Numerical Approach and Verification Method for Improving the Sensitivity of Ferrous Particle Sensors with a Permanent Magnet
Abstract
1. Introduction
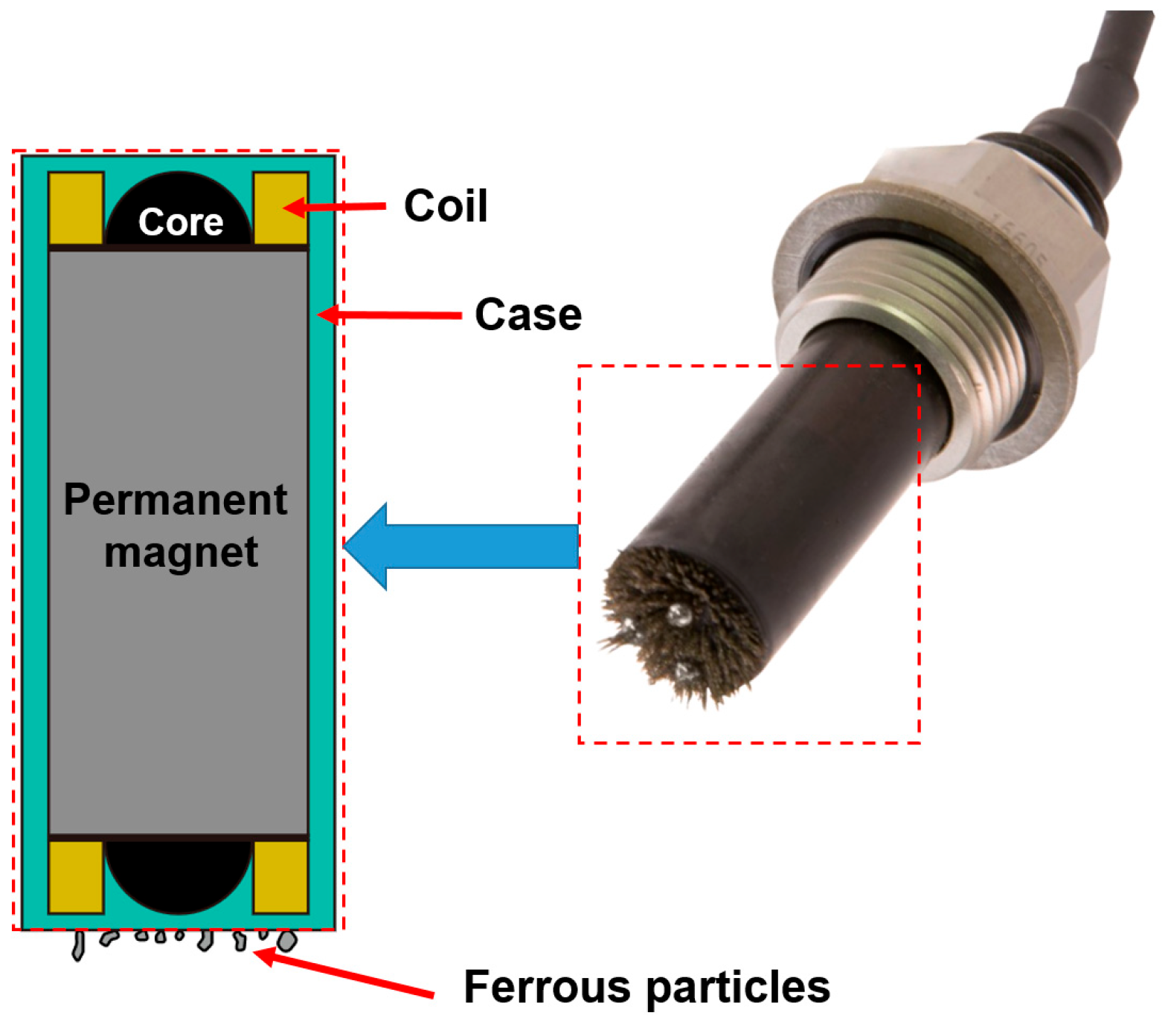
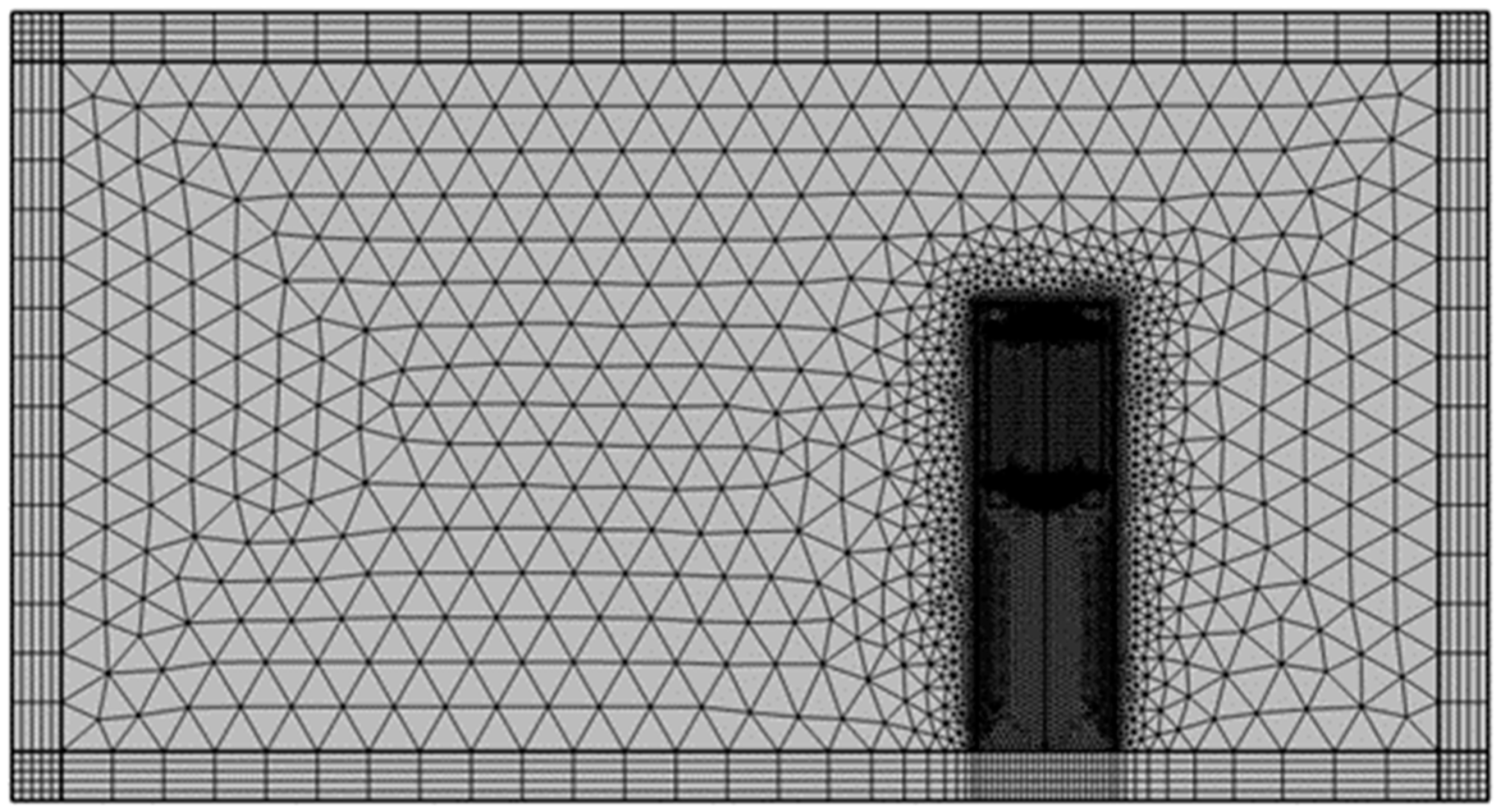
2. Numerical Model and Analysis
2.1. Analysis of Magnetic Flux Density for Changes in the Sensor’s Internal Design Parameters
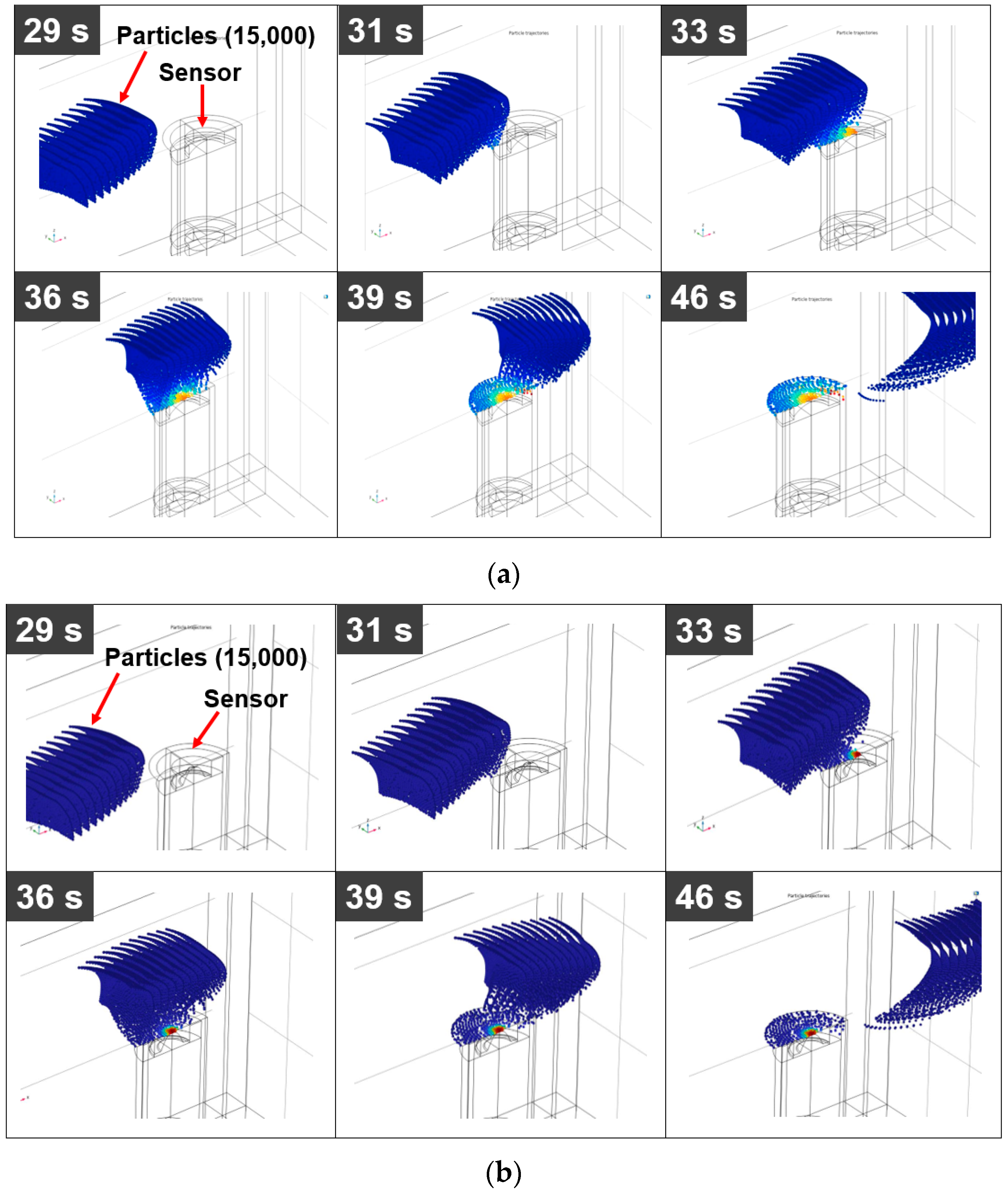
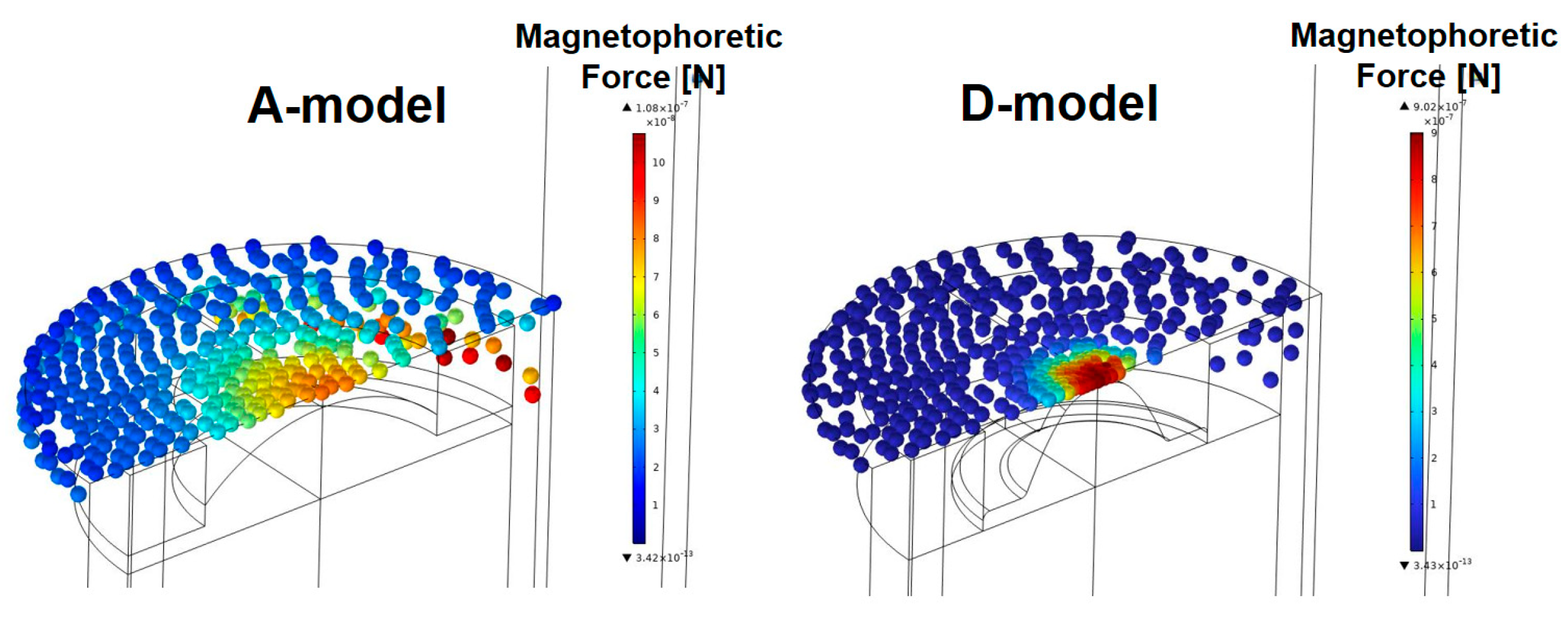
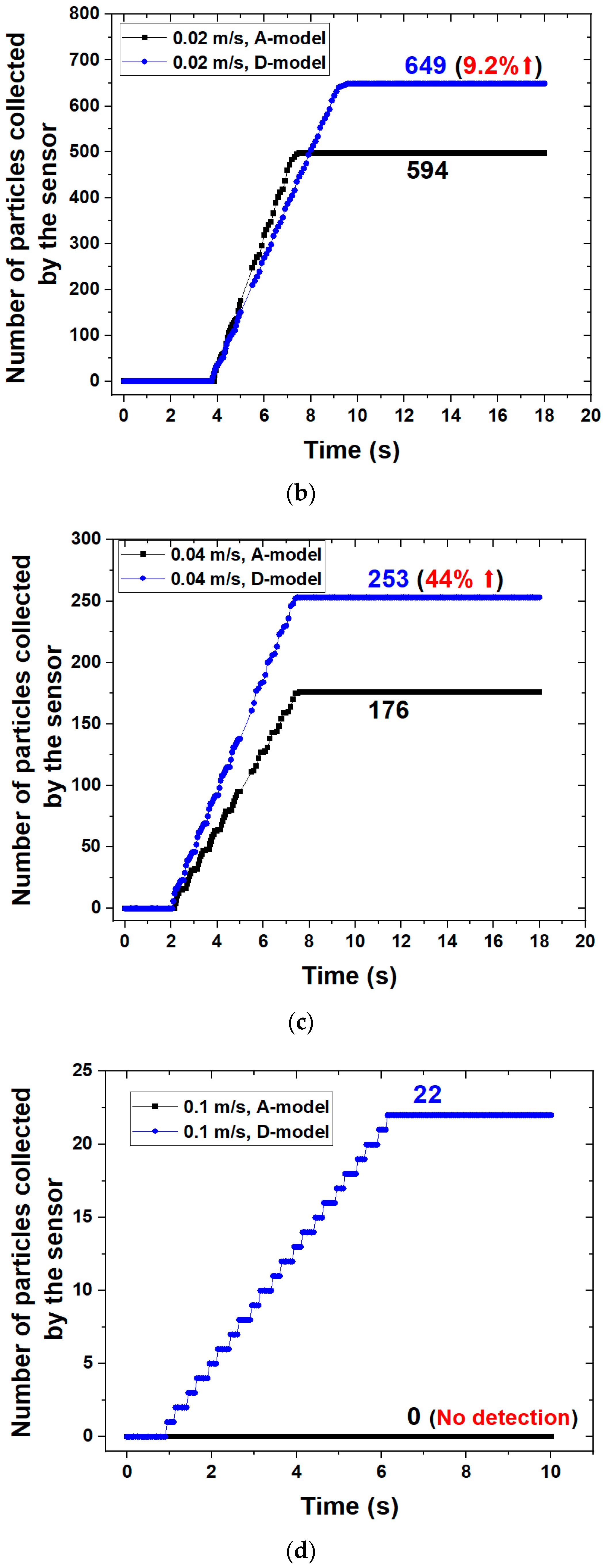
2.2. Evaluating the Sensitivity of the Sensor in the Flow Field
3. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Height of the permanent magnet [mm] |
| B | Magnetic flux density [T] |
| b | Width of the permanent magnet [mm] |
| c | Height of the coil [mm] |
| D | Magnetic vector potential [A] |
| d | Width of the coil [mm] |
| dp | Particle diameter [mm] |
| E | Magnetic field [V/m] |
| e | Height of the core [mm] |
| F | Volume force [N/m3] |
| FD | Drag force [N] |
| Fext | Magnetophoretic force [N] |
| f | Length of the core from the central axis to the core [mm] |
| g | Thickness of the core under the coil [mm] |
| H | Magnetic field intensity [A/m] |
| h | Thickness of the case at the top of the core [mm] |
| I | Identity matrix |
| J | Current density [A/m2] |
| Je | Externally generated current density [A/m2] |
| K | Non-dimensional parameter [1] |
| mp | Particle mass [kg] |
| p | Fluid pressure [Pa] |
| r | Position vector [m] |
| r1 | Curvature radius in the A-model [mm] |
| rp | Particle radius [m] |
| T | Unit of magnetic flux density [Wb/m2] |
| v | Velocity of the fluid [m/s] |
| v1 | Velocity factor of the particle [m/s] |
| ρ | Density of the fluid [kg/m3] |
| ρp | Density of the particle [kg/m3] |
| σ | Permittivity |
| τ | Shear stress [Pa] |
| τp | Mean particle velocity response time [s] |
| μ | Viscosity of the fluid [Pa∙s] |
| μ0 | Vacuum permeability [kg∙m∙s/A2] |
| μr | Relative permeability |
| Ω | Mean angular velocity [1/s] |
References
- Kumar, M.; Mukherjee, P.S.; Misra, N.M. Advancement and current status of wear debris analysis for machine condition monitoring: A review. Ind. Lubr. Tribol. 2013, 65, 3–11. [Google Scholar] [CrossRef]
- Hong, S.H. Lit Literature review of machine condition monitoring with oil sensors—Types of Sensors and their functions. Tribol. Lubr. 2020, 36, 297–306. [Google Scholar]
- Hong, S.H.; Jeon, H.G. Monitoring the conditions of hydraulic oil with integrated oil sensors in construction equipment. Lubricants 2022, 10, 278. [Google Scholar] [CrossRef]
- Hong, S.H. Machine Condition Diagnosis Based on Oil Analysis—Fundamental Course, 1st ed.; Hanteemedia: Seoul, Republic of Korea, 2021; pp. 94–96. [Google Scholar]
- Fasihi, P.; Kendall, O.; Abrahams, R.; Mutton, P.; Qiu, C.; Schlafer, T.; Yan, W. Tribological properties of laser cladded alloys for repair of rail components. Materials 2022, 15, 7466. [Google Scholar] [CrossRef] [PubMed]
- Du, L.; Zhe, J.; Carletta, J.; Veillette, R.; Choy, F. Real-time monitoring of wear debris in lubricating oil using a microfluidic inductive coulter counting device. Microfluid. Nanofluidics 2010, 9, 1241–1245. [Google Scholar] [CrossRef]
- Du, L.; Zhe, J. A high throughput inductive pulse sensor for online oil debris monitoring. Tribol. Int. 2011, 44, 175–179. [Google Scholar] [CrossRef]
- Du, L.; Zhe, J. Parallel sensing of metallic wear debris in lubricants using under-sampling data processing. Tribol. Int. 2012, 53, 28–34. [Google Scholar] [CrossRef]
- Du, L.; Zhu, X.; Han, Y.; Zhao, L.; Zhe, J. Improving sensitivity of an inductive pulse sensor for detection of metallic wear debris in lubricants using parallel LC resonance method. Meas. Sci. Technol. 2013, 24, 75106. [Google Scholar] [CrossRef]
- Wang, C.; Bai, C.; Yang, Z.; Zhang, H.; Li, W.; Wang, X.; Zheng, Y.; Ilerioluwa, L.; Sun, Y. Research on High Sensitivity Oil Debris Detection Sensor Using High Magnetic Permeability Material and Coil Mutual Inductance. Sensors 2022, 22, 1833. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, T.; Wu, D.; Zhu, L.; Qing, X.; Xue, W. A new in situ coaxial capacitive sensor network for debris monitoring of lubricating oil. Sensors 2022, 22, 1777. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, S.; Raihan, M.K.; Zhu, D.; Yu, K.; Wang, F.; Pan, X. The optimization of parallel resonance circuit for wear debris detection by adjusting Capacitance. Energies 2022, 15, 7318. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, Y.; Li, N.; Qian, Z.; Liu, D.; Qian, Z.; Zhang, C. A new inductive debris sensor based on dual-excitation coils and dual-sensing coils for online debris monitoring. Sensors 2021, 21, 7556. [Google Scholar] [CrossRef]
- Zeng, L.; Zhang, H.; Wang, Q.; Zhang, X. Monitoring of non-ferrous wear debris in hydraulic oil by detecting the equivalent resistance of inductive sensors. Micromachines 2018, 9, 117. [Google Scholar] [CrossRef]
- Li, W.; Bai, C.; Wang, C.; Zhang, H.; Ilerioluwa, L.; Wang, X.; Yu, S.; Li, G. Design and research of inductive oil pollutant detection sensor based on high gradient magnetic field structure. Micromachines 2021, 12, 638. [Google Scholar] [CrossRef]
- Wu, S.; Liu, Z.; Yu, K.; Fan, Z.; Yuan, Z.; Sui, Z.; Yin, Y.; Pan, X. A novel multichannel inductive wear debris sensor based on time division multiplexing. IEEE Sens. J. 2021, 21, 11131–11139. [Google Scholar] [CrossRef]
- Hong, W.; Li, T.; Wang, S.; Zhou, Z. A general framework for aliasing corrections of inductive oil debris detection based on artificial neural networks. IEEE Sens. J. 2020, 20, 10724–10732. [Google Scholar] [CrossRef]
- Muthuvel, P.; George, B.; Ramadass, G.A. A highly sensitive in-line oil wear debris sensor based on passive wireless LC sensing. IEEE Sens. J. 2021, 21, 6888–6896. [Google Scholar] [CrossRef]
- Wu, X.; Liu, H.; Qian, Z.; Qian, Z.; Liu, D.; Li, K.; Wang, G. On the investigation of frequency characteristics of a novel inductive debris sensor. Micromachines 2023, 14, 669. [Google Scholar] [CrossRef]
- Du, L.; Zhe, J. An integrated ultrasonic-inductive pulse sensor for wear debris detection. Smart Mater. Struct. 2013, 22, 25003. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, P.; Wang, H.; Li, Y.; Lv, C. Ultrasonic echo wave shape features extraction based on QPSO-matching pursuit for online wear debris discrimination. Mech. Syst. Signal Process. 2015, 60, 301–315. [Google Scholar] [CrossRef]
- Hamilton, A.; Cleary, A.; Quail, F. Development of a novel wear detection system for wind turbine gearboxes. IEEE Sens. J. 2014, 14, 465–473. [Google Scholar] [CrossRef]
- Wu, T.; Wu, H.; Du, Y.; Kwok, N.; Peng, Z. Imaged wear debris separation for on-line monitoring using gray level and integrated morphological features. Wear 2014, 316, 19–29. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Y.; Zuo, H.; Wang, H.; Chen, Z. An oil wear particles inline optical sensor based on motion characteristics for rotating machines condition monitoring. Machines 2022, 10, 727. [Google Scholar] [CrossRef]
- Jing, Y.; Zheng, H.; Lin, C.; Zheng, W.; Dong, K.; Li, X. Foreign object debris detection for optical imaging sensors based on random forest. Sensors 2022, 22, 2463. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wang, H.; Yi, H.; Xue, Y.; Wen, D.; Wang, F.; Shen, Y.; Pan, Y. Space debris detection and positioning technology based on multiple star trackers. Appl. Sci. 2022, 12, 3593. [Google Scholar] [CrossRef]
- Fan, B.; Liu, Y.; Zhang, P.; Wang, L.; Zhang, C.; Wang, J. A permanent magnet ferromagnetic wear debris sensor based on axisymmetric high-gradient magnetic field. Sensors 2022, 22, 8282. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Z.; Ren, X.; Wu, S.; Meng, M.; Wang, Y.; Pan, X. A novel method for detecting ferromagnetic wear debris with high flow velocity. Sensors 2022, 22, 4912. [Google Scholar] [CrossRef]
- Jeon, H.G.; Kim, J.K.; Na, S.J.; Kim, M.S.; Hong, S.H. Application of condition monitoring for hydraulic oil using tuning fork sensor: A case on hydraulic system of earth moving machinery. Materials 2022, 15, 7657. [Google Scholar] [CrossRef]
- Hong, S.H.; Jeon, H.G. Assessment of condition diagnosis system for axles with ferrous particle sensor. Materials 2023, 16, 1426. [Google Scholar] [CrossRef]
- Ren, Y.; Li, W.; Zhao, G.; Feng, Z. Inductive debris sensor using one energizing coil with multiple sensing coils for sensitivity improvement and high throughput. Tribol. Int. 2018, 128, 96–103. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, X.; Li, H.; Luo, J.; Fong, S. An Inductive debris sensor for large-diameter lubricating oil circuit based on a high-gradient magnetic field. Appl. Sci. 2019, 9, 1546. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, H.; Qiao, W.; Han, X.; Zeng, L.; Shi, H. Oil metal debris detection sensor using ferrite core and flat channel for sensitivity improvement and high throughput. IEEE Sens. J. 2020, 20, 7303–7309. [Google Scholar] [CrossRef]
- Zeng, L.; Yu, Z.; Zhang, H.; Zhang, X.; Chen, H. A high sensitive multi-parameter micro sensor for detection of multi-contamination in hydraulic oil. Sens. Actuators A Phys. 2018, 282, 197–205. [Google Scholar] [CrossRef]
- Jia, R.; Ma, B.; Zheng, C.; Ba, X.; Wang, L.; Du, Q.; Wang, K. Compressive improvement of the sensitivity and detectability of a large-aperture electromagnetic wear particle detector. Sensors 2019, 19, 3162. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, H.; Zheng, W.; Shi, H.; Wang, C.; Xie, Y. Investigation on the effect of debris position on the sensitivity of the inductive debris sensor. IEEE Sens. J. 2023, 23, 4438–4444. [Google Scholar] [CrossRef]
- COMSOL. COMSOL Manual, version 6.0; Massachusetts, USA, 2023; pp. 84, 272–304. Available online: https://doc.comsol.com/6.0/docserver/#!/com.comsol.help.comsol/html_ModelManagerReferenceManual.html (accessed on 28 April 2023).
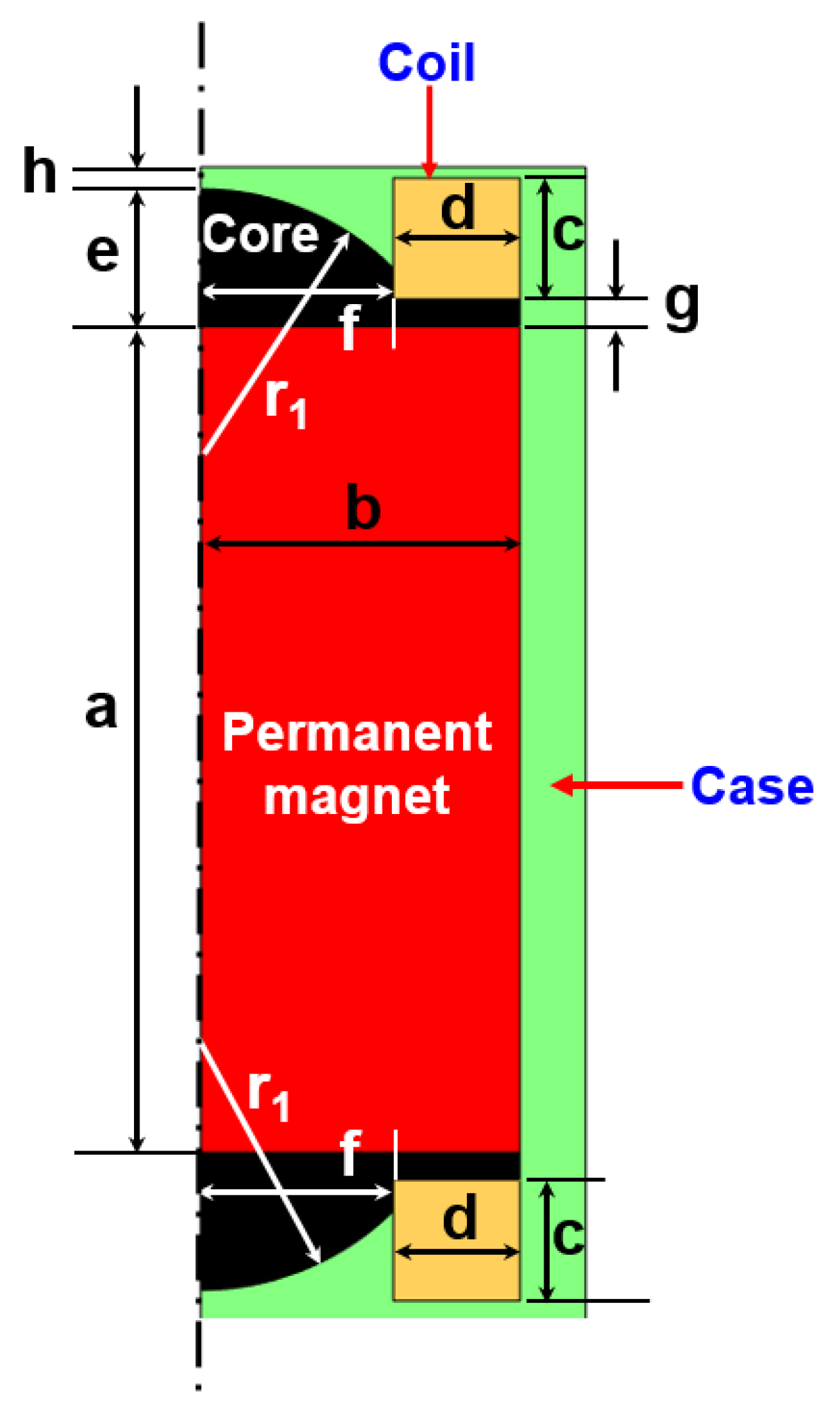


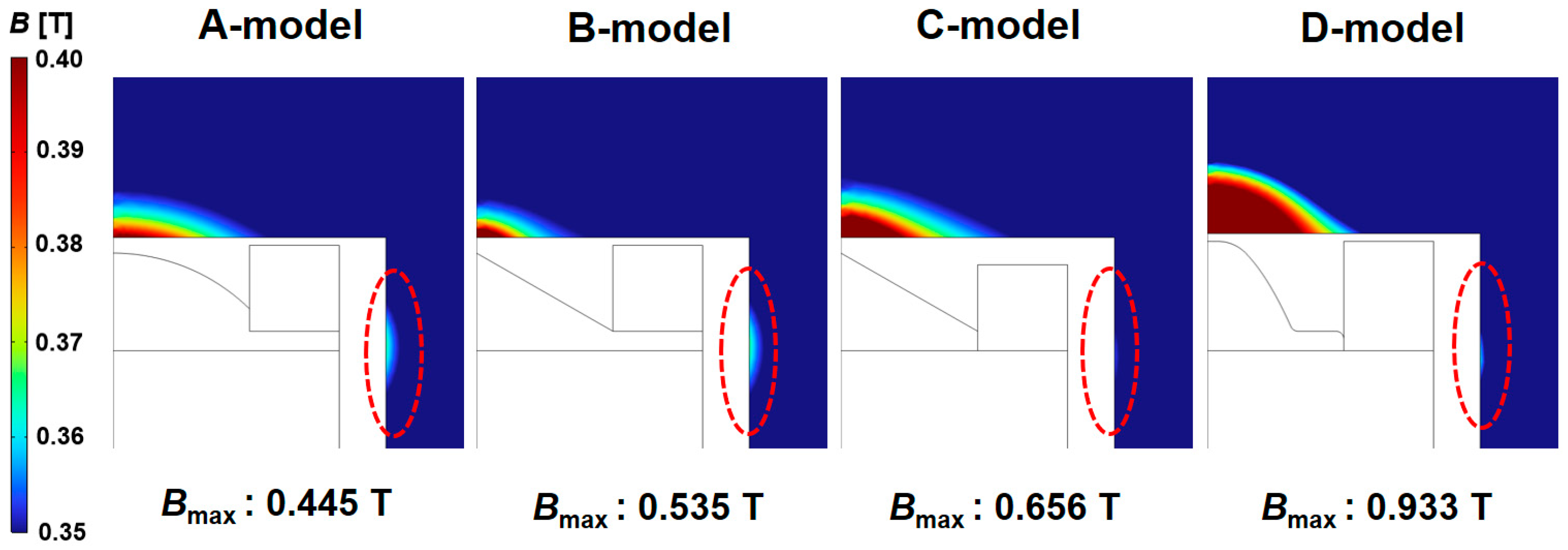
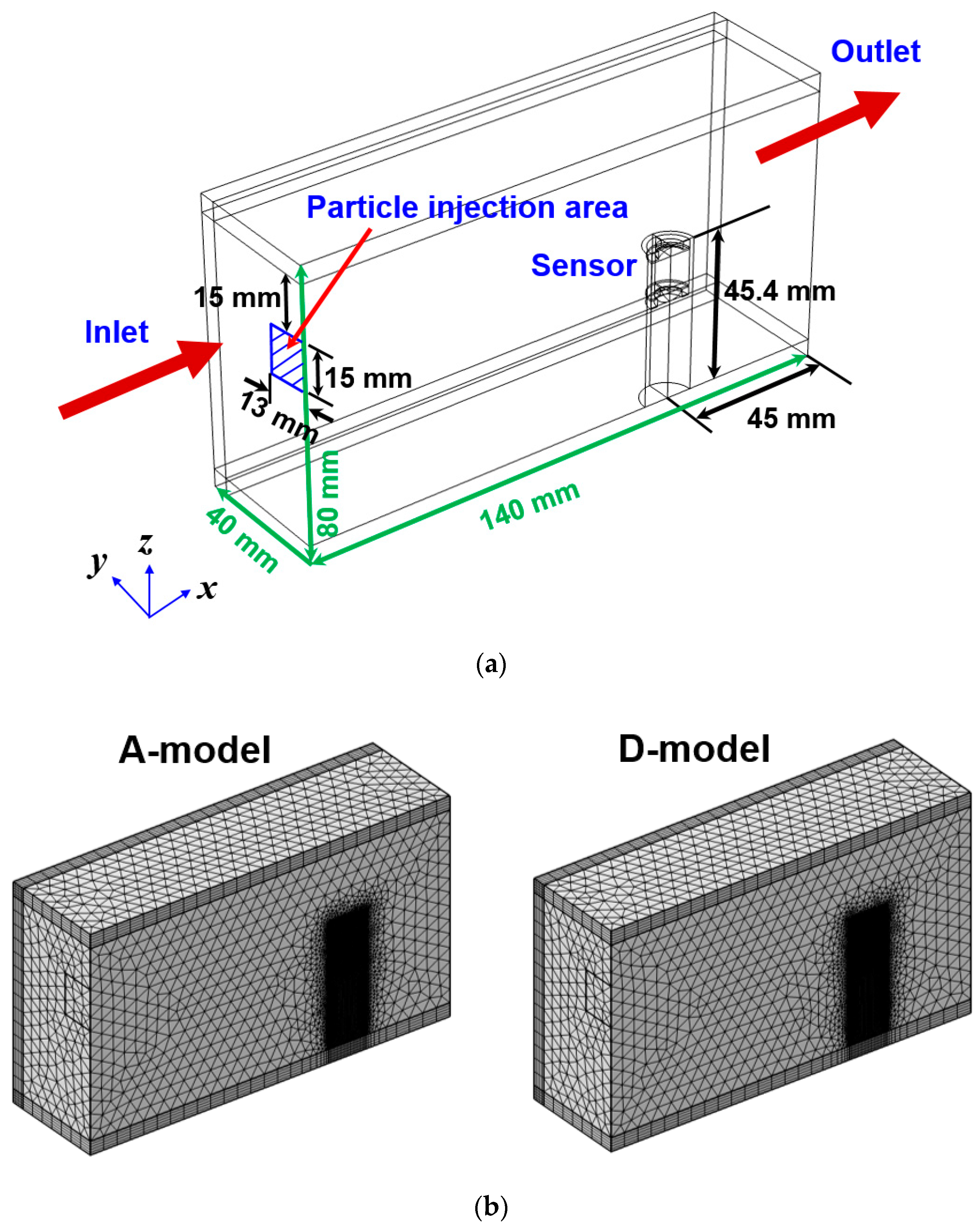


| Model | A-Model | B-Model | C-Model | D-Model |
|---|---|---|---|---|
| a [mm] | 15 | 15 | 15 | 15 |
| b [mm] | 5.8 | 5.8 | 5.8 | 5.8 |
| c [mm] | 2.2 | 2.2 | 2.2 | 2.8 |
| d [mm] | 2.3 | 2.3 | 2.3 | 2.3 |
| e [mm] | 2.5 | 2.5 | 2.5 | 2.8 |
| f [mm] | 3.5 | 3.5 | 3.5 | 3.5 |
| g [mm] | 0.5 | 0.5 | 0 | 0 |
| h [mm] | 0.4 | 0.4 | 0.4 | 0.2 |
| r1 [mm] | 5 | - | - | - |
| Items | Condition | Items | Condition |
|---|---|---|---|
| Inlet (velocity) | 0.02 m/s | Outlet | Outflow |
| Number of particles | 15,000 | Particle diameter | 10 μm |
| Shape of the particles | Sphere | Material of particle | Steel |
| Particle relative Permeability | 1000 | Particle density | 8030 kg/m3 |
| Density of the lubricant | 870 kg/m3 | Absolute viscosity of the lubricant | 0.04 Pa∙s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.-H. Numerical Approach and Verification Method for Improving the Sensitivity of Ferrous Particle Sensors with a Permanent Magnet. Sensors 2023, 23, 5381. https://doi.org/10.3390/s23125381
Hong S-H. Numerical Approach and Verification Method for Improving the Sensitivity of Ferrous Particle Sensors with a Permanent Magnet. Sensors. 2023; 23(12):5381. https://doi.org/10.3390/s23125381
Chicago/Turabian StyleHong, Sung-Ho. 2023. "Numerical Approach and Verification Method for Improving the Sensitivity of Ferrous Particle Sensors with a Permanent Magnet" Sensors 23, no. 12: 5381. https://doi.org/10.3390/s23125381
APA StyleHong, S.-H. (2023). Numerical Approach and Verification Method for Improving the Sensitivity of Ferrous Particle Sensors with a Permanent Magnet. Sensors, 23(12), 5381. https://doi.org/10.3390/s23125381







