A New Temperature Correction Method for NaI(Tl) Detectors Based on Pulse Deconvolution
Abstract
1. Introduction
2. Materials and Methods
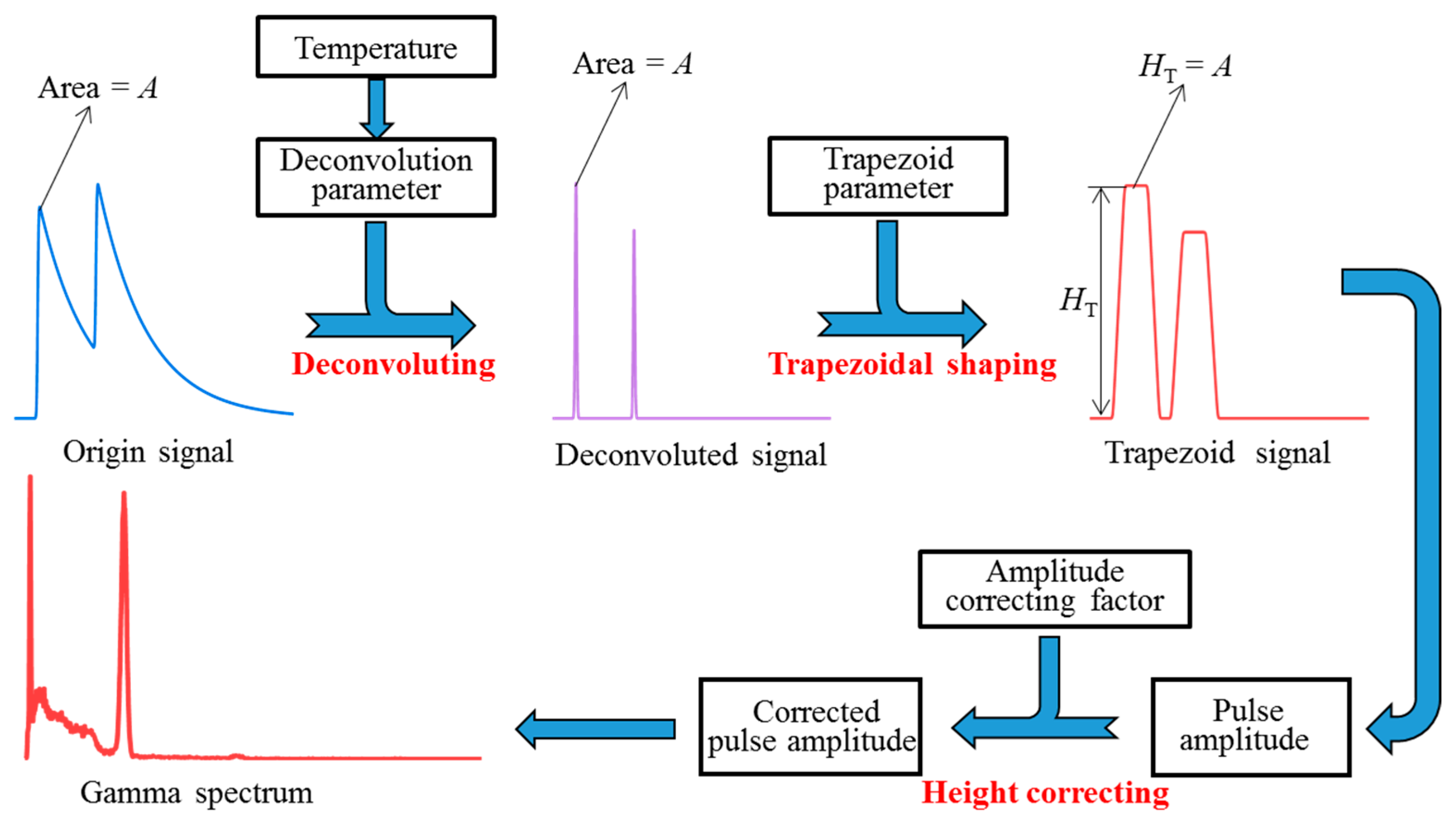
2.1. Method Description
2.1.1. Pulse Model and Deconvolution
2.1.2. Trapezoidal Shaping and Amplitude Correction
2.2. Pulse Data Acquisition and Preprocessing
3. Results
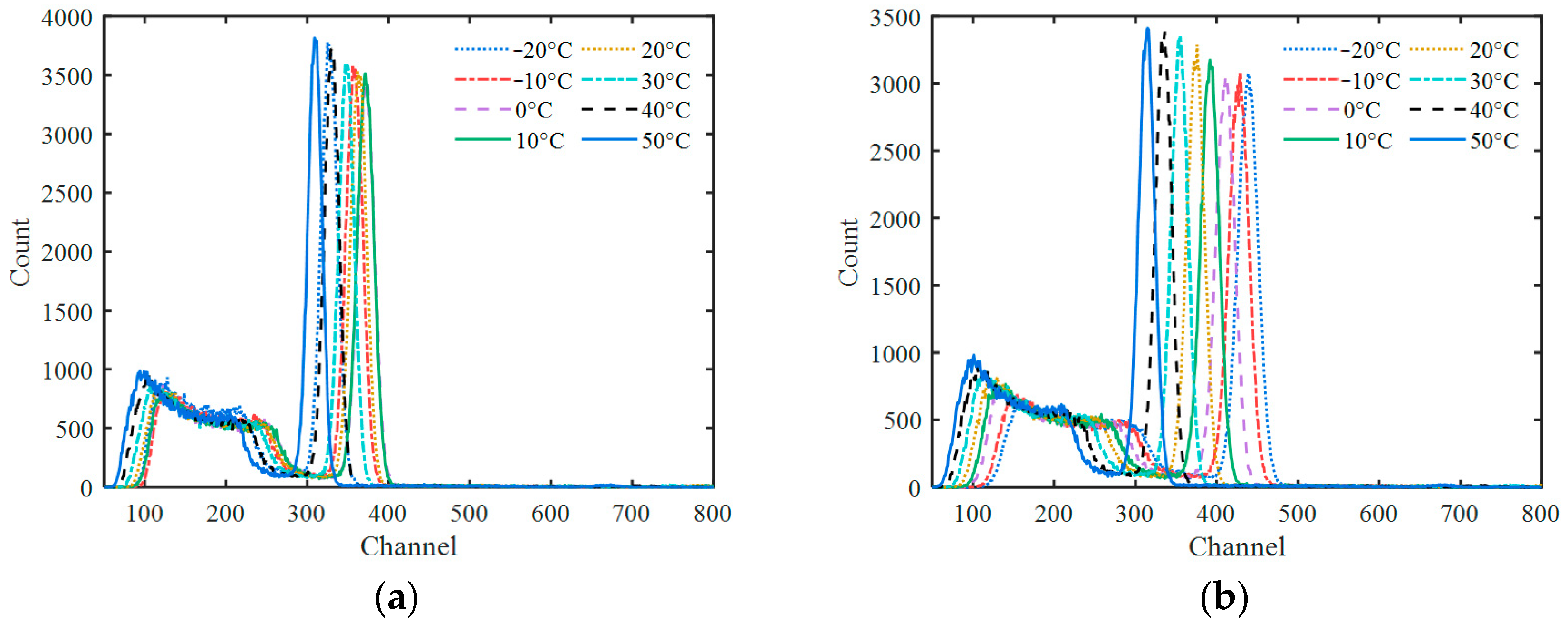
3.1. Pulse Model Parameter Fit Result
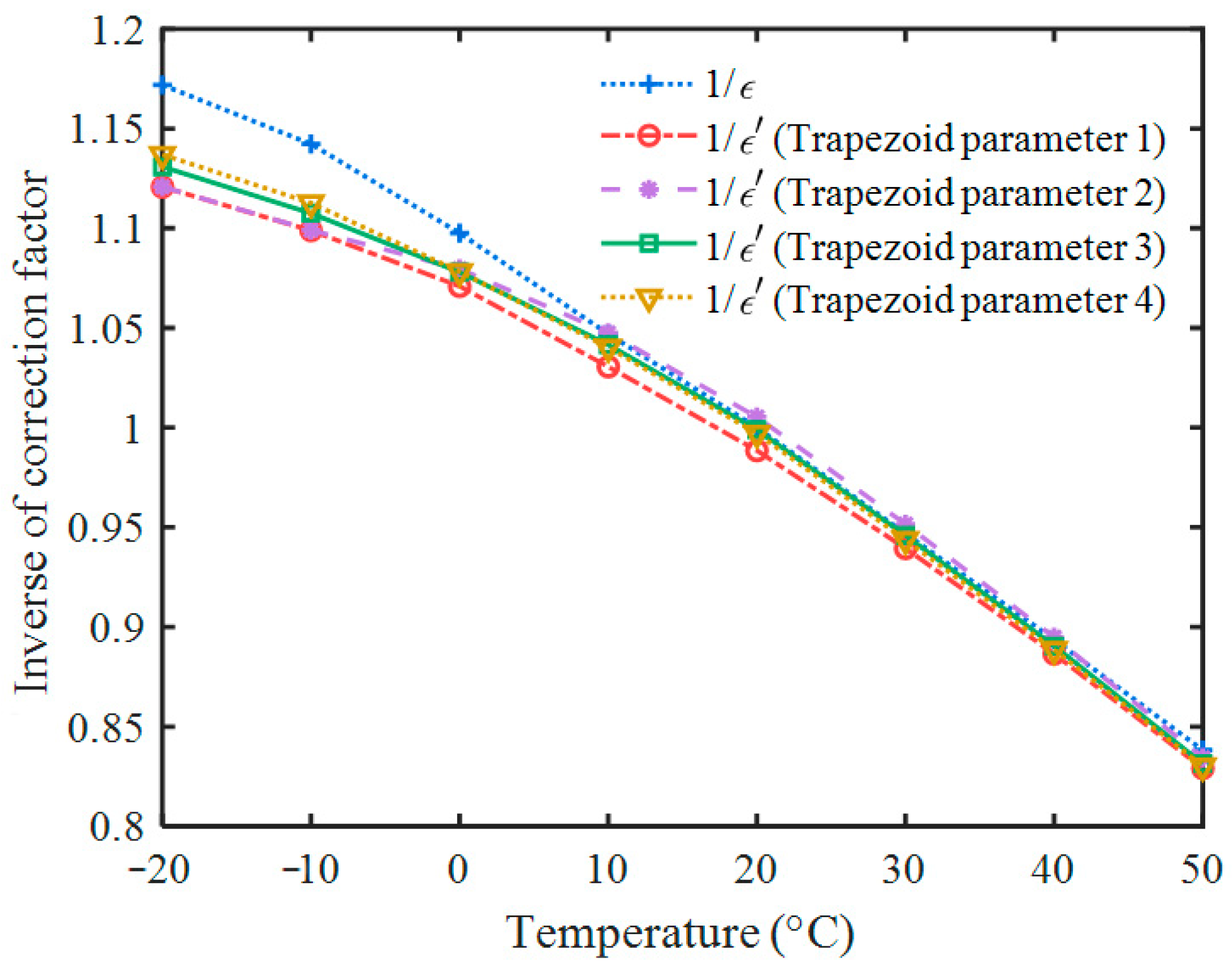
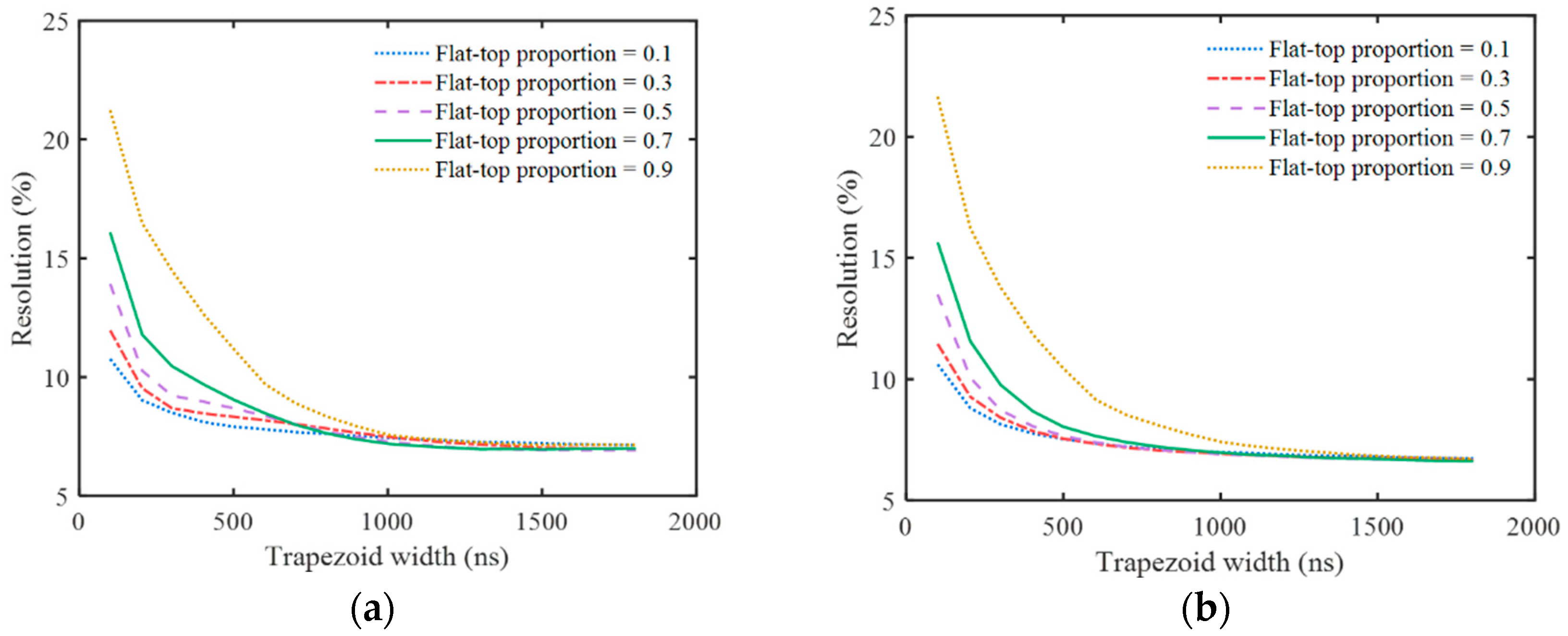
3.2. Temperature Correction Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gilmore, G. Scintillation Spectrometry. In Practical Gamma-Ray Spectroscopy, 2nd ed.; John Wiley & Sons Nuclear: Warrington, UK, 2008; p. 207. [Google Scholar]
- Schweitzer, J.S.; Ziehl, W. Temperature dependence of NaI(Tl) decay constant. IEEE Trans. Nucl. Sci. 1983, 30, 380–382. [Google Scholar] [CrossRef]
- Moszyński, M.; Nassalski, A.; Syntfeld-Każuch, A.; Szczęśniak, T.; Czarnacki, W.; Wolski, D.; Stein, J. Temperature dependences of LaBr3 (Ce), LaCl3 (Ce) and NaI(Tl) scintillators. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2006, 568, 739–751. [Google Scholar] [CrossRef]
- Knoll, G.F. Inorganic Scintilltors. In Radiation Detection and Measurement, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; p. 241. [Google Scholar]
- Dudley, R.A.; Scarpatetti, R. Ṡtabilization of a gamma scintillator spectrometer against zero and gain drifts. Nucl. Instrum. Methods 1963, 25, 297–313. [Google Scholar] [CrossRef]
- Patwardhan, P.K. Spectrum stabilization with variable reactance gain control. Nucl. Instrum. Methods 1964, 31, 169–172. [Google Scholar] [CrossRef]
- Stromswold, D.C.; Meisner, J.E. Gamma-ray spectrum stabilization in a borehole probe using a light emitting diode. IEEE Trans. Nucl. Sci. 1979, 26, 395–397. [Google Scholar] [CrossRef]
- Tsankov, L.T.; Mitev, M.G. A simple method for stabilization of arbitrary spectra. In Proceedings of the Sixteen International Scientific and Applied Science Conference ELECTRONICS ET, Sozopol, Bulgaria, 19–21 September 2007; pp. 3–8. [Google Scholar]
- Chen, Y.; Li, J.; Zhang, Y.; Xiao, W. Gamma spectrum stabilization method based on nonlinear least squares optimization. Appl. Radiat. Isot. 2021, 169, 109515. [Google Scholar] [CrossRef] [PubMed]
- Pommé, S.; Sibbens, G. Concept for an off-line gain stabilisation method. Appl. Radiat. Isot. 2004, 60, 151–154. [Google Scholar] [CrossRef] [PubMed]
- Casanovas, R.; Morant, J.J.; Salvadó, M. Temperature peak-shift correction methods for NaI(Tl) and LaBr3(Ce) gamma-ray spectrum stabilisation. Radiat. Meas. 2012, 47, 588–595. [Google Scholar] [CrossRef]
- Pausch, G.; Stein, J.; Kreuels, A.; Lueck, F.; Teofilov, N. Multifunctional application of pulse width analysis in a LED-stabilized digital NaI(Tl) gamma spectrometer. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, Fajardo, PR, USA, 23–29 October 2005. [Google Scholar]
- Stein, J.; Neuer, M.J.; Herbach, C.M.; Pausch, G.; Ruhnau, K. Radiation detector signal processing using sampling kernels without bandlimiting constraints. In Proceedings of the 2007 IEEE Nuclear Science Symposium Conference Record, Honolulu, HI, USA, 26 October–3 November 2007. [Google Scholar]
- Xiao, W.; Farsoni, A.T.; Yang, H.; Hamby, D.H. A new pulse model for NaI(Tl) detection systems. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2014, 763, 170–173. [Google Scholar] [CrossRef]
- Radeka, V. Trapezoidal filtering of signals from large germanium detectors at high rates. Nucl. Instrum. Methods 1972, 99, 525–539. [Google Scholar] [CrossRef]
- Xiao, W.; Farsoni, A.T.; Yang, H.; Hamby, D.M. Model-based pulse deconvolution method for NaI(Tl) detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2015, 769, 5–8. [Google Scholar] [CrossRef]
- Photomultiplier CR173 with an End Window. Available online: http://www.bhphoton.com/upload/1/content/1662094262625.pdf (accessed on 9 May 2023). (In Chinese).
- N6730/N6725 8-Channel 14-bit 500/250 MS/s Waveform Digitizer. Available online: https://www.caen.it/?downloadfile=7499 (accessed on 9 May 2023).
- Alexandrov, B.S.; Ianakiev, K.D.; Littlewood, P.B. Branching transport model of NaI (Tl) alkali-halide scintillator. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2008, 586, 432–438. [Google Scholar] [CrossRef]
- Payne, S.A.; Moses, W.W.; Sheets, S.; Ahle, L.; Cherepy, N.J.; Choong, W.S. Nonproportionality of scintillator detectors: Theory and experiment. II. IEEE Trans. Nucl. Sci. 2011, 58, 3392–3402. [Google Scholar] [CrossRef]
- Khodyuk, I.V.; Dorenbos, P. Trends and patterns of scintillator nonproportionality. IEEE Trans. Nucl. Sci. 2012, 59, 3320–3331. [Google Scholar] [CrossRef]





| Temperature/°C | A | τ0/ns | τ1/ns | τ2/ns | φ | t0/ns |
|---|---|---|---|---|---|---|
| −20 | 3.382 × 105 | 9.784 | 160.8 | 842.9 | 0.2682 | 933.3 |
| −10 | 3.302 × 105 | 9.343 | 218.8 | 603.0 | 0.3202 | 933.3 |
| 0 | 3.194 × 105 | 11.67 | 271.2 | 404.9 | 0.3778 | 937.4 |
| 10 | 3.059 × 105 | 18.05 | 281.1 | 281.3 | 0.8297 | 930.6 |
| 20 | 2.935 × 105 | 23.05 | 236.2 | 236.4 | 0.8120 | 929.4 |
| 30 | 2.785 × 105 | 25.34 | 199.7 | 200.0 | 0.9993 | 929.3 |
| 40 | 2.625 × 105 | 25.24 | 174.0 | 200.0 | 1.000 | 929.4 |
| 50 | 2.453 × 105 | 23.93 | 155.9 | 200.0 | 1.000 | 929.7 |
| a0 | a1 | a2 | R2 | ||
|---|---|---|---|---|---|
| ε | −1.537 × 10−5 | −4.398 × 10−3 | 1.095 | 0.9993 | |
| ε′ | tWidth = 500 ns, tTop = 100 ns | −2.928 × 10−5 | −3.335 × 10−3 | 1.068 | 0.9997 |
| tWidth = 500 ns, tTop = 250 ns | −4.033 × 10−5 | −2.900 × 10−3 | 1.078 | 0.9993 | |
| tWidth = 1000 ns, tTop = 200 ns | −3.214 × 10−5 | −3.345 × 10−3 | 1.077 | 0.9998 | |
| tWidth = 1000 ns, tTop = 500 ns | −2.861 × 10−5 | −3.563 × 10−3 | 1.078 | 0.9998 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Yang, L.; Li, J.; Qi, S.; Chen, W.; Xu, H.; Xiao, W. A New Temperature Correction Method for NaI(Tl) Detectors Based on Pulse Deconvolution. Sensors 2023, 23, 5083. https://doi.org/10.3390/s23115083
Xie J, Yang L, Li J, Qi S, Chen W, Xu H, Xiao W. A New Temperature Correction Method for NaI(Tl) Detectors Based on Pulse Deconvolution. Sensors. 2023; 23(11):5083. https://doi.org/10.3390/s23115083
Chicago/Turabian StyleXie, Jianming, Liu Yang, Jinglun Li, Sheng Qi, Wenzhuo Chen, Hang Xu, and Wuyun Xiao. 2023. "A New Temperature Correction Method for NaI(Tl) Detectors Based on Pulse Deconvolution" Sensors 23, no. 11: 5083. https://doi.org/10.3390/s23115083
APA StyleXie, J., Yang, L., Li, J., Qi, S., Chen, W., Xu, H., & Xiao, W. (2023). A New Temperature Correction Method for NaI(Tl) Detectors Based on Pulse Deconvolution. Sensors, 23(11), 5083. https://doi.org/10.3390/s23115083






