Energy-Efficient Algorithms for Path Coverage in Sensor Networks
Abstract
1. Introduction
2. Related Work
3. Least Movement of Sensors on Path Coverage
3.1. Problem Description
3.2. The Least Movement Algorithm
3.2.1. Path Disjunction
| Algorithm 1: Curve disjunction |
| 1. Let step-size d be (big-coordinate − min-coordinate)/n; 2. Let the collection Q be NULL; 3. For i from 1 to n do 4. xi = (i − 1/2)d; 5. Insert the fetched point (h(xi), xi) into collection Q; 6. Return collection Q. |
3.2.2. Initial Movement
| Algorithm 2: Initializing movement |
| /* Input: points in collection Q with size n in path P, deployed node collection S with size m. Output: move S shortest such that for si in S, there exists pj in Q, where |si, pj| ≤ R2; */ 1. For i from 1 to m do 2. If |si, every point in Q| > R2, then 3. move si to its closest point pj such that |si, pj| = R2; 4. Return. |
3.2.3. Last Movement
| Algorithm 3: Find-redundant-nodes |
| /* Input: points collection Q with size n in P, nodes collection S with size m, point i. Output: the closest redundant node in S(i) to N(pos(i)).*/ 1. For (1≤ i ≤ n) & (Pi ≥ d), then 2. If Pi < d after moving s, then 3. Return Ø; 4. If orient = left, then 5. Set N(pos(i)) as Mj(pi) 6. Else if orient = right, then 7. Set N(pos(i)) as Nj(pi) 8. Else if orient = self 9. Set N(pos(i)) as i; 10. Take i out of Q; 11. If exist a closest redundant node s to N(pos(i)), then 12. Insert i into Q; 13. Return s. |
| Algorithm 4: PCP solution |
| /* Input: points collection Q with size n in P, nodes collection S with size m. Output: move S shortest distance to cover P, or report failure.*/ 1. Rank all points in line with x-axis; 2. Compute covering probability of all elements in collection Q; 3. Let mv_len = 0; 4. Initializing node movement; /*Algorithm 2*/ 5. For (0 ≤ i ≤ n) & For (1 ≤ j ≤ n) 6. If exists redundant node s in S(Mi(pj)) or S(Ni(pj)), then 7. When (i = 0), move s to s0 according to Regulation 1; 8. mv_len = mv_len + |s0, s|; else 9. If s in S(Mi(pj)), then let orient be left 10. Else let orient be right. 11. If x0 in Mi(pj) or Ni(pj) possesses a redundant node; 12. Note path (pf, pf−1, …, p1); 13. For (r = f, r--, r ≥ 1) 14. If exists redundant node s in S(pr), then 15. When (r ≥ 2) then move node according to Regulation 2. 16. Else move s according to Regulation 1; 17. Move node to s0; add |s0, s| to mv_len. |
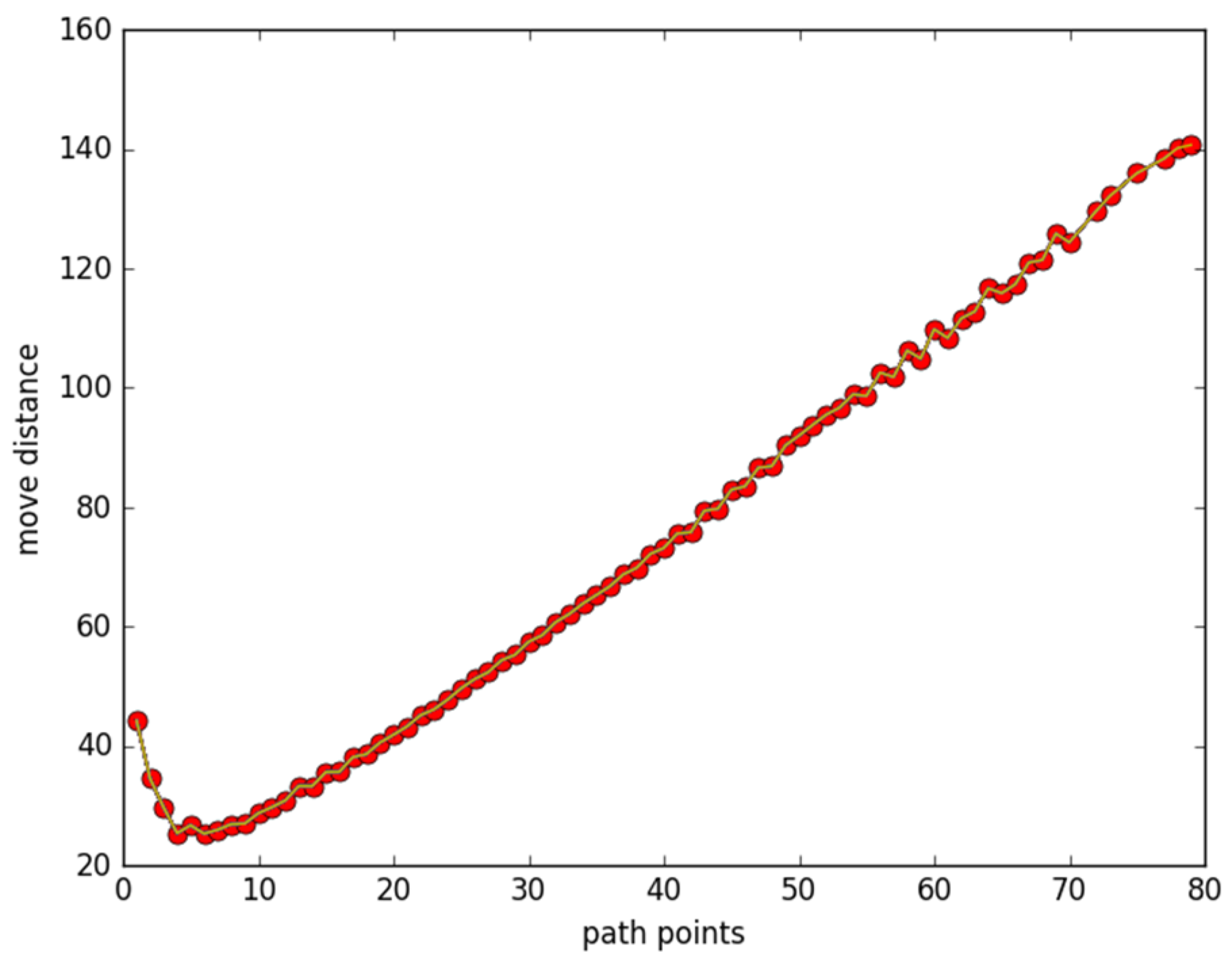
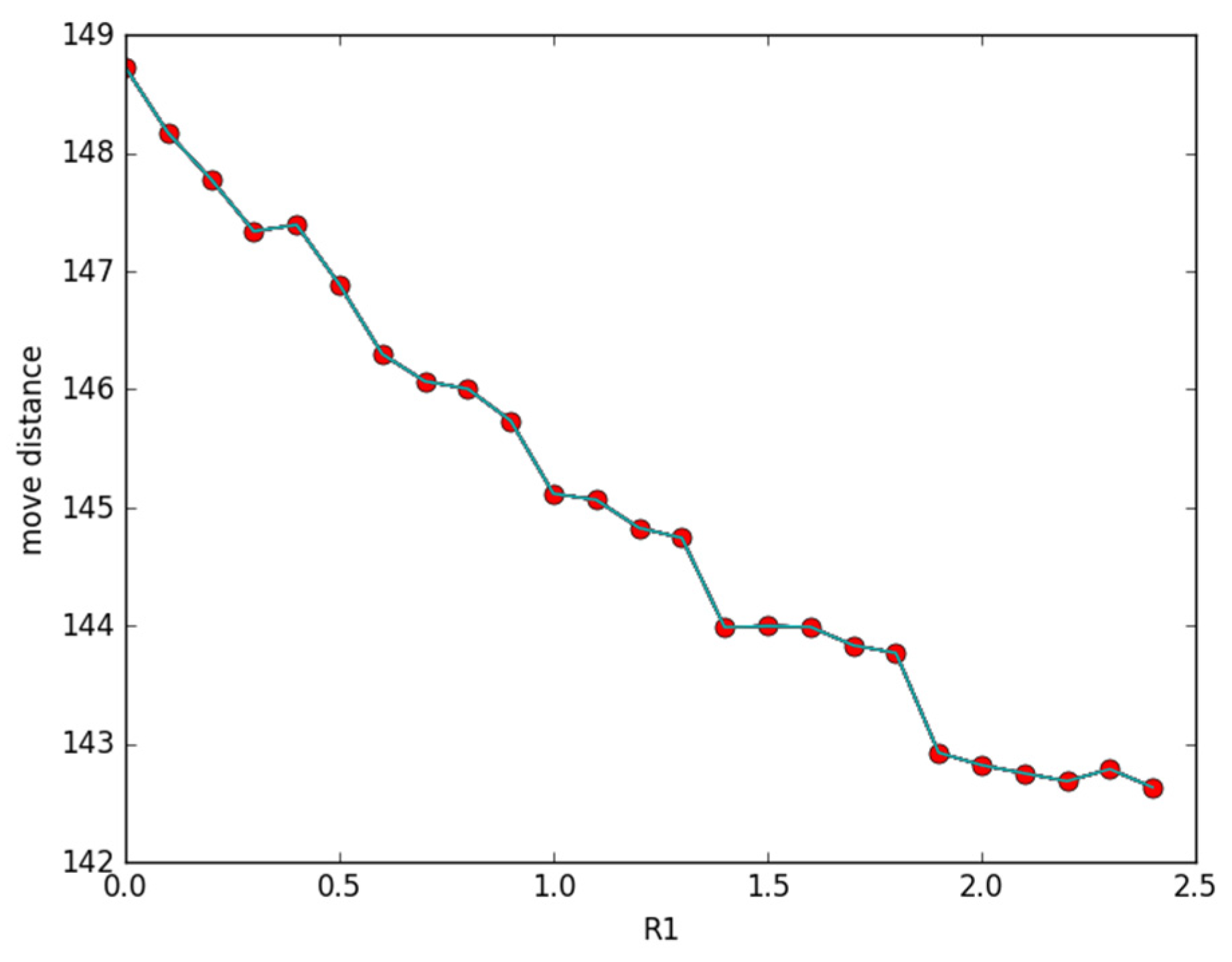
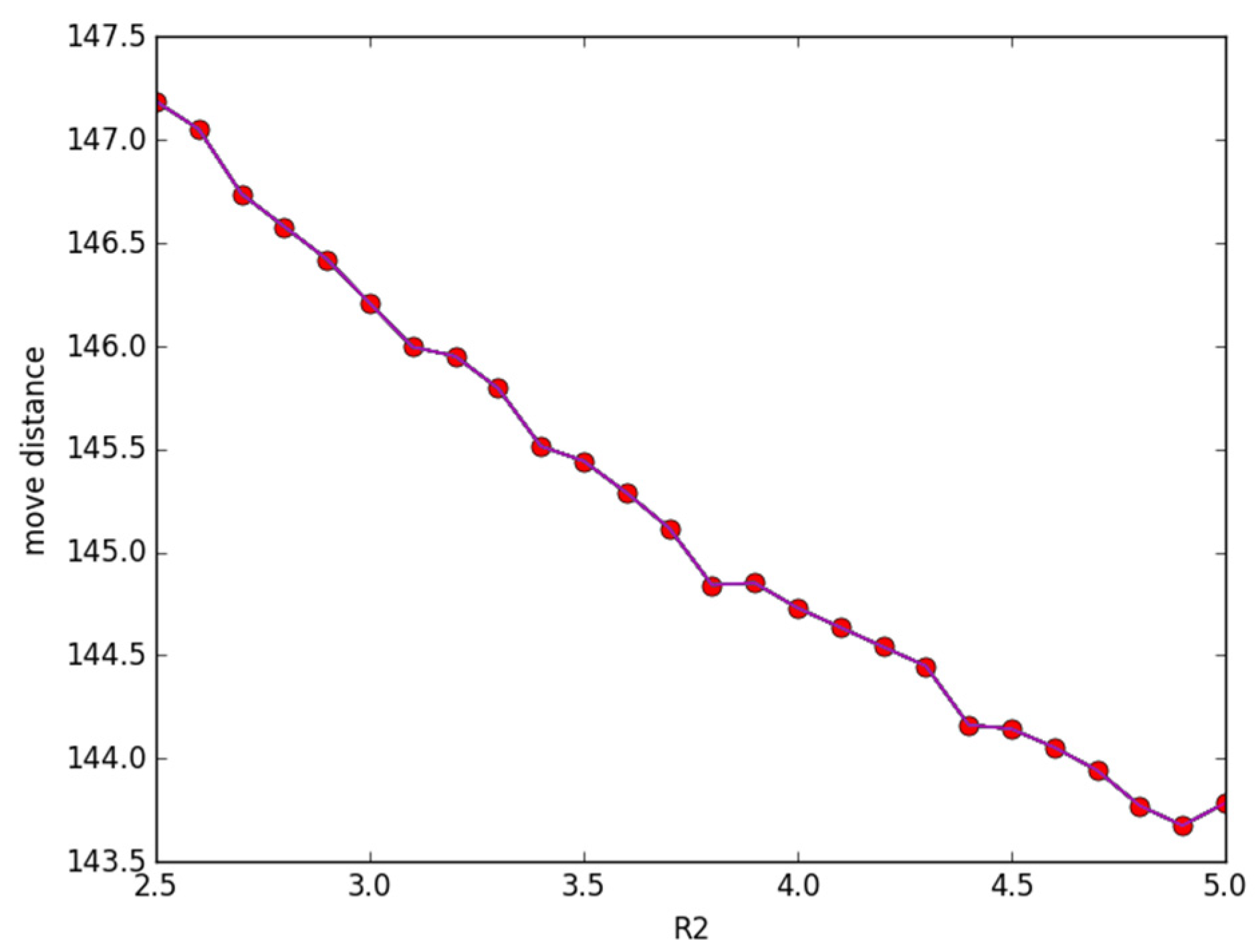
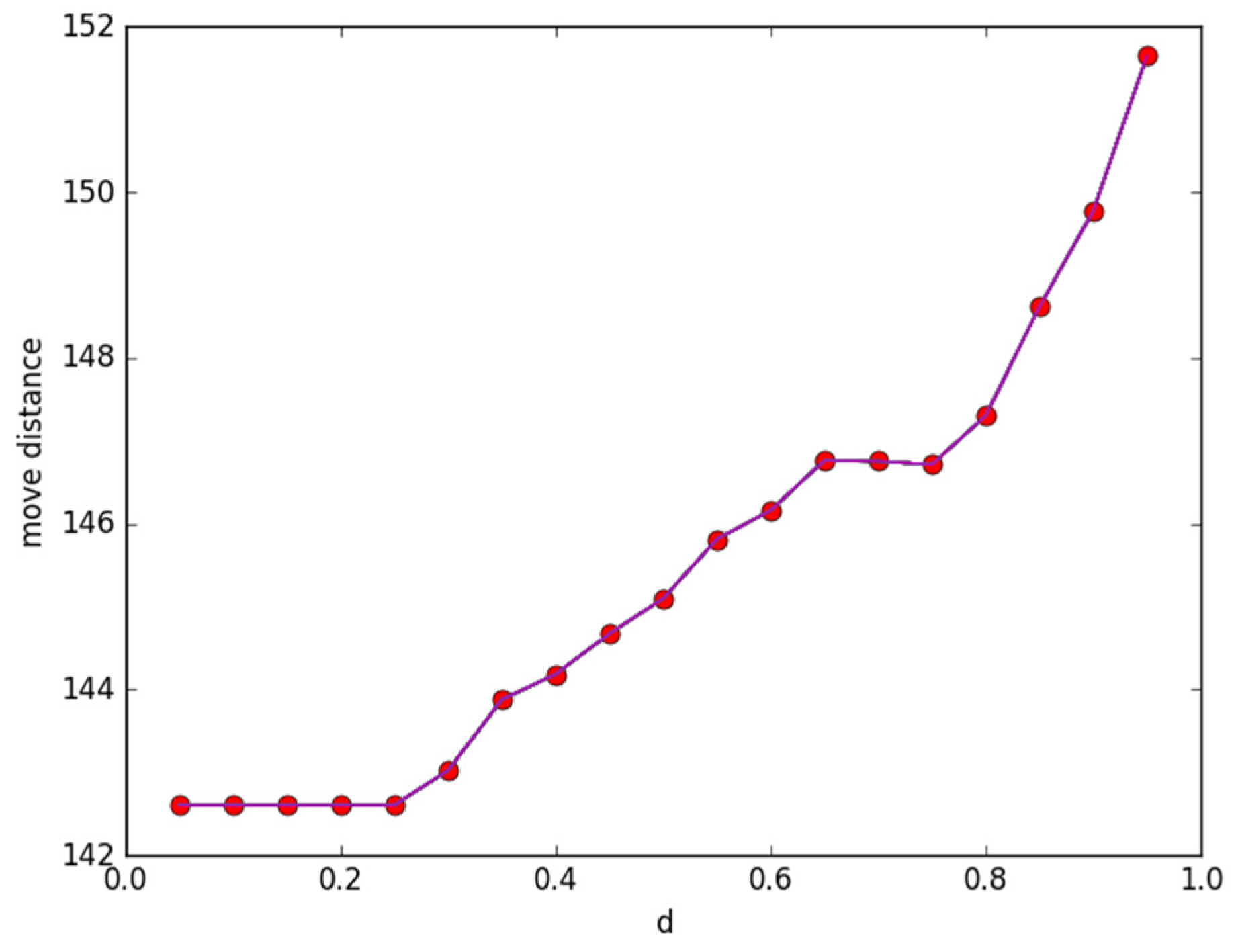
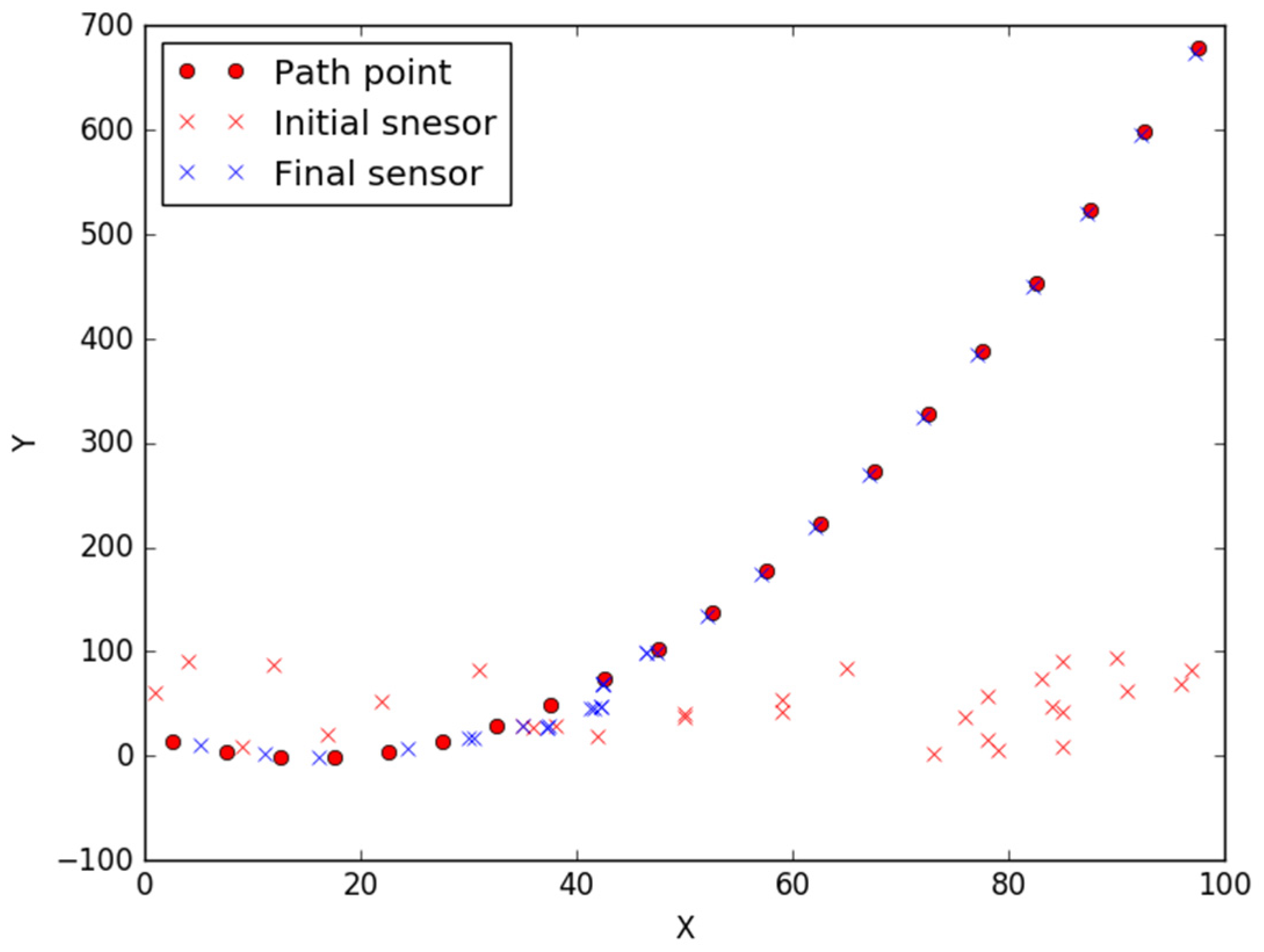
3.2.4. Simulations
4. Largest Path Coverage Lifetime
4.1. Problem Analysis
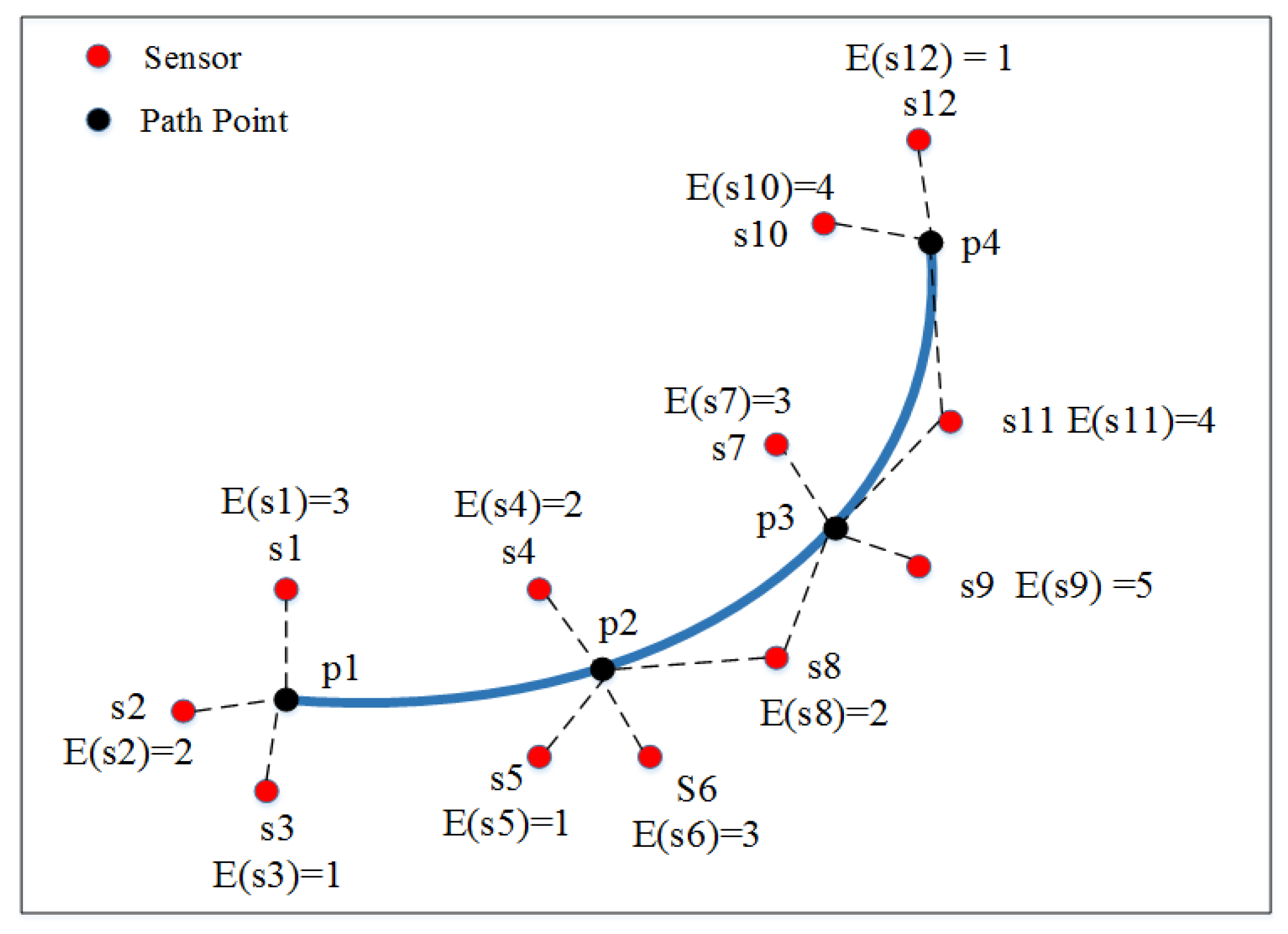
4.1.1. Marks
- E(s): The remaining battery level of node s, which is also called the lifetime of s;
- S(v): The collection of nodes that covered point v;
- C(s): The collection of points within the covering region of node s.
4.1.2. Preliminaries
4.1.3. Problem Description
4.2. Largest Path Coverage Lifetime Algorithm
4.2.1. Nodes Partitioning
| Algorithm 5: Nodes-partition (S, Q) |
| /* Input: deploy nodes collection S = {v1, v2, …, vn}, and points collection Q = {p1,…,pm} in P. Output: partitions collection of nodes. */ 1. Note S(pi) be the collection of nodes covering point pi; 2. Note T1, T2, …, Th be collection of node partitions; 3. S1 = Ø; 4. For (1 ≤ i ≤ h) & (1 ≤ j ≤ m) 5. randomly pitch a subset S0 of S(pj); 6. Ti = Ti + (S0 − S1); 7. S(pj) = S(pj) − (S′ − S1); 8. S1 = S1 + (S0 − S1); 9. Return T1, T2, …, Th. |
4.2.2. Combine Partitions
| Algorithm 6: Combine-partition (T, Q) |
| /* Input: collection T = {T1, T2,…, Th} of node partitions, collection Q = {p1,…,pm} of points in P Output: new partition collections W1, W2, …, Wr (r ≤ h), each covers all points in collection Q. */ 1. Arrange T by quantity of covered points by Ti, denoted by T = {T1, T2, …, Th}. 2. r = 1; T0 = T; S0 = Q; 3. If (r ≤ h) 4. Set Wr be zero, j be one, respectively; 5. If (T0 is not null) & (S0 is not null) & (j ≤ h) & (|C(Tj) − (Q − S0)| ≤ 0) 6. j++; Wr = Wr + { Tj }; T0 = T0 − Tj; S0 = S0 − C(Tj); j++; 7. If (S0 is null collection) 8. r++; else if (r ≤ 1) 9. Return zero; else 10. Merge all collections in T0 with Wr − 1; Merge all collections in Wr with Wr − 1; r--; 11. Return W1, …, Wr. |
4.2.3. Partition Schedule
| Algorithm 7: Partition schedule (W) |
| /* Input: partition collections W = {W1, W2, …, Wr} (r ≤ h), each covers all points in Q = {p1,…,pm}. Output: the schedule of collections in W */ 1. Calculate expected lifetime for each Wi; 2. For (1 ≤ i ≤ r) 3. Command nodes in collection Wi covering points in collection P; 4. Return. |
4.2.4. Intra-Schedule
| Algorithm 8: Intra-partition scheduling (Wi, Q) |
| /* Input: node collection Wi covering all points in collection Q = {p1,..,pm}. Output: schedule of nodes */ 1. While nodes in Wi cover all points in Q 2. Produce G = (V1,V2,E), where V1 denotes nodes set in Wi, and V2 denotes points set in Q; 3. Find a LRM (noted as M) in G; 4. For each vertex without matching in V2 5. Denote unmatched vertices set by V2′ in V2; 6. Induce a new sub-graph G0 from V1 and V2′; 7. Find a LRM in G0; 8. For element v in V2, note M(v) as the element in collection V1 matching some element of v in collection V2, and the one in M(v) with least battery be ver0; 9. For element v in collection V2, schedule M(v) to cover point v and point M(v), thus each element in collection Vi cost ver0 battery; 10. Delete elements in Wi out of service. 11. Return. |
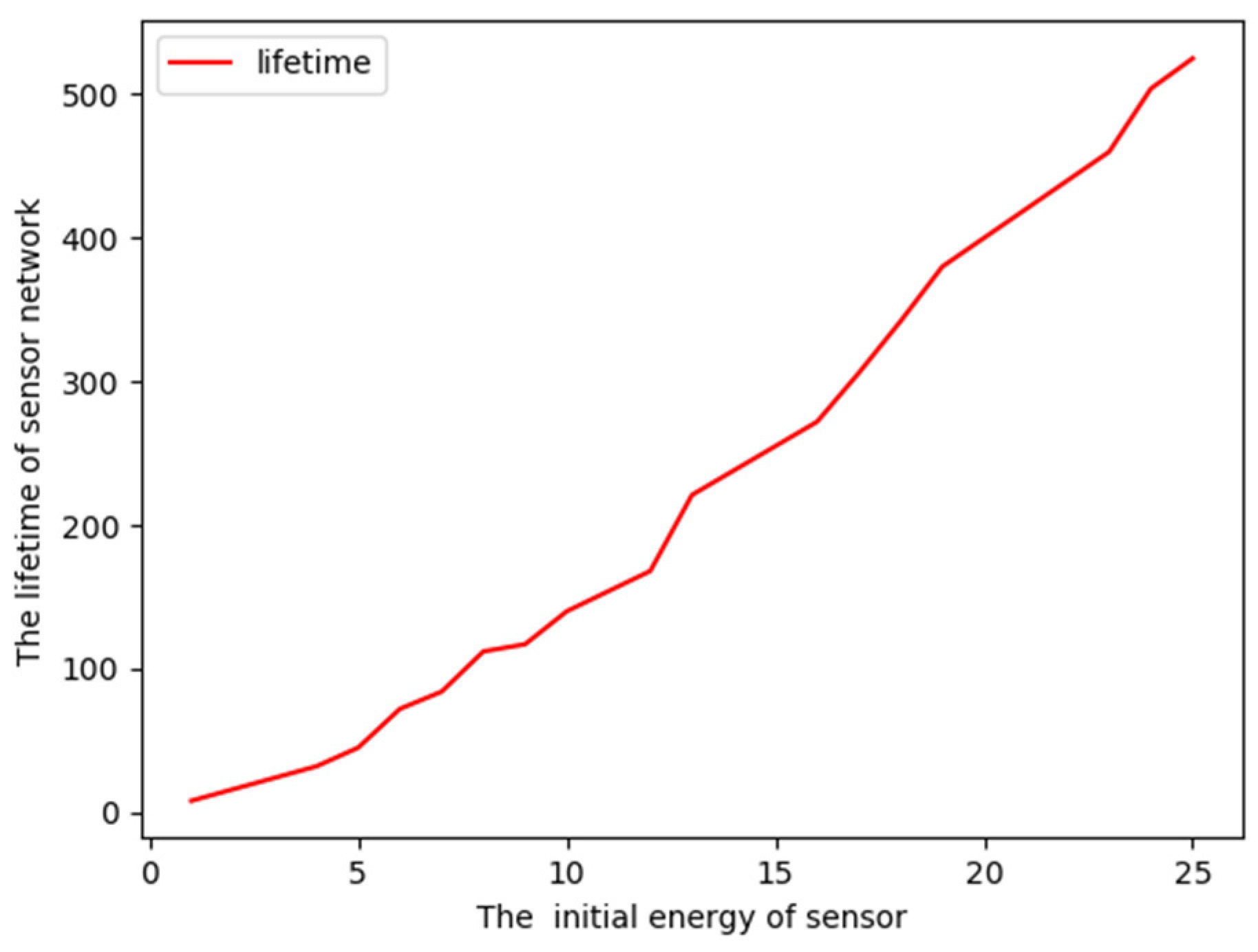
4.3. Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, S.; Mao, X.; Li, X.Y. Optimal k-support coverage paths in wireless sensor networks. In Proceedings of the IEEE International Conference on Pervasive Computing & Communications, Washington, DC, USA, 9 March 2009. [Google Scholar]
- Bose, P.; Morin, B.; Stojmenovic, I. Routing with guaranteed delivery in ad hoc wireless networks. ACM J. Wirel. Netw. 1999, 7, 609–616. [Google Scholar] [CrossRef]
- Tan, R.; Xing, G.; Wang, J. Exploiting reactive mobility for collaborative target detection in wireless sensor networks. IEEE Trans. Mob. Comput. 2010, 9, 317–332. [Google Scholar] [CrossRef]
- Somasundara, A.; Ramamoorthy, A.; Srivastava, M. Mobile element scheduling with dynamic deadlines. IEEE Trans. Mob. Comput. 2007, 6, 395–410. [Google Scholar] [CrossRef]
- Liao, Z.; Wang, J.; Zhang, S. Minimizing movement for target coverage and network connectivity in mobile sensor networks. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 1971–1983. [Google Scholar] [CrossRef]
- Hefeeda, M.; Bagheri, M. Randomized k-Coverage algorithms for dense sensor networks. In Proceedings of the International Conference on Computer Communications, Anchorage, AK, USA, 6 May 2007. [Google Scholar]
- Zhang, Y.; Huang, H.; Sun, P. Improving path-coverage for moving targets in wireless multimedia sensor networks. J. Commun. 2014, 9, 843–850. [Google Scholar] [CrossRef]
- Attea, B.A.; Hameed, S.M. A genetic algorithm for minimum set covering problem in reliable and efficient wireless sensor networks. Iraqi J. Sci. 2015, 55, 224–240. [Google Scholar]
- Han, R.S.; Wei, Y.; Li, Z. Achieving Crossed Strong Barrier Coverage in Wireless Sensor Network. Sensors 2018, 18, 534. [Google Scholar] [CrossRef] [PubMed]
- Dhawan, A. Maximum lifetime scheduling in wireless sensor networks. In Wireless Sensor Networks, Technology and Protocols; Intech: London, UK, 2012. [Google Scholar]
- Mini, S.; Udgata, S.K.; Sabat, S.L. Sensor deployment and scheduling for target coverage problem in wireless sensor networks. IEEE Nodes J. 2014, 14, 636–644. [Google Scholar] [CrossRef]
- Abrams, Z.E.; Ashish, G.; Serge, P. Set k-cover algorithms for energy efficient monitoring in wireless sensor networks. In Proceedings of the International Symposium on Information Processing in Sensor Networks, Berkeley, CA, USA, 27 April 2004. [Google Scholar]
- Cardei, M.; Du, D.Z. Improving wireless sensor network lifetime through power aware organization. Wirel. Netw. 2005, 11, 333–340. [Google Scholar] [CrossRef]
- Lu, Z.; Li, W.W.; Pan, M. Maximizing lifetime scheduling for target coverage and data collection in wireless sensor networks. IEEE Trans. Veh. Technol. 2015, 64, 714–727. [Google Scholar] [CrossRef]
- Gu, Y.; Pan, M.; Li, W. Maximizing the lifetime of delay-sensitive sensor networks via joint routing and sleep scheduling. In Proceedings of the IEEE International Conference on Computing, Networking and Communications, Honolulu, HI, USA, 15 January 2014. [Google Scholar]
- Weng, C.I.; Chang, C.Y.; Hsiao, C.Y. On-supporting energy balanced k-barrier coverage in wireless sensor networks. IEEE Access 2018, 99, 274–278. [Google Scholar] [CrossRef]
- Yoon, Y.; Kim, Y.H. Maximizing the coverage of sensor deployments using a memetic algorithm and fast coverage estimation. IEEE Trans. Cybern. 2021, 99, 6531–6542. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.; Duan, Q. A hybrid-strategy-improved butterfly optimization algorithm applied to the node coverage problem of wireless sensor networks. Math. Biosci. Eng. 2022, 19, 3928–3952. [Google Scholar] [CrossRef] [PubMed]



| Algorithms | Application Field | Object |
|---|---|---|
| MND [5] | point coverage | nodes movement |
| MTPCA [7] | point/region coverage | nodes movement |
| MSCP [8] | point/region coverage | nodes movement |
| MSPA [9] | barrier coverage | nodes movement |
| ABC [11] | point coverage | network lifetime |
| MC-MIP [13] | point coverage | network lifetime |
| MLCS [14] | point coverage | network lifetime |
| MSPA [16] | barrier coverage | network lifetime |
| HBOA [18] | point coverage | network lifetime |
| Our proposal | path coverage | nodes movement/network lifetime |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhou, W. Energy-Efficient Algorithms for Path Coverage in Sensor Networks. Sensors 2023, 23, 5026. https://doi.org/10.3390/s23115026
Liu Z, Zhou W. Energy-Efficient Algorithms for Path Coverage in Sensor Networks. Sensors. 2023; 23(11):5026. https://doi.org/10.3390/s23115026
Chicago/Turabian StyleLiu, Zhixiong, and Wei Zhou. 2023. "Energy-Efficient Algorithms for Path Coverage in Sensor Networks" Sensors 23, no. 11: 5026. https://doi.org/10.3390/s23115026
APA StyleLiu, Z., & Zhou, W. (2023). Energy-Efficient Algorithms for Path Coverage in Sensor Networks. Sensors, 23(11), 5026. https://doi.org/10.3390/s23115026







