Bayesian Noise Modelling for State Estimation of the Spread of COVID-19 in Saudi Arabia with Extended Kalman Filters
Abstract
1. Introduction
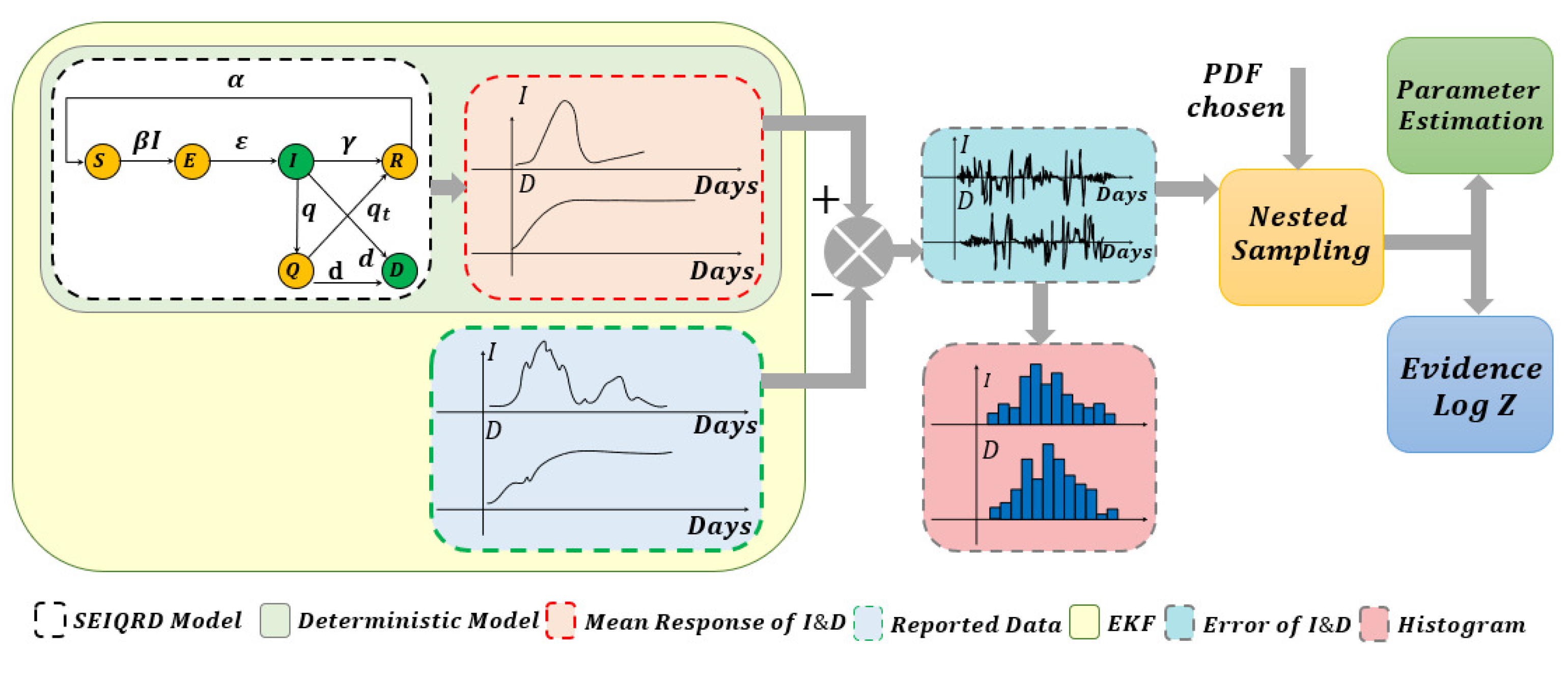
2. Kalman Filtering and the Pandemic Model
Multivariate Distributions
3. Methodology for Model Parameters and Uncertainty Estimation
4. Results and Discussions
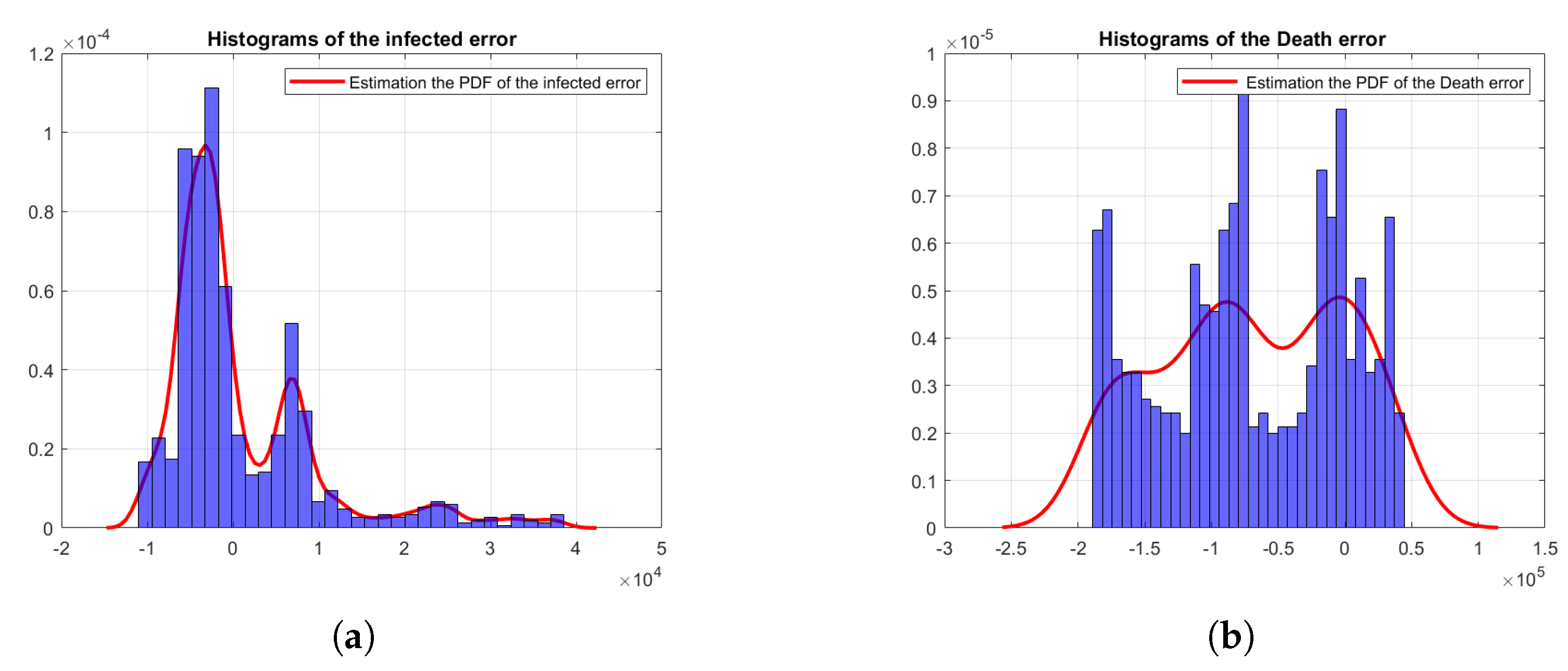
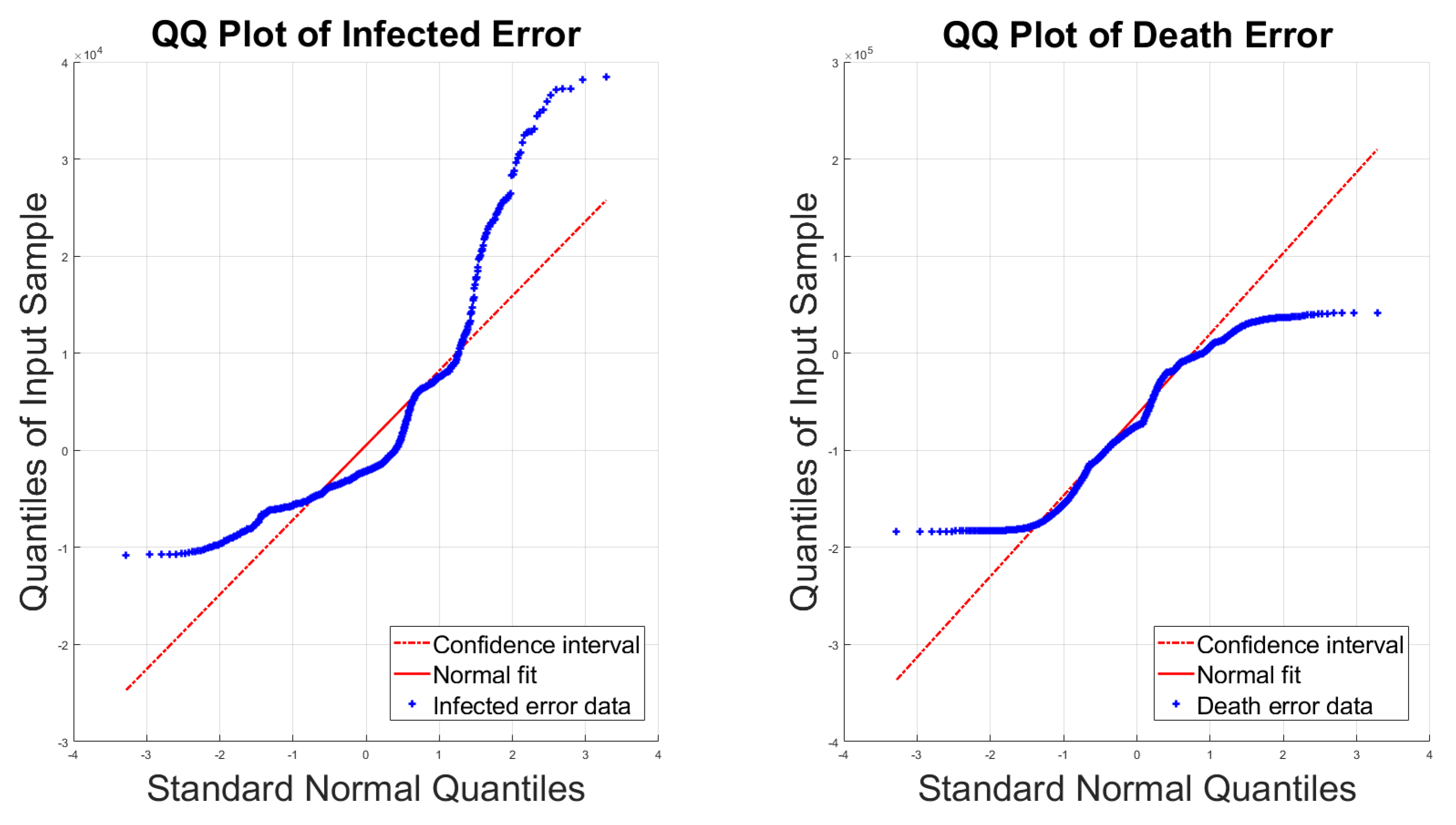
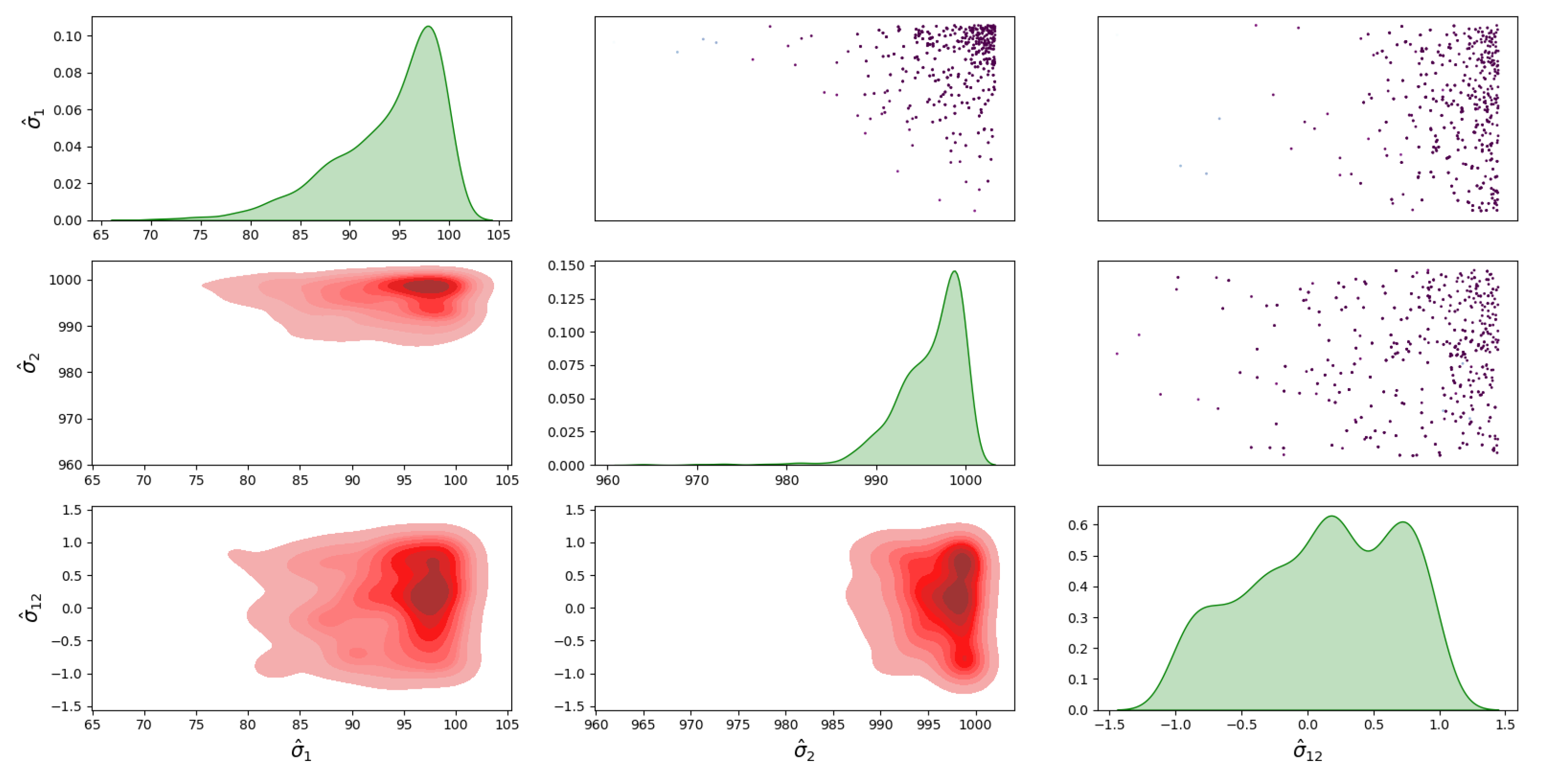
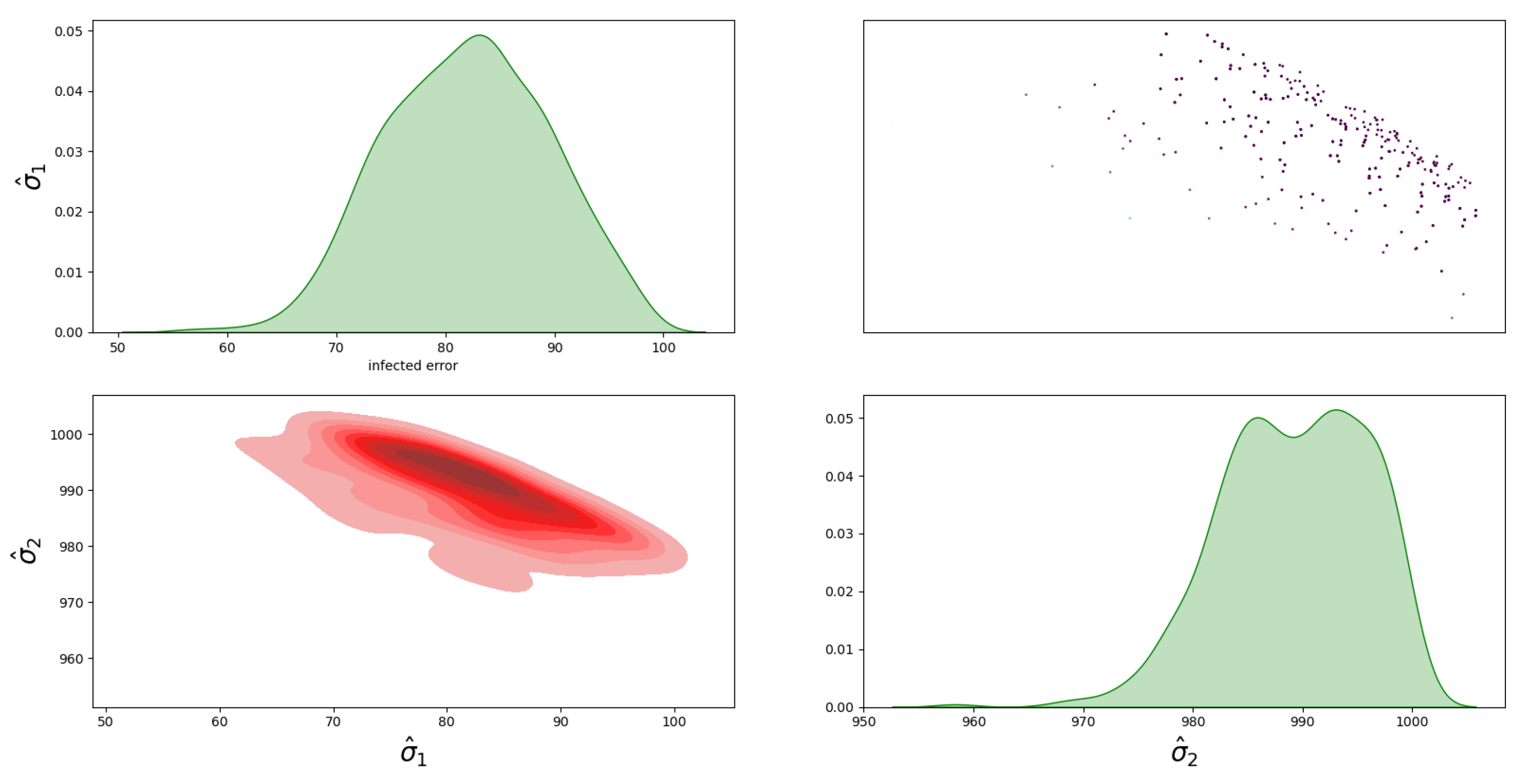
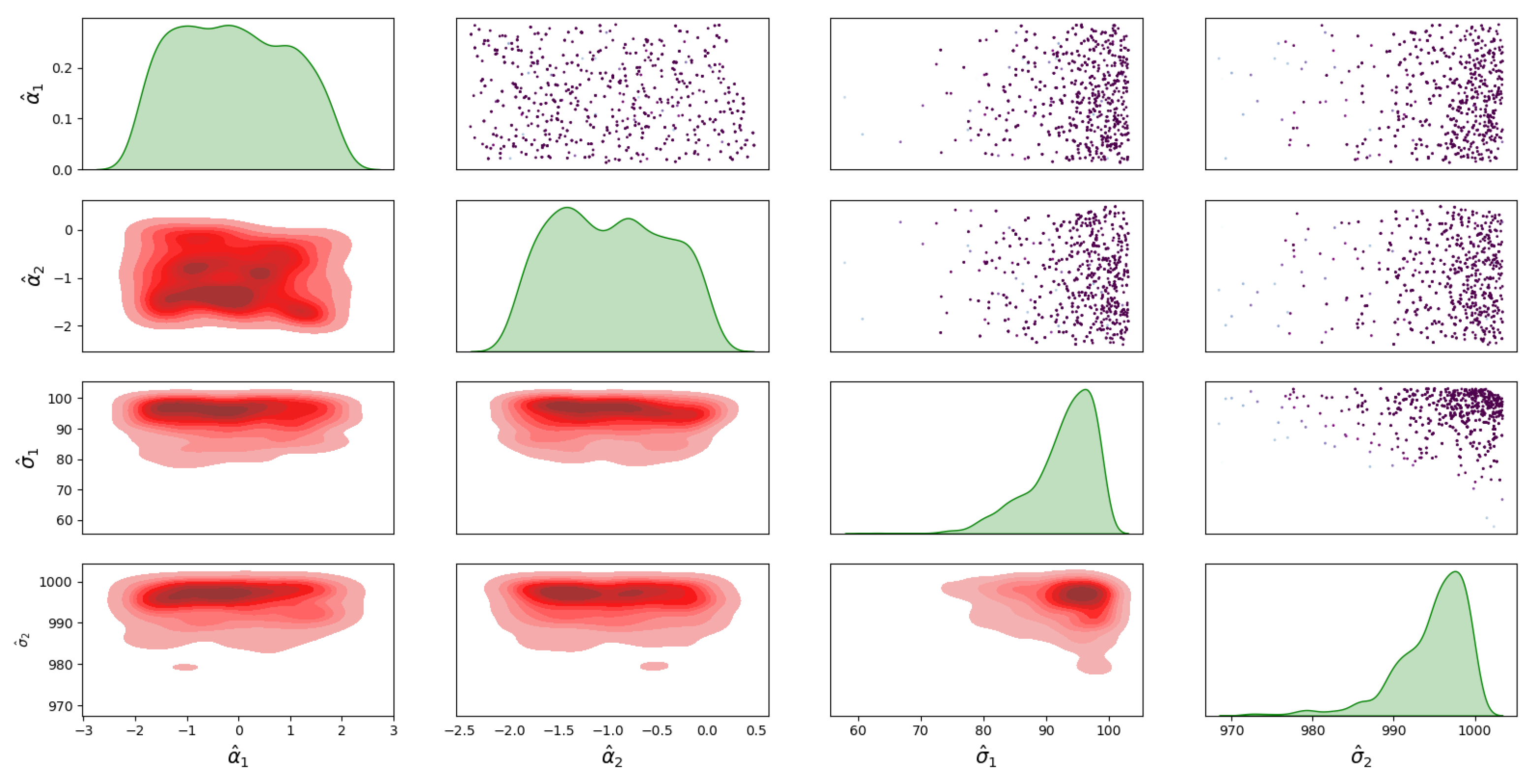
4.1. Bayesian Inference Results and Error Distributions
4.2. Assumptions on the Error Distributions
- The distribution with a full covariance matrix between I and D;
- The distribution with no correlation between I and D, i.e., diagonal covariance matrix ;
- The distribution with a full covariance matrix, , between I and D;
- The distribution with no correlation between I and D, i.e., diagonal covariance matrix, .
4.3. Sampling from the Posterior of the Unknown Noise Parameters Using Nested Sampling
4.4. Bayesian Model Comparison for Selecting the Best Noise Distribution
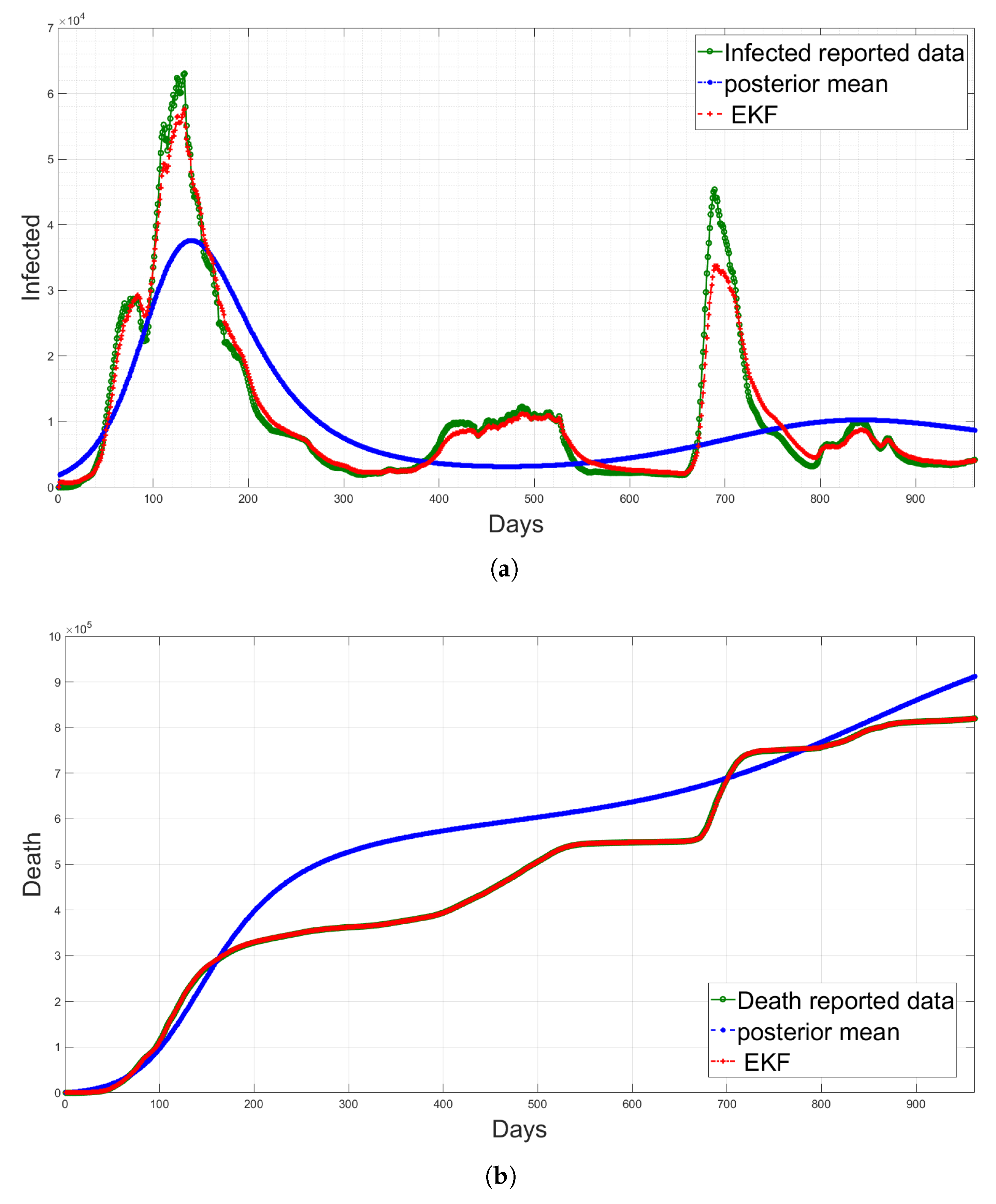
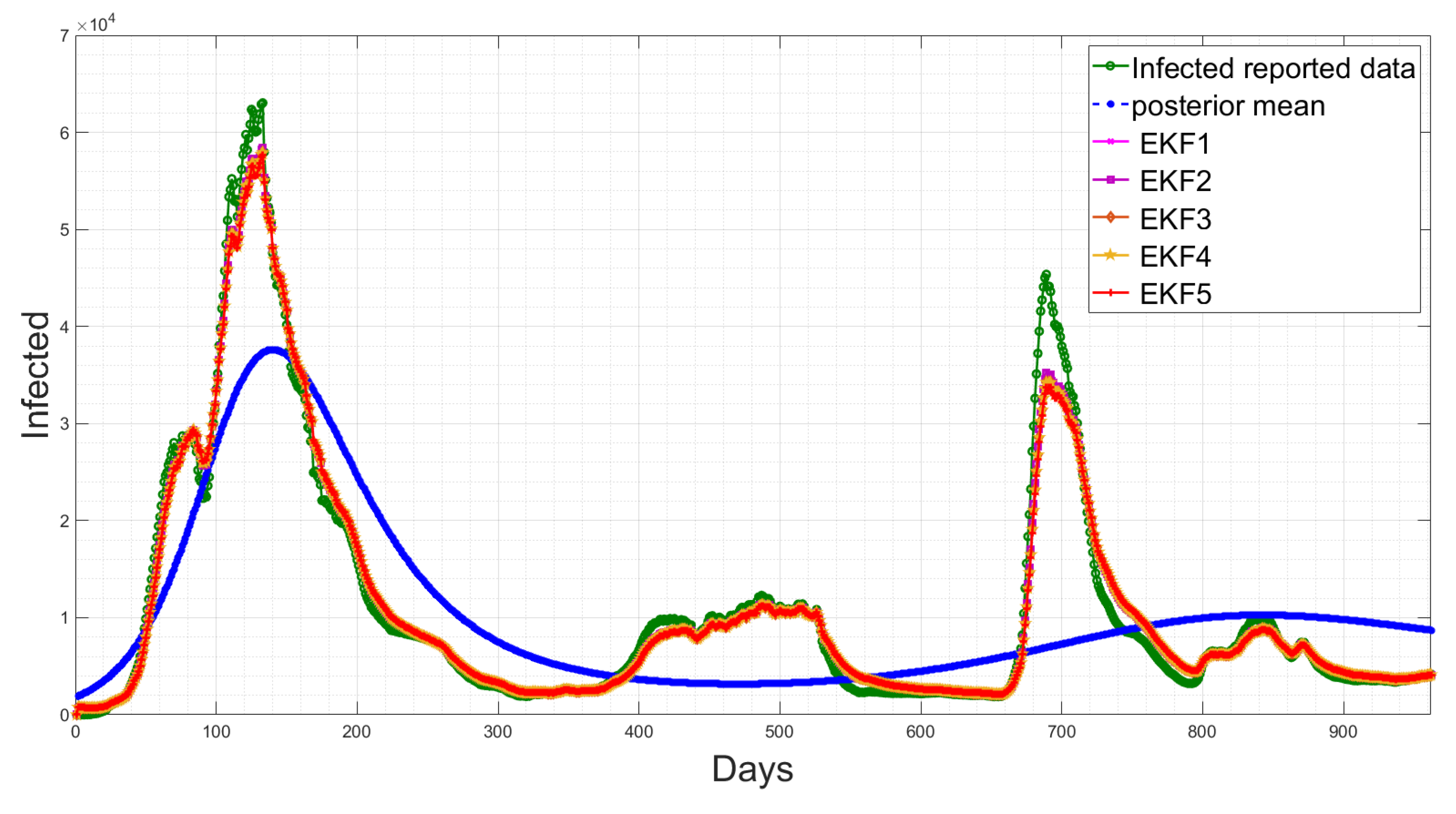
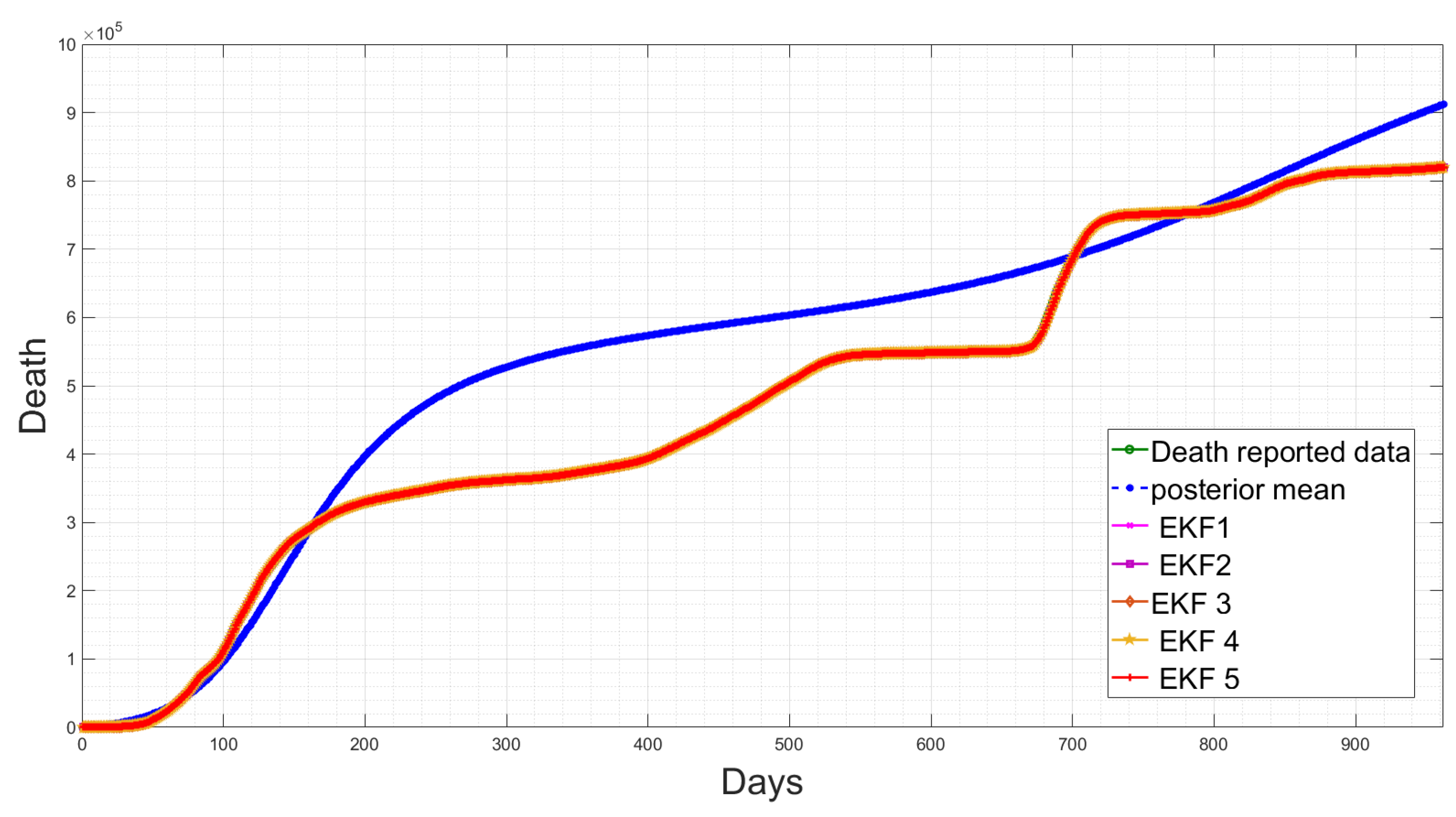
4.5. State Estimation Using Extended Kalman Filters with the Estimated Noise Distributions
5. Conclusions
5.1. Main Contributions and Limitations
5.2. Future Work
- This work can be further extended with other, more complex nonlinear epidemiological compartmental models under the EKF framework with more experimental evidence.
- Another possible future direction is to include more model comparisons within different skewness distribution families using similar approaches such as the class of skewness distributions presented in [52]. However, the challenge with this class is dealing with the extra parameters as well as prior range selection, which should be carried out carefully as there is a lack of interpretability in the literature which needs further investigation.
- Unknown microbes or microorganisms that arrive from space, which are called panspermia, as discussed in [54,55]; however, there is a lack of evidence for this hypothesis and microbial data collection in space is limited due to the high cost, the complexity of the experimental setup and the high level of risk involved. As there are no clear findings of microorganisms coming from asteroids, comets or spacecraft, the evidence of possible infection is rather low. COVID-19 data can help in improving modelling of unknown pandemics from outer space.
- The outbreak of experimental microbes in scientific laboratories, due to accidents or poor management practices, can result in infections such as Brucella abortus, which can cause foetal death in pregnant women. Moreover, the origin of COVID-19 is still unknown, and whether it emerged through natural spillover, trans-species migration or a laboratory accident is still uncertain. However, a laboratory accident cannot be excluded as a potential risk for similar or even larger future pandemics, as discussed in [56,57].
- Future pandemics may also be caused by anthropogenic roots such as political conflicts or wars between countries, continents and specific genotypes, which can be modelled and controlled using the COVID-19 data as a test scenario [58,59]. This may also include manipulating the birth rate and other constants between the model compartments related to the health system’s infrastructure, such as the hospital capacity, quarantine period and reinfection rate in a country or region.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| KF | Kalman filter |
| EKF | Extended Kalman filter |
| MVN | Multivariate normal distribution |
| MSN | Multivariate skew normal distribution |
| Probability density function | |
| CDF | Cumulative density function |
| KDE | Kernel density estimate |
| MAP | Maximum a posteriori estimate |
| RMSE | Root Mean Squared Error |
References
- Alyami, L.; Das, S. State Estimation of the Spread of COVID-19 in Saudi Arabia using Extended Kalman Filter. In Proceedings of the 2022 Sensor Signal Processing for Defence Conference (SSPD), London, UK, 13–14 September 2022; pp. 1–5. [Google Scholar]
- Skilling, J. Nested sampling for general Bayesian computation. Bayesian Anal. 2006, 1, 833–859. [Google Scholar] [CrossRef]
- Odelson, B.J.; Lutz, A.; Rawlings, J.B. The autocovariance least-squares method for estimating covariances: Application to model-based control of chemical reactors. IEEE Trans. Control. Syst. Technol. 2006, 14, 532–540. [Google Scholar] [CrossRef]
- Odelson, B.J.; Rajamani, M.R.; Rawlings, J.B. A new autocovariance least-squares method for estimating noise covariances. Automatica 2006, 42, 303–308. [Google Scholar] [CrossRef]
- Åkesson, B.M.; Jørgensen, J.B.; Poulsen, N.K.; Jørgensen, S.B. A generalized autocovariance least-squares method for Kalman filter tuning. J. Process. Control 2008, 18, 769–779. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H∞, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Julier, S.J. Skewed approach to filtering. In Proceedings of the Signal and Data Processing of Small Targets, Orlando, FL, USA, 14–16 April 1998; Volume 3373, pp. 271–282. [Google Scholar]
- Genton, M.G. Skew-Elliptical Distributions and Their Applications: A Journey Beyond Normality; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Zhu, X.; Gao, B.; Zhong, Y.; Gu, C.; Choi, K.S. Extended Kalman filter based on stochastic epidemiological model for COVID-19 modelling. Comput. Biol. Med. 2021, 137, 104810. [Google Scholar] [CrossRef] [PubMed]
- Lal, R.; Huang, W.; Li, Z. An application of the ensemble Kalman filter in epidemiological modelling. PLoS ONE 2021, 16, e0256227. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Xie, H.; Gao, B.; Zhong, Y.; Gu, C.; Choi, K.S. Maximum likelihood-based extended Kalman filter for COVID-19 prediction. Chaos Solitons Fractals 2021, 146, 110922. [Google Scholar] [CrossRef]
- Arroyo-Marioli, F.; Bullano, F.; Kucinskas, S.; Rondón-Moreno, C. Tracking R of COVID-19: A new real-time estimation using the Kalman filter. PLoS ONE 2021, 16, e0244474. [Google Scholar] [CrossRef]
- Bansal, R.; Kumar, A.; Singh, A.K.; Kumar, S. Stochastic filtering based transmissibility estimation of novel coronavirus. Digit. Signal Process. 2021, 112, 103001. [Google Scholar] [CrossRef]
- Zeng, X.; Ghanem, R. Dynamics identification and forecasting of COVID-19 by switching Kalman filters. Comput. Mech. 2020, 66, 1179–1193. [Google Scholar] [CrossRef] [PubMed]
- Nanda, S.K.; Kumar, G.; Bhatia, V.; Singh, A.K. Kalman-based compartmental estimation for COVID-19 pandemic using advanced epidemic model. Biomed. Signal Process. Control 2023, 84, 104727. [Google Scholar] [CrossRef] [PubMed]
- Marques, J.A.L.; Gois, F.N.B.; Xavier-Neto, J.; Fong, S.J. Predictive Models for Decision Support in the COVID-19 Crisis; Springer: Cham, Switzeralnd, 2021. [Google Scholar]
- Saudi Ministry of Health. Available online: https://covid19.moh.gov.sa (accessed on 30 November 2022).
- Zhang, Z.; Zeb, A.; Hussain, S.; Alzahrani, E. Dynamics of COVID-19 mathematical model with stochastic perturbation. Adv. Differ. Eqs. 2020, 2020, 451. [Google Scholar] [CrossRef]
- Khan, T.; Zaman, G.; El-Khatib, Y. Modeling the dynamics of novel coronavirus (COVID-19) via stochastic epidemic model. Results Phys. 2021, 24, 104004. [Google Scholar] [CrossRef] [PubMed]
- Hussain, S.; Madi, E.N.; Khan, H.; Etemad, S.; Rezapour, S.; Sitthiwirattham, T.; Patanarapeelert, N. Investigation of the stochastic modeling of COVID-19 with environmental noise from the analytical and numerical point of view. Mathematics 2021, 9, 3122. [Google Scholar] [CrossRef]
- Azzalini, A.; Valle, A.D. The multivariate skew-normal distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Statistical applications of the multivariate skew normal distribution. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1999, 61, 579–602. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Dey, D.K. Bayesian model choice: Asymptotics and exact calculations. J. R. Stat. Soc. Ser. B (Methodol.) 1994, 56, 501–514. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. On Monte Carlo methods for estimating ratios of normalizing constants. Ann. Stat. 1997, 25, 1563–1594. [Google Scholar] [CrossRef]
- Chib, S. Marginal likelihood from the Gibbs output. J. Am. Stat. Assoc. 1995, 90, 1313–1321. [Google Scholar] [CrossRef]
- Llorente, F.; Martino, L.; Delgado, D.; Lopez-Santiago, J. Marginal likelihood computation for model selection and hypothesis testing: An extensive review. SIAM Rev. 2023, 65, 3–58. [Google Scholar] [CrossRef]
- Bos, C.S. A comparison of marginal likelihood computation methods. In Proceedings of the COMPSTAT: Proceedings in Computational Statistics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 111–116. [Google Scholar]
- Friel, N.; Wyse, J. Estimating the evidence—A review. Stat. Neerl. 2012, 66, 288–308. [Google Scholar] [CrossRef]
- Robert, C.P.; Wraith, D. Computational methods for Bayesian model choice. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2009; Volume 1193, pp. 251–262. [Google Scholar]
- Ardia, D.; Baştürk, N.; Hoogerheide, L.; Van Dijk, H.K. A comparative study of Monte Carlo methods for efficient evaluation of marginal likelihood. Comput. Stat. Data Anal. 2012, 56, 3398–3414. [Google Scholar] [CrossRef]
- Chopin, N.; Robert, C.P. Properties of nested sampling. Biometrika 2010, 97, 741–755. [Google Scholar] [CrossRef]
- Mukherjee, P.; Parkinson, D.; Liddle, A.R. A nested sampling algorithm for cosmological model selection. Astrophys. J. 2006, 638, L51. [Google Scholar] [CrossRef]
- Vegetti, S.; Koopmans, L.V. Bayesian strong gravitational-lens modelling on adaptive grids: Objective detection of mass substructure in Galaxies. Mon. Not. R. Astron. Soc. 2009, 392, 945–963. [Google Scholar] [CrossRef]
- Li, Y.I.; Turk, G.; Rohrbach, P.B.; Pietzonka, P.; Kappler, J.; Singh, R.; Dolezal, J.; Ekeh, T.; Kikuchi, L.; Peterson, J.D.; et al. Efficient Bayesian inference of fully stochastic epidemiological models with applications to COVID-19. R. Soc. Open Sci. 2021, 8, 211065. [Google Scholar] [CrossRef]
- Das, S.; Hobson, M.P.; Feroz, F.; Chen, X.; Phadke, S.; Goudswaard, J.; Hohl, D. Microseismic event detection in large heterogeneous velocity models using Bayesian multimodal nested sampling. Data-Centric Eng. 2021, 2, e1. [Google Scholar] [CrossRef]
- Pártay, L.B.; Csányi, G.; Bernstein, N. Nested sampling for materials. Eur. Phys. J. B 2021, 94, 159. [Google Scholar] [CrossRef]
- Buchner, J. A statistical test for nested sampling algorithms. Stat. Comput. 2016, 26, 383–392. [Google Scholar] [CrossRef]
- Ferreira, J.T.; Steel, M.F. Model comparison of coordinate-free multivariate skewed distributions with an application to stochastic frontiers. J. Econom. 2007, 137, 641–673. [Google Scholar] [CrossRef]
- Ferreira, J.T.; Steel, M.F. On describing multivariate skewed distributions: A directional approach. Can. J. Stat. 2006, 34, 411–429. [Google Scholar] [CrossRef]
- Rubio, F.; Steel, M. Bayesian modelling of skewness and kurtosis with Two-Piece Scale and shape distributions. Electron. J. Stat. 2015, 9, 1884–1912. [Google Scholar] [CrossRef]
- Joanes, D.N.; Gill, C.A. Comparing measures of sample skewness and kurtosis. J. R. Stat. Soc. Ser. D (Stat.) 1998, 47, 183–189. [Google Scholar] [CrossRef]
- Serfling, R.J. Approximation Theorems of Mathematical Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Demir, S. Comparison of normality tests in terms of sample sizes under different skewness and Kurtosis coefficients. Int. J. Assess. Tools Educ. 2022, 9, 397–409. [Google Scholar] [CrossRef]
- Bulmer, M.G. Principles of Statistics; Courier Corporation: Gloucester, MA, USA, 1979. [Google Scholar]
- Tabachnick, B.G.; Fidell, L.S.; Ullman, J.B. Using Multivariate Statistics; Pearson: Boston, MA, USA, 2013; Volume 6. [Google Scholar]
- Field, A. Discovering Statistics Using IBM SPSS Statistics; Sage: Thousand Oaks, CA, USA, 2013. [Google Scholar]
- Feroz, F.; Hobson, M.; Bridges, M. MultiNest: An efficient and robust Bayesian inference tool for cosmology and particle physics. Mon. Not. R. Astron. Soc. 2009, 398, 1601–1614. [Google Scholar] [CrossRef]
- Verdinelli, I.; Wasserman, L. Computing Bayes factors using a generalization of the Savage-Dickey density ratio. J. Am. Stat. Assoc. 1995, 90, 614–618. [Google Scholar] [CrossRef]
- Dickey, J.M. The weighted likelihood ratio, linear hypotheses on normal location parameters. Ann. Math. Stat. 1971, 42, 204–223. [Google Scholar] [CrossRef]
- DiCiccio, T.J.; Kass, R.E.; Raftery, A.; Wasserman, L. Computing Bayes factors by combining simulation and asymptotic approximations. J. Am. Stat. Assoc. 1997, 92, 903–915. [Google Scholar] [CrossRef]
- Jeffreys, H. Theory of Probability; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Gonzalez-Farias, G.; Dominguez-Molina, A.; Gupta, A.K. Additive properties of skew normal random vectors. J. Stat. Plan. Inference 2004, 126, 521–534. [Google Scholar] [CrossRef]
- Thoradeniya, T.; Jayasinghe, S. COVID-19 and future pandemics: A global systems approach and relevance to SDGs. Glob. Health 2021, 17, 59. [Google Scholar] [CrossRef]
- Wesson, P.S. Panspermia, past and present: Astrophysical and biophysical conditions for the dissemination of life in space. Space Sci. Rev. 2010, 156, 239–252. [Google Scholar] [CrossRef]
- Steele, E.J.; Gorczynski, R.M.; Lindley, R.A.; Tokoro, G.; Temple, R.; Wickramasinghe, N.C. Origin of new emergent Coronavirus and Candida fungal diseases—Terrestrial or cosmic? Adv. Genet. 2020, 106, 75–100. [Google Scholar] [PubMed]
- Bloom, J.D.; Chan, Y.A.; Baric, R.S.; Bjorkman, P.J.; Cobey, S.; Deverman, B.E.; Fisman, D.N.; Gupta, R.; Iwasaki, A.; Lipsitch, M.; et al. Investigate the origins of COVID-19. Science 2021, 372, 694. [Google Scholar] [CrossRef] [PubMed]
- Maxmen, A.; Mallapaty, S. The COVID lab-leak hypothesis: What scientists do and don’t know. Nature 2021, 594, 313–315. [Google Scholar] [CrossRef] [PubMed]
- Merrin, W. Anthropocenic war: Coronavirus and total demobilization. Digit. War 2020, 1, 36–49. [Google Scholar] [CrossRef]
- Lyon, R.F. The COVID-19 response has uncovered and increased our vulnerability to biological warfare. Mil. Med. 2021, 186, 193–196. [Google Scholar] [CrossRef]
- Pan, X.; Ojcius, D.M.; Gao, T.; Li, Z.; Pan, C.; Pan, C. Lessons learned from the 2019-nCoV epidemic on prevention of future infectious diseases. Microbes Infect. 2020, 22, 86–91. [Google Scholar] [CrossRef]




| Model | |||||
|---|---|---|---|---|---|
| with correlation | - | - | |||
| without correlation | - | - | - | ||
| with correlation | |||||
| without correlation | - |
| Model | log | ||
|---|---|---|---|
| Model-1: with correlation | 60 | −263.215 ± 0.329 | 715 |
| Model-2: without correlation | 40 | −266.940 ± 0.403 | 463 |
| Model-3: with correlation | 100 | −263.546 ± 0.265 | 1239 |
| Model-4: without correlation | 80 | −263.548 ± 0.297 | 989 |
| EKF | Covariance Matrices | Infected RMSE | Death RMSE |
|---|---|---|---|
| EKF1 with correlation | = 500 × , = | 67.1907 | 26.9871 |
| EKF2 without correlation | = 500 × , = diag[82.017, 989.20] | 61.2482 | 26.6587 |
| EKF3 with correlation | = 500 × , = | 66.5684 | 26.9649 |
| EKF4 without correlation | = 500 × , = diag[93.17, 994.56] | 66.8042 | 26.9032 |
| EKF5 | = 500 × , = diag[100, 1000], Ref. [1] | 70.1258 | 27.0861 |
| Parameter | Parameter Value | ||
|---|---|---|---|
| Description | Mean | Standard Deviation | |
| infection rate | 3 | 4.4 | |
| reinfection rate | 0.0028 | 1.4 | |
| incubation period | 0.0353 | 0.00361 | |
| q | quarantine rate | 0.9593 | 0.0033 |
| quarantine period | 0.5939 | 0.0521 | |
| d | death rate | 4 | 2.7 |
| recovery rate | 0.9586 | 0.0031 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alyami, L.; Panda, D.K.; Das, S. Bayesian Noise Modelling for State Estimation of the Spread of COVID-19 in Saudi Arabia with Extended Kalman Filters. Sensors 2023, 23, 4734. https://doi.org/10.3390/s23104734
Alyami L, Panda DK, Das S. Bayesian Noise Modelling for State Estimation of the Spread of COVID-19 in Saudi Arabia with Extended Kalman Filters. Sensors. 2023; 23(10):4734. https://doi.org/10.3390/s23104734
Chicago/Turabian StyleAlyami, Lamia, Deepak Kumar Panda, and Saptarshi Das. 2023. "Bayesian Noise Modelling for State Estimation of the Spread of COVID-19 in Saudi Arabia with Extended Kalman Filters" Sensors 23, no. 10: 4734. https://doi.org/10.3390/s23104734
APA StyleAlyami, L., Panda, D. K., & Das, S. (2023). Bayesian Noise Modelling for State Estimation of the Spread of COVID-19 in Saudi Arabia with Extended Kalman Filters. Sensors, 23(10), 4734. https://doi.org/10.3390/s23104734








