Highly Sensitive SPAD-Based Receiver for Dimming Control in LiFi Networks †
Abstract
1. Introduction
1.1. Related Works
1.2. Contributions
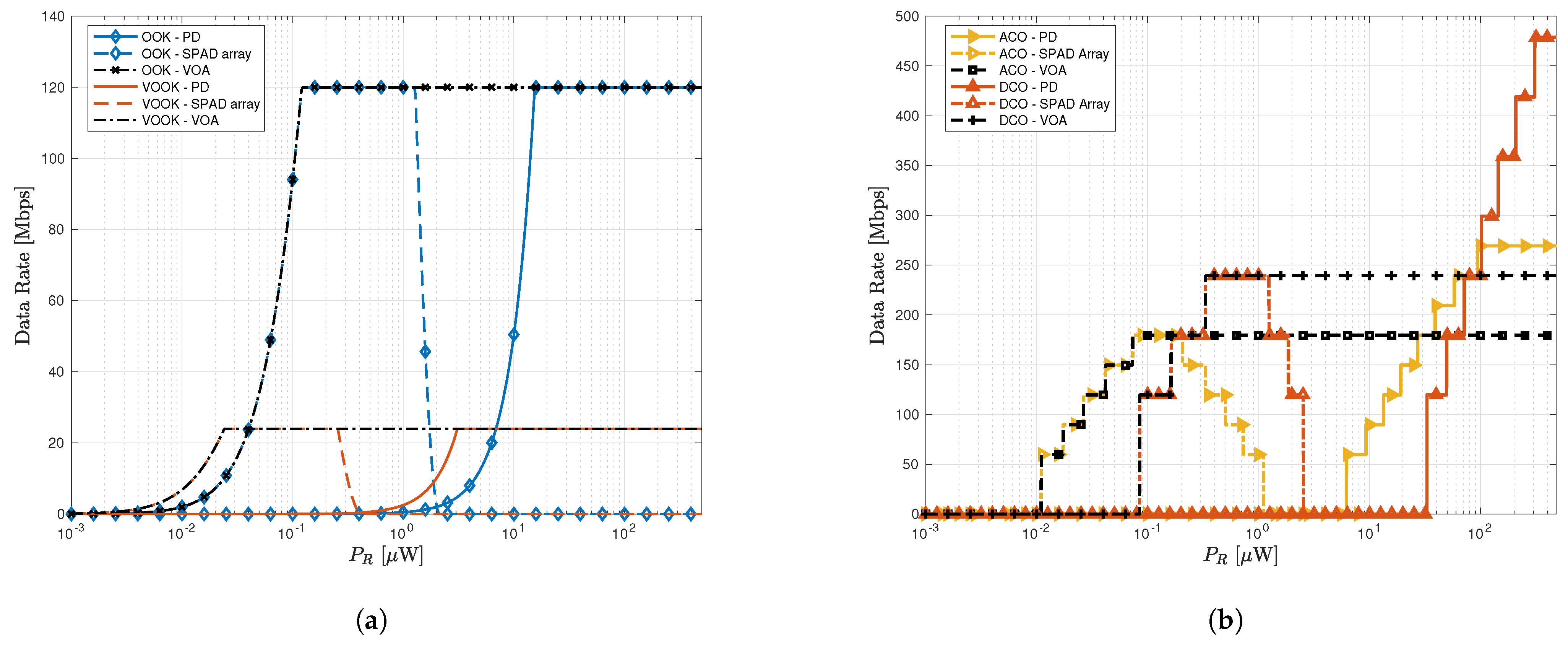
- We propose a novel adaptive receiver employing a SPAD array with a VOA to improve the overall performance of indoor VLC links and satisfy a wide range of dimming requirements.
- The analytical expressions of the signal-to-noise ratio (SNR), BER, and achievable data rate of the VLC dimming systems with the proposed receiver when various modulation schemes are employed are derived. The considered modulation schemes include the single-carrier schemes OOK and VOOK, and also the multi-carrier schemes DCO- and ACO-OFDM.
- We show that in low dimming levels, the proposed receiver benefits from the SPAD’s high sensitivity, but as light brightness increases, the receiver utilizes the VOA to avoid significant non-linear distortion in the SPAD array and maintains superior performance.
- The extensive numerical results demonstrate that the proposed adaptive receiver outperforms both PIN PD and traditional PIN PD and SPAD receivers in terms of BER and achievable data rate under various dimming levels and a wide range of channel conditions.
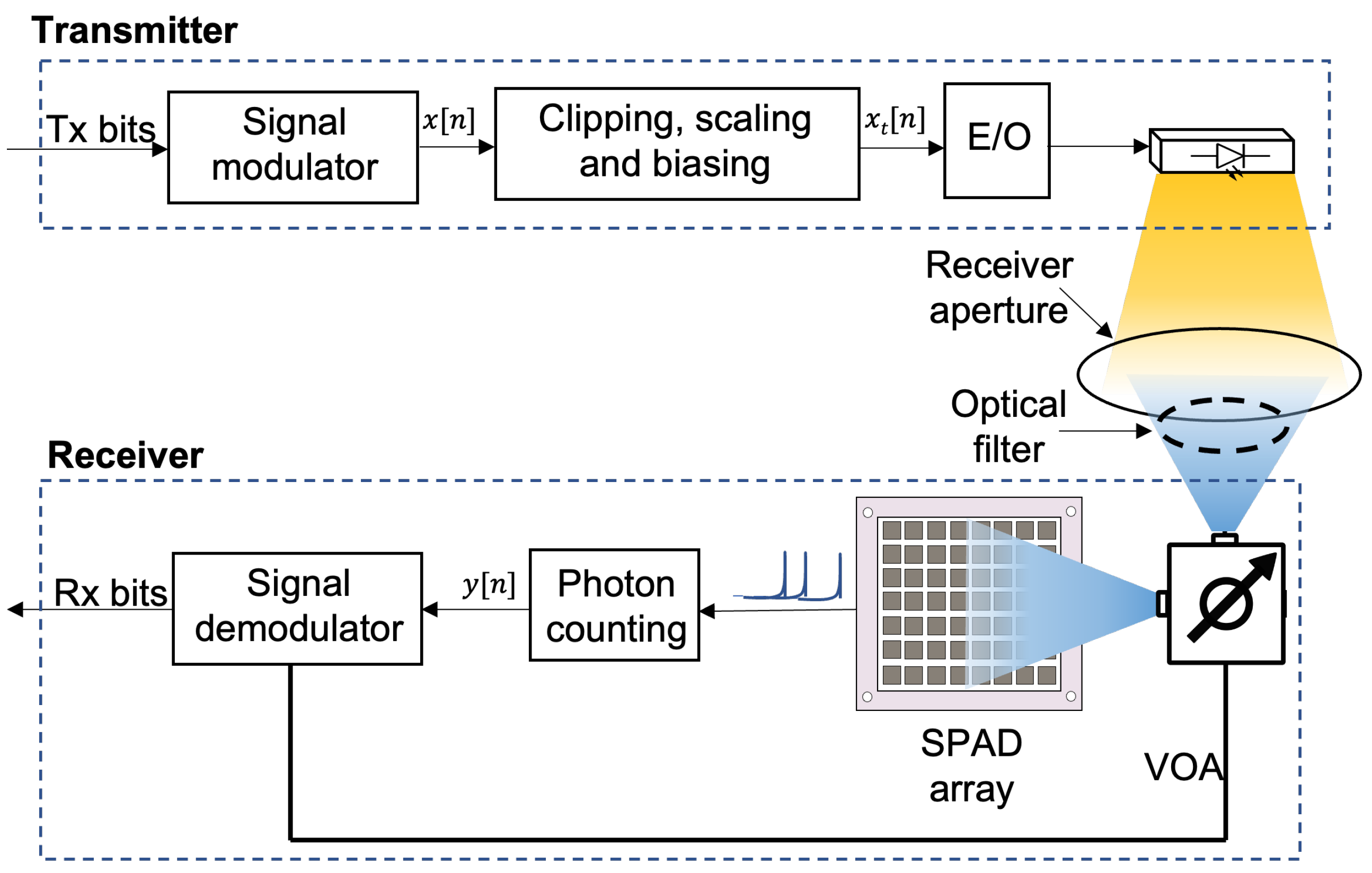
2. System Model
3. Single-Carrier Transmission Schemes with Dimming Control
3.1. On-Off Keying (OOK)—Analogue Dimming
3.1.1. PD Receivers
3.1.2. Adaptive SPAD Receivers
3.2. Variable On–Off Keying (VOOK)—Digital Dimming
3.2.1. PD Receivers
3.2.2. Adaptive SPAD Receivers
4. Multi-Carrier Transmission Schemes with Dimming Control
4.1. DCO-OFDM
4.1.1. PD Receivers
4.1.2. Adaptive SPAD Receivers
4.2. ACO-OFDM
4.2.1. PD Receivers
4.2.2. Adaptive SPAD Receivers
5. Numerical Results and Discussion
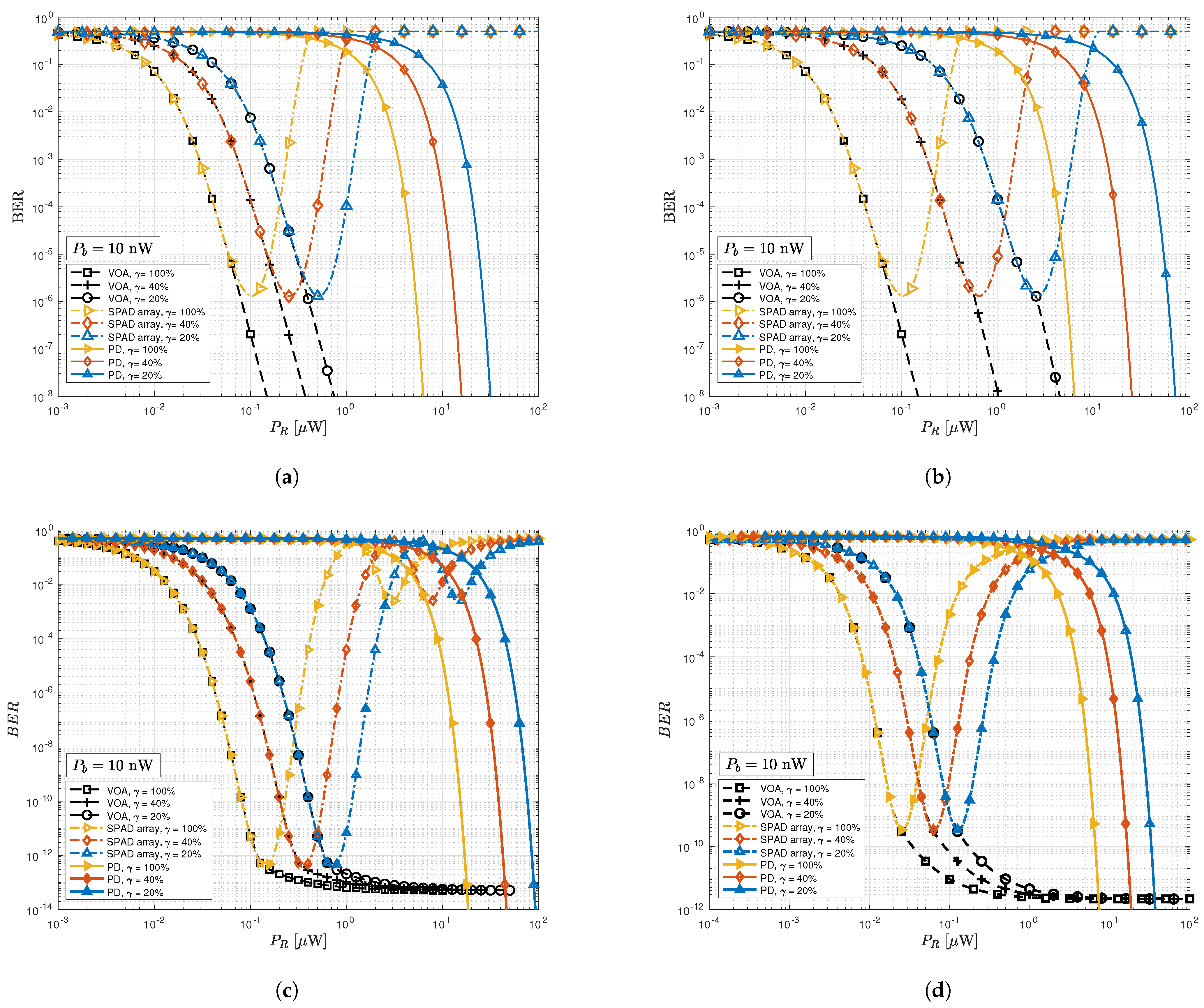
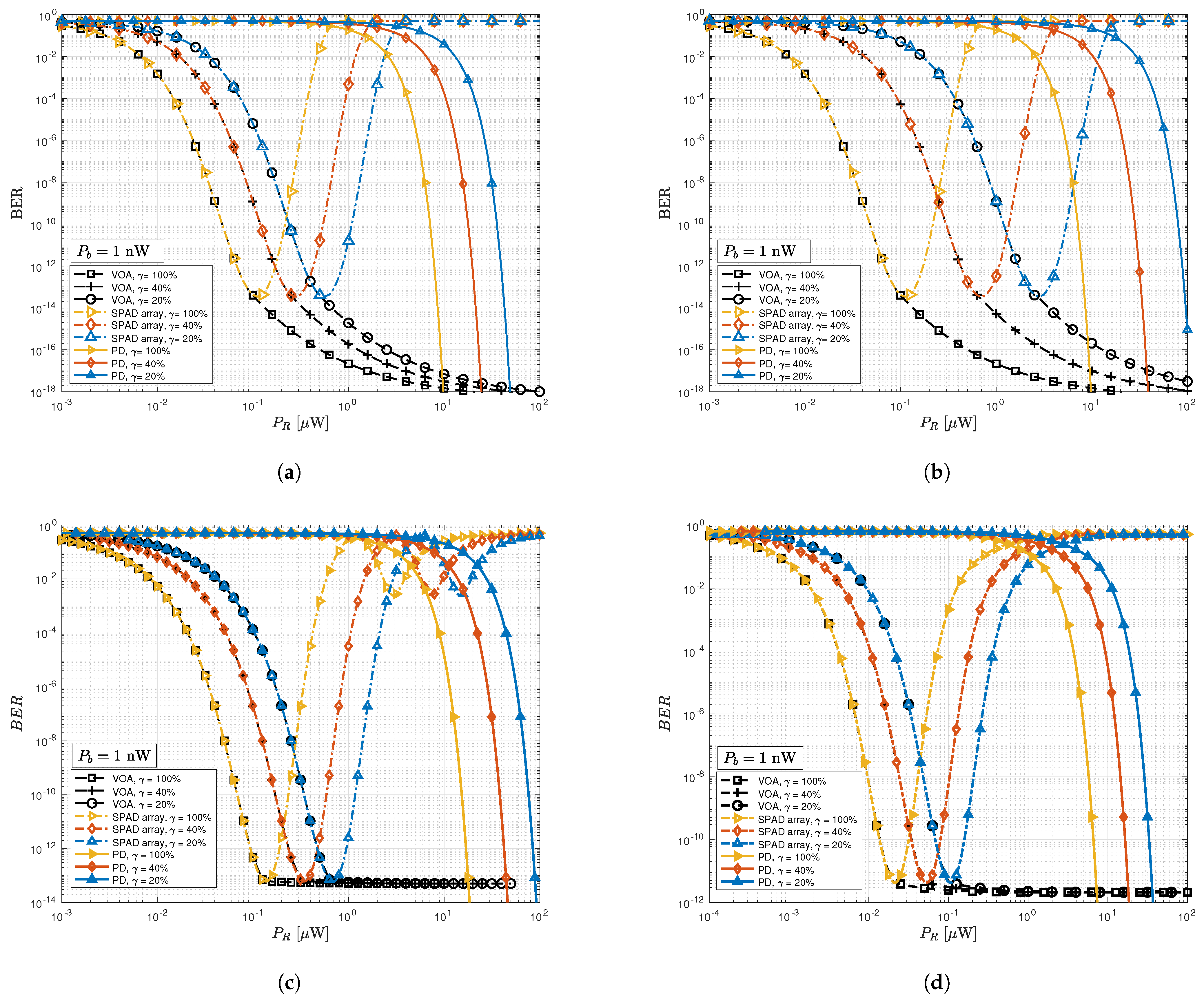
5.1. BER Performance
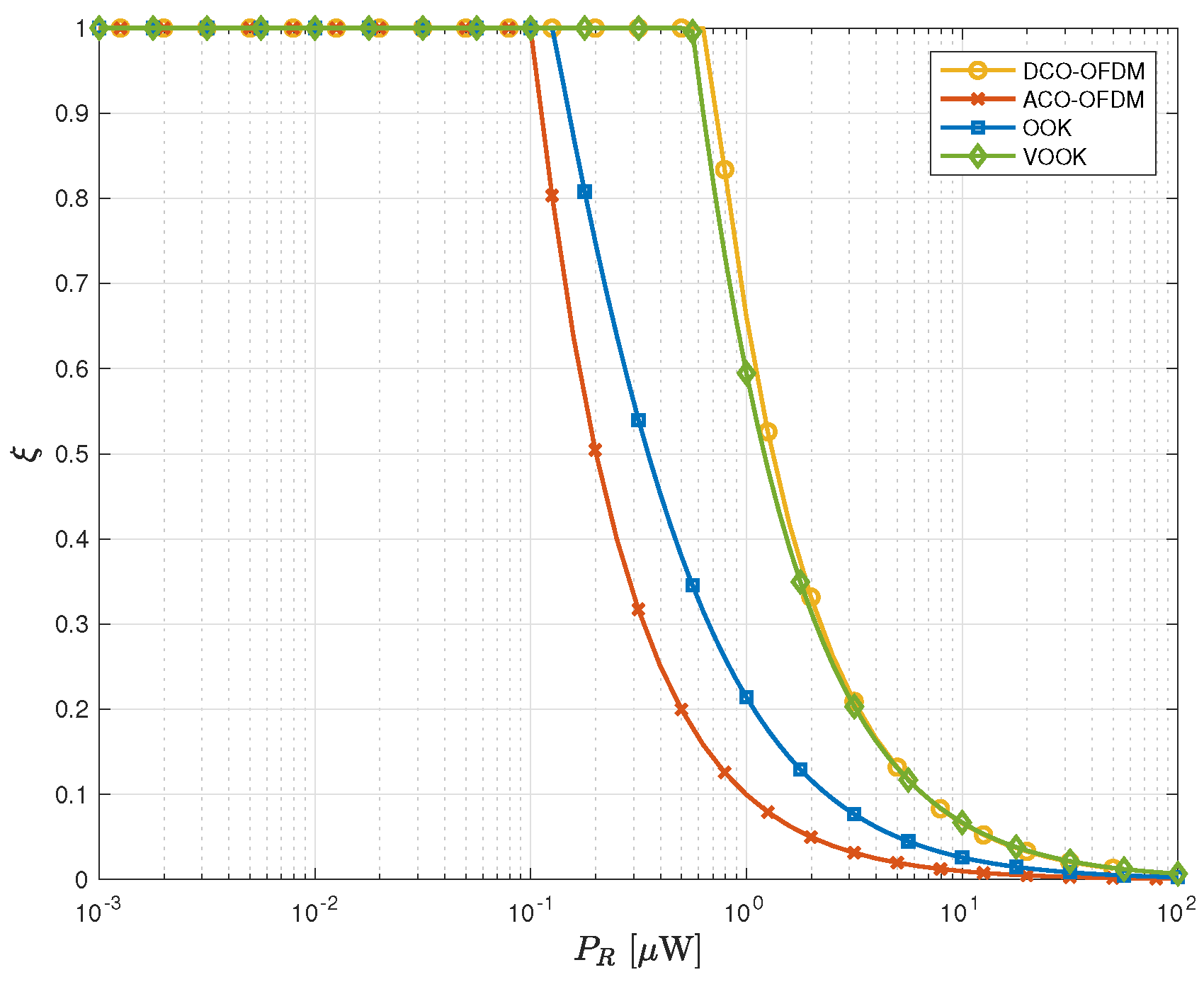
5.2. Spectral Efficiency
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ghassemlooy, Z.; Arnon, S.; Uysal, M.; Xu, Z.; Cheng, J. Emerging Optical Wireless Communications-Advances and Challenges. IEEE J. Sel. Areas Commun. 2015, 33, 1738–1749. [Google Scholar] [CrossRef]
- Elayan, H.; Amin, O.; Shihada, B.; Shubair, R.M.; Alouini, M.S. Terahertz Band: The Last Piece of RF Spectrum Puzzle for Communication Systems. IEEE Open J. Commun. Soc. 2020, 1, 1–32. [Google Scholar] [CrossRef]
- Minotto, A.; Haigh, P.A.; Łukasiewicz, Ł.G.; Lunedei, E.; Gryko, D.T.; Darwazeh, I.; Cacialli, F. Visible light communication with efficient far-red/near-infrared polymer light-emitting diodes. Light Sci. Appl. 2020, 9, 70. [Google Scholar] [CrossRef] [PubMed]
- Haas, H.; Yin, L.; Wang, Y.; Chen, C. What is LiFi? J. Light. Technol. 2016, 34, 1533–1544. [Google Scholar] [CrossRef]
- Yoo, J.H.; Lee, R.; Oh, J.K.; Seo, H.W.; Kim, J.Y.; Kim, H.C.; Jung, S.Y. Demonstration of vehicular visible light communication based on LED headlamp. In Proceedings of the 2013 Fifth International Conference on Ubiquitous and Future Networks (ICUFN), Da Nang, Vietnam, 2–5 July 2013; pp. 465–467. [Google Scholar] [CrossRef]
- Yang, H.; Zhong, W.D.; Chen, C.; Alphones, A.; Du, P. QoS-Driven Optimized Design-Based Integrated Visible Light Communication and Positioning for Indoor IoT Networks. IEEE Internet Things J. 2020, 7, 269–283. [Google Scholar] [CrossRef]
- Shakil Sejan, M.A.; Chung, W.Y. Indoor Fine Particulate Matter Monitoring in a Large Area Using Bidirectional Multihop VLC. IEEE Internet Things J. 2021, 8, 7214–7228. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, M.; Ren, X. Design and Implementation of Wireless Optical Access System for VLC-IoT Networks. J. Light. Technol. 2023, 41, 2369–2380. [Google Scholar] [CrossRef]
- Amran, N.A.; Soltani, M.D.; Yaghoobi, M.; Safari, M. Learning Indoor Environment for Effective LiFi Communications: Signal Detection and Resource Allocation. IEEE Access 2022, 10, 17400–17416. [Google Scholar] [CrossRef]
- Li, Y.; Safari, M.; Henderson, R.; Haas, H. Nonlinear Distortion in SPAD-Based Optical OFDM Systems. In Proceedings of the 2015 IEEE Globecom Workshops (GC Wkshps), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Huang, S.; Safari, M. SPAD-Based Optical Wireless Communication With Signal Pre-Distortion and Noise Normalization. IEEE Trans. Commun. 2022, 70, 2593–2605. [Google Scholar] [CrossRef]
- Fisher, E.; Underwood, I.; Henderson, R. A Reconfigurable Single-Photon-Counting Integrating Receiver for Optical Communications. IEEE J.-Solid-State Circuits 2013, 48, 1638–1650. [Google Scholar] [CrossRef]
- Hadfield, R. Single-photon detectors for optical quantum information applications. Nat. Photonics 2009, 3, 696–705. [Google Scholar] [CrossRef]
- Niclass, C.; Soga, M.; Matsubara, H.; Ogawa, M.; Kagami, M. A 0.18-μm CMOS SoC for a 100-m-Range 10-Frame/s 200 ×96-Pixel Time-of-Flight Depth Sensor. IEEE J.-Solid-State Circuits 2014, 49, 315–330. [Google Scholar] [CrossRef]
- Niclass, C.; Rochas, A.; Besse, P.A.; Charbon, E. Design and characterization of a CMOS 3-D image sensor based on single photon avalanche diodes. IEEE J.-Solid-State Circuits 2005, 40, 1847–1854. [Google Scholar] [CrossRef]
- Tosi, A.; Calandri, N.; Sanzaro, M.; Acerbi, F. Low-Noise, Low-Jitter, High Detection Efficiency InGaAs/InP Single-Photon Avalanche Diode. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 192–197. [Google Scholar] [CrossRef]
- Chick, S.; Coath, R.; Sellahewa, R.; Turchetta, R.; Leitner, T.; Fenigstein, A. Dead Time Compensation in CMOS Single Photon Avalanche Diodes With Active Quenching and External Reset. IEEE Trans. Electron. Devices 2014, 61, 2725–2731. [Google Scholar] [CrossRef]
- Bronzi, D.; Tisa, S.; Villa, F.; Bellisai, S.; Tosi, A.; Zappa, F. Fast Sensing and Quenching of CMOS SPADs for Minimal Afterpulsing Effects. IEEE Photonics Technol. Lett. 2013, 25, 776–779. [Google Scholar] [CrossRef]
- Wayne, M.A.; Bienfang, J.C.; Migdall, A.L. Low-noise photon counting above 100 × 106 counts per second with a high-efficiency reach-through single-photon avalanche diode system. Appl. Phys. Lett. 2021, 118, 134002. [Google Scholar] [CrossRef]
- Xu, H.; Pancheri, L.; Braga, L.H.C.; Betta, G.F.D.; Stoppa, D. Cross-talk characterization of dense single-photon avalanche diode arrays in CMOS 150-nm technology. Opt. Eng. 2016, 55, 067102. [Google Scholar] [CrossRef]
- Lee, K. Modulations for Visible Light Communications With Dimming Control. IEEE Photonics Technol. Lett. 2011, 23, 1136–1138. [Google Scholar] [CrossRef]
- Noshad, M.; Brandt-Pearce, M. Application of Expurgated PPM to Indoor Visible Light Communications—Part I: Single-User Systems. J. Light. Technol. 2014, 32, 875–882. [Google Scholar] [CrossRef]
- Carruthers, J.; Kahn, J. Multiple-subcarrier modulation for nondirected wireless infrared communication. IEEE J. Sel. Areas Commun. 1996, 14, 538–546. [Google Scholar] [CrossRef]
- Armstrong, J.; Lowery, A. Power efficient optical OFDM. Electron. Lett. 2006, 42, 370–372. [Google Scholar] [CrossRef]
- Lee, S.C.J.; Randel, S.; Breyer, F.; Koonen, A.M.J. PAM-DMT for Intensity-Modulated and Direct-Detection Optical Communication Systems. IEEE Photonics Technol. Lett. 2009, 21, 1749–1751. [Google Scholar] [CrossRef]
- Elgala, H.; Little, T.D.C. Reverse polarity optical-OFDM (RPO-OFDM): Dimming compatible OFDM for gigabit VLC links. Opt. Express 2013, 21, 24288–24299. [Google Scholar] [CrossRef]
- Yang, Y.; Zeng, Z.; Cheng, J.; Guo, C. An Enhanced DCO-OFDM Scheme for Dimming Control in Visible Light Communication Systems. IEEE Photonics J. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Bai, R.; Wang, Q.; Wang, Z. Asymmetrically Clipped Absolute Value Optical OFDM for Intensity-Modulated Direct-Detection Systems. J. Light. Technol. 2017, 35, 3680–3691. [Google Scholar] [CrossRef]
- Shafique, T.; Amin, O.; Abdallah, M.; Ansari, I.S.; Alouini, M.S.; Qaraqe, K. Performance Analysis of Single-Photon Avalanche Diode Underwater VLC System Using ARQ. IEEE Photonics J. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Anisimova, E.; Nikulov, D.; Hu, S.; Bourgon, M.; Neumann, S.; Ursin, R.; Jennewein, T.; Makarov, V. A low-noise single-photon detector for long-distance free-space quantum communication. EPJ Quantum Technol. 2021, 8, 23. [Google Scholar] [CrossRef]
- Matthews, W.; Ahmed, Z.; Ali, W.; Collins, S. A 3.45 Gigabits/s SiPM-Based OOK VLC Receiver. IEEE Photonics Technol. Lett. 2021, 33, 487–490. [Google Scholar] [CrossRef]
- Huang, S.; Safari, M. Hybrid SPAD/PD Receiver for Reliable Free-Space Optical Communication. IEEE Open J. Commun. Soc. 2020, 1, 1364–1373. [Google Scholar] [CrossRef]
- Zafar, F.; Karunatilaka, D.; Parthiban, R. Dimming schemes for visible light communication: The state of research. IEEE Wirel. Commun. 2015, 22, 29–35. [Google Scholar] [CrossRef]
- Dimitrov, S.; Sinanovic, S.; Haas, H. Clipping Noise in OFDM-Based Optical Wireless Communication Systems. IEEE Trans. Commun. 2012, 60, 1072–1081. [Google Scholar] [CrossRef]
- Tsonev, D.; Sinanovic, S.; Haas, H. Complete Modeling of Nonlinear Distortion in OFDM-Based Optical Wireless Communication. J. Light. Technol. 2013, 31, 3064–3076. [Google Scholar] [CrossRef]
- Cova, S.; Ghioni, M.; Lacaita, A.; Samori, C.; Zappa, F. Avalanche photodiodes and quenching circuits for single-photon detection. Appl. Opt. 1996, 35, 1956–1976. [Google Scholar] [CrossRef]
- Eisele, A.; Henderson, R.; Schmidtke, B.; Funk, T.; Grant, L.; Richardson, J.; Freude, W. 185 MHz Count Rate, 139 dB Dynamic Range Single-Photon Avalanche Diode with Active Quenching Circuit in 130 nm CMOS Technology. In Proceedings of the International Image Sensor Workshop (IISW’11), Hokkaido, Japan, 8–11 June 2011; pp. 278–280. [Google Scholar]
- Khalighi, M.A.; Akhouayri, H.; Hranilovic, S. Silicon-Photomultiplier-Based Underwater Wireless Optical Communication Using Pulse-Amplitude Modulation. IEEE J. Ocean. Eng. 2020, 45, 1611–1621. [Google Scholar] [CrossRef]
- Omote, K. Dead-time effects in photon counting distributions. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1990, 293, 582–588. [Google Scholar] [CrossRef]
- Yu, D.F.; Fessler, J.A. Mean and variance of single photon counting with deadtime. Phys. Med. Biol. 2000, 45, 2043–2056. [Google Scholar] [CrossRef]
- Kahn, J.; Barry, J. Wireless infrared communications. Proc. IEEE 1997, 85, 265–298. [Google Scholar] [CrossRef]
- Sarbazi, E.; Safari, M.; Haas, H. Photon detection characteristics and error performance of SPAD array optical receivers. In Proceedings of the 2015 4th International Workshop on Optical Wireless Communications (IWOW), Istanbul, Turkey, 7–8 September 2015; pp. 132–136. [Google Scholar] [CrossRef]
- Hijazi, M.; Huang, S.; Safari, M. Adaptive SPAD-based Receiver for Dimmable Visible Light Communication. In Proceedings of the 2022 IEEE Wireless Communications and Networking Conference (WCNC), Austin, TX, USA, 10–13 April 2022; pp. 2685–2690. [Google Scholar] [CrossRef]
- Dimitrov, S.; Haas, H. Information Rate of OFDM-Based Optical Wireless Communication Systems With Nonlinear Distortion. J. Light. Technol. 2013, 31, 918–929. [Google Scholar] [CrossRef]
- Bussgang, J.J.; Bussgang, J.J. Crosscorrelation Functions of Amplitude-Distorted Gaussian Signals; Technical report 216; Research Laboratory of Electronics: Cambridge, MA, USA, 1952. [Google Scholar]
- Randel, S.; Breyer, F.; Lee, S.C.J.; Walewski, J.W. Advanced Modulation Schemes for Short-Range Optical Communications. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1280–1289. [Google Scholar] [CrossRef]
- Huang, S.; Li, Y.; Chen, C.; Soltani, M.D.; Henderson, R.; Safari, M.; Haas, H. Performance Analysis of SPAD-Based Optical Wireless Communication with OFDM. J. Opt. Commun. Netw. 2022, 15, 174–186. [Google Scholar] [CrossRef]
- Huang, S.; Chen, C.; Soltani, M.D.; Henderson, R.; Haas, H.; Safari, M. SPAD-Based Optical Wireless Communication with ACO-OFDM. arXiv 2022, arXiv:2210.14101. [Google Scholar] [CrossRef]
- Safari, M. Efficient optical wireless communication in the presence of signal-dependent noise. In Proceedings of the 2015 IEEE International Conference on Communication Workshop (ICCW), London, UK, 8–12 June 2015; pp. 1387–1391. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.D.; Gao, Q.; Luo, Y.; Gu, D. Exact BEP Analysis for Coherent M-ary PAM and QAM over AWGN and Rayleigh Fading Channels. In Proceedings of the VTC Spring 2008—IEEE Vehicular Technology Conference, Singapore, 11–14 May 2008; pp. 390–394. [Google Scholar] [CrossRef]
- Alonso, O.; Franch, N.; Canals, J.; Arias-Alpízar, K.; de la Serna, E.; Baldrich, E.; Diéguez, A. An internet of things-based intensity and time-resolved fluorescence reader for point-of-care testing. Biosens. Bioelectron. 2020, 154, 112074. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Chitnis, D.; Chun, H.; Rajbhandari, S.; Faulkner, G.; O’Brien, D.; Collins, S. A Comparison of APD- and SPAD-Based Receivers for Visible Light Communications. J. Light. Technol. 2018, 36, 2435–2442. [Google Scholar] [CrossRef]
| (%) | Codeword |
|---|---|
| 100 | |
| 80 | |
| 60 | |
| 40 | |
| 20 | |
| 0 | 0000000000 |
| Symbol | Definition | Value |
|---|---|---|
| Optical wavelength | 450 nm | |
| Background light power | 1 nW and 10 nW | |
| Maximal LED power | 1 mW | |
| Minimal LED power | 0 mW | |
| LED bandwidth | 120 MHz | |
| K | FFT and IFFT size | 1024 |
| ℜ | Photo-diode responsivity | A/W |
| Load-resistor temperature | 297 K | |
| Load resistance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hijazi, M.; Huang, S.; Safari, M. Highly Sensitive SPAD-Based Receiver for Dimming Control in LiFi Networks. Sensors 2023, 23, 4673. https://doi.org/10.3390/s23104673
Hijazi M, Huang S, Safari M. Highly Sensitive SPAD-Based Receiver for Dimming Control in LiFi Networks. Sensors. 2023; 23(10):4673. https://doi.org/10.3390/s23104673
Chicago/Turabian StyleHijazi, Mohamad, Shenjie Huang, and Majid Safari. 2023. "Highly Sensitive SPAD-Based Receiver for Dimming Control in LiFi Networks" Sensors 23, no. 10: 4673. https://doi.org/10.3390/s23104673
APA StyleHijazi, M., Huang, S., & Safari, M. (2023). Highly Sensitive SPAD-Based Receiver for Dimming Control in LiFi Networks. Sensors, 23(10), 4673. https://doi.org/10.3390/s23104673








