Interrogation Method with Temperature Compensation Using Ultra-Short Fiber Bragg Gratings in Silica and Polymer Optical Fibers as Edge Filters
Abstract
:1. Introduction
2. Theoretical Concepts
3. Materials and Methods
3.1. Gratings Inscription Setup
3.2. USFBGs Production in Silica Fiber
3.3. USFBGs Production in PMMA mPOF
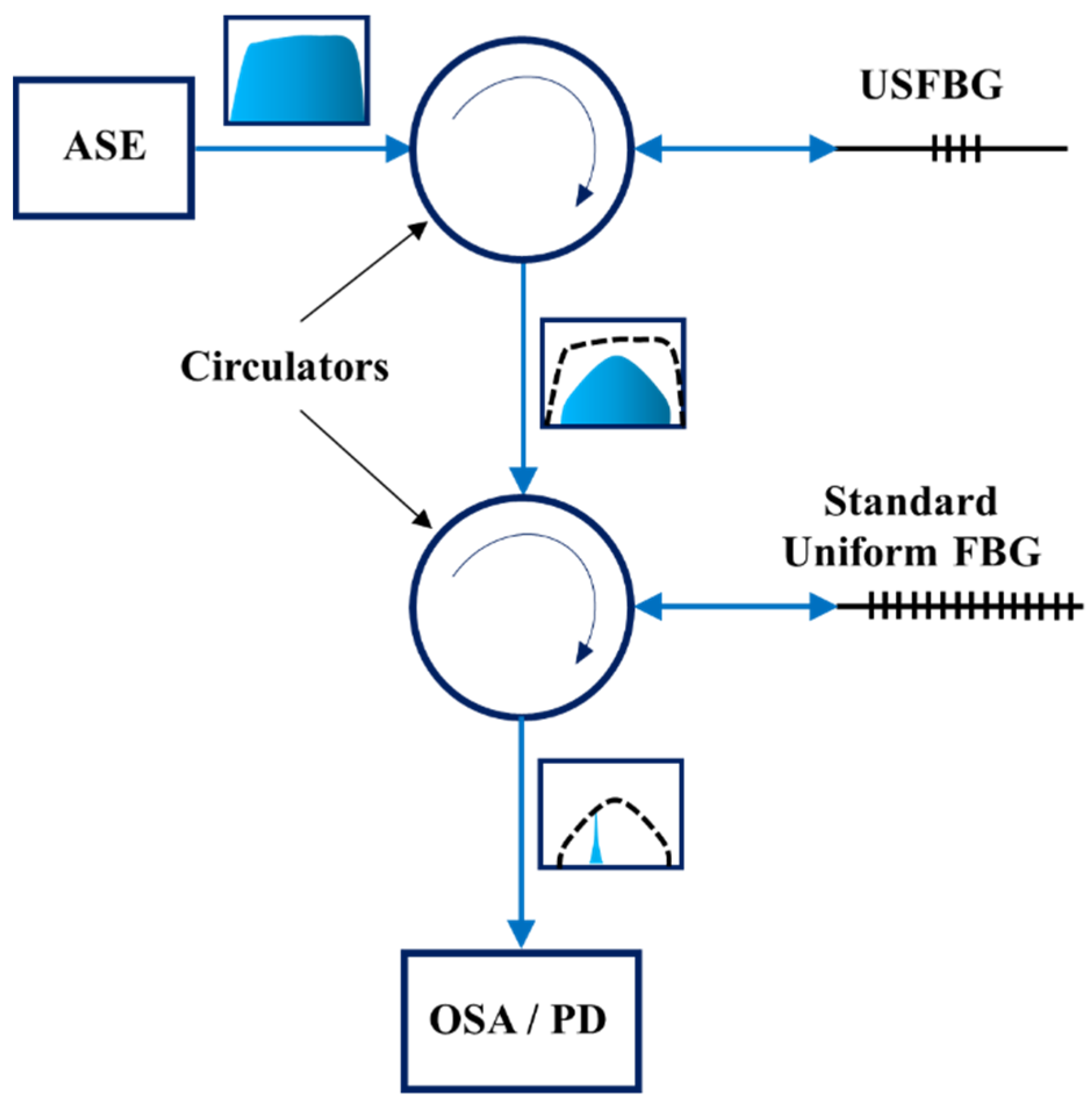
3.4. Sensing Configuration Description
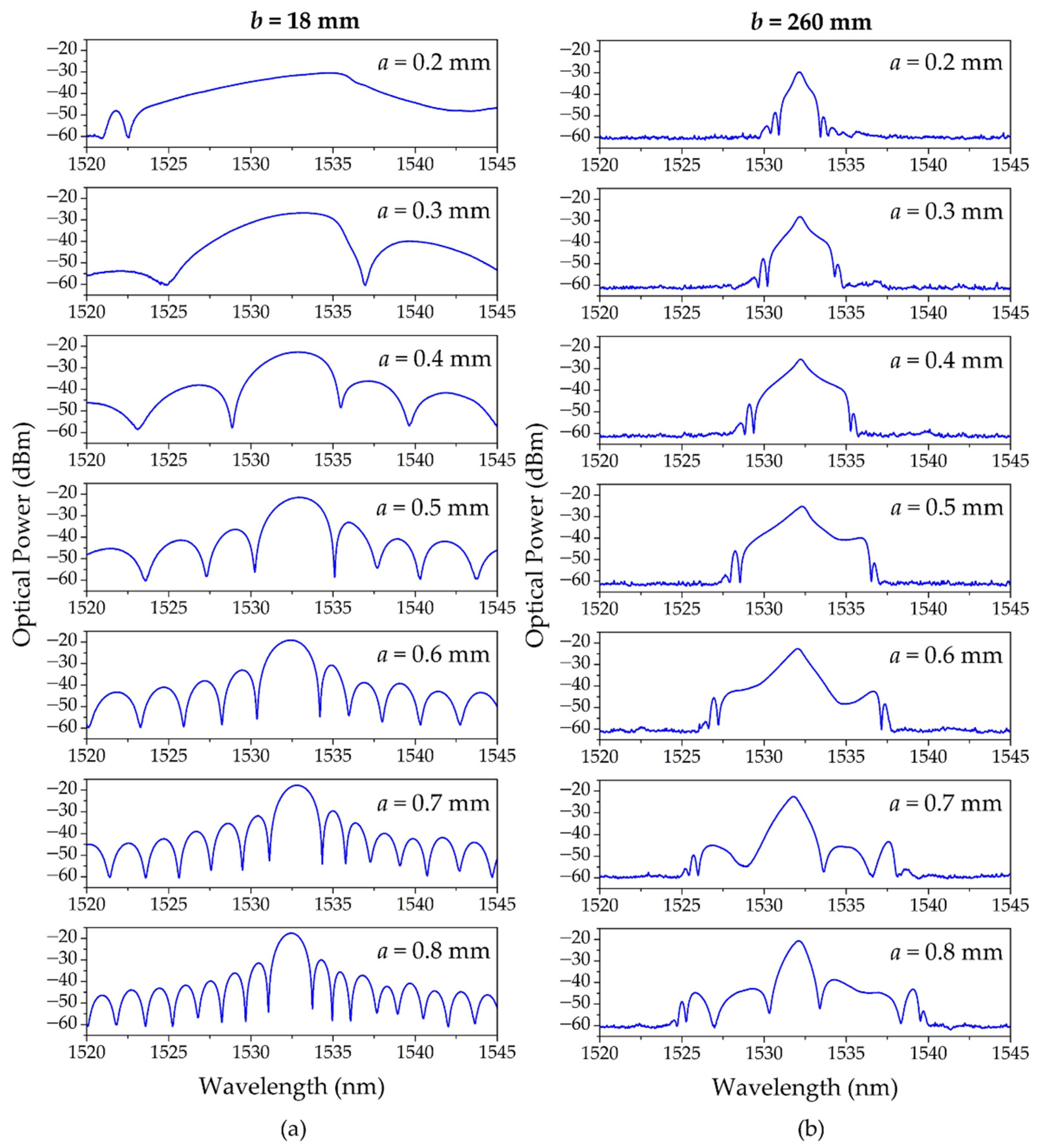
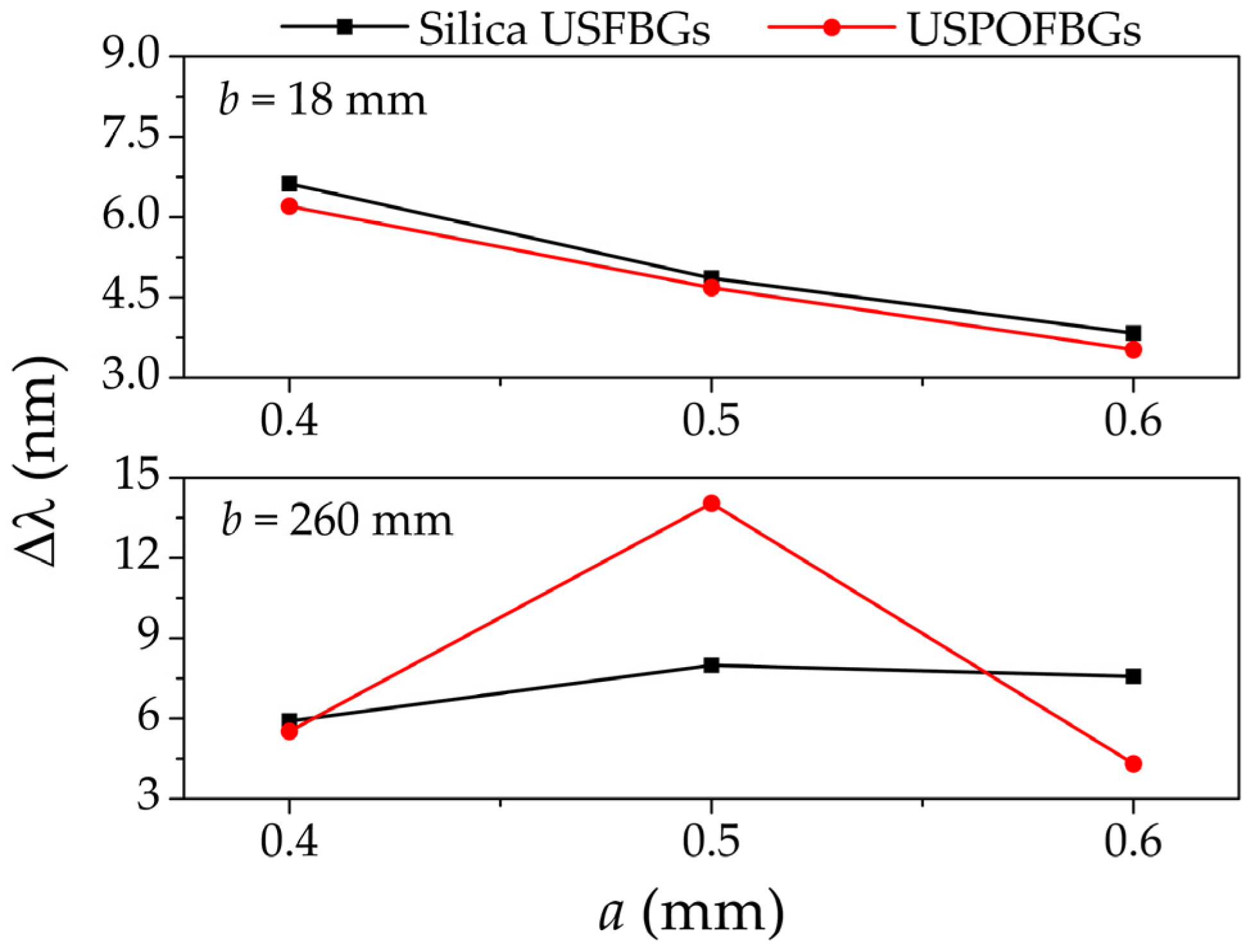
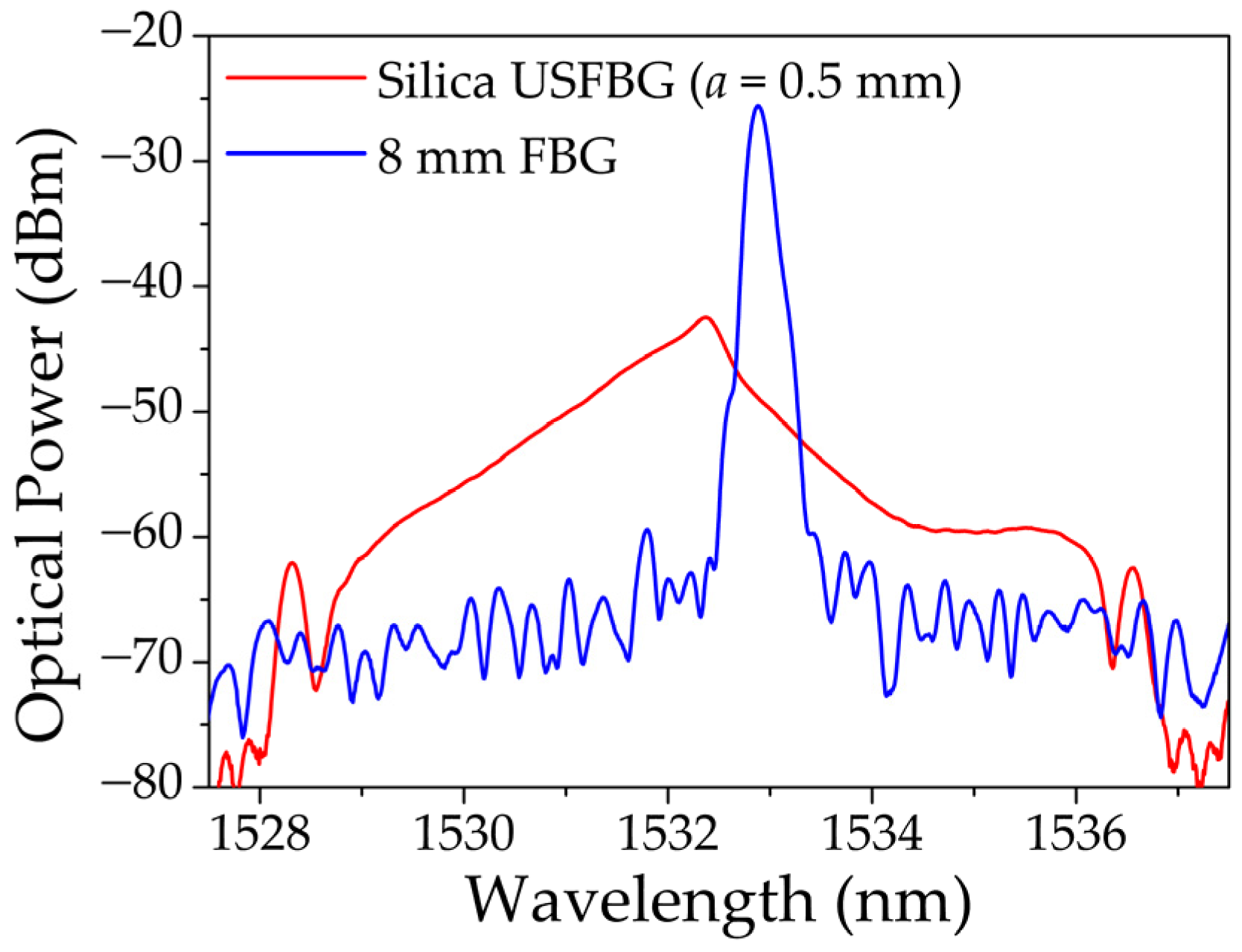
4. Results and Discussion
4.1. Silica USFBGs
4.2. PMMA mPOF USFBGs
4.3. Sensing Characterization
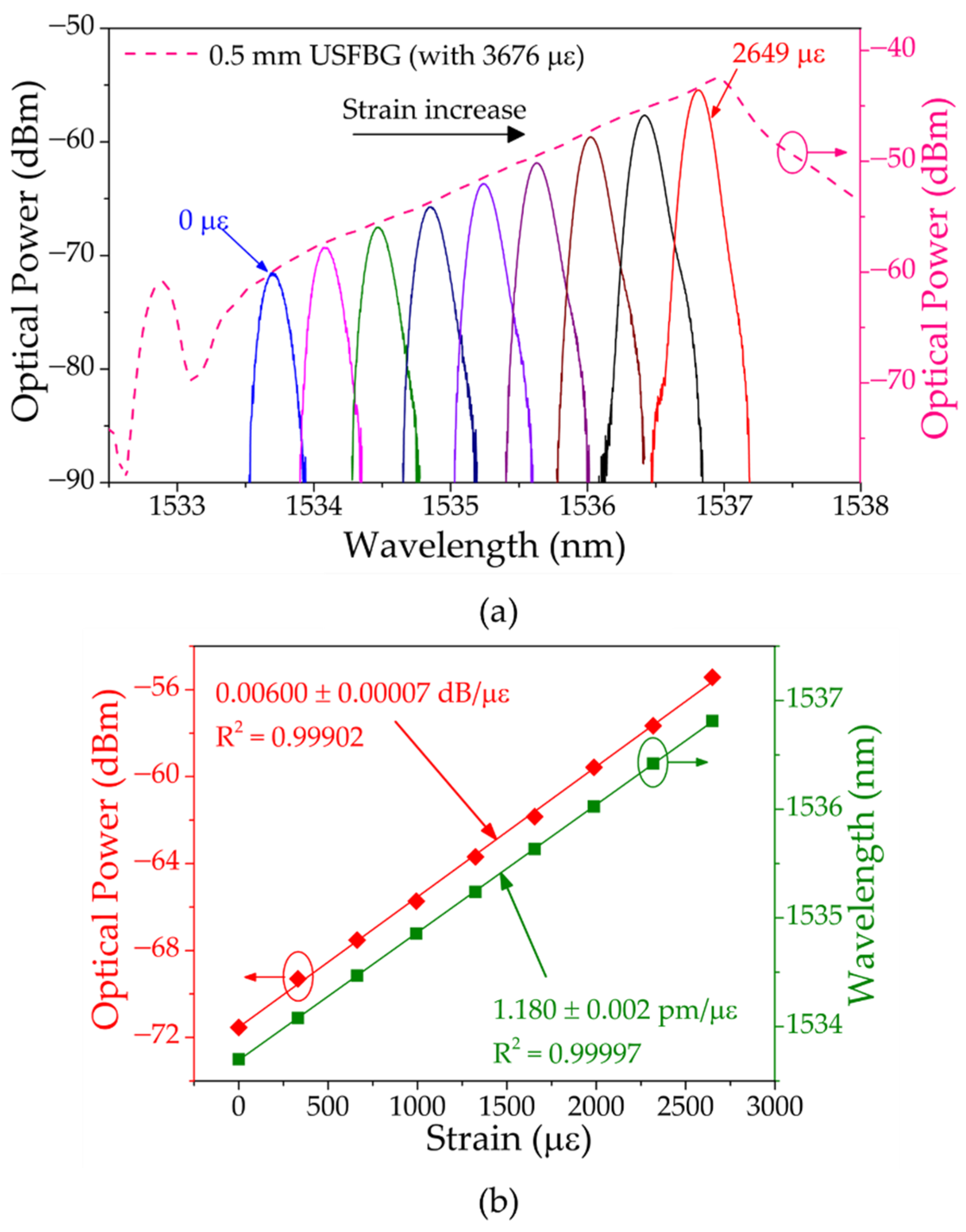
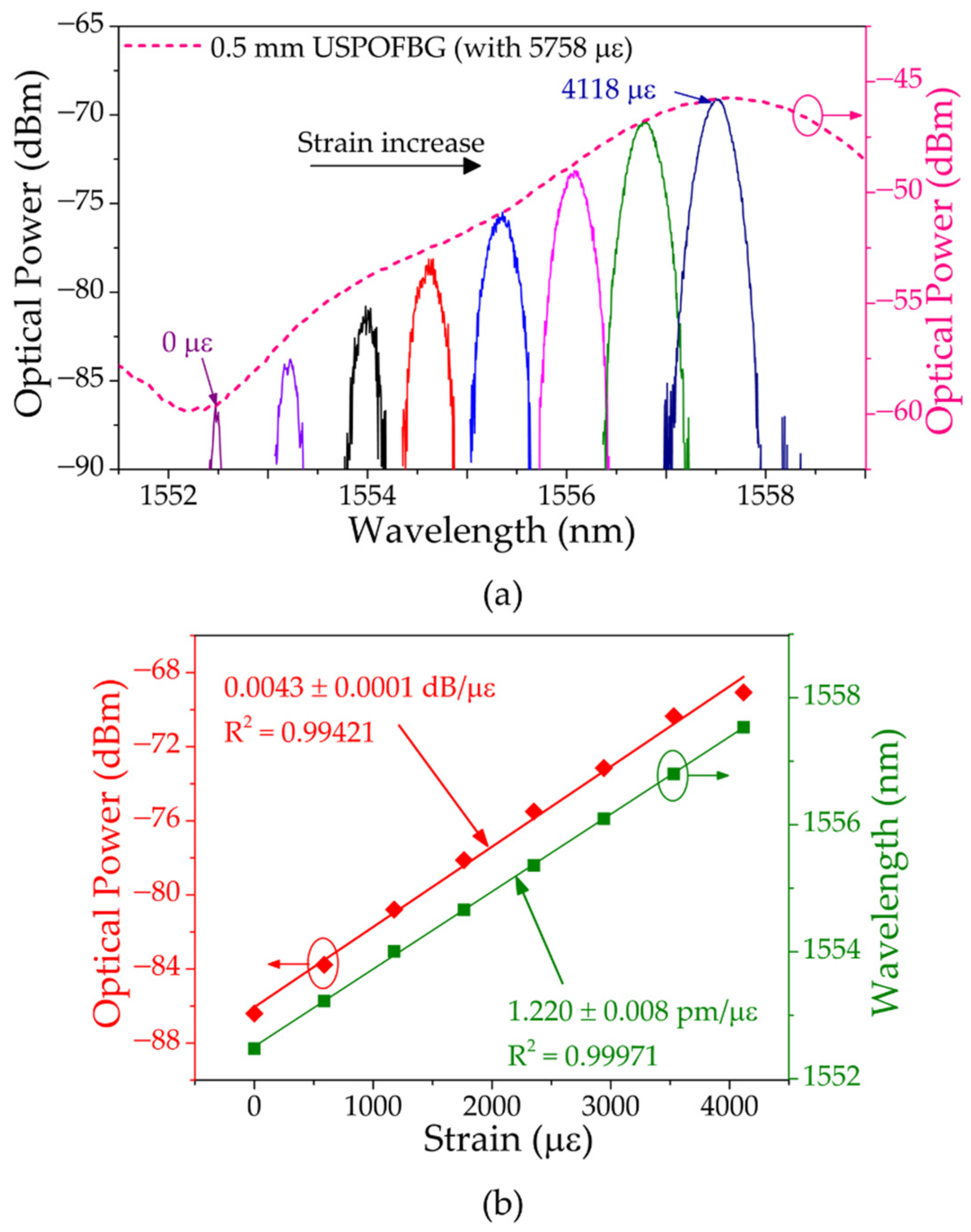
4.3.1. Strain Response
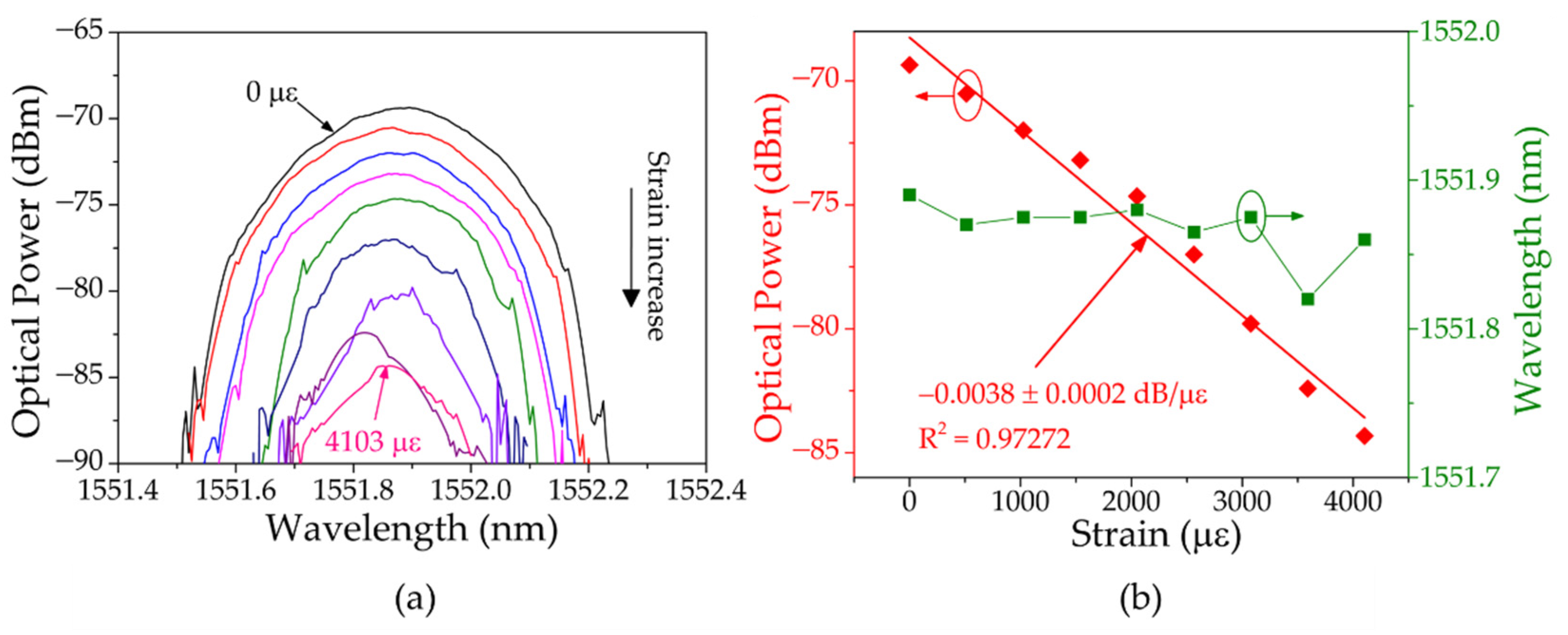
4.3.2. Temperature Response
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hill, K.O.; Fujii, Y.; Johnson, D.C.; Kawasaki, B.S. Photosensitivity in optical fiber waveguides: Application to reflection filter fabrication. Appl. Phys. Lett. 1978, 32, 647–649. [Google Scholar] [CrossRef]
- Meltz, G.; Morey, W.W.; Glenn, W.H. Formation of Bragg gratings in optical fibers by a transverse holographic method. Opt. Lett. 1989, 14, 823–825. [Google Scholar] [CrossRef] [PubMed]
- Hill, O.K.; Malo, B.; Bilodeau, F.; Johnson, D.C.; Albert, J. Bragg grating fabricated in monomode photosensitive optical fiber by UV exposure through a phase mask. Appl. Phys. Lett. 1993, 62, 1035–1037. [Google Scholar] [CrossRef] [Green Version]
- Webb, D.J. Fibre Bragg grating sensors in polymer optical fibres. Meas. Sci. Technol. 2015, 26, 092004. [Google Scholar] [CrossRef]
- Mesquita, E.; Pereira, L.; Theodosiou, A.; Alberto, N.; Melo, J.; Marques, C.; Kalli, K.; André, P.; Varum, H.; Antunes, P. Optical sensors for bond-slip characterization and monitoring of RC structures. Sens. Actuators A Phys. 2018, 280, 332–339. [Google Scholar] [CrossRef]
- Sampath, U.; Kim, D.; Kim, H.; Song, M. Polymer-coated FBG sensor for simultaneous temperature and strain monitoring in composite materials under cryogenic conditions. Appl. Opt. 2018, 57, 492–497. [Google Scholar] [CrossRef]
- James, S.W.; Dockney, M.I.; Tatam, R.P. Simultaneous independent temperature and strain measurement using in-fibre bragg grating sensors. Electron. Lett. 1996, 32, 1133–1134. [Google Scholar] [CrossRef]
- Pereira, D.; Frazão, O.; Santos, J.L. Fiber bragg grating sensing system for simultaneous measurement of salinity and temperature. Opt. Eng. 2004, 43, 299–304. [Google Scholar] [CrossRef]
- Shu, X.; Zhao, D.; Zhang, L.; Bennion, I. Use of dual-grating sensors formed by different types of fiber Bragg gratings for simultaneous temperature and strain measurements. Appl. Opt. 2004, 43, 2006–2012. [Google Scholar] [CrossRef] [Green Version]
- Bhowmik, K.; Peng, G.-D.; Luo, Y.; Ambikairajah, E.; Lovric, V.; Walsh, W.R.; Rajan, G. High intrinsic sensitivity etched polymer fiber bragg grating pair for simultaneous strain and temperature measurements. IEEE Sens. J. 2016, 16, 2453–2459. [Google Scholar] [CrossRef]
- Woyessa, G.; Pedersen, J.K.M.; Fasano, A.; Nielsen, K.; Markos, C.; Rasmussen, H.K.; Bang, O. Zeonex-PMMA microstructured polymer optical FBGs for simultaneous humidity and temperature sensing. Opt. Lett. 2017, 42, 1161–1164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, W.; Stefani, A.; Bang, O. Tunable polymer Fiber Bragg Grating (FBG) inscription: Fabrication of dual-FBG temperature compensated polymer optical fiber strain sensors. IEEE Photonics Technol. Lett. 2012, 24, 401–403. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.B.; Liu, H.Y.; Peng, G.D.; Chu, P.L. Strain and temperature sensor using a combination of polymer and silica fibre bragg gratings. Opt. Commun. 2003, 219, 139–142. [Google Scholar] [CrossRef]
- Patrick, H.J.; Williams, G.M.; Kersey, A.D.; Pedrazzani, J.P.; Vengsarkar, A.M. Hybrid fiber Bragg grating/long period fiber grating sensor for strain/temperature discrimination. IEEE Photonics Technol. Lett. 1996, 8, 1223–1225. [Google Scholar] [CrossRef]
- Liu, Q.; Ran, Z.L.; Rao, Y.J.; Luo, S.C.; Yang, H.Q.; Huang, Y. Highly Integrated FP/FBG Sensor for Simultaneous Measurement of High Temperature and Strain. IEEE Photonics Technol. Lett. 2014, 26, 1715–1717. [Google Scholar] [CrossRef]
- Wu, Q.; Okabe, Y.; Wo, J. Fiber Sensor Based on Interferometer and Bragg Grating for Multiparameter Detection. IEEE Photonics Technol. Lett. 2015, 27, 1345–1348. [Google Scholar] [CrossRef]
- Oliveira, R.; Marques, T.H.R.; Bilro, L.; Nogueira, R.; Cordeiro, C.M.B. Multiparameter POF Sensing Based on Multimode Interference and Fiber Bragg Grating. J. Light. Technol. 2017, 35, 3–9. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Diaz, C.; Marques, C.; Frizera, A.; Pontes, M.J. 3D-Printing Techniques on the development of multiparameter sensors using one FBG. Sensors 2019, 19, 3514. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.K.; Berggren, S.; Zhu, Y.; Han, M.; Huang, H. Simultaneous strain and temperature measurement using a single fiber bragg grating embedded in a composite laminate. Smart Mater. Struct. 2017, 26, 115025. [Google Scholar] [CrossRef]
- Lima, H.F.; Antunes, P.F.; Pinto, J.L.; Nogueira, R.N. Simultaneous Measurement of Strain and Temperature With a Single Fiber Bragg Grating Written in a Tapered Optical Fiber. IEEE Sens. J. 2010, 10, 269–273. [Google Scholar] [CrossRef]
- Pereira, L.; Min, R.; Paixão, T.; Marques, C.; Woyessa, G.; Bang, O.; Pinto, J.L.; Antunes, P.F.C. Compact Dual-Strain Sensitivity Polymer Optical Fiber Grating for Multi-Parameter Sensing. J. Light. Technol. 2021, 39, 2230–2240. [Google Scholar] [CrossRef]
- Min, R.; Pereira, L.; Paixão, T.; Woyessa, G.; Hu, X.; Antunes, P.; Bang, O.; Pinto, J.; Ortega, B.; Marques, C. Chirped POF Bragg grating production utilizing UV cure Adhesive coating for multiparameter sensing. Opt. Fiber Technol. 2021, 65, 102593. [Google Scholar] [CrossRef]
- Rohit, E.S.; Gautam, A.; Singh, R.R.; Kumar, A.; Priye, V. Analysis and Optimization of Edge-Filter Interrogation Scheme for FBG Sensors. In Proceedings of the Frontiers in Optics/Laser Science, Washington, DC, USA, 16–20 September 2018. [Google Scholar]
- Fernández, M.P.; Rossini, L.A.B.; Cruz, J.L.; Andrés, M.V.; Caso, P.A.C. High-speed and high-resolution interrogation of FBG sensors using wavelength-to-time mapping and Gaussian filters. Opt. Express 2019, 27, 36815–36823. [Google Scholar] [CrossRef] [PubMed]
- Díaz, C.A.R.; Leitão, C.; Marques, C.A.; Domingues, M.F.; Alberto, N.; Pontes, M.J.; Frizera, A.; Ribeiro, M.R.N.; André, P.S.B.; Antunes, P.F.C. Low-Cost Interrogation Technique for Dynamic Measurements with FBG-Based Devices. Sensors 2017, 17, 2414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fallon, R.W.; Zhang, L.; Everall, L.A.; Williams, J.A.R.; Bennion, I. All-fibre optical sensing system: Bragg grating sensor interrogated by a long-period grating. Meas. Sci. Technol. 1998, 9, 1969–1973. [Google Scholar] [CrossRef]
- Antunes, P.; Varum, H.; André, P. Uniaxial fiber Bragg grating accelerometer system with temperature and cross axis insensitivity. Measurement 2011, 44, 55–59. [Google Scholar] [CrossRef]
- Cui, J.; Hu, Y.; Feng, K.; Li, J.; Tan, J. FBG Interrogation Method with High Resolution and Response Speed Based on a Reflective-Matched FBG Scheme. Sensors 2015, 15, 16516–16535. [Google Scholar] [CrossRef] [Green Version]
- Dante, A.; Bacurau, R.M.; Spengler, A.W.; Ferreira, E.C.; Dias, J.A.S. A Temperature-Independent Interrogation Technique for FBG Sensors Using Monolithic Multilayer Piezoelectric Actuators. IEEE Trans. Instrum. Meas. 2016, 65, 2476–2484. [Google Scholar] [CrossRef]
- Wu, Q.; Semenova, Y.; Sun, A.; Wang, P.; Farell, G. High resolution temperature insensitive interrogation technique for FBG sensors. Opt. Laser Technol. 2010, 42, 653–656. [Google Scholar] [CrossRef] [Green Version]
- Miao, Y.; Liu, B.; Zhang, W.; Dong, B.; Zhou, H.; Zhao, Q. Dynamic Temperature Compensating Interrogation Technique for Strain Sensors With Tilted Fiber Bragg Gratings. IEEE Photonics Technol. Lett. 2008, 20, 1393–1395. [Google Scholar] [CrossRef]
- Cheng, R.; Xia, L. Interrogation of weak Bragg grating sensors based on dual-wavelength differential detection. Opt. Lett. 2016, 41, 5254–5257. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Xia, L.; Ran, Y.; Rohollahnejad, J.; Zhou, J.; Wen, Y. Interrogation of Ultrashort Bragg Grating Sensors Using Shifted Optical Gaussian Filters. IEEE Photonics Technol. Lett. 2015, 27, 1833–1836. [Google Scholar] [CrossRef]
- Wang, Z.; Shen, F.; Song, L.; Wang, X.; Wang, A. Multiplexed Fiber Fabry-Pérot Interferometer Sensors Based on Ultrashort Bragg Gratings. IEEE Photonics Technol. Lett. 2007, 19, 622–624. [Google Scholar] [CrossRef]
- Li, X.; Sun, Q.; Liu, D.; Liang, R.; Zhang, J.; Wo, J.; Shum, P.P.; Liu, D. Simultaneous wavelength and frequency encoded microstructure based quasi-distributed temperature sensor. Opt. Express 2012, 20, 12076–12084. [Google Scholar] [CrossRef] [PubMed]
- Cheng, R.; Xia, L.; Sima, C.; Ran, Y.; Rohollahnejad, J.; Zhou, J.; Wen, Y.; Yu, C. Ultra-short FBG based distributed sensing using shifted optical Gaussian filters and microwave-network analysis. Opt. Express 2016, 24, 2466–2484. [Google Scholar] [CrossRef]
- Erdogan, T. Fiber Grating Spectra. J. Light. Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef] [Green Version]
- Kashyap, R. Theory of Fiber Bragg Gratings. In Fiber Bragg Gratings, 2nd ed.; Academic Press: San Diego, CA, USA, 2009; pp. 119–187. [Google Scholar]
- Ziemann, O.; Krauser, J.; Zamzow, P.E.; Daum, W. POF Handbook: Optical Short Range Transmission Systems, 2nd ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Large, M.; Poladian, L.; Barton, G.; Eijkelenborg, M.A. Microstructured Polymer Optical Fibres, 1st ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Peters, K. Polymer optical fiber sensors—A review. Smart Mater. Struct. 2011, 20, 013002. [Google Scholar] [CrossRef]
- Woyessa, G.; Fasano, A.; Markos, C. Microstructured polymer optical fibre gratings and sensors. In Handbook of Optical Fibres, 1st ed.; Peng, G.-D., Ed.; Springer: Singapore, 2019; pp. 2037–2078. [Google Scholar]
- Wu, M.C.; Rogowski, R.S. Fabrication of self-apodized short-length fiber Bragg gratings. Appl. Opt. 2003, 42, 5017–5023. [Google Scholar] [CrossRef]
- Wu, M.C.; Rogowski, R.S.; Tedjojuwono, K.K. Fabrication of extremely short length fiber Bragg gratings for sensor applications. In Proceedings of the Sensors, IEEE 2002, Orlando, FL, USA, 12–14 June 2002. [Google Scholar]
- Stefani, A.; Nielsen, K.; Rasmussen, H.K.; Bang, O. Cleaving of TOPAS and PMMA microstructured polymer optical fibers: Core-shift and statistical quality optimization. Opt. Commun. 2012, 285, 1825–1833. [Google Scholar] [CrossRef] [Green Version]
- Kopietz, M.; Lechner, M.D.; Steinmeier, D.G.; Marotz, J.; Franke, H.; Krätzig, E. Light-induced refractive index changes in polymethylmethacrylate (PMMA) blocks. Polym. Photochem. 1984, 5, 109–119. [Google Scholar] [CrossRef]
- Wochnowski, C.; Eldin, M.A.S.; Metev, S. UV-laser-assisted degradation of poly(methylmethacrylate). Polym. Degrad. Stab. 2005, 89, 252–264. [Google Scholar] [CrossRef]
- Eve, S.; Mohr, J. Study of the surface modification of the PMMA by UV-radiation. Procedia Eng. 2009, 1, 237–240. [Google Scholar] [CrossRef] [Green Version]
- Monsores, K.G.C.; Silva, A.O.; Oliveira, S.S.; Rodrigues, J.G.P.; Weber, R.P. Influence of ultraviolet radiation on polymethylmethacrylate (PMMA). J. Mater. Res. Technol. 2019, 8, 3713–3718. [Google Scholar] [CrossRef]









| a (mm) | b = 18 mm | b = 260 mm | ||
|---|---|---|---|---|
| NF | 3-dB Bandwidth (nm) | NF | 3-dB Bandwidth (nm) | |
| 0.2 | 2.089 | 5.195 | 0.145 | 0.580 |
| 0.3 | 4.699 | 4.375 | 0.325 | 0.645 |
| 0.4 | 8.354 | 2.965 | 0.578 | 0.720 |
| 0.5 | 13.054 | 2.170 | 0.904 | 0.935 |
| 0.6 | 18.797 | 1.725 | 1.301 | 0.855 |
| 0.7 | 25.585 | 1.430 | 1.771 | 0.810 |
| 0.8 | 33.417 | 1.195 | 2.314 | 0.785 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, L.; Min, R.; Woyessa, G.; Bang, O.; Marques, C.; Varum, H.; Antunes, P. Interrogation Method with Temperature Compensation Using Ultra-Short Fiber Bragg Gratings in Silica and Polymer Optical Fibers as Edge Filters. Sensors 2023, 23, 23. https://doi.org/10.3390/s23010023
Pereira L, Min R, Woyessa G, Bang O, Marques C, Varum H, Antunes P. Interrogation Method with Temperature Compensation Using Ultra-Short Fiber Bragg Gratings in Silica and Polymer Optical Fibers as Edge Filters. Sensors. 2023; 23(1):23. https://doi.org/10.3390/s23010023
Chicago/Turabian StylePereira, Luís, Rui Min, Getinet Woyessa, Ole Bang, Carlos Marques, Humberto Varum, and Paulo Antunes. 2023. "Interrogation Method with Temperature Compensation Using Ultra-Short Fiber Bragg Gratings in Silica and Polymer Optical Fibers as Edge Filters" Sensors 23, no. 1: 23. https://doi.org/10.3390/s23010023
APA StylePereira, L., Min, R., Woyessa, G., Bang, O., Marques, C., Varum, H., & Antunes, P. (2023). Interrogation Method with Temperature Compensation Using Ultra-Short Fiber Bragg Gratings in Silica and Polymer Optical Fibers as Edge Filters. Sensors, 23(1), 23. https://doi.org/10.3390/s23010023












