Research on Dual-Frequency Electromagnetic False Alarm Interference Effect of a Typical Radar
Abstract
:1. Introduction
2. Imaging Mechanism of False Alarm Signal
2.1. Time-Frequency Decoupling Angle Analysis
2.2. Analysis of Signal Processing Angle of Receiver
3. Interference Mechanism of Dual Frequency Electromagnetic False Alarm
3.1. Imaging Mechanism of Dual Frequency Non-Intermodulation False Alarm Signal
3.2. Imaging Mechanism of Second Order Intermodulation False Alarm Signal
4. Electromagnetic False Alarm Interference Effect Test and Results
4.1. Pre-Test Preparation
4.2. Electromagnetic Sensitive Frequency Band Test and Result Analysis of False Alarm Interference
4.3. Characteristic Test Results and Analysis of Dual-Frequency Non-Intermodulation False Alarm Interference
4.4. Test Results and Analysis of Radar Second-Order Intermodulation False Alarm Interference
5. Conclusions
- The electromagnetic sensitive bandwidth of the false alarm signal is about ±75 MHz, which is smaller than its working bandwidth.
- The position of the single-frequency electromagnetic false alarm interference signal of the tested radar is affected by the local oscillator phase, and the position shows random performance.
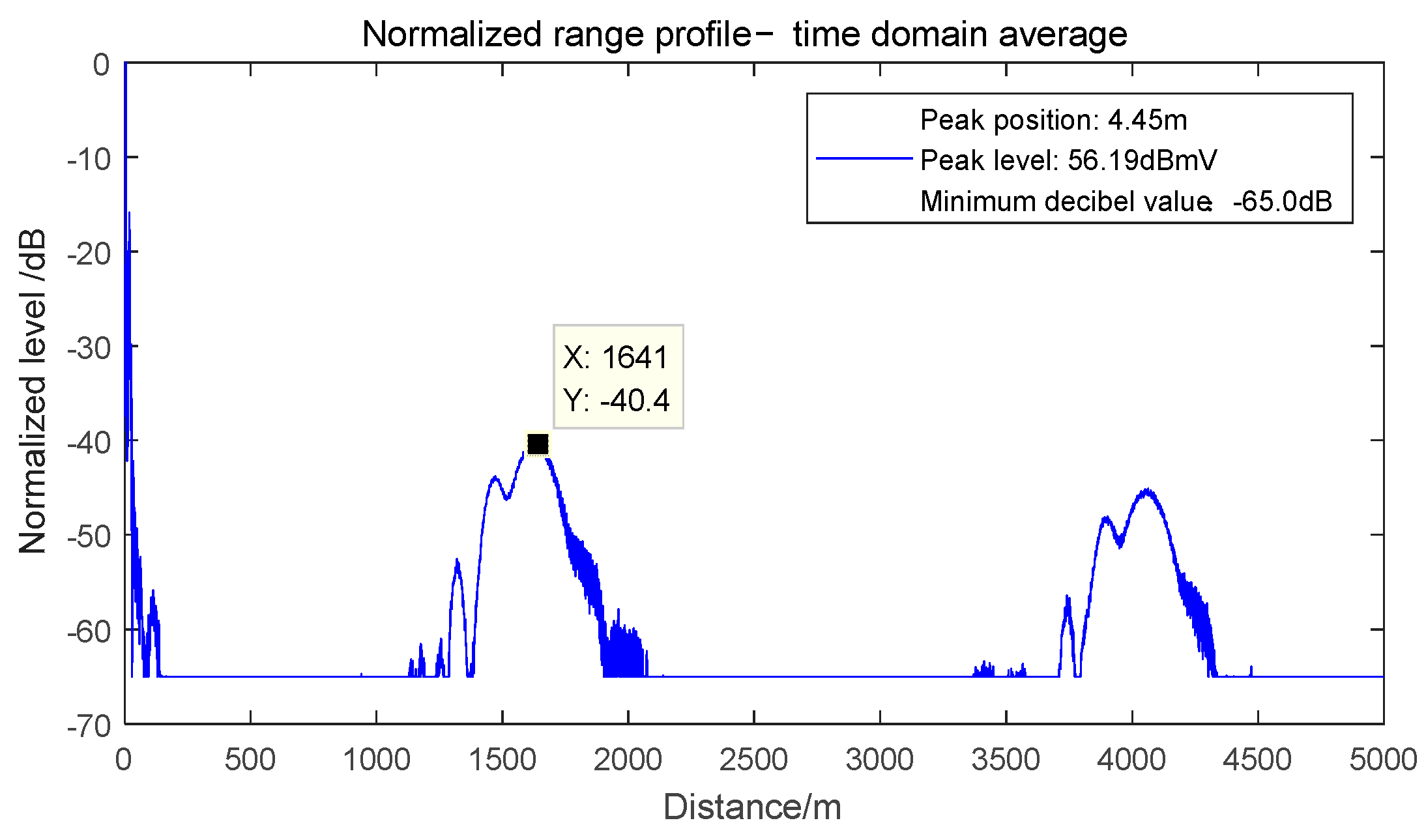
- Without considering the intermodulation, the dual-frequency electromagnetic interference makes the test radar generate two false alarm signals with wide waveform. The dual frequency non-intermodulation false alarm signal distance difference is related to the interference frequency difference. Under the condition of tight constraints, the frequency offset of dual-frequency interference can be substituted into the test radar according to Formula (26) to obtain the distance difference between the two false alarm targets of −2925 m and 4575 m, and the test results are consistent with the theory.
- The second-order intermodulation false alarm signal is ‘spike’ shaped; its position is related to the frequency offset of dual-frequency interference, the relative error is less than 0.1, and the test data is stable.
6. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zou, L.; Wang, X.T.; Wang, W. Ku-Band High Performance Monopulse Microstrip Array Antenna Based on Waveguide Coupling Slot Array Feeding Network. Radioengineering 2020, 29, 59–66. [Google Scholar] [CrossRef]
- Tang, Z.Y.; Yu, C.R.; Deng, Y.K. Evaluation of Deceptive Jamming Effect on SAR Based on Visual Consistency. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 11, 12246–12262. [Google Scholar] [CrossRef]
- Du, X.; Wei, G.H.; Zhao, K. Study on Electromagnetic Sensitivity of Ku-band Stepped Frequency Radar. In Proceedings of the 13th Global Symposium on Millimeter-Waves & Terahertz (GSMM), Nanjing, China, 23–26 May 2021; Volume 5, pp. 1–3. [Google Scholar]
- Wang, L.; Shen, X.; Zhou, B. Review on cognition of complex electromagnetic environment. Aerosp. Electron. Warf. 2020, 36, 1–6. [Google Scholar]
- Du, X.; Wei, G.H.; Ren, S.Z.; Zhao, K. Analysis of Blocking Effect of Single Frequency Continuous Wave Electromagnetic Radiation in Swept Frequency Radar. Syst. Eng. Electron. 2020, 42, 2742–2746. [Google Scholar]
- Zhao, K.; Wei, G. Dual frequency blocking interference laws with high order nonlinear distortion. Syst. Eng. Electron. 2021, 32, 61–66. [Google Scholar]
- Zhao, K.; Wei, G.H.; Wang, Y.P. Prediction model of in-band blocking interference under the electromagnetic radiation of dual-frequency continuous wave. Int. J. Antennasand Propag. 2020, 2, 1–8. [Google Scholar] [CrossRef]
- Du, X. Research on Continuous Wave Electromagnetic Effect in Swept Frequency Radar. Math. Probl. Eng. 2021, 2021, 4862451. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Liu, Z.; Li, G.; Xiong, S.; Luo, Y. An Anti-Jamming Method against Interrupted Sampling Repeater Jamming Based on Compressed Sensing. Sensors 2022, 22, 2239. [Google Scholar] [CrossRef] [PubMed]
- Olivier, K.; Cilliers, J.E. Design and performance of wideband DRFM for radar test and evaluation. Electron. Lett. 2011, 47, 824–825. [Google Scholar] [CrossRef] [Green Version]
- Hill, P.C.; Truffert, V. Statistical processing techniques for detecting DRFM repeat-jamradar signals. Signal Process. Tech. Electron. Warf. IEE Colloq. 1992, 2, 1–6. [Google Scholar]
- Weng, Y.X. Simultaneous Multi-target Interference Technology Based on Digital Reconfigurability. J. Caeit 2019, 14, 1270–1275. [Google Scholar]
- Lu, G.; Tang, B. Deception jammer rejection using pulse diversity in joint slow/fast-time domain. J. Chin. Inst. Eng. 2013, 36, 405–410. [Google Scholar] [CrossRef]
- Li, W.; Huang, F.; Yang, H.M. Efficiency Analysis of adar Noise Jamming and Multiple. J. CAEIT 2013, 8, 403–406. [Google Scholar]
- Li, D.; Long, T. Target’s Redundance Removed Algorithms of Step Frequency Radar. Acta Electron. Sin. 2000, 28, 60–64. [Google Scholar]
- Long, T.; Li, D.; Wu, Q. Design Methods for Step Frequency Waveform and the Target Pick-up Algorithm. Syst. Eng. Electron. 2001, 23, 26–31. [Google Scholar]
- Lu, X.F.; Wei, G.H.; Pan, X.D. A directional coupler based injection device aimed at radiated susceptibility verification of antenna systems against HIRF. J. Electromagn. Waves Appl. 2013, 27, 1351–1364. [Google Scholar] [CrossRef]
- Lu, X.F.; Wei, G.H.; Pan, X.D. A double differential-mode current injection method based on directional couplers for HIRF verification testing of interconnected systems. J. Electromagn. Waves Appl. 2014, 28, 346–359. [Google Scholar] [CrossRef]
- Xu, T.; Chen, Y.Z.; Wang, Y.M.; Zhao, M. Research on In-band Continuous Wave Electromagnetic Interference Effect of UAV Data Link. Trans. Beijing Inst. Technol. 2021, 41, 1084–1094. [Google Scholar]
- Fan, Y.; Cheng, E.; Wei, M.; Zhang, Q.; Chen, Y. Effects of CW interference on the BDS receiver and analysis on the coupling path of electromagnetic energy. IEEE Access 2019, 7, 155885–155893. [Google Scholar] [CrossRef]
- Du, X.; Wei, G.; Zhao, H. Research on the Continuous Wave Electromagnetic Environmental Effect of Radar Equipment. J. Army Eng. Univ. PLA 2022, 1, 1–8. [Google Scholar]
- GJB8848-2016; Electromagnetic Environmental Effects Test Methods for Systems. Equipment Development Department of the Central Military Commission: Beijing, China, 2016.
- GJB 151B-2013; Electromagnetic Emission and Susceptibility Requirements and Measurements for Military Equipment and Subsystems. Military Standard Press of General Equipment Department: Beijing, China, 2013.




| False Alarm Signal Characteristics | Single-Frequency | Dual-Frequency | |
|---|---|---|---|
| Non-Intermodulation | Second-Order Intermodulation | ||
| Waveform | Spike type | Waveform broadening | Spike type |
| Position | Rj1′ | ΔR = Rj1′ − Rj2′ | Rjm2 |
| Ej/(dBV/m) | R0/m | R1/m | R2/m | R3/m | R4/m |
|---|---|---|---|---|---|
| −19 | 2676 | 4404 | 3913 | 1594 | 1829 |
| −16 | 1428 | 2510 | 3463 | 2226 | 1371 |
| −12 | 2906 | 2455 | 2003 | 4103 | 2081 |
| −9 | 626 | 3988 | 3645 | 4573 | 1432 |
| −6 | 1085 | 1823 | 1738 | 546.7 | 4544 |
| −3 | 3149 | 2287 | 4198 | 2533 | 4376 |
| 0 | 503 | 999.1 | 3187 | 3505 | 1258 |
| 3 | 1368 | 932 | 4924 | 1654 | 2137 |
| 6 | 2550 | 263 | 4908 | 3587 | 710.9 |
| 9 | 2708 | 1834 | 1131 | 1767 | 1924 |
| 12 | 1172 | 437 | 4075 | 1822 | 431.9 |
| Serial Number | R1′/m | R2′/m | ΔR/m |
|---|---|---|---|
| 1 | 4771 | 1876 | −2895 |
| 2 | 4963 | 2083 | −2880 |
| 3 | 3694 | 775 | −2919 |
| 4 | 4182 | 1277 | −2905 |
| 5 | 4318 | 1423 | −2895 |
| 6 | 328 | 4923 | 4595 |
| 7 | 3017 | 128 | −2889 |
| 8 | 3535 | 640 | −2895 |
| 9 | 3179 | 278 | −2901 |
| 10 | 4081 | 1176 | −2905 |
| Serial Number | R1′/m | R2′/m | ΔR/m |
|---|---|---|---|
| 1 | 3647 | 701 | −2946 |
| 2 | 4761 | 1815 | −2946 |
| 3 | 3668 | 746 | −2922 |
| 4 | 4818 | 1888 | −2930 |
| 5 | 3886 | 943 | −2943 |
| 6 | 230 | 4791 | 4561 |
| 7 | 4263 | 1320 | −2943 |
| 8 | 4795 | 1877 | −2918 |
| 9 | 4293 | 1378 | −2915 |
| 10 | 3336 | 381 | −2955 |
| Δfj2/kHz | Rjm2/m | Rav/m | ||||
|---|---|---|---|---|---|---|
| 1.65 | 1270 | 1270 | 1270 | 1271 | 1269 | 1270 |
| 3.60 | 2718 | 2722 | 2721 | 2719 | 2723 | 2721 |
| 6.60 | 4936 | 4932 | 4928 | 4927 | 4920 | 4929 |
| 14.51 | 4113 | 4115 | 4118 | 4120 | 4120 | 4117 |
| 18.51 | 1150 | 1152 | 1153 | 1155 | 1153 | 1153 |
| 20.57 | 350 | 349 | 349 | 349 | 348 | 349 |
| 23.50 | 2596 | 2596 | 2593 | 2594 | 2592 | 2594 |
| 26.38 | 4839 | 4835 | 4834 | 4833 | 4833 | 4835 |
| 58.38 | 1210 | 1210 | 1211 | 1211 | 1211 | 1211 |
| 84.38 | 3280 | 3278 | 3278 | 3278 | 3277 | 3278 |
| Δfj2/kHz | Rav/m | Rc′/m | Rt′/m |
|---|---|---|---|
| 1.65 | 1270 | 1238 | 1238 |
| 3.60 | 2721 | 2700 | 2700 |
| 6.60 | 4929 | 4950 | 4950 |
| 14.51 | 4117 | 10,883 | 4118 |
| 18.51 | 1153 | 13,883 | 1118 |
| 20.57 | 349 | 15,360 | 360 |
| 23.50 | 2594 | 17,625 | 2625 |
| 26.38 | 4835 | 19,785 | 4785 |
| 58.38 | 1211 | 43,785 | 1215 |
| 84.38 | 3278 | 63,285 | 3285 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Wei, G.; Zhao, K.; Zhao, H.; Lyu, X. Research on Dual-Frequency Electromagnetic False Alarm Interference Effect of a Typical Radar. Sensors 2022, 22, 3574. https://doi.org/10.3390/s22093574
Du X, Wei G, Zhao K, Zhao H, Lyu X. Research on Dual-Frequency Electromagnetic False Alarm Interference Effect of a Typical Radar. Sensors. 2022; 22(9):3574. https://doi.org/10.3390/s22093574
Chicago/Turabian StyleDu, Xue, Guanghui Wei, Kai Zhao, Hongze Zhao, and Xuxu Lyu. 2022. "Research on Dual-Frequency Electromagnetic False Alarm Interference Effect of a Typical Radar" Sensors 22, no. 9: 3574. https://doi.org/10.3390/s22093574
APA StyleDu, X., Wei, G., Zhao, K., Zhao, H., & Lyu, X. (2022). Research on Dual-Frequency Electromagnetic False Alarm Interference Effect of a Typical Radar. Sensors, 22(9), 3574. https://doi.org/10.3390/s22093574







