Super-Resolution and Feature Extraction for Ocean Bathymetric Maps Using Sparse Coding
Abstract
:1. Introduction
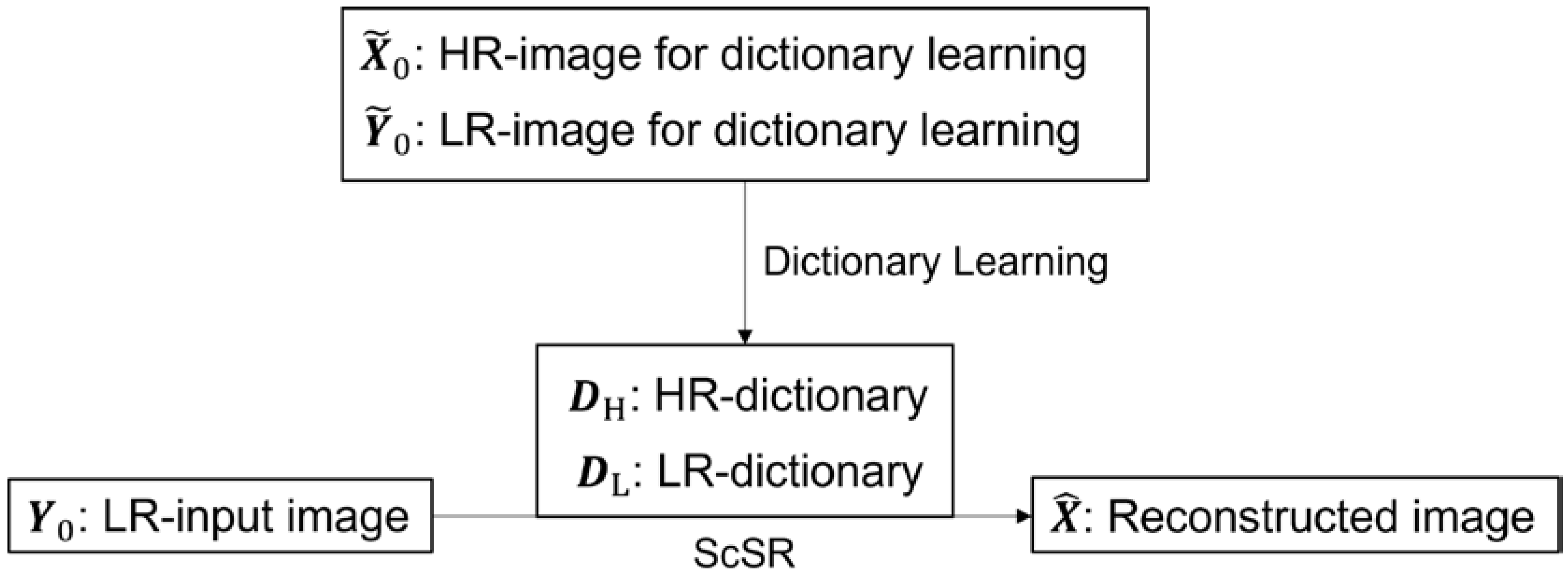
2. Method
2.1. Dictionary Learning
2.2. Sparse-Coding and Reconstruction
| Algorithm 1. Reconstruction algorithm for sparse coding super-resolution (ScSR). |
| 0: Learn HR and LR dictionaries, and 1: Input: dictionaries, and , edge components of an LR image 2: Split an LR image into high- and low-frequency components, and . 3: Extract LR patches from the edge components of . 4: 5: Generate the HR patch: . 6: Up-sample the high-frequency component of the LR image, 7: Superpose the adjacent patches and add : 8: Find which satisfies the constraint: . 9: Up-sample the low-frequency component of the LR image: . 10: Take a summation of reconstructed component and up-sampled component : . 11: Output: SR image . |
3. Data and Implementation
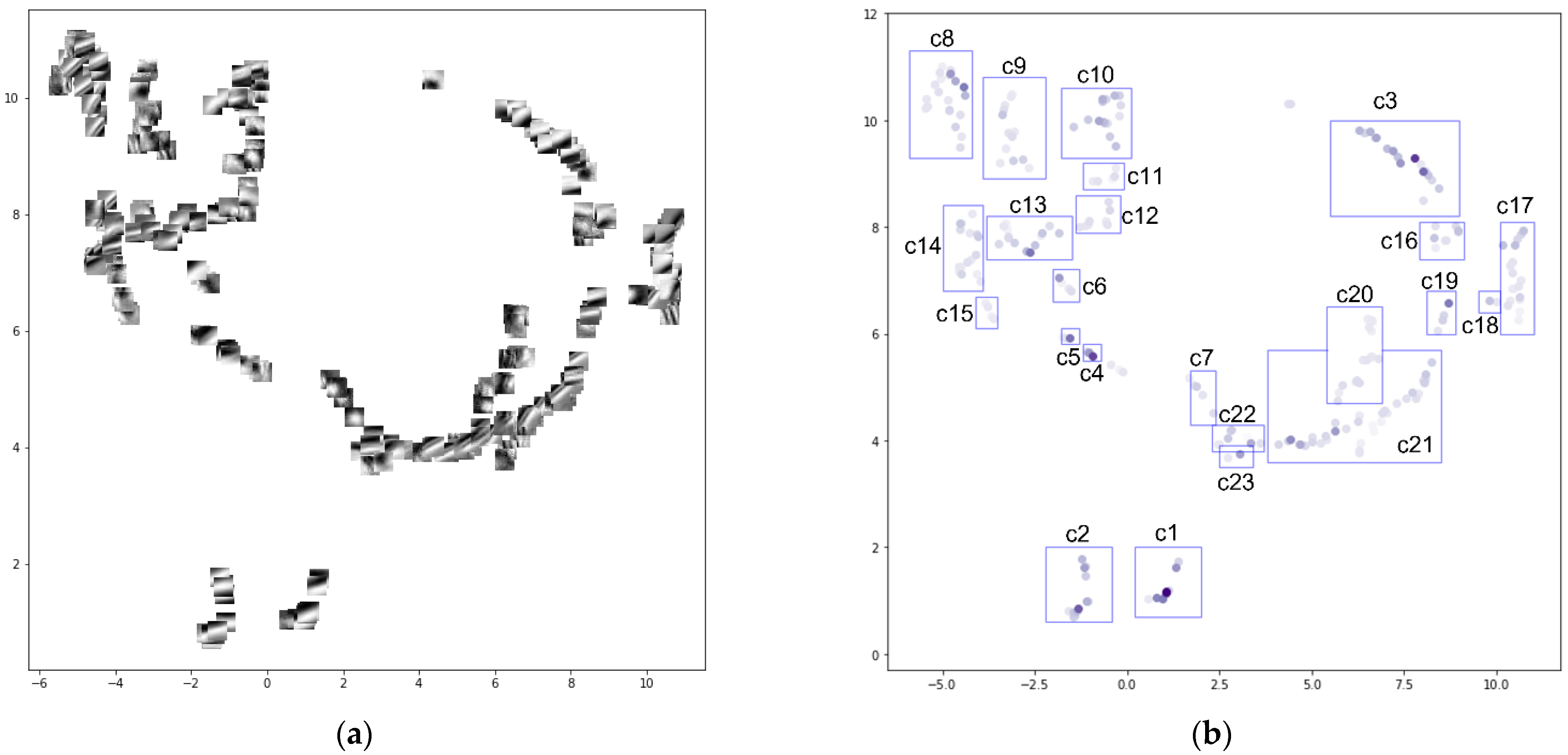
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- GEBCO_2021. Available online: https://www.gebco.net/data_and_products/gridded_bathymetry_data/ (accessed on 10 February 2022).
- Mayer, L.; Jakobsson, M.; Allen, G.; Dorschel, B.; Falconer, R.; Ferrini, V.; Lamarche, G.; Snaith, H.; Weatherall, P. The Nippon Foundation-GEBCO Seabed 2030 Project: The Quest to See the World’s Oceans Completely Mapped by 2030. Geosciences 2018, 8, 63. [Google Scholar] [CrossRef] [Green Version]
- DeSET Project. Available online: https://deset-en.lne.st/ (accessed on 10 February 2022).
- Yang, J.; Wright, J.; Huang, T.; Ma, Y. Image Super-Resolution as Sparse Representation of Raw Image Patches. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Kim, K.I.; Kwon, Y. Single-Image Super-Resolution Using Sparse Regression and Natural Image Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1127–1133. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Dong, W.; Zhang, L.; Shi, G.; Wu, X. Image Deblurring and Super-Resolution by Adaptive Sparse Domain Selection and Adaptive Regularization. IEEE Trans. Image Process. 2011, 20, 1838–1857. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, D.; Timofte, R.; van Gool, L. Jointly Optimized Regressors for Image Super-Resolution. Computer Graphics Forum. 2015, 34, 95–104. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image Denoising via Sparse and Redundant Representations over Learned Dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- Kato, T.; Hino, H.; Murata, N. Multi-Frame Image Super Resolution Based on Sparse Coding. Neural Netw. 2015, 66, 64–78. [Google Scholar] [CrossRef]
- Kato, T.; Hino, H.; Murata, N. Doubly Sparse Structure in Image Super Resolution. In Proceedings of the IEEE International Workshop on Machine Learning for Signal Processing, MLSP, Vietri sul Mare, Italy, 13–16 September 2016; IEEE Computer Society: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Kato, T.; Hino, H.; Murata, N. Double Sparsity for Multi-Frame Super Resolution. Neurocomputing 2017, 240, 115–126. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Rivenson, Y.; Jin, Y.; Wei, Z.; Gao, R.; Günaydın, H.; Bentolila, L.A.; Kural, C.; Ozcan, A. Deep Learning Enables Cross-Modality Super-Resolution in Fluorescence Microscopy. Nat. Methods 2019, 16, 103–110. [Google Scholar] [CrossRef]
- Liu, T.; de Haan, K.; Rivenson, Y.; Wei, Z.; Zeng, X.; Zhang, Y.; Ozcan, A. Deep Learning-Based Super-Resolution in Coherent Imaging Systems. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ito, K. Efficient Bathymetry by Learning-Based Image Super Resolution. Fish. Eng. 2019, 56, 47–50. [Google Scholar]
- Sonogashira, M.; Shonai, M.; Iiyama, M. High-Resolution Bathymetry by Deep-Learning-Based Image Superresolution. PLoS ONE 2020, 15, e0235487. [Google Scholar] [CrossRef] [PubMed]
- Hidaka, M.; Matsuoka, D.; Kuwatani, T.; Kaneko, J.; Kasaya, T.; Kido, Y.; Ishikawa, Y.; Kikawa, E. Super-resolution for Ocean Bathymetric Maps Using Deep Learning Approaches: A Comparison and Validation. Geoinformatics 2021, 32, 3–13. [Google Scholar] [CrossRef]
- Nock, K.; Bonanno, D.; Elmore, P.; Smith, L.; Ferrini, V.; Petry, F. Applying Single-Image Super-Resolution to Enhancment of Deep-Water Bathymetry. Heliyon 2019, 5, e02570. [Google Scholar] [CrossRef]
- Belthangady, C.; Royer, L.A. Applications, Promises, and Pitfalls of Deep Learning for Fluorescence Image Reconstruction. Nat. Methods 2019, 16, 1215–1225. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Moore, E.H. On the Reciprocal of the General Algebraic Matrix. Bull. Am. Math. Soc. 1920, 26, 394–395. [Google Scholar]
- Penrose, R. A Generalized Inverse for Matrices. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1955; Volume 51, pp. 406–413. [Google Scholar] [CrossRef] [Green Version]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal Matching Pursuit: Recursive Function Approximation with Applications to Wavelet Decomposition. In Proceedings of the Conference Record of the Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 1–3 November 1993; IEEE: Piscataway, NJ, USA, 1993; Volume 1, pp. 40–44. [Google Scholar]
- Kasaya, T.; Machiyama, H.; Kitada, K.; Nakamura, K. Trial Exploration for Hydrothermal Activity Using Acoustic Measurements at the North Iheya Knoll. Geochem. J. 2015, 49, 597–602. [Google Scholar] [CrossRef]
- Nakamura, K.; Kawagucci, S.; Kitada, K.; Kumagai, H.; Takai, K.; Okino, K. Water Column Imaging with Multibeam Echo-Sounding in the Mid-Okinawa Trough: Implications for Distribution of Deep-Sea Hydrothermal Vent Sites and the Cause of Acoustic Water Column Anomaly. Geochem. J. 2015, 49, 579–596. [Google Scholar] [CrossRef] [Green Version]
- Ishibashi, J.I.; Ikegami, F.; Tsuji, T.; Urabe, T. Okinawa Trough: Hydrothermal Activity in the Okinawa Trough Back-Arc Basin: Geological Background and Hydrothermal Mineralization. In Subseafloor Biosphere Linked to Hydrothermal Systems: TAIGA Concept; Springer: Tokyo, Japan, 2015; pp. 337–360. ISBN 9784431548652. [Google Scholar]
- Kasaya, T.; Kaneko, J.; Iwamoto, H. Observation and confirmation based on survey protocol for seafloor massive sulfide deposits using acoustic survey technique and self-potential surveys. BUTSURI-TANSA 2020, 73, 42–52. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv preprint 2018, arXiv:1802.03426. [Google Scholar]
- Elad, M. Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]








| Reconstruct Area | 0_0 | 0_1 | 0_2 | 0_3 | 1_0 | 1_1 | 1_2 | 1_3 | Mean |
|---|---|---|---|---|---|---|---|---|---|
| ScSR | 0.803 | 1.183 | 1.156 | 1.853 | 1.193 | 1.259 | 1.414 | 1.723 | 1.323 |
| bicubic | 1.066 | 1.458 | 1.713 | 2.501 | 1.794 | 1.789 | 2.293 | 2.524 | 1.892 |
| ScSR/bicubic | 0.753 | 0.812 | 0.675 | 0.741 | 0.665 | 0.703 | 0.617 | 0.682 | 0.709 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yutani, T.; Yono, O.; Kuwatani, T.; Matsuoka, D.; Kaneko, J.; Hidaka, M.; Kasaya, T.; Kido, Y.; Ishikawa, Y.; Ueki, T.; et al. Super-Resolution and Feature Extraction for Ocean Bathymetric Maps Using Sparse Coding. Sensors 2022, 22, 3198. https://doi.org/10.3390/s22093198
Yutani T, Yono O, Kuwatani T, Matsuoka D, Kaneko J, Hidaka M, Kasaya T, Kido Y, Ishikawa Y, Ueki T, et al. Super-Resolution and Feature Extraction for Ocean Bathymetric Maps Using Sparse Coding. Sensors. 2022; 22(9):3198. https://doi.org/10.3390/s22093198
Chicago/Turabian StyleYutani, Taku, Oak Yono, Tatsu Kuwatani, Daisuke Matsuoka, Junji Kaneko, Mitsuko Hidaka, Takafumi Kasaya, Yukari Kido, Yoichi Ishikawa, Toshiaki Ueki, and et al. 2022. "Super-Resolution and Feature Extraction for Ocean Bathymetric Maps Using Sparse Coding" Sensors 22, no. 9: 3198. https://doi.org/10.3390/s22093198
APA StyleYutani, T., Yono, O., Kuwatani, T., Matsuoka, D., Kaneko, J., Hidaka, M., Kasaya, T., Kido, Y., Ishikawa, Y., Ueki, T., & Kikawa, E. (2022). Super-Resolution and Feature Extraction for Ocean Bathymetric Maps Using Sparse Coding. Sensors, 22(9), 3198. https://doi.org/10.3390/s22093198






