Abstract
Objective: Non-invasive estimation of serum potassium, , and calcium, , can help to prevent life-threatening ventricular arrhythmias in patients with advanced renal disease, but current methods for estimation of electrolyte levels have limitations. We aimed to develop new markers based on the morphology of the QRS complex of the electrocardiogram (ECG). Methods: ECG recordings from 29 patients undergoing hemodialysis (HD) were processed. Mean warped QRS complexes were computed in two-minute windows at the start of an HD session, at the end of each HD hour and 48 h after it. We quantified QRS width, amplitude and the proposed QRS morphology-based markers that were computed by warping techniques. Reference and were determined from blood samples acquired at the time points where the markers were estimated. Linear regression models were used to estimate electrolyte levels from the QRS markers individually and in combination with T wave morphology markers. Leave-one-out cross-validation was used to assess the performance of the estimators. Results: All markers, except for QRS width, strongly correlated with (median Pearson correlation coefficients, r, ranging from 0.81 to 0.87) and with (r ranging from 0.61 to 0.76). QRS morphology markers showed very low sensitivity to heart rate (HR). Actual and estimated serum electrolyte levels differed, on average, by less than 0.035 mM (relative error of 0.018) for and 0.010 mM (relative error of 0.004) for when patient-specific multivariable estimators combining QRS and T wave markers were used. Conclusion: QRS morphological markers allow non-invasive estimation of and with low sensitivity to HR. The estimation performance is improved when multivariable models, including T wave markers, are considered. Significance: Markers based on the QRS complex of the ECG could contribute to non-invasive monitoring of serum electrolyte levels and arrhythmia risk prediction in patients with renal disease.
1. Introduction
Patients with chronic kidney disease (CKD), particularly at the most severe stages, are at high risk for life-threatening arrhythmias and sudden cardiac death [1,2,3,4], and millions of them die every year due to lack of access to affordable treatment. Between five and seven million end-stage renal disease (ESRD) patients need renal replacement therapy worldwide [5]. ESRD patients undergoing hemodialysis (HD) frequently have serum electrolyte levels outside normal ranges, which can increase the mortality risk [1,2,3,4].
Non-invasive monitoring of electrolyte levels can be useful for risk prediction and the triggering of early warnings. Electrocardiogram (ECG) ventricular depolarization and repolarization are, in particular, altered by variations in serum potassium () and calcium () [1,2,6,7,8]. ECG markers have been proposed for the continuous monitoring of these two electrolyte levels, which could facilitate timely therapies for ESRD patients.
Most ECG-based estimators of and , such as those based on the QT interval or on T wave amplitude, slope and slope-to-amplitude ratio, are based exclusively on ventricular repolarization and commonly refer to a specific time interval, to an amplitude at a given time point or to a particular portion of the T wave [9,10,11,12,13,14,15]. Although the QT interval has long been used to monitor CKD patients during HD [16,17,18,19,20,21], contradictory findings have been presented, with many studies reporting QT prolongation [18,19,21,22,23] and others showing QT shortening or no effects during HD [24,25]. Other recent studies have investigated changes in markers of sympathetic activity-related T wave instability during HD [26] and in model-based descriptors of T wave morphology in the interdialytic interval [27]. These studies, however, have not established a tight correlation between the proposed markers and , thus limiting their possibilities for ambulatory monitoring. In previous studies, we used nonlinear dynamics and time-warping techniques to characterize changes in the whole T wave at varying and in patients and simulated ECGs [28,29,30,31,32,33]. We found a strong relationship between and T wave linear and nonlinear features.
Assessment of ventricular depolarization for serum electrolyte estimation has been less explored. Similarly to QT studies, research on QRS complex duration has rendered inconsistent results, with some works reporting widened QRS complexes [1,34] and others reporting narrowed QRS complexes at high [2,35]. Other works have assessed the time voltage area, amplitude and sine wave shape of the QRS complex, but limitations in terms of their significance or their dependence on blood volume have been acknowledged [14,36,37,38]. None of these studies have, however, quantitatively characterized overall variations in the morphology of the QRS complex during HD. We hypothesized that QRS morphology could provide complementary information on and , in addition to that provided by repolarization.
The aim of this study was to quantify changes in the QRS amplitude, duration and morphology, the latter both in the time and amplitude domains, at varying , and heart rate (HR) in ESRD patients. Univariable and multivariable electrolyte estimators, including novel QRS morphological markers in combination with already proposed T wave markers [28,29,30,39], were devised, and the contribution of depolarization analysis to and monitoring was assessed.
2. Materials
Forty-eight-hour 12-lead ECGs with 3.75 V resolution and a sampling frequency of 1 kHz (H12+, Mortara Instruments, Milwaukee, WI, USA) were acquired from 29 ESRD patients of Hospital Clínico Universitario de Zaragoza (HCUZ). ECG acquisition started 5 minutes before HD and lasted for 48 hours (Figure 1, bottom blue line), with patients in the supine position. Concurrently, six blood samples were taken during and after the HD session: the first one at HD onset and the next three samples every hour during the HD session (Figure 1, to in red). The fifth blood sample () was obtained at the end of the HD (minute 215 or 245, depending on the patient) while the sixth blood sample was taken after 48 h (), immediately before the next HD session. Serum and were measured at those six time points, as shown in Figure 1 [28,29,30], using a Cobas 6000 c501 analyzer (Roche Diagnostics, Germany) by an indirect ion selective electrode method. We defined another time point for ECG analysis, corresponding to a segment taken two minutes before the end of HD (minute 213 or 243, depending on the patient), which we denoted by . The value at was assumed to be the same as at , as the time difference between these two segments was just two minutes. All patients signed informed consent. The study protocol was approved by the Research Ethics Committee of Aragón (CEICA, ref. PI18/003, 25 January 2018). Table 1 shows the population characteristics.
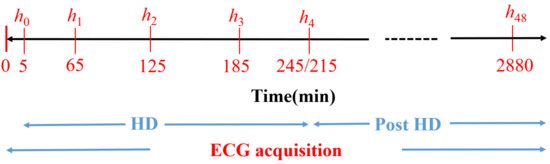
Figure 1.
Diagram of the study protocol. to are the time points (in minutes) for blood sample extraction. Reproduced with permission from Bukhari et al., Computers in Biology and Medicine; published by Elsevier, 2022.

Table 1.
Characteristics of the study population. Values are expressed as number (%) for categorical variables and median (interquartile range, IQR) for continuous variables. Reproduced with permission from Bukhari et al., Computers in Biology and Medicine; published by Elsevier, 2022.
3. Methods
A flow chart showing all the stages of the signal processing starting with 12-lead ECG pre-processing, followed by principal component analysis (PCA) transformation, computation of mean warped QRS (MWQRS) complexes and QRS morphological markers, and finishing with the estimation of and is shown in Figure 2.
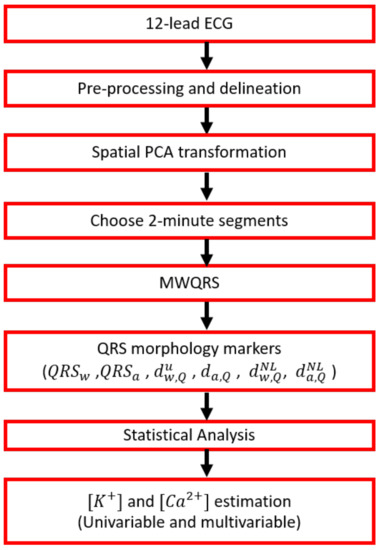
Figure 2.
Flow chart showing the ECG processing steps performed in this study, from the collection of raw ECGs to the estimation of and .
3.1. ECG Pre-Processing
A band-pass filter (0.5 to 40 Hz) was used to remove baseline wander, muscular noise and powerline interference from measured ECG signals. A wavelet-based single-lead delineation method [40] was used for QRS detection and wave delineation. Spatial principal component (PC) analysis was performed on the complete ECG of the eight independent leads [41] to enhance QRS complex energy. PCs were obtained from the eigenvectors of the inter-lead auto-correlation matrix of QRS complexes extracted from a stable (in terms of HR) 10-min ECG segment at the end of the HD session to emphasize the QRS complex components. This segment corresponded to the time when the patient was discharged from hospital with restored serum and . The ECG recording from each time point during and after HD was subsequently projected onto the direction of the first PC. The QRS complexes from each time point in the first PC were delineated [40] to mark their onsets, peaks and ends.
3.2. QRS Descriptors
3.2.1. Computation of Mean Warped QRS Complexes
MWQRS complexes, which are optimal representative averages in both temporal and amplitude domains, were calculated from the two-minute ECG segment at the end of each HD hour following the methodology described in [39]. The two-minute ECG segment was short enough to maintain the assumption of stability for both electrolyte and HR values [30]. Only QRS complexes in each analyzed two-minute window that presented the dominant polarity were considered for MWQRS calculation, with the polarity defined as:
where represents the QRS complex under analysis. An average of of QRS complexes in each analyzed two-minute ECG segment were found to present such dominant polarity (see Figure S1 in Supplementary Material). An initial MWQRS was computed after aligning the QRS complexes having the dominant polarity with respect to their gravity center so that the calculated MWQRS was not affected by potential outlier QRS complex polarities and morphologies [39]. Outliers, defined as those QRS complexes having a Spearman’s correlation coefficient with an initial MWQRS lower than , were rejected. The final MWQRS was computed from the remaining QRS complexes.
The QRS descriptors defined in the next sections were computed from MWQRS complexes for ECG segments during and after HD (, , , , , and ).
3.2.2. QRS Duration and Amplitude Markers
For each MWQRS, the following descriptors were computed:
- , which represented the QRS width calculated from QRS onset to end (expressed in ms) [40].
- , which represented the QRS amplitude calculated from the minimum to maximum amplitude of the QRS complex (expressed in mV).
3.2.3. QRS Morphology Markers
Morphology-based QRS descriptors were computed using the time-warping methodology, as previously described [39]. For each patient, a reference QRS complex, , was calculated from the MWQRS at the end of the HD session, the time when the patient was discharged from hospital with restored serum ion levels. Representative QRS complexes for each HD stage, , were calculated from the MWQRS at two-minute windows at the end of each hour during the HD session and 48 h after it. is expressed as and the reference QRS complex as . The vectors and are the uniformly sampled time vectors corresponding to the QRS complexes and , respectively. and represent the total duration, in samples, of and , respectively. Figure 3a shows an example of and , with their respective time domains, and .
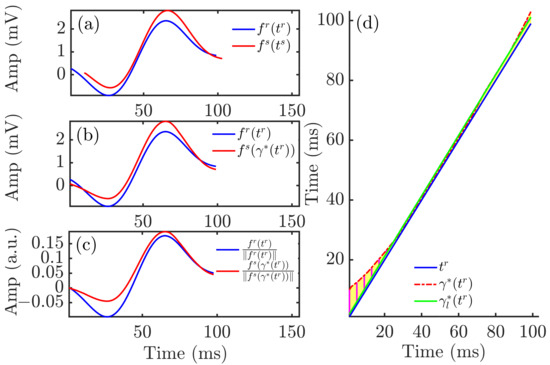
Figure 3.
Time warping of QRS complexes. Panel (a) shows the reference (blue) and investigated (red) QRS complexes obtained from an ECG segment during HD. Panel (b) shows the warped QRS complexes, which had the same duration whilst keeping the original amplitude. Panel (c) depicts the warped QRS complexes after normalization by their L2-norms. The yellow area in panel (d) represents , which quantified the total amount of warping. The green solid line is the linear regression function best fitted to .
Let be the warping function that relates and such that denotes the time-domain warping of using . The square-root slope function (SRSF) transformation was used to find the optimal warping function [39]. This transformation was defined as:
The optimal warping function was determined as the one minimizing the amplitude difference between the SRSF of and :
A dynamic programming algorithm was used to obtain the function that optimally warped into . This function is shown in Figure 3d. The warped QRS complex, , is shown in Figure 3b, together with the reference QRS complex, .
The descriptor, , was used to quantify the level of warping required to optimally align the QRS complexes and :
The amplitude descriptor, , was computed from the area contained between and normalized by the L2-norm of , thus quantifying amplitude differences after time warping the two QRS complexes:
where was used to account for the sign.
The above described marker accounted for both linear and nonlinear warping required to fit the two QRS complexes in the time domain. The nonlinear component marker was quantified as:
where (green line in Figure 3d) was derived by linearly fitting using the least absolute residual method.
The nonlinear amplitude marker was defined by computing the norm of the difference between -normalized versions of and :
Figure 3a shows and , referring to their respective time domains, and . The warped QRS complex (red), , is shown in Figure 3b, together with the reference QRS complex (blue), .
The analyzed warping-based QRS descriptors, computed from MWQRS during and after HD stages, , included:
- , which represented temporal variations in QRS morphology (expressed in ms),
- , which represented amplitude variations in QRS morphology (expressed as a percentage),
- , which represented nonlinear temporal variations in QRS morphology (expressed in ms),
- , which represented nonlinear amplitude variations in QRS morphology (expressed as a percentage).
3.3. Statistical Analysis
Pearson correlation coefficients (r) were computed to assess the strength of the linear relationship between , or RR and each of the investigated QRS descriptors in each patient individually.
A Wilcoxon signed-rank test was applied to test for significant differences () in , , RR, , , , , and between consecutive HD stages. The reason for using a non-parametric statistical test was that, according to the Shapiro–Wilk test, the data distributions were not normal.
To test whether the Pearson correlation coefficient between each QRS marker and , or RR was significantly different from 0, a Student’s t-test was used after transforming the statistical distribution of r into a normal distribution using Fisher’s z transform [42].
All statistical analyses were performed using MATLAB version R2020b for Windows (MathWorks Inc., Novi, MI, USA).
3.4. Uni- and Multivariable Estimation of and
To estimate and , univariable and multivariable estimators were developed. Of all the analyzed QRS descriptors, was selected to build univariable estimators because it presented high median absolute Pearson correlation with and and a relatively low IQR range, particularly for . Univariable estimators were additionally built using the repolarization descriptor , which had shown strong correlation with electrolyte levels [29,30]. was calculated analogously to but for the T wave instead of the QRS complex. Multivariable estimators were tested using both and .
The univariable (, respectively) and multivariable (, respectively) estimators were of the following form:
and
where . The performance of the estimators was tested by using the leave-one-out cross-validation approach.
For the univariable estimators, the coefficient vector or was estimated as [43,44]:
with . Three different types of estimators were considered, namely stage-specific, patient-specific and global estimators, as described in the following paragraphs. The definition of , and was different for each type of estimator:
- For an HD stage-specific (S) estimator, which estimates the electrolyte level at stage of a given patient q from the marker’s values of the remaining patients at that stage, the vector was calculated from the vector of dimension 1, with Q being the total number of patients minus 1, the vector containing the values of the marker b = or at stage i from patients 1, …, Q (all except for patient q) and the vector containing the measured values at stage i. The vector was defined analogously for . This procedure was carried out for each HD stage, , separately.
- For a patient-specific (P) estimator, which estimates the electrolyte level at stage of a given patient q from the marker’s values at the remaining stages for that same patient, the vector was calculated from the vector of dimension 1 (if is or ) or 1 (if was different from or ), = containing the values of the marker b = or for patient q at the different time points except for , with and being duplicated. The vector was defined as containing the measured values for patient q at all time points except for . An analogous definition of vector was applied for . This process was repeated for each patient individually.
- For a global (G) estimator, which estimates the electrolyte level at stage of a given patient q from the marker values at all other time points from all other patients, the vector was calculated by defining vectors and to contain the marker values and the electrolyte measures from all patients at all stages except for patient q at time i.
For the multivariable estimators, was estimated using Equation (11), where the matrix , with = and = , was calculated as described for the univariable estimators depending on the type of estimator (stage-specific, patient-specific or global).
The error, e, between actual (or ) and estimated (or ) was computed as
The relative error, , with respect to the range of electrolyte measurements was computed as
where was defined as the difference between the 75th and 25th percentiles of across patients at each HD stage. An analogous definition for was used.
The relative error, , with respect to the actual electrolyte measurement for each patient at each HD stage (analogously for ) was computed as
The mean absolute error was computed by averaging the absolute value of e defined in Equation (12). The root mean square error was computed by taking the root mean square of e defined in Equation (12).
To assess the agreement between actual and estimated and values, Bland–Altman analysis was performed [45], in which the differences between the actual and estimated and were plotted as a function of their averages, for all patients at all HD time points (see Supplementary Material). and estimation accuracy using our investigated markers was also compared with those of the previously proposed markers [10,11] and [12] (see Supplementary Material):
- represented the ratio between the maximal downward slope (in absolute value) and the amplitude of the T wave [10,11].
- represented the ratio between the maximal downward slope (in absolute value) and the square root of the amplitude of the T wave [12].
It should be noted that estimations of and could not be performed at the end of the HD session () since the morphological QRS complex markers were zero by definition due to the fact that the reference was taken at that time stage. Therefore, we defined an extra time point just before the HD end (reference) so as to improve the estimation accuracy based on one additional HD point.
4. Results
4.1. Characterization of QRS Complex Changes during and after HD
The top panels in Figure 4 show the results for the QRS markers (, , , , and ) together with , and RR variations during and after HD for all patients. Statistically significant differences between consecutive HD stages were found for , , , and as well as for and variations, but not for RR.
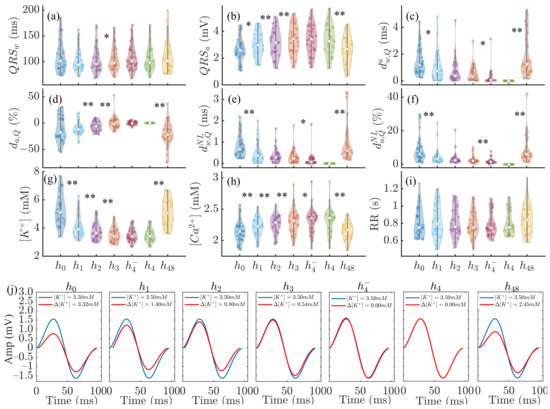
Figure 4.
Panels (a–f): changes in , , , , and during HD stages. Panels (g–i): corresponding variations in , and RR. In panels (a–i), * denotes and ** denotes . In each panel, the central white dot indicates the median. Each dot corresponds to an individual patient. Panel (j): MWQRS (red) of a patient at different HD stages and reference MWQRS (blue). denotes the change in with respect to the end of HD ().
The bottom panels of Figure 4 show MWQRS during and after HD (red) compared to the reference MWQRS (blue) computed at the end of HD. Lower values could be observed at and , corresponding to the highest and the lowest .
4.2. Contribution of , and HR Variations to QRS Complex Changes
Figure 5 shows the Pearson correlation coefficient, r, between the analyzed QRS markers and (black), (red) and RR (blue). , , , and were the most highly correlated, in median, with (median r being , , , and , respectively) and (, , , and , respectively). The IQR of r was the lowest for when the correlation with was analyzed, and for in the case of . Poor association between all the analyzed markers and RR was found.
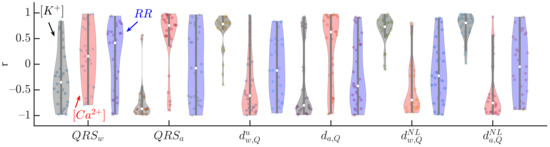
Figure 5.
Pearson correlation coefficients between QRS markers (, , , , and ) and (black), (red) and RR (blue) for all patients at all HD points. The central white dot indicates the median. Each dot corresponds to an individual patient.
Table 2 shows the p-values from the Student’s t-test used to determine the statistical significance of non-zero mean Fisher z-transformed Pearson correlation coefficients between QRS markers and each of , and RR in the patient population, during and after HD. All the analyzed QRS markers showed significant association with and most of them (all but ) with . On the other hand, no marker presented significant association with RR.

Table 2.
p-values from the parametric test (t-test) to evaluate statistical significance of non-zero mean Fisher z-transformed Pearson correlation coefficients between QRS markers and , and RR.
4.3. Uni- and Multivariable Estimation of and
Figure 6 shows an illustrative example of the comparison between measured and estimated and using stage-specific (S), patient-specific (P) and global (G) approaches during (, , , , ) and after () HD for a particular patient, for both univariable (panels a–b) and multivariable (panel c) estimators. The patient-specific approach provided better results in terms of reduced errors, particularly using multivariable estimation (mean over HD points being 0.071 (S), −0.008 (P), 0.001 (G) for and 0.019 (S), 0.001 (P), 0.031 (G) for ).
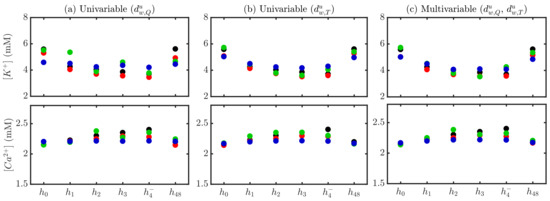
Figure 6.
Actual (black) and estimated and for a patient using stage-specific (red), patient-specific (green) and global (blue) approaches. Univariable -based estimation is shown in (panel a), -based in (panel b) and multivariable - -based in (panel c).
Figure 7 shows the relative errors, , for all patients and HD stages in the estimation of and using stage-specific (top panel), patient-specific (middle panel) and global (bottom panel) approaches. Figure S2 in the Supplementary Material shows the relative errors, .
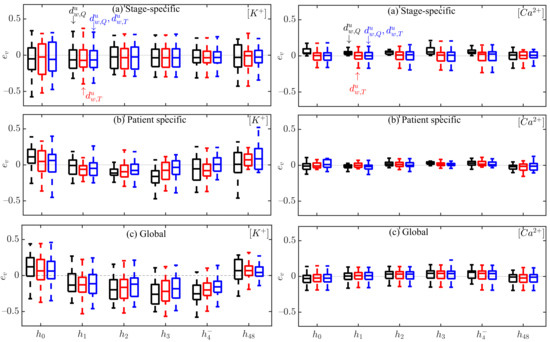
Figure 7.
Box plots of and estimation errors during HD stages for all patients using (black), (red) and the combination of and (blue) for stage-specific (top), patient-specific (middle) and global (bottom) approaches. The central line indicates the median, whereas top and bottom edges show the 25th and 75th percentiles.
Table 3 shows actual and estimated and values over the study population at each HD stage. Multivariable estimation results using stage-specific, patient-specific and global approaches are presented.

Table 3.
Actual and estimated and values over the study population at each HD stage using multivariable (m) estimation and stage-specific (S), patient-specific (P) and global (G) approaches. Values are expressed as median (IQR) and the units are mM.
Table 4 and Table 5 show the median and IQR values of intra-patient Pearson correlation coefficients between actual and estimated (, respectively) using univariable and multivariable estimators.

Table 4.
Intra-patient Pearson correlation coefficient r between actual and estimated using univariable and multivariable estimators, with stage-specific (S), patient-specific (P) and global (G) approaches. Values are expressed as median (IQR).

Table 5.
Intra-patient Pearson correlation coefficient r between actual and estimated using univariable and multivariable estimators, with stage-specific (S), patient-specific (P) and global (G) approaches. Values are expressed as median (IQR).
Bland–Altman plots between actual and estimated and for the proposed markers are shown in Supplementary Material (Figures S3–S12).
Table 6 and Table 7 show a comparison between estimation errors obtained for the markers analyzed in this study and in previous studies. Tables S6–S9 in the Supplementary Material show mean absolute and root mean square errors for the analyzed markers.

Table 6.
Estimation errors (e) using stage-specific (S), patient-specific (P) and global (G) approach-based estimators, from all patients at all HD time points. Values are expressed as mean ± standard deviation and the units are mM.

Table 7.
Estimation errors (e) using stage-specific (S), patient-specific (P) and global (G) approach-based estimators, from all patients at all HD time points. Values are expressed as mean ± standard deviation and the units are mM.
5. Discussion
We investigated changes in QRS duration, amplitude and morphology at varying , and HR in ESRD patients. We designed and estimators based on our proposed QRS morphological characteristics, taken both individually and in combination with T wave morphology markers. We showed the accuracy of our proposed estimators using three different approaches, stage-specific, patient-specific and global estimation, which outperformed previously proposed methods. Our results offered new non-invasive tools to monitor serum and , which could have a significant role in clinical practice and could contribute to reduce the mortality risk associated with abnormal electrolyte levels in ESRD patients.
5.1. Characterization of QRS Complex Amplitude, Duration and Morphology in ESRD Patients during and after HD
In ECG recordings of ESRD patients, we evaluated QRS duration and amplitude, measured by markers and , and QRS morphological characteristics, measured by markers , , and , which was proposed here for the first time. All markers except for presented significant changes during and after HD. These changes were strongly associated with variations in and but not in HR. The inconsistent relationship between QRS markers, such as , and HR has been investigated in previous works, including the study by Hnatkova et al. [46], who reported increases in QRS duration with increasing HR in 35% of their patients and decreases in QRS duration in the remaining 65%. In line with these results, we found that QRS became markedly wider at higher RR intervals for 34% of the patients; it became markedly narrower for 21% of the patients; its width moderately changed with RR for 21% of the patients; and it showed poor association with RR for the remaining 24% of the patients (see Table S2 in Supplementary Material). This led to a median r value of between and RR over the 29 ESRD patients, reflecting a notably weaker relationship between and RR as compared to other depolarization markers. Regarding QRS amplitude, even if we found to remarkably change during HD, this marker depended on ECG amplitudes at specific time points, which, in noisy ambulatory recordings, could lead to large changes not associated with variations in electrolyte levels. On the other hand, changes in warping-based markers accounted for deviations in the whole QRS waveform and could thus be better suited for ambulatory monitoring. In particular, if QRS duration on top of amplitude changes occurred in the inter-dialytic interval, as, e.g., reported during advanced ischemia [47,48], these changes could be reflected in our proposed QRS warping markers.
On top of investigating the relationship between QRS markers and or , we also investigated the relationship between these markers and sodium concentration (). variations were less remarkable than those of and during HD in our patients (see Table S3 in Supplementary Material). Importantly, none of the markers were strongly associated with (see Figure S13 and Table S4 in Supplementary Material). could have been expected to play a more important role in modulating depolarization markers because the fast sodium current was primarily responsible for phase 0 of the action potential and its changes might have manifested in QRS complex alterations. However, we found that the QRS complex became markedly wider at higher for 43% of the patients; it became markedly narrower for 7% of the patients; its width moderately changed with for 14% of the patients; and it showed poor association with for the remaining 36% of the patients (see Table S5 in Supplementary Material).
High inter-individual variability was found in the relationship between the analyzed QRS markers and or . This was especially remarkable in the case of , which presented high IQR in the intra-patient correlation coefficients with and . Such high dispersion could be explained by QRS polarity effects, as a reduction (increase, respectively) in the absolute amplitude could be reflected as either positive or negative , depending on QRS being predominantly positive or negative.
Changes in ECG characteristics induced by variations in and have been extensively investigated in terms of ventricular repolarization. A number of studies have characterized changes in T wave width, amplitude, slope or slope-to-amplituderatio [10,11,13,49,50]. We have recently quantified changes in T wave nonlinear dynamics and morphology and have shown their relationship with and variations [28,29,31,33,51].
The analysis of electrolyte-induced alterations in ventricular depolarization remains, however, much more limited. In a study including 923 patients with severe hyperkalemia, sine wave-shaped QRS complexes were observed in almost 36.7% of patients [38]. In the present study, we could observe such behavior in most of the patients (Figure 4). Inconsistent results have been reported in relation to the effects of on QRS duration, with a larger proportion of studies reporting QRS widening [1,34,52,53,54,55,56] and others reporting QRS narrowing [2,35] with increased . Here, we observed no significant changes in QRS width during and after HD. Regarding QRS amplitude, we found to be strongly negatively correlated with and positively correlated with , in accordance with the increase in with decreasing , as described by Astan et al. [35]. We observed similar results for the QRS morphology-based amplitude marker . Our study characterized additional QRS morphological changes by the warping markers , and further extended these results to provide a robust characterization of QRS changes during and after HD in ESRD patients. Figure 8 illustrates QRS complexes and T waves at the start and end of HD.
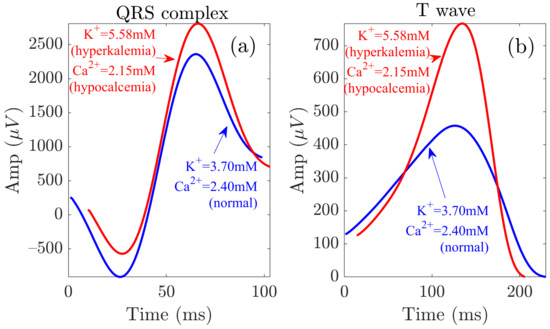
Figure 8.
QRS and T wave variations at the start (red) and end (blue) of the HD session. Panels (a,b) show the waveforms related to the QRS complex and the T wave, respectively.
5.2. Multivariable Predictors of and Based on Depolarization and Repolarization Characteristics
Based on the novel QRS morphology markers of this study and on already proposed T wave markers [29,30,39], we designed linear univariable and multivariable and estimators. In particular, we used (QRS marker) and (T wave marker), as these were strongly correlated with and and poorly related to each other (see Table S1 in the Supplementary Material), thus potentially providing complementary information to monitor electrolyte variations.
For each of the constructed and linear estimators, we used stage-specific, patient-specific and global estimation approaches. Overall, the stage-specific approach rendered results with both mean and median estimation errors very close to zero but with higher dispersion than in the patient-specific approach. The latter approach would be suitable for clinical application, as electrolyte levels could be predicted in each patient based on a short ECG recording of the same patient.
Multivariable estimators combining information from and outperformed univariable estimators (the ones proposed by us and other authors [10,11,12]). The estimation errors for the multivariable estimators were lower (Figure 7, Figures S3–S12 in Supplementary Material, Table 6 and Table 7) and the correlation coefficients r between actual and estimated electrolyte levels were higher than for univariable estimators, both for the patient-specific and global estimation approaches (see Table 4 and Table 5). In particular, for the patient-specific approach, median, r, in estimation was for the combination of and , while it was for and for . Similarly, for the global approach, median, r, in estimation was for the combination compared to for and for . It should be noted that these correlation coefficient values were computed between actual and estimated while the correlation between each of the tested markers and was higher, both for the QRS marker proposed here and for the T wave marker analyzed in our previous studies [29,30].
These results supported the use of our proposed QRS markers to improve prediction of and by ECG repolarization markers. ECG depolarization-based estimators have been scarcely investigated in the literature for serum electrolyte monitoring. In [57], an ECG-based estimator was designed using QRS duration in addition to T wave markers, but QRS duration was found not to be highly correlated with , in agreement with our present results for . Pilia et al. [14] reviewed studies evaluating QRS amplitude and width features, but no improved serum electrolyte prediction by incorporating these features into repolarization-based estimators was provided. Here, we proposed univariable and multivariable and estimators that included information from the whole morphology of the QRS complex. By accounting for characteristics beyond QRS amplitude and width, these estimators could offer more robust performance for ambulatory monitoring of ESRD patients and overcome some limitations of previously proposed markers, such as their dependence on blood volume [36,37].
For all the estimators we built, we found that the values of and at the beginning of each of the two HD sessions, i.e., time points and , were the more challenging to estimate, as could be observed from the largest estimation errors at those time points (Figure 4). Here, we duplicated the values of the ECG markers at and to give them more weight in the training step, as all other measures corresponding to , , and were more similar to one another and the learning could otherwise be biased towards such measures.
5.3. Study Limitations and Future Research
This study investigated 29 ECG recordings of ESRD patients. Although the dataset was originally planned to include a larger number of patients, ECG acquisition had to be stopped due to the situation generated by the COVID-19 pandemic. Future studies should investigate the application of the proposed methods to larger numbers of patients.
For each patient, six blood samples were available, five of them taken during an HD session and the sixth one at the beginning of the following HD session. Future studies could be designed to have more frequent and measurements, especially during the first HD hour, when electrolyte levels vary most remarkably. This could help to improve the learning of the estimators.
We used linear estimators due to the small number of samples, particularly when using a patient-specific approach. Future work could investigate the use of nonlinear estimators [11,32], which could prove to be particularly relevant for the estimation of and at the start of HD sessions when these take values far from those at other HD stages.
We did not have access to measurements of blood volume or of other variables that could be used to infer them. Studies on other datasets where such measurements were available could test the relationship between the markers and used in our and estimators and the blood volume. In addition, some of the patients analyzed in the study had diseases, such as diabetes mellitus. We did not find significant differences in the analyzed markers between diabetic and non-diabetic patients. Nevertheless, future studies addressing larger patient cohorts could investigate the impact of diseases additional to ESRD on the relationship between QRS markers and electrolytes.
Some publications have reported the use of deep learning methods for hypo- and hyperkalemia screening from the ECG. While such methods require large amounts of training data and could not be addressed with the database analyzed here, further investigations could extend the present work to include machine learning techniques for the same purpose [58,59,60].
We focused our research on and estimation. was found to present less notable variations during HD and none of our analyzed QRS markers showed significant association with it in the reduced dataset analyzed in this study, which should be further tested in larger patient cohorts. Although variations in other electrolytes, such as magnesium , have also been shown to alter the ECG to some extent [2,24,61,62,63], measurements were not available for the present study.
An additional future research line related to this work will be aimed at extending the present investigations to include patient-specific electrophysiological simulations in biventricular models embedded in torso models. From those simulations, realistic ECGs could be computed and used to gain understanding on the relationship between ECG characteristics and or .
6. Conclusions
Our proposed QRS morphology markers presented remarkable changes during and after HD, which were strongly associated with and in the ESRD patients. Multivariable estimators based on combined QRS and T wave morphological variability allowed accurate prediction of and , outperforming estimators based on only ECG depolarization or repolarization. These results could pave the way to ambulatory, non-invasive monitoring of electrolyte levels, which could help to prevent fatal ventricular arrhythmias in ESRD patients.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/s22082951/s1, Figure S1: QRS complexes, including dominant and non-dominant polarity; Figure S2: Box plots of and estimation errors ; Figures S3–S12: Bland-Altman plots between actual and estimated and ; Figure S13: Changes in sodium levels () along HD stages; Table S1: Pearson correlation coefficient (r) to assess the association between QRS and T waves based multivariable estimators; Table S2: Pearson correlation coefficient (r) between QRS complex width and RR interval in 29 ESRD patients; Table S3: p-values to assess differences in between consecutive time stages; Table S4: Pearson (r) and Spearman () correlation coefficients between QRS complex markers and in 29 ESRD patients; Table S5: Pearson correlation coefficient (r) between QRS complex width and in 29 ESRD patients; Tables S6–S9: Mean absolute errors () and Root mean square errors () using stage-specific (S), patient-specific (P) and global (G) approach based and estimators.
Author Contributions
Conceptualization, H.A.B., C.S., M.P., P.L. and E.P.; data curation, J.E.R., P.L. and E.P.; formal analysis, H.A.B.; funding acquisition, E.P.; investigation, H.A.B., C.S., P.L. and E.P.; methodology, H.A.B., P.L. and E.P.; project administration, J.E.R., P.L. and E.P.; resources, E.P.; software, H.A.B.; supervision, C.S., M.P., P.L. and E.P.; validation, H.A.B., C.S., P.L. and E.P.; visualization, H.A.B.; writing—original draft, H.A.B.; writing—review and editing, H.A.B., C.S., M.P., P.L. and E.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by projects PID2019-105674RB-I00 and PID2019-104881RB-I00 (Ministerio de Ciencia e Innovación), ERC-StG 638284 (ERC), Marie Skłodowska-Curie grant 764738 (European Commission) and by European Social Fund (EU) and Aragón Government through project LMP94_21 and BSICoS group T39_20R. M. Potse was funded by the French National Research Agency, grant reference ANR-10-IAHU04-LIRYC.
Institutional Review Board Statement
The study was approved by the Research Ethics Committee of Aragón (CEICA, ref. PI18/003, 25 January 2018).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The dataset is still ongoing and it is available upon request to the corresponding author.
Acknowledgments
Computations were performed by the ICTS NANBIOSIS (HPC Unit at University of Zaragoza).
Conflicts of Interest
The authors declare no conflict of interest. The funders had role in the design of the study but they had no role in the collection, analyses, or interpretation of data nor in the writing of the manuscript, or in the decision to publish the results.
References
- Weiss, J.N.; Qu, Z.; Shivkumar, K. Electrophysiology of hypokalemia and hyperkalemia. Circ. Arrhythmia Electrophysiol. 2017, 10, e004667. [Google Scholar] [CrossRef] [Green Version]
- Noordam, R.; Young, W.J.; Salman, R.; Kanters, J.K.; van den Berg, M.E.; van Heemst, D.; Lin, H.J.; Barreto, S.M.; Biggs, M.L.; Biino, G.; et al. Effects of calcium, magnesium, and potassium concentrations on ventricular repolarization in unselected individuals. J. Am. Coll. Cardiol. 2019, 73, 3118–3131. [Google Scholar] [CrossRef] [PubMed]
- Soar, J.; Perkins, G.D.; Abbas, G.; Alfonzo, A.; Barelli, A.; Bierens, J.J.; Brugger, H.; Deakin, C.D.; Dunning, J.; Georgiou, M.; et al. European Resuscitation Council Guidelines for Resuscitation 2010 Section 8. Cardiac arrest in special circumstances: Electrolyte abnormalities, poisoning, drowning, accidental hypothermia, hyperthermia, asthma, anaphylaxis, cardiac surgery, trauma, pregnancy, electrocution. Resuscitation 2010, 81, 1400–1433. [Google Scholar] [PubMed]
- Levis, J.T. ECG diagnosis: Hypokalemia. Perm. J. 2012, 16, 57. [Google Scholar] [CrossRef] [PubMed]
- Lv, J.C.; Zhang, L.X. Prevalence and disease burden of chronic kidney disease. Adv. Exp. Med. Biol. 2019, 1165, 3–15. [Google Scholar] [PubMed]
- El-Sherif, N.; Turitto, G. Electrolyte disorders and arrhythmogenesis. Cardiol. J. 2011, 18, 233–245. [Google Scholar]
- Lanari, A.; Chait, L.O.; Capurro, C. Electrocardiographic effects of potassium. I. Perfusion through the coronary bed. Am. Heart J. 1964, 67, 357–363. [Google Scholar] [CrossRef]
- Van Mieghem, C.; Sabbe, M.; Knockaert, D. The clinical value of the ECG in noncardiac conditions. Chest 2004, 125, 1561–1576. [Google Scholar] [CrossRef] [PubMed]
- Severi, S.; Corsi, C.; Haigney, M.; DeBie, J.; Mortara, D. Noninvasive potassium measurements from ECG analysis during hemodialysis sessions. In Proceedings of the 2009 36th Annual Computers in Cardiology Conference (CinC), Park City, UT, USA, 13–16 September 2009; pp. 821–824. [Google Scholar]
- Corsi, C.; DeBie, J.; Napolitano, C.; Priori, S.; Mortara, D.; Severi, S. Validation of a novel method for non-invasive blood potassium quantification from the ECG. In Proceedings of the 2012 Computing in Cardiology, Krakow, Poland, 9–12 September 2012; pp. 105–108. [Google Scholar]
- Corsi, C.; Cortesi, M.; Callisesi, G.; De Bie, J.; Napolitano, C.; Santoro, A.; Mortara, D.; Severi, S. Noninvasive quantification of blood potassium concentration from ECG in hemodialysis patients. Sci. Rep. 2017, 7, 42492. [Google Scholar] [CrossRef] [Green Version]
- Attia, Z.I.; DeSimone, C.V.; Dillon, J.J.; Sapir, Y.; Somers, V.K.; Dugan, J.L.; Bruce, C.J.; Ackerman, M.J.; Asirvatham, S.J.; Striemer, B.L.; et al. Novel bloodless potassium determination using a signal-processed single-lead ECG. J. Am. Heart Assoc. Cardiovasc. Cerebrovasc. Dis. 2016, 5, 1. [Google Scholar] [CrossRef] [Green Version]
- Dillon, J.J.; DeSimone, C.V.; Sapir, Y.; Somers, V.K.; Dugan, J.L.; Bruce, C.J.; Ackerman, M.J.; Asirvatham, S.J.; Striemer, B.L.; Bukartyk, J.; et al. Noninvasive potassium determination using a mathematically processed ECG: Proof of concept for a novel “blood-less, blood test”. J. Electrocardiol. 2015, 48, 12–18. [Google Scholar] [CrossRef] [Green Version]
- Pilia, N.; Severi, S.; Raimann, J.G.; Genovesi, S.; Dössel, O.; Kotanko, P.; Corsi, C.; Loewe, A. Quantification and classification of potassium and calcium disorders with the electrocardiogram: What do clinical studies, modeling, and reconstruction tell us? APL Bioeng. 2020, 4, 041501. [Google Scholar] [CrossRef] [PubMed]
- Yoon, D.; Lim, H.S.; Jeong, J.C.; Kim, T.Y.; Choi, J.; Jang, J.; Jeong, E.; Park, C.M. Quantitative evaluation of the relationship between T-wave-based features and serum potassium level in real-world clinical practice. BioMed Res. Int. 2018, 2018, 3054316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di Iorio, B.; Bellasi, A. QT interval in CKD and haemodialysis patients. Clin. Kidney J. 2013, 6, 137–143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khosoosi Niaki, M.R.; Saravi, M.; Oliaee, F.; Akbari, R.; Noorkhomami, S.; Bozorgi Rad, S.H.; Fallahpoor, K.; Ramezani, M.S. Changes in QT interval before and after hemodialysis. Casp. J. Intern. Med. 2013, 4, 590–594. [Google Scholar]
- Sohal, P.M.; Goel, A.; Gupta, D.; Aslam, N.; Sandhu, J.; Sandhu, J.S.; John, E.E.; Sharma, D. Effect of hemodialysis on corrected QT interval and QTc dispersion. Indian J. Nephrol. 2018, 28, 335–338. [Google Scholar]
- Matsumoto, Y.; Mori, Y.; Kageyama, S.; Arihara, K.; Sato, H.; Nagata, K.; Shimada, Y.; Nojima, Y.; Iguchi, K.; Sugiyama, T. Changes in QTc interval in long-term hemodialysis patients. PLoS ONE 2019, 14, e0209297. [Google Scholar] [CrossRef] [Green Version]
- Malhis, M.; Al-Bitar, S.; Farhood, S.; Zaiat, K.A. Changes in QT intervals in patients with end-stage renal disease before and after hemodialysis. Saudi J. Kidney Dis. Transplant. 2010, 21, 460–465. [Google Scholar]
- Kim, E.D.; Watt, J.; Tereshchenko, L.G.; Jaar, B.G.; Sozio, S.M.; Kao, W.; Estrella, M.M.; Parekh, R.S. Associations of serum and dialysate electrolytes with QT interval and prolongation in incident hemodialysis: The predictors of arrhythmic and cardiovascular risk in end-stage renal disease (PACE) study. BMC Nephrol. 2019, 20, 133. [Google Scholar] [CrossRef] [Green Version]
- Lorincz, I.; Mátyus, J.; Zilahi, Z.; Kun, C.; Karányi, Z.; Kakuk, G. QT dispersion in patients with end-stage renal failure and during hemodialysis. J. Am. Soc. Nephrol. JASN 1999, 10, 1297–1302. [Google Scholar] [CrossRef]
- Covic, A.; Diaconita, M.; Gusbeth-Tatomir, P.; Covic, M.; Botezan, A.; Ungureanu, G.; Goldsmith, D.J. Haemodialysis increases QTc interval but not QTc dispersion in ESRD patients without manifest cardiac disease. Nephrol. Dial. Transplant. 2002, 17, 2170–2177. [Google Scholar] [CrossRef] [Green Version]
- Ozportakal, H.; Ozkok, A.; Alkan, O.; Bulut, A.S.; Boyraz, M.; Inanir, M.; Acar, G.; Odabas, A.R. Hemodialysis-induced repolarization abnormalities on ECG are influenced by serum calcium levels and ultrafiltration volumes. Int. Urol. Nephrol. 2017, 49, 509–515. [Google Scholar] [CrossRef]
- Floccari, F.; Aloisi, E.; Nostro, L.; Caccamo, C.; Crisafulli, A.; Barillà, A.; Aloisi, C.; Romeo, A.; Corica, F.; Ientile, R.; et al. QTc interval and QTc dispersion during haemodiafiltration. Nephrology 2004, 9, 335–340. [Google Scholar] [CrossRef] [PubMed]
- Schüttler, D.; Schönermarck, U.; Wenner, F.; Toepfer, M.; Rizas, K.D.; Bauer, A.; Brunner, S.; Hamm, W. Large potassium shifts during dialysis enhance cardiac repolarization instability. J. Nephrol. 2021, 34, 1301–1305. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, A.S.; Petrėnas, A.; Paliakaitė, B.; Kušleikaitė-Pere, N.; Jaruševičius, G.; Bumblytė, I.A.; Laguna, P.; Marozas, V. Noninvasive monitoring of potassium fluctuations during the long interdialytic interval. IEEE Access 2020, 8, 88488–188502. [Google Scholar] [CrossRef]
- Bukhari, H.A.; Palmieri, F.; Ferreira, D.; Potse, M.; Ramírez, J.; Laguna, P.; Sánchez, C.; Pueyo, E. Transmural ventricular heterogeneities play a major role in determining T-wave morphology at different extracellular potassium levels. In Proceedings of the 2019 Computing in Cardiology (CinC), Singapore, 8–11 September 2019; pp. 1–4. [Google Scholar]
- Bukhari, H.A.; Palmieri, F.; Ramirez, J.; Laguna, P.; Ruiz, J.E.; Ferreira, D.; Potse, M.; Sanchez, C.; Pueyo, E. Characterization of T wave amplitude, duration and morphology changes during hemodialysis: Relationship with serum electrolyte levels and heart rate. IEEE Trans. Biomed. Eng. 2021, 68, 2467–2478. [Google Scholar] [CrossRef] [PubMed]
- Palmieri, F.; Gomis, P.; Ferreira, D.; Ruiz, J.E.; Bergasa, B.; Martín-Yebra, A.; Bukhari, H.A.; Pueyo, E.; Martínez, J.P.; Ramírez, J.; et al. Monitoring blood potassium concentration in hemodialysis patients by quantifying T-wave morphology dynamics. Sci. Rep. 2021, 11, 3883. [Google Scholar] [CrossRef]
- Srinivasan, S.; Bukhari, H.A.; Laguna, P.; Sánchez, C.; Pueyo, E. Analysis of T wave nonlinear dynamics for serum potassium monitoring in end-stage renal disease patients. In Proceedings of the 2020 Computing in Cardiology, Rimini, Italy, 13–16 September 2020; pp. 1–4. [Google Scholar]
- Palmieri, F.; Gomis, P.; Ruiz, J.E.; Ferreira, D.; Martín-Yebra, A.; Pueyo, E.; Martínez, J.P.; Ramírez, J.; Laguna, P. Nonlinear T-wave time warping-based sensing model for non-invasive personalized blood potassium monitoring in hemodialysis patients. Sensors 2021, 21, 2710. [Google Scholar] [CrossRef]
- Bukhari, H.A.; Sánchez, C.; Srinivasan, S.; Palmieri, F.; Potse, M.; Laguna, P.; Pueyo, E. Estimation of potassium levels in hemodialysis patients by T wave nonlinear dynamics and morphology markers. Comput. Biol. Med. 2022, 143, 105304. [Google Scholar] [CrossRef]
- Parham, W.A.; Mehdirad, A.A.; Biermann, K.M.; Fredman, C.S. Hyperkalemia revisited. Tex. Heart Inst. J. 2006, 33, 40–47. [Google Scholar]
- Astan, R.; Akpinar, I.; Karan, A.; Kacmaz, F.; Sokmen, E.; Baysal, E.; Ozeke, O.; Selçuk, M.T. The effect of hemodialysis on electrocardiographic parameters. Ann. Noninvasive Electrocardiol. 2015, 20, 253–257. [Google Scholar] [CrossRef]
- Curione, M.; Castro, C.; Cammarota, C.; Tonnarini, G.; Pasquali, M. Progressive loss in circulating volume during haemodialysis can be monitored by time voltage integral area of QRS complex: Pilot study. Arch. Med Sci. AMS 2013, 9, 544–547. [Google Scholar] [CrossRef] [PubMed]
- Ojanen, S.; Kööbi, T.; Korhonen, P.; Mustonen, J.; Pasternack, A. QRS amplitude and volume changes during hemodialysis. Am. J. Nephrol. 1999, 19, 423–427. [Google Scholar] [CrossRef] [PubMed]
- An, J.N.; Lee, J.P.; Jeon, H.J.; Kim, D.H.; Oh, Y.K.; Kim, Y.S.; Lim, C.S. Severe hyperkalemia requiring hospitalization: Predictors of mortality. Crit. Care 2012, 16, R225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramirez, J.; Orini, M.; Tucker, J.D.; Pueyo, E.; Laguna, P. Variability of ventricular repolarization dispersion quantified by Time-warping the morphology of the T-Waves. IEEE Trans. Biomed. Eng. 2017, 64, 1619–1630. [Google Scholar]
- Martínez, J.P.; Almeida, R.; Olmos, S.; Rocha, A.P.; Laguna, P. A wavelet-based ECG delineator: Evaluation on standard databases. IEEE Trans. Biomed. Eng. 2004, 51, 570–581. [Google Scholar] [CrossRef] [PubMed]
- Castells, F.; Laguna, P.; Sörnmo, L.; Bollmann, A.; Roig, J.M. Principal component analysis in ECG signal processing. EURASIP J. Adv. Signal Process. 2007, 2007, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Fisher, R.A. Statistical methods for research workers. In Breakthroughs in Statistics: Methodology and Distribution; Ser. Springer Series in Statistics, Kotz, S., Johnson, N.L., Eds.; Springer: New York, NY, USA, 1992; pp. 66–70. [Google Scholar]
- Rencher, A.C.; Christensen, W.F. Methods of Multivariate Analysis; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Freedman, D. Statistical Models: Theory and Practice; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Hnatkova, K.; Smetana, P.; Toman, O.; Schmidt, G.; Malik, M. Sex and race differences in QRS duration. Europace 2016, 18, 1842–1849. [Google Scholar] [CrossRef]
- Pueyo, E.; Sornmo, L.; Laguna, P. QRS slopes for detection and characterization of myocardial ischemia. IEEE Trans. Biomed. Eng. 2008, 55, 468–477. [Google Scholar] [CrossRef]
- Romero, D.; Ringborn, M.; Laguna, P.; Pahlm, O.; Pueyo, E. Evaluation of depolarization changes during acute myocardial ischemia by analysis of QRS slopes. J. Electrocardiol. 2011, 44, 416–424. [Google Scholar]
- Kharche, S.; Callisesi, G.; Stary, T.; Bracci, A.; Severi, S. Simulating the effects of serum potassium on the ECG. In Proceedings of the 2012 Computing in Cardiology, Krakow, Poland, 9–12 September 2012; pp. 225–228. [Google Scholar]
- Frohnert, P.P.; Giuliani, E.R.; Friedberg, M.; Johnson, W.J.; Tauxe, W.N. Statistical investigation of correlations between serum potassium levels and electrocardiographic findings in patients on intermittent hemodialysis therapy. Circulation 1970, 41, 667–676. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palmieri, F.; Gomis, P.; Ferreira, D.; Ruiz, J.E.; Bergasa, B.; Martín-Yebra, A.; Bukhari, H.A.; Pueyo, E.; Martínez, J.P.; Ramírez, J.; et al. T-wave morphology changes as surrogate for blood potassium concentration in hemodialysis patients. In Proceedings of the 2019 Computing in Cardiology (CinC), Singapore, 8–11 September 2019; pp. 1–4. [Google Scholar]
- Ettinger, P.O.; Regan, T.J.; Oldewurtel, H.A. Hyperkalemia, cardiac conduction, and the electrocardiogram: A review. Am. Heart J. 1974, 88, 360–371. [Google Scholar] [CrossRef]
- Aslam, S.; Friedman, E.A.; Ifudu, O. Electrocardiography is unreliable in detecting potentially lethal hyperkalaemia in haemodialysis patients. Nephrol. Dial. Transplant. 2002, 17, 1639–1642. [Google Scholar] [CrossRef] [Green Version]
- Montague, B.T.; Ouellette, J.R.; Buller, G.K. Retrospective review of the frequency of ECG changes in hyperkalemia. Clin. J. Am. Soc. Nephrol. CJASN 2008, 3, 324–330. [Google Scholar] [CrossRef]
- Martinez-Vea, A.; Bardají, A.; Garcia, C.; Oliver, J.A. Severe hyperkalemia with minimal electrocardiographic manifestations: A report of seven cases. J. Electrocardiol. 1999, 32, 45–49. [Google Scholar] [CrossRef]
- Fisch, C. Relation of electrolyte disturbances to cardiac arrhythmias. Circulation 1973, 47, 408–419. [Google Scholar] [CrossRef] [Green Version]
- Velagapudi, V.; O’Horo, J.C.; Vellanki, A.; Baker, S.P.; Pidikiti, R.; Stoff, J.S.; Tighe, D.A. Computer-assisted image processing 12 lead ECG model to diagnose hyperkalemia. J. Electrocardiol. 2017, 50, 31–138. [Google Scholar] [CrossRef]
- Lin, C.S.; Lin, C.; Fang, W.H.; Hsu, C.J.; Chen, S.J.; Huang, K.H.; Lin, W.S.; Tsai, C.S.; Kuo, C.C.; Chau, T.; et al. A deep-learning algorithm (ECG12Net) for detecting hypokalemia and hyperkalemia by electrocardiography: Algorithm development. JMIR Med. Inform. 2020, 8, 3. [Google Scholar] [CrossRef]
- Galloway, C.D.; Valys, A.V.; Shreibati, J.B.; Treiman, D.L.; Petterson, F.L.; Gundotra, V.P.; Albert, D.E.; Attia, Z.I.; Carter, R.E.; Asirvatham, S.J.; et al. Development and validation of a deep-learning model to screen for hyperkalemia from the electrocardiogram. JAMA Cardiol. 2019, 4, 428–436. [Google Scholar] [CrossRef]
- Kwon, J.M.; Jung, M.S.; Kim, K.H.; Jo, Y.Y.; Shin, J.H.; Cho, Y.H.; Lee, Y.J.; Ban, J.H.; Jeon, K.H.; Lee, S.Y.; et al. Artificial intelligence for detecting electrolyte imbalance using electrocardiography. Ann. Noninvasive Electrocardiol. 2021, 26, e12839. [Google Scholar] [CrossRef] [PubMed]
- Naksuk, N.; Hu, T.; Krittanawong, C.; Thongprayoon, C.; Sharma, S.; Park, J.Y.; Rosenbaum, A.N.; Gaba, P.; Killu, A.M.; Sugrue, A.M.; et al. Association of serum magnesium on mortality in patients admitted to the intensive cardiac care unit. Am. J. Med. 2017, 130, 229.e5–229.e13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jhang, W.K.; Lee, Y.J.; Kim, Y.A.; Park, S.J.; Park, Y.S. Severe hypermagnesemia presenting with abnormal electrocardiographic findings similar to those of hyperkalemia in a child undergoing peritoneal dialysis. Korean J. Pediatr. 2013, 56, 308–311. [Google Scholar] [CrossRef] [PubMed]
- Van den Bergh, W.M.; Algra, A.; Rinkel, G.J. Electrocardiographic abnormalities and serum magnesium in patients with subarachnoid hemorrhage. Stroke 2004, 35, 644–648. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).