Use of Genetic Algorithms for Design an FPGA-Integrated Acoustic Camera
Abstract
:1. Introduction
2. The Acoustic Camera Designs
- A prototype of a hemisphere-shaped acoustic camera—Acoustic Camera 1;
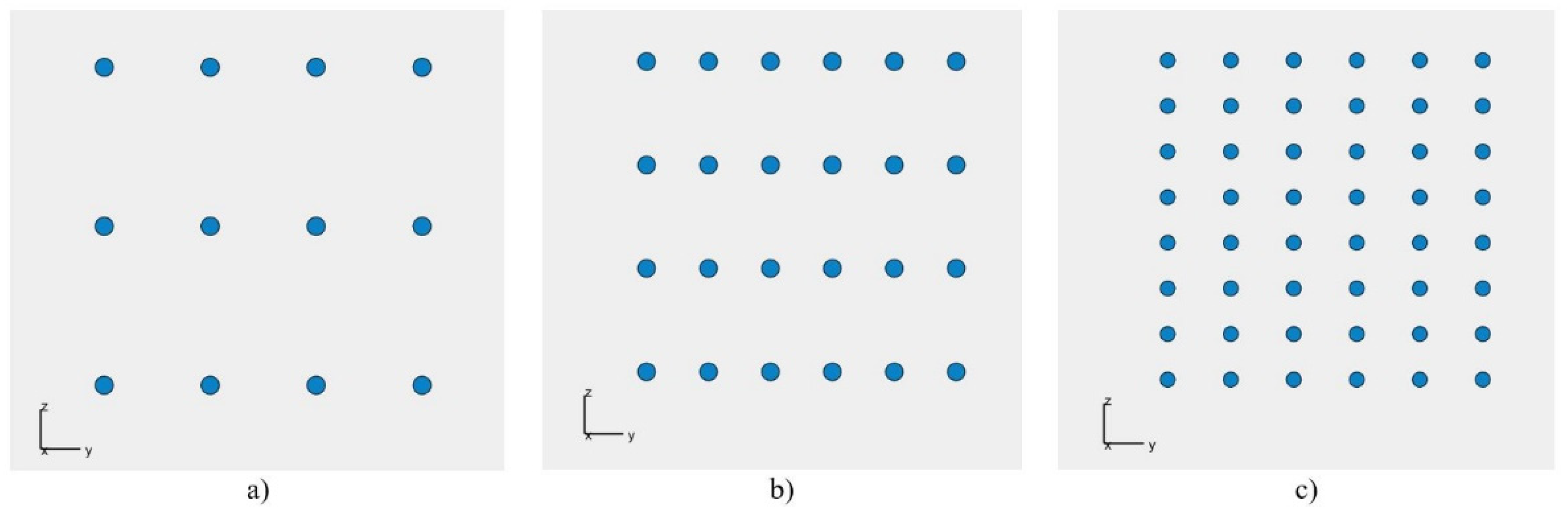
- A prototype of a plate-shaped acoustic camera (i.e., in the form of a plate consisting of four plates measuring 20 × 20 cm with a uniform distribution of microphone arrays)—Acoustic Camera 2, and
- A prototype of a plate-shaped acoustic camera (i.e., in the form of a plate consisting of four optimal acoustic plates with 24 microphones)—Acoustic Camera 3.
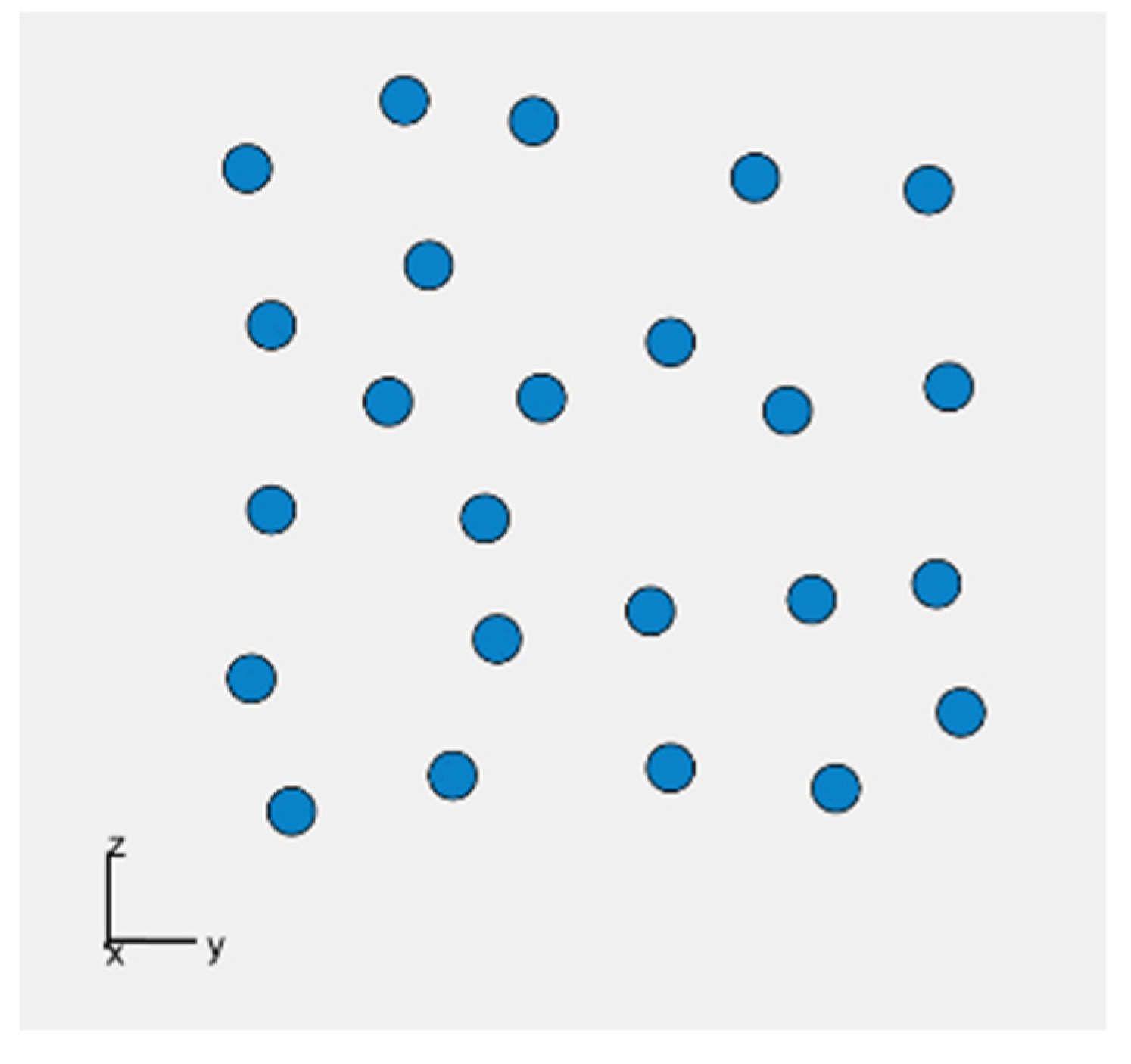
2.1. A Hemisphere-Shaped Acoustic Camera—Acoustic Camera 1
2.1.1. Implementation of Genetic Algorithm (GA) in Case of Acoustic Camera 1
2.1.2. Developing a Prototype of a Hemisphere-Shaped Acoustic Camera—Acoustic Camera 1
2.2. Plate-Shaped Acoustic Cameras—Acoustic Camera 2 and Acoustic Camera 3
2.2.1. Implementation of Genetic Algorithm (GA) in Case of Plate-Shaped Acoustic Cameras
2.2.2. Developing the Prototypes of Plate-Shaped Acoustic Cameras—Acoustic Camera 2 and Acoustic Camera 3
3. The Comparison of Different Acoustic Camera Prototypes
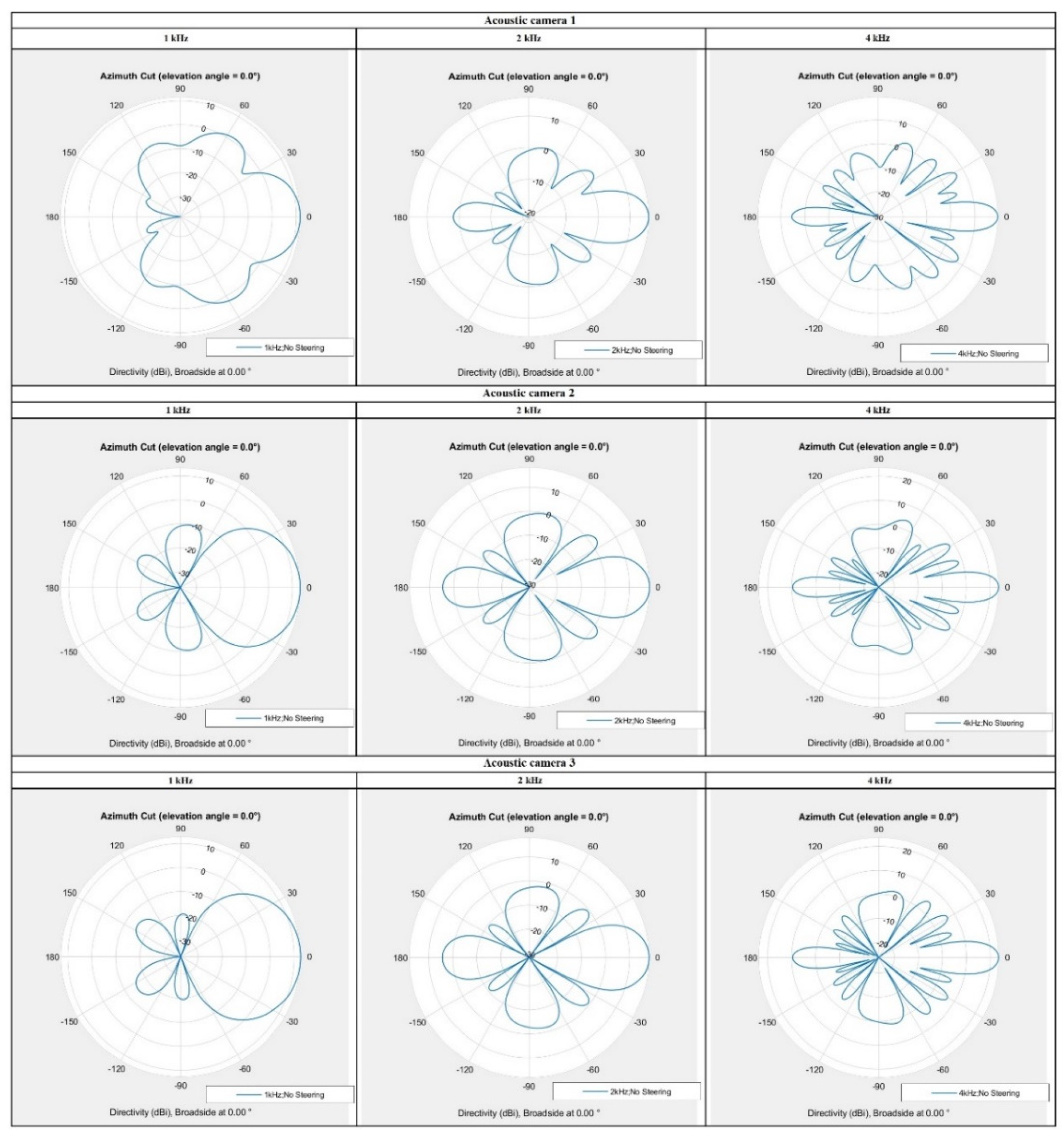
3.1. The Simulation Results of Acoustic Camera Prototypes
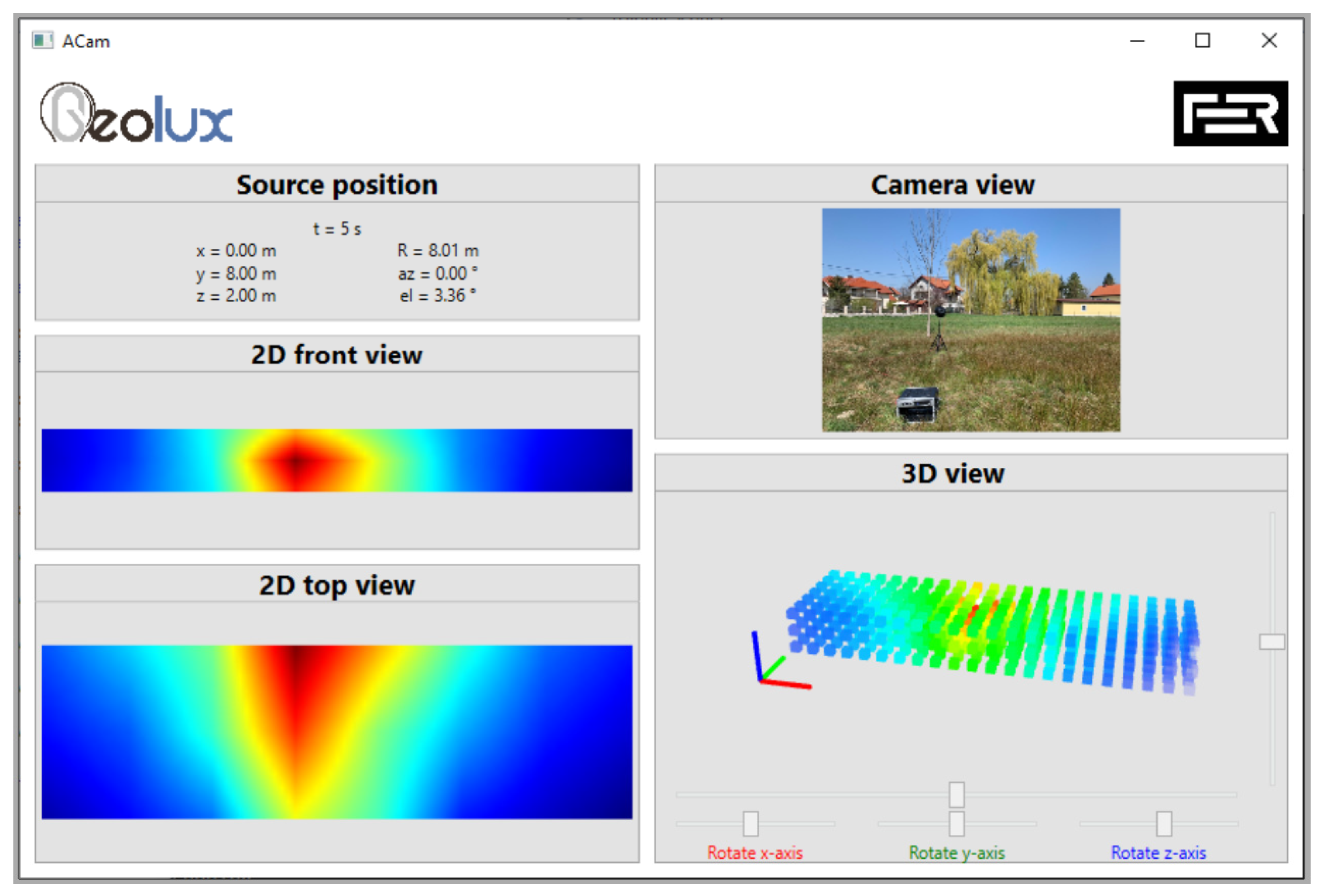
3.2. The Measurement Results of Acoustic Camera Prototypes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Organized Crime around the World. Available online: http://old.heuni.fi/material/attachments/heuni/reports/6KdD32kXX/Hreport_31.pdf (accessed on 24 January 2022).
- Agius, C. Ordering without bordering: Drones, the unbordering of late modern warfare and ontological insecurity. Postcolonial Stud. Abbr. J. Name 2017, 20, 370–386. [Google Scholar] [CrossRef]
- Park, S.; Kim, Y.; Lee, K.; Smith, A.H.; Dietz, J.E.; Matson, E.T. Accessible Real-Time Surveillance Radar System for Object Detection. Sensors 2020, 20, 2215. [Google Scholar] [CrossRef] [PubMed]
- Zyczkowski, M.; Szustakowski, M.; Ciurapinski, W.; Karol, M.; Markowski, P. Integrated radar-camera security system: Range test. In Radar Sensor Technology XVI. International Society for Optics and Photonics; SPIE Defense, Security, and Sensing: Baltimore, MD, USA, 2012. [Google Scholar] [CrossRef]
- Perimeter Security Sensor Technologies Handbook. Available online: https://www.ojp.gov/ncjrs/virtual-library/abstracts/perimeter-security-sensor-technologies-handbook (accessed on 24 January 2022).
- Lohar, S.; Zhu, L.; Young, S.; Graf, P.; Blanton, M. Sensing Technology Survey for Obstacle Detection in Vegetation. Future Transp. 2021, 1, 672–685. [Google Scholar] [CrossRef]
- Koutrouvelis, A.I.; Sherson, T.W.; Heusdens, R.; Hendriks, R.C. A Low-Cost Robust Distributed Linearly Constrained Beamformer for Wireless Acoustic Sensor Networks with Arbitrary Topology. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1434–1448. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Huang, J.; Song, E.; Liu, H.; Li, B.; Yuan, X. Design of Small MEMS Microphone Array Systems for Direction Finding of Outdoors Moving Vehicles. Sensors 2014, 14, 4384–4398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zu, X.; Guo, F.; Huang, J.; Zhao, Q.; Liu, H.; Li, B.; Yuan, X. Design of an Acoustic Target Intrusion Detection System Based on Small-Aperture Microphone Array. Sensors 2017, 17, 514. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perez, P.G.; Cuinas, I. Degradation of ground-based RADAR performance due to vegetation cover. Measurement 2016, 92, 230–235. [Google Scholar] [CrossRef]
- Norsonic Acoustic Camera. Available online: https://web2.norsonic.com/product_single/acoustic-camera/ (accessed on 10 January 2022).
- Acoustic Camera—The Original. Available online: https://www.gfaitech.com/products/acoustic-camera (accessed on 10 January 2022).
- Product Data: BK Connect Acoustic Camera (BP2534). Available online: https://www.bksv.com/-/media/literature/Product-Data/bp2534.ashx (accessed on 10 January 2022).
- Tontiwattnakul, K.; Hongweing, J.; Trakulsatjawat, P.; Noimai, P. Design and build of a planar acoustic camera using digital microphones. In Proceedings of the 2019 5th International Conference on Engineering, Applied Sciences and Technology (ICEAST), Luang Prabang, Laos, 2–5 July 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Bauer, R.; Zhang, Y.; Jackson, J.C.; Whitmer, W.M.; Brimijoin, W.O.; Akeroyd, M.A.; Uttamchandani, D.; Windmill, J.F.C. Influence of Microphone Housing on the Directional Response of Piezoelectric MEMS Microphones Inspired by Ormia Ochracea. IEEE Sens. J. 2017, 17, 5529–5536. [Google Scholar] [CrossRef]
- Tutorial for MEMS Microphones. Available online: https://www.st.com/resource/en/application_note/dm00103199-tutorial-for-mems-microphones-stmicroelectronics.pdf (accessed on 22 December 2021).
- Walser, S.; Siegel, C.; Winter, M.; Feiertag, G.; Loibl, M.; Leidl, A. MEMS microphones with narrow sensitivity distribution. Sens. Actuators A Phys. 2016, 247, 663–670. [Google Scholar] [CrossRef]
- Industry’s Strongest MEMS Microphone Portfolio Driven by TDK. Available online: https://invensense.tdk.com/news-media/industrys-strongest-mems-microphone-portfolio-driven-by-tdk/ (accessed on 22 December 2021).
- Stamac, J.; Grubesa, S.; Petosic, A. Designing the Acoustic Camera using MATLAB with respect to different types of microphone arrays. In Proceedings of the 2019 2nd International Colloquium on Smart Grid Metrology (SMAGRIMET), Split, Croatia, 9–12 April 2019. [Google Scholar]
- Grubesa, S.; Stamac, J.; Suhanek, M. Acoustic Camera Design with Different Types of MEMS Microphone Arrays. Am. J. Environ. Sci. Eng. 2019, 3, 88–93. [Google Scholar] [CrossRef]
- Brandstein, M.; Ward, D. Microphone Arrays: Signal Processing Techniques and Applications; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Vaca, K.; Jefferies, M.M.; Yang, X. An Open Audio Processing Platform with Zync FPGA. In Proceedings of the 2019 IEEE International Symposium on Measurement and Control in Robotics (ISMCR), Houston, TX, USA, 19–21 September 2019; pp. D1-2-1–D1-2-6. [Google Scholar] [CrossRef]
- Zhang, J.; Ning, G.; Zhang, S. Design of Audio Signal Processing and Display System Based on SoC. In Proceedings of the 4th International Conference on Computer Science and Network Technology (ICCSNT), Virtual, 22–23 October 2015; pp. 824–828. [Google Scholar]
- Björklund, S. Signal Processing for Radar with Array Antennas and for Radar with Micro-Doppler Measurements. Ph.D. Dissertation, Blekinge Institute of Technology, Faculty of Engineering, Department of Mathematics and Natural Sciences, Swedish Defence Research, Karlskrona, Sweden, 2017. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Reading: Boston, MA, USA, 1989. [Google Scholar]
- Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]
- Zhao, L.; Benesty, J.; Chen, J. Optimal design of directivity patterns for endfire linear microphone arrays. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 295–299. [Google Scholar] [CrossRef]
- Thomas, M.R.P.; Ahrens, J.; Tashev, I.J. Beamformer Design Using Measured Microphone Directivity Patterns: Robustness to Modelling Error. In Proceedings of the 2012 Asia Pacific Signal and Information Processing Association Annual Summit and Conference, Hollywood, CA, USA, 3–6 December 2012. [Google Scholar]
- Parthy, A.; Jin, C.; Schaik, A. Measured and theoretical performance comparison of a co-centred rigid and open spherical microphone array. In Proceedings of the 2008 International Conference on Audio, Language and Image Processing, Shanghai, China, 7–9 July 2008; pp. 1289–1294. [Google Scholar] [CrossRef]

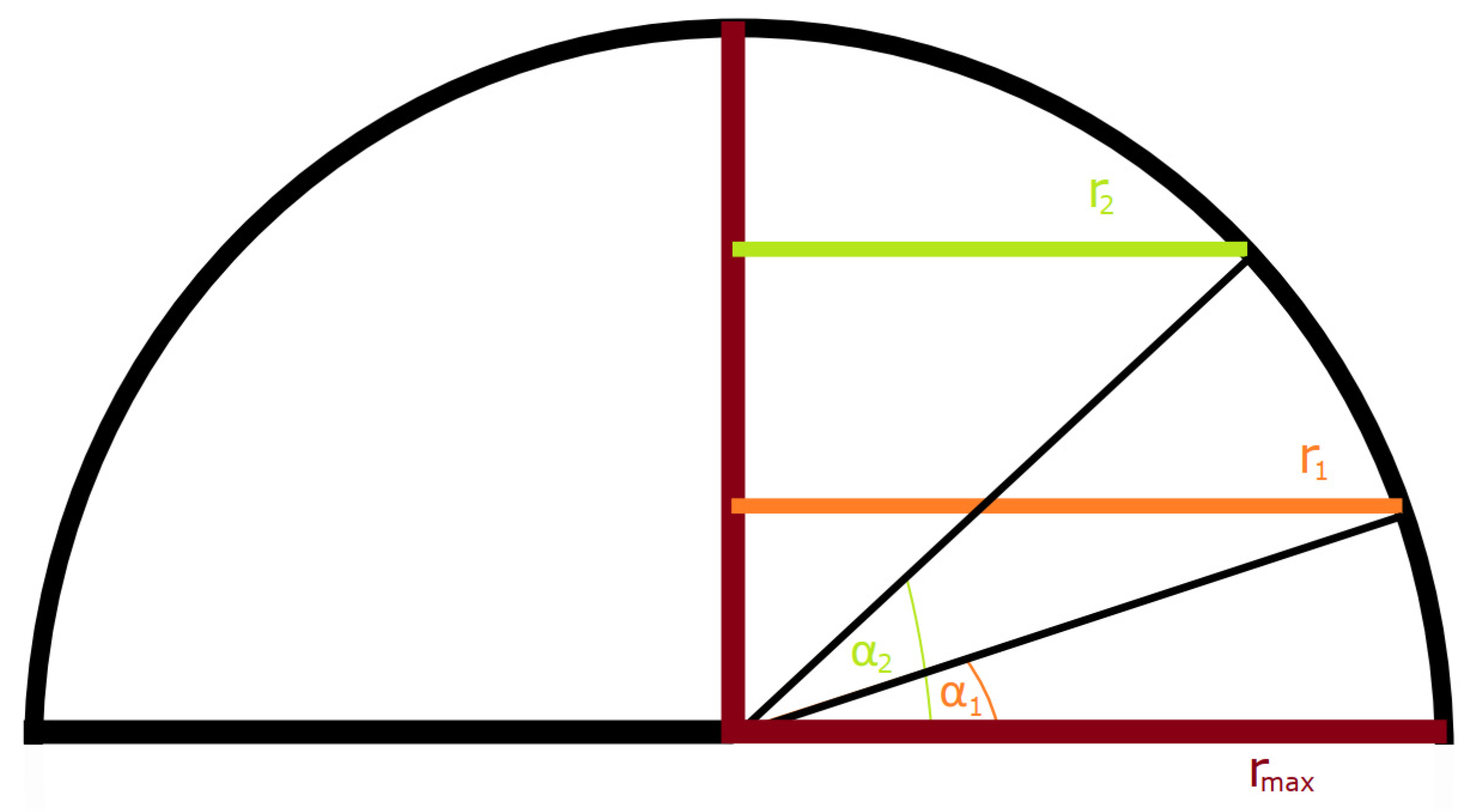










| rmax | 0.200 m |
| d | 0.170 m |
| α1 | 20° |
| r1 | 0.188 m |
| n1 | 7 |
| α2 | 35° |
| r2 | 0.164 m |
| n2 | 6 |
| G | 13.2 dBi |
| A | 16.3 dBi |
| n | 14 |
| Population Mark | Population Size = x (Best from Previous Iteration) + y (New Ones Created Using Crossover) + z (New Ones Created Randomly) |
|---|---|
| 1 | 40 = 12 + 12 + 16 |
| 2 | 40 = 4 + 12 + 24 |
| 3 | 40 = 4 + 4 + 32 |
| 4 | 40 = 2 + 12 + 26 |
| 5 | 40 = 4 + 12 + 24 STEP 1° |
| Population Mark | Population Size = x (Best from Previous Iteration) + y (New Ones Created Using Crossover) + z (Newly Created Randomly) | Score SC1 and the Overall Score SC |
|---|---|---|
| 2 | 40 = 4 + 12 + 24 | SC1: [15.2827 17.2282 18.6894] SC: 51.2003 |
| 4 | 40 = 2 + 12 + 26 | SC1: [14.8595 17.3148 18.9160] SC: 51.0903 |
| 3 | 40 = 4 + 4 + 32 | SC1: [16.8706 16.4777 17.7411] SC: 51.0894 |
| 1 | 40 = 12 + 12 + 16 | SC1: [16.7452 16.7217 17.6133] SC: 51.0802 |
| 5 | 40 = 4 + 12 + 24 STEP 1° | SC1: [16.5735 16.4258 17.6911] SC: 50.6904 |
| Population Mark | The Circle Position on the Acoustic Camera [°] and the Number of Microphones (in Brackets) | The Total Number of Microphones on the Acoustic Camera |
|---|---|---|
| 2 | 0° (48), 65° (24) | 48 + 24 = 72 |
| 4 | 0° (45), 65° (15) | 45 + 15 = 60 |
| 3 | 35° (33), 90° (1) | 33 + 1 = 34 |
| 1 | 35° (30) | 30 |
| 5 | 33° (35), 90° (1) | 35 + 1 = 36 |
| Frequency (Hz) | 1000 | 2000 | 4000 | |||
|---|---|---|---|---|---|---|
| G (dBi) | A (dBi) | G (dBi) | A (dBi) | G (dBi) | A (dBi) | |
| Square array with 12 microphones | 8.8709 | N/A | 13.8558 | 14.8744 | 14.3310 | 11.8358 |
| Square array with 24 microphones | 8.2234 | N/A | 13.5240 | 17.9620 | 18.5997 | 13.0778 |
| Square array with 48 microphones | 7.8124 | N/A | 13.1172 | 17.9620 | 18.5501 | 13.0778 |
| SC1 (1 kHz) | SC1 (2 kHz) | SC1 (4 kHz) | SC | |
|---|---|---|---|---|
| Square array with 12 microphones | 13.5484 | 16.5340 | 16.5215 | 46.6038 |
| Square array with 24 microphones | 13.2894 | 16.6071 | 18.3117 | 48.2082 |
| Square array with 48 microphones | 13.1249 | 16.4444 | 18.2919 | 47.8612 |
| Frequency (Hz) | 1000 | 2000 | 4000 | |||
|---|---|---|---|---|---|---|
| G (dBi) | A (dBi) | G (dBi) | A (dBi) | G (dBi) | A (dBi) | |
| Acoustic Camera 1 | 11.6869 | 9.1196 | 15.8550 | 13.2938 | 19.5723 | 12.9075 |
| Acoustic Camera 2 | 13.3476 | 23.6101 | 18.4138 | 15.7453 | 23.6812 | 15.2169 |
| Acoustic Camera 3 | 12.7201 | 27.0348 | 18.1426 | 21.2696 | 23.3653 | 18.4144 |
| SC1 (1 kHz) | SC1 (2 kHz) | SC1 (4 kHz) | SC | |
|---|---|---|---|---|
| Acoustic Camera 1 | 15.2827 | 17.2282 | 18.6894 | 51.2003 |
| Acoustic Camera 2 | 16.9130 | 18.4152 | 20.4869 | 55.8151 |
| Acoustic Camera 3 | 16.8904 | 18.6750 | 20.5737 | 56.1391 |
| Sound Source—Loudspeaker Sphere at a Distance R = 8 m—Pink Noise | ||
|---|---|---|
| The Placement of Loudspeaker Sphere with Respect to the Sound Level Meter and Acoustic Camera | Sound Level Meter Measurement Values LZeq [dB] | Acoustic Camera Prototype Measurement Values LZeq [dB] |
| 0° | 83.4 | 83 |
| 15° left | 83.4 | 84 |
| 30° left | 83.5 | 84 |
| 45° left | 83.3 | 85 |
| 60° left | 83.5 | 85 |
| 75° left | 84.4 | 85 |
| 90° left | 84.0 | 86 |
| 15° right | 83.6 | 84 |
| 30° right | 83.2 | 84 |
| 45° right | 83.8 | 84 |
| 60° right | 83.8 | 86 |
| 75° right | 83.8 | 85 |
| 90° right | 84.0 | 86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grubeša, S.; Stamać, J.; Suhanek, M.; Petošić, A. Use of Genetic Algorithms for Design an FPGA-Integrated Acoustic Camera. Sensors 2022, 22, 2851. https://doi.org/10.3390/s22082851
Grubeša S, Stamać J, Suhanek M, Petošić A. Use of Genetic Algorithms for Design an FPGA-Integrated Acoustic Camera. Sensors. 2022; 22(8):2851. https://doi.org/10.3390/s22082851
Chicago/Turabian StyleGrubeša, Sanja, Jasna Stamać, Mia Suhanek, and Antonio Petošić. 2022. "Use of Genetic Algorithms for Design an FPGA-Integrated Acoustic Camera" Sensors 22, no. 8: 2851. https://doi.org/10.3390/s22082851
APA StyleGrubeša, S., Stamać, J., Suhanek, M., & Petošić, A. (2022). Use of Genetic Algorithms for Design an FPGA-Integrated Acoustic Camera. Sensors, 22(8), 2851. https://doi.org/10.3390/s22082851








