Denoising for 3D Point Cloud Based on Regularization of a Statistical Low-Dimensional Manifold
Abstract
:1. Introduction
- (1)
- A denoising algorithm was designed for Gaussian noise and Laplace noise to denoise the two kinds of noise together;
- (2)
- Using the regularization term of the manifold and the fidelity term of the noise, the basic structure of a denoised point cloud was maintained;
- (3)
- Discrete sampling was used to construct low-dimensional manifolds to avoid a large number of calculations.
2. Related Works
3. Methods
3.1. Low-Dimensional Manifold Model
3.2. Point Cloud Denoising Model
3.2.1. 3D Point Cloud and Noise Model
3.2.2. Statistical Low-Dimensional Manifold Model
3.3. Solution of Point Cloud Denoising Model
3.3.1. Solution Principle
3.3.2. Algorithm Design
| Algorithm 1: Denoising for 3D point cloud based on R- |
| Input: , , , , . Output: Denoised cloud . 1: Initializing with ; 2: for = 1, 2, … do; 3: Sampling points from as a block center; 4: Find the nearest neighbors of the center of each block to form a surface block; 5: Optimizing objective function: , subject to: ; 6: ; 7:; 8: ; ; 9: converges; 10: end for |
3.3.3. Performance Evaluation
4. Results and Discussion
4.1. Comparative Analysis of Denoising Performance
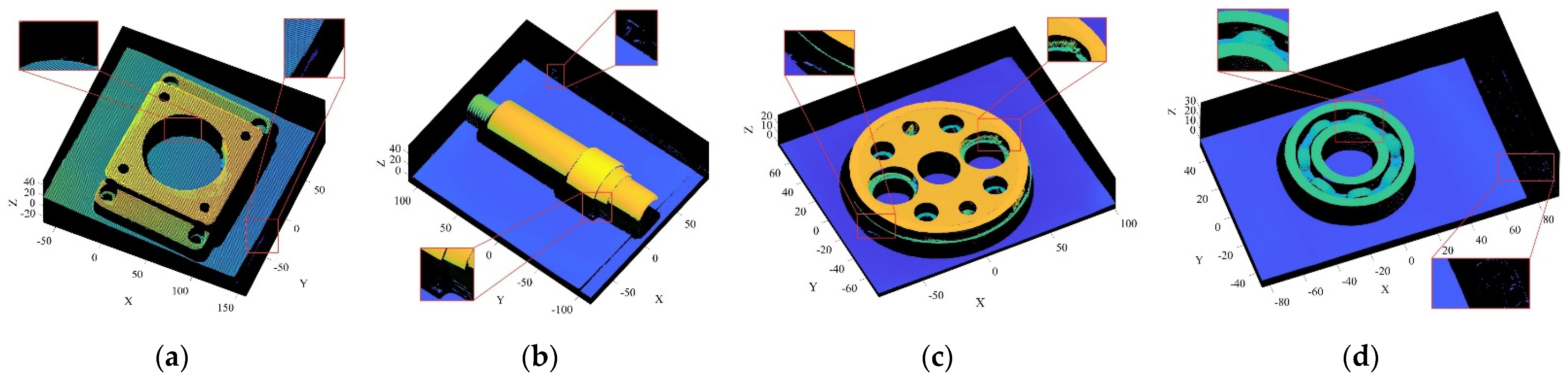
4.2. Denoising Application for 3D Point Cloud
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| observation image | |
| position matrix of block center | |
| , , | constant |
| number | |
| dimension of block manifold | |
| distance threshold | |
| diagonal matrix | |
| coordinate function | |
| Gaussian noise | |
| count | |
| number of nearest fields | |
| Laplace noise | |
| Laplacian matrix of combined graph | |
| global graph Laplace matrix | |
| number of samples | |
| position of point cloud | |
| point cloud with noise | |
| number of samples | |
| number of samples of ground-truth point cloud | |
| number of samples of observed point cloud after denoising | |
| block set | |
| point of | |
| block coordinates | |
| position matrix of point cloud | |
| midpoint coordinate vector in x-direction | |
| midpoint coordinate vector in y-direction | |
| midpoint coordinate vector in z-direction | |
| index of coordinates, | |
| radius of neighborhood | |
| number field with size of | |
| number field with size of | |
| sampling rate of block center | |
| length of pixel block | |
| width of pixel block | |
| sampling matrix | |
| average distance | |
| multiple threshold of standard deviation | |
| image | |
| set of ground-truth point cloud | |
| set of observed point cloud after denoising | |
| ideal model | |
| edge weight | |
| adjacency matrix | |
| pixel | |
| coordinate function, = 1,…, | |
| constant | |
| manifold dimension | |
| perturbing noise. | |
| reset parameter | |
| maximum number of iteration | |
| parameter | |
| parameter in penalty item | |
| mean value of | |
| mean value of | |
| standard deviation | |
| standard deviation of | |
| standard deviation of | |
| covariance of and | |
| edge set | |
| metric operator | |
| discrete graph | |
| manifold | |
| manifold size | |
| set of point cloud with noise | |
| visible surface block | |
| pixel index |
References
- Li, J.; Zhou, Q.; Li, X.; Chen, R.; Ni, K. An improved low-noise processing methodology combined with PCL for industry inspection based on laser line scanner. Sensors 2019, 19, 3398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dumic, E.; Bjelopera, A.; Nüchter, A. Dynamic Point Cloud Compression Based on Projections, Surface Reconstruction and Video Compression. Sensors 2021, 22, 197. [Google Scholar] [CrossRef]
- Mueller, C.A.; Birk, A. Visual object categorization based on hierarchical shape motifs learned from noisy point cloud decompositions. J. Intell. Robot. Syst. 2020, 97, 313–338. [Google Scholar] [CrossRef] [Green Version]
- Ping, G.; Esfahani, M.A.; Chen, J.; Wang, H. Visual enhancement of single-view 3D point cloud reconstruction. Comput. Graph. 2022, 102, 112–119. [Google Scholar] [CrossRef]
- Lazzarotto, D.; Ebrahimi, T. Sampling color and geometry point clouds from ShapeNet dataset. arXiv 2022, arXiv:2201.06935. [Google Scholar]
- Han, S.; Huo, L.; Wang, Y.; Zhou, J.; Li, H. Rapid Reconstruction of 3D Structural Model Based on Interactive Graph Cuts. Buildings 2021, 12, 22. [Google Scholar] [CrossRef]
- Haleem, A.; Gupta, P.; Bahl, S.; Javaid, M.; Kumar, L. 3D scanning of a carburetor body using COMET 3D scanner supported by COLIN 3D software: Issues and solutions. Mater. Today Proc. 2021, 39, 331–337. [Google Scholar] [CrossRef]
- Maru, M.B.; Lee, D.; Tola, K.D.; Park, S. Comparison of depth camera and terrestrial laser scanner in monitoring structural deflections. Sensors 2020, 21, 201. [Google Scholar] [CrossRef] [PubMed]
- Neuville, R.; Bates, J.S.; Jonard, F. Estimating forest structure from UAV-mounted LiDAR point cloud using machine learning. Remote Sens. 2021, 13, 352. [Google Scholar] [CrossRef]
- Hu, S.; Xiao, S.; Zhang, A.; Deng, Y.; Wang, B. Continuous-Time Laser Frames Associating and Mapping via Multilayer Optimization. Sensors 2020, 21, 97. [Google Scholar] [CrossRef]
- Luo, S.; Hu, W. Differentiable manifold reconstruction for point cloud denoising. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 1330–1338. [Google Scholar]
- Zhou, J.; Jin, W.; Wang, M.; Liu, X.; Li, Z.; Liu, Z. Fast and Accurate Normal Estimation for Point Clouds Via Patch Stitching. Comput.-Aided Des. 2022, 142, 103121. [Google Scholar] [CrossRef]
- Zeng, J.; Cheung, G.; Ng, M.; Pang, J.; Yang, C. 3D point cloud denoising using graph Laplacian regularization of a low dimensional manifold model. IEEE Trans. Image Process. 2019, 29, 3474–3489. [Google Scholar] [CrossRef] [Green Version]
- Dinesh, C.; Cheung, G.; Bajic, I.V.; Yang, C. Fast 3D point cloud denoising via bipartite graph approximation & total variation. arXiv 2018, arXiv:1804.10831. [Google Scholar]
- Duan, C.; Chen, S.; Kovačević, J. Weighted multi-projection: 3d point cloud denoising with estimated tangent planes. arXiv 2018, arXiv:1807.00253. [Google Scholar]
- Hu, W.; Gao, X.; Cheung, G.; Guo, Z. Feature graph learning for 3D point cloud denoising. IEEE Trans. Signal Process. 2020, 68, 2841–2856. [Google Scholar] [CrossRef] [Green Version]
- Alexa, M.; Behr, J.; Cohen-Or, D.; Fleishman, S.; Levin, D.; Silva, C.T. Computing and rendering point set surfaces. IEEE Trans. Vis. Comput. Graph. 2003, 9, 3–15. [Google Scholar] [CrossRef] [Green Version]
- Guennebaud, G.; Gross, M. Algebraic point set surfaces. In Proceedings of the ACM SIGGRAPH 2007 Papers, San Diego, CA, USA, 5–9 August 2007; pp. 5–9. [Google Scholar]
- Öztireli, A.C.; Guennebaud, G.; Gross, M. Feature preserving point set surfaces based on non-linear kernel regression. Comput. Graph. Forum 2009, 28, 493–501. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Schaefer, S.; Wang, W. Denoising point sets via L0 minimization. Comput. Aided Geom. Des. 2015, 35, 2–15. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, G.; Wu, S.; Liu, Y.; Gao, Y. Guided point cloud denoising via sharp feature skeletons. Vis. Comput. 2017, 33, 857–867. [Google Scholar] [CrossRef]
- Lipman, Y.; Cohen-Or, D.; Levin, D.; Tal-Ezer, H. Parameterization-free projection for geometry reconstruction. ACM Trans. Graph. (TOG) 2007, 26, 22. [Google Scholar] [CrossRef]
- Huang, H.; Li, D.; Zhang, H.; Ascher, U.; Cohen-Or, D. Consolidation of unorganized point clouds for surface reconstruction. ACM Trans. Graph. (TOG) 2009, 28, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Wu, S.; Gong, M.; Cohen-Or, D.; Ascher, U.; Zhang, H. Edge-aware point set resampling. ACM Trans. Graph. (TOG) 2013, 32, 1–12. [Google Scholar] [CrossRef]
- Dinesh, C.; Cheung, G.; Bajić, I.V. Point cloud denoising via feature graph laplacian regularization. IEEE Trans. Image Process. 2020, 29, 4143–4158. [Google Scholar] [CrossRef] [PubMed]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Rosman, G.; Dubrovina, A.; Kimmel, R. Patch-Collaborative Spectral Point-Cloud Denoising. Comput. Graph. Forum 2013, 32, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Deschaud, J.E.; Goulette, F. Point cloud non local denoising using local surface descriptor similarity. IAPRS 2010, 38, 109–114. [Google Scholar]
- Shi, Z.; Osher, S.; Zhu, W. Generalization of the weighted nonlocal laplacian in low dimensional manifold model. J. Sci. Comput. 2018, 75, 638–656. [Google Scholar] [CrossRef]
- Osher, S.; Shi, Z.; Zhu, W. Low dimensional manifold model for image processing. SIAM J. Imaging Sci. 2017, 10, 1669–1690. [Google Scholar] [CrossRef]
- Carlsson, G.; Ishkhanov, T.; De Silva, V.; Zomorodian, A. On the local behavior of spaces of natural images. Int. J. Comput. Vis. 2008, 76, 1–12. [Google Scholar] [CrossRef]
- Shuman, D.I.; Narang, S.K.; Frossard, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Zeng, J.; Pang, J.; Sun, W.; Cheung, G. Deep graph Laplacian regularization for robust denoising of real images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Pang, J.; Cheung, G. Graph Laplacian regularization for image denoising: Analysis in the continuous domain. IEEE Trans. Image Process. 2017, 26, 1770–1785. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hein, M. Uniform convergence of adaptive graph-based regularization. In Proceedings of the International Conference on Computational Learning Theory, Pittsburgh, PA, USA, 22–25 June 2006; pp. 50–64. [Google Scholar]
- Liu, X.; Cheung, G.; Wu, X. Random walk graph Laplacian-based smoothness prior for soft decoding of JPEG images. IEEE Trans. Image Process. 2016, 26, 509–524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]







| Noise Levels | Means | |||||
|---|---|---|---|---|---|---|
| Noise | 47.31 | 46.73 | 46.14 | 45.26 | 44.96 | 46.08 |
| APSS | 48.12 | 47.52 | 46.87 | 45.96 | 45.48 | 46.79 |
| NLD | 47.93 | 46.28 | 46.71 | 45.78 | 45.38 | 46.42 |
| FGL | 48.05 | 48.29 | 46.22 | 46.75 | 45.83 | 47.03 |
| R-SLDM | 49.78 | 48.77 | 48.26 | 47.36 | 46.98 | 48.23 |
| Noise Levels | Means | |||||
|---|---|---|---|---|---|---|
| Noise | 0.196 | 0.231 | 0.283 | 0.315 | 0.356 | 0.276 |
| APSS | 0.187 | 0.216 | 0.267 | 0.289 | 0.313 | 0.255 |
| WLOP | 0.179 | 0.208 | 0.257 | 0.273 | 0.308 | 0.245 |
| FGL | 0.174 | 0.192 | 0.236 | 0.274 | 0.301 | 0.235 |
| R-SLDM | 0.139 | 0.153 | 0.162 | 0.169 | 0.172 | 0.159 |
| Noise Levels | Means | |||||
|---|---|---|---|---|---|---|
| Noise | 0. 944 | 0.921 | 0.913 | 0.895 | 0.856 | 0.906 |
| APSS | 0.954 | 0.936 | 0.967 | 0.949 | 0.913 | 0.944 |
| WLOP | 0.959 | 0.948 | 0.957 | 0.931 | 0.928 | 0.945 |
| FGL | 0.981 | 0.953 | 0.931 | 0.937 | 0.931 | 0.947 |
| R-SLDM | 0.979 | 0.983 | 0.962 | 0.961 | 0.952 | 0.967 |
| Objects | a | b | c | d | Means |
|---|---|---|---|---|---|
| Noise | 45.21 | 47.51 | 48.42 | 44.23 | 46.34 |
| APSS | 46.63 | 48.63 | 48.98 | 45.63 | 47.47 |
| NLD | 46.75 | 47.74 | 48.78 | 46.14 | 47.35 |
| FGL | 46.92 | 47.82 | 48,83 | 47.81 | 47.85 |
| R-SLDM | 47.83 | 48.64 | 49.74 | 47.73 | 48.49 |
| Objects | a | b | c | d | Means |
|---|---|---|---|---|---|
| Noise | 4.734 | 4.348 | 5.378 | 5.134 | 4.989 |
| APSS | 4.257 | 3.789 | 4.898 | 4.568 | 4.378 |
| WLOP | 4.191 | 3.695 | 4.788 | 4.414 | 4.272 |
| FGL | 3.933 | 2.978 | 3.764 | 3.789 | 3.616 |
| R-SLDM | 3.275 | 2.784 | 3.356 | 3.246 | 3.165 |
| Objects | a | b | c | d | Means |
|---|---|---|---|---|---|
| Noise | 0.884 | 0.912 | 0.878 | 0.934 | 0.902 |
| APSS | 0.913 | 0.941 | 0.918 | 0.968 | 0.935 |
| WLOP | 0.931 | 0.965 | 0.908 | 0.944 | 0.937 |
| FGL | 0.956 | 0.953 | 0.928 | 0.954 | 0.950 |
| R-SLDM | 0.975 | 0.984 | 0.956 | 0.976 | 0.973 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zou, B.; Xu, J.; Yang, S.; Li, Y. Denoising for 3D Point Cloud Based on Regularization of a Statistical Low-Dimensional Manifold. Sensors 2022, 22, 2666. https://doi.org/10.3390/s22072666
Liu Y, Zou B, Xu J, Yang S, Li Y. Denoising for 3D Point Cloud Based on Regularization of a Statistical Low-Dimensional Manifold. Sensors. 2022; 22(7):2666. https://doi.org/10.3390/s22072666
Chicago/Turabian StyleLiu, Youyu, Baozhu Zou, Jiao Xu, Siyang Yang, and Yi Li. 2022. "Denoising for 3D Point Cloud Based on Regularization of a Statistical Low-Dimensional Manifold" Sensors 22, no. 7: 2666. https://doi.org/10.3390/s22072666
APA StyleLiu, Y., Zou, B., Xu, J., Yang, S., & Li, Y. (2022). Denoising for 3D Point Cloud Based on Regularization of a Statistical Low-Dimensional Manifold. Sensors, 22(7), 2666. https://doi.org/10.3390/s22072666







