Machine Learning Meets Compressed Sensing in Vibration-Based Monitoring
Abstract
:1. Introduction
Contribution
- Input data. It is investigated how CS methodologies, which reduce the probability of network congestion, may affect the classification process. Temperature values are provided as additional input data for the NN machine to inherently model the dependency of modal features on environmental factors.
- Knowledge distillation. A reduction in the complexity of the NN models is performed by shrinking the number of neurons in the hidden layers, without affecting the classification accuracy with respect to more redundant configurations.
- MEMS noise density. Acceleration waveforms are corrupted with the intrinsic noise density characterizing MEMS-based sensors, which are the most widely adopted sensing technology in this kind of application and, thus, need to be properly handled in view of real installations. Hence, the robustness of the classification process under this technological limitation is evaluated.
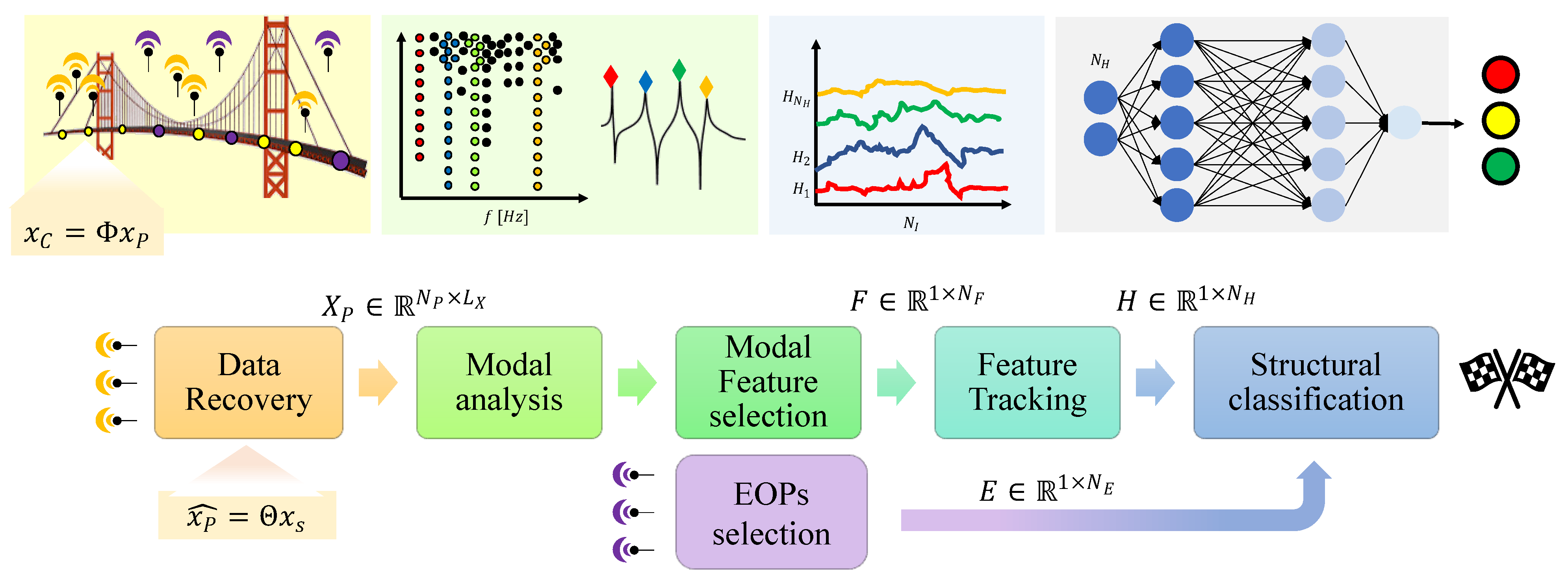
2. From Data Acquisition to Classification
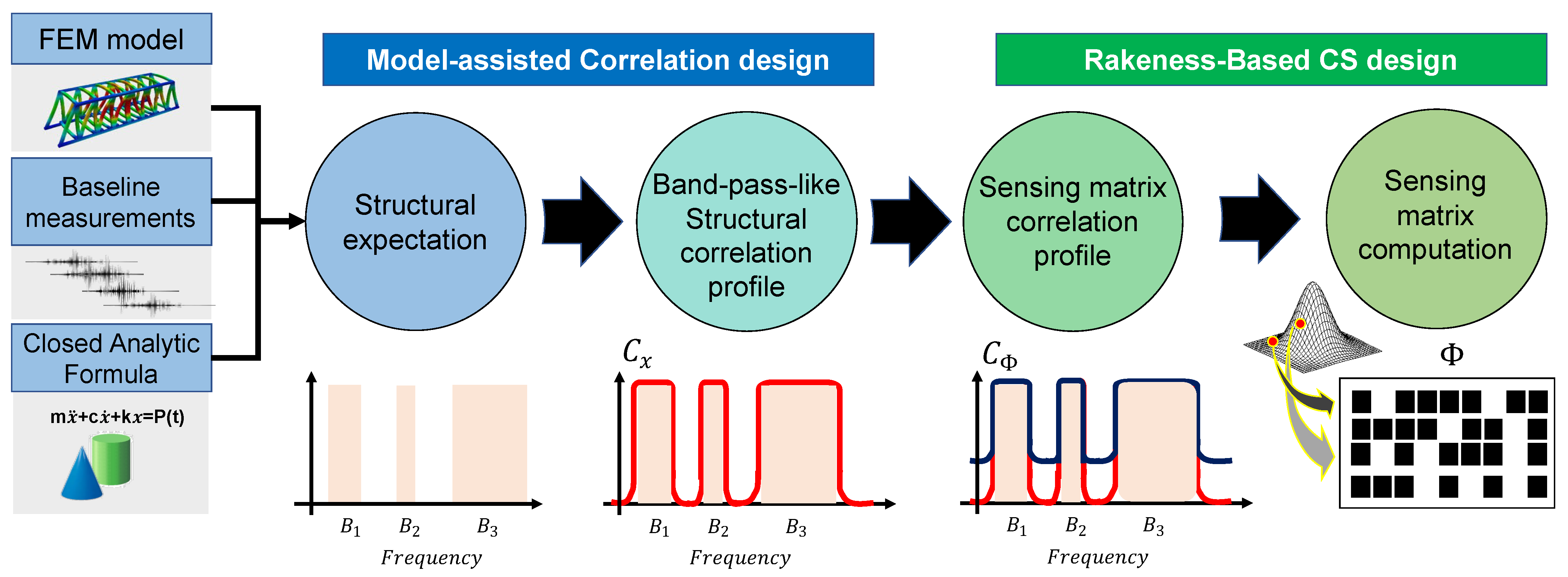
2.1. Data Compression and Recovery
2.2. Modal Parameter Extraction
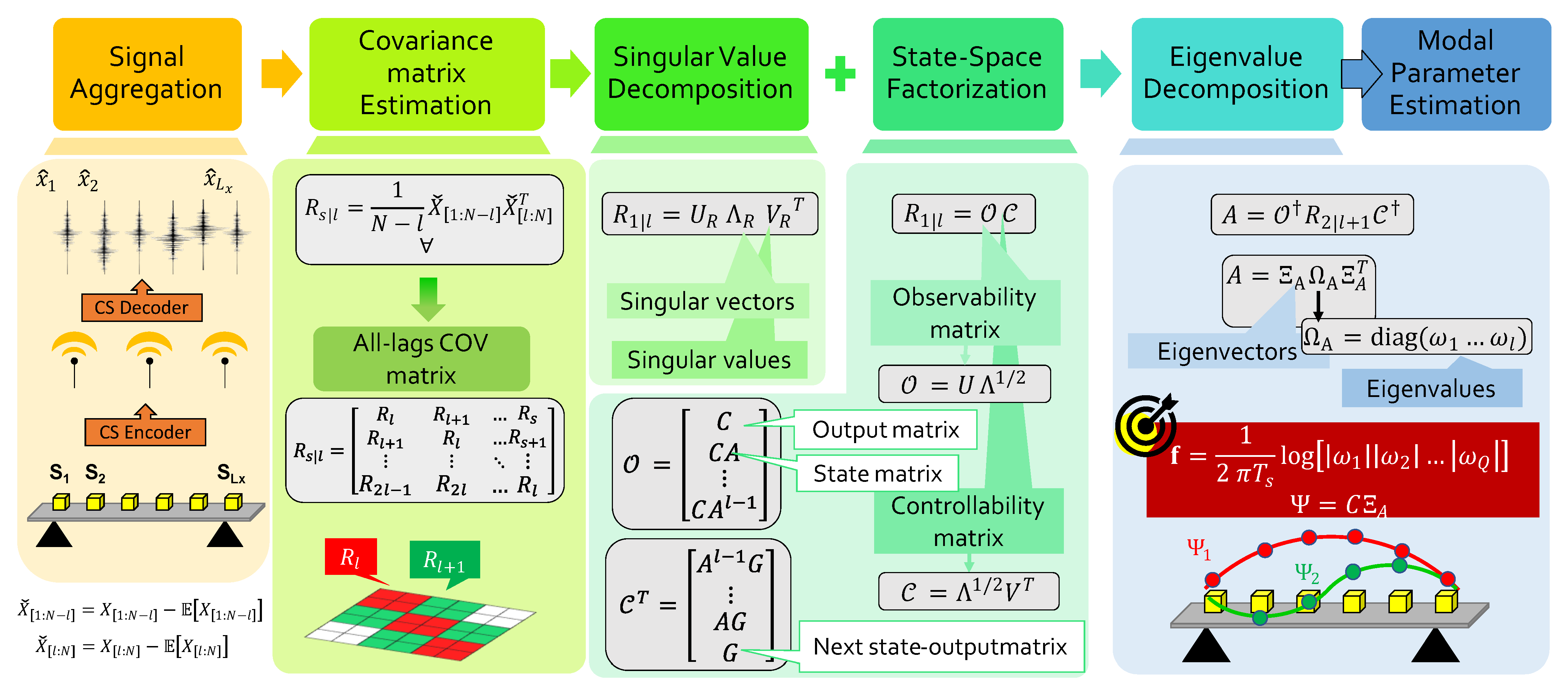
A Covariance-Based SSI Approach
- Compute, for fixed time lag l and time shift s, the block Toeplitz matrix of dimensionin which the internal blocks:are nothing but the covariance matrix between the aggregated output signals acquired in the interval and , respectively.
- Perform the Singular Value Decomposition (SVD) of (), returning , with the rectangular matrix of left singular vectors and the diagonal matrix of singular values.
- Apply the state–space factorization of the covariance matrix. Starting from the pure algebraic manipulation of the SVD, one may write . This means that can be decomposed into the product of two matrices: The so-called observability matrix and the controllability matrix . The advantage in pursuing such factorization is that the two latter quantities admit an alternative state–space formulation as and uniquely determined by the state output matrix A, the state matrixC and the next state–output matrix G. While C and G can be easily extracted from the first Q rows (columns) of the controllability and observability matrix, respectively, the computation of A is given by ( being the Moore–Penrose pseudoinverse operator).
- Execute the eigenvalue decomposition of the above-computed state matrix. This is decomposed as , corresponding to the product of the eigenvector matrix and the diagonal matrix of Q eigenvalues , namely .
- Estimate the sought natural frequencies of vibration f and mode shapes from ( being the sampling time):
2.3. Environmental Analysis
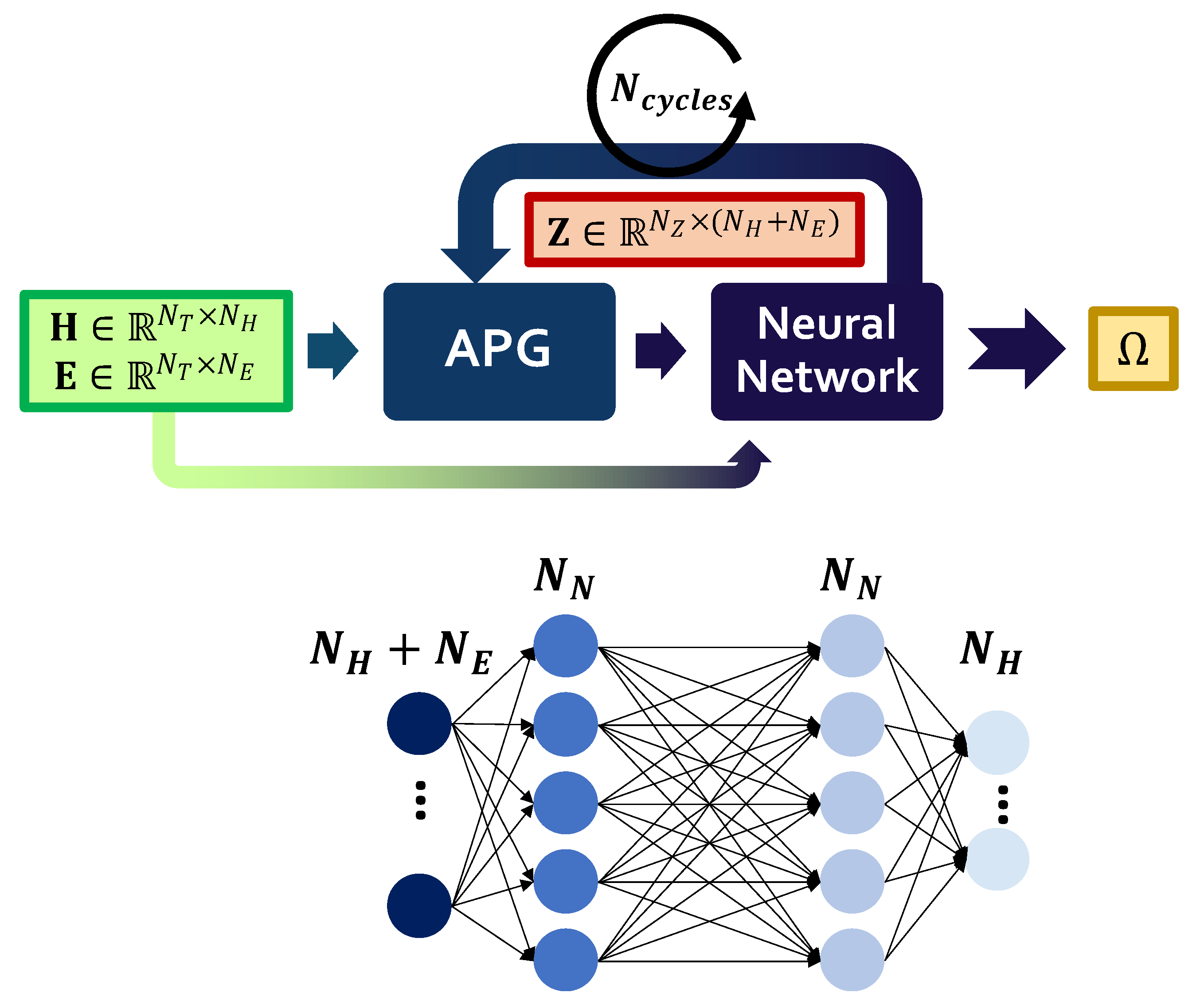
2.4. Neural Network Design
2.4.1. OCCNN
2.4.2. Autoassociative Neural Network
3. Experimental Validation
3.1. Z24-Bridge Dataset
3.2. Data Compression and Recovery
3.3. Feature Extraction
3.3.1. Modal Identification
3.3.2. EOP Selection
3.4. Neural Network Models
3.5. Noise Density in MEMS Accelerometers
4. Results
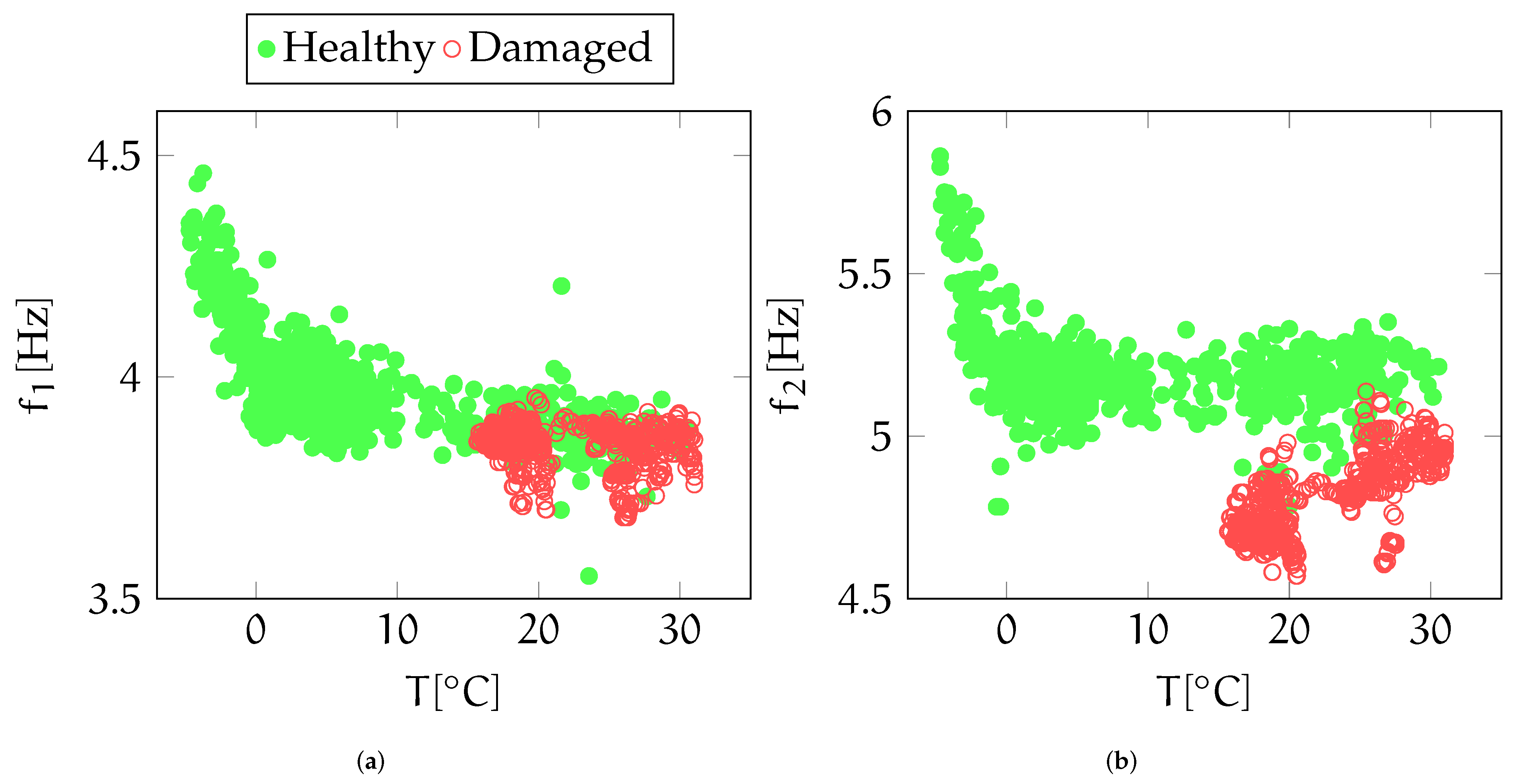
4.1. Effect of Temperature Data
4.2. Effect of Data Compression
4.3. Effect of NN Distillation
4.4. Effect of Intrinsic Noise Density in MEMS Accelerometers
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN | Autoassociative Neural Network |
| CS | Compressed Sensing |
| DCT | Discrete Cosine Transform |
| OCC | One-Class Classifier |
| OCCNN | One-Class Classifier Neural Network |
| EOP | Environmental and Operational Parameters |
| MRAK-CS | Model-assisted Rakeness-based Compressed Sensing |
| SHM | Structural Health Monitoring |
References
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Mohd Ghazali, M.H.; Rahiman, W. Vibration Analysis for Machine Monitoring and Diagnosis: A Systematic Review. Shock Vib. 2021, 2021, 9469318. [Google Scholar] [CrossRef]
- Toh, G.; Park, J. Review of vibration-based structural health monitoring using deep learning. Appl. Sci. 2020, 10, 1680. [Google Scholar] [CrossRef]
- Carvalho, T.P.; Soares, F.A.; Vita, R.; Francisco, R.d.P.; Basto, J.P.; Alcalá, S.G. A systematic literature review of machine learning methods applied to predictive maintenance. Comput. Ind. Eng. 2019, 137, 106024. [Google Scholar] [CrossRef]
- Esfandabadi, Y.K.; Bilodeau, M.; Masson, P.; Marchi, L.D. Deep learning for enhancing wavefield image quality in fast non-contact inspections. Struct. Health Monit. 2020, 19, 1003–1016. [Google Scholar] [CrossRef]
- Bloemheuvel, S.; van den Hoogen, J.; Atzmueller, M. A computational framework for modeling complex sensor network data using graph signal processing and graph neural networks in structural health monitoring. Appl. Netw. Sci. 2021, 6, 1–24. [Google Scholar] [CrossRef]
- Mylonas, C.; Tsialiamanis, G.; Worden, K.; Chatzi, E. Bayesian Graph Neural Networks for Strain-Based Crack Localization. In Data Science in Engineering; Springer: Berlin/Heidelberg, Germany, 2022; Volume 9, pp. 253–261. [Google Scholar]
- Zonzini, F.; Bogomolov, D.; Dhamija, T.; Testoni, N.; De Marchi, L.; Marzani, A. Deep Learning Approaches for Robust Time of Arrival Estimation in Acoustic Emission Monitoring. Sensors 2022, 22, 1091. [Google Scholar] [CrossRef]
- Pang, L.; Liu, J.; Harkin, J.; Martin, G.; McElholm, M.; Javed, A.; McDaid, L. Case Study—Spiking Neural Network Hardware System for Structural Health Monitoring. Sensors 2020, 20, 5126. [Google Scholar] [CrossRef]
- Barchi, F.; Zanatta, L.; Parisi, E.; Burrello, A.; Brunelli, D.; Bartolini, A.; Acquaviva, A. Spiking Neural Network-Based Near-Sensor Computing for Damage Detection in Structural Health Monitoring. Future Internet 2021, 13, 219. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, D.; Chen, M.; Hong, X. Continual Learning for Multimode Dynamic Process Monitoring with Applications to an Ultra-Supercritical Thermal Power Plant. IEEE Trans. Autom. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Li, J.; He, H.; He, H.; Li, L.; Xiang, Y. An End-to-End Framework with Multisource Monitoring Data for Bridge Health Anomaly Identification. IEEE Trans. Instrum. Meas. 2020, 70, 3500909. [Google Scholar] [CrossRef]
- Graff, K.F. Wave Motion in Elastic Solids; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures; Springer: New York, NY, USA, 2014; Volume 142, p. 143. [Google Scholar]
- Zonzini, F.; Girolami, A.; De Marchi, L.; Marzani, A.; Brunelli, D. Cluster-based Vibration Analysis of Structures with Graph Signal Processing. IEEE Trans. Ind. Electron. 2020, 68, 3465–3474. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Bao, Y.; Tang, Z.; Li, H. Compressive-sensing data reconstruction for structural health monitoring: A machine-learning approach. Struct. Health Monit. 2020, 19, 293–304. [Google Scholar] [CrossRef]
- Perelli, A.; De Marchi, L.; Flamigni, L.; Marzani, A.; Masetti, G. Best basis compressive sensing of guided waves in structural health monitoring. Digit. Signal Process. 2015, 42, 35–42. [Google Scholar] [CrossRef]
- Zonzini, F.; Zauli, M.; Mangia, M.; Testoni, N.; De Marchi, L. Model-assisted Compressed Sensing for Vibration-based Structural Health Monitoring. IEEE Trans. Ind. Inform. 2021, 17, 7338–7347. [Google Scholar] [CrossRef]
- Xu, B.; Wu, Z.; Chen, G.; Yokoyama, K. Direct identification of structural parameters from dynamic responses with neural networks. Eng. Appl. Artif. Intell. 2004, 17, 931–943. [Google Scholar] [CrossRef]
- Yu, Y.; Wu, X.; Yuan, S. Anomaly detection for internet of things based on compressed sensing and online extreme learning machine autoencoder. J. Phys. Conf. Ser. 2020, 1544, 012027. [Google Scholar] [CrossRef]
- Moussa, M.A. Data Gathering and Anomaly Detection in Wireless Sensors Networks. Ph.D. Thesis, Paris Est, Champs-sur-Marne, Marne-la-Vallée, France, 2017. [Google Scholar]
- Fowler, J.E.; Du, Q. Anomaly Detection and Reconstruction From Random Projections. IEEE Trans. Image Process. 2012, 21, 184–195. [Google Scholar] [CrossRef] [Green Version]
- Azimi, M.; Eslamlou, A.D.; Pekcan, G. Data-Driven Structural Health Monitoring and Damage Detection through Deep Learning: State-of-the-Art Review. Sensors 2020, 20, 2778. [Google Scholar] [CrossRef]
- Yuan, F.G.; Zargar, S.A.; Chen, Q.; Wang, S. Machine learning for structural health monitoring: Challenges and opportunities. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2020, International Society for Optics and Photonics, Online, 26 May 2020; Volume 11379, p. 1137903. [Google Scholar]
- Warden, P.; Situnayake, D. Tinyml: Machine Learning with Tensorflow Lite on Arduino and Ultra-Low-Power Microcontrollers; O’Reilly Media, Inc.: Newton, MA, USA, 2019. [Google Scholar]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Gentile, C.; Guidobaldi, M.; Saisi, A. One-year dynamic monitoring of a historic tower: Damage detection under changing environment. Meccanica 2016, 51, 2873–2889. [Google Scholar] [CrossRef] [Green Version]
- Plaza, E.G.; López, P.N. Surface roughness monitoring by singular spectrum analysis of vibration signals. Mech. Syst. Signal Process. 2017, 84, 516–530. [Google Scholar] [CrossRef]
- Bhowmik, B.; Krishnan, M.; Hazra, B.; Pakrashi, V. Real-time unified single-and multi-channel structural damage detection using recursive singular spectrum analysis. Struct. Health Monit. 2019, 18, 563–589. [Google Scholar] [CrossRef]
- Luong, P.; Wang, W. Smart Sensor-Based Synergistic Analysis for Rotor Bar Fault Detection of Induction Motors. IEEE/ASME Trans. Mechatron. 2020, 25, 1067–1075. [Google Scholar] [CrossRef]
- Liu, J.; Qu, F.; Hong, X.; Zhang, H. A small-sample wind turbine fault detection method with synthetic fault data using generative adversarial nets. IEEE Trans. Ind. Inform. 2018, 15, 3877–3888. [Google Scholar] [CrossRef]
- Peng, Y.; Qiao, W.; Qu, L.; Wang, J. Sensor fault detection and isolation for a wireless sensor network-based remote wind turbine condition monitoring system. IEEE Trans. Ind. Appl. 2017, 54, 1072–1079. [Google Scholar] [CrossRef]
- Iqbal, R.; Maniak, T.; Doctor, F.; Karyotis, C. Fault detection and isolation in industrial processes using deep learning approaches. IEEE Trans. Ind. Inform. 2019, 15, 3077–3084. [Google Scholar] [CrossRef]
- Lu, W.; Li, Y.; Cheng, Y.; Meng, D.; Liang, B.; Zhou, P. Early fault detection approach with deep architectures. IEEE Trans. Instrum. Meas. 2018, 67, 1679–1689. [Google Scholar] [CrossRef]
- Favarelli, E.; Giorgetti, A. Machine Learning for Automatic Processing of Modal Analysis in Damage Detection of Bridges. IEEE Trans. Instrum. Meas. 2020, 70, 2504013. [Google Scholar] [CrossRef]
- Reynders, E.; Roeck, G.D. Continuous Vibration Monitoring and Progressive Damage Testing on the Z24 Bridge. Encycl. Struct. Health Monit. 2009. [Google Scholar] [CrossRef]
- Langone, R.; Reynders, E.; Mehrkanoon, S.; Suykens, J.A. Automated structural health monitoring based on adaptive kernel spectral clustering. Mech. Syst. Signal Process. 2017, 90, 64–78. [Google Scholar] [CrossRef] [Green Version]
- Sen, D.; Erazo, K.; Zhang, W.; Nagarajaiah, S.; Sun, L. On the effectiveness of principal component analysis for decoupling structural damage and environmental effects in bridge structures. J. Sound Vib. 2019, 457, 280–298. [Google Scholar] [CrossRef]
- Swartz, R.A. Decentralized algorithms for SHM over wireless and distributed smart sensor networks. In Earthquakes and Health Monitoring of Civil Structures; Springer: Berlin/Heidelberg, Germany, 2013; pp. 109–131. [Google Scholar]
- Jayawardhana, M.; Zhu, X.; Liyanapathirana, R.; Gunawardana, U. Compressive sensing for efficient health monitoring and effective damage detection of structures. Mech. Syst. Signal Process. 2017, 84, 414–430. [Google Scholar] [CrossRef] [Green Version]
- Gade, S.; Møller, N.B.; Herlufsen, H.; Konstantin-Hansen, H. Frequency domain techniques for operational modal analysis. In Proceedings of the 1st International Operational Modal Analysis Conference, Copenhagen, Denmark, 26–27 April 2005; pp. 261–271. [Google Scholar]
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Rahimian Koloor, S.S.; Petrù, M. Health Monitoring of Civil Infrastructures by Subspace System Identification Method: An Overview. Appl. Sci. 2020, 10, 2786. [Google Scholar] [CrossRef] [Green Version]
- Yi, L.; Deng, X.; Yang, L.T.; Wu, H.; Wang, M.; Situ, Y. Reinforcement-Learning-Enabled Partial Confident Information Coverage for IoT-Based Bridge Structural Health Monitoring. IEEE Internet Things J. 2020, 8, 3108–3119. [Google Scholar] [CrossRef]
- Bhowmik, B.; Tripura, T.; Hazra, B.; Pakrashi, V. Real time structural modal identification using recursive canonical correlation analysis and application towards online structural damage detection. J. Sound Vib. 2020, 468, 115101. [Google Scholar] [CrossRef]
- Favarelli, E.; Testi, E.; Giorgetti, A. One class classifier neural network for anomaly detection in low dimensional feature spaces. In Proceedings of the 2019 13th International Conference on Signal Processing and Communication Systems (ICSPCS), Gold Coast, Australia, 16–18 December 2019; pp. 1–7. [Google Scholar]
- Pollard, J. On distance estimators of density in randomly distributed forests. Biometrics 1971, 27, 991–1002. [Google Scholar] [CrossRef]
- Gu, J.; Gul, M.; Wu, X. Damage detection under varying temperature using artificial neural networks. Struct. Control Health Monit. 2017, 24, e1998. [Google Scholar] [CrossRef]
- Klis, R.; Chatzi, E.N. Vibration monitoring via spectro-temporal compressive sensing for wireless sensor networks. Struct. Infrastruct. Eng. 2017, 13, 195–209. [Google Scholar] [CrossRef]
- Van den Berg, E.; Friedlander, M.P. SPGL1: A Solver for Large-Scale Sparse Reconstruction. 2019. Available online: https://friedlander.io/spgl1 (accessed on 26 February 2022).
- Rani, M.; Dhok, S.B.; Deshmukh, R.B. A Systematic Review of Compressive Sensing: Concepts, Implementations and Applications. IEEE Access 2018, 6, 4875–4894. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Peeters, B.; De Roeck, G. One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]
- Laine, J.; Mougenot, D. Benefits of MEMS based seismic accelerometers for oil exploration. In Proceedings of the TRANSDUCERS 2007-2007 International Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007; pp. 1473–1477. [Google Scholar]
- Testoni, N.; Aguzzi, C.; Arditi, V.; Zonzini, F.; De Marchi, L.; Marzani, A.; Cinotti, T.S. A Sensor Network with Embedded Data Processing and Data-to-Cloud Capabilities for Vibration-Based Real-Time SHM. J. Sens. 2018, 2018, 2107679. [Google Scholar] [CrossRef]
- Vlahović, N.; Kvaščev, G. Noise reduction by using autoassociative neural networks. In Proceedings of the 2016 13th Symposium on Neural Networks and Applications (NEUREL), Belgrade, Serbia, 22–24 November 2016; pp. 1–5. [Google Scholar]



| Feature | Unity of Measure | MA | MB |
|---|---|---|---|
| Sensitivity @ | 61.0 | 3.9 | |
| Zero-g level offset | 40 | 25 | |
| Noise ( | 80 | 25 | |
| Zero-g change vs temperature | |||
| Sensitivity change vs temperature | [%/C] |
| ∞ | MA | MB | ||||
|---|---|---|---|---|---|---|
| Model size [] | 13.232 | 6.824 | 3.304 | 2.312 | ||
| parameters | 2852 | 1250 | 370 | 122 | ||
| Accuracy [%] | 95.73 | 96.98 | 96.04 | 97.16 | 93.49 | 90.12 |
| Precision [%] | 94.12 | 95.78 | 94.59 | 96.25 | 92.65 | 89.25 |
| Recall [%] | 99.93 | 99.93 | 99.87 | 99.67 | 99.37 | 100 |
| F1 [%] | 96.94 | 97.81 | 97.16 | 97.93 | 96.18 | 94.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zonzini, F.; Carbone, A.; Romano, F.; Zauli, M.; De Marchi, L. Machine Learning Meets Compressed Sensing in Vibration-Based Monitoring. Sensors 2022, 22, 2229. https://doi.org/10.3390/s22062229
Zonzini F, Carbone A, Romano F, Zauli M, De Marchi L. Machine Learning Meets Compressed Sensing in Vibration-Based Monitoring. Sensors. 2022; 22(6):2229. https://doi.org/10.3390/s22062229
Chicago/Turabian StyleZonzini, Federica, Antonio Carbone, Francesca Romano, Matteo Zauli, and Luca De Marchi. 2022. "Machine Learning Meets Compressed Sensing in Vibration-Based Monitoring" Sensors 22, no. 6: 2229. https://doi.org/10.3390/s22062229
APA StyleZonzini, F., Carbone, A., Romano, F., Zauli, M., & De Marchi, L. (2022). Machine Learning Meets Compressed Sensing in Vibration-Based Monitoring. Sensors, 22(6), 2229. https://doi.org/10.3390/s22062229







