Garmin GPSMAP 66sr: Assessment of Its GNSS Observations and Centimeter-Accurate Positioning
Abstract
:1. Introduction
2. Observation Data and Data Processing
3. Assessment of Observation Quality and Antenna Calibration
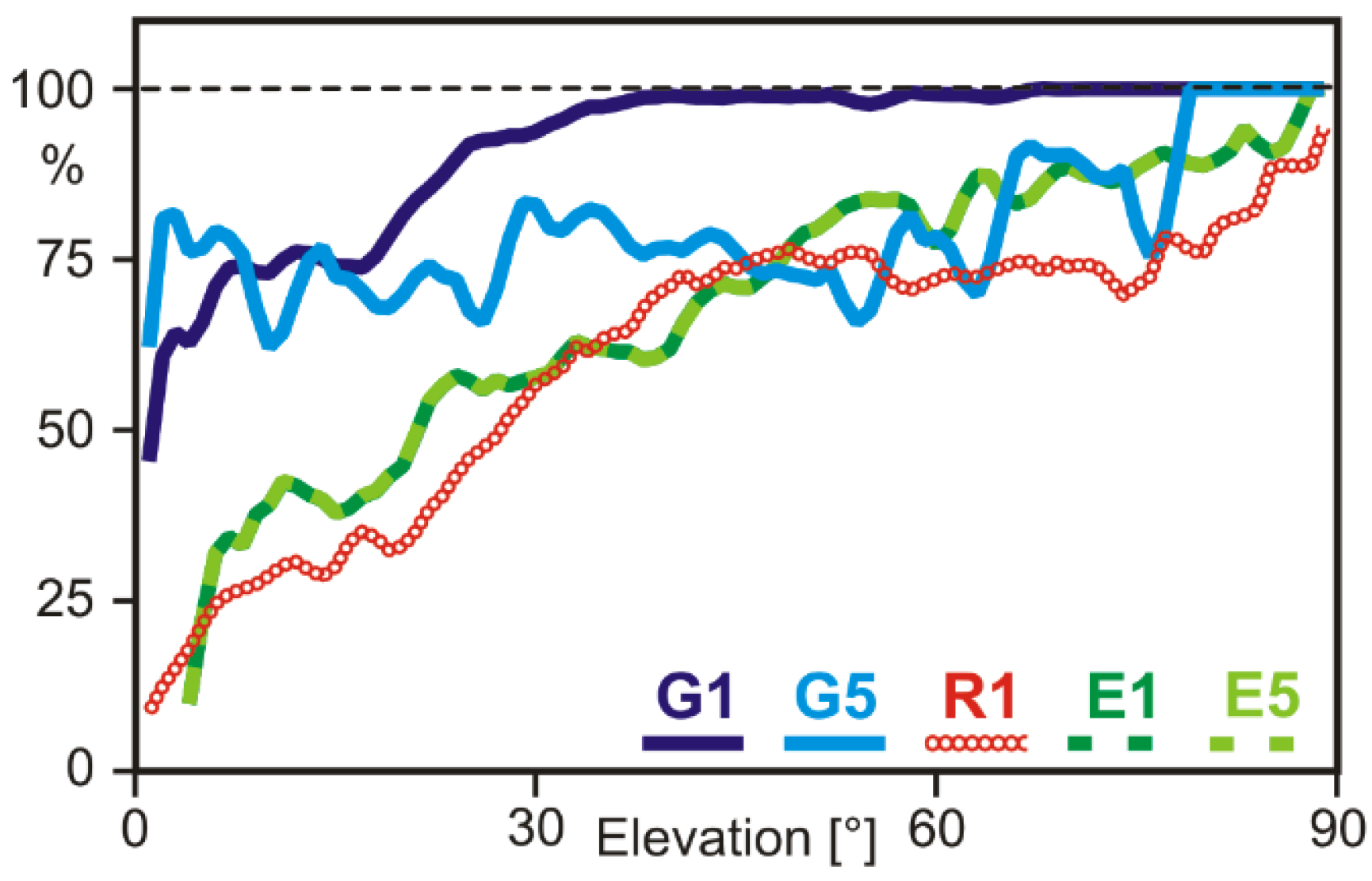
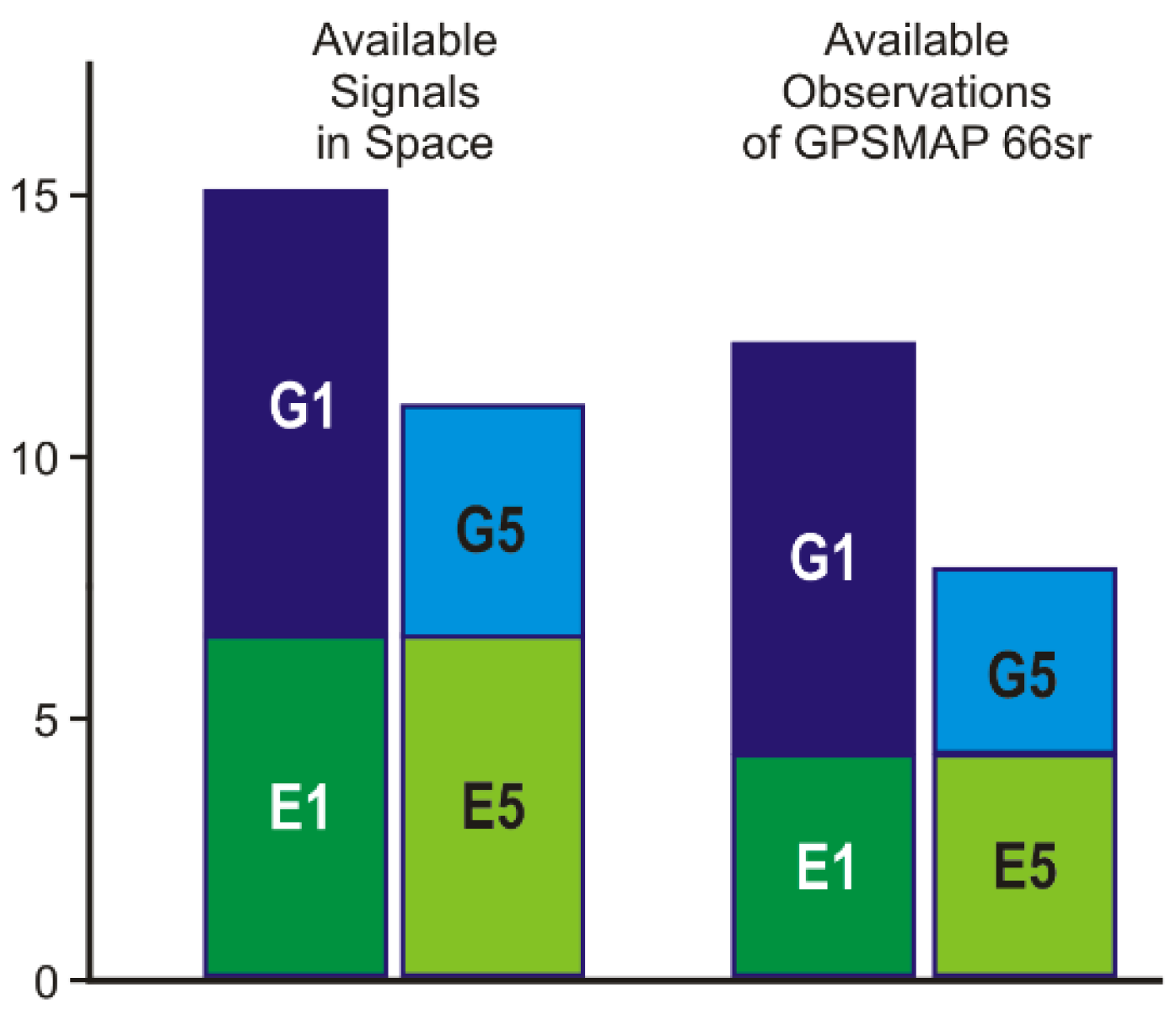
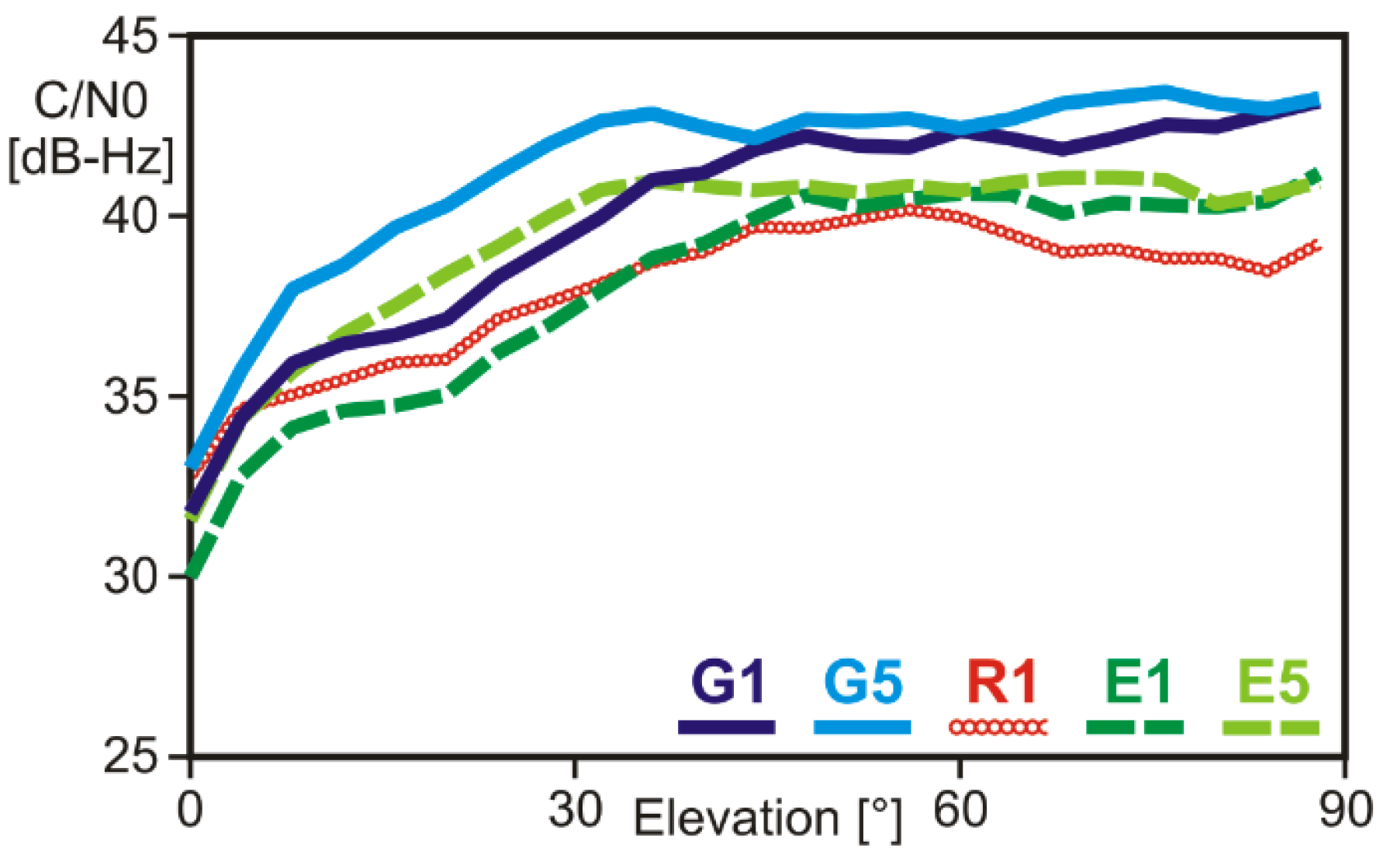
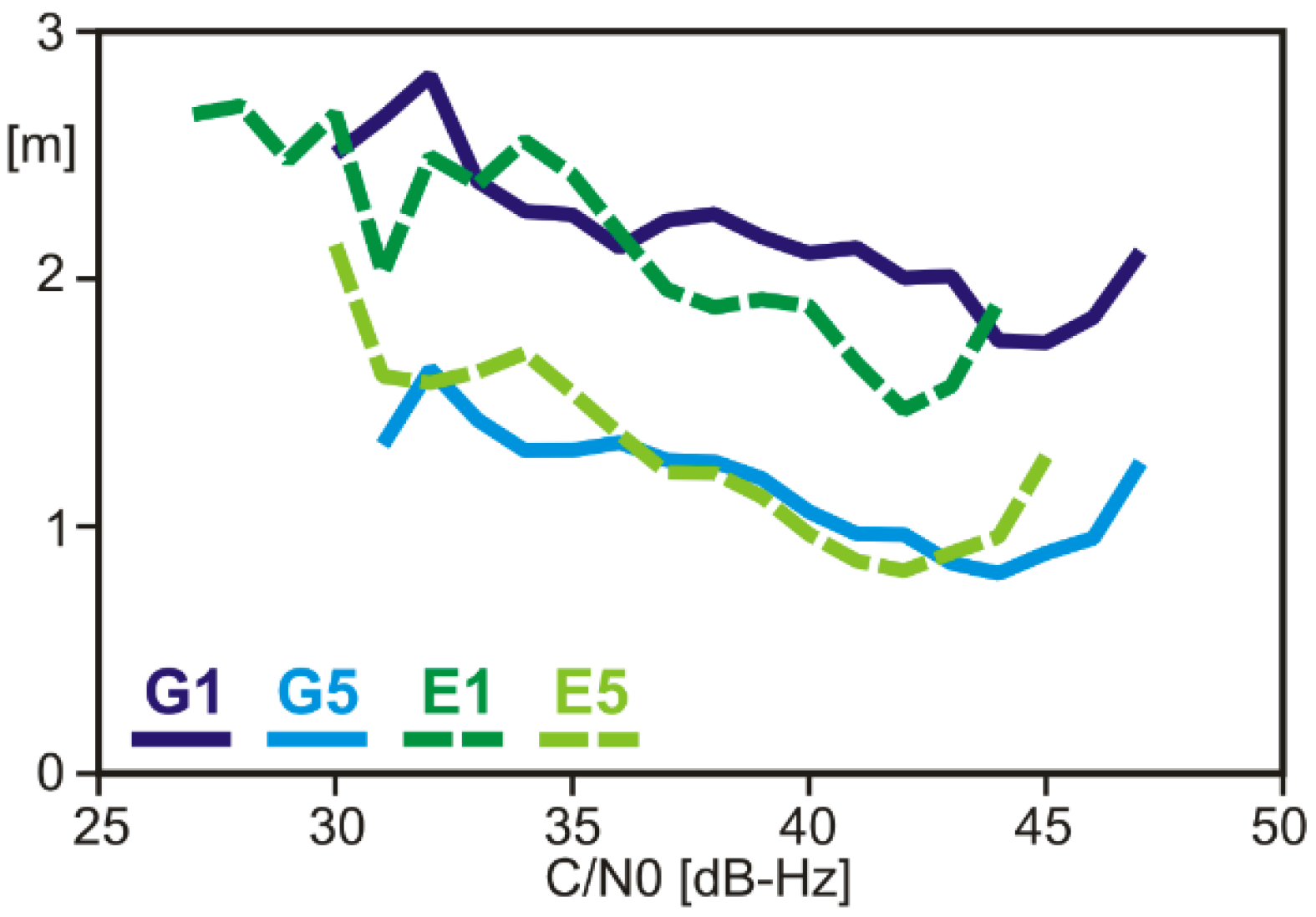
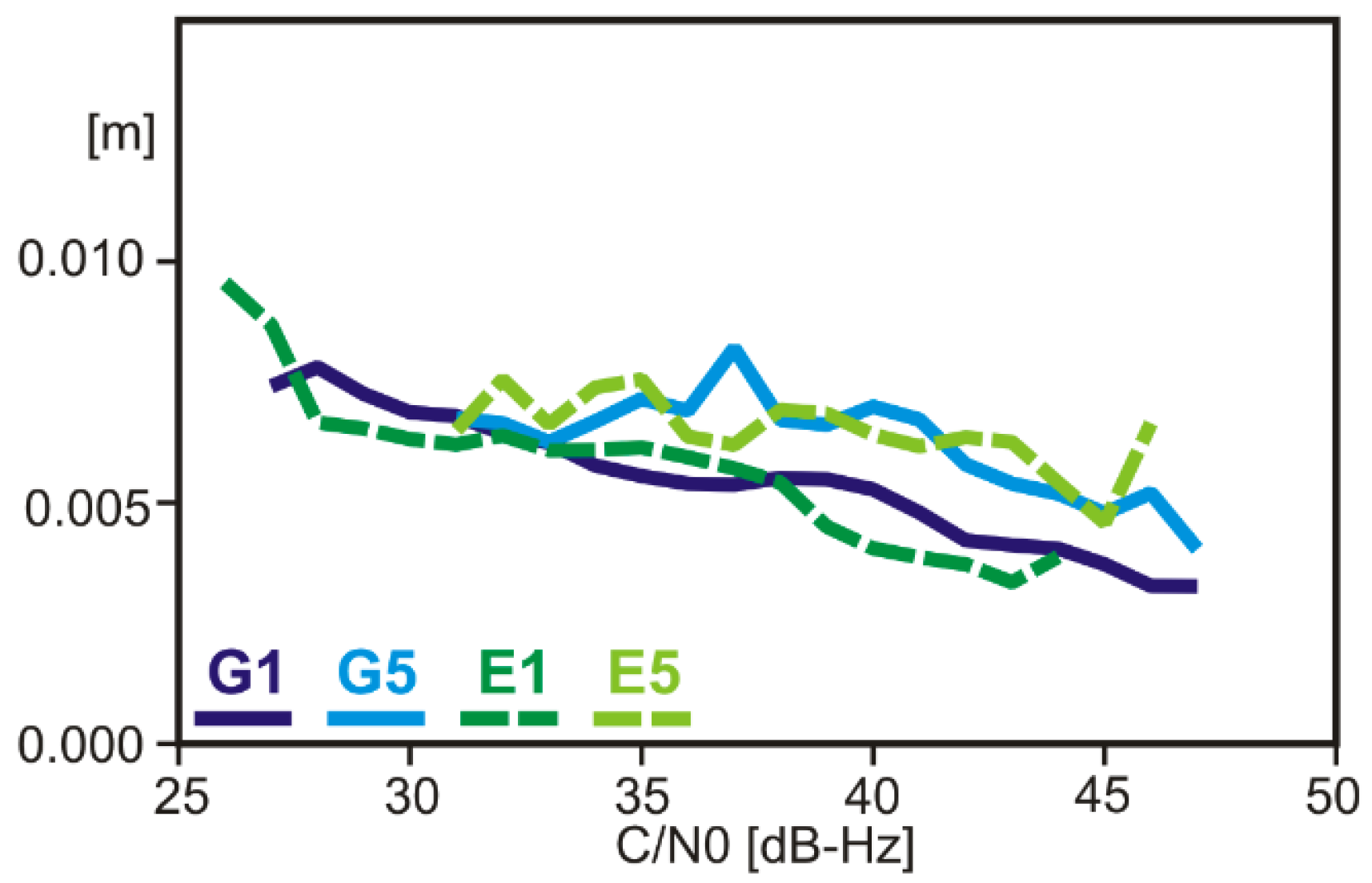
3.1. Observation Quality
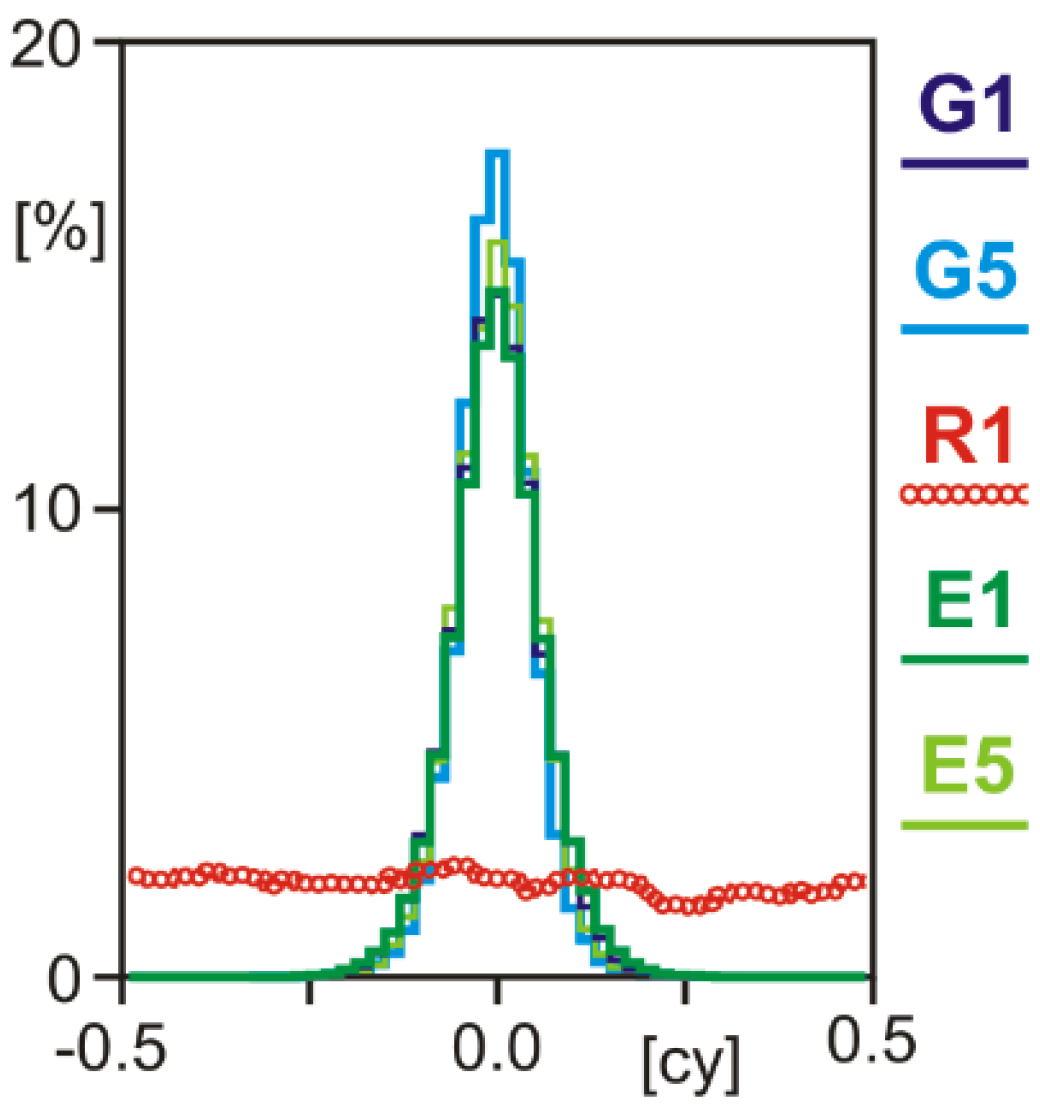
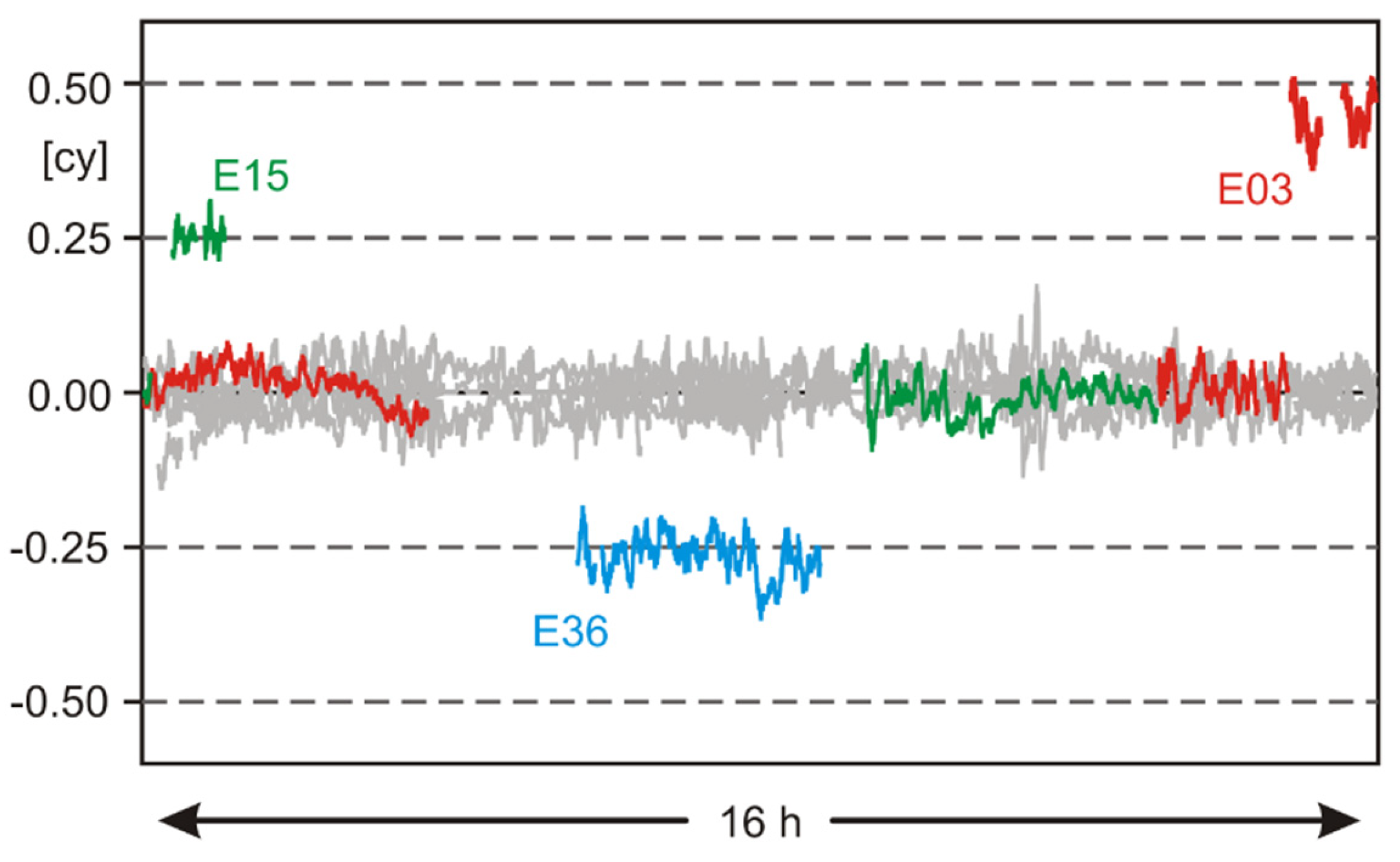
3.2. Integer Property of Estimated Ambiguities
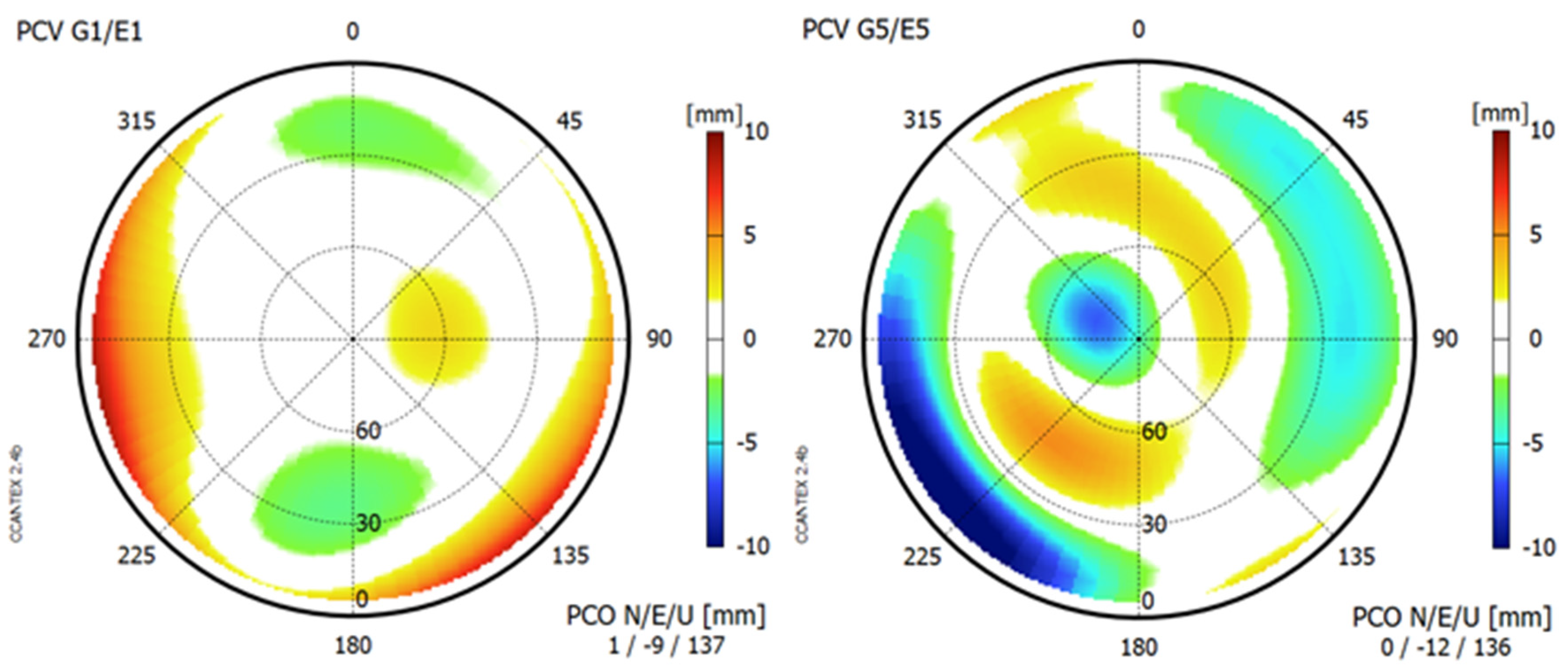
3.3. Antenna Phase-Center Calibration
4. Precise Positioning Results
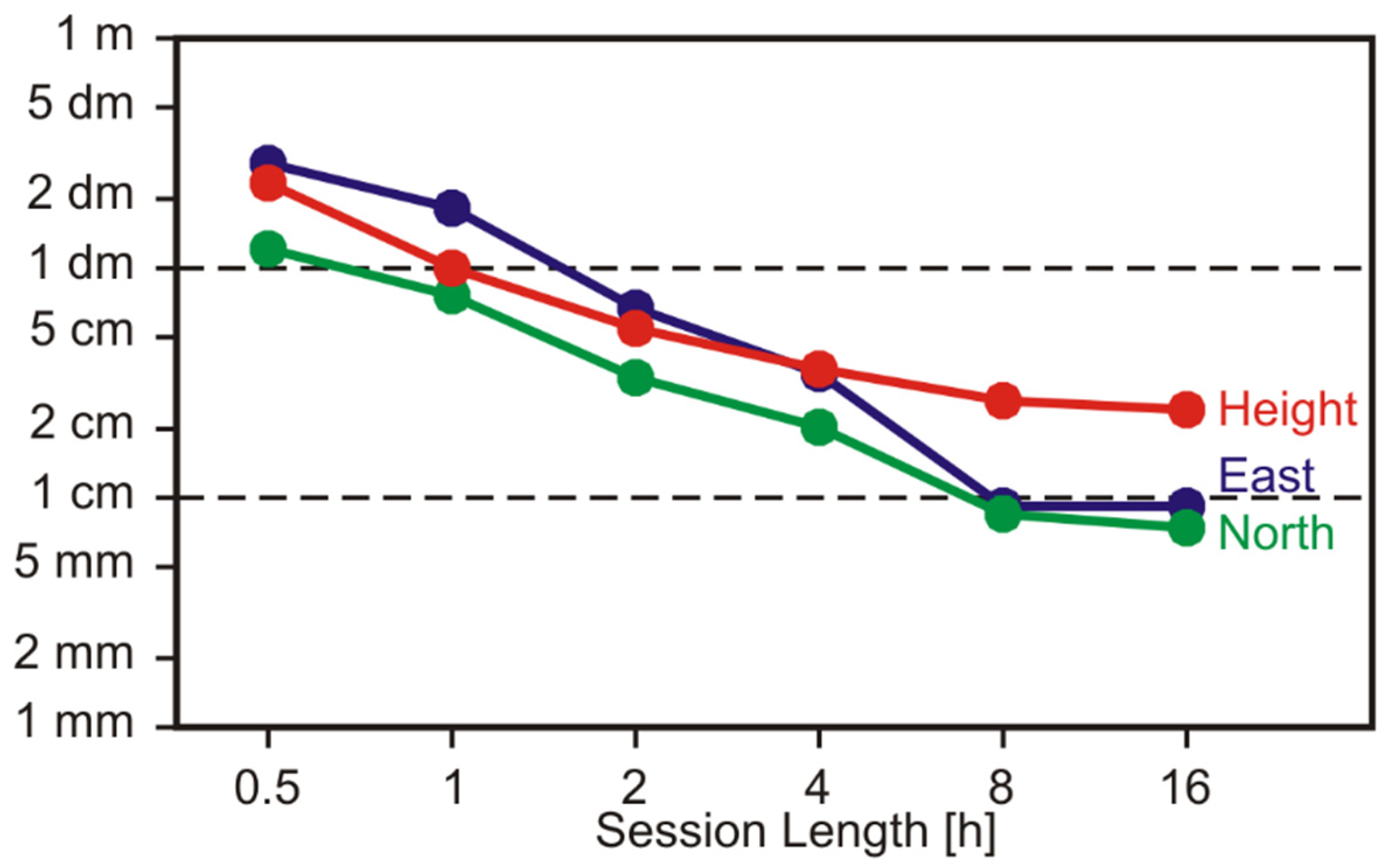
4.1. Dual-Frequency GPS/Galileo Precise Point Positioning
- The processing service does not accept G5 and/or Galileo observations but only the GPS (+GLONASS) traditional signal frequencies 1 and 2;
- The GPSMAP 66sr antenna does not belong to the group of antennas supported by the processing service.
- Code biases between different signals (frequencies and modulations), which are determined from the observation data of globally distributed GNSS reference station networks and are available either as differential code biases (DCBs) [17] or as pseudo-absolute code biases (observable-specific bias (OSB)) [18]. We applied the appropriate GPS DCBs produced by DLR and obtained from CDDIS [19], similar to their application described in [20].
- In the case of GPS Block IIF satellites, pronounced inter-frequency clock biases exist between G5 and G1/G2, with periods of several hours and amplitudes of up to many centimeters. They can be determined from triple-frequency GPS observations from a set of globally distributed GNSS reference stations, as described in [21]. For each of our observation days, we selected 10 globally distributed sites of the IGS (CIBG, DAV1, DGAR, KOUR, MAL2, MKEA, NKLG, NYA2, PNGM, and WTZS) and computed G1/G5—G1/G2 clock corrections, with a temporal resolution of 5 min. We applied them to the CODE GPS Block IIF clock corrections prior to the G1/G5 PPP processing.
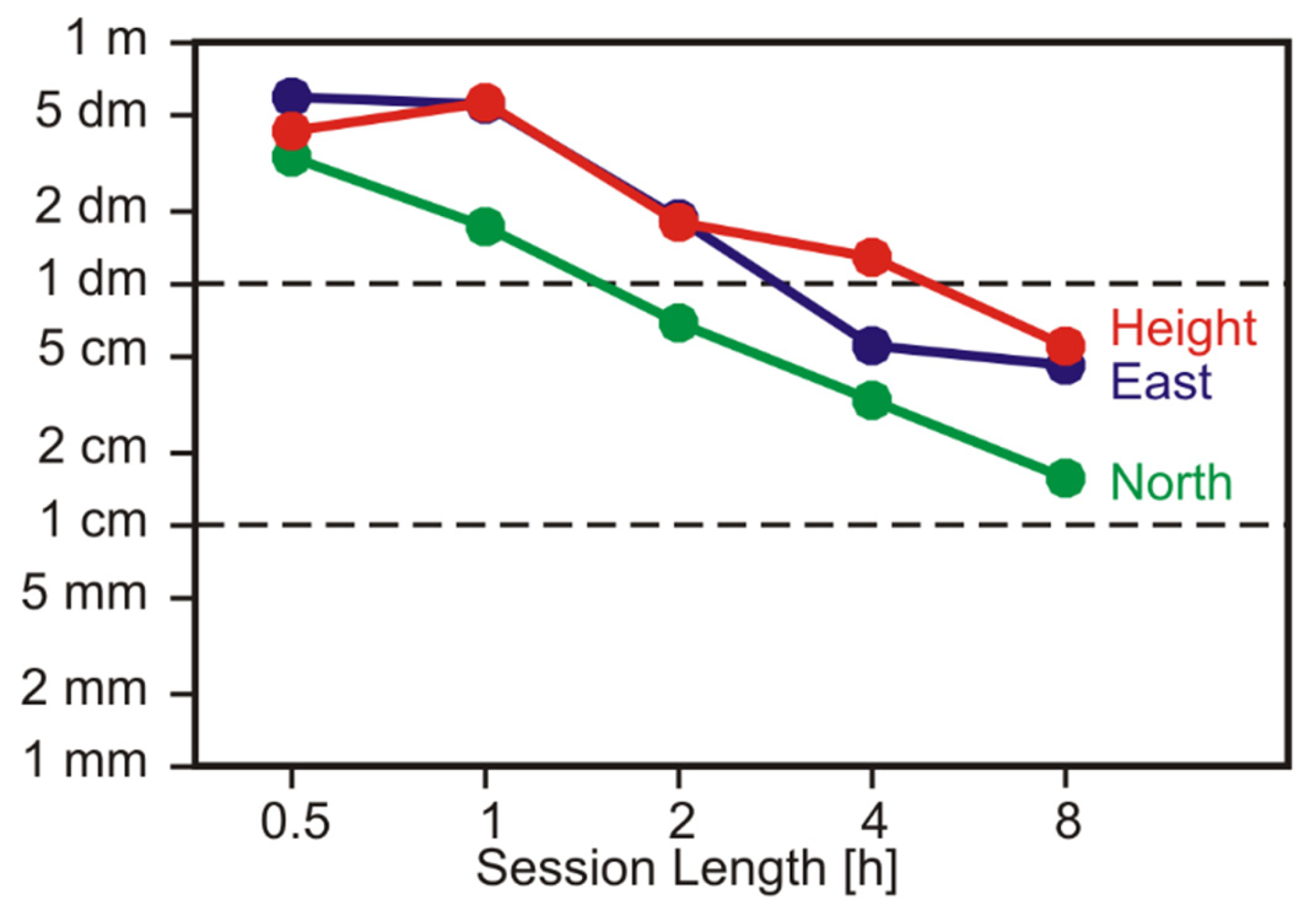
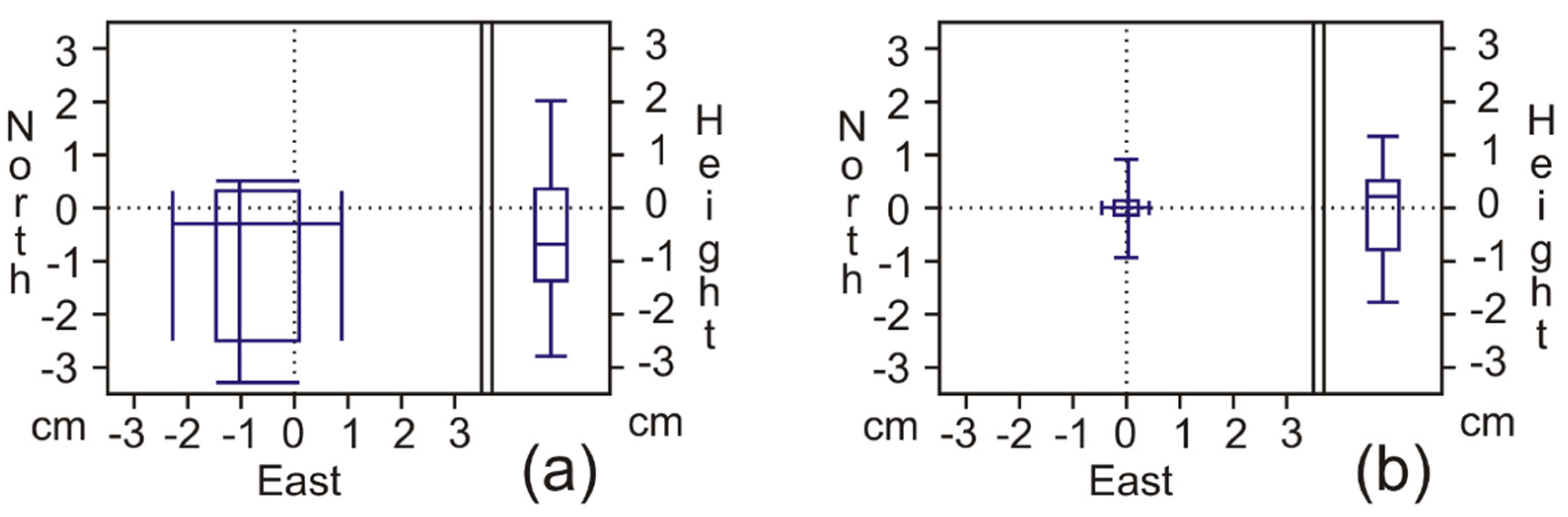
4.2. Relative Carrier-Phase Positioning with Respect to VRS
5. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niu, Z.; Nie, P.; Tao, L.; Sun, J.; Zhu, B. RTK with the Assistance of an IMU-Based Pedestrian Navigation Algorithm for Smartphones. Sensors 2019, 19, 3228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wanninger, L.; Hesselbarth, A. GNSS code and carrier phase observations of a Huawei P30 smartphone: Quality assessment and centimeter-accurate positioning. GPS Solut. 2020, 24, 64. [Google Scholar] [CrossRef] [Green Version]
- Darugna, F.; Wübbena, J.B.; Wübbena, G.; Schmitz, M.; Schön, S.; Warneke, A. Impact of robot antenna calibration on dual-frequency smartphone-based high-accuracy positioning: A case study using the Huawei Mate20X. GPS Solut. 2021, 25, 15. [Google Scholar] [CrossRef]
- Garmin GPSMAP 66sr. Available online: https://www.garmin.com/ (accessed on 13 January 2022).
- Hesselbarth, A.; Wanninger, L. Towards centimeter accurate positioning with smartphones. In Proceedings of the 2020 European Navigation Conference (ENC), IEEE (2020), Virtual Event, 23–24 November 2020; pp. 1–8. Available online: https://ieeexplore.ieee.org/document/9317392 (accessed on 13 January 2022).
- Wanninger, L.; Thiemig, M.; Frevert, V. Multi-frequency quadrifilar helix antennas for cm-accurate GNSS positioning. J. Appl. Geod. 2022, 16, 25–35. [Google Scholar] [CrossRef]
- IGS/RTCM. RINEX—The Receiver Independent Exchange Format Version 3.04. International GNSS Service (IGS), RINEX Working Group and Radio Technical Commission for Maritime Services Special Committee 104 (RTCM–SC104). 2018. Available online: https://files.igs.org/pub/data/format/rinex304.pdf (accessed on 13 January 2022).
- Noll, C.E. The crustal dynamics data information system: A resource to support scientific analysis using space geodesy. Adv. Space Res. 2010, 45, 1421–1440. [Google Scholar] [CrossRef] [Green Version]
- WaSoft Software Package. Available online: http://www.wasoft.de/e (accessed on 13 January 2022).
- Braasch, M.S. Multipath. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 443–468. [Google Scholar]
- Schmolke, A.; Wanninger, L.; Frevert, V. Erste GNSS-Antennenkalibrierungen im Feldverfahren auf neuen Signalfrequenzen. Z. Geodäsie Geoinfo. Landm. 2015, 140, 283–289. Available online: http://geodaesie.info/zfv/zfv-52015/4892 (accessed on 13 January 2022).
- Rothacher, M.; Schmid, R. ANTEX: The Antenna Exchange Format, Version 1.4. 2010. Available online: https://files.igs.org/pub/station/general/antex14.txt (accessed on 13 January 2022).
- Canadian Spatial Reference System—Precise Point Positioning (CSRS-PPP). Available online: https://webapp.geod.nrcan.gc.ca/geod/tools-outils/ppp.php (accessed on 13 January 2022).
- Trimble CenterPoint RTX Post-Processing Service. Available online: https://trimblertx.com (accessed on 13 January 2022).
- GNSS Analysis and Positioning Software (GAPS). Available online: http://gaps.gge.unb.ca (accessed on 13 January 2022).
- Kouba, J.; Lahaye, F.; Tétreault, P. Precise Point Positioning. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 723–751. [Google Scholar]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential Code Bias Estimation using Multi-GNSS Observations and Global Ionosphere Maps: Mulit-GNSS DCB Estimation. J. Inst. Navig. 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Schaer, S.; Villiger, A.; Arnold, D.; Dach, R.; Prange, L.; Jäggi, A. The CODE ambiguity-fixed clock and phase bias analysis products: Generation, properties, and performance. J. Geod. 2021, 95, 81. [Google Scholar] [CrossRef]
- Crustal Dynamics Data Information System (CDDIS). Available online: https://cddis.nasa.gov (accessed on 13 January 2022).
- Elmezayen, A.; El-Rabbany, A. Precise Point Positioning Using World’s First Dual-Frequency GPS/GALILEO Smartphone. Sensors 2019, 19, 2593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, F.; Chai, H.; Li, L.; Xiao, G.; Du, Z. Estimation and analysis of GPS inter-fequency clock biases from long-term triple-frequency observations. GPS Solut. 2021, 25, 126. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- SAPOS GPPS-PrO Sachsen. Available online: https://www.landesvermessung.sachsen.de/sapos (accessed on 13 January 2022).
- Odijk, D.; Wanninger, L. Differential Positioning. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 753–780. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wanninger, L.; Heßelbarth, A.; Frevert, V. Garmin GPSMAP 66sr: Assessment of Its GNSS Observations and Centimeter-Accurate Positioning. Sensors 2022, 22, 1964. https://doi.org/10.3390/s22051964
Wanninger L, Heßelbarth A, Frevert V. Garmin GPSMAP 66sr: Assessment of Its GNSS Observations and Centimeter-Accurate Positioning. Sensors. 2022; 22(5):1964. https://doi.org/10.3390/s22051964
Chicago/Turabian StyleWanninger, Lambert, Anja Heßelbarth, and Volker Frevert. 2022. "Garmin GPSMAP 66sr: Assessment of Its GNSS Observations and Centimeter-Accurate Positioning" Sensors 22, no. 5: 1964. https://doi.org/10.3390/s22051964
APA StyleWanninger, L., Heßelbarth, A., & Frevert, V. (2022). Garmin GPSMAP 66sr: Assessment of Its GNSS Observations and Centimeter-Accurate Positioning. Sensors, 22(5), 1964. https://doi.org/10.3390/s22051964





