A Modified Complex Variational Mode Decomposition Method for Analyzing Nonstationary Signals with the Low-Frequency Trend
Abstract
:1. Introduction
2. Related Work
2.1. Variational Mode Decomposition
2.2. Complex Variational Mode Decomposition
3. Problem Statement
4. Modified Complex Variational Mode Decomposition
4.1. MCVMD Algorithm
4.2. MCVMD Hilbert Spectrum
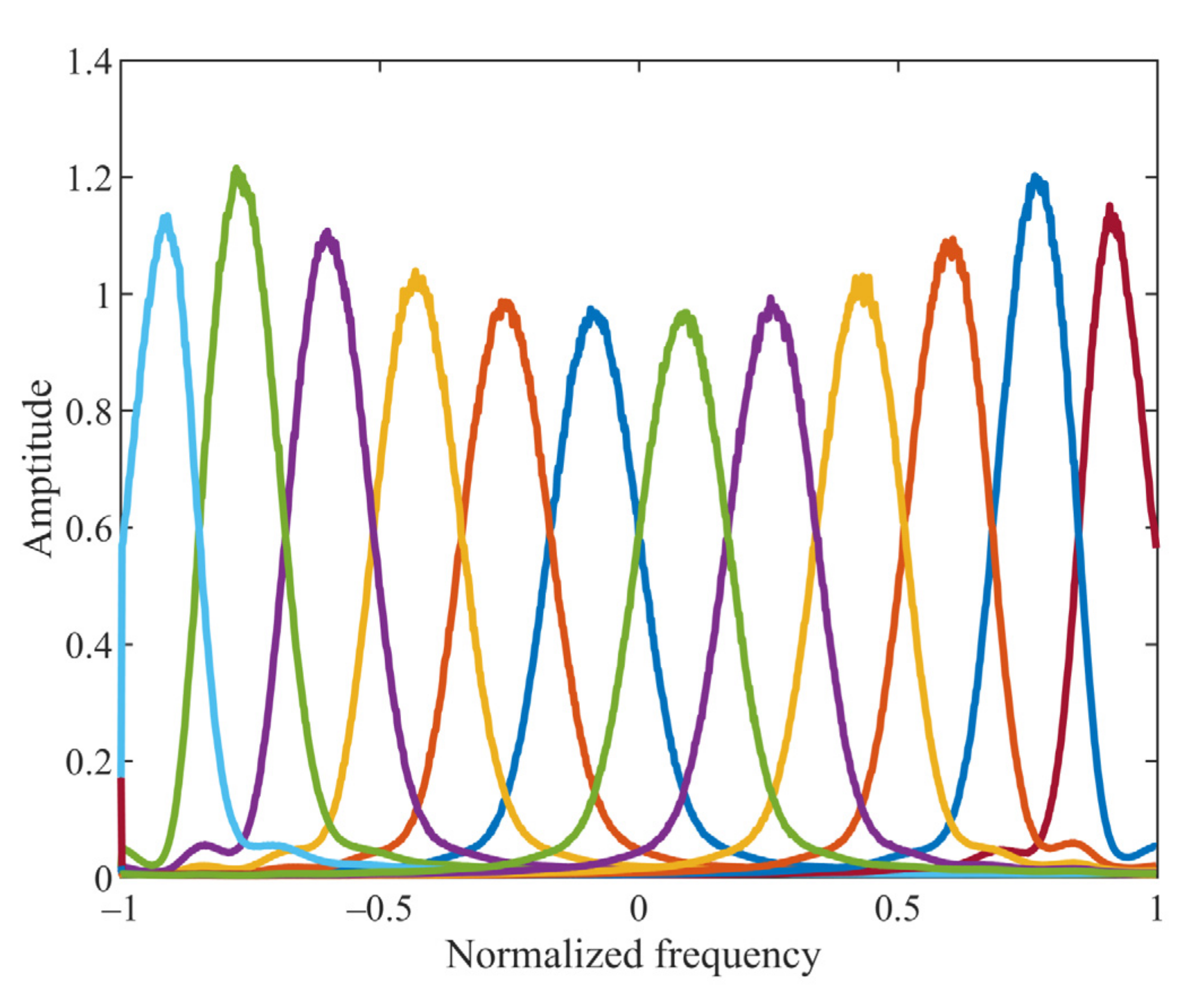
4.3. MCVMD Equivalent Filter Bank
5. Results and Discussion
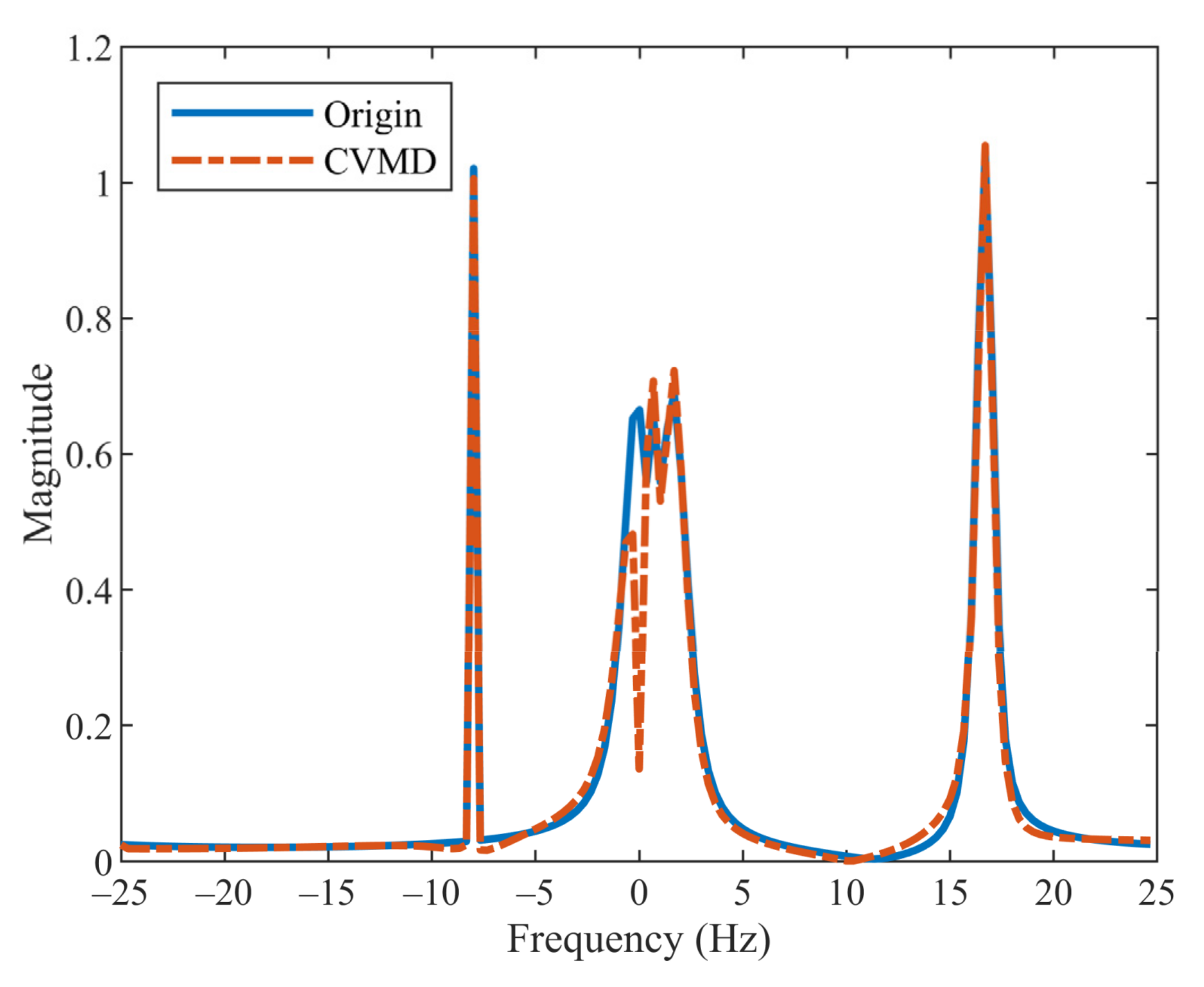
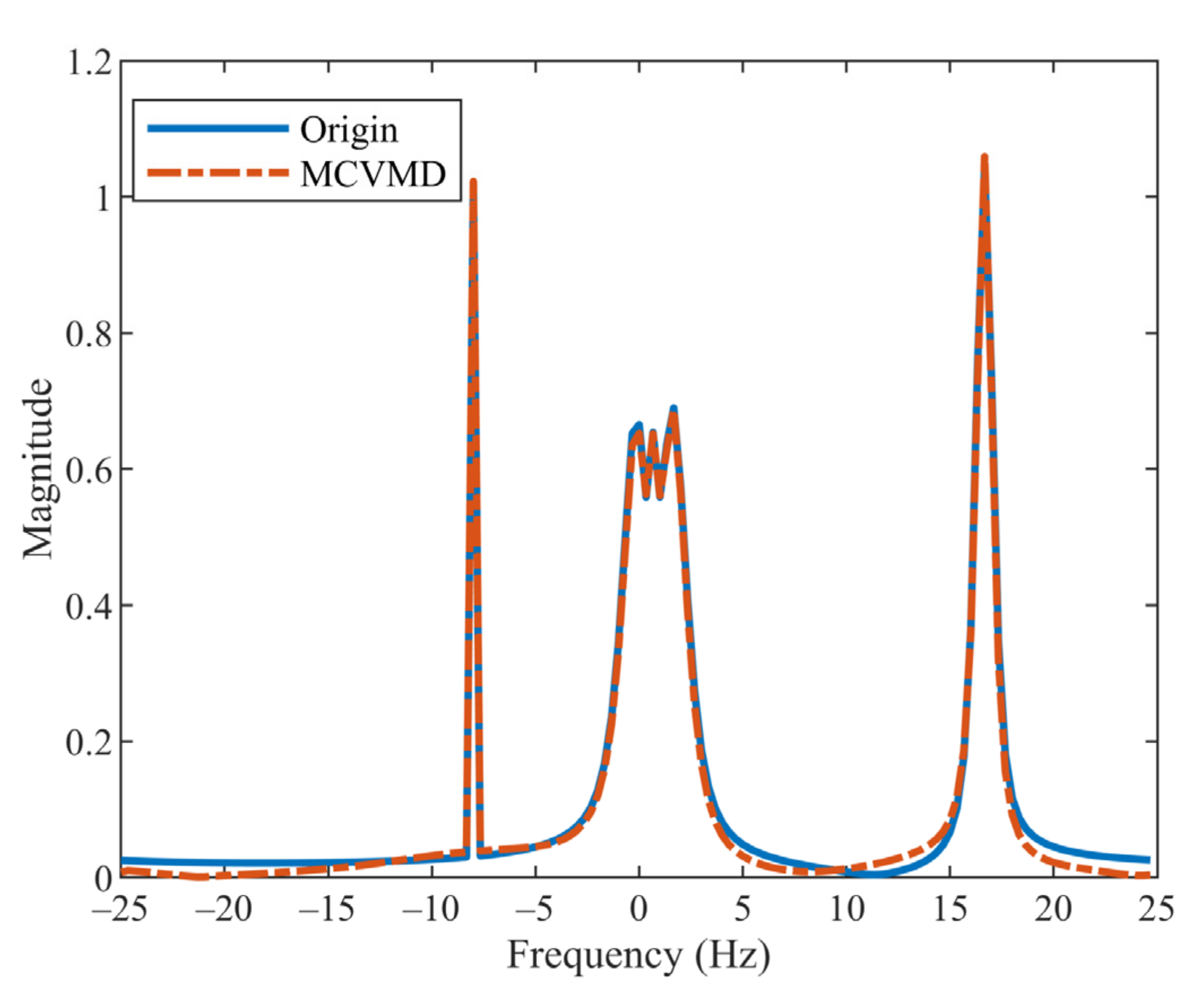
5.1. Synthetic Signal Analysis
5.1.1. Example 1
5.1.2. Example 2
5.1.3. Example 3
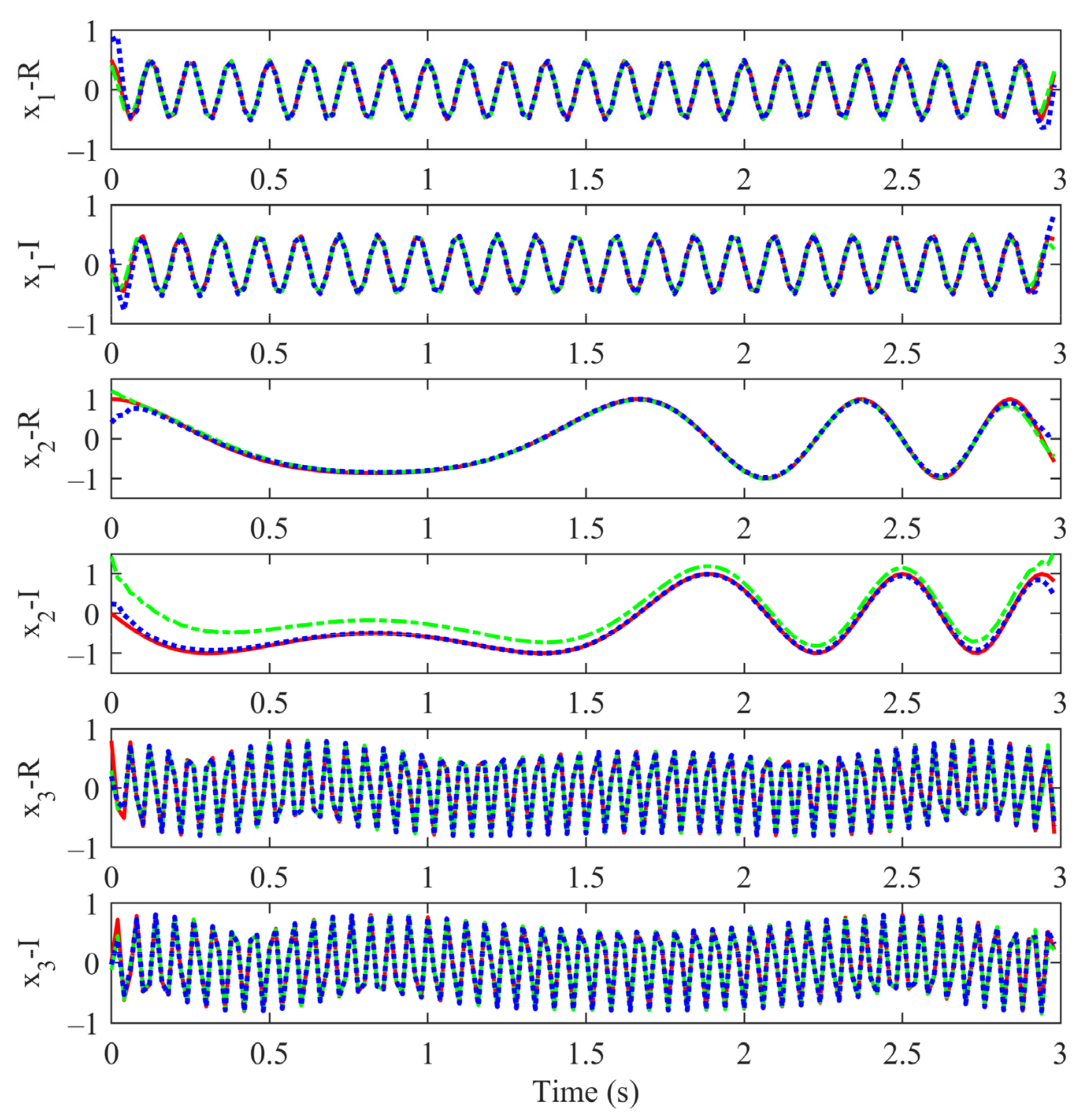
5.2. Real-World Data Analysis
5.2.1. Analysis of Float Drift Data
5.2.2. Analysis of Wind Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Allen, J.B.; Rabiner, L.R. A unified approach to short-time fourier analysis and synthesis. Proc. IEEE 1977, 65, 1558–1564. [Google Scholar] [CrossRef]
- Daubechies, I. Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef] [Green Version]
- Stockwell, R.G.; Mansinha, L.; Lowe, R.P. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Cohen, L. Time-frequency distributions-a review. Proc. IEEE 1989, 77, 941–981. [Google Scholar] [CrossRef] [Green Version]
- Hlawatsch, F.; Boudreaux-Bartels, G.F. Linear and quadratic time-frequency signal representations. IEEE Signal Process. Mag. 1992, 9, 21–67. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–998. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, S.S.P. Hilbert-Huang Transform and Its Applications; Interdisciplinary Mathematical Sciences; World Scientific: Singapore, 2005; pp. 2–15. ISBN 978-981-256-376-7. [Google Scholar]
- Huang, N.E.; Wu, Z.; Long, S.R.; Arnold, K.C.; Chen, X.; Blank, K. On instantaneous frequency. Adv. Adapt. Data Anal. 2009, 1, 177–229. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Nazari, M.; Sakhaei, S.M. Successive variational mode decomposition. Signal Process. 2020, 174, 107610. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R. Filter bank property of variational mode decomposition and its applications. Signal Process. 2016, 120, 509–521. [Google Scholar] [CrossRef]
- Mohanty, S.; Gupta, K.K.; Raju, K.S. Hurst based vibro-acoustic feature extraction of bearing using EMD and VMD. Measurement 2018, 117, 200–220. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, G.; Li, M.; Yin, H. Variational mode decomposition denoising combined the detrended fluctuation analysis. Signal Process. 2016, 125, 349–364. [Google Scholar] [CrossRef]
- Lu, Q.; Shen, X.; Wang, X.; Li, M.; Li, J.; Zhang, M. Fault diagnosis of rolling bearing based on improved VMD and KNN. Math. Probl. Eng. 2021, 2021, e2530315. [Google Scholar] [CrossRef]
- Civera, M.; Surace, C. A comparative analysis of signal decomposition techniques for structural health monitoring on an experimental benchmark. Sensors 2021, 21, 1825. [Google Scholar] [CrossRef] [PubMed]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Adali, T.; Schreier, P.J.; Scharf, L.L. Complex-valued signal processing: The proper way to deal with impropriety. IEEE Trans. Signal Process. 2011, 59, 5101–5125. [Google Scholar] [CrossRef]
- Magarey, J.; Kingsbury, N. Motion estimation using a complex-valued wavelet transform. IEEE Trans. Signal Process. 1998, 46, 1069–1084. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J. Complex variational mode decomposition for slop-preserving denoising. IEEE Trans. Geosci. Remote Sens. 2018, 56, 586–597. [Google Scholar] [CrossRef]
- Stanković, L.; Mandić, D.; Daković, M.; Brajović, M. Time-frequency decomposition of multivariate multicomponent signals. Signal Process. 2018, 142, 468–479. [Google Scholar] [CrossRef]
- Sony, S. Towards Multiclass Damage Detection and Localization Using Limited Vibration Measurements. Ph.D. Thesis, Western University, London, ON, Canada, 2021. [Google Scholar]
- Huang, G.; Su, Y.; Kareem, A.; Liao, H. Time-frequency analysis of nonstationary process based on multivariate empirical mode decomposition. J. Eng. Mech. 2016, 142, 04015065. [Google Scholar] [CrossRef]
- Rilling, G.; Flandrin, P.; Goncalves, P.; Lilly, J.M. Bivariate empirical mode decomposition. IEEE Signal Process. Lett. 2007, 14, 936–939. [Google Scholar] [CrossRef] [Green Version]
- Rehman, N.; Mandic, D.P. Multivariate empirical mode decomposition. Proc. R. Soc. Math. Phys. Eng. Sci. 2010, 466, 1291–1302. [Google Scholar] [CrossRef]
- ur Rehman, N.; Aftab, H. Multivariate variational mode decomposition. IEEE Trans. Signal Process. 2019, 67, 6039–6052. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Liu, F.; Jiang, Z.; He, S.; Mo, Q. Complex variational mode decomposition for signal processing applications. Mech. Syst. Signal Process. 2017, 86, 75–85. [Google Scholar] [CrossRef]
- Tanaka, T.; Mandic, D.P. Complex empirical mode decomposition. IEEE Signal Process. Lett. 2007, 14, 101–104. [Google Scholar] [CrossRef]
- Xia, S.; Yang, J.; Cai, W.; Zhang, C.; Hua, L.; Zhou, Z. Adaptive complex variational mode decomposition for micro-motion signal processing applications. Sensors 2021, 21, 1637. [Google Scholar] [CrossRef]
- Doroslovački, M.I. On nontrivial analytic signals with positive instantaneous frequency. Signal Process. 2003, 83, 655–658. [Google Scholar] [CrossRef]
- Xu, W.; Stewart, W.K. Multiresolution-signal direction-of-arrival estimation: A wavelets approach. IEEE Signal Process. Lett. 2000, 7, 66–68. [Google Scholar] [CrossRef]
- Goh, S.L.; Chen, M.; Popović, D.H.; Aihara, K.; Obradovic, D.; Mandic, D.P. Complex-valued forecasting of wind profile. Renew. Energy 2006, 31, 1733–1750. [Google Scholar] [CrossRef]
- Yaroslavsky, L. Fast Transform Methods in Digital Signal Processing: Theory, Applications, Efficient Algorithms; Digital Signal Processing in Experimental Research; Bentham eBooks: Oak Park, IL, USA, 2011; ISBN 978-1-60805-230-1. [Google Scholar]
- Streamlining Digital Signal Processing: A Tricks of the Trade Guidebook|IEEE EBooks|IEEE Xplore. Available online: https://ieeexplore.ieee.org/book/6241055 (accessed on 23 January 2022).
- Huang, N.E.; Wu, M.L.; Qu, W.; Long, S.R.; Shen, S.S.P. Applications of Hilbert-Huang Transform to Non-Stationary Financial Time Series Analysis. Appl. Stoch. Models Bus. Ind. 2010, 19, 245–268. [Google Scholar] [CrossRef]
- Richardson, P.L.; Price, J.F.; Walsh, D.; Armi, L.; Schröder, M. Tracking three meddies with SOFAR floats. J. Phys. Oceanogr. 1989, 19, 371–383. [Google Scholar] [CrossRef]










| CVMD | 0.020 | 0.020 | 0.042 | 0.334 | 0.012 | 0.015 |
| MCVMD | 0.010 | 0.013 | 0.027 | 0.033 | 0.005 | 0.006 |
| Mode 1-F 1 | Mode 1-A | Mode 2-F | Mode 2-A | |
|---|---|---|---|---|
| CVMD | 0.0538 | 3.3954 | 0.1202 | 0.3566 |
| MCVMD | 0.0149 | 0.9334 | 0.0104 | 0.0780 |
| - | (1,0) | (2,0) | (3,0) | |
| (0,1) | (1,1) | (2,1) | (3,1) | |
| (0,2) | (1,2) | (2,2) | (3,2) | |
| (0,3) | (1,3) | (2,3) | (3,3) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, Q.; Shu, Q.; Wu, B.; Sun, X.; Song, K. A Modified Complex Variational Mode Decomposition Method for Analyzing Nonstationary Signals with the Low-Frequency Trend. Sensors 2022, 22, 1801. https://doi.org/10.3390/s22051801
Miao Q, Shu Q, Wu B, Sun X, Song K. A Modified Complex Variational Mode Decomposition Method for Analyzing Nonstationary Signals with the Low-Frequency Trend. Sensors. 2022; 22(5):1801. https://doi.org/10.3390/s22051801
Chicago/Turabian StyleMiao, Qiuyan, Qingxin Shu, Bin Wu, Xinglin Sun, and Kaichen Song. 2022. "A Modified Complex Variational Mode Decomposition Method for Analyzing Nonstationary Signals with the Low-Frequency Trend" Sensors 22, no. 5: 1801. https://doi.org/10.3390/s22051801
APA StyleMiao, Q., Shu, Q., Wu, B., Sun, X., & Song, K. (2022). A Modified Complex Variational Mode Decomposition Method for Analyzing Nonstationary Signals with the Low-Frequency Trend. Sensors, 22(5), 1801. https://doi.org/10.3390/s22051801






