A Multi-Frequency Tomographic Inverse Scattering Using Beam Basis Functions
Abstract
:1. Introduction
- a.
- Data localization: The phase–space processing of the scattered data extract the local direction of arrival. The phase space representation of the data is therefore localized along well defined trajectories corresponding to the local direction and time of arrival from the relevant regions in the target domain.
- b.
- Under the Born approximation, the beam-wave scattering mechanism by the medium inhomogeneities is described by local Snell’s reflections from the local stratification, which is related to the local Radon transform (LRT) of the medium inhomogeneities (Section 5 in [36]).
- c.
- As follows from the discussion in items a and b, the phase space data is directly related to the LRT of the medium inhomogeneities about a given region.
- d.
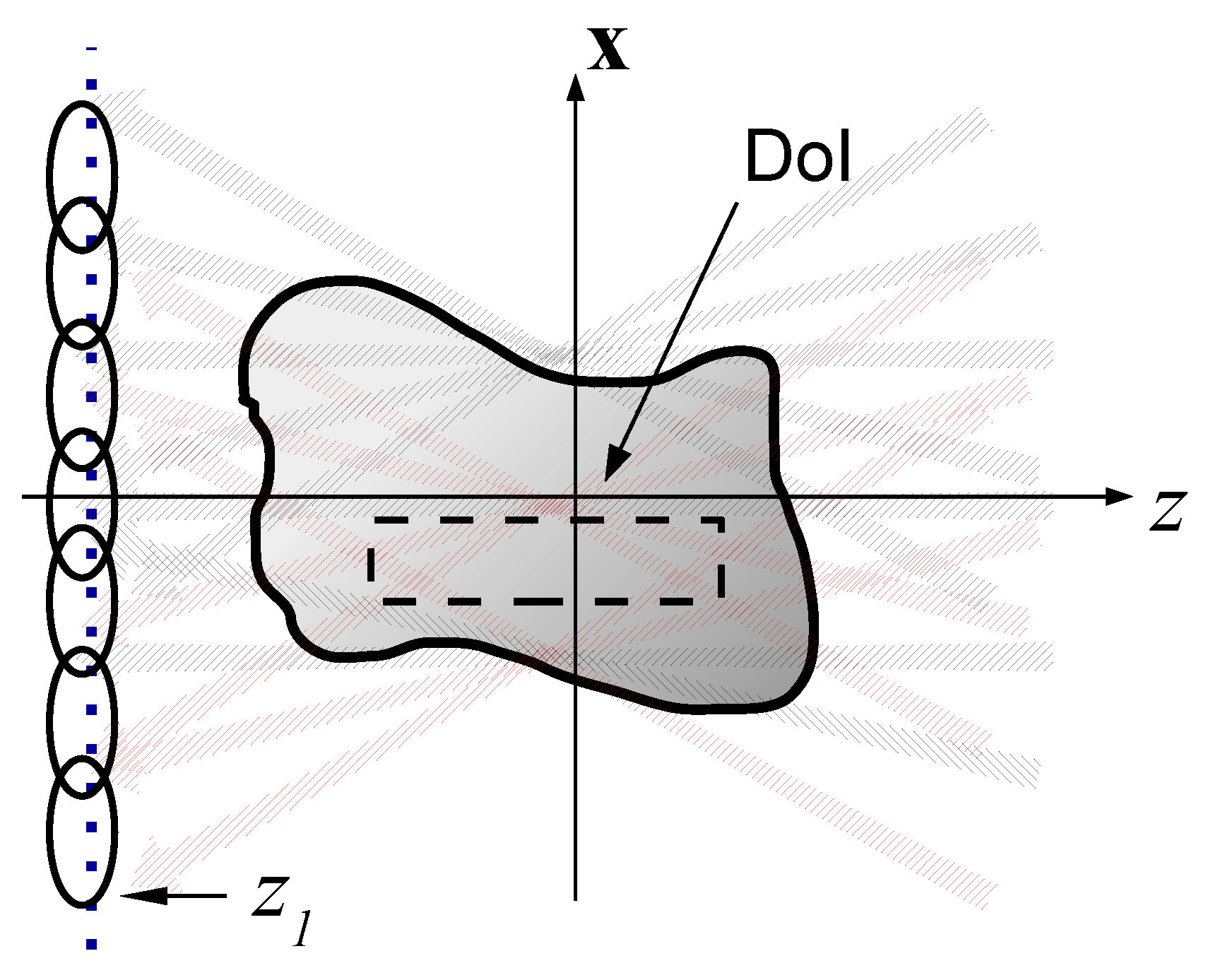
- The beam-based imaging enables local imaging within a given domain of interest (DoI) by considering only the data that correspond to beams that pass through or near the DoI. This not only reduces the problem complexity, but also reduces the noise level, since data and noise arriving from other regions are a priori filtered out.
- e.
- The beam-based imaging enables backpropagation and imaging over a non-homogeneous background.
2. UWB Diffraction Tomography in the Spectral Plane-Wave Domain: A Review
2.1. Problem Description—Physical Configuration
2.2. The DT Identity
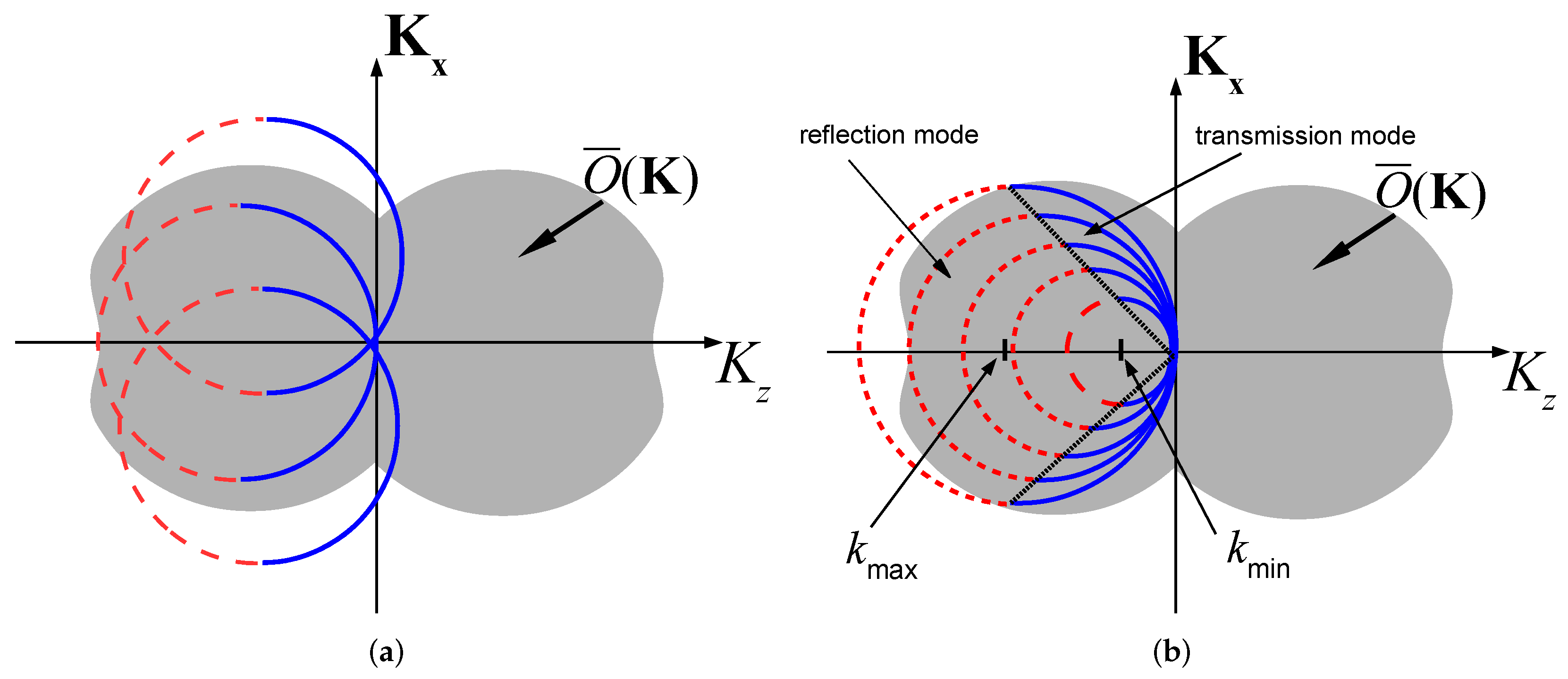
2.3. Object Reconstruction via Angular Diversity
2.4. Object Reconstruction via Frequency Diversity (UWB Tomography)
3. Mathematical Background on the UWB-PS-BS
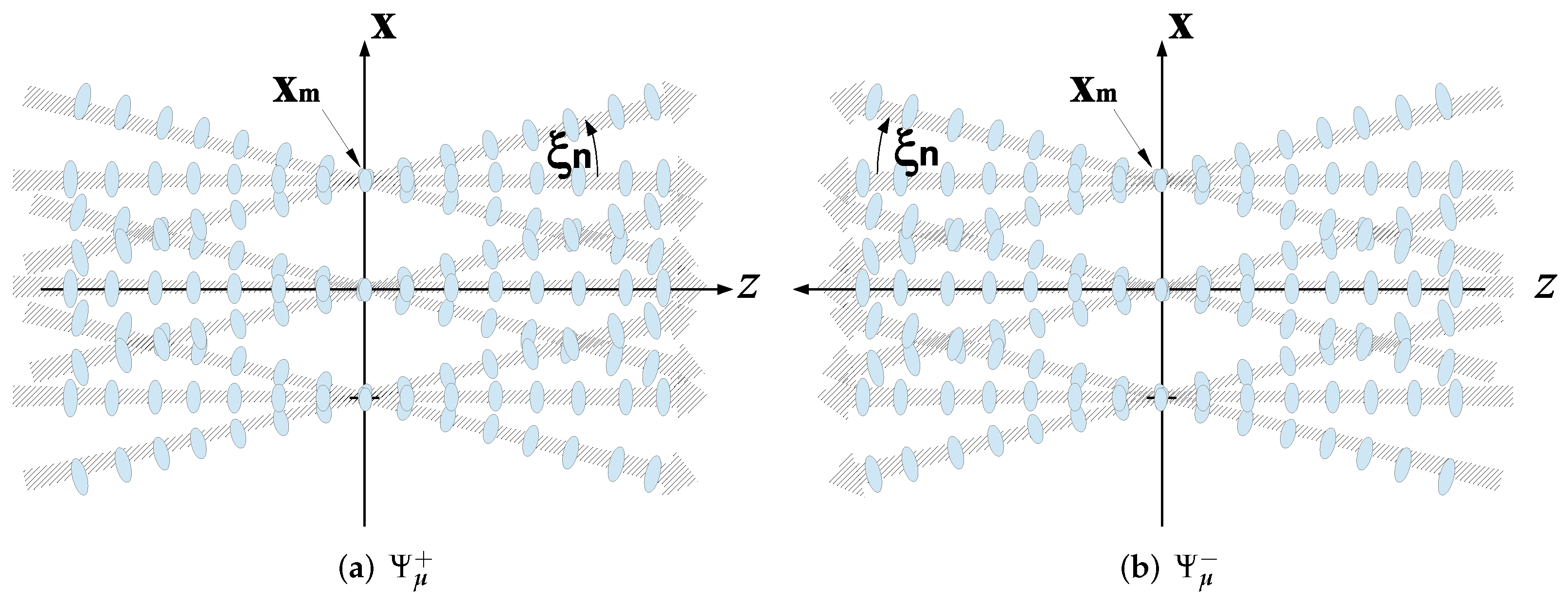
3.1. The Windowed Fourier Transform (WFT) Frame Representation of the Field
3.2. UWB Considerations
3.3. The Beam Frame Theorem
4. UWB Beam-Based Diffraction Tomography: Multi-Frequency Formulation
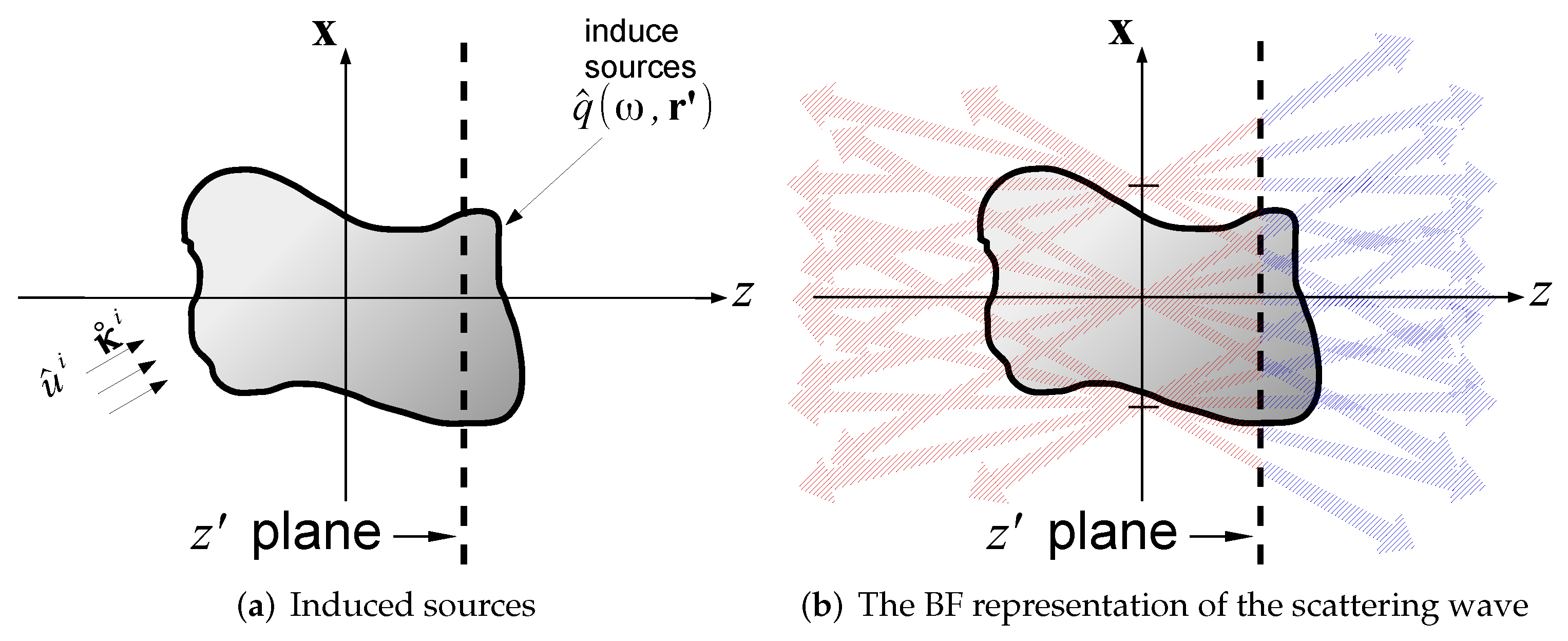
4.1. The Inversion Algorithm
4.2. Interpretation within the Born Approximation
5. Numerical Examples
5.1. A Step by Step Summary of the Algorithm
- 1.
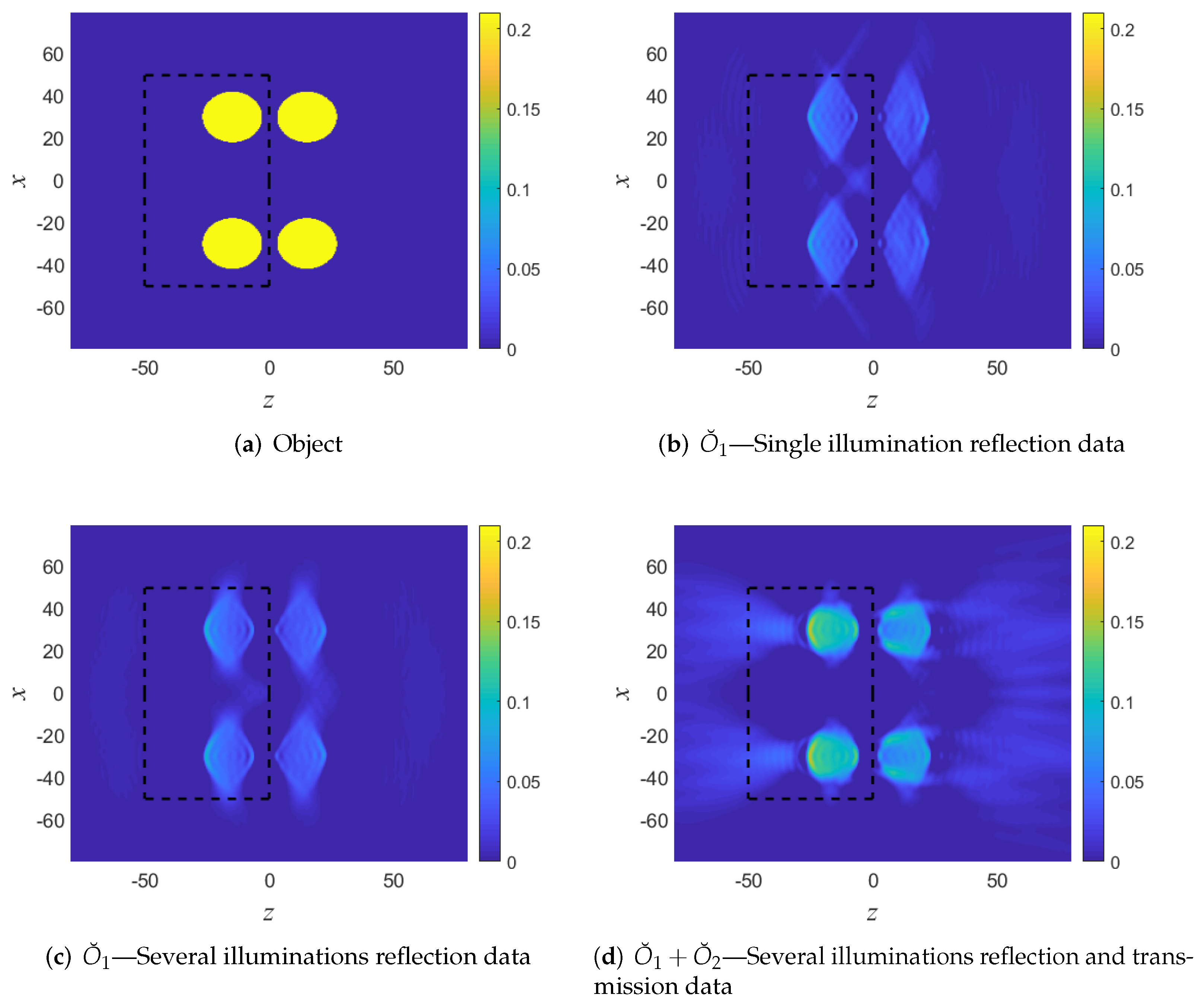
- We consider a realistic case where the object is illuminated by an array of M independent point transducers over the plane, as illustrated in Figure 5a. We illustrate here only the reflected data on the plane, since in many applications (e.g., geophysics) the transmission field cannot be measures, and in some cases this data is not needed (see discussion in Section 2.4). If, however, the transmitted data at is available, then the receiver array considerations are similar.
- 2.
- The data is measured by exciting the sources one at a time by short pulse that spans the desired frequency band as needed to obtain the desired -space coverage. The result is an data matrix describing the response at the p receiver due to an excitation by the q source.
- 3.
- The data is sampled at the proper Nyquist rate and then converted to the FD via FFT, giving rise to the data matrix . Before the calculation, the time-series are padded by zeros to avoid aliasing of the final image when it is generated by integration over all the frequencies. Note that in some applications, may be measure directly in the FD.
- 4.
- The response to time-harmonic PW excitations at different angles is synthesized from by q-stacking the array data with proper phase terms. The result provides the PW data to the phase–space beam-based processing.One may also calculate the time-harmonic PW spectrum of the scattered field via p-stacking with proper phase terms. The result is an data matrix describing the spectral PW due to an excitation by the incident PW. As noted earlier, before we do the stacking, the array dimensions should be zero- padded to avoid aliasing of the final image when the images are generated by spectral integrations.
- 5.
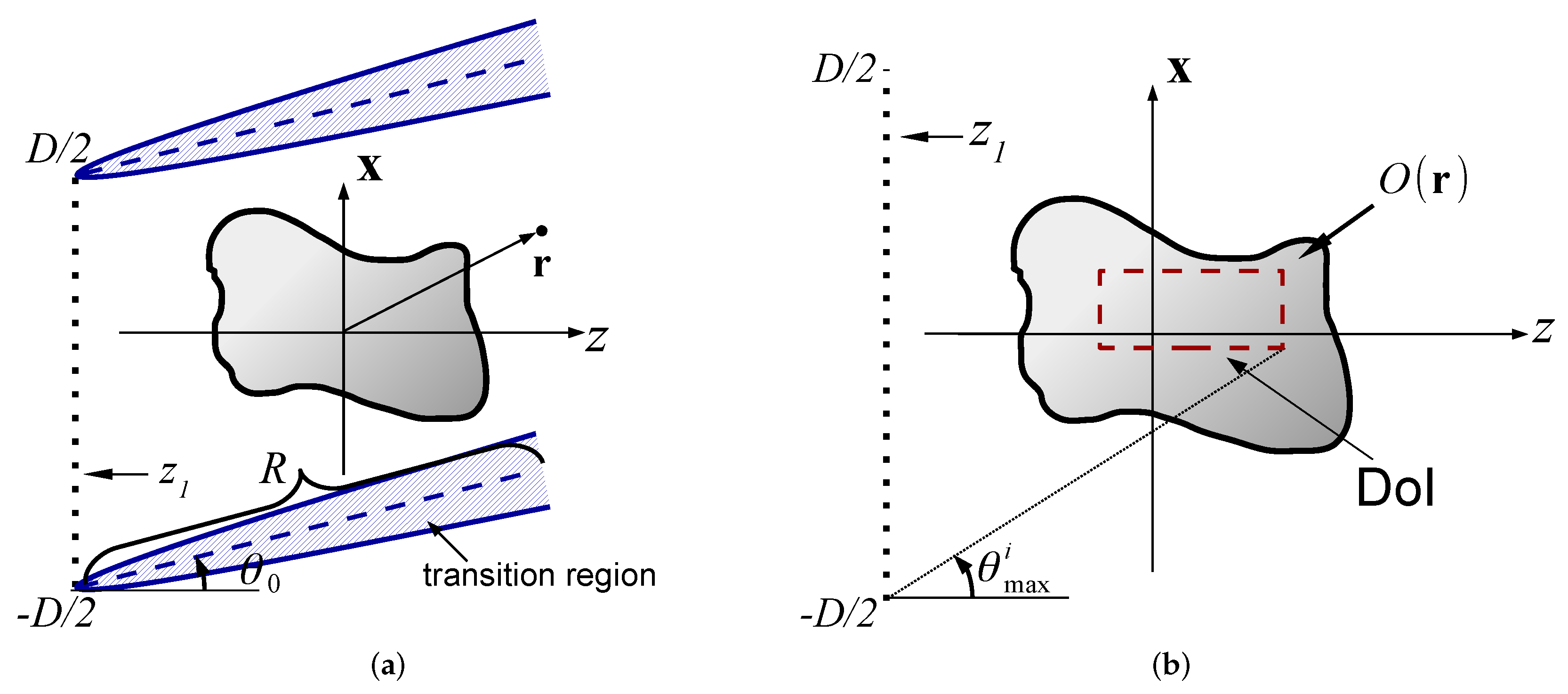
- As illustrated in Figure 5a, the spectral information that can be covered by the array is determined by the size of the array and by the target range R. The size of the array should be chosen to provide sufficient spectral coverage of the target. In general, R should be within the Fresnel zone of the array, i.e., . Note also that due to the finite size of the array, one should avoid the array transition zone illustrated in Figure 5a.
- 6.
- The array elements inner spacing should, in general, satisfy the Nyquist sampling rate . However, since the target range satisfies , it is only required that the phase difference between adjacent elements will be small, yielding a sparser array with .
- 1.
- Choosing the beam parameter b: As discussed in Section 3.2, the ID Gaussian windows in (23) are fully determined by the parameter b. The considerations of choosing b were widely studied in [21,36] for the application of local inverse scattering. This parameter balances between the beam collimation length and the beamwidth. We choose b to be on the order of the DoI domain so that the beams are collimated throughout the DoI while being small enough for transversal resolution.
- 2.
- The phase–space lattice: The guidelines for constructing the UWB beam lattice are discussed in Section 3.2. As discussed there, we choose which balances between stable expansion frame and moderate over-completeness (relatively small number of elements). The optimal values for are given by (24).
- 3.
- The phase–space propagators: The frame elements are calculated via (26). For the Gaussian windows (23), the results are ID-GB propagators (see explicit expressions in (Appendices A,C [21]).
- 4.
- Limited physical data: We need to consider only beams whose initiation point are supported by the array size. The maximal value of is determined by the scan angle. If, for example, the scan angle is , then .
- 1.
- Calculating the expansion coefficients: The coefficients are calculated via (30).
- 2.
- Filtering out low amplitude data: As discussed in Section 4.2, the beam data is related to the local Snell’s reflections of the beams by the local stratification in , which in turns are determined by the LRT of . We therefore threshold low amplitude beams at a level of 40 dB.
- 1.
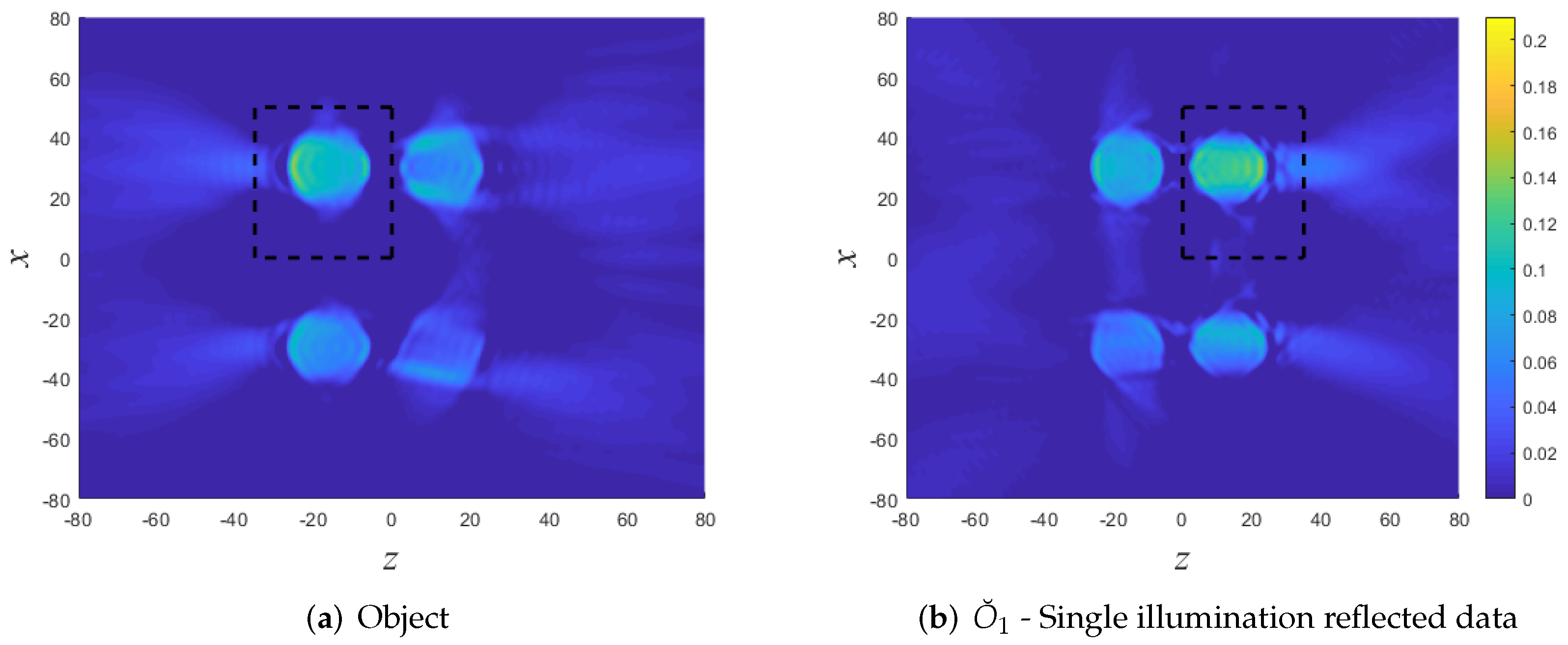
- Beam backpropagation within the DoI: Next, following Section 4.1, we backpropagate the beams whose amplitudes are larger than the threshold set above. We consider only the beams passing through the DoI (see Figure 6) or no further than 3 beam-widths away from the DoI (this distance is consistent with an effective threshold of 40 dB).
- 2.
- The image: The imaging fields are calculated via (31), and finally the image is calculated via Equations (12)–(13).
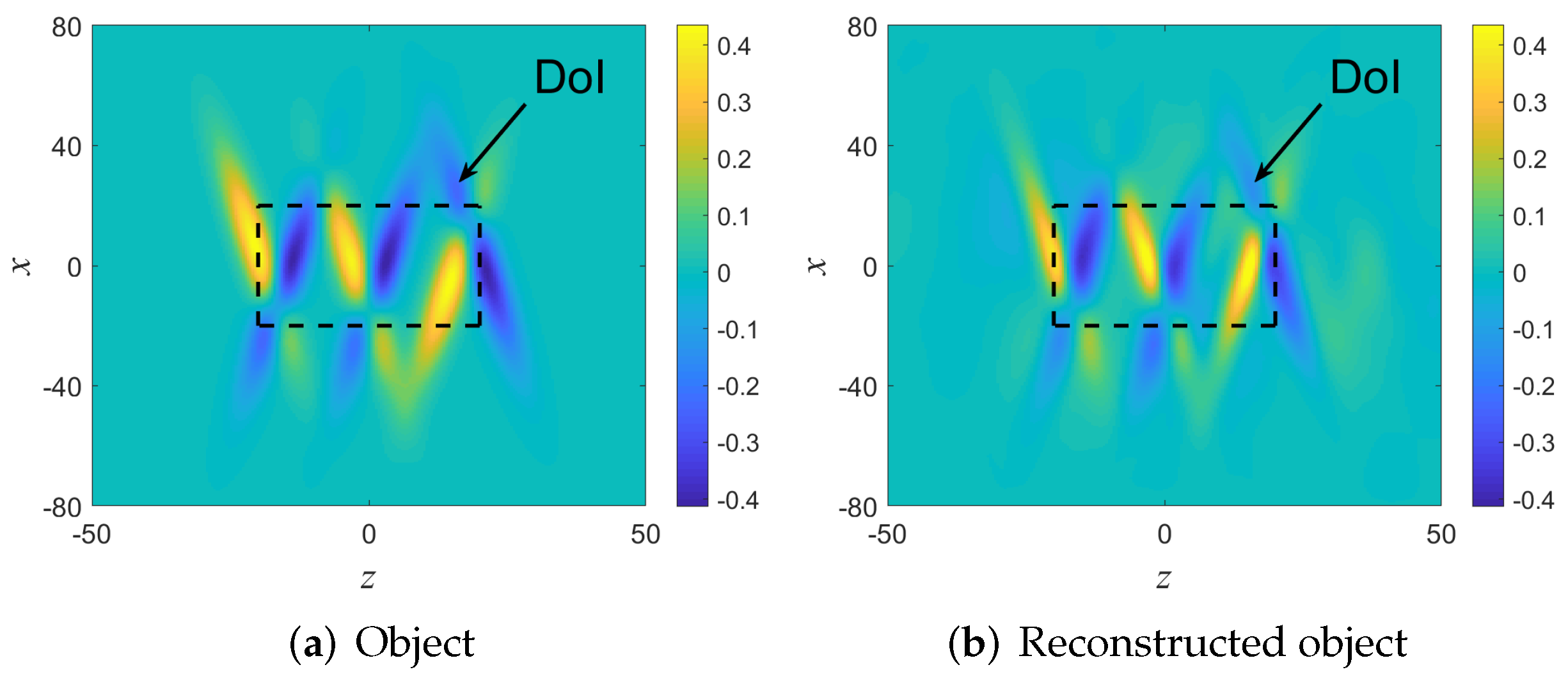
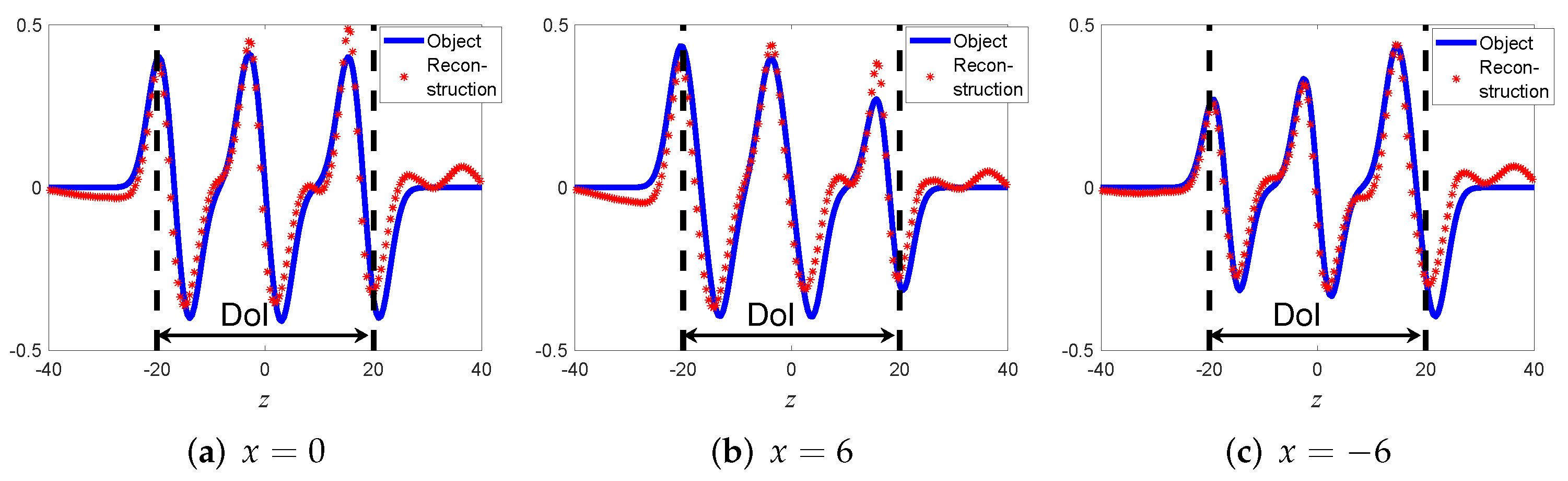
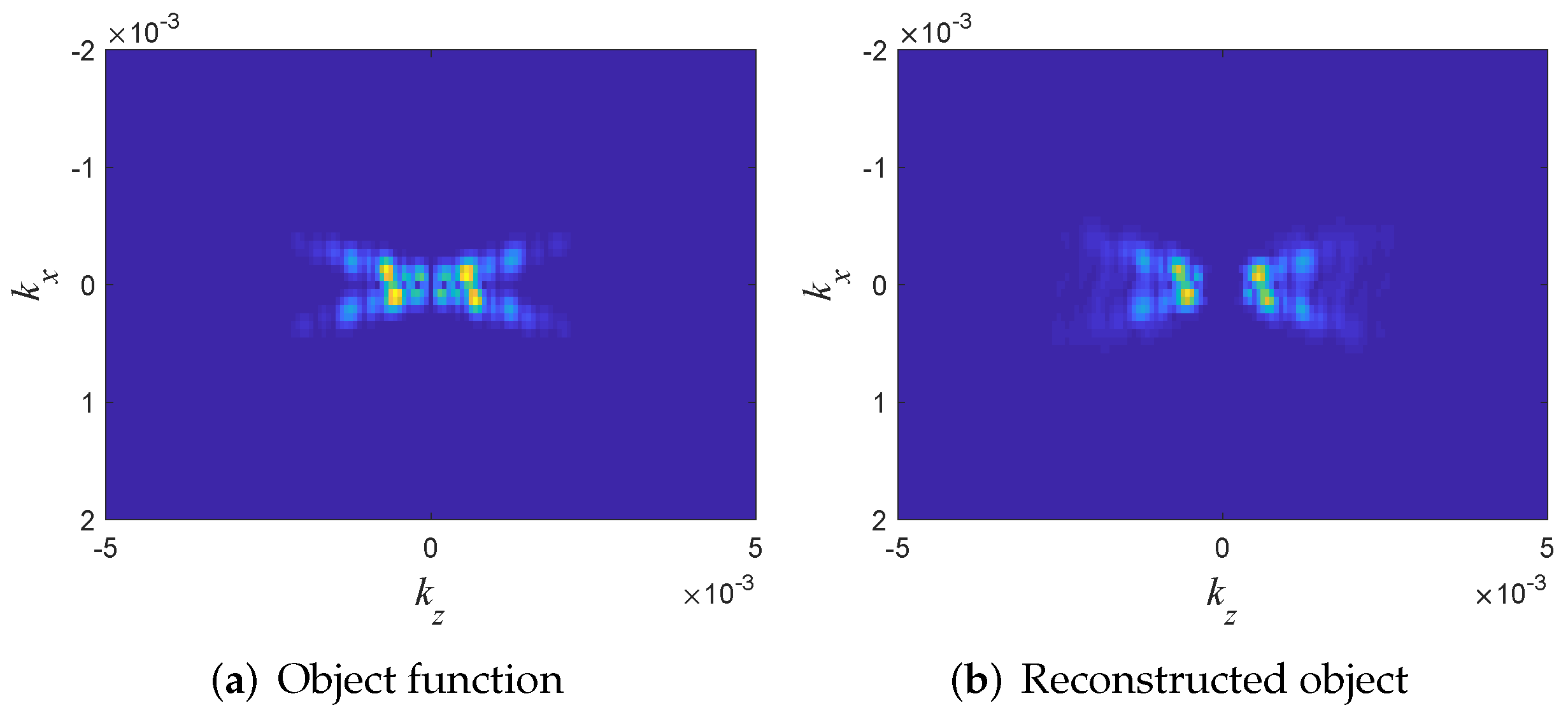
5.2. Example A: A Smooth and Quasi Stratified Medium. UWB Reflection Mode Data
5.3. Example B: An Object with Sharp Boundaries. Reflection and Transmission Data
6. Discussion and Conclusions
- 1.
- Local imaging within a given domain of interest (DoI).
- 2.
- Reduced complexity since it accounts only for the beam basis-functions that cover the DoI.
- 3.
- Reduced noise level since data and noise arriving from other regions are a priori filtered out.
- 4.
- Backpropagation and imaging over a non-homogeneous background.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Claerbout, J.F. Fundamentals of Geophysical Data Processing; Citeseer; McGraw-Hill Inc.: New York, NY, USA, 1976; Volume 274. [Google Scholar]
- Langenberg, K.J. Applied inverse problems for acoustic, electromagnetic and elastic wave scattering. In Basic Methods of Tomography and Inverse Problems; Sabatier, P.C., Ed.; Malvern Physics Series; Adam Hilger: Bristol, UK, 1987. [Google Scholar]
- Colton, D.; Kress, R. Inverse Acoustic and Electromagnetic Scattering Theory; Springer: Berlin/Heidelberg, Germany, 1998; Volume 93. [Google Scholar]
- Cakoni, F.; Colton, D. A Qualitative Approach to Inverse Scattering Theory; Springer: New York, NY, USA, 2014; Volume 188. [Google Scholar]
- Devaney, A.J. Mathematical Foundations of Imaging, Tomography and Wavefield Inversion; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Devaney, A.J. Diffraction tomography. In Inverse Methods in Electromagnetic Imaging; Part 2; Boerner, W.M., Ed.; D. Reidel Publ. Comp.: Dordrecht, The Netherlands, 1985; pp. 1107–1135. [Google Scholar]
- Heyman, E.; Felsen, L.B. Gaussian beam and pulsed beam dynamics: Complex-source and complex spectrum formulations within and beyond paraxial asymptotics. JOSAA 2001, 18, 1588–1611. [Google Scholar] [CrossRef]
- Heyman, E. Pulsed beam solution for propagation and scattering problems. In Scattering and Inverse Scattering in Pure and Applied Science; Pike, R., Sabatier, P., Eds.; Academic Press: London, UK, 2002; Chapter 1.5.4; pp. 295–315. [Google Scholar]
- Popov, M.M. A new method of computation of wave fields using Gaussian beams. Wave Motion 1982, 4, 85–97. [Google Scholar] [CrossRef]
- Červenỳ, V. Expansion of a plane wave into Gaussian beams. Stud. Geophys. Geod. 1982, 26, 120–131. [Google Scholar] [CrossRef]
- Norris, A.N. Complex point-source representation of real sources and the Gaussian beam summation method. J. Opt. Soc. A. 1986, 3, 205–210. [Google Scholar] [CrossRef]
- Heyman, E. Complex source pulsed beam expansion of transient radiation. Wave Motion 1989, 11, 337–349. [Google Scholar] [CrossRef]
- Bastiaans, M.J. The expansion of an optical signal into a discrete set of Gaussian beams. Optik 1980, 57, 95–102. [Google Scholar]
- Einziger, P.D.; Raz, S.; Shapira, M. Gabor representation and aperture theory. JOSAA 1986, 3, 508–522. [Google Scholar] [CrossRef]
- Steinberg, B.Z.; Heyman, E.; Felsen, L.B. Phase space beam summation for time-harmonic radiation from large apertures. JOSAA 1991, 8, 41–59. [Google Scholar] [CrossRef]
- Maciel, J.J.; Felsen, L.B. Gaussian beam analysis of propagation from an extended plane aperture distribution through dielectric layers, Part I—Plane layer. IEEE Trans. Antennas Propag. 1990, 38, 1107–1617. [Google Scholar]
- Shlivinski, A.; Heyman, E.; Boag, A.; Letrou, C. A phase-space beam summation formulation for ultra wideband radiation. IEEE Trans. Antennas Propag. 2004, 52, 2042–2056. [Google Scholar] [CrossRef]
- Shlivinski, A.; Heyman, E.; Boag, A. A phase-space beam summation formulation for ultrawide-band radiation. II: A multiband scheme. IEEE Trans. Antennas Propag. 2005, 53, 948–957. [Google Scholar] [CrossRef]
- Shlivinski, A.; Heyman, E.; Boag, A. A pulsed beam summation formulation for short pulse radiation based on windowed radon transform (WRT) frames. IEEE Trans. Antennas Propag. 2005, 53, 3030–3048. [Google Scholar] [CrossRef]
- Leibovich, M.; Heyman, E. Beam summation theory for waves in fluctuating media. part I: The beam frame and the beam-domain scattering matrix. IEEE Trans. Antennas Propag. 2017, 65, 5431–5442. [Google Scholar] [CrossRef]
- Tuvi, R.; Heyman, E.; Melamed, T. Beam frame representation for ultrawideband radiation from volume source distributions: Frequency-domain and time-domain formulations. IEEE Trans. Antennas Propag. 2019, 67, 1010–1024. [Google Scholar] [CrossRef]
- Hill, N.R. Gaussian beam migration. Geophysics 1990, 55, 1416–1428. [Google Scholar] [CrossRef]
- Hill, N.R. Prestack Gaussian-beam depth migration. Geophysics 2001, 66, 1240–1250. [Google Scholar] [CrossRef]
- Nowack, R.L.; Sen, M.K.; Paul, S.L. Gassuian beam migration for sparse common-shot and common-receiver data. In Proceedings of the 2003 SEG Annual Meeting, Dallas, TX, USA, 26–31 October 2003; Society of Exploration Geophysicists: Tulsa, OK, USA, 2003. [Google Scholar]
- Bleistein, N. Mathematics of modeling, migration and inversion with Gassuian beams. In Proceedings of the 70th EAGE Conference and Exhibition-Workshops and Fieldtrips, Rome, Italy, 9–12 June 2008; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2008; p. 41. [Google Scholar]
- Nowack, R.L. Dynamically focused Gaussian beams for seismic imaging. Int. J. Geophys. 2011, 2011, 316581. [Google Scholar] [CrossRef] [Green Version]
- Gray, S.H. Gaussian beam migration of common-shot records. Geophysics 2005, 70, S71–S77. [Google Scholar] [CrossRef]
- Gray, S.H.; Bleistein, N. True-amplitude Gaussian-beam migration. Geophysics 2009, 74, 11. [Google Scholar] [CrossRef]
- Popov, M.M.; Semtchenok, N.M.; Popov, P.M.; Verde, A.R. Depth migration by the Gaussian beam summation method. Geophysics 2010, 75, 1MA-Z39. [Google Scholar] [CrossRef]
- Zacek, K. Gaussian packet pre-stack depth migration. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 2004; pp. 957–960. [Google Scholar]
- Melamed, T.; Heyman, E.; Felsen, L.B. Local spectral analysis of short-pulse-excited scattering from weakly inhomogenous media: Part I–forward scattering. IEEE Trans. Antennas Propag. 1999, 47, 1208–1217. [Google Scholar] [CrossRef] [Green Version]
- Melamed, T.; Heyman, E.; Felsen, L.B. Local spectral analysis of short-pulse-excited scattering from weakly inhomogeneous media: Part II–inverse scattering. IEEE Trans. Antennas Propag. 1999, 47, 1218–1227. [Google Scholar] [CrossRef]
- Shlivinski, A.; Heyman, E.; Langenberg, K.J. Migration based imaging using the UWB beam summation algorithm. In Proceedings of the XXVII General Assembly of the Int. Union of Radio Science (URSI), New Delhi, India, 12–17 September 2005. [Google Scholar]
- Heilpern, T.; Shlivinski, A.; Heyman, E. Back-propagation and correlation imaging using phase-space Gaussian-beams processing. IEEE Trans. Antennas Propag. 2013, 61, 5676–5688. [Google Scholar] [CrossRef]
- Heilpern, T.; Heyman, E. MUSIC imaging using phase-space Gaussian-beams processing. IEEE Trans. Antennas Propag. 2014, 62, 1270–1281. [Google Scholar] [CrossRef]
- Tuvi, R.; Heyman, E.; Melamed, T. UWB beam-based local diffraction tomography. part I: Phase-space processing and physical interpretation. IEEE Trans. Antennas Propag. 2020, 68, 7144–7157. [Google Scholar] [CrossRef]
- Tuvi, R.; Heyman, E.; Melamed, T. UWB beam-based local diffraction tomography. part II: The inverse problem. IEEE Trans. Antennas Propag. 2020, 68, 7158–7169. [Google Scholar] [CrossRef]
- Wu, R.S.; Wangand, Y.; Gao, J. Beamlet migration based on local perturbation theory. In Proceedings of the 2000 SEG Annual Meeting, Calgary, AB, Canada, 6–11 August 2000; Society of Exploration Geophysicists: Tulsa, OK, USA, 2000. [Google Scholar]
- Wu, R.S.; Chen, L. Beamlet migration using gabor-daubechies frame propagator. In Proceedings of the 63rd EAGE Conference & Exhibition, Amsterdam, The Netherlands, 11–15 June 2001; Netherlands European Association of Geoscientists & Engineers: Houten, The Netherlands, 2001. [Google Scholar]
- Wu, R.S.; Wang, Y.; Luo, M. Beamlet migration using local cosine basis. Geophysics 2008, 73, S207–S217. [Google Scholar] [CrossRef]
- Melamed, T. Phase-space Green’s functions for modeling time-harmonic scattering from smooth inhomogeneous objects. J. Math. Phys. 2004, 46, 2232–2246. [Google Scholar] [CrossRef] [Green Version]
- Tuvi, R.; Zhao, Z.; Sen, M.K. Multi frequency beam-based migration in inhomogeneous media using windowed Fourier transform frames. Geophys. J. Int. 2020, 8, 1086–1099. [Google Scholar] [CrossRef]
- Tuvi, R.; Zhao, Z.; Sen, M.K. A compressed data approach for image-domain least-squares migration. Geophysics 2021, 86, 1–37. [Google Scholar] [CrossRef]
- Tuvi, R.; Zhao, Z.; Sen, M.K. A fast least-squares migration with ultra-wide-band phase-space beam summation method. J. Phys. Commun. 2021, 5, 105013. [Google Scholar] [CrossRef]
- Melamed, T.; Ehrlich, Y.; Heyman, E. Short-pulse inversion of inhomogeneous media: A time-domain diffraction tomography. Inverse Probl. 1996, 12, 977. [Google Scholar] [CrossRef]
- Dean, S.R. The Radon Transform and Some of Its Applications; Wiley—Interscience: New York, NY, USA, 1983. [Google Scholar]
- Devaney, A.J. A filtered backpropagation algorithm for diffraction tomography. Ultrason. Imaging 1982, 4, 336–350. [Google Scholar] [CrossRef] [PubMed]
- Kak, A.C. Computerized tomography with X-ray, emission, and ultrasound sources. Proc. IEEE 1979, 67, 1245–1272. [Google Scholar] [CrossRef]
- Heyman, E. Pulsed beam propagation in inhomogeneous medium. IEEE Trans. Antennas Propag. 1994, 42, 311–319. [Google Scholar] [CrossRef]
- Tuvi, R.; Zhao, Z.; Sen, M.K. A time domain seismic imaging method with a sparse pulsed-beams data. IEEE Trans. Geosci. Remote Sens. 2021, 1. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuvi, R. A Multi-Frequency Tomographic Inverse Scattering Using Beam Basis Functions. Sensors 2022, 22, 1684. https://doi.org/10.3390/s22041684
Tuvi R. A Multi-Frequency Tomographic Inverse Scattering Using Beam Basis Functions. Sensors. 2022; 22(4):1684. https://doi.org/10.3390/s22041684
Chicago/Turabian StyleTuvi, Ram. 2022. "A Multi-Frequency Tomographic Inverse Scattering Using Beam Basis Functions" Sensors 22, no. 4: 1684. https://doi.org/10.3390/s22041684
APA StyleTuvi, R. (2022). A Multi-Frequency Tomographic Inverse Scattering Using Beam Basis Functions. Sensors, 22(4), 1684. https://doi.org/10.3390/s22041684





