Complex Pearson Correlation Coefficient for EEG Connectivity Analysis
Abstract
1. Introduction
2. Methods
2.1. Complex Pearson Correlation Coefficient as a Measure of Undirected Connectivity
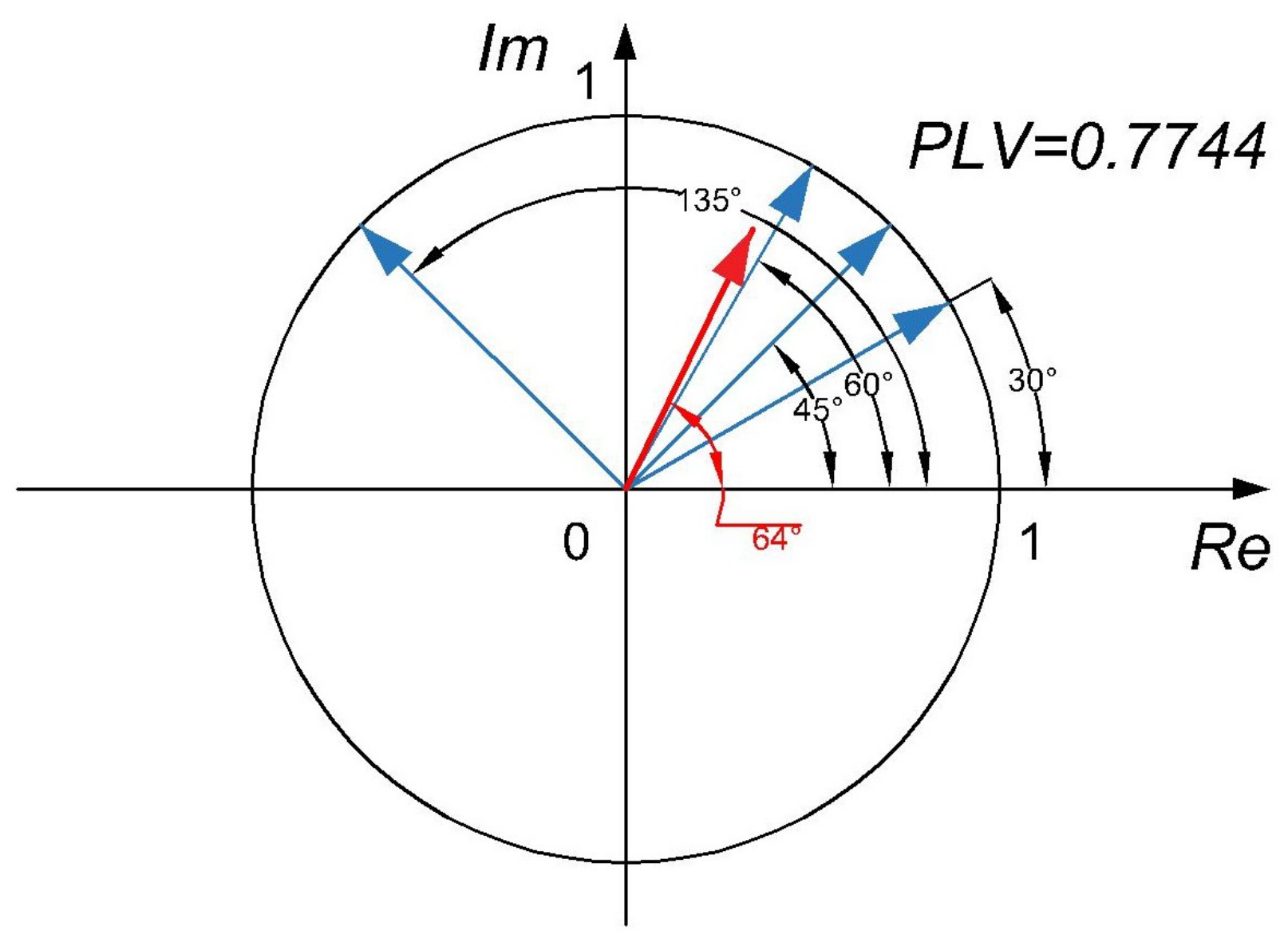
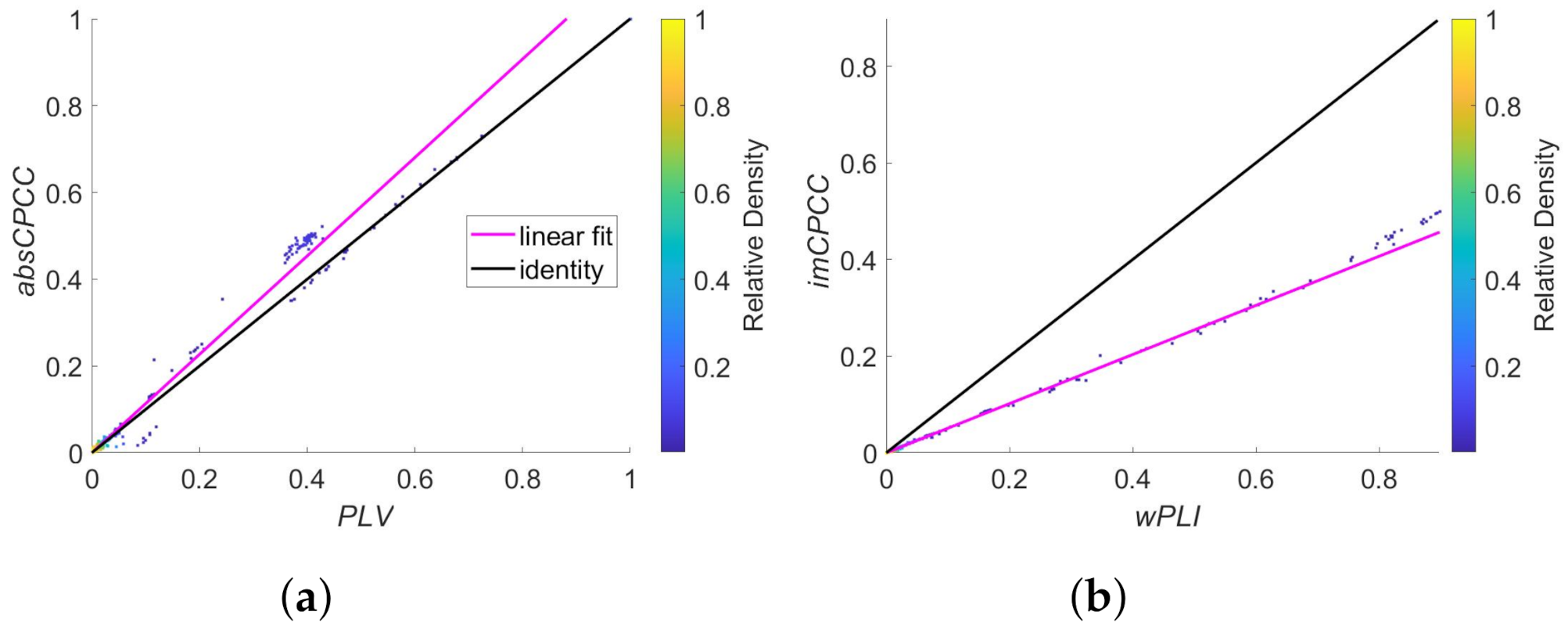
2.2. Phase Locking Value PLV and Its Relation to CPCC
2.3. Weighted Phase Lag Index wPLI and Its Relation to CPCC
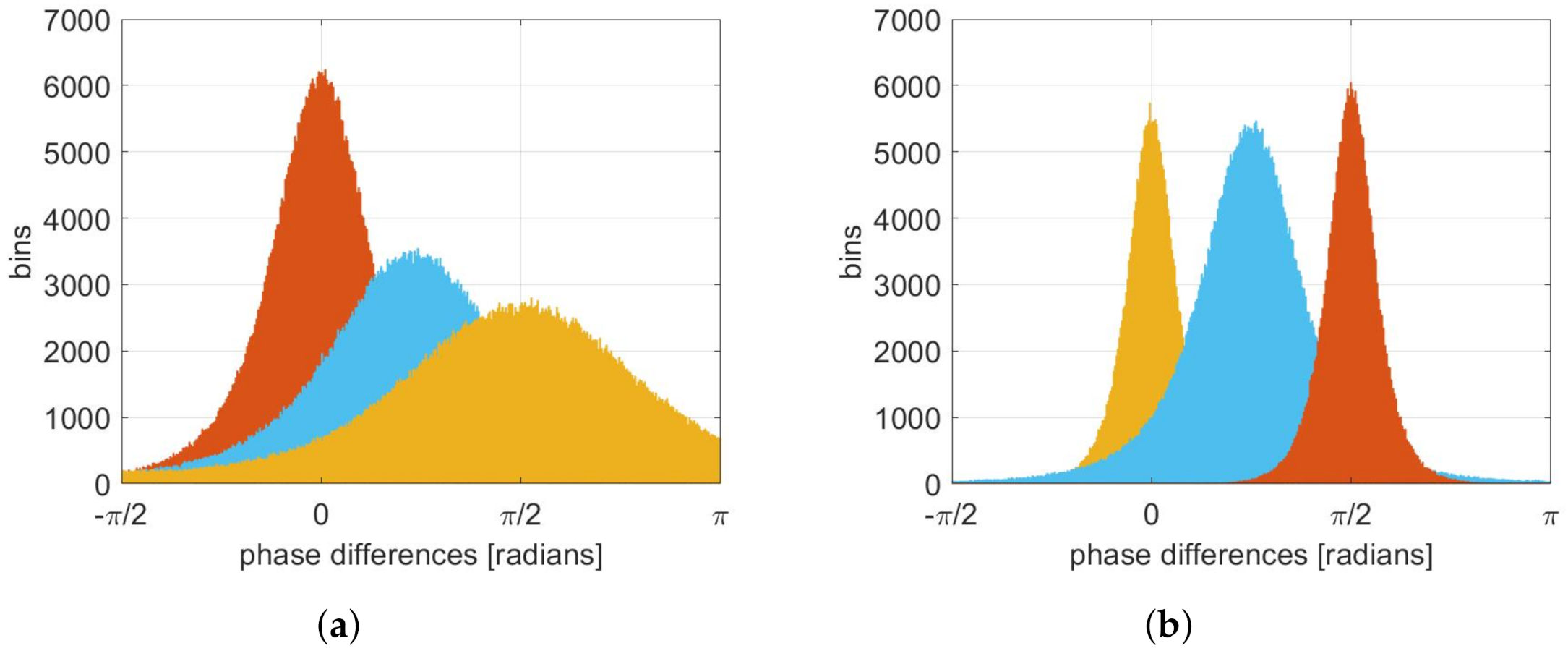
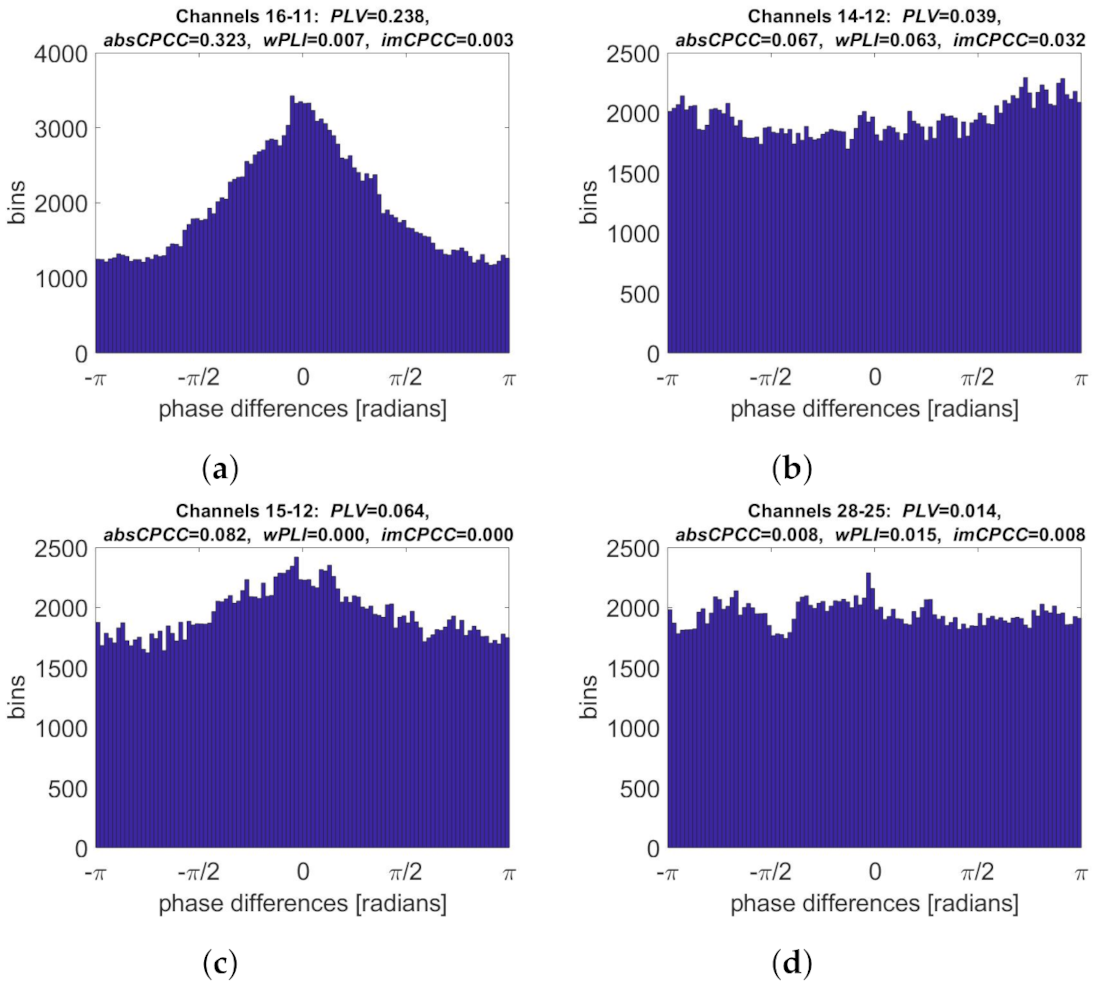
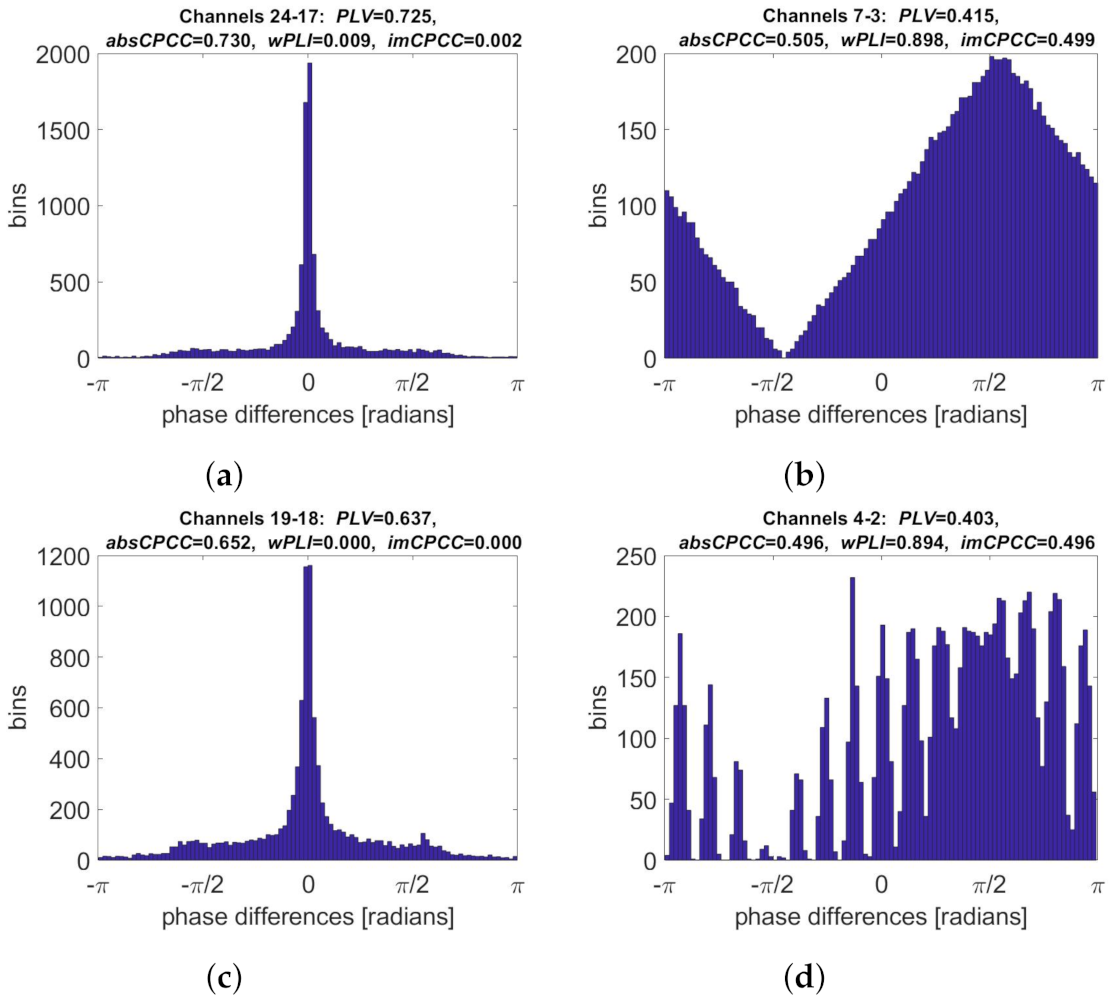
2.4. Connectivity Estimation Based on Phase Difference Histograms
3. Results
3.1. Synthetic Signals from the MRC Brain Network Dynamics Unit (University of Oxford)
3.2. Synthetic Signals Generated with the Kuramoto Model
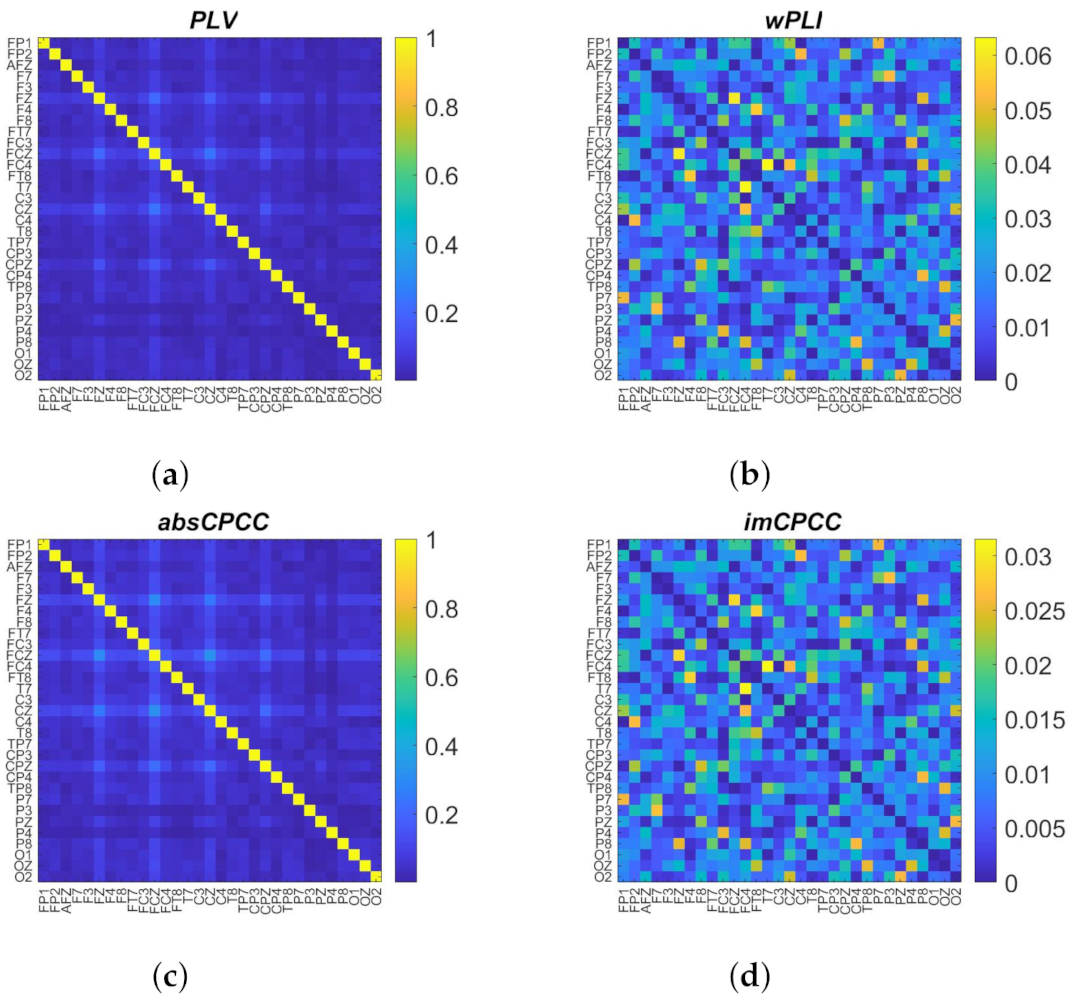
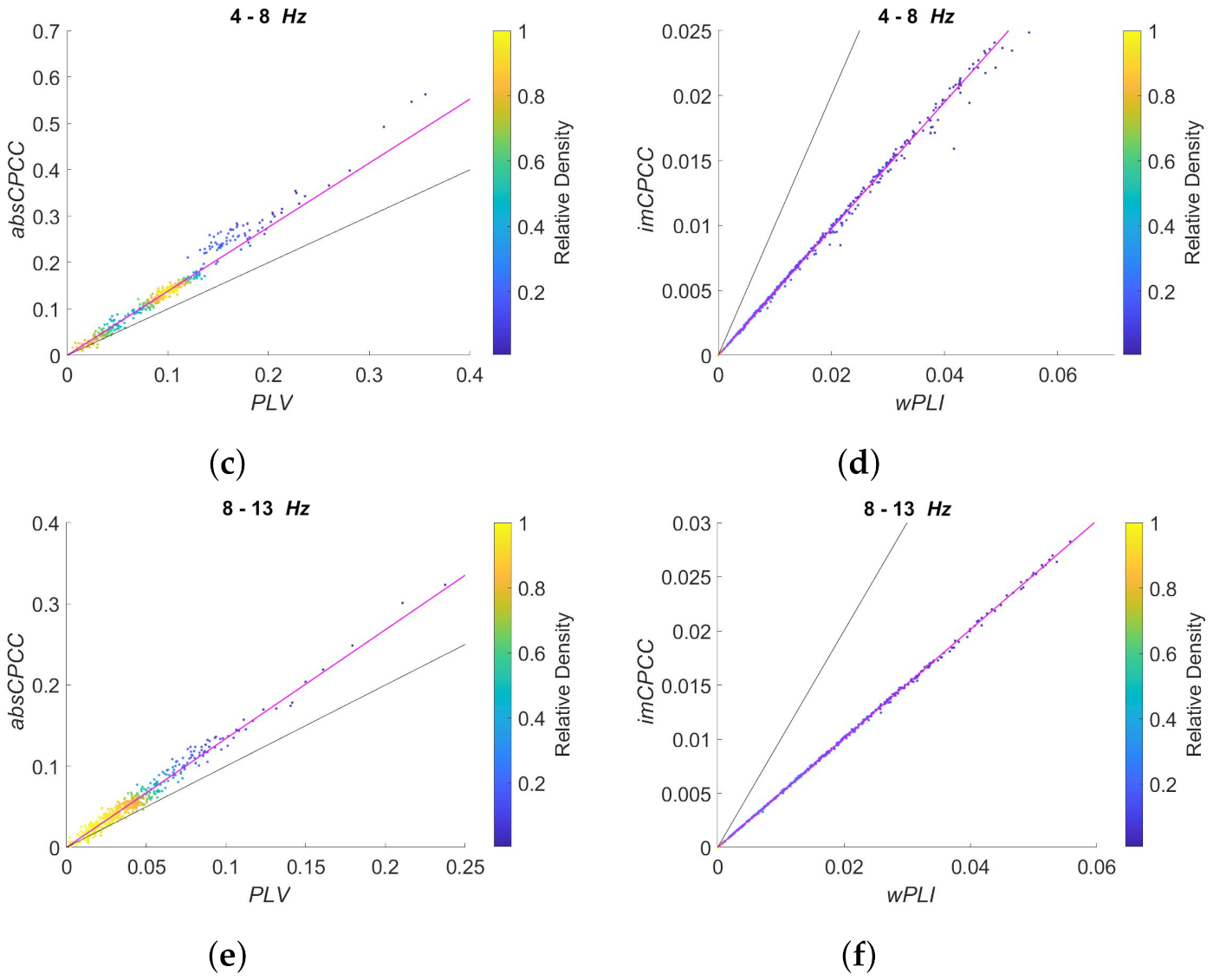
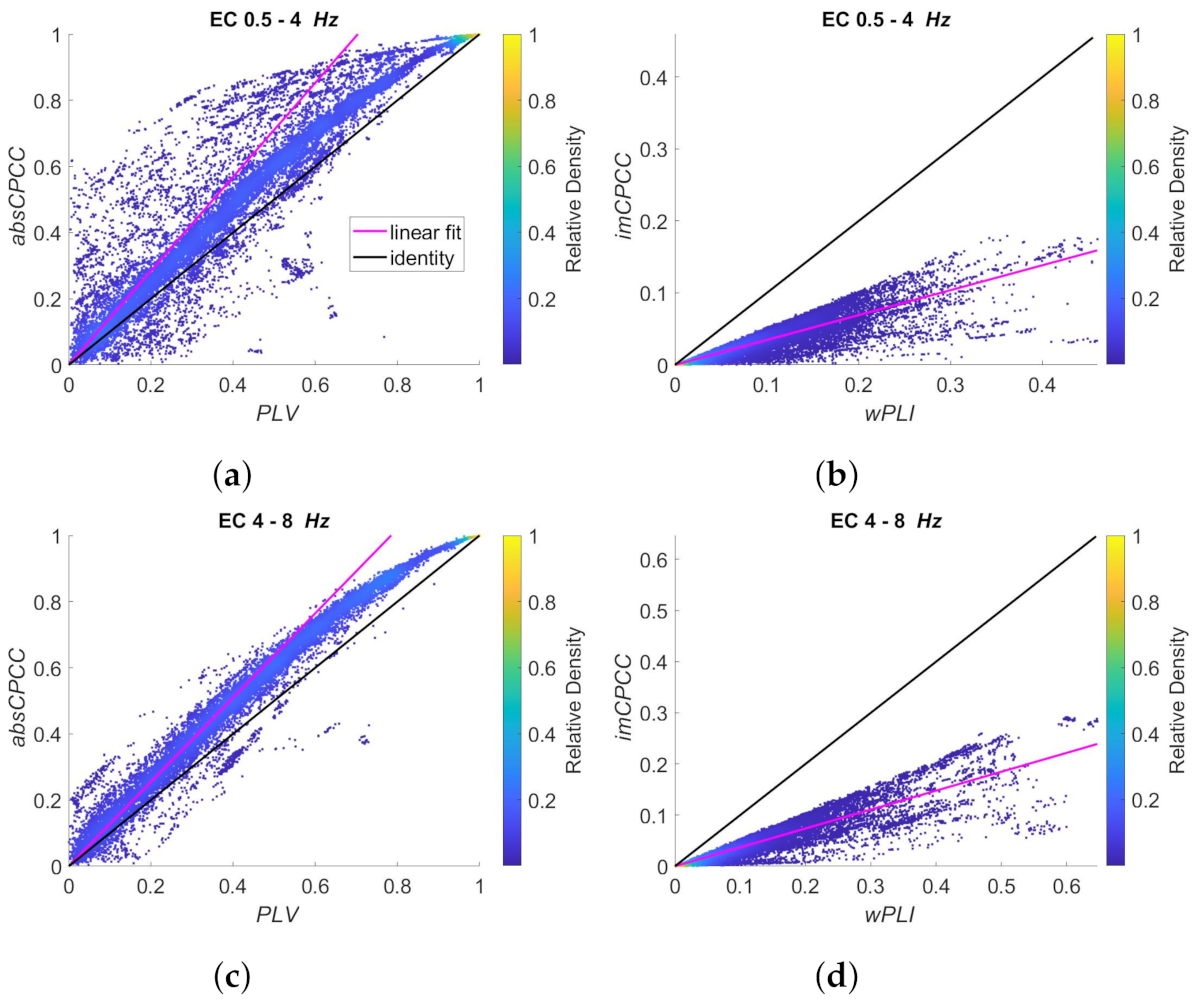
3.3. Real-Life Signals
- The raw brain activity data were imported into MATLAB using the EEGLAB toolbox;
- Electrode positions (also called channel locations) were defined in the software;
- The data were referenced to average;
- The data were filtered with a band pass filter limited to 0.5 and 45 Hz;
- Automatic spectral-based channel suppression (z = 5) was performed using the EEGLAB “pop rejchan” function;
- Artifacts were removed using the ICLabel plugin for EEGLAB (thresholds for removing components were less than or equal to 0.05 for brain activity and greater than or equal to 0.9 for artifacts);
- The data were re-referenced to average;
- Sub-bands of the EEG signal were extracted (delta 0.5–4 Hz, theta 4–8 Hz, alpha 8–13 Hz, low beta 13–18 Hz, high beta 18–30 Hz, gamma 35–45 Hz).
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| absCPCC | absolute value of complex Pearson correlation coefficient |
| CPCC | complex Pearson correlation coefficient |
| DTI | diffusion tensor imaging |
| EC | eyes closed |
| EEG | electroencephalography |
| EO | eyes open |
| HT | Hilbert transform |
| imCPCC | imaginary component of complex Pearson correlation coefficient |
| MEG | magnetoencephalography |
| MRI | magnetic resonance imaging |
| PLV | phase locking value |
| PLI | phase lag index |
| wPLI | weighted phase lag index |
References
- Fornito, A.; Zalesky, A.; Bullmore, E. Fundamentals of Brain Network Analysis, 1st ed.; Academic Press: London, UK, 2016; pp. 1–3. [Google Scholar]
- Sanei, S.; Chambers, J.A. EEG Signal Processing, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 1–8. [Google Scholar]
- Olejarczyk, E.; Marzetti, L.; Pizzella, V.; Zappasodi, F. Comparison of connectivity analyses for resting state EEG data. J. Neural Eng. 2017, 14, 036017. [Google Scholar] [CrossRef] [PubMed]
- Koch, M.A.; Norris, D.G.; Hund-Georgiadis, M. An investigation of functional and anatomical connectivity using magnetic resonance imaging. Neuroimage 2002, 16, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Rose, S.; Pannek, K.; Bell, C.; Baumann, F.; Hutchinson, N.; Coulthard, A.; McCombe, P.; Henderson, R. Direct evidence of intra- and interhemispheric corticomotor network degeneration in amyotrophic lateral sclerosis: An automated MRI structural connectivity study. Neuroimage 2012, 59, 2661–2669. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.; Han, C.E.; Uhlhaas, P.J.; Kaiser, M. Preferential detachment during human brain development: Age-and sex-specific structural connectivity in diffusion tensor imaging (DTI) data. Cereb. Cortex 2015, 25, 1477–1489. [Google Scholar] [CrossRef]
- Singer, W. Neuronal synchrony: A versatile code for the definition of relations? Neuron 1999, 24, 49–65. [Google Scholar] [CrossRef]
- Varela, F.; Lachaux, J.P.; Rodriguez, E.; Martinerie, J. The brainweb: Phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2001, 2, 229–239. [Google Scholar] [CrossRef]
- Fries, P. A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. Trends Cogn. Sci. 2005, 9, 474–480. [Google Scholar] [CrossRef]
- Fries, P. Rhythms for cognition: Communication through coherence. Neuron 2015, 88, 220–235. [Google Scholar] [CrossRef]
- Siegel, M.; Donner, T.H.; Engel, A.K. Spectral fingerprints of large-scale neuronal interactions. Nat. Rev. Neurosci. 2012, 13, 121–134. [Google Scholar] [CrossRef]
- Bastos, A.M.; Schoffelen, J.M. A tutorial review of functional connectivity analysis methods and their interpretational pitfalls. Front. Syst. Neurosci. 2016, 9, 175. [Google Scholar] [CrossRef]
- Sakkalis, V. Review of advanced techniques for the estimation of brain connectivity measured with EEG/MEG. Comput. Biol. Med. 2011, 41, 1110–1117. [Google Scholar] [CrossRef]
- Hwa, R.C.; Ferree, T.C. Scaling properties of fluctuations in the human electroencephalogram. Phys. Rev. E 2002, 66, 021901. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.X.; Jiang, T. Visual working memory load-related changes in neural activity and functional connectivity. PLoS ONE 2011, 6, e22357. [Google Scholar] [CrossRef]
- Stam, C.J.; Van Dijk, B.W. Synchronization likelihood: An unbiased measure of generalized synchronization in multivariate data sets. Phys. D 2002, 163, 236–251. [Google Scholar] [CrossRef]
- Stam, C.J.; Nolte, G.; Daffertshofer, A. Phase lag index: Assessment of functional connectivity from multi channel EEG and MEG with diminished bias from common sources. Hum. Brain Mapp. 2007, 28, 1178–1193. [Google Scholar] [CrossRef]
- Lachaux, J.P.; Rodriguez, E.; Martinerie, J.; Varela, F.J. Measuring phase synchrony in brain signals. Hum. Brain Mapp. 1999, 8, 194–208. [Google Scholar] [CrossRef]
- Vinck, M.; Oostenveld, R.; Van Wingerden, M.; Battaglia, F.; Pennartz, C.M. An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias. Neuroimage 2011, 55, 1548–1565. [Google Scholar] [CrossRef]
- Schreier, P.J. A unifying discussion of correlation analysis for complex random vectors. IEEE Trans. Signal Process 2008, 56, 1327–1336. [Google Scholar] [CrossRef]
- Ma, G.; Li, L. Depth and structural index estimation of 2D magnetic source using correlation coefficient of analytic signal. J. Appl. Geophys. 2013, 91, 9–13. [Google Scholar] [CrossRef]
- Fuhrmann, D.R.; San Antonio, G. Transmit beamforming for MIMO radar systems using signal cross-correlation. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 171–186. [Google Scholar] [CrossRef]
- Makita, S.; Kurokawa, K.; Hong, Y.J.; Miura, M.; Yasuno, Y. Noise-immune complex correlation for optical coherence angiography based on standard and Jones matrix optical coherence tomography. Biomed. Opt. Express 2016, 7, 1525–1548. [Google Scholar] [CrossRef]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Tass, P.; Rosenblum, M.G.; Weule, J.; Kurths, J.; Pikovsky, A.; Volkmann, J.; Schnitzler, A.; Freund, H.J. Detection of n:m Phase Locking from Noisy Data: Application to Magnetoencephalography. Phys. Rev. Lett. 1998, 81, 3291–3294. [Google Scholar] [CrossRef]
- Mäkinen, V.; Tiitinen, H.; May, P. Auditory event-related responses are generated independently of ongoing brain activity. NeuroImage 2005, 24, 961–968. [Google Scholar] [CrossRef]
- Šverko, Z.; Sajovic, J.; Drevenšek, G.; Vlahinić, S.; Rogelj, P. Generation of Oscillatory Synthetic Signal Simulating Brain Network Dynamics. In Proceedings of the 2021 44th International Convention on Information, Communication and Electronic Technology (MIPRO), MEET—Microelectronics, Electronics and Electronic Technology, Opatija, Croatia, 27 September–1 October 2021. [Google Scholar]
- Torkamani Azar, M.; Kanik, S.D.; Aydin, S.; Cetin, M. Prediction of reaction time and vigilance variability from spatio-spectral features of resting-state EEG in a long sustained attention task. IEEE J. Biomed. Health Inform. 2020, 24, 2550–2558. [Google Scholar] [CrossRef]
- Fraschini, M.; Pani, S.M.; Didaci, L.; Marcialis, G.L. Robustness of functional connectivity metrics for EEG-based personal identification over task-induced intra-class and inter-class variations. Pattern Recognit. Lett. 2019, 125, 49–54. [Google Scholar] [CrossRef]
- Hardmeier, M.; Hatz, F.; Bousleiman, H.; Schindler, C.; Stam, C.J.; Fuhr, P. Reproducibility of functional connectivity and graph measures based on the phase lag index (PLI) and weighted phase lag index (wPLI) derived from high resolution EEG. PLoS ONE 2014, 9, e108648. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, Z. EEG Signal Processing and Feature Extraction; Springer: Singapore, 2019; pp. 241–266. [Google Scholar]
- Sarmukadam, K.; Bitsika, V.; Sharpley, C.F.; McMillan, M.M.; Agnew, L.L. Comparing different EEG connectivity methods in young males with ASD. Behav. Brain Res. 2020, 383, 112482. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, J.; Zhu, L.; Tang, J.; Lin, G.; Kong, W.; Lei, X.; Zhu, L. EEG-Based Sleep Staging Analysis with Functional Connectivity. Sensors 2021, 21, 1988. [Google Scholar] [CrossRef]
- Caicedo-Acosta, J.; Castaño, G.A.; Acosta-Medina, C.; Alvarez-Meza, A.; Castellanos-Dominguez, G. Deep Neural Regression Prediction of Motor Imagery Skills Using EEG Functional Connectivity Indicators. Sensors 2021, 21, 1932. [Google Scholar] [CrossRef]
- Hag, A.; Handayani, D.; Pillai, T.; Mantoro, T.; Kit, M.H.; Al-Shargie, F. EEG Mental Stress Assessment Using Hybrid Multi-Domain Feature Sets of Functional Connectivity Network and Time-Frequency Features. Sensors 2021, 21, 6300. [Google Scholar] [CrossRef] [PubMed]
- Katmah, R.; Al-Shargie, F.; Tariq, U.; Babiloni, F.; Al-Mughairbi, F.; Al-Nashash, H. A Review on Mental Stress Assessment Methods Using EEG Signals. Sensors 2021, 21, 5043. [Google Scholar] [CrossRef]
- Formoso, M.A.; Ortiz, A.; Martinez-Murcia, F.J.; Gallego, N.; Luque, J.L. Detecting Phase-Synchrony Connectivity Anomalies in EEG Signals. Application to Dyslexia Diagnosis. Sensors 2021, 21, 7061. [Google Scholar] [CrossRef] [PubMed]
- Anzolin, A.; Toppi, J.; Petti, M.; Cincotti, F.; Astolfi, L. SEED-G: Simulated EEG Data Generator for Testing Connectivity Algorithms. Sensors 2021, 21, 3632. [Google Scholar] [CrossRef] [PubMed]
- Chikara, R.K.; Ko, L.-W. Modulation of the Visual to Auditory Human Inhibitory Brain Network: An EEG Dipole Source Localization Study. Brain Sci. 2019, 9, 216. [Google Scholar] [CrossRef] [PubMed]
- Perez-Ortiz, C.X.; Gordillo, J.L.; Mendoza-Montoya, O.; Antelis, J.M.; Caraza, R.; Martinez, H.R. Functional Connectivity and Frequency Power Alterations during P300 Task as a Result of Amyotrophic Lateral Sclerosis. Sensors 2021, 21, 6801. [Google Scholar] [CrossRef] [PubMed]
- García-Murillo, D.G.; Alvarez-Meza, A.; Castellanos-Dominguez, G. Single-Trial Kernel-Based Functional Connectivity for Enhanced Feature Extraction in Motor-Related Tasks. Sensors 2021, 21, 2750. [Google Scholar] [CrossRef]
- Vecchio, F.; Pappalettera, C.; Miraglia, F.; Alù, F.; Orticoni, A.; Judica, E.; Cotelli, M.; Pistoia, F.; Rossini, P.M. Graph Theory on Brain Cortical Sources in Parkinson’s Disease: The Analysis of ‘Small World’ Organization from EEG. Sensors 2021, 21, 7266. [Google Scholar] [CrossRef]





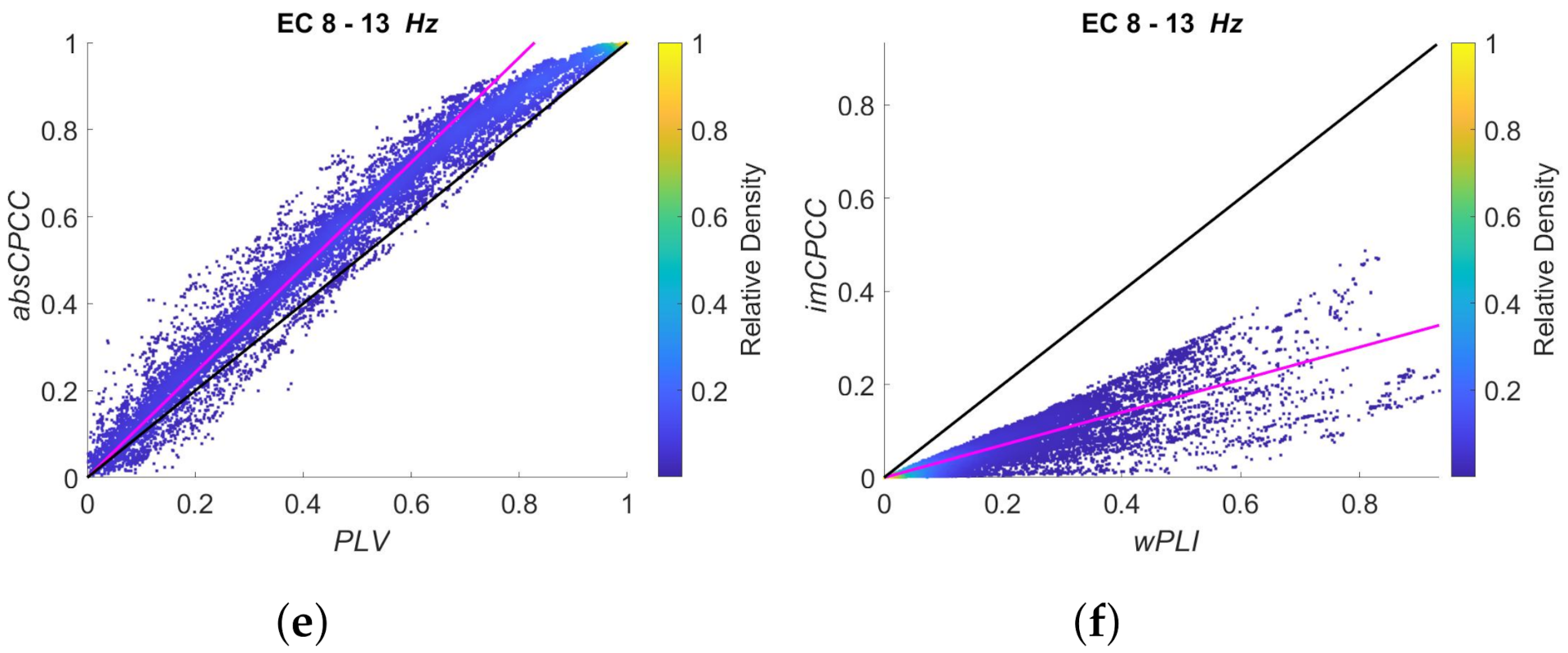
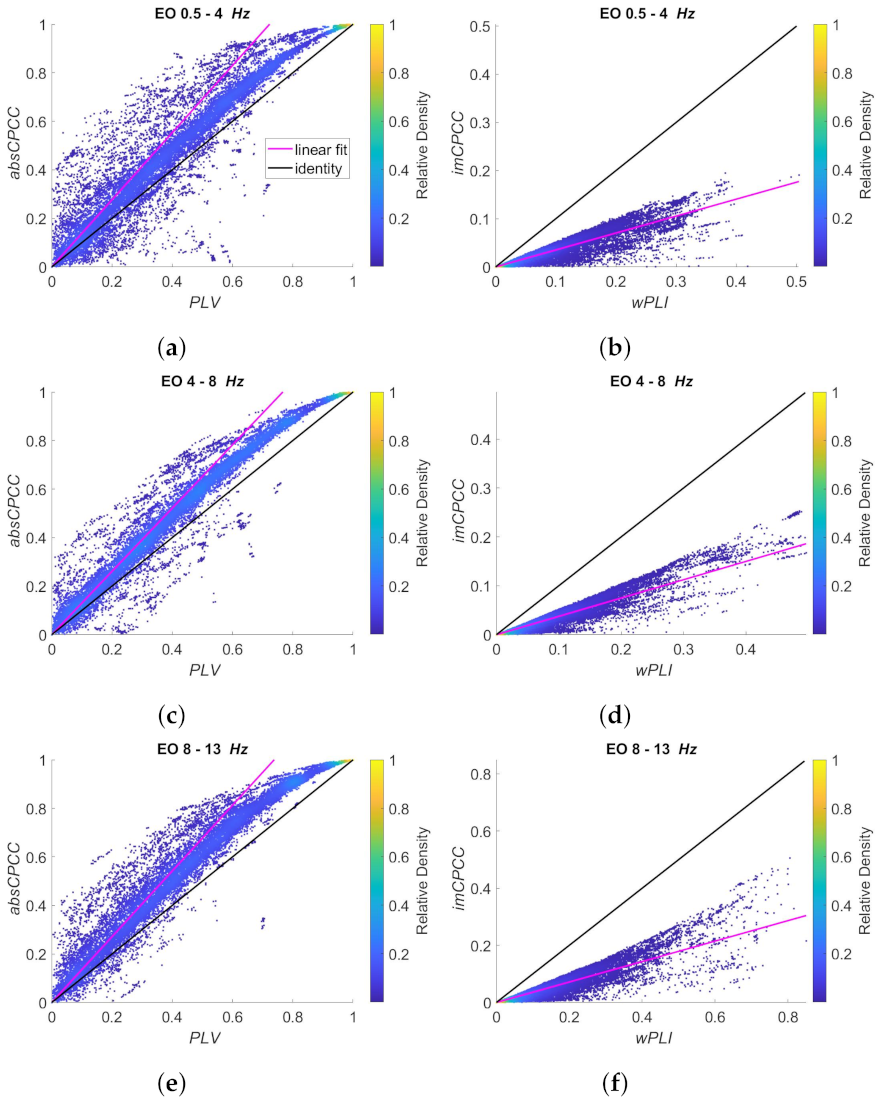

| Frequency | State-EC | State-EO | ||
|---|---|---|---|---|
| (Hz) | ||||
| 0.5–4 | 0.93 | 0.86 | 0.94 | 0.89 |
| 4–8 | 0.98 | 0.91 | 0.97 | 0.94 |
| 8–13 | 0.98 | 0.86 | 0.97 | 0.91 |
| 13–18 | 0.99 | 0.94 | 0.99 | 0.96 |
| 18–30 | 0.98 | 0.96 | 0.99 | 0.96 |
| 35–45 | 0.96 | 0.95 | 0.99 | 0.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šverko, Z.; Vrankić, M.; Vlahinić, S.; Rogelj, P. Complex Pearson Correlation Coefficient for EEG Connectivity Analysis. Sensors 2022, 22, 1477. https://doi.org/10.3390/s22041477
Šverko Z, Vrankić M, Vlahinić S, Rogelj P. Complex Pearson Correlation Coefficient for EEG Connectivity Analysis. Sensors. 2022; 22(4):1477. https://doi.org/10.3390/s22041477
Chicago/Turabian StyleŠverko, Zoran, Miroslav Vrankić, Saša Vlahinić, and Peter Rogelj. 2022. "Complex Pearson Correlation Coefficient for EEG Connectivity Analysis" Sensors 22, no. 4: 1477. https://doi.org/10.3390/s22041477
APA StyleŠverko, Z., Vrankić, M., Vlahinić, S., & Rogelj, P. (2022). Complex Pearson Correlation Coefficient for EEG Connectivity Analysis. Sensors, 22(4), 1477. https://doi.org/10.3390/s22041477








