Doppler Measurement of Modulated Light for High Speed Vehicles
Abstract
:1. Introduction
2. Optical Waveform for Doppler Radar Application
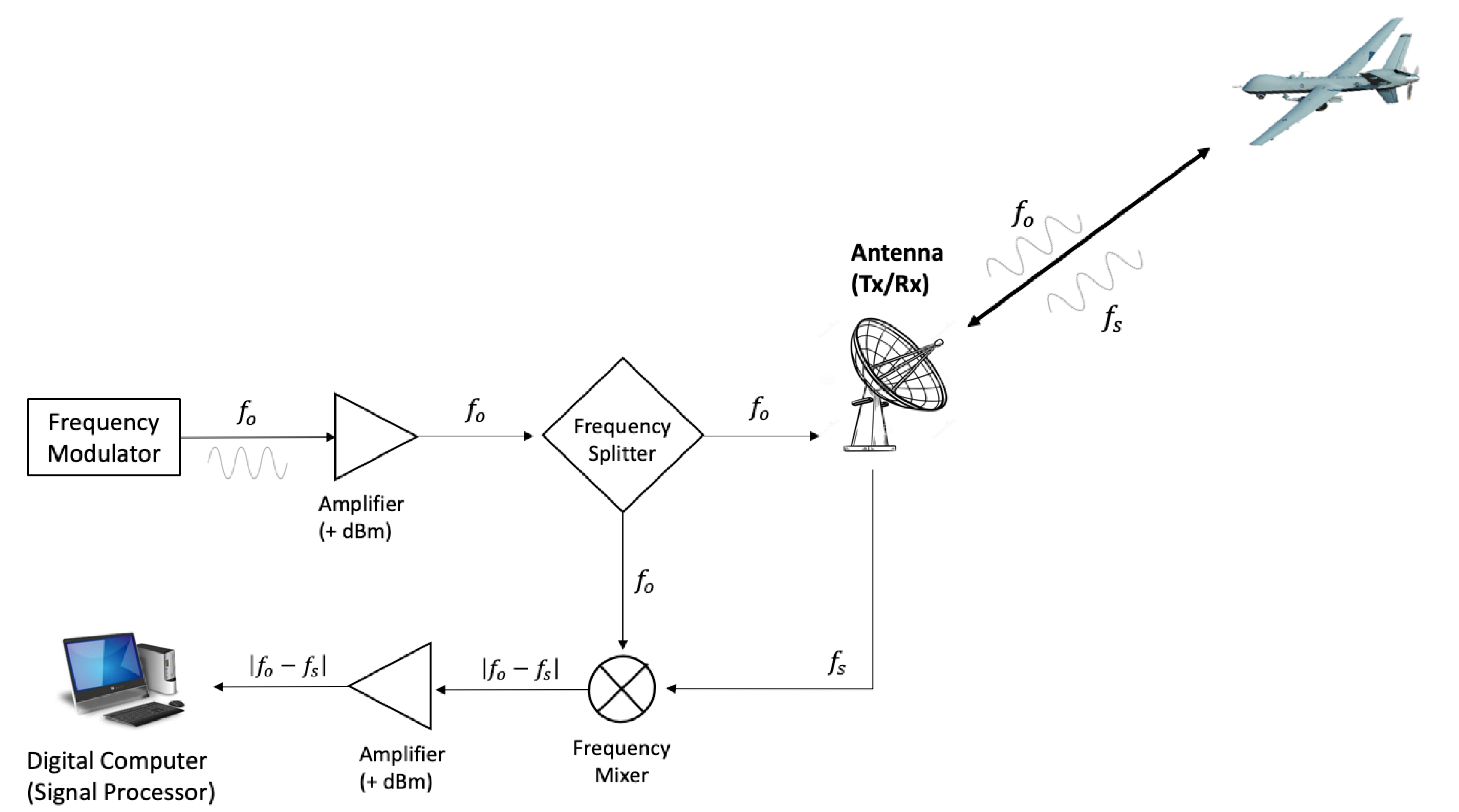
2.1. Principles of Doppler Radar
2.2. Photonic Doppler Sensing
2.2.1. Optical Modulation
- Thermal noise (Johnson noise): This unavoidable noise is generated by random thermal motion of charge carriers. It is generated regardless of the voltage applied.
- Flicker noise: The flicker electronic noise has a PSD (power spectral density) of 1/(frequency). This is a low-frequency phenomenon because higher frequencies are overshadowed by white noise. Typically, this noise affects the DC components of the circuit.
2.2.2. Doppler Shift in Modulated Light
2.2.3. Modulation Bandwidth of LED
2.2.4. Trans-Impedance Amplifier (TIA): Operation and Noise
3. Sensor Design
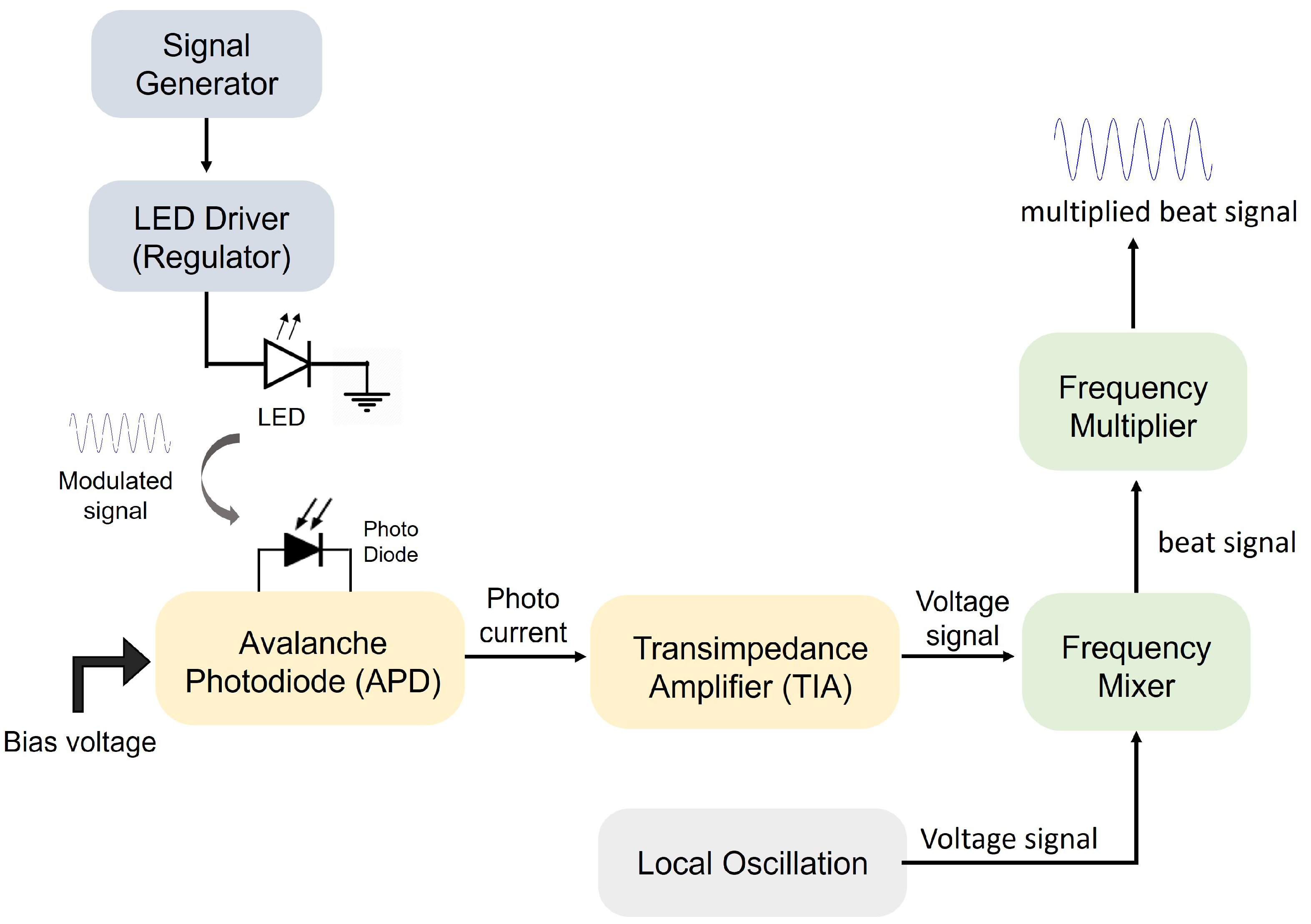
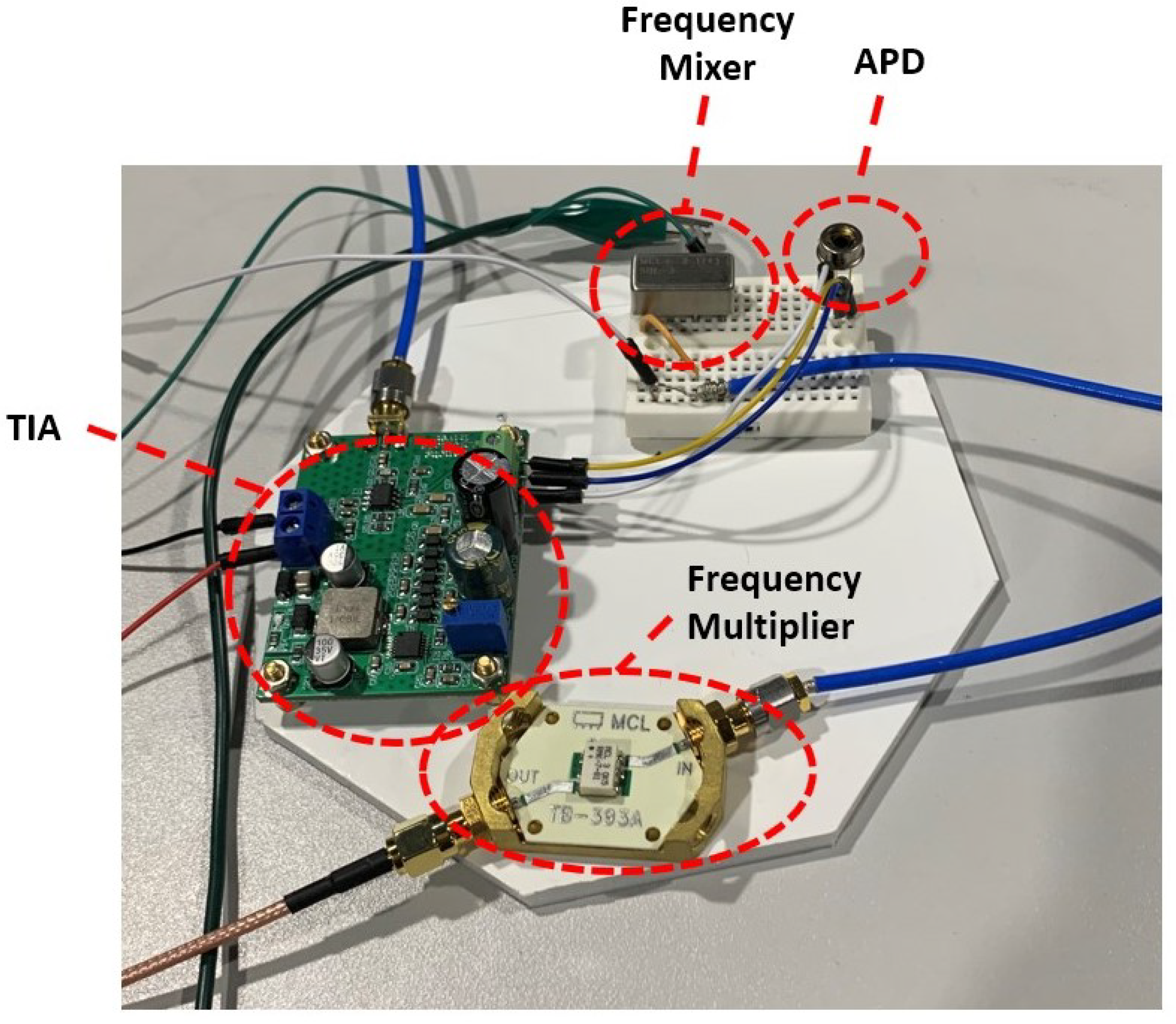
3.1. Sensor Description
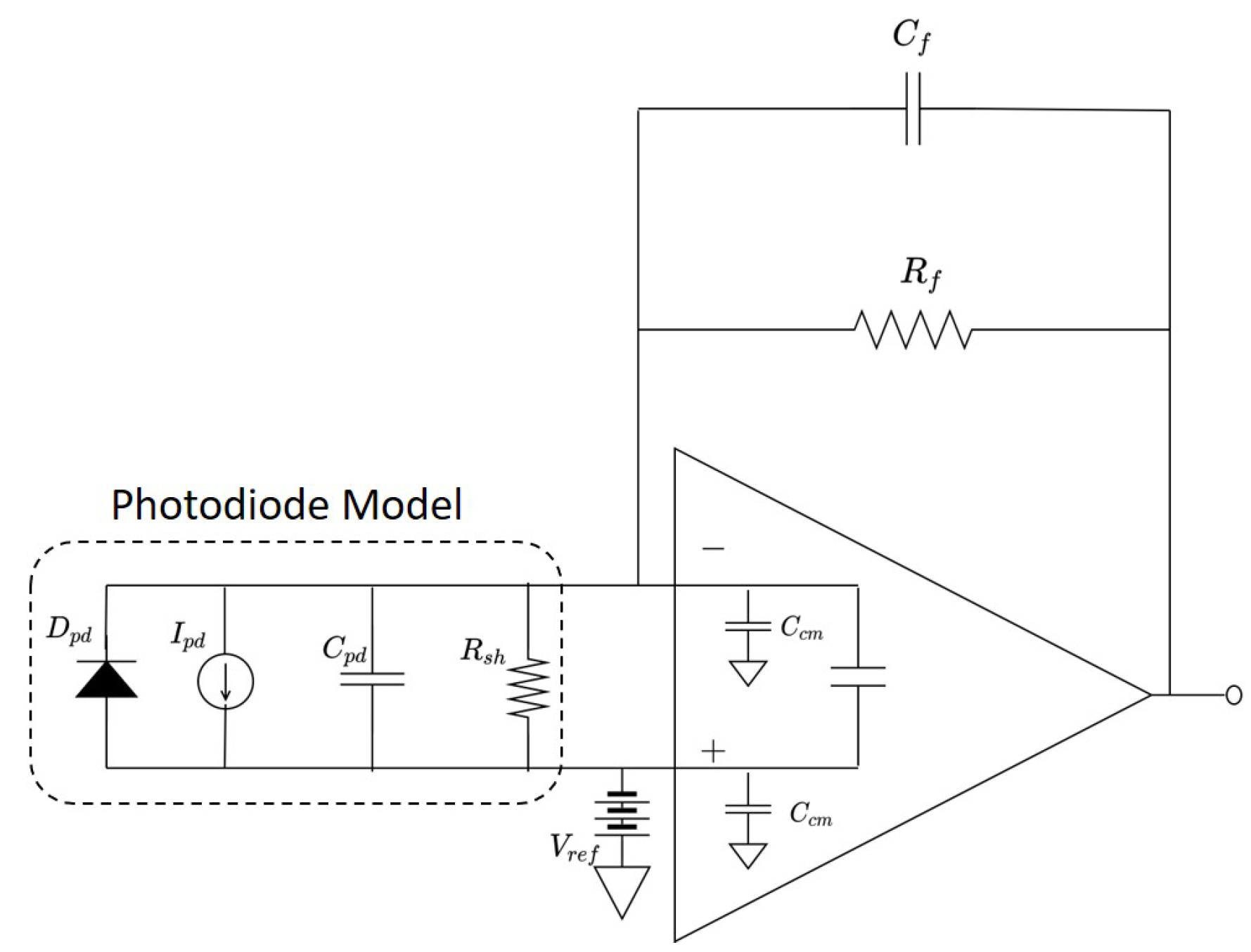
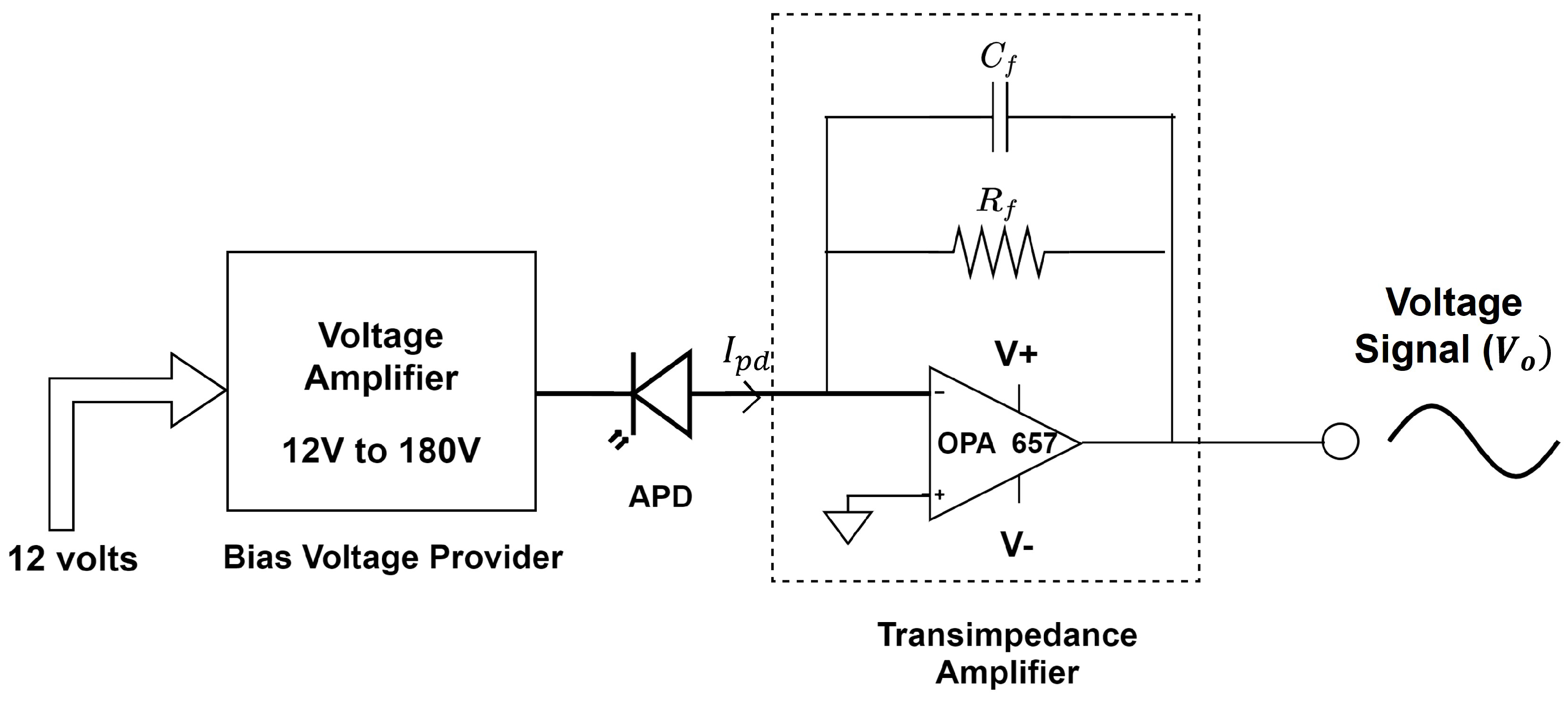
3.1.1. Photodetector
3.1.2. Transimpedance Amplifier (TIA)
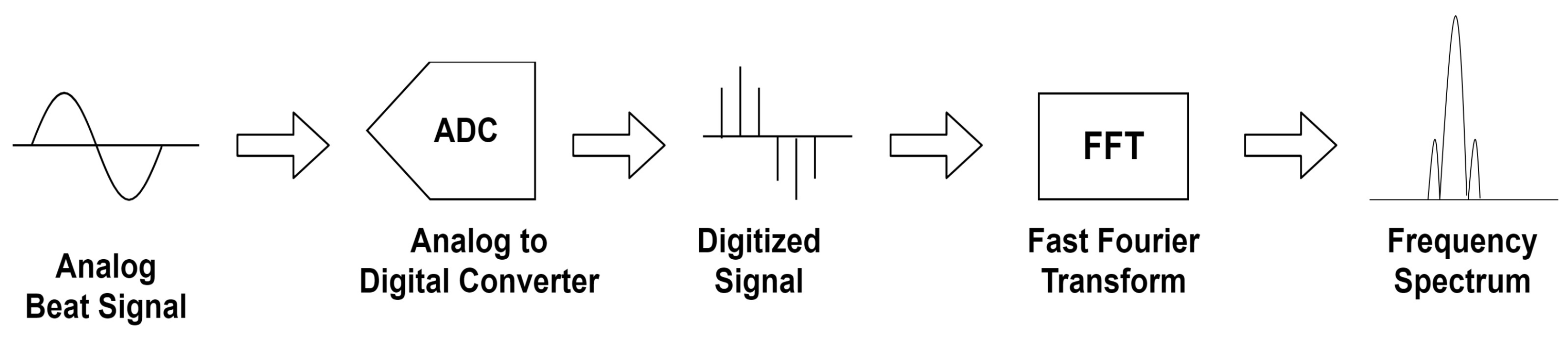
3.2. Signal Processing
4. Experiment
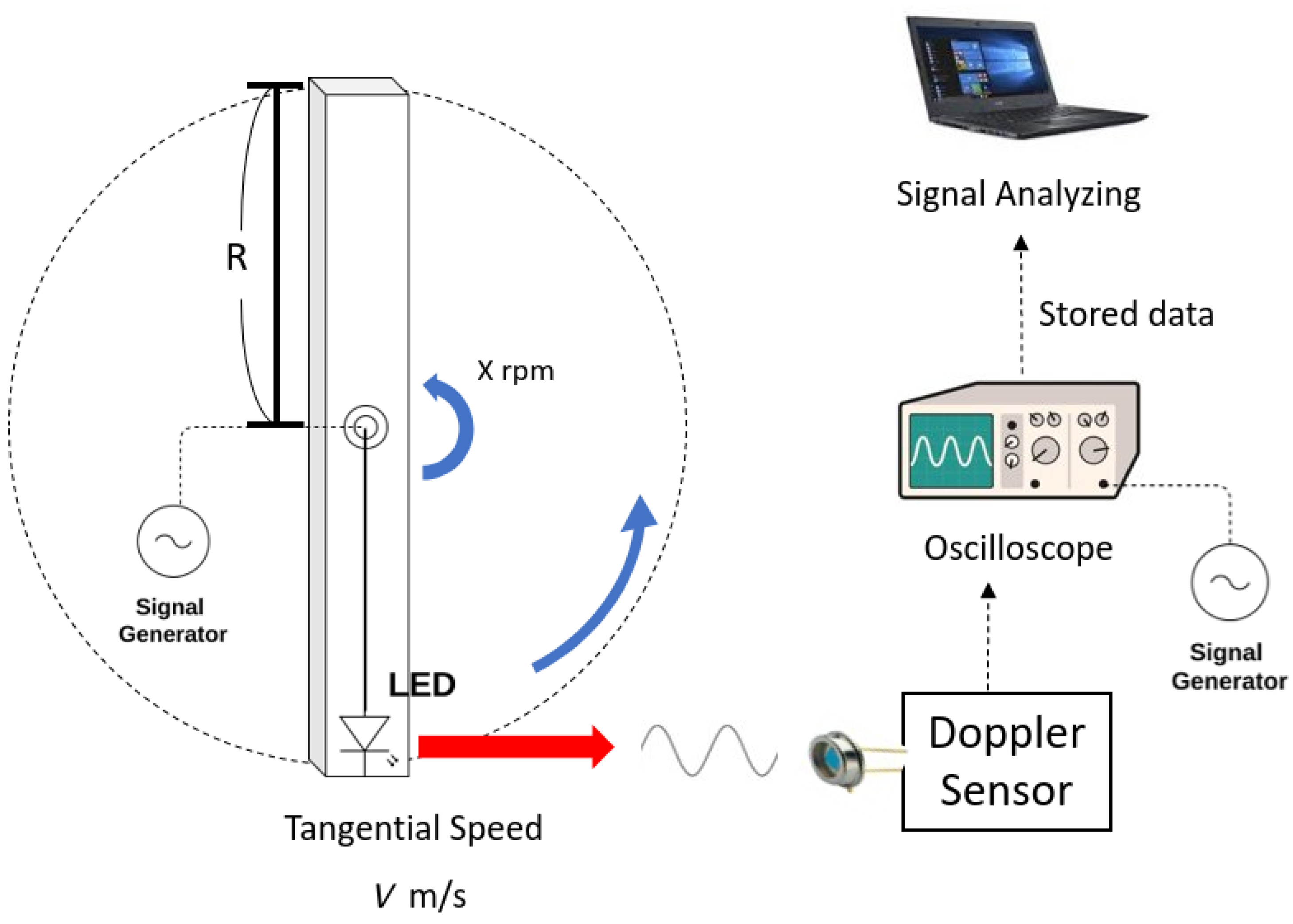
4.1. Benchtop Experiment Setup
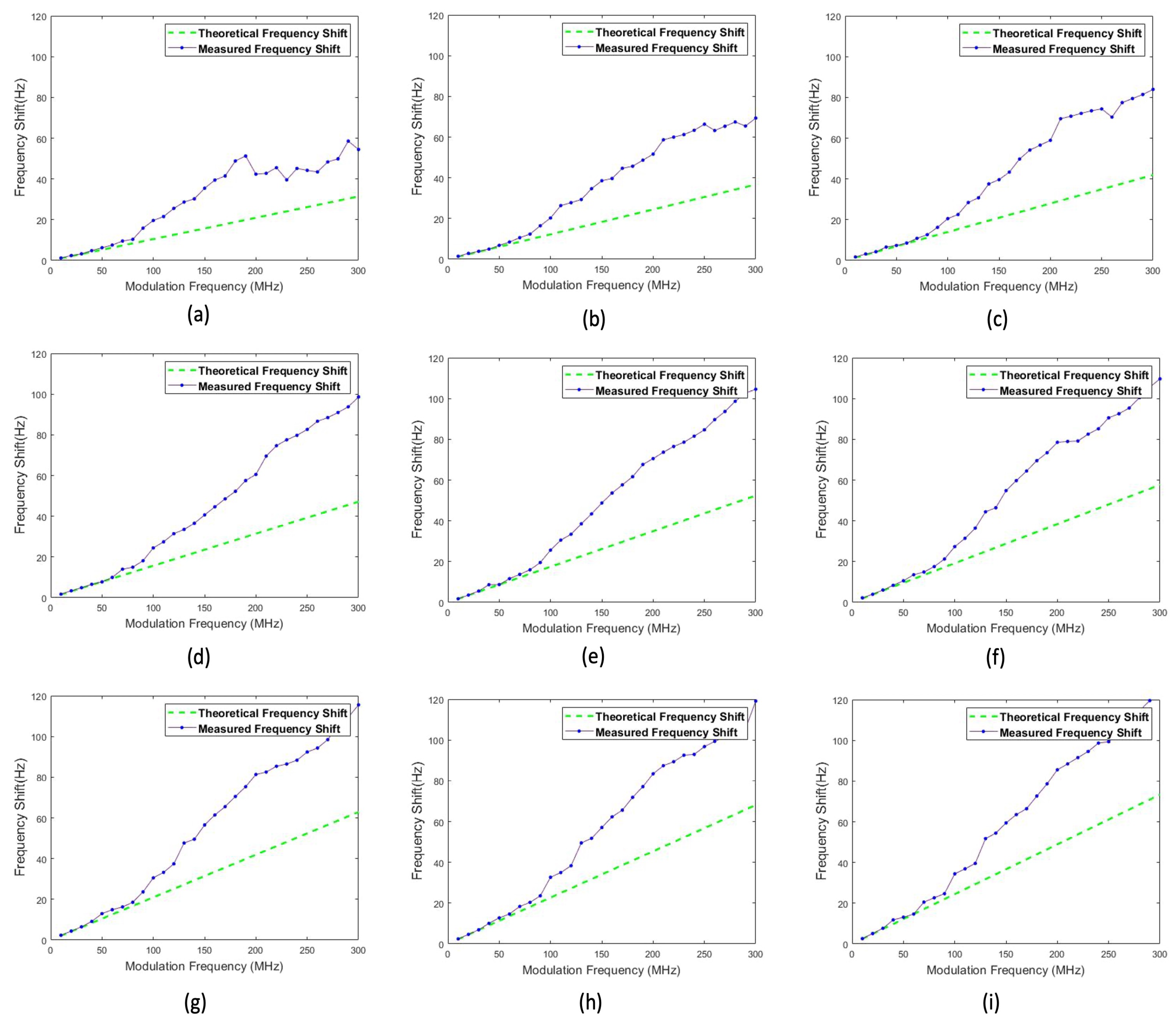
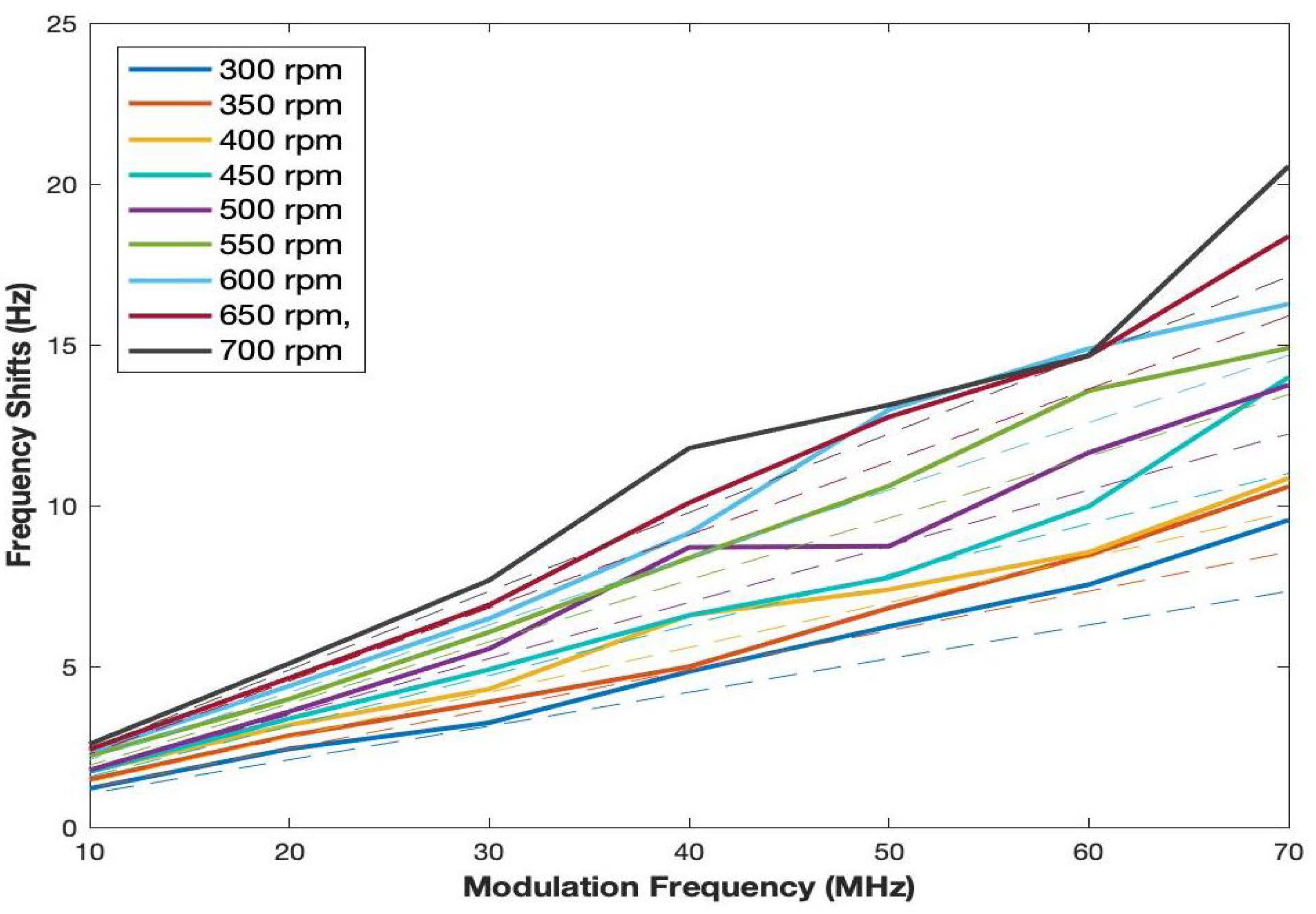
4.2. Experimental Result
4.3. Velocity Conversion
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kayton, M.; Fried, W.R. Avionics Navigation Systems; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- El-Rabbany, A. Introduction to GPS: The Global Positioning System; Artech House: London, UK, 2002. [Google Scholar]
- Grewal, M.; Weill, L. GPS Positioning Systems, Inertial Navigation, and Integration; Willey-Inter Science, Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Ramasubramanian, K.; Ramaiah, K. Moving from legacy 24 GHz to state-of-the-art 77-GHz radar. ATZelektronik Worldw. 2018, 13, 46–49. [Google Scholar] [CrossRef]
- Charvat, G.L. Small and Short-Range Radar Systems; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Dickmann, J.; Klappstein, J.; Hahn, M.; Appenrodt, N.; Bloecher, H.L.; Werber, K.; Sailer, A. Automotive radar the key technology for autonomous driving: From detection and ranging to environmental understanding. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Li, C.; Peng, Z.; Huang, T.Y.; Fan, T.; Wang, F.K.; Horng, T.S.; Munoz-Ferreras, J.M.; Gomez-Garcia, R.; Ran, L.; Lin, J. A review on recent progress of portable short-range noncontact microwave radar systems. IEEE Trans. Microw. Theory Tech. 2017, 65, 1692–1706. [Google Scholar] [CrossRef]
- Junkins, J.L.; Hughes, D.C.; Wazni, K.P.; Pariyapong, V. Vision-based navigation for rendezvous, docking and proximity operations. In Proceedings of the 22nd Annual AAS Guidance and Control Conference, Breckenridge, CO, USA, 3–7 February 1999; Volume 99, p. 021. [Google Scholar]
- Gunnam, K.K.; Hughes, D.C.; Junkins, J.L.; Kehtarnavaz, N. A vision-based DSP embedded navigation sensor. IEEE Sens. J. 2002, 2, 428–442. [Google Scholar] [CrossRef]
- Wong, X.I.; Majji, M. A Structured Light System for Relative Navigation Applications. IEEE Sens. J. 2016, 16, 6662–6679. [Google Scholar] [CrossRef]
- Wolff, C. Doppler-Radar. Available online: http://www.radartutorial.eu/index.en.html (accessed on 4 September 2021).
- Kaushal, H.; Kaddoum, G. Optical communication in space: Challenges and mitigation techniques. IEEE Commun. Surv. Tutor. 2016, 19, 57–96. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Miyashita, L.; Watanabe, Y.; Ishikawa, M. Robust 6-DOF motion sensing for an arbitrary rigid body by multi-view laser Doppler measurements. Opt. Express 2017, 25, 30371–30387. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Miyashita, L.; Watanabe, Y.; Ishikawa, M. Visual Calibration for Multiview Laser Doppler Speed Sensing. Sensors 2019, 19, 582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Belmonte, A.; Torres, J.P. Optical Doppler shift with structured light. Opt. Lett. 2011, 36, 4437–4439. [Google Scholar] [CrossRef] [PubMed]
- Bernal, L.; Bilbao, L. Optical Doppler shift measurement using a rotating mirror. Am. J. Phys. 2007, 75, 216–219. [Google Scholar] [CrossRef] [Green Version]
- Heide, F.; Heidrich, W.; Hullin, M.; Wetzstein, G. Doppler time-of-flight imaging. ACM Trans. Graph. (ToG) 2015, c 34, 36. [Google Scholar]
- Schetzen, M. Airborne Doppler Radar: Applications, Theory, and Philosophy; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar]
- Berger, F.B. The design of airborne Doppler velocity measuring systems. IRE Trans. Aeronaut. Navig. Electron. 1957, ANE-4, 157–175. [Google Scholar] [CrossRef]
- Desk, E.C. Electronic Warfare and Radar Systems Engineering Handbook; Electronic Warfare Division: Pont Mugu, CA, USA, 1997.
- Graeme, J.G.; Graeme, J.G. Photodiode Amplifiers: Op Amp Solutions; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Pei, Y.; Zhu, S.; Yang, H.; Zhao, L.; Yi, X.; Wang, J.J.; Li, J. LED modulation characteristics in a visible-light communication system. Opt. Photonics J. 2013, 3, 139. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, G.P. Fiber-Optic Communication Systems; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 222. [Google Scholar]
- Keiser, G. Optical Fiber Communications; McGraw-Hill: New York, NY, USA, 2000; Volume 2. [Google Scholar]
- Keiser, G. Biophotonics; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Censor, D. The group doppler effect. J. Frankl. Inst. 1975, 299, 333–338. [Google Scholar] [CrossRef]
- Fang, H.; Maslov, K.; Wang, L.V. Photoacoustic Doppler effect from flowing small light-absorbing particles. Phys. Rev. Lett. 2007, 99, 184501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sobolev, V.S.; Utkin, E.N.; Kashcheeva, G.A.; Zhuravel, F.A.; Shcherbachenko, A.M. Doppler shift of the modulation frequency of laser radiation scattered by a moving object. Opt. Spectrosc. 2015, 119, 291–294. [Google Scholar] [CrossRef]
- Brown, B. Noise Analysis of FET Transimpedance Amplifiers; Technical Report; Texas Instrum: Dallas, TX, USA, 1994; Available online: http://www.ti.com/lit/an/sboa060/sboa060.pdf (accessed on 2 January 2022).
- Baker, B. Design Transimpedance Amplifiers for Precision Opto-Sensing. Available online: https://www.digikey.com/en/articles/design-transimpedance-amplifiers-for-precision-opto-sensing (accessed on 22 October 2021).
- Kim, J.H.; Jeon, S.J.; Ji, M.G.; Park, J.H.; Choi, Y.W. Analysis on frequency response of trans-impedance amplifier (TIA) for signal-to-noise ratio (SNR) enhancement in optical signal detection system using lock-in amplifier (LIA). In Proceedings of the Smart Photonic and Optoelectronic Integrated Circuits XIX, San Francisco, CA, USA, 31 January–20 February 2017; Volume 10107, p. 1010713. [Google Scholar]
- Optomet, Laser Vibrometry. Available online: https://www.optomet.com/ (accessed on 14 December 2021).
- Mao, X.; Inoue, D.; Kato, S.; Kagami, M. Amplitude-modulated laser radar for range and speed measurement in car applications. IEEE Trans. Intell. Transp. Syst. 2011, 13, 408–413. [Google Scholar] [CrossRef]




| RPM | Linear Velocity (m/s) | Bias (m/s) | Standard Deviation |
|---|---|---|---|
| 300 | 31.416 | 5.3433 | 5.8233 |
| 350 | 36.652 | 5.0225 | 5.6661 |
| 400 | 41.888 | 4.5603 | 5.5447 |
| 450 | 47.124 | 3.8572 | 5.5050 |
| 500 | 52.36 | 4.3629 | 6.0143 |
| 550 | 57.596 | 5.9297 | 6.5108 |
| 600 | 62.832 | 7.3232 | 8.4667 |
| 650 | 68.068 | 5.5096 | 6.4170 |
| 700 | 73.304 | 6.5142 | 8.5092 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sung, K.; Majji, M. Doppler Measurement of Modulated Light for High Speed Vehicles. Sensors 2022, 22, 1444. https://doi.org/10.3390/s22041444
Sung K, Majji M. Doppler Measurement of Modulated Light for High Speed Vehicles. Sensors. 2022; 22(4):1444. https://doi.org/10.3390/s22041444
Chicago/Turabian StyleSung, Kookjin, and Manoranjan Majji. 2022. "Doppler Measurement of Modulated Light for High Speed Vehicles" Sensors 22, no. 4: 1444. https://doi.org/10.3390/s22041444
APA StyleSung, K., & Majji, M. (2022). Doppler Measurement of Modulated Light for High Speed Vehicles. Sensors, 22(4), 1444. https://doi.org/10.3390/s22041444






