1. Introduction
The Internet of Things (IoT) is a core technology leading the fourth industrial revolution through the convergence and integration of various advanced technologies. Recently, the convergence of artificial intelligence (AI) is expected to be a solution that helps data processing in IoT quickly and safely. The development of AIoT (Artificial Intelligence Internet of Things), a combination of AI and IoT, is expected to improve and broaden IoT products’ performance [
1,
2,
3].
AIoT is the latest research topic among AI semiconductors [
4,
5]. Before the AIoT topic, a wide range of research has been conducted in implementing AI, that is, a neural network that mimics human neurons. As research on AIoT is advancing, the challenges of resource-constrained IoT devices are also emerging. A survey on such challenges is being conducted by [
6], where the potential solutions for challenges in communication overhead, convergence guarantee and energy reduction are summarized. Most of the studies on accelerators of the neural network have focused on the architecture and circuit structure in the forward direction that determines the accuracy of input data, such as image data [
7,
8]. However, to mimic the neural network of humans or animals as much as possible, it is necessary to implement a neural network circuit in the backpropagation that provides feedback through accuracy. Significant research is being conducted on studying the neural network circuit in the back direction [
9,
10]. Among the various applications of AIoT, wearable and smart home technologies have strict area and power constraints. Therefore, we need higher performance while consuming low power and size [
11].
As explained in [
12], learning in deployed neural networks can be of two types, which are on-chip learning [
13,
14] and off-chip learning [
15,
16]. Previously, high-speed servers were used to analyze the data, but several studies have concluded that it is more efficient to use edge devices to collect, process, and analyze data [
17,
18]. Edge devices that require repeated interactions with the server are prone to significant battery charge reduction. Minimizing the depreciation of battery power while interacting with the server is challenging. Kumar et al. [
19] developed a tree-based algorithm for predicting resource-constrained IoT devices; still, they did not perform the training operation. Therefore, one of the key motivations in designing the optimized low power/area on-chip neural network is its ability to self-train its lightweight neural network model using various data inputs. For the realization of low power, it is essential to choose the appropriate format for the mathematical computations involved. The literature has shown that Integer operations are sufficient to design a low power inference accelerator [
20,
21]. However, considerable research is still required to train a neural network with reasonable accuracy as well. Empirical results from these studies suggest that at least 16-bit precision is required to train a neural network [
22,
23]. Mixed precision training using Integer operations is implemented in [
22], which multiplies the two INT16 numbers and stores the output into an INT32 accumulator. One drawback mentioned by the authors in [
22] was the lower dynamic range. The deficiency of Integer operators to represent a broad range of numbers served as the main obstacle to using them in training engines. The floating-point operators are used in [
24] to train the weights to counter this problem.
Floating-point operation demonstrates superior accuracy over fixed-point operation when employed in training neural networks [
25,
26]. Conventional neural network circuit design studies have been conducted using floating-point operations provided by GPUs or fixed-point computation hardware [
27,
28]. However, most of the existing floating-point-based neural networks are limited to inference operation, and only a few incorporate training engines that are aimed at high-speed servers, not low-power mobile devices. Since FP operations dissipate enormous power and consume a larger area to implement on-chip, the need to optimize the FP operation has emerged. One of the most used methods to reduce the complexity of the computation is the computing approximation technique, which can minimize significant energy consumption by FP operators [
29]. While computing approximation has shown promising results concerning energy efficiency and throughput optimization, recent studies have focused on maintaining the precision of weight updates during backpropagation. In [
30], mixed precision training is implemented by maintaining the master copy of FP32 weights, and another copy in FP16 is used during forward and backward pass. Then, the weight gradient updates the FP32 master copy and the process is repeated for each iteration. Although the overall memory usage was reduced, maintaining the copy of weights increased the memory requirement of weights by two times as well as the latency due to additional memory access. We came up with a novel technique to counter the shortcomings in precision reduction. An algorithm is designed to find the optimal floating format without sacrificing significant accuracy. Our method uses a mixed-precision architecture in which the layers requiring higher precision are assigned more bits, while those layers requiring less precision are assigned with lesser bits.
This paper evaluates different floating-point formats and their combinations to implement FP operators, providing accurate results with less consumption of resources. We have implemented a circuit that infers accuracy using CNN (convolutional neural network) and a floating-point training circuit. We have used MNIST handwritten digit dataset for evaluation purposes. The prominent contributions of our paper are summarized below:
Designing optimized floating-point operators, i.e., Adder, Multiplier, and Divider, in different precisions.
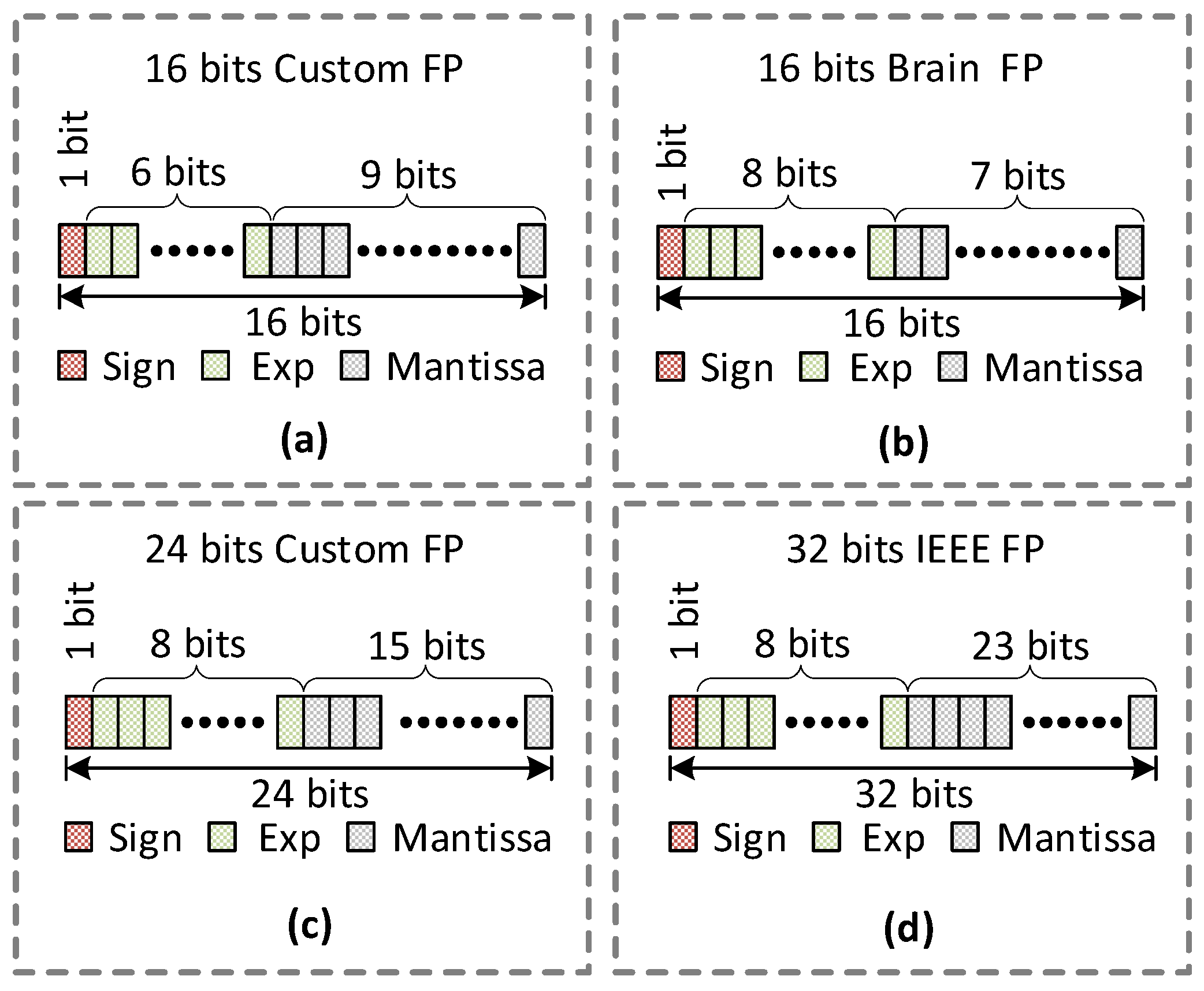
Proposing two custom floating-point formats for evaluation purposes.
Designing an inference engine and a training engine of CNN to calculate the effect of precision on energy, area, and accuracy of CNN accelerator.
Designing a mixed-precision accelerator in which convolutional block is implemented in higher precision to obtain better results.
Section 2 describes the overview of different floating-point formats and the basic principles of CNN training architecture.
Section 3 explains the proposed architecture of floating-point arithmetic operators and their usage in the CNN training accelerator.
Section 4 focuses on the results of both FP operators individually and the whole CNN training accelerator with multiple configurations.
Section 5 is reserved for the conclusion of this paper.
4. Proposed Architecture
4.1. Division Calculation Using Signed Array
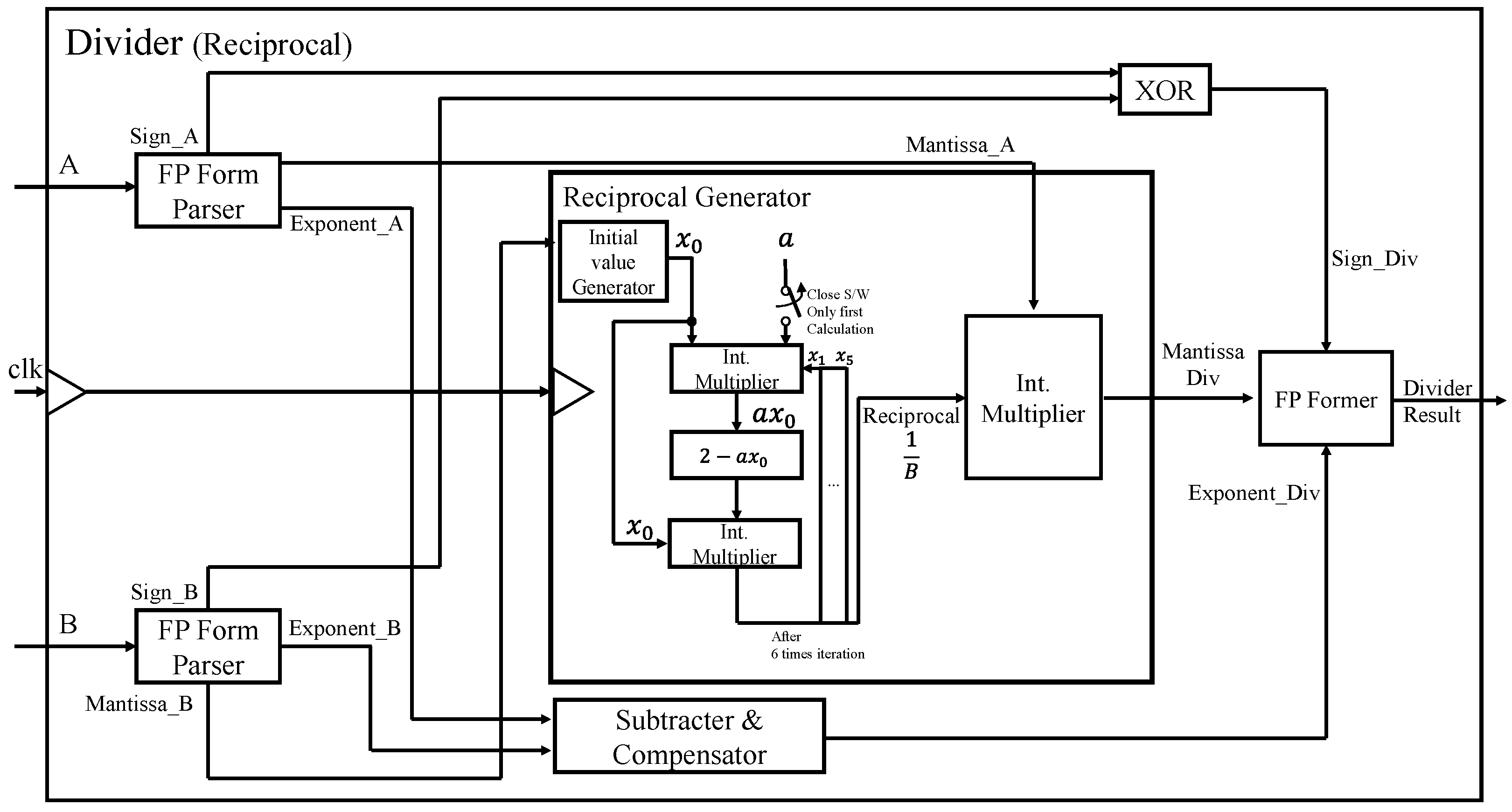
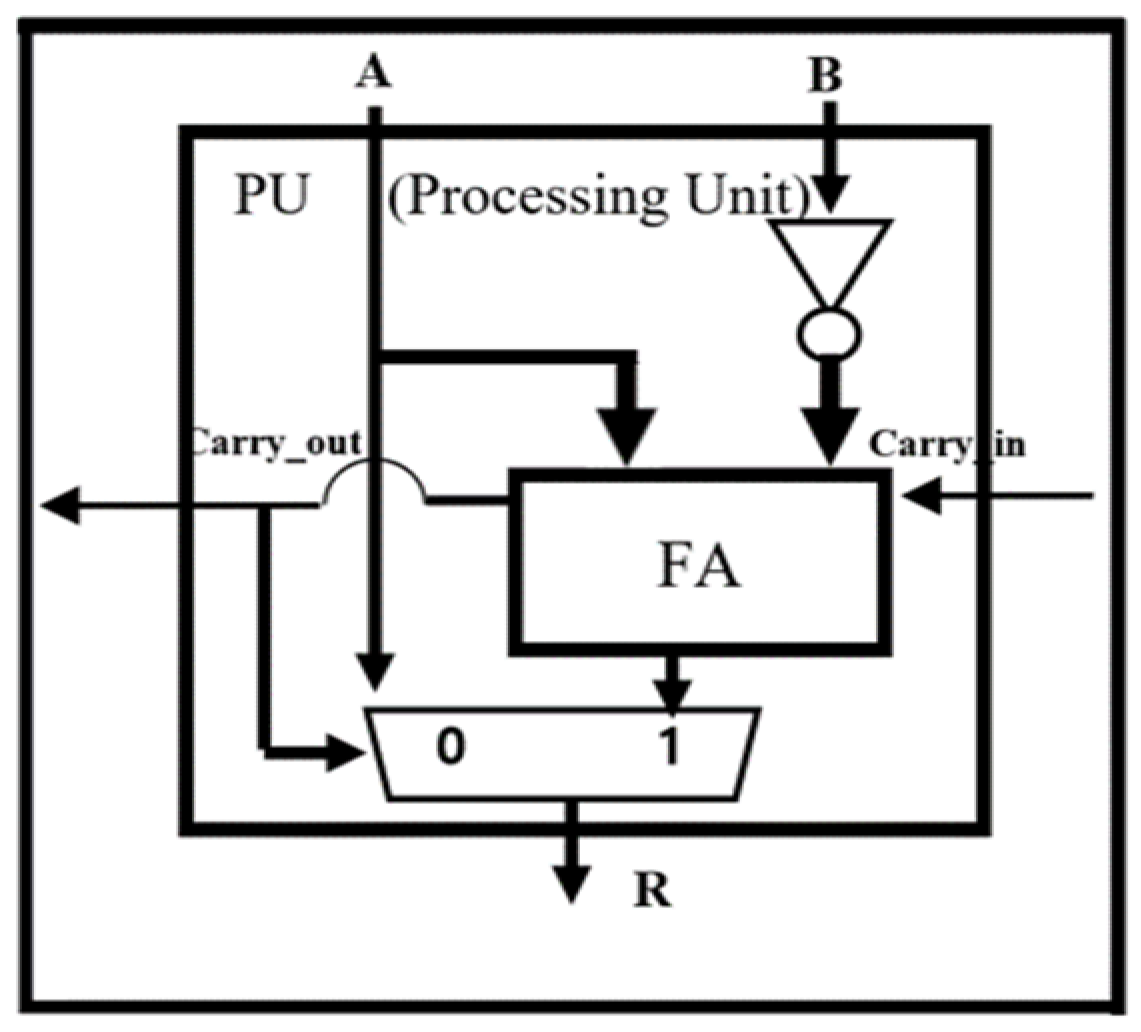
Since the reciprocal-based divider requires many iterations and multipliers, it suffers from long processing delay and an excessive hardware area overhead. We have proposed a division structure using a Signed Array to calculate a division calculation of binary numbers to counter these issues. Since Signed Array division does not have repetitive multiplication operations compared to division calculations using reciprocals, it offers significantly shorter processing delay than the reciprocal-based divider. It uses a specially designed Processing Unit (PU), as shown in
Figure 6, optimized for division. It selects the quotient through the subtraction calculation and feedback of carry-out.
The structure of the overall Signed Array division operator is shown in
Figure 7. It first calculates the Mantissa in the signed array module, exponent using a subtractor and compensator block, and the sign bit of the result using XOR independently. Every row in the signed array module computes the partial division (subtracting from the previous partial division) and then passes it to the next row. Each row is shifted to the right by 1 bit to align each partial division corresponding to the next bit position of the dividend. Finally, just like the hand calculation of A divided B in binary numbers, each row of the array divider determines the next highest bit of quotient. Finally, it merges these three components to obtain the final divider result.
As emphasized in the introduction section, the architecture of our accelerator minimizes the energy and hardware size to the level that suffices the requirement for IoT applications. To compare the size, the operation delay, and the total consumption, we implemented the two dividers using a synthesis tool, Design Compiler, with TSMC 55 nm standard cells, which are analyzed in
Table 2.
The proposed Signed Array divider is 6.1 and 4.5 times smaller than the reciprocal-based divider for operation clocks of 50 MHz and 100 MHz, respectively. The operation delay of the Signed Array divider is 3.3 and 6 times shorter for the two clocks, respectively. Moreover, it significantly reduces the energy consumption by 17.5~22.5 times compared with the reciprocal-based divider. Therefore, we chose the proposed Signed Array divider in implementing the SoftMax function of the CNN training accelerator.
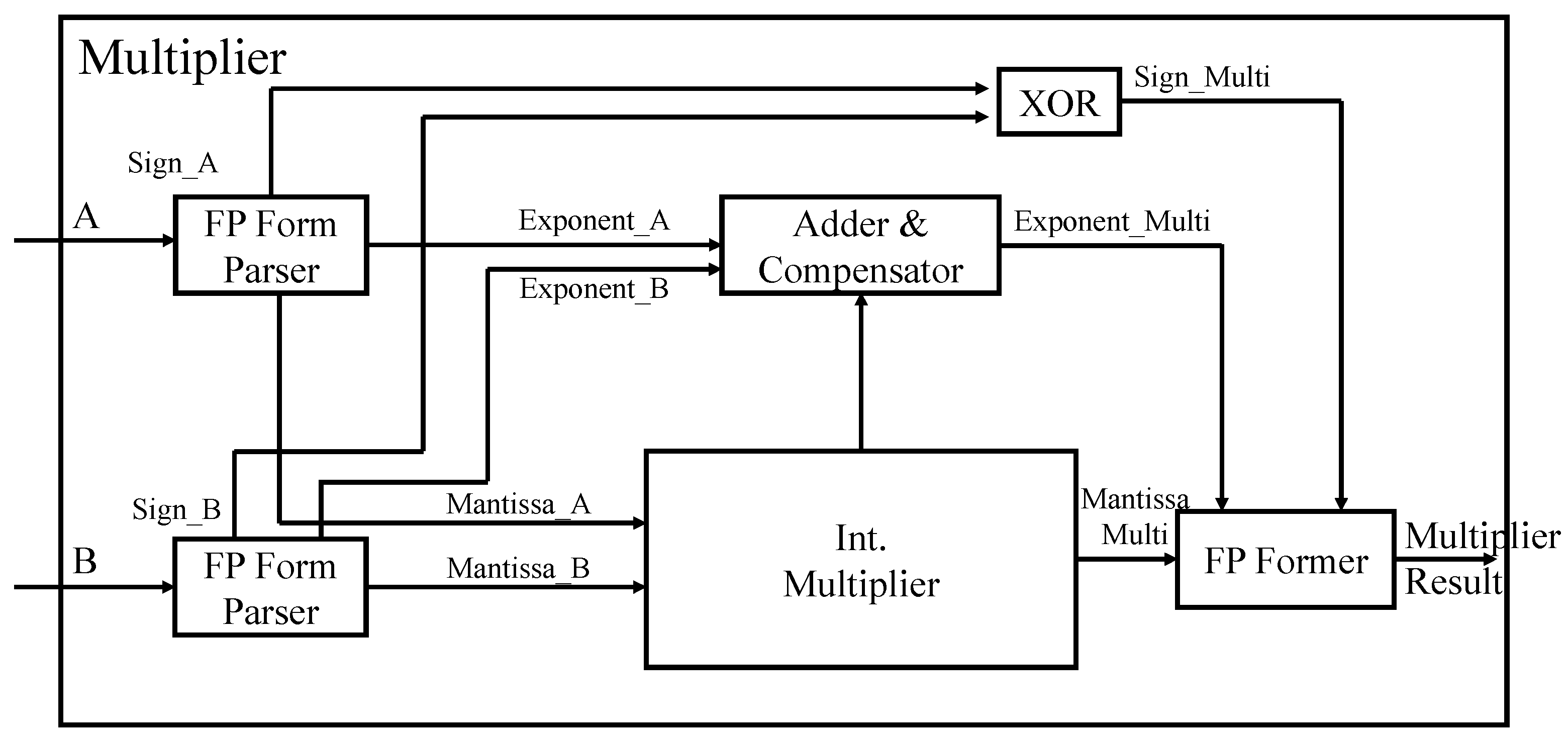
4.2. Floating Point Multiplier
Unlike floating-point adder/subtracter, floating-point multipliers calculate Mantissa and exponent independent of the sign bit. The sign bit is calculated through a 2-input XOR gate. The adder and compensator block in
Figure 8 calculates the resulting exponent by adding the exponents of the two input numbers and subtracting the offset ‘127’ from the result. However, if the calculated exponent result is not between 0 and 255, it is considered overflow/underflow and saturated to the bound as follows. Any value less than zero (underflow) is saturated to zero, while a value greater than 255 (overflow) is saturated to 255. The Mantissa output is calculated through integer multiplication of two input Mantissa. Finally, the Mantissa bits are rearranged using the Exponent value and then merged to produce the final floating-point format.
4.3. Overall Architecture of the Proposed CNN Accelerator
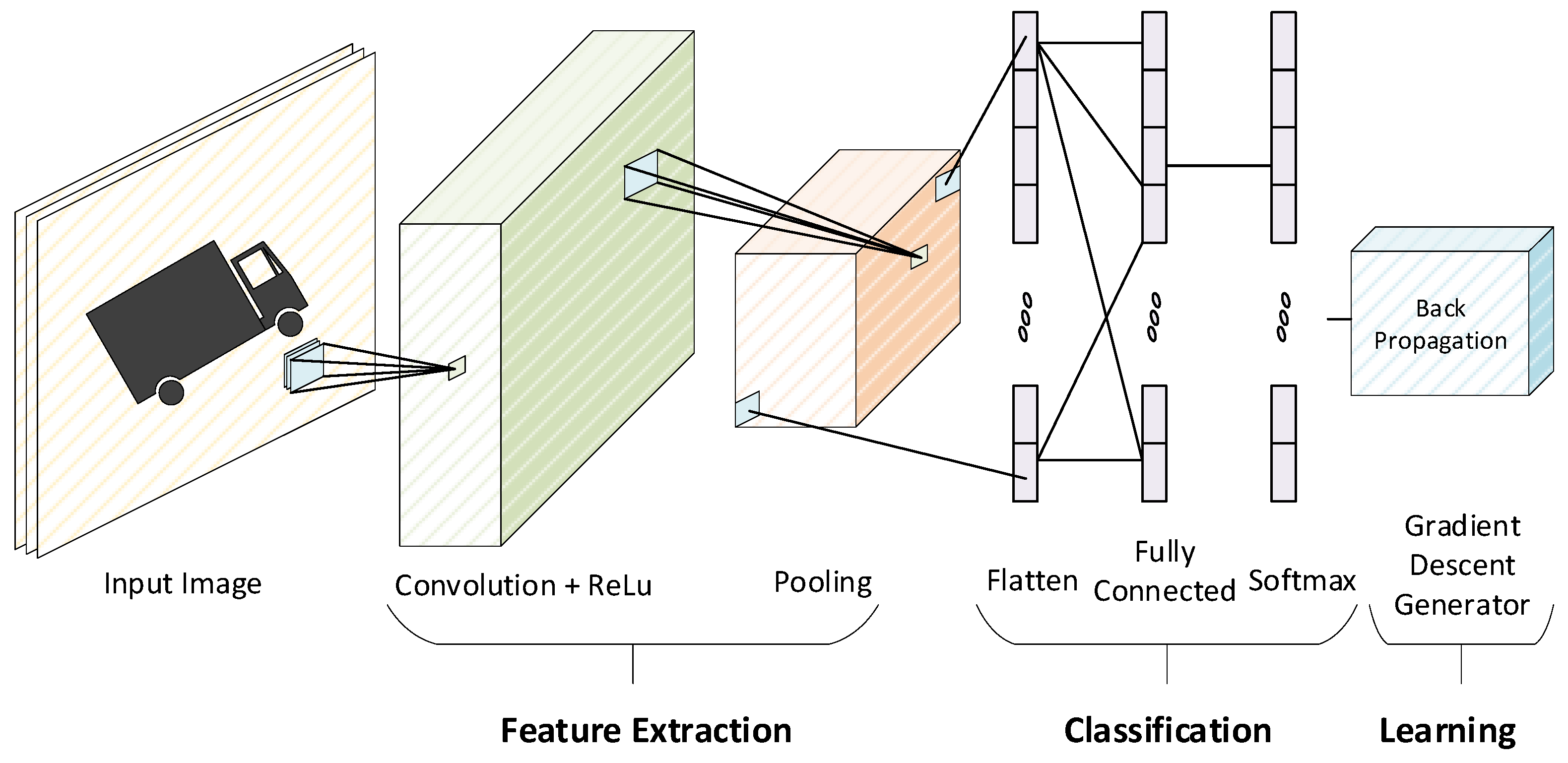
To evaluate the performance of the proposed floating-point operators, we have designed a CNN accelerator that supports two modes of operation, i.e., Inference and Training.
Figure 9 shows the overall architecture of our accelerator with an off-chip interface used for sending the images, filters, weights, and control signals from outside of the chip.
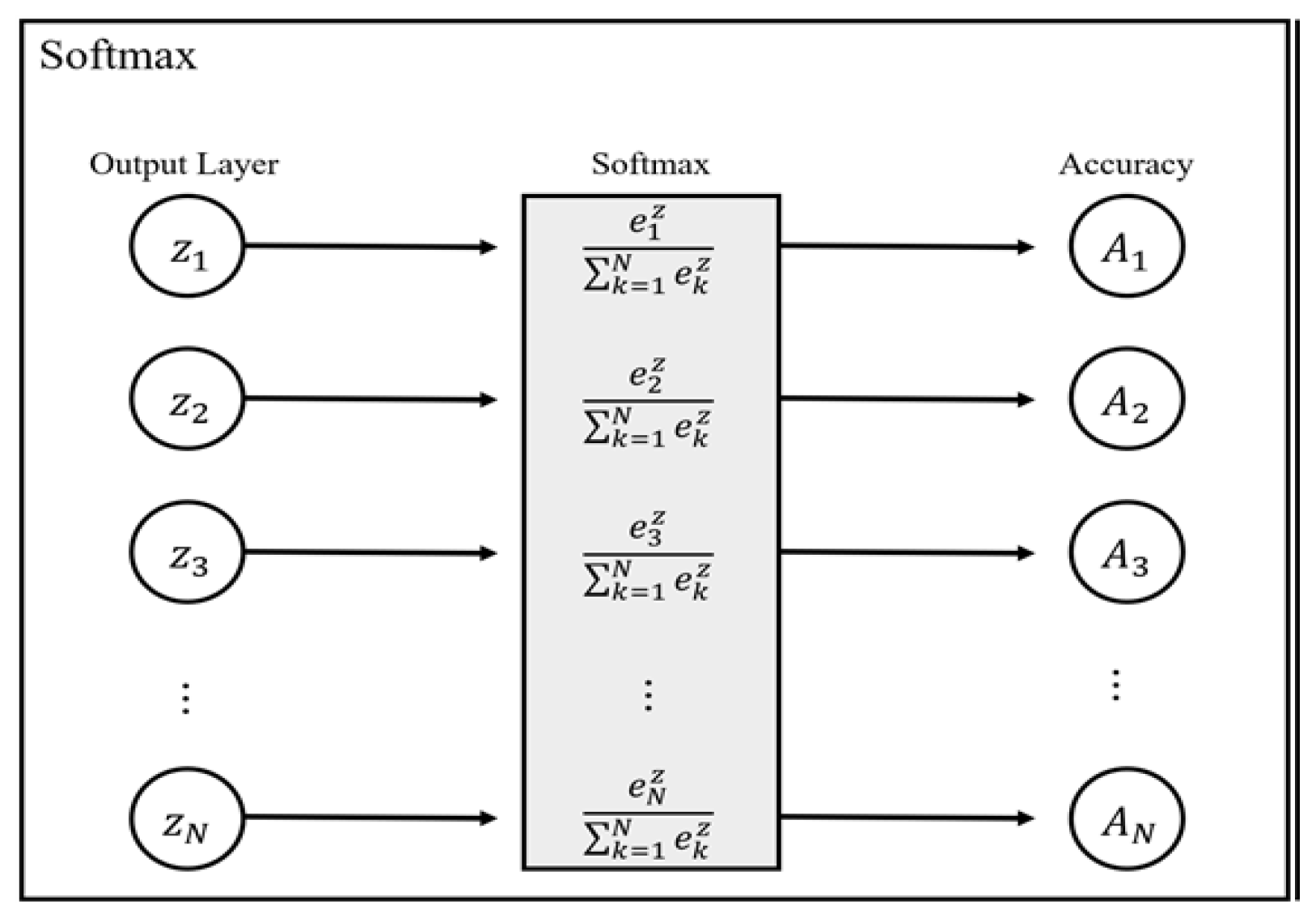
Before sending the MNIST training images with size 28 × 28, the initial weights of four filters of size 3 × 3, FC1 with size 196 × 10, along with FC2 with size 10 × 10 are written in the on-chip memory through an off-chip interface. Upon receiving the start signal, the training image and the filter weights are passed to the convolution module, and the convolution is calculated based on the dot product of a matrix. The Max Pooling module down-samples the output of the convolution module by selecting the maximum value in every 2 × 2 subarray of the output feature data. Then, the two fully connected layers, FC1 and FC2, followed by the Softmax operation, predict the classification of the input image as the inference result.
During training mode, the backpropagation calculates gradient descent in matrix dot products in the reverse order of the CNN layers. Softmax and backpropagation layers are also involved to further train the partially trained weights. As evident from
Figure 9, fully connected layers are divided into two modules, i.e., dout and dW. The dout module is used to calculate the gradient, while the dW module is used to calculate weight derivatives. Since back convolution is the final layer, there is therefore no dout module for this block. In this way, we train the weight values for each layer by calculating dout and dW repeatedly until the weight values achieve the desired accuracy. Those trained weights are stored in the respective memories which are used for inference in the next iteration of the training process.
4.4. CNN Structure Optimization
This section explains how we optimize the CNN architecture by finding the optimal floating-point format. We initially calculated the Training/Test accuracies along with the dynamic power of representative precision format to find the starting point with reasonable accuracies, as shown in
Table 3.
For our evaluation purposes, we chose the target accuracy in this paper of 93%. Although the custom 24-bit format satisfies the accuracy threshold of 93%, it incurs dynamic power of 30 mW, which is 58% higher than the IEEE-16 floating-point format. Therefore, we developed an algorithm that searches optimal floating-point formats of individual layers to achieve minimal power consumption while satisfying the target accuracy.
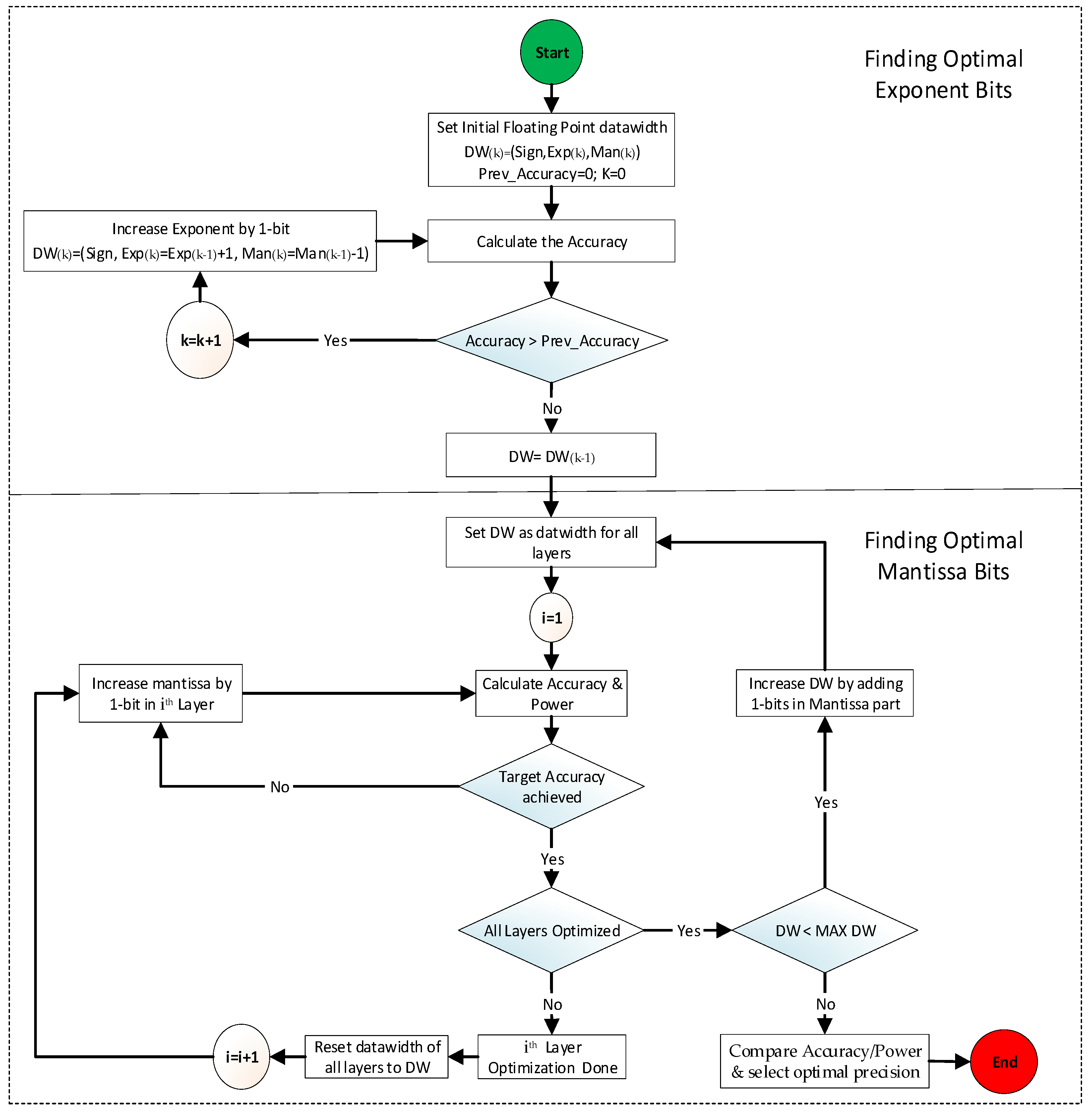
The algorithm shown in
Figure 10 first calculates the accuracy using the initial floating-point format which is set to IEEE-16 in this paper, and using Equation (5), it gradually increases the exponent by 1 bit until the accuracy stops increasing or starts decreasing.
As shown in Equation (5), the exponent bit in the kth-iteration is increased while the overall data width (DW) remains constant as the Mantissa bit is consequently decreased. After fixing the exponent bit width, the algorithm calculates the performance metric (accuracy and power) using the new floating-point data format. In the experiment of this paper, the new floating-point format before Mantissa optimization was found to be (Sign, Exp, DW-Exp-1) with DW of 16 bits, Exp = 8, and Mantissa = 16 – 8 – 1 = 7 bits. Then, the algorithm optimizes each layer’s precision format by gradually increasing the Mantissa by 1 bit until the target accuracy is met using the current DW. When all layers are optimized for minimal power consumption while meeting the target accuracy, it stores a combination of optimal formats for all layers. Then, it increases the data width DW by 1 bit for all layers and repeats the above procedure to search for other optimal formats, which can offer a trade-off between accuracy and area/power consumption. The above procedure is repeated until the DW reaches maximum data width (MAX DW), which is set to 32 bits in our experiment. Once the above search procedure is completed, the final step compares the accuracy and power of all search results and determines the best combination of formats with minimum power while maintaining the target accuracy.