Tunnel Magnetoresistance Sensor with AC Modulation and Impedance Compensation for Ultra-Weak Magnetic Field Measurement
Abstract
:1. Introduction
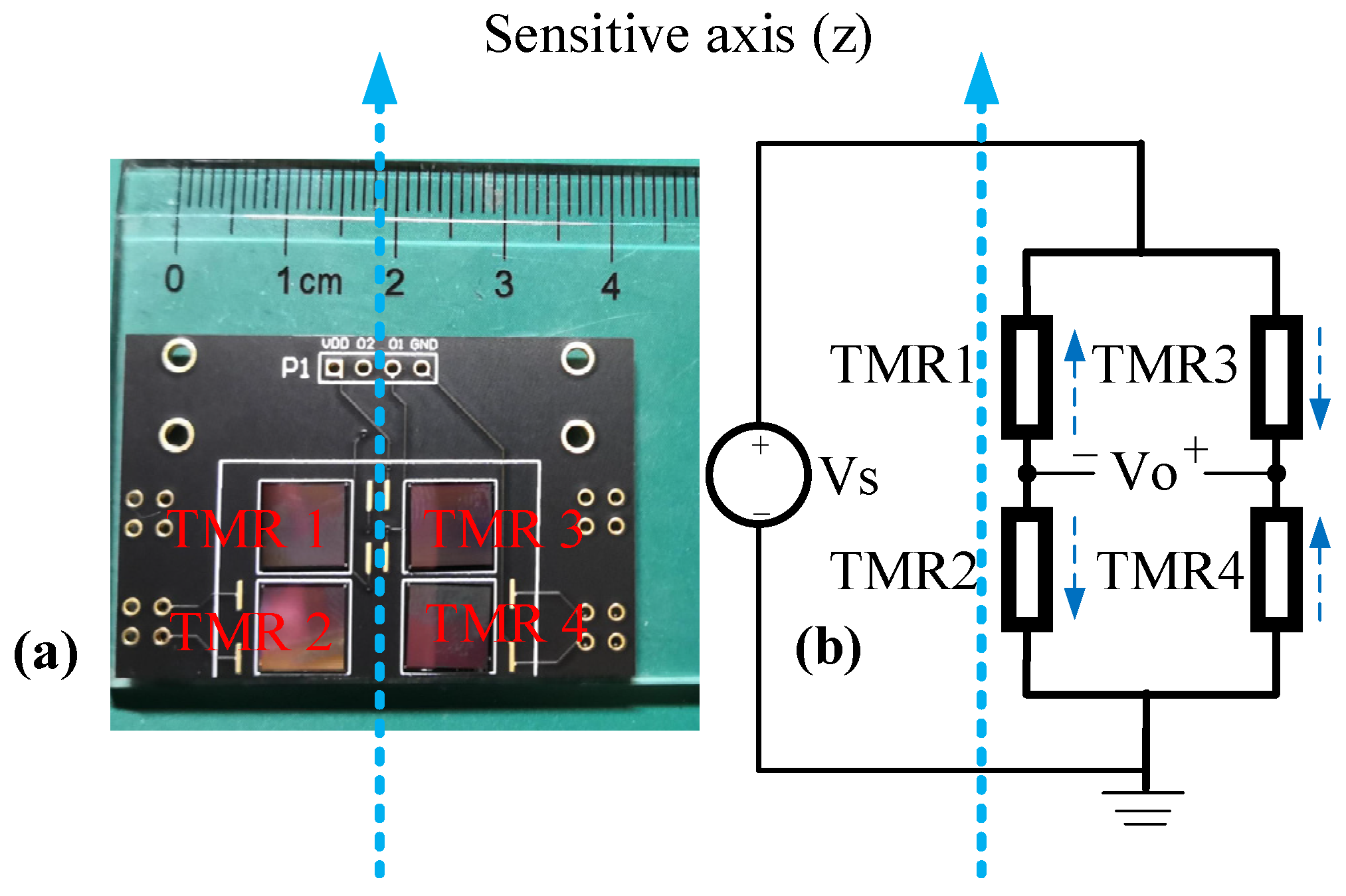
2. Characteristics of Sensor
2.1. Response of Push–Pull TMR Bridge with DC Driving
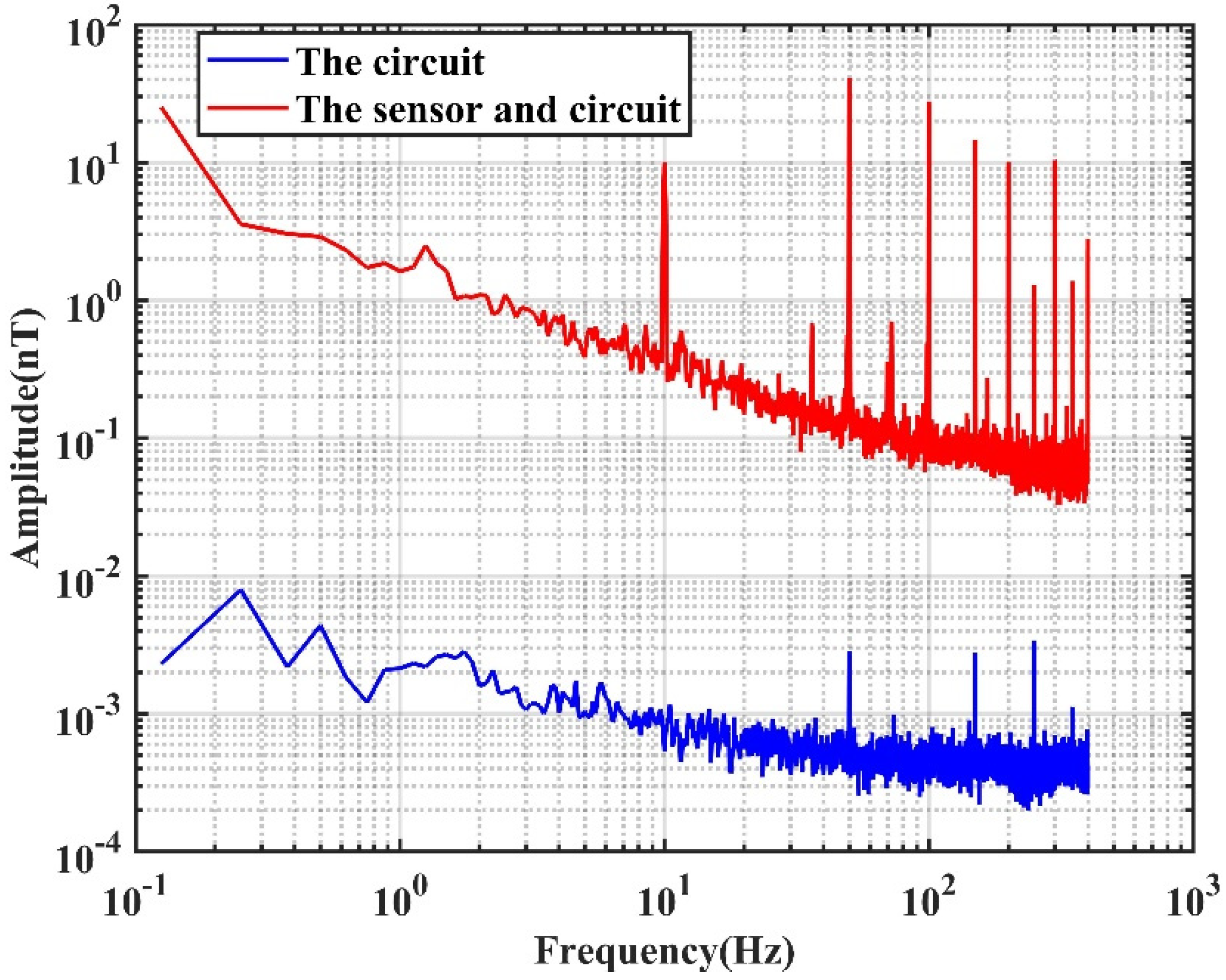
2.2. Noise Spectrum
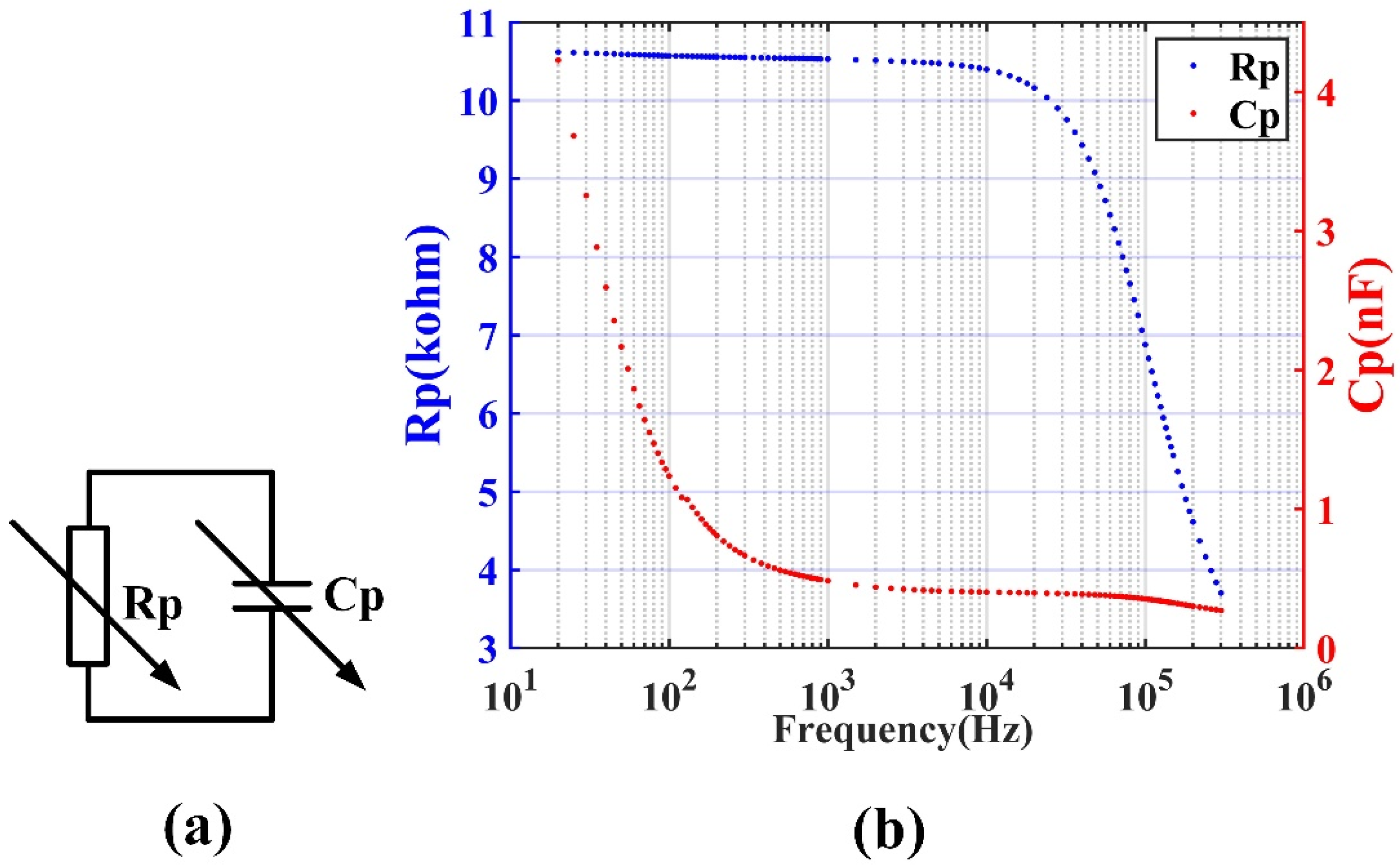
2.3. Impedance of the TMR Sensor
3. AC Modulation Method
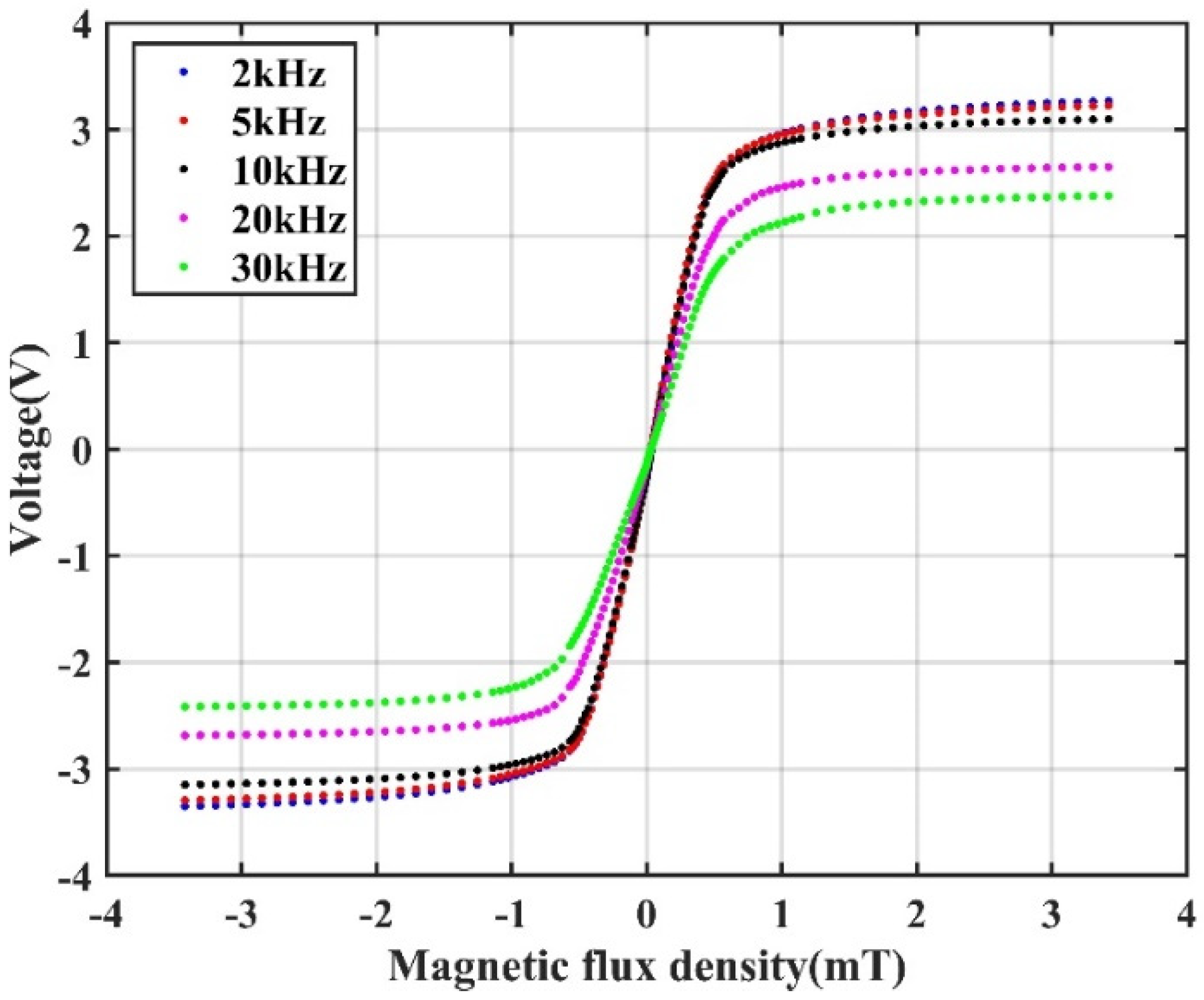
3.1. Response of a Push–Pull TMR Bridge with AC Modulation
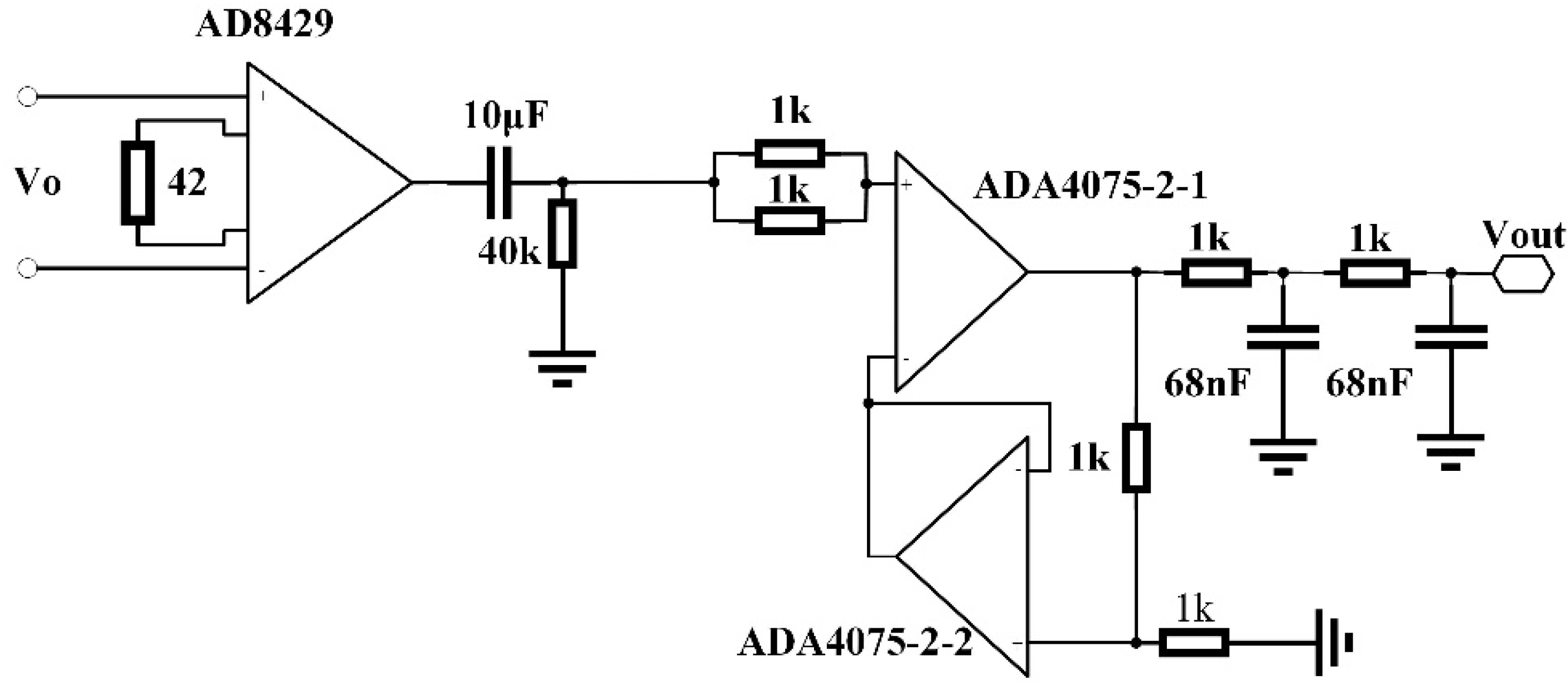
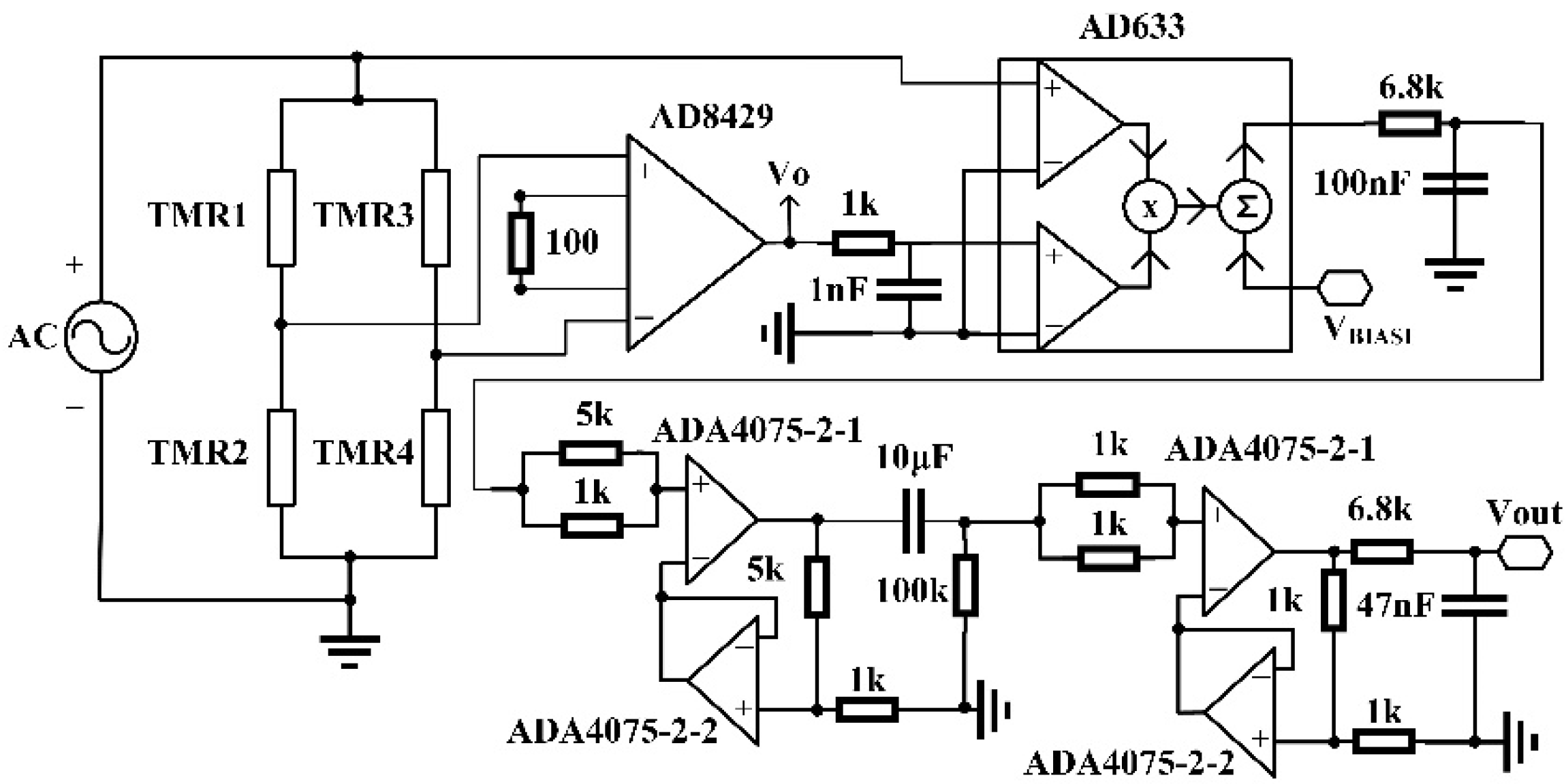
3.2. Measurement with Impedance Compensation
4. Magnetocardiography Measurement
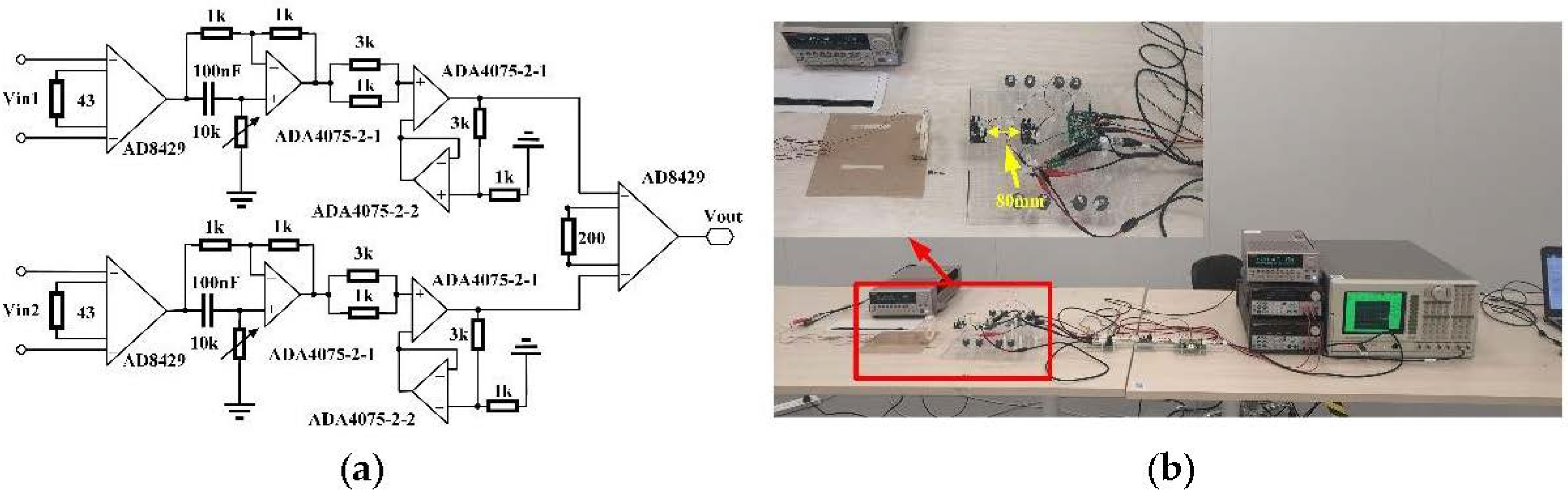
4.1. Gradiometer
4.2. Experiment Setup
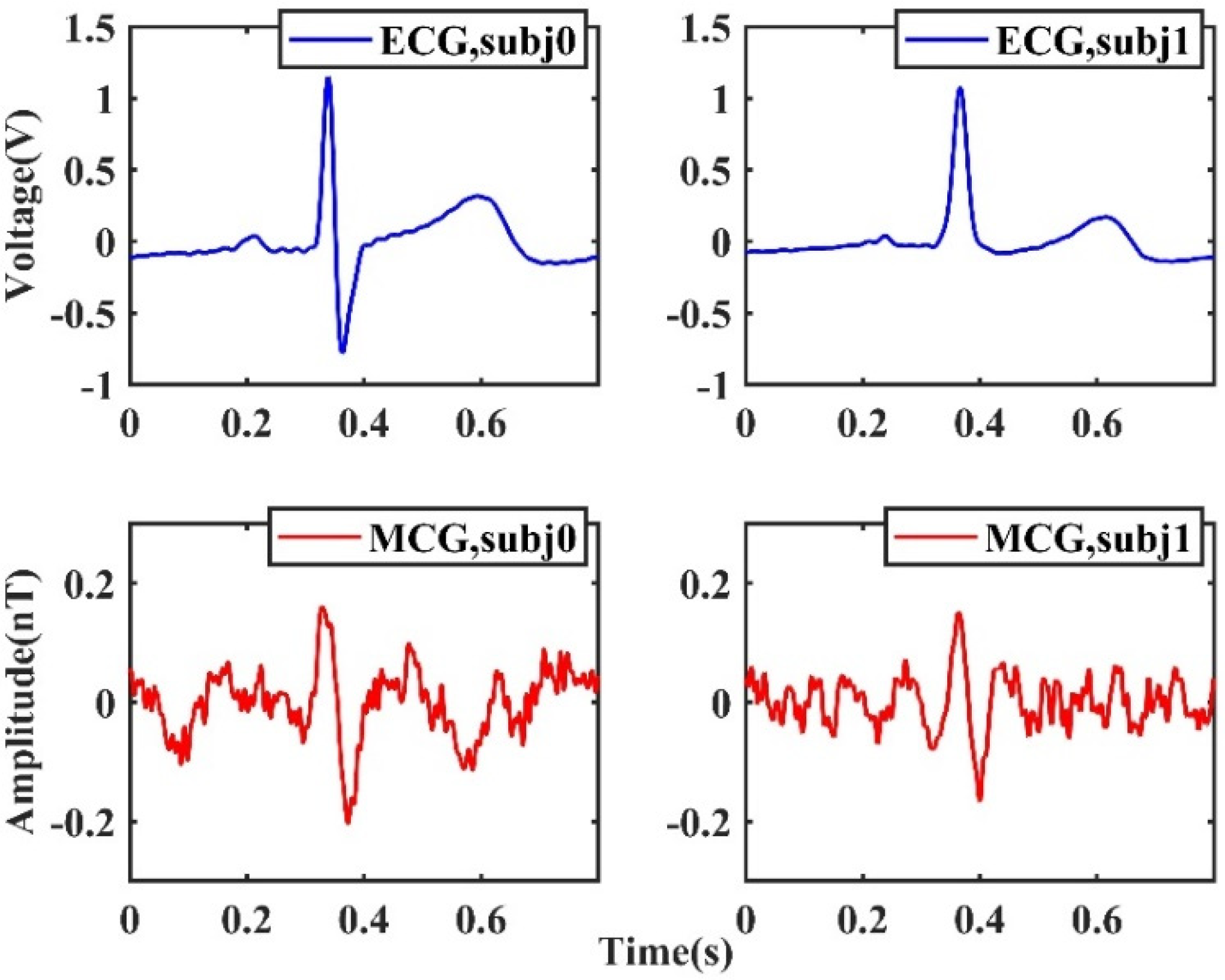
4.3. Result and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Swain, P.P.; Sengottuvel, S.; Patel, R.; Mani, A.; Gireesan, K. A feasibility study to measure magnetocardiography (MCG) in unshielded environment using first order gradiometer. Biomed. Signal Process. Control. 2020, 55, 101664. [Google Scholar] [CrossRef]
- Kwong, J.S.W.; Leithäuser, B.; Park, J.-W.; Yu, C.-M. Diagnostic value of magnetocardiography in coronary artery disease and cardiac arrhythmias: A review of clinical data. Int. J. Cardiol. 2013, 167, 1835–1842. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, K.; Yang, R.; Kong, X.; Chen, W. SQUID Gradiometer Module for Fetal Magnetocardiography Measurements Inside a Thin Magnetically Shielded Room. IEEE Trans. Appl. Supercond. 2019, 29, 1–4. [Google Scholar] [CrossRef]
- Hämäläinen, M.; Hari, R.; Ilmoniemi, R.J.; Knuutila, J.; Lounasmaa, O.V. Magnetoencephalography—theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev. Mod. Phys. 1993, 65, 413–497. [Google Scholar] [CrossRef] [Green Version]
- Kominis, I.K.; Kornack, T.W.; Allred, J.C.; Romalis, M.V. A subfemtotesla multichannel atomic magnetometer. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Tang, J.; Yin, Y.; Wang, Y.; Zhou, B.; Han, B. Single-Beam Atomic Magnetometer Based on the Transverse Magnetic-Modulation or DC-Offset. IEEE Sens. J. 2020, 20, 5827–5833. [Google Scholar] [CrossRef]
- Knappe, S.; Sander, T.; Trahms, L. Optically-Pumped Magnetometers for MEG. In Magnetoencephalography; Supek, S., Aine, C.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 993–999. ISBN 978-3-642-33044-5. [Google Scholar] [CrossRef]
- Borna, A.; Carter, T.R.; Goldberg, J.D.; Colombo, A.P.; Jau, Y.-Y.; Berry, C.; McKay, J.; Stephen, J.; Weisend, M.; Schwindt, P.D.D. A 20-channel magnetoencephalography system based on optically pumped magnetometers. Phys. Med. Biol. 2017, 62, 8909–8923. [Google Scholar] [CrossRef]
- Strand, S.; Lutter, W.; Strasburger, J.F.; Shah, V.; Baffa, O.; Wakai, R.T. Low-Cost Fetal Magnetocardiography: A Comparison of Superconducting Quantum Interference Device and Optically Pumped Magnetometers. JAHA 2019, 8, e013436. [Google Scholar] [CrossRef]
- Kim, Y.J.; Savukov, I.; Newman, S. Magnetocardiography with a 16-channel fiber-coupled single-cell Rb optically pumped magnetometer. Appl. Phys. Lett. 2019, 114, 143702. [Google Scholar] [CrossRef] [Green Version]
- Zheng, W.; Su, S.; Zhang, G.; Bi, X.; Lin, Q. Vector magnetocardiography measurement with a compact elliptically polarized laser-pumped magnetometer. Biomed. Opt. Express 2020, 11, 649–659. [Google Scholar] [CrossRef]
- Sulai, I.A.; DeLand, Z.J.; Bulatowicz, M.D.; Wahl, C.P.; Wakai, R.T.; Walker, T.G. Characterizing atomic magnetic gradiometers for fetal magnetocardiography. Rev. Sci. Instrum. 2019, 90, 085003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, R.; Mhaskar, R.; Smith, K.; Prouty, M. Portable intrinsic gradiometer for ultra-sensitive detection of magnetic gradient in unshielded environment. Appl. Phys. Lett. 2020, 116, 143501. [Google Scholar] [CrossRef] [Green Version]
- Shah, V.; Romalis, M.V. Spin-exchange relaxation-free magnetometry using elliptically polarized light. Phys. Rev. A 2009, 80, 013416. [Google Scholar] [CrossRef] [Green Version]
- Uchiyama, T.; Nakayama, S.; Mohri, K.; Bushida, K. Biomagnetic field detection using very high sensitivity magnetoimpedance sensors for medical applications. Phys. Status Solidi 2009, 206, 639–643. [Google Scholar] [CrossRef]
- Janosek, M.; Butta, M.; Dressler, M.; Saunderson, E.; Novotny, D.; Fourie, C. 1-pT Noise Fluxgate Magnetometer for Geomagnetic Measurements and Unshielded Magnetocardiography. IEEE Trans. Instrum. Meas. 2020, 69, 2552–2560. [Google Scholar] [CrossRef]
- Kaiju, H.; Takei, M.; Misawa, T.; Nagahama, T.; Nishii, J.; Xiao, G. Large magnetocapacitance effect in magnetic tunnel junctions based on Debye-Fröhlich model. Appl. Phys. Lett. 2015, 107, 132405. [Google Scholar] [CrossRef] [Green Version]
- Luong, V.S.; Nguyen, A.T.; Hoang, Q.K. Resolution enhancement in measuring low-frequency magnetic field of tunnel magnetoresistance sensors with AC-bias polarity technique. Measurement 2018, 127, 512–517. [Google Scholar] [CrossRef]
- Fujiwara, K.; Oogane, M.; Kanno, A.; Imada, M.; Jono, J.; Terauchi, T.; Okuno, T.; Aritomi, Y.; Morikawa, M.; Tsuchida, M.; et al. Magnetocardiography and magnetoencephalography measurements at room temperature using tunnel magneto-resistance sensors. Appl. Phys. Express 2018, 11, 023001. [Google Scholar] [CrossRef]
- Adachi, Y.; Oyama, D.; Terazono, Y.; Hayashi, T.; Shibuya, T.; Kawabata, S. Calibration of Room Temperature Magnetic Sensor Array for Biomagnetic Measurement. IEEE Trans. Magn. 2019, 55, 1–6. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Peng, L.; Ye, C. Measurement of Triaxial Magnetocardiography Using High Sensitivity Tunnel Magnetoresistance Sensor. IEEE Sens. J. 2019, 19, 9610–9615. [Google Scholar] [CrossRef]
- Dieny, B.; Prejbeanu, I.L.; Garello, K.; Gambardella, P.; Freitas, P.; Lehndorff, R.; Raberg, W.; Ebels, U.; Demokritov, S.O.; Akerman, J.; et al. Opportunities and challenges for spintronics in the microelectronics industry. Nat. Electron. 2020, 3, 446–459. [Google Scholar] [CrossRef]

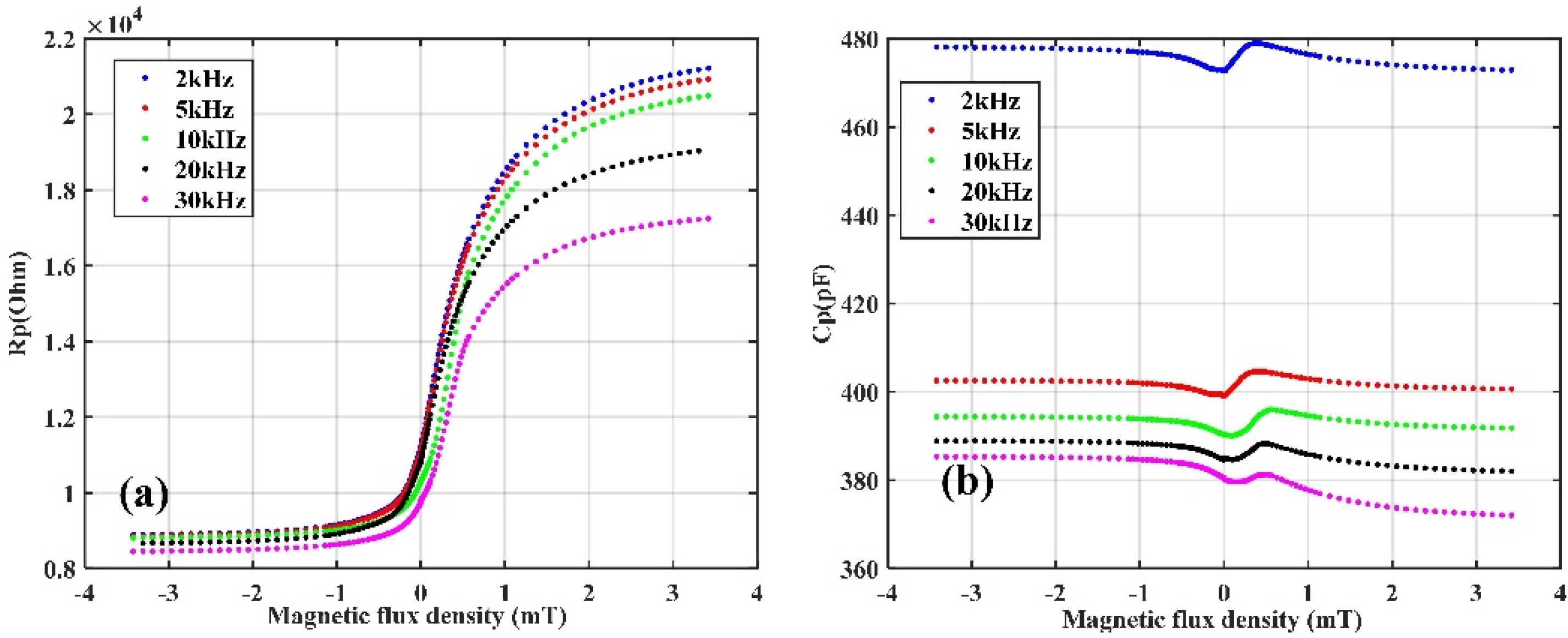



| Frequency (kHz) | Rp (kOhm) | Cp (pF) |
|---|---|---|
| 2 kHz | 11.026 kOhm | 472.6 pF |
| 5 kHz | 11.031 kOhm | 399.0 pF |
| 10 kHz | 10.310 kOhm | 390.3 pF |
| 20 kHz | 10.813 kOhm | 384.6 pF |
| 30 kHz | 9.756 kOhm | 380.5 pF |
| Frequency (kHz) | ξ without Impedance Compensation (mV/V/mT) |
|---|---|
| 2 kHz | 136.8 mV/V/mT |
| 5 kHz | 165.2 mV/V/mT |
| 10 kHz | 145.5 mV/V/mT |
| 20 kHz | 107.4 mV/V/mT |
| 30 kHz | 94.3 mV/V/mT |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Tao, X.; Ye, C.; Tao, Y. Tunnel Magnetoresistance Sensor with AC Modulation and Impedance Compensation for Ultra-Weak Magnetic Field Measurement. Sensors 2022, 22, 1021. https://doi.org/10.3390/s22031021
Zhao W, Tao X, Ye C, Tao Y. Tunnel Magnetoresistance Sensor with AC Modulation and Impedance Compensation for Ultra-Weak Magnetic Field Measurement. Sensors. 2022; 22(3):1021. https://doi.org/10.3390/s22031021
Chicago/Turabian StyleZhao, Wenlei, Xinchen Tao, Chaofeng Ye, and Yu Tao. 2022. "Tunnel Magnetoresistance Sensor with AC Modulation and Impedance Compensation for Ultra-Weak Magnetic Field Measurement" Sensors 22, no. 3: 1021. https://doi.org/10.3390/s22031021
APA StyleZhao, W., Tao, X., Ye, C., & Tao, Y. (2022). Tunnel Magnetoresistance Sensor with AC Modulation and Impedance Compensation for Ultra-Weak Magnetic Field Measurement. Sensors, 22(3), 1021. https://doi.org/10.3390/s22031021






