Towards Outdoor Electromagnetic Field Exposure Mapping Generation Using Conditional GANs
Abstract
1. Introduction
- Generating a new simulated dataset called “LilleExposureMap”, which consists of EMF exposure maps in Lille, France.
- Develop the generator and discriminator for the proposed EMGAN utilizing the deep convolutional structure and auto-encoders analogy to learn about signal propagation and calculate the map of EMF exposure.
2. Related Work
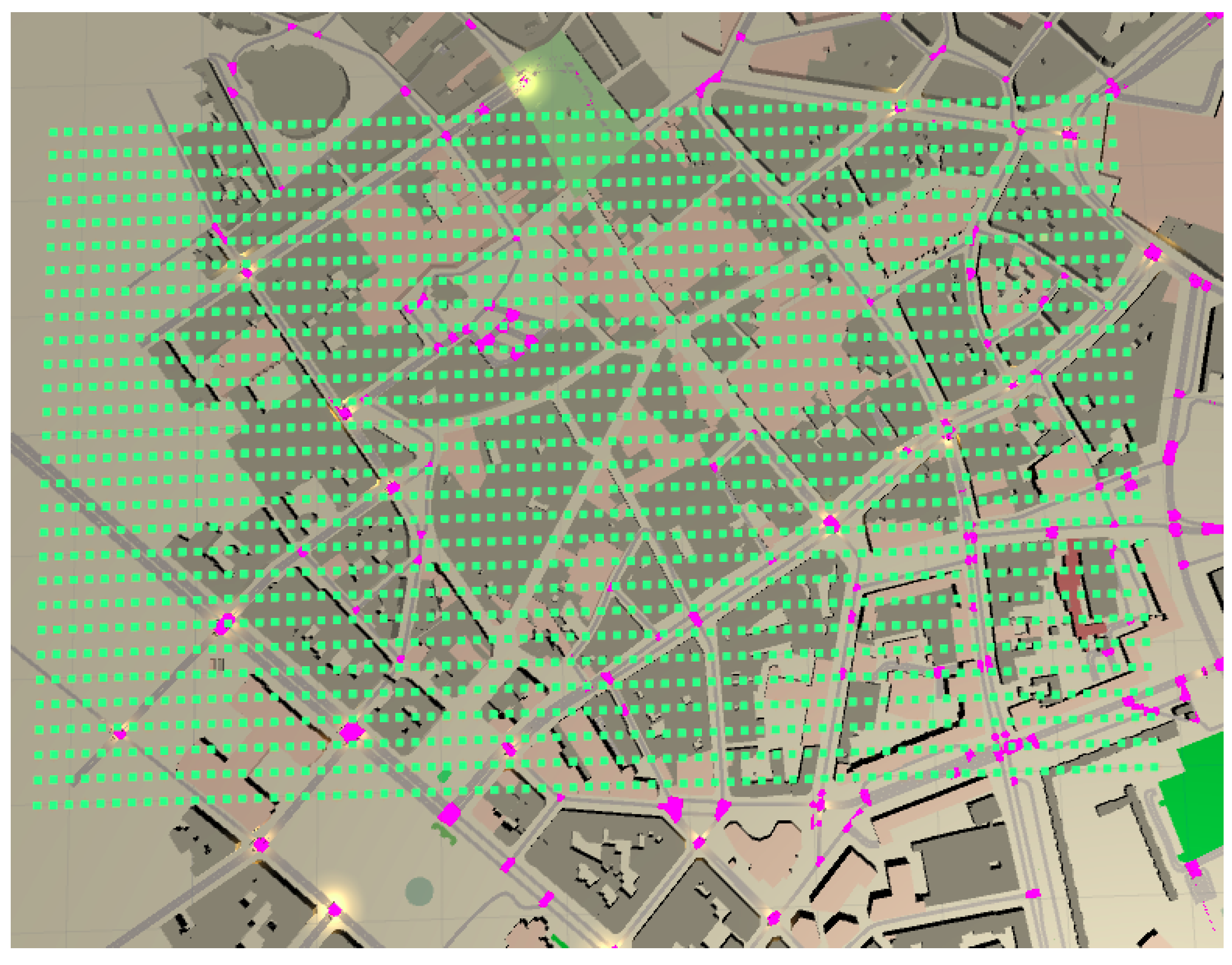
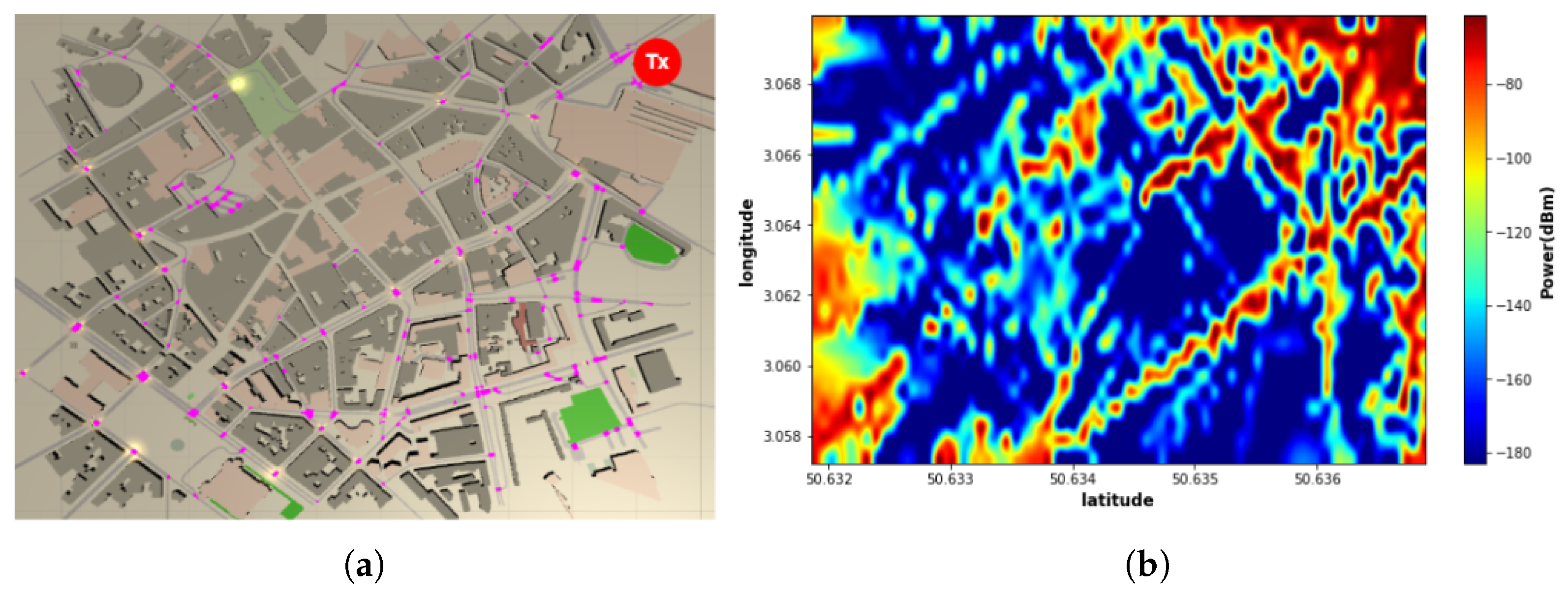
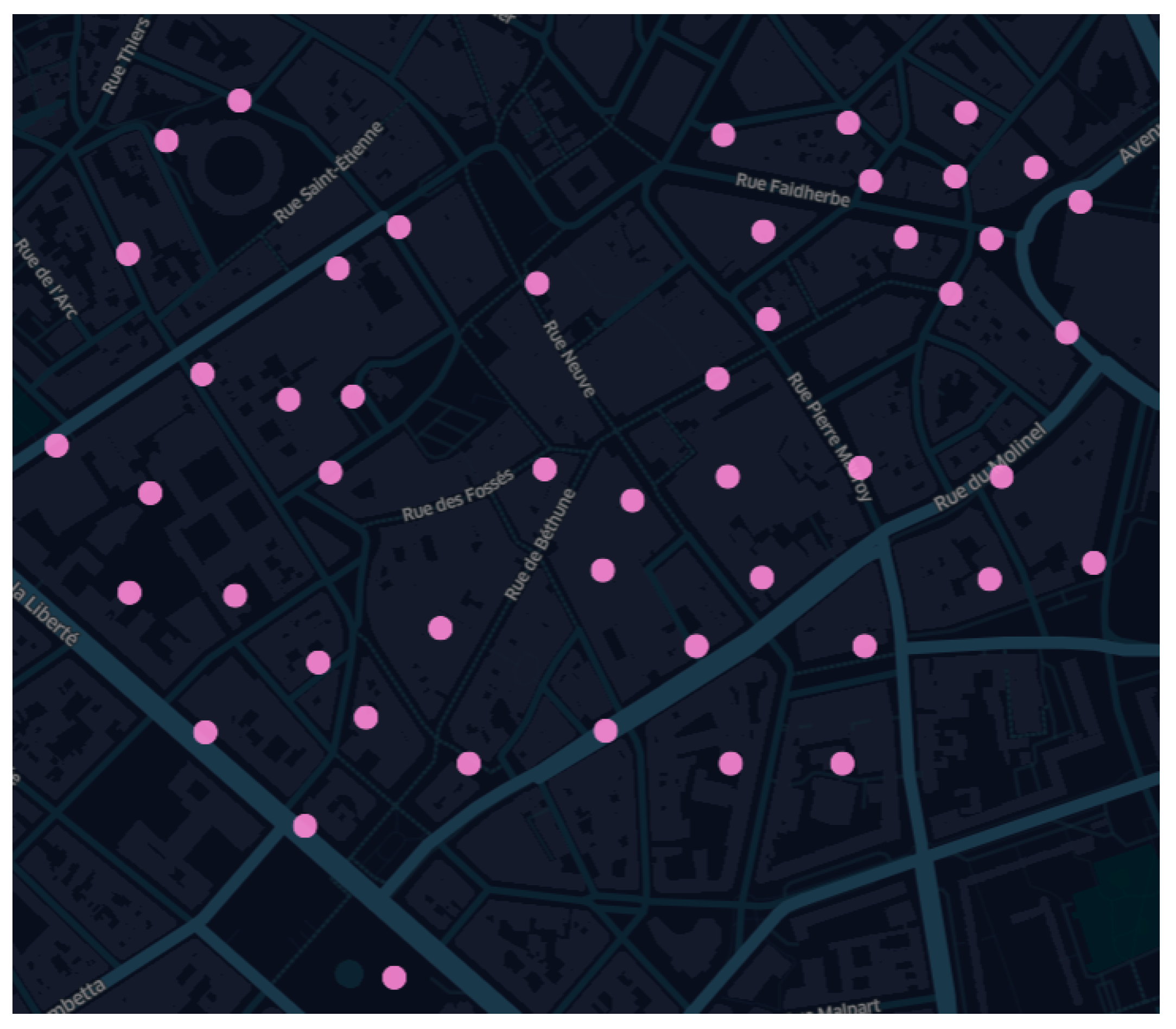
3. Dataset and Simulator
4. The Proposed EMGAN Model
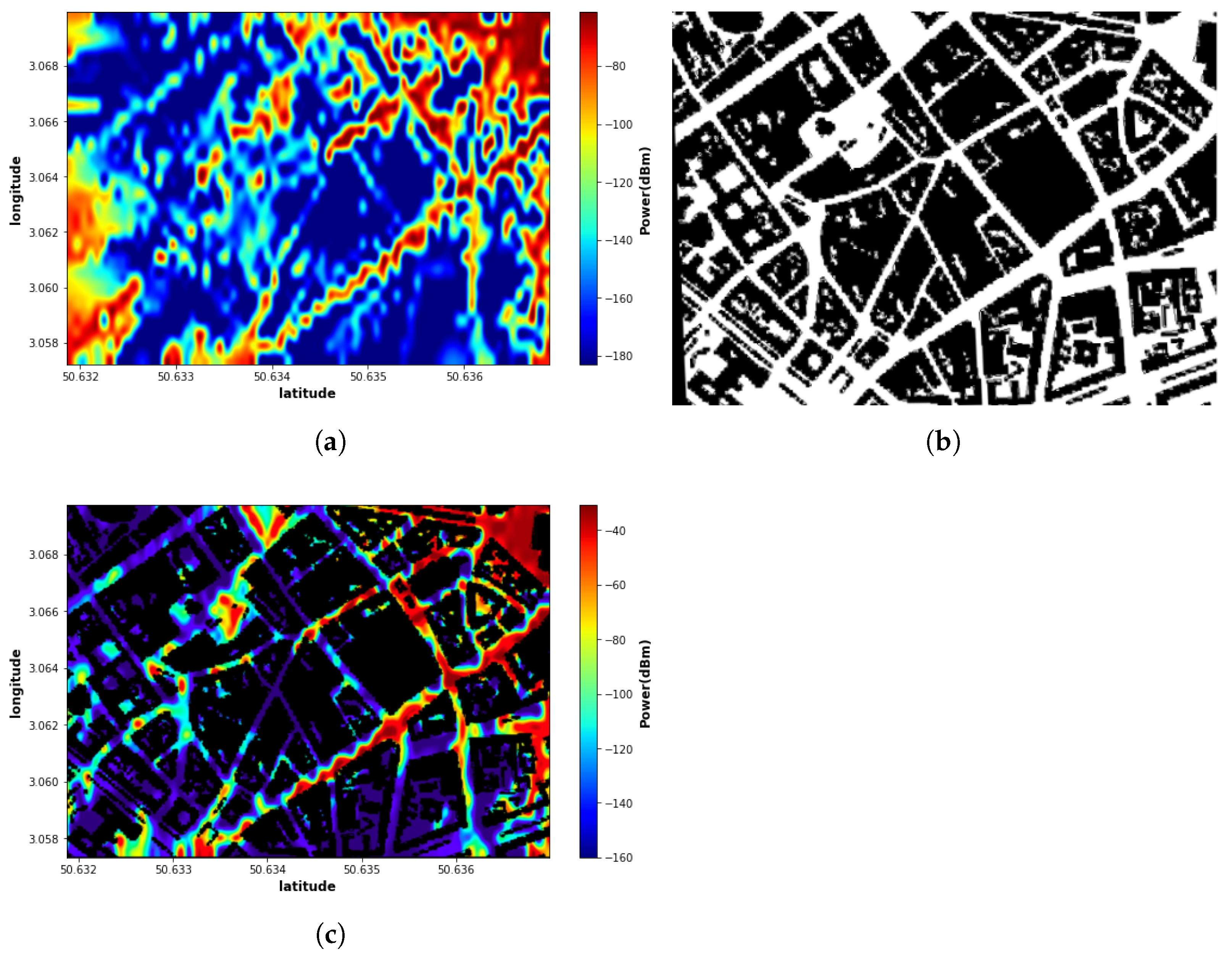
4.1. Input and Output Data
4.2. Network Architecture
4.2.1. U-Net Generator
- Using a kernel size of and a stride of 1, two convolutional layers are applied in succession. The input layer uses tensors of a size of , which represent a three-dimensional sensor map picture. This results in new dimensions with 16 channels and raises the feature map’s channel count.
- The rectified linear unit (ReLU) is the activation function that is being used. This function enables us to take only positive values after convolution operation.
- A max-pooling layer connects previous layers. This layer downsamples the feature map by taking the biggest value in each patch of each feature map. This creates new dimensions of .
4.2.2. Discriminator
4.3. Loss Functions
5. Results
5.1. Training Set-Up
5.2. Evaluation Metrics
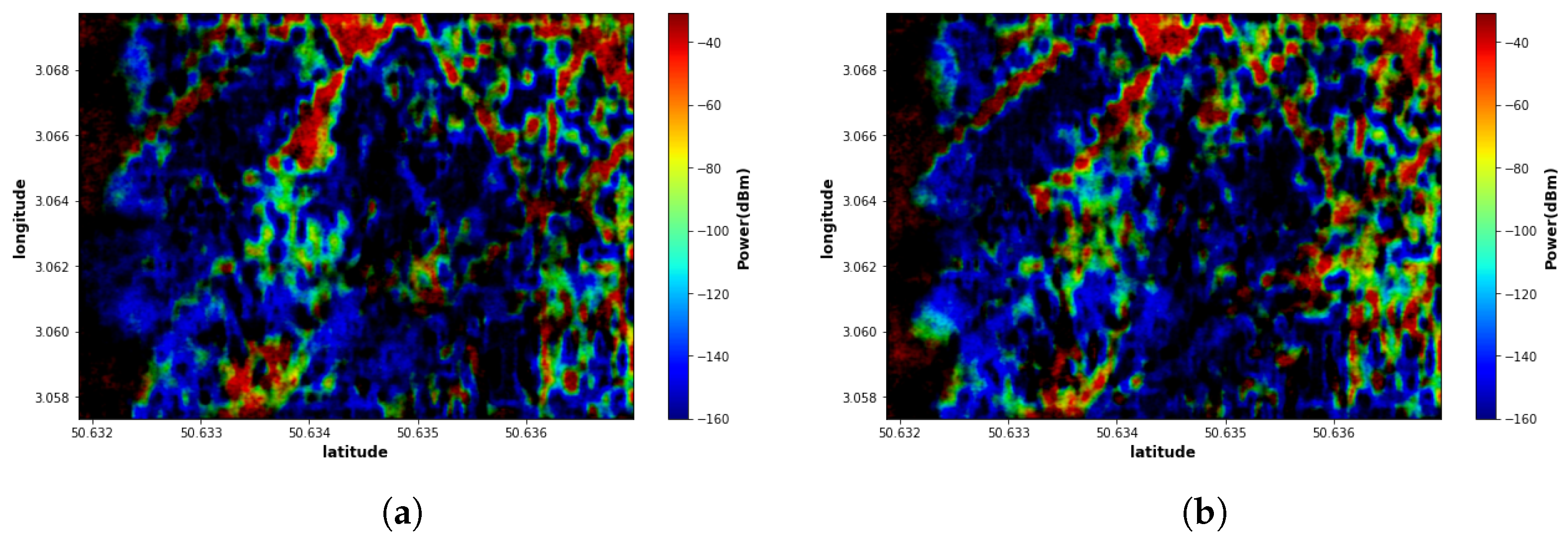
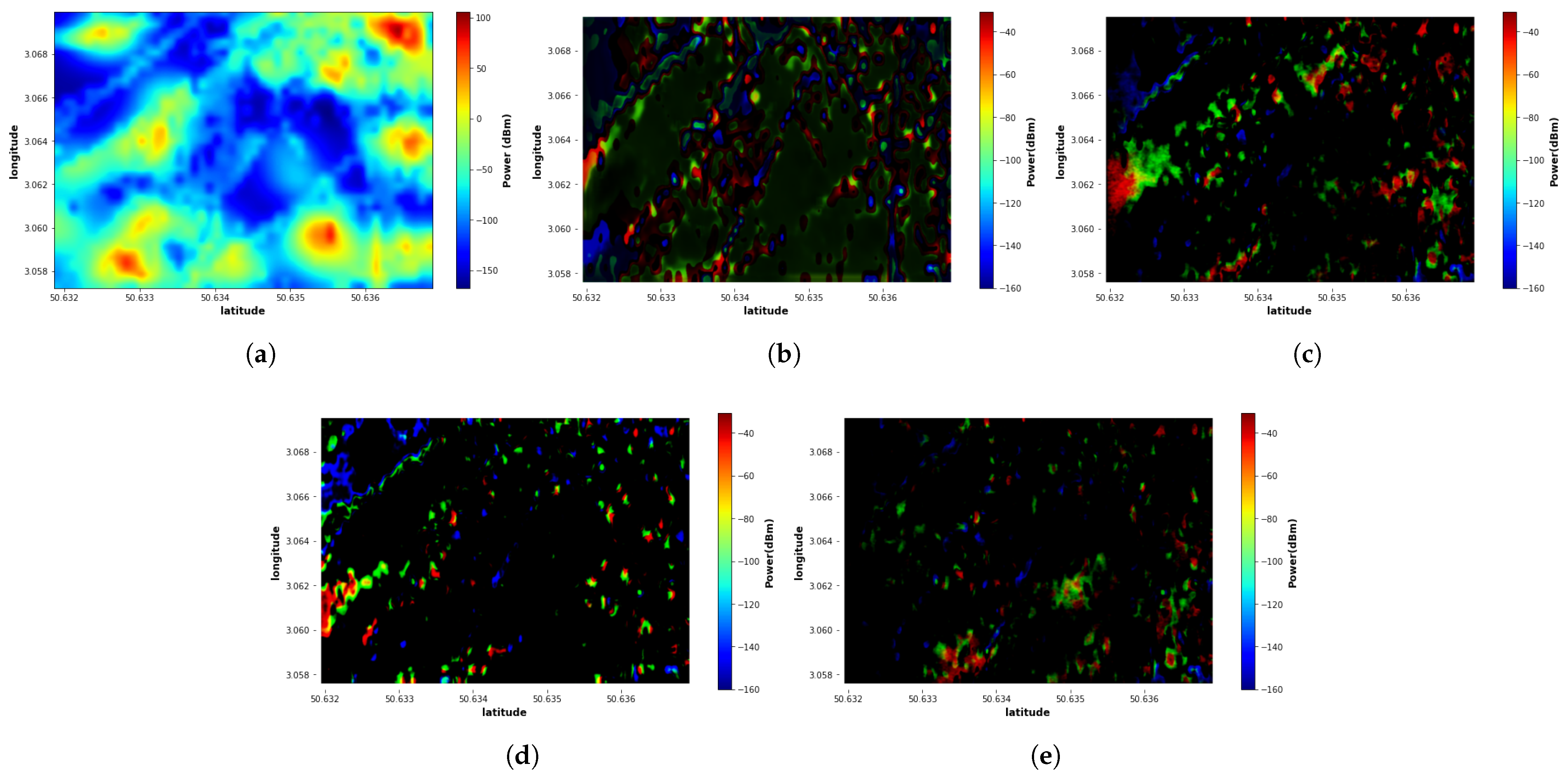
5.3. Visual Analysis
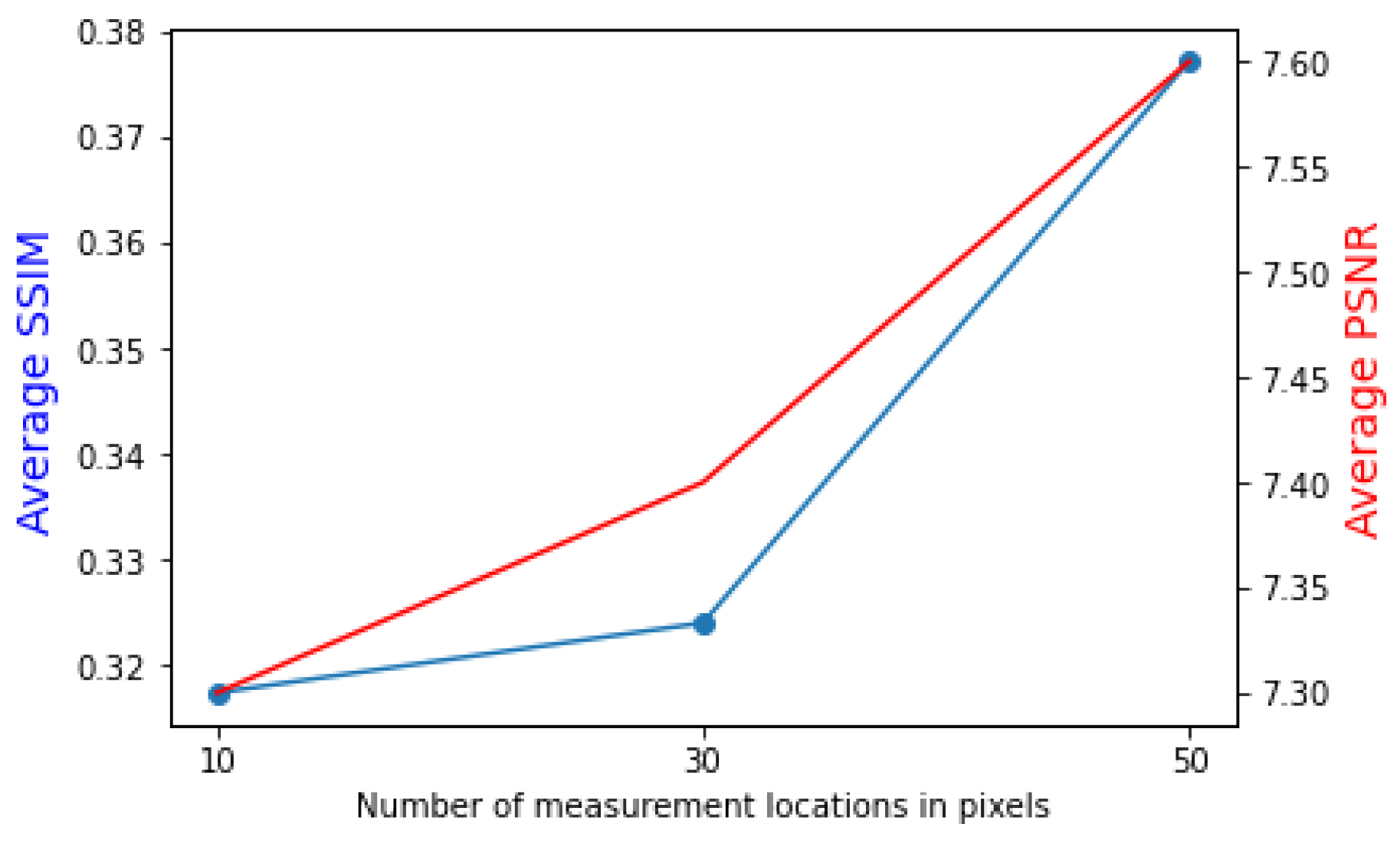
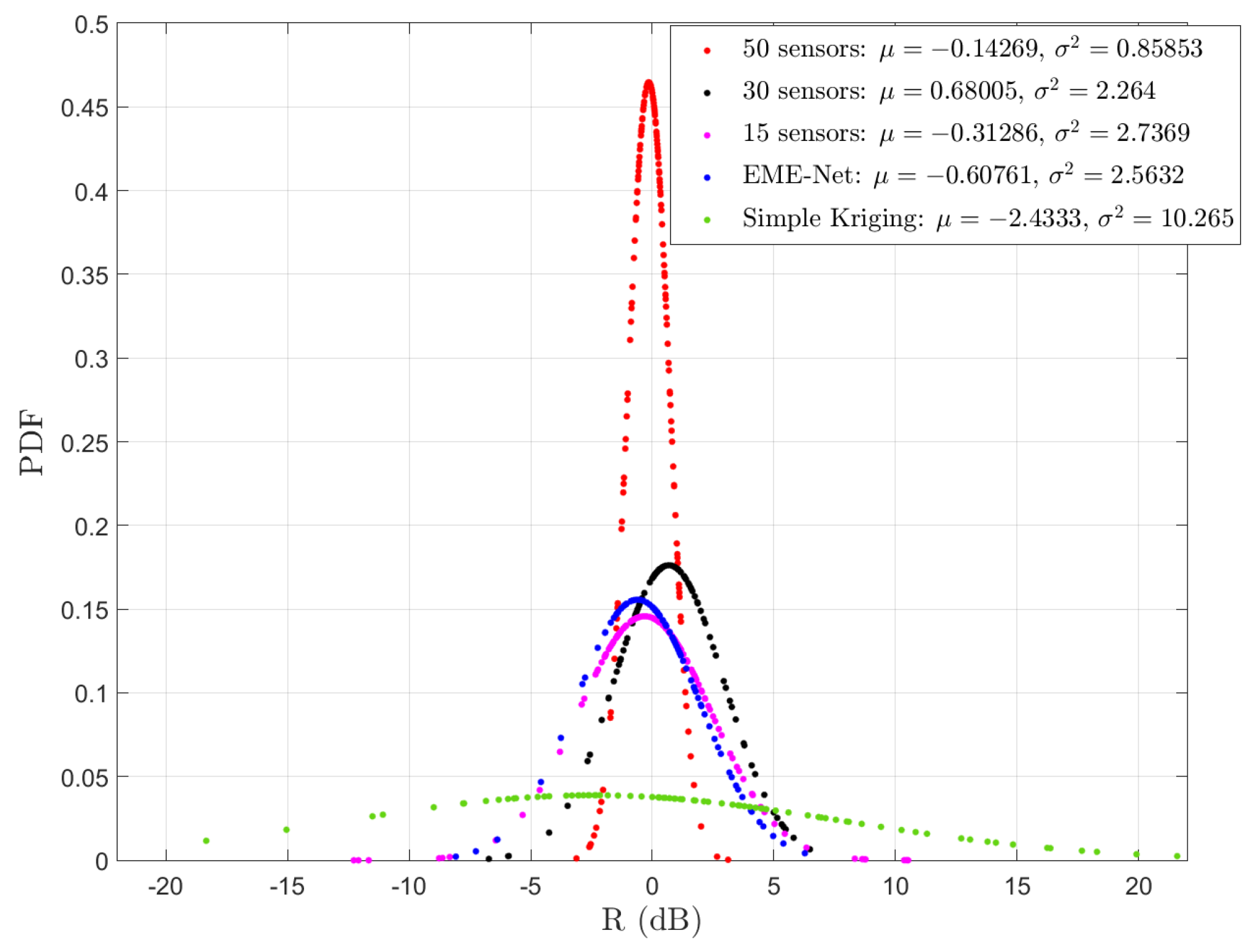
5.4. Quantified Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niknejad, A.M.; Thyagarajan, S.; Alon, E.; Wang, Y.; Hull, C. A circuit designer’s guide to 5G mm-wave. In Proceedings of the 2015 IEEE Custom Integrated Circuits Conference (CICC), San Jose, CA, USA, 28–30 September 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Ahokangas, P.; Matinmikko-Blue, M.; Yrjölä, S.; Hämmäinen, H. Platform configurations for local and private 5G networks in complex industrial multi-stakeholder ecosystems. Telecommun. Policy 2021, 45, S0308596121000331. [Google Scholar] [CrossRef]
- Gajšek, P.; Ravazzani, P.; Wiart, J.; Grellier, J.; Samaras, T.; Thuróczy, G. Electromagnetic field exposure assessment in Europe radiofrequency fields (10 MHz–6 GHz). J. Expo. Sci. Environ. Epidemiol. 2015, 25, 37–44. [Google Scholar] [CrossRef] [PubMed]
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Guidelines for limiting exposure to electromagnetic fields (100 KHz to 300 GHz). Health Phys. 2020, 118, 483–524. [Google Scholar] [CrossRef]
- Bailey, W.H.; Bodemann, R.; Bushberg, J.; Chou, C.K.; Cleveland, R.; Faraone, A.; Foster, K.R.; Gettman, K.E.; Graf, K.; Harrington, T.; et al. Synopsis of IEEE Std C95. 1™-2019 “IEEE Standard for Safety Levels With Respect to Human Exposure to Electric, Magnetic, and Electromagnetic Fields, 0 Hz to 300 GHz”. IEEE Access 2019, 7, 171346–171356. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- MacCartney, G.R.; Zhang, J.; Nie, S.; Rappaport, T.S. Path loss models for 5G millimeter wave propagation channels in urban microcells. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 3948–3953. [Google Scholar] [CrossRef]
- Piersanti, S.; Annoni, L.A.; Cassioli, D. Millimeter waves channel measurements and path loss models. In Proceedings of the 2012 IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 4552–4556. [Google Scholar] [CrossRef]
- Andersen, J.; Rappaport, T.; Yoshida, S. Propagation measurements and models for wireless communications channels. IEEE Commun. Mag. 1995, 33, 42–49. [Google Scholar] [CrossRef]
- Wahl, R.; Wölfle, G.; Wertz, P.; Wildbolz, P.; Landstorfer, F. Dominant path prediction model for urban scenarios. In Proceedings of the 14th IST Mobile and Wireless Communications Summit, Dresden, Germany, 19–23 June 2005. [Google Scholar]
- Rizk, K.; Wagen, J.F.; Gardiol, F. Two-dimensional ray-tracing modeling for propagation prediction in microcellular environments. IEEE Trans. Veh. Technol. 1997, 46, 508–518. [Google Scholar] [CrossRef]
- Balanis, C.A. Advanced Engineering Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Zugno, T.; Drago, M.; Giordani, M.; Polese, M.; Zorzi, M. Toward standardization of millimeter-wave vehicle-to-vehicle networks: Open challenges and performance evaluation. IEEE Commun. Mag. 2020, 58, 79–85. [Google Scholar] [CrossRef]
- Yun, Z.; Iskander, M.F. Ray tracing for radio propagation modeling: Principles and applications. IEEE Access 2015, 3, 1089–1100. [Google Scholar] [CrossRef]
- Boban, M.; Barros, J.; Tonguz, O.K. Geometry-based vehicle-to-vehicle channel modeling for large-scale simulation. IEEE Trans. Veh. Technol. 2014, 63, 4146–4164. [Google Scholar] [CrossRef]
- Stein, M.L. Interpolation of Spatial Data: Some Theory for Kriging; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Knotters, M.; Brus, D.; Voshaar, J.O. A comparison of kriging, co-kriging and kriging combined with regression for spatial interpolation of horizon depth with censored observations. Geoderma 1995, 67, 227–246. [Google Scholar] [CrossRef]
- Tesfay, A.A.; Clavier, L. Gaussian Process-based Spatial Reconstruction of Electromagnetic fields. arXiv 2022, arXiv:2203.01869. [Google Scholar] [CrossRef]
- Han, X.; Xue, L.; Shao, F.; Xu, Y. A Power Spectrum Maps Estimation Algorithm Based on Generative Adversarial Networks for Underlay Cognitive Radio Networks. Sensors 2020, 20, 311. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Annual Conference on Neural Information Processing Systems 2014, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Imai, T.; Kitao, K.; Inomata, M. Radio propagation prediction model using convolutional neural networks by deep learning. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–5. [Google Scholar]
- Saito, K.; Jin, Y.; Kang, C.; Takada, J.i.; Leu, J.S. Two-step path loss prediction by artificial neural network for wireless service area planning. IEICE Commun. Express 2019, 8, 611–616. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Popoola, S.I.; Jefia, A.; Atayero, A.A.; Kingsley, O.; Faruk, N.; Oseni, O.F.; Abolade, R.O. Determination of neural network parameters for path loss prediction in very high frequency wireless channel. IEEE Access 2019, 7, 150462–150483. [Google Scholar] [CrossRef]
- Sotiroudis, S.P.; Goudos, S.K.; Gotsis, K.A.; Siakavara, K.; Sahalos, J.N. Application of a composite differential evolution algorithm in optimal neural network design for propagation path-loss prediction in mobile communication systems. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 364–367. [Google Scholar] [CrossRef]
- Popescu, I.; Nafomita, I.; Constantinou, P.; Kanatas, A.; Moraitis, N. Neural networks applications for the prediction of propagation path loss in urban environments. In Proceedings of the IEEE VTS 53rd Vehicular Technology Conference, Spring 2001. Proceedings (Cat. No. 01CH37202), Rhodes, Greece, 6–9 May 2001; Volume 1, pp. 387–391. [Google Scholar]
- Teganya, Y.; Romero, D. Deep Completion Autoencoders for Radio Map Estimation. IEEE Trans. Wirel. Commun. 2022, 21, 1710–1724. [Google Scholar] [CrossRef]
- Zhang, Y. A Better Autoencoder for Image: Convolutional Autoencoder. 2018. ICONIP17-DCEC. Available online: http://users.cecs.anu.edu.au/Tom.Gedeon/conf/ABCs2018/paper/ABCs2018_paper_58.pdf (accessed on 23 March 2017).
- Egea-Lopez, E.; Losilla, F.; Pascual-Garcia, J.; Molina-Garcia-Pardo, J.M. Vehicular networks simulation with realistic physics. IEEE Access 2019, 7, 44021–44036. [Google Scholar] [CrossRef]
- Haas, J.K. A History of the Unity Game Engine; Worcester Polytechnic Institute: Worcester, MA, USA, 2014. [Google Scholar]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.P.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wießner, E. Microscopic Traffic Simulation using SUMO. In Proceedings of the 21st IEEE International Conference on Intelligent Transportation Systems, Maui, HI, USA, 4–7 November 2018. [Google Scholar]
- Egea-Lopez, E.; Molina-Garcia-Pardo, J.M.; Lienard, M.; Degauque, P. Opal: An open source ray-tracing propagation simulator for electromagnetic characterization. PLoS ONE 2021, 16, e0260060. [Google Scholar] [CrossRef]
- OpenStreetMap Contributors. Planet Dump Retrieved from https://planet.osm.org. 2017. Available online: https://www.openstreetmap.org (accessed on 15 May 2022).
- Xu, C.; Zhao, B. Satellite image spoofing: Creating remote sensing dataset with generative adversarial networks (short paper). In Proceedings of the 10th International Conference on Geographic Information Science (GIScience 2018), Melbourne, Australia, 28–31 August 2018. [Google Scholar]
- Sun, J.; Du, Y.; Li, C.; Wu, T.H.; Yang, B.; Mok, G.S. Pix2Pix generative adversarial network for low dose myocardial perfusion SPECT denoising. Quant. Imaging Med. Surg. 2022, 12, 3539. [Google Scholar] [CrossRef] [PubMed]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Mallik, M.; Kharbech, S.; Mazloum, T.; Wang, S.; Wiart, J.; Gaillot, D.P.; Clavier, L. EME-Net: A U-net-based Indoor EMF Exposure Map Reconstruction Method. In Proceedings of the 2022 16th European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- RGBA Color Model. 2021. Available online: https://en.wikipedia.org/wiki/RGBA_color_model (accessed on 21 June 2022).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]



| Parameters | Value |
|---|---|
| Total number of images | 6006 |
| Input samples | 2500 |
| Test set | 503 |
| Optimizer | ADAM |
| Learning rate | |
| Batch size | 2 |
| Decay rate | |
| Epochs | 4000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallik, M.; Tesfay, A.A.; Allaert, B.; Kassi, R.; Egea-Lopez, E.; Molina-Garcia-Pardo, J.-M.; Wiart, J.; Gaillot, D.P.; Clavier, L. Towards Outdoor Electromagnetic Field Exposure Mapping Generation Using Conditional GANs. Sensors 2022, 22, 9643. https://doi.org/10.3390/s22249643
Mallik M, Tesfay AA, Allaert B, Kassi R, Egea-Lopez E, Molina-Garcia-Pardo J-M, Wiart J, Gaillot DP, Clavier L. Towards Outdoor Electromagnetic Field Exposure Mapping Generation Using Conditional GANs. Sensors. 2022; 22(24):9643. https://doi.org/10.3390/s22249643
Chicago/Turabian StyleMallik, Mohammed, Angesom Ataklity Tesfay, Benjamin Allaert, Redha Kassi, Esteban Egea-Lopez, Jose-Maria Molina-Garcia-Pardo, Joe Wiart, Davy P. Gaillot, and Laurent Clavier. 2022. "Towards Outdoor Electromagnetic Field Exposure Mapping Generation Using Conditional GANs" Sensors 22, no. 24: 9643. https://doi.org/10.3390/s22249643
APA StyleMallik, M., Tesfay, A. A., Allaert, B., Kassi, R., Egea-Lopez, E., Molina-Garcia-Pardo, J.-M., Wiart, J., Gaillot, D. P., & Clavier, L. (2022). Towards Outdoor Electromagnetic Field Exposure Mapping Generation Using Conditional GANs. Sensors, 22(24), 9643. https://doi.org/10.3390/s22249643







