Experimental Study of Ghost Imaging in Underwater Environment
Abstract
:1. Introduction
2. Method
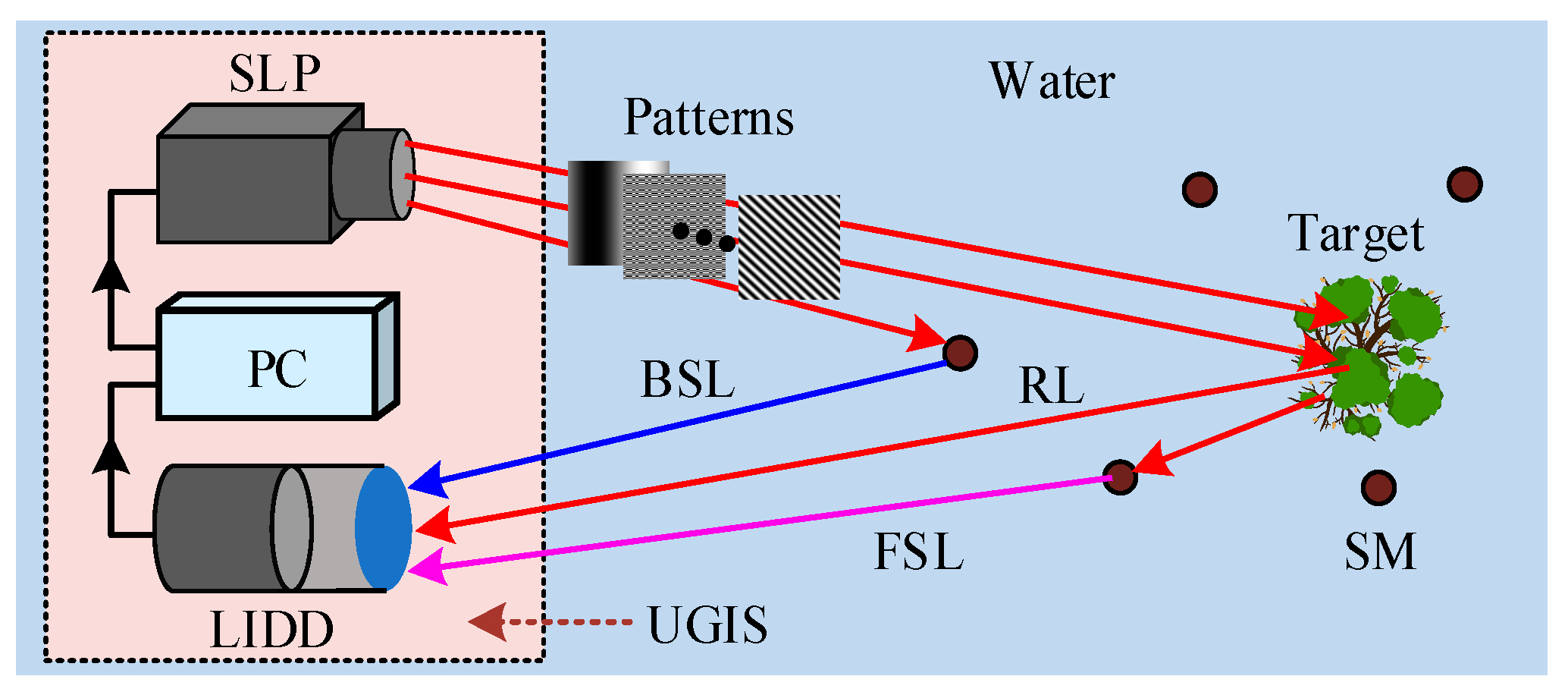
2.1. Underwater Ghost Imaging Model
2.2. GI Image Reconstruction
2.3. Image Reconstruction with Other Methods
3. Results
3.1. Simulation Results and Analysis
3.1.1. Results without WGN
3.1.2. Results with WGN
3.2. Experimental Results and Analysis
3.2.1. GI without Water
3.2.2. GI with Water
3.2.3. GI with Water and Turbulence
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moghimi, M.K.; Mohanna, F. Real-time underwater image enhancement: A systematic review. J. Real-Time Image Process. 2021, 18, 1509–1525. [Google Scholar] [CrossRef]
- Liu, R.; Fan, X.; Zhu, M.; Hou, M.; Luo, Z. Real-world Underwater Enhancement: Challenges, Benchmarks, and Solutions under Natural Light. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 4861–4875. [Google Scholar] [CrossRef]
- Luo, Z.; Tang, Z.; Jiang, L.; Wang, C. An underwater-imaging-model-inspired no-reference quality metric for images in multi-colored environments. Expert Syst. Appl. 2022, 191, 116361. [Google Scholar] [CrossRef]
- Zhao, F.; Lu, R.; Chen, X.; Jin, C.; Chen, S.; Shen, Z.; Zhang, C.; Yang, Y. Metalens-assisted system for underwater imaging. Laser Photonics Rev. 2021, 15, 2100097. [Google Scholar] [CrossRef]
- Hu, H.; Qi, P.; Li, X.; Cheng, Z.; Liu, T. Underwater imaging enhancement based on a polarization filter and histogram attenuation prior. J. Phys. D Appl. Phys. 2021, 54, 175102. [Google Scholar] [CrossRef]
- Liu, T.; Guan, Z.; Li, X.; Cheng, Z.; Hu, H. Polarimetric underwater image recovery for color image with crosstalk compensation. Opt. Lasers Eng. 2020, 124, 105833. [Google Scholar] [CrossRef]
- Li, T.; Wang, J.; Yao, K. Visibility enhancement of underwater images based on active polarized illumination and average filtering technology. Alex. Eng. J. 2022, 61, 701–708. [Google Scholar] [CrossRef]
- Zhu, Y.; Zeng, T.; Liu, K.; Ren, Z.; Lam, E.Y. Full scene underwater imaging with polarization and an untrained network. Opt. Express 2021, 29, 41865–41881. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, Y.; Li, X.; Lin, Y.; Liu, T. Polarimetric underwater image recovery via deep learning. Opt. Lasers Eng. 2020, 133, 106152. [Google Scholar] [CrossRef]
- Chen, Q.; Mathai, A.; Xu, X.; Wang, X. A study into the effects of factors influencing an underwater, single-pixel imaging system’s performance. Photonics 2019, 6, 123. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, M.; Li, F.; Tian, Z.; Zhao, M. Underwater polarization-based single pixel imaging. J. Soc. Inf. Display 2020, 28, 157–163. [Google Scholar] [CrossRef]
- Gong, W. Performance comparison of computational ghost imaging versus single-pixel camera in light disturbance environment. Opt. Laser Technol. 2022, 152, 108140. [Google Scholar] [CrossRef]
- Pittman, T.B.; Shih, Y.H.; Strekalov, D.V.; Sergienko, A.V. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 1995, 52, R3429–R3432. [Google Scholar] [CrossRef]
- Cheng, J.; Han, S. Incoherent coincidence imaging and its applicability in X-ray diffraction. Phys. Rev. Lett. 2004, 92, 93903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, J.; Cao, D.; Huang, F.; Li, H.; Sun, X.; Wang, K. Experimental observation of classical subwavelength interference with a pseudothermal light source. Phys. Rev. Lett. 2005, 94, 173601. [Google Scholar] [CrossRef] [Green Version]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 61802. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, J. Single-pixel imaging and its application in three-dimensional reconstruction: A brief review. Sensors 2019, 19, 732. [Google Scholar] [CrossRef] [Green Version]
- Edgar, M.P.; Gibson, G.M.; Padgett, M.J. Principles and prospects for single-pixel imaging. Nat. Photonics 2019, 13, 13–20. [Google Scholar] [CrossRef]
- Wan, W.; Luo, C.; Guo, F.; Zhou, J.; Wang, P.; Huang, X. Demonstration of asynchronous computational ghost imaging through strong scattering media. Opt. Laser Technol. 2022, 154, 108346. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, W.; Zhang, E.; Li, Q.; Dai, H.; Chen, P. Is ghost imaging intrinsically more powerful against scattering? Opt. Express 2015, 23, 32993–33000. [Google Scholar] [CrossRef]
- Gao, Z.; Yin, J.; Bai, Y.; Fu, X. Imaging quality improvement of ghost imaging in scattering medium based on Hadamard modulated light field. Appl. Opt. 2020, 59, 8472–8477. [Google Scholar] [CrossRef]
- Li, F.; Zhao, M.; Tian, Z.; Willomitzer, F.; Cossairt, O. Compressive ghost imaging through scattering media with deep learning. Opt. Express 2020, 28, 17395–17408. [Google Scholar] [CrossRef]
- Fu, Q.; Bai, Y.; Huang, X.; Nan, S.; Xie, P.; Fu, X. Positive influence of the scattering medium on reflective ghost imaging. Photonics Res. 2019, 7, 1468–1472. [Google Scholar] [CrossRef]
- Bina, M.; Magatti, D.; Molteni, M.; Gatti, A.; Lugiato, L.; Ferri, F. Backscattering differential ghost imaging in turbid media. Phys. Rev. Lett. 2013, 110, 083901. [Google Scholar] [CrossRef]
- Liu, B.; Yang, Z.; Qu, S.; Zhang, A. Influence of turbid media at different locations in computational ghost imaging. Acta Opt. Sin. 2016, 36, 1026017. [Google Scholar]
- Yuan, Y.; Chen, H. Unsighted ghost imaging for objects completely hidden inside turbid media. New J. Phys. 2022, 24, 43034. [Google Scholar] [CrossRef]
- Shi, X.; Huang, X.; Nan, S.; Li, H.; Bai, Y.; Fu, X. Image quality enhancement in low-light-level ghost imaging using modified compressive sensing method. Laser Phys. Lett. 2018, 15, 45204. [Google Scholar] [CrossRef]
- Huang, J.; Shi, D. Multispectral computational ghost imaging with multiplexed illumination. J. Opt. 2017, 19, 75701. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Liu, Z.; Wu, J.; Li, E.; Hu, C.; Tong, Z.; Shen, X.; Han, S. Hyperspectral ghost imaging camera based on a flat-field grating. Opt. Express 2018, 26, 17705–17716. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, W.; Wu, H.; Chen, Y.; Su, X.; Xiao, Y.; Wang, Z.; Gu, Y. High-visibility underwater ghost imaging in low illumination. Opt. Commun. 2019, 441, 45–48. [Google Scholar] [CrossRef]
- Gao, Y.; Fu, X.; Bai, Y. Ghost imaging in transparent liquid. J. Opt. 2017, 46, 410–414. [Google Scholar] [CrossRef]
- Luo, C.; Wan, W.; Chen, S.; Long, A.; Peng, L.; Wu, S.; Qi, H. High-quality underwater computational ghost imaging with shaped Lorentz sources. Laser Phys. Lett. 2020, 17, 105209. [Google Scholar] [CrossRef]
- Wang, M.; Bai, Y.; Zou, X.; Peng, M.; Zhou, L.; Fu, Q.; Jiang, T.; Fu, X. Effect of uneven temperature distribution on underwater computational ghost imaging. Laser Phys. 2022, 32, 65205. [Google Scholar] [CrossRef]
- Ming, Z.; Yu, W.; Zhiming, T.; Meijing, Z. Method of Push-Broom Underwater Ghost Imaging Computation. Laser Optoelectron. Prog. 2019, 56, 161101. [Google Scholar] [CrossRef]
- Wang, T.; Chen, M.; Wu, H.; Xiao, H.; Luo, S.; Cheng, L. Underwater compressive computational ghost imaging with wavelet enhancement. Appl. Opt. 2021, 60, 6950–6957. [Google Scholar] [CrossRef]
- Yang, X.; Yu, Z.; Xu, L.; Hu, J.; Wu, L.; Yang, C.; Zhang, W.; Zhang, J.; Zhang, Y. Underwater ghost imaging based on generative adversarial networks with high imaging quality. Opt. Express 2021, 29, 28388–28405. [Google Scholar] [CrossRef]
- Le, M.; Wang, G.; Zheng, H.; Liu, J.; Zhou, Y.; Xu, Z. Underwater computational ghost imaging. Opt. Express 2017, 25, 22859–22868. [Google Scholar] [CrossRef]
- Luo, C.; Li, Z.; Xu, J.; Liu, Z. Computational ghost imaging and ghost diffraction in turbulent ocean. Laser Phys. Lett. 2018, 15, 125205. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, W.; Liu, K.; Zhou, L.; Wang, Z.; Gu, Y. Effect of oceanic turbulence on the visibility of underwater ghost imaging. JOSA A 2019, 36, 397–402. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Liu, L.; Wang, F.; Zhang, Y.; Cai, Y. Ghost imaging with a partially coherent beam carrying twist phase in a turbulent ocean: A numerical approach. Appl. Sci. 2019, 9, 3023. [Google Scholar] [CrossRef] [Green Version]
- Yin, M.; Wang, L.; Zhao, S. Experimental demonstration of influence of underwater turbulence on ghost imaging. Chin. Phys. B 2019, 28, 94201. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, Z.; Tang, Z. Experimental Study on Anti-Disturbance Ability of Underwater Ghost Imaging. Laser Optoelectron. Prog. 2021, 58, 611002. [Google Scholar]
- Zhang, Z.; Ma, X.; Zhong, J. Single-pixel imaging by means of Fourier spectrum acquisition. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Wang, X.; Zheng, G.; Zhong, J. Hadamard single-pixel imaging versus Fourier single-pixel imaging. Opt. Express 2017, 25, 19619–19639. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Lu, R.; Han, S.; Xie, H.; Du, G.; Xiao, T.; Zhu, D. Fourier-transform ghost imaging with hard X-rays. Phys. Rev. Lett. 2016, 117, 113901. [Google Scholar] [CrossRef] [Green Version]
- Ferri, F.; Magatti, D.; Lugiato, L.A.; Gatti, A. Differential ghost imaging. Phys. Rev. Lett. 2010, 104, 253603. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Welsh, S.S.; Edgar, M.P.; Shapiro, J.H.; Padgett, M.J. Normalized ghost imaging. Opt. Express 2012, 20, 16892–16901. [Google Scholar] [CrossRef] [Green Version]
- Sun, M.; Meng, L.; Edgar, M.P.; Padgett, M.J.; Radwell, N. A Russian Dolls ordering of the Hadamard basis for compressive single-pixel imaging. Sci. Rep. 2017, 7, 3464. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Zhao, G.; Wang, R.; Xiao, H.; Wang, D.; Liang, J.; Cheng, L.; Liang, R. Computational ghost imaging system with 4-connected-region-optimized Hadamard pattern sequence. Opt. Lasers Eng. 2020, 132, 106105. [Google Scholar] [CrossRef]
- Wu, H.; Wu, W.; Chen, M.; Luo, S.; Zhao, R.; Xu, L.; Xiao, H.; Cheng, L.; Zhang, X.; Xu, Y. Computational ghost imaging with 4-step iterative rank minimization. Phys. Lett. A 2021, 394, 127199. [Google Scholar] [CrossRef]
- Wu, H.; Wang, R.; Huang, Z.; Xiao, H.; Liang, J.; Wang, D.; Tian, X.; Wang, T.; Cheng, L. Online adaptive computational ghost imaging. Opt. Lasers Eng. 2020, 128, 106028. [Google Scholar] [CrossRef]
- Yi, K.; Leihong, Z.; Hualong, Y.; Mantong, Z.; Kanwal, S.; Dawei, Z. Camouflaged optical encryption based on compressive ghost imaging. Opt. Lasers Eng. 2020, 134, 106154. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef] [Green Version]
- Li, C. An Efficient Algorithm for Total Variation Regularization with Applications to the Single Pixel Camera and Compressive Sensing. Master’s Thesis, Rice University, Houston, TX, USA, 2010. [Google Scholar]
- Yu, W. Super Sub-Nyquist Single-Pixel Imaging by Means of Cake-Cutting Hadamard Basis Sort. Sensors 2019, 19, 4122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, X.; Suo, J.; Yue, T.; Bian, L.; Dai, Q. Patch-primitive driven compressive ghost imaging. Opt. Express 2015, 23, 11092–11104. [Google Scholar] [CrossRef] [PubMed]
- Bian, L.; Suo, J.; Dai, Q.; Chen, F. Experimental comparison of single-pixel imaging algorithms. JOSA A 2018, 35, 78–87. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Q.; Gong, W. Distorted point spread function and image reconstruction for ghost imaging. Opt. Lasers Eng. 2021, 139, 106486. [Google Scholar] [CrossRef]
- Gong, W. High-resolution pseudo-inverse ghost imaging. Photonics Res. 2015, 3, 234–237. [Google Scholar] [CrossRef]
- Czajkowski, K.M.; Pastuszczak, A.; Kotyński, R. Real-time single-pixel video imaging with Fourier domain regularization. Opt. Express 2018, 26, 20009–20022. [Google Scholar] [CrossRef]
- Pastuszczak, A.; Stojek, R.; Wróbel, P.; Kotyński, R. Differential real-time single-pixel imaging with fourier domain regularization: Applications to VIS-IR imaging and polarization imaging. Opt. Express 2021, 29, 26685–26700. [Google Scholar] [CrossRef]
- Luo, K.; Huang, B.; Zheng, W.; Wu, L. Nonlocal imaging by conditional averaging of random reference measurements. Chin. Phys. Lett. 2012, 29, 74216. [Google Scholar] [CrossRef] [Green Version]
- Tong, Z.; Liu, Z.; Hu, C.; Wang, J.; Han, S. Preconditioned deconvolution method for high-resolution ghost imaging. Photonics Res. 2021, 9, 1069–1077. [Google Scholar] [CrossRef]
- Guo, K.; Jiang, S.; Zheng, G. Multilayer fluorescence imaging on a single-pixel detector. Biomed. Opt. Express 2016, 7, 2425–2431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, C.; Wang, C.; Guan, J.; Zhang, C.; Guo, S.; Gong, W.; Gao, F. Scalar-matrix-structured ghost imaging. Photonics Res. 2016, 4, 281–285. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, S. Fast reconstructed and high-quality ghost imaging with fast Walsh–Hadamard transform. Photonics Res. 2016, 4, 240–244. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.; Xiao, X.; Ren, C.; Zhang, D.; Li, Z.; Cao, D. Denoising in SVD-based ghost imaging. Opt. Express 2022, 30, 6248–6257. [Google Scholar] [CrossRef]
- Wang, F.; Wang, H.; Wang, H.; Li, G.; Situ, G. Learning from simulation: An end-to-end deep-learning approach for computational ghost imaging. Opt. Express 2019, 27, 25560–25572. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Zhao, G.; Chen, M.; Cheng, L.; Xiao, H.; Xu, L.; Wang, D.; Liang, J.; Xu, Y. Hybrid neural network-based adaptive computational ghost imaging. Opt. Lasers Eng. 2021, 140, 106529. [Google Scholar] [CrossRef]
- Ni, Y.; Zhou, D.; Yuan, S.; Bai, X.; Xu, Z.; Chen, J.; Li, C.; Zhou, X. Color computational ghost imaging based on a generative adversarial network. Opt. Lett. 2021, 46, 1840–1843. [Google Scholar] [CrossRef]
- Wang, F.; Wang, C.; Chen, M.; Gong, W.; Zhang, Y.; Han, S.; Situ, G. Far-field super-resolution ghost imaging with a deep neural network constraint. Light Sci. Appl. 2022, 11, 1. [Google Scholar] [CrossRef]











| Pattern Type | GI Methods |
|---|---|
| Random | GI [13,14], DGI [46], NGI [47], OGI [52], TV [53], TR [56,57], SPGI [57], PSF [58], PGI [59], CI [62], PreGI [63], APGI [64], SMGI [65], and TSGI [67] |
| Orthogonal | WGI [35], FSPI [43], RD [48], CR [49], LGI [50], ZzGI [51], CC [55], DRI [60], DDRI [61], and FWHT [66] |
| Group | Adding WGN? | Noise Level |
|---|---|---|
| 1 | No | / |
| 2 | Yes | 50 |
| 3 | Yes | 45 |
| OGI | TV | TR | PSF | FWHT | RD | CR | |
|---|---|---|---|---|---|---|---|
| PSNR | 14.86 | 13.45 | 20.26 | 18.63 | 14.70 | 14.88 | 17.74 |
| 15.96 | 12.25 | 18.60 | 18.50 | 18.04 | 18.96 | 20.27 | |
| RMSE | 0.18 | 0.21 | 0.10 | 0.12 | 0.18 | 0.18 | 0.13 |
| 0.16 | 0.24 | 0.12 | 0.12 | 0.13 | 0.11 | 0.10 | |
| ZzGI | CC | LGI | WGI | FSPI | DRI | DDRI | |
| PSNR | 18.73 | 19.07 | 18.79 | 19.31 | 20.96 | 23.29 | 22.66 |
| 19.28 | 20.53 | 18.60 | 20.76 | 20.34 | 21.15 | 20.15 | |
| RMSE | 0.12 | 0.12 | 0.11 | 0.11 | 0.09 | 0.07 | 0.07 |
| 0.11 | 0.09 | 0.12 | 0.09 | 0.10 | 0.09 | 0.10 |
| OGI | TV | TR | PSF | FWHT | RD | CR | |
|---|---|---|---|---|---|---|---|
| PSNR | 11.53 | 12.93 | 11.91 | 13.64 | 14.70 | 14.91 | 17.70 |
| 9.23 | 11.62 | 9.03 | 11.79 | 18.03 | 18.94 | 20.28 | |
| RMSE | 0.27 | 0.23 | 0.25 | 0.21 | 0.18 | 0.18 | 0.13 |
| 0.35 | 0.26 | 0.35 | 0.26 | 0.13 | 0.11 | 0.10 | |
| ZzGI | CC | LGI | WGI | FSPI | DRI | DDRI | |
| PSNR | 18.75 | 19.06 | 18.77 | 19.30 | 18.15 | 17.36 | 16.50 |
| 19.20 | 20.53 | 18.59 | 20.87 | 16.74 | 12.94 | 12.27 | |
| RMSE | 0.12 | 0.11 | 0.12 | 0.11 | 0.12 | 0.14 | 0.15 |
| 0.12 | 0.09 | 0.12 | 0.09 | 0.15 | 0.23 | 0.24 |
| OGI | TV | TR | PSF | FWHT | RD | CR | |
|---|---|---|---|---|---|---|---|
| PSNR | 9.37 | 12.50 | 9.73 | 11.11 | 14.71 | 14.93 | 17.67 |
| 6.92 | 11.02 | 7.03 | 7.52 | 18.03 | 18.92 | 20.28 | |
| RMSE | 0.34 | 0.24 | 0.33 | 0.29 | 0.18 | 0.18 | 0.13 |
| 0.45 | 0.28 | 0.44 | 0.42 | 0.13 | 0.11 | 0.10 | |
| ZzGI | CC | LGI | WGI | FSPI | DRI | DDRI | |
| PSNR | 18.75 | 19.05 | 18.80 | 19.29 | 16.16 | 13.99 | 13.78 |
| 19.13 | 20.53 | 18.58 | 20.87 | 13.63 | 10.14 | 9.58 | |
| RMSE | 0.12 | 0.11 | 0.11 | 0.11 | 0.16 | 0.20 | 0.20 |
| 0.11 | 0.09 | 0.12 | 0.09 | 0.21 | 0.31 | 0.33 |
| FWHT | RD | CR | ZzGI | DRI | |
|---|---|---|---|---|---|
| PSNR | 15.29 | 15.32 | 16.79 | 16.93 | 13.73 |
| RMSE | 0.17 | 0.17 | 0.14 | 0.14 | 0.21 |
| CC | LGI | WGI | FSPI | DDRI | |
| PSNR | 17.30 | 17.72 | 18.71 | 17.78 | 12.17 |
| RMSE | 0.14 | 0.13 | 0.12 | 0.13 | 0.25 |
| FWHT | RD | CR | ZzGI | DRI | |
|---|---|---|---|---|---|
| PSNR | 14.41 | 14.06 | 14.97 | 15.80 | 11.14 |
| RMSE | 0.19 | 0.20 | 0.19 | 0.16 | 0.28 |
| CC | LGI | WGI | FSPI | DDRI | |
| PSNR | 15.98 | 16.53 | 17.08 | 16.40 | 10.62 |
| RMSE | 0.16 | 0.15 | 0.14 | 0.15 | 0.29 |
| FWHT | RD | CR | ZzGI | DRI | |
|---|---|---|---|---|---|
| PSNR | 13.38 | 13.13 | 14.11 | 14.40 | 10.78 |
| RMSE | 0.21 | 0.22 | 0.20 | 0.19 | 0.29 |
| CC | LGI | WGI | FSPI | DDRI | |
| PSNR | 14.93 | 15.83 | 15.55 | 14.39 | 9.99 |
| RMSE | 0.18 | 0.16 | 0.17 | 0.19 | 0.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Chen, Z.; He, C.; Cheng, L.; Luo, S. Experimental Study of Ghost Imaging in Underwater Environment. Sensors 2022, 22, 8951. https://doi.org/10.3390/s22228951
Wu H, Chen Z, He C, Cheng L, Luo S. Experimental Study of Ghost Imaging in Underwater Environment. Sensors. 2022; 22(22):8951. https://doi.org/10.3390/s22228951
Chicago/Turabian StyleWu, Heng, Ziyan Chen, Chunhua He, Lianglun Cheng, and Shaojuan Luo. 2022. "Experimental Study of Ghost Imaging in Underwater Environment" Sensors 22, no. 22: 8951. https://doi.org/10.3390/s22228951
APA StyleWu, H., Chen, Z., He, C., Cheng, L., & Luo, S. (2022). Experimental Study of Ghost Imaging in Underwater Environment. Sensors, 22(22), 8951. https://doi.org/10.3390/s22228951







