Polarization Domain Spectrum Sensing Algorithm Based on AlexNet
Abstract
:1. Introduction
1.1. Motivation
1.2. Novelty
2. Polarization Domain Signal Model
2.1. Jones Vector
2.2. Signal Model
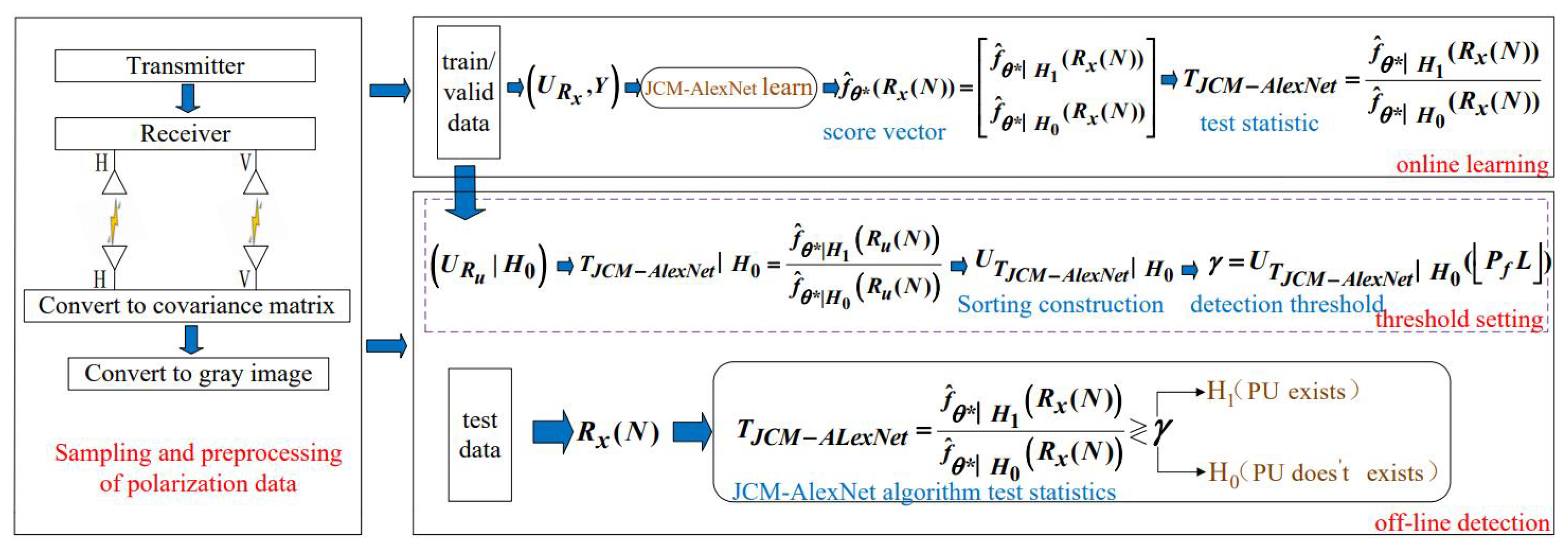
3. JCM-AlexNet Spectrum Sensing Algorithm
3.1. Data Preprocessing of Polarization Signal
3.2. Online Learning of JCM-AlexNet Algorithm
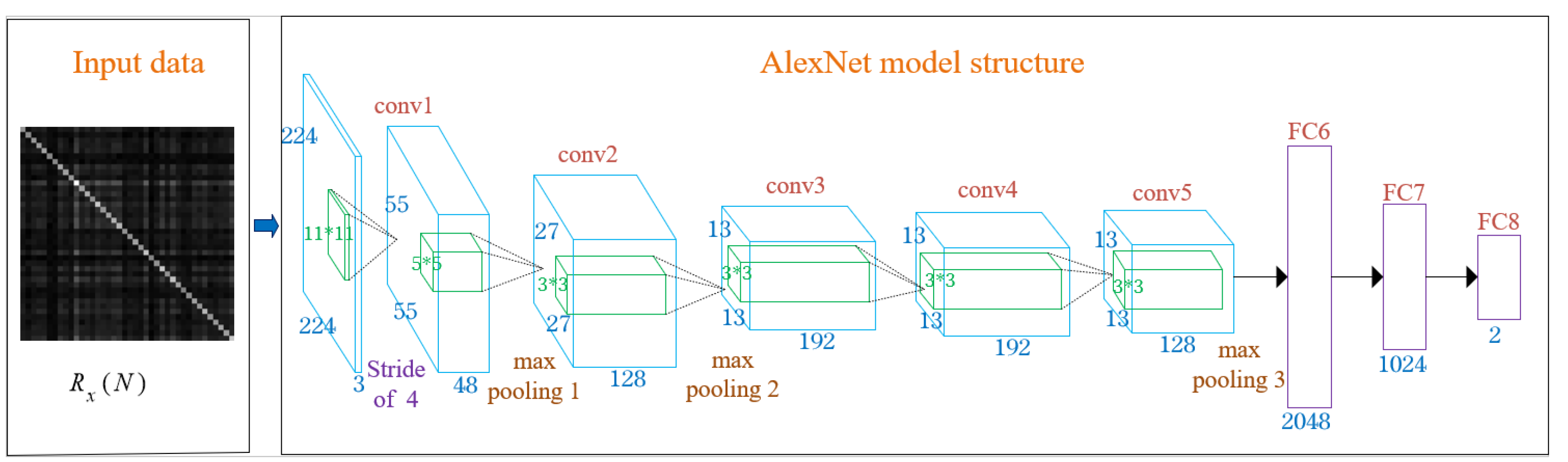
3.2.1. AlexNet Model Structure
3.2.2. Learning Phase
3.2.3. Test Statistic Design
3.3. Off-Line Detection of JCM-AlexNet Algorithm
3.3.1. Design of Detection Threshold
3.3.2. Determination of Detection Results
4. Simulation Analysis
4.1. Structural Analysis
4.2. Parameter Analysis
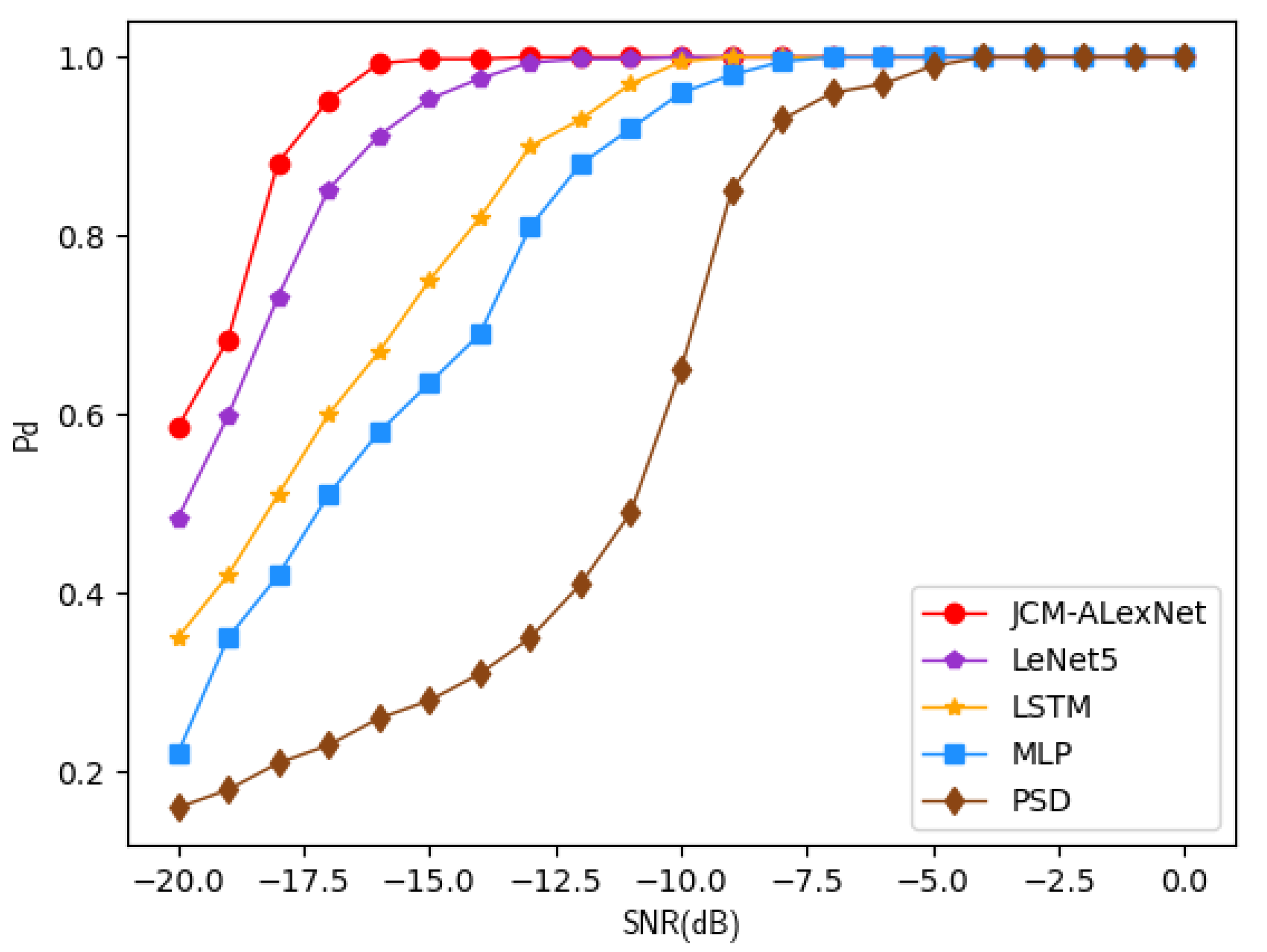
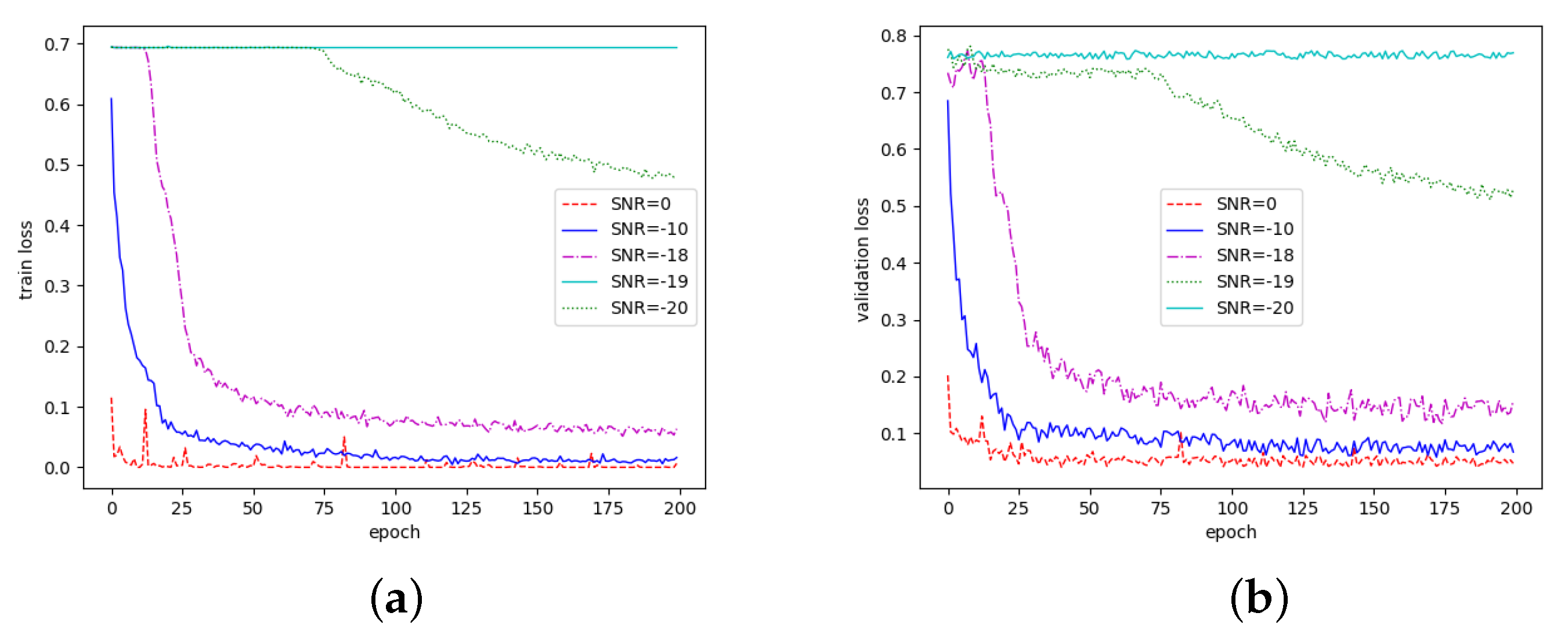
4.3. Performance Analysis
4.3.1. Performance Analysis of Detection Probability
4.3.2. Analysis of Loss Value Change
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sazia, P.; Farookh Khadeer, H.; Omar Khadeer, H. Cognitive radio network security: A survey. J. Netw. Comput. Appl. 2012, 35, 1691–1708. [Google Scholar]
- Sharma, S.K.; Chatzinotas, S.; Ottersten, B. Exploiting polarization for spectrum sensing in cognitive SatComs. In Proceedings of the 2012 7th International ICST Conference on Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM), Stockholm, Sweden, 18–20 June 2012. [Google Scholar]
- Lu, J.; Huang, M.; Yang, J. Polarized Antenna Aided Spectrum Sensing Based on Stochastic Resonance. Wirel. Pers. Commun. 2020, 114, 3383–3394. [Google Scholar] [CrossRef]
- Cali, G.; Hanyang, L.; Shuo, C. Study of spectrum sensing exploiting polarization: From optimal LRT to practical detectors. Digit. Signal Process. 2016, 114, 1–13. [Google Scholar]
- Deng, Y. Research of Spectrum Sensing Algirthm in Cognitive Radio Based on Polarization Information. Master’s Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2012. [Google Scholar]
- Janu, D.; Singh, K.; Kumar, S. Machine learning for cooperative spectrum sensing and sharing: A survey. Trans. Emerg. Telecommun. Technol. 2022, 33, e4352. [Google Scholar] [CrossRef]
- Khamaysa, S.; Halawani, A. Cooperative Spectrum Sensing in Cognitive Radio Networks: A Survey on Machine Learning-based Methods. J. Telecommun. Inf. Technol. 2020, 3, 36–46. [Google Scholar] [CrossRef]
- Tavares, C.; Filho, J.; Proenca, M. Machine Learning-based Models for Spectrum Sensing in Cooperative Radio Networks. IET Commun. 2020, 14, 3102–3109. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 6, 386–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soni, B.; Patel, D.; Lopez-Benitez, M. Long Short-Term Memory Based Spectrum Sensing Scheme for Cognitive Radio Using Primary Activity Statistics. IEEE Access. 2020, 8, 97437–97451. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Wang, J.; Liu, X. Deep CM-CNN for Spectrum Sensing in Cognitive Radio. IEEE J. Sel. Areas Commun. 2019, 37, 2306–2321. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y. Gradient-based learning applied to document recognition. Proc. IEEE. 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Tekbiyik, K.; Akbunar, O.; Ekti, A. Spectrum Sensing and Signal Identification With Deep Learning Based on Spectral Correlation Function. IEEE Trans. Veh. Technol. 2021, 70, 10514–10527. [Google Scholar] [CrossRef]
- Mengbo, Z.; Lunwen, W.; Yanqing, F. A Spectrum Sensing Algorithm for OFDM Signal Based on Deep Learning and Covariance Matrix Graph. IEICE Trans. Commun. 2018, E101.B, 2435–2444. [Google Scholar]
- Jiandong, X.; Jun, F.; Chang, L. Deep Learning-Based Spectrum Sensing in Cognitive Radio: A CNN-LSTM Approach. IEEE Commun. Lett. 2020, 24, 2196–2200. [Google Scholar]
- Guyon, L.; Elisseeff, A. An Introduction of Variable and Feature Selection. J. Mach. Learn. Res. Spec. Issue Var. Feature Sel. 2003, 3, 1157–1182. [Google Scholar]
- Fangfang, L.; Chunyan, F.; Caili, G. Polarization Spectrum Sensing Scheme for Cognitive Radios. In Proceedings of the 2009 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 24–26 September 2009. [Google Scholar]
- Huanyao, D.; Xuesong, W. Connotation and Representation of Spatial Polarization Characteristic; Springer: Singapore, 2018; pp. 29–56. [Google Scholar]
- Di, B.; Baldassare. Classical Theory of Electromagnetism, 3rd ed.; WORLD SCIENTIFIC, Boston College: Newton, MA, USA, 2018; p. 720. [Google Scholar]



| Layer (Type) | Output Shape | Param |
|---|---|---|
| Conv2d-1 | [−1, 48, 55, 55] | 17472 |
| ReLU-2 | [−1, 48, 55, 55] | 0 |
| MaxPool2d-3 | [−1, 48, 27, 27] | 0 |
| Conv2d-4 | [−1, 128, 27, 27] | 153728 |
| ReLU-5 | [−1, 128, 27, 27] | 0 |
| MaxPool2d-6 | [−1, 128, 13, 13] | 0 |
| Conv2d-7 | [−1, 192, 13, 13] | 221376 |
| ReLU-8 | [−1, 192, 13, 13] | 0 |
| Conv2d-9 | [−1, 192, 13, 13] | 331968 |
| ReLU-10 | [−1, 192, 13, 13] | 0 |
| Conv2d-11 | [−1, 128, 13, 13] | 221312 |
| ReLU-12 | [−1, 128, 13, 13] | 0 |
| MaxPool2d-13 | [−1, 128, 6, 6] | 0 |
| Dropout-14 | [−1, 4608] | 0 |
| Linear-15 | [−1, 2048] | 9439232 |
| ReLU-16 | [−1, 2048] | 0 |
| Dropout-17 | [−1, 2048] | 0 |
| Linear-18 | [−1, 1024] | 2098176 |
| ReLU-19 | [−1, 1024] | 0 |
| Linear-20 | [−1, 2] | 2050 |
| Parameter Value | AlexNet_Pd | LeNet5_Pd | LSTM_Pd | MLP_Pd | |
|---|---|---|---|---|---|
| Learning rate | 0.952 | 0.894 | 0.724 | 0.589 | |
| 0.998 | 0.923 | 0.752 | 0.643 | ||
| 0.973 | 0.856 | 0.681 | 0.635 | ||
| Batch_size | 32 | 0.981 | 0.905 | 0.736 | 0.614 |
| 64 | 0.998 | 0.923 | 0.752 | 0.635 | |
| epoch | 50 | 0.984 | 0.916 | 0.732 | 0.635 |
| 100 | 0.992 | 0.923 | 0.752 | 0.602 | |
| 200 | 0.998 | 0.895 | 0.744 | 0.608 | |
| loss function | binary_crossentropy | 0.995 | 0.923 | 0.749 | 0.635 |
| categorical_crossentropy | 0.998 | 0.921 | 0.752 | 0.635 | |
| Optimization function | SGD | 0.856 | 0.828 | 0.724 | 0.596 |
| Adam | 0.998 | 0.923 | 0.752 | 0.635 | |
| Rmsprop | 0.926 | 0.854 | 0.738 | 0.614 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, S.; Wu, H.; Chen, W.; Li, D. Polarization Domain Spectrum Sensing Algorithm Based on AlexNet. Sensors 2022, 22, 8946. https://doi.org/10.3390/s22228946
Ren S, Wu H, Chen W, Li D. Polarization Domain Spectrum Sensing Algorithm Based on AlexNet. Sensors. 2022; 22(22):8946. https://doi.org/10.3390/s22228946
Chicago/Turabian StyleRen, Shiyu, Hailong Wu, Wantong Chen, and Dongxia Li. 2022. "Polarization Domain Spectrum Sensing Algorithm Based on AlexNet" Sensors 22, no. 22: 8946. https://doi.org/10.3390/s22228946
APA StyleRen, S., Wu, H., Chen, W., & Li, D. (2022). Polarization Domain Spectrum Sensing Algorithm Based on AlexNet. Sensors, 22(22), 8946. https://doi.org/10.3390/s22228946





