A Neural Network Based Approach to Inverse Kinematics Problem for General Six-Axis Robots
Abstract
:1. Introduction
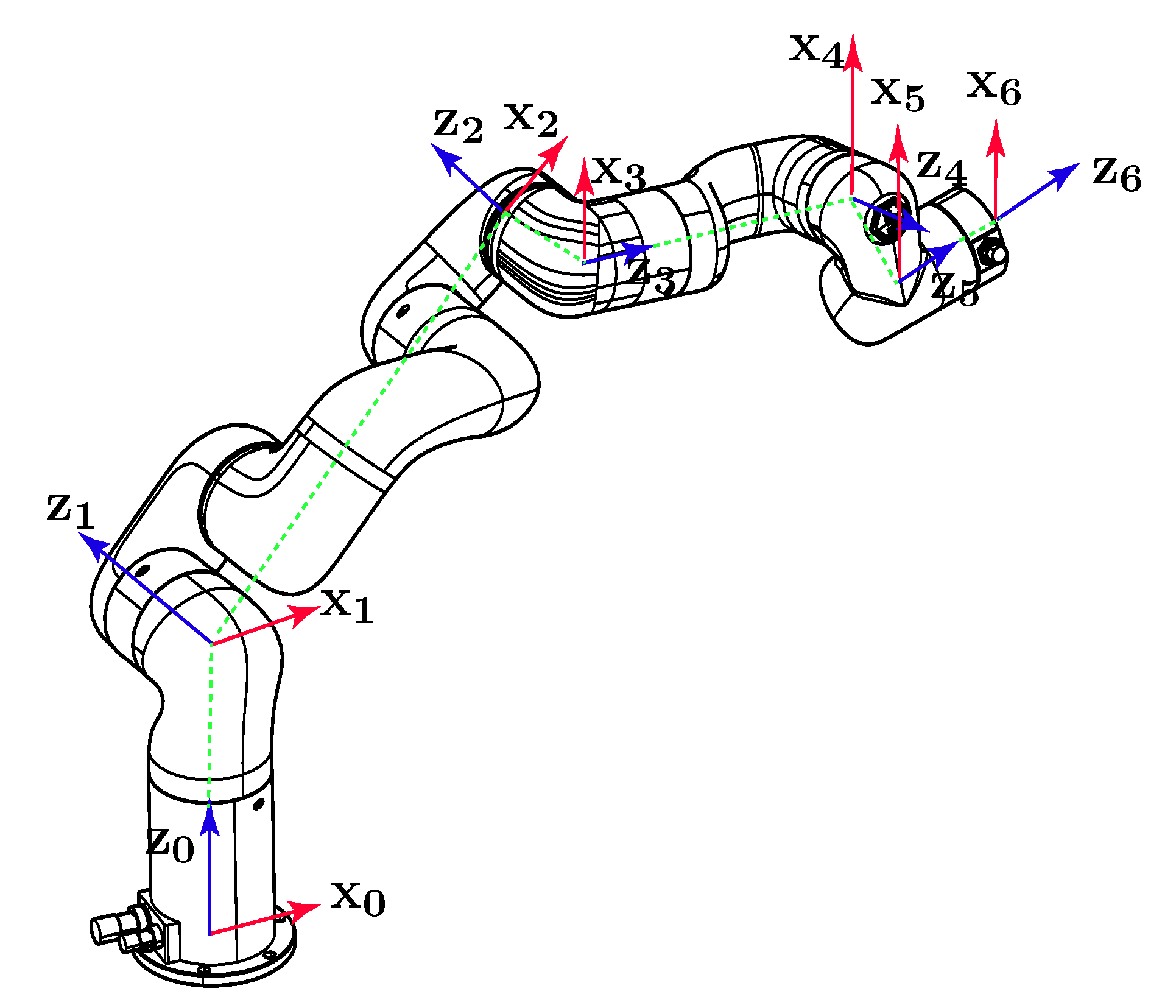
2. Robot Architecture and Kinematic Modeling
3. Neural Network with Error Minimization
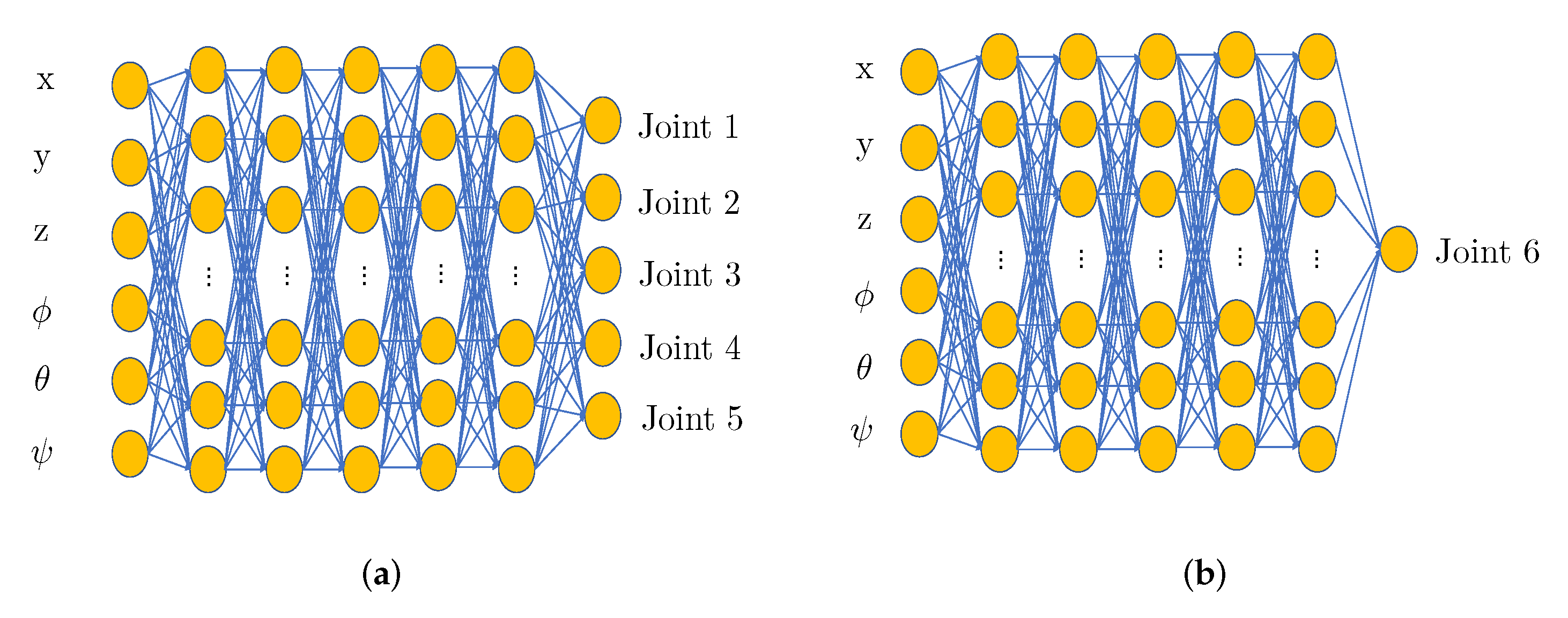
3.1. Neural Network
3.2. Numerical Error Minimization
4. Implementation
4.1. Obtain the Training Data
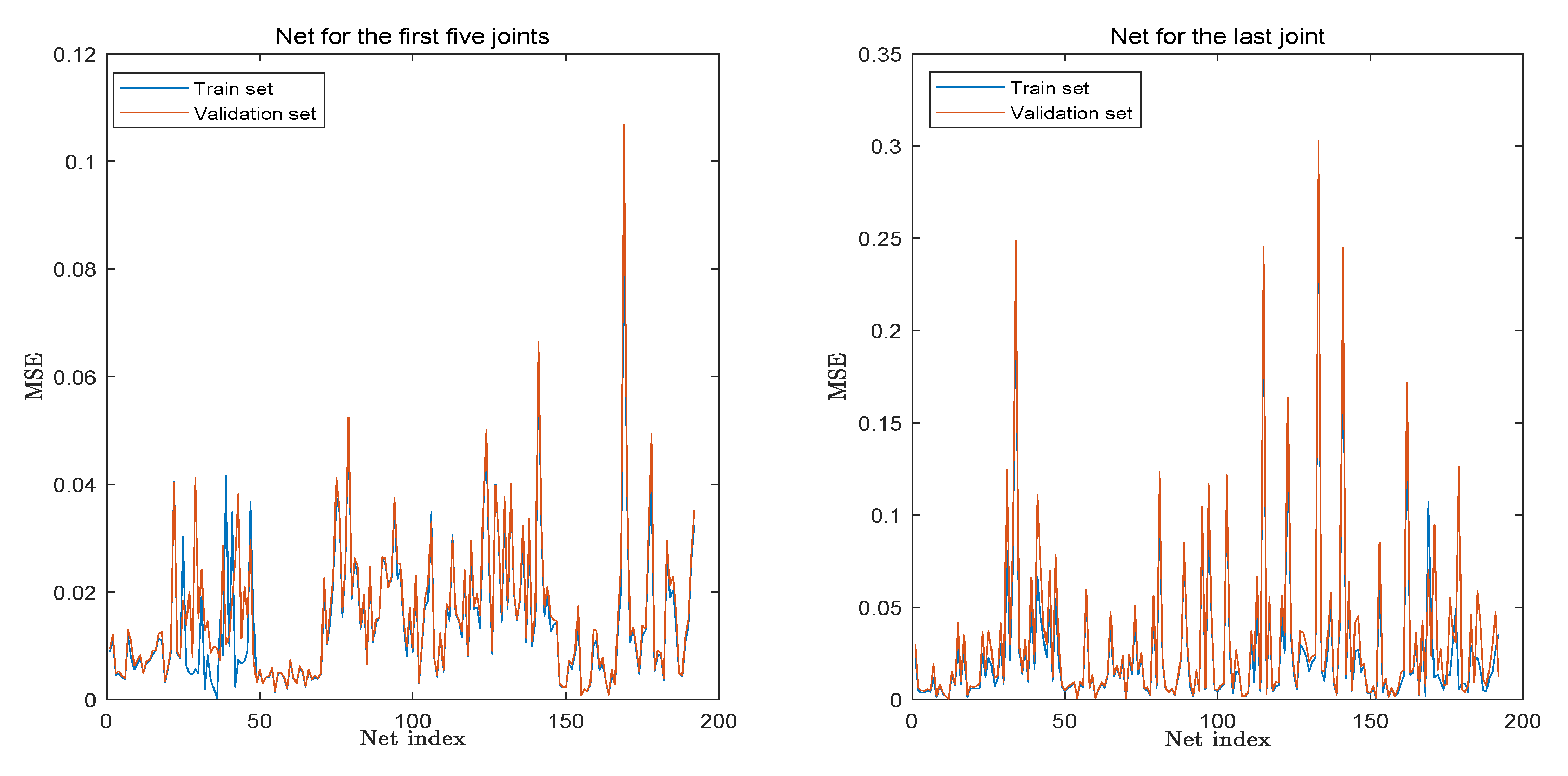
4.2. IKP Simplification and NN Training
- The maximum iteration epochs: 2000;
- The maximum amount of hidden layers: 5;
- The maximum amount of training data: 200,000.
- Amount of neurons per hidden layer: 20;
- Training method: L-M;
- Split of dataset: 70%, 15% and 15% for training set, cross validation set and test set, respectively.
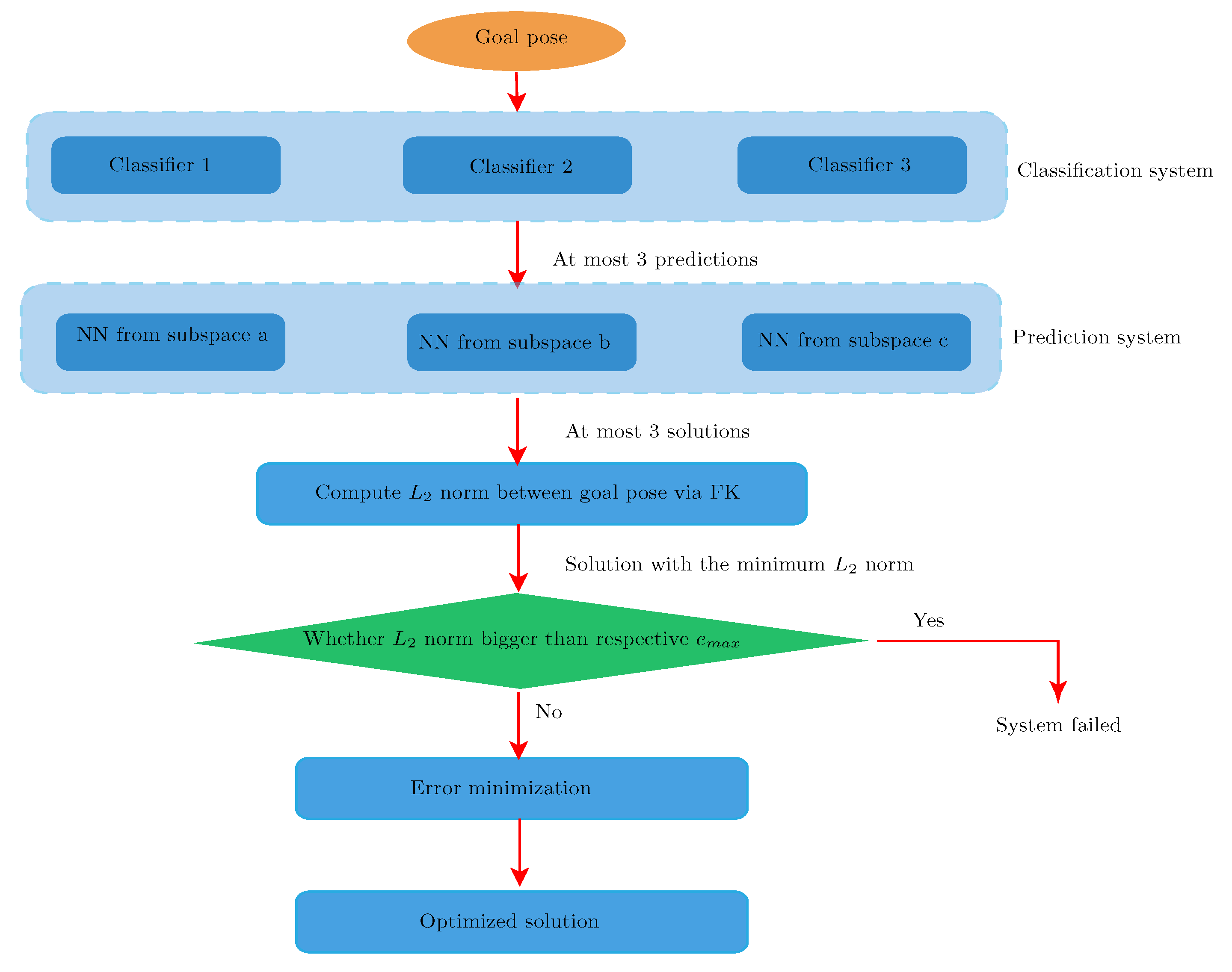
4.3. Selection of the Optimum Prediction
5. Results and Discussion
5.1. Simplification vs. Non-Simplification
5.2. Test with Random Pose
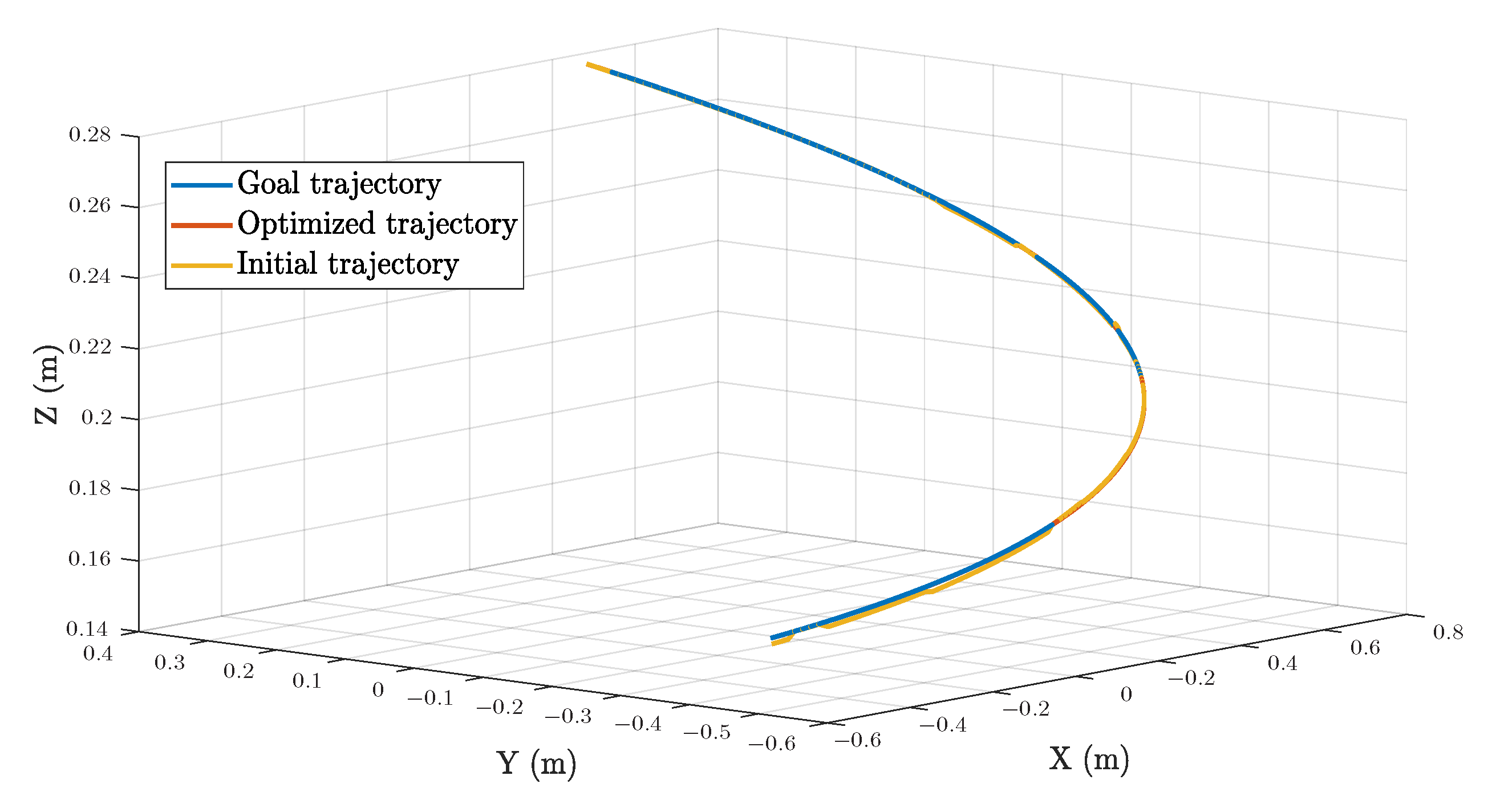
5.3. Trajectory Tracking
5.4. Efficiency and Singularity
- Failures due to the singularity problem.
- Failures due to joint limitation. The solution exceeds joint limitation.
- Success. The algorithm gives a desired answer.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koceska, N.; Koceski, S.; Beomonte Zobel, P.; Trajkovik, V.; Garcia, N. A telemedicine robot system for assisted and independent living. Sensors 2019, 19, 834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, S.; Zhou, M.; Luo, X. Modified primal-dual neural networks for motion control of redundant manipulators with dynamic rejection of harmonic noises. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 4791–4801. [Google Scholar] [CrossRef]
- Yang, G.; Nelson, B.J.; Murphy, R.R.; Choset, H.; Christensen, H.; Collins, S.H.; Dario, P.; Goldberg, K.; Ikuta, K.; Jacobstein, N.; et al. Combating COVID-19—The role of robotics in managing public health and infectious diseases. Sci. Robot. 2020, 5, eabb5589. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 3rd ed.; Pearson Education International: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Tsai, L.W.; Morgan, A.P. Solving the kinematics of the most general six-and five-degree-of-freedom manipulators by continuation methods. J. Mech. Transm. Autom. Des. 1985, 107, 189–200. [Google Scholar] [CrossRef]
- Pieper, D.L. The Kinematics of Manipulators under Computer Control. Ph.D. Thesis, Stanford University, Standford, CA, USA, 1968. [Google Scholar]
- Mavroidis, C.; Roth, B. Structural parameters which reduce the number of manipulator configurations. J. Mech. Des. 1994, 116, 3–10. [Google Scholar] [CrossRef]
- Xiao, F.; Li, G.; Jiang, D.; Xie, Y.; Yun, J.; Liu, Y.; Huang, L.; Fang, Z. An effective and unified method to derive the inverse kinematics formulas of general six-DOF manipulator with simple geometry. Mech. Mach. Theory 2021, 159, 104265. [Google Scholar] [CrossRef]
- Leoro, J.; Hsiao, T.; Betancourt, C. A New Geometric Subproblem to Extend Solvability of Inverse Kinematics Based on Screw Theory for 6R Robot Manipulators. Int. J. Control Autom. Syst. 2021, 19, 562–573. [Google Scholar] [CrossRef]
- Raghavan, M.; Roth, B. Inverse kinematics of the general 6R manipulator and related linkages. Trans. ASME 1993, 115, 502–508. [Google Scholar] [CrossRef]
- Manocha, D.; Canny, J.F. Efficient inverse kinematics for general 6R manipulators. IEEE Trans. Robot. Autom. 1994, 10, 648–657. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Yu, H.; Shen, N.; Zhong, Z.; Lu, Y.; Fan, J. A novel inverse kinematics method for 6-DOF robots with non-spherical wrist. Mech. Mach. Theory 2021, 157, 104180. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, C.; Wang, X.; Zhang, P.; Li, P.; Liu, H. Inverse kinematics of a 7-DOF spraying robot with 4R 3-DOF non-spherical wrist. J. Intell. Robot. Syst. 2021, 101, 68. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, J.; Liu, H. Solving the Inverse Kinematics Problem of Multiple Redundant Manipulators with Collision Avoidance in Dynamic Environments. J. Intell. Robot. Syst. 2021, 101, 30. [Google Scholar] [CrossRef]
- Wu, H.; Yu, J.; Pan, J.; Li, G.; Pei, X. CRRIK: A Fast Heuristic Algorithm for the Inverse Kinematics of Continuum Robot. J. Intell. Robot. Syst. 2022, 105, 55. [Google Scholar] [CrossRef]
- Karlik, B.; Aydin, S. An improved approach to the solution of inverse kinematics problems for robot manipulators. Eng. Appl. Artif. Intell. 2000, 13, 159–164. [Google Scholar] [CrossRef]
- Zhang, P.Y.; Lü, T.S.; Song, L.B. RBF networks-based inverse kinematics of 6R manipulator. Int. J. Adv. Manuf. Technol. 2005, 26, 144–147. [Google Scholar] [CrossRef]
- Köker, R. Reliability-based approach to the inverse kinematics solution of robots using Elman’s networks. Eng. Appl. Artif. Intell. 2005, 18, 685–693. [Google Scholar] [CrossRef]
- Chiddarwar, S.S.; Ramesh Babu, N. Comparison of RBF and MLP neural networks to solve inverse kinematic problem for 6R serial robot by a fusion approach. Eng. Appl. Artif. Intell. 2010, 23, 1083–1092. [Google Scholar] [CrossRef]
- Hasan, A.T.; Ismail, N.; Hamouda, A.M.S.; Aris, I.; Marhaban, M.H.; Al-Assadi, H. Artificial neural network-based kinematics Jacobian solution for serial manipulator passing through singular configurations. Adv. Eng. Softw. 2010, 41, 359–367. [Google Scholar] [CrossRef] [Green Version]
- KöKer, R. A genetic algorithm approach to a neural-network-based inverse kinematics solution of robotic manipulators based on error minimization. Inf. Sci. 2013, 222, 528–543. [Google Scholar] [CrossRef]
- Koker, R.; Cakar, T.o.k. A neuro-genetic-simulated annealing approach to the inverse kinematics solution of robots: A simulation based study. Eng. Comput. 2016, 32, 553–565. [Google Scholar] [CrossRef]
- Feng, Y.; Yao-nan, W.; Yi-min, Y. Inverse kinematics solution for robot manipulator based on neural network under joint subspace. Int. J. Comput. Commun. Control 2014, 7, 459–472. [Google Scholar] [CrossRef] [Green Version]
- Almusawi, A.R.J.; Dülger, L.C.; Kapucu, S. A New Artificial Neural Network Approach in Solving Inverse Kinematics of Robotic Arm (Denso VP6242). Comput. Intell. Neurosci. 2016, 2016, 5720163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sherbiny, A.; Elhosseini, M.A.; Haikal, A.Y. A comparative study of soft computing methods to solve inverse kinematics problem. Ain Shams Eng. J. 2018, 9, 2535–2548. [Google Scholar] [CrossRef]
- Ren, H.; Ben-Tzvi, P. Learning inverse kinematics and dynamics of a robotic manipulator using generative adversarial networks. Robot. Auton. Syst. 2020, 124, 103386. [Google Scholar] [CrossRef]
- Šegota, S.B.; Anđelić, N.; Mrzljak, V.; Lorencin, I.; Kuric, I.; Car, Z. Utilization of multilayer perceptron for determining the inverse kinematics of an industrial robotic manipulator. Int. J. Adv. Robot. Syst. 2021, 18, 1–11. [Google Scholar] [CrossRef]
- Jiménez-López, E.; Servín de la Mora-Pulido, D.; Reyes-Ávila, L.A.; Servín de la Mora-Pulido, R.; Melendez-Campos, J.; López-Martínez, A.A. Modeling of Inverse Kinematic of 3-DoF Robot, Using Unit Quaternions and Artificial Neural Network. Robotica 2021, 39, 1230–1250. [Google Scholar] [CrossRef]
- Jiang, G.; Luo, M.; Bai, K.; Chen, S. A precise positioning method for a puncture robot based on a PSO-optimized BP neural network algorithm. Appl. Sci. 2017, 7, 969. [Google Scholar] [CrossRef]
- Bai, Y.; Luo, M.; Pang, F. An algorithm for solving robot inverse kinematics based on FOA optimized BP neural network. Appl. Sci. 2021, 11, 7129. [Google Scholar] [CrossRef]
- Pinkus, A. Approximation theory of the MLP model in neural networks. Acta Numer. 1999, 8, 143–195. [Google Scholar] [CrossRef]
- Mukherjee, I.; Routroy, S. Comparing the performance of neural networks developed by using Levenberg–Marquardt and Quasi-Newton with the gradient descent algorithm for modelling a multiple response grinding process. Expert Syst. Appl. 2012, 39, 2397–2407. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Cambridge, MA, USA, 2006. [Google Scholar]
- Diederik, P.; Kingma, J.L.B. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015.
- Csiszar, A.; Eilers, J.; Verl, A. On solving the inverse kinematics problem using neural networks. In Proceedings of the 2017 24th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Auckland, New Zealand, 21–23 November 2017; pp. 1–6. [Google Scholar]
- Demby’s, J.; Gao, Y.; DeSouza, G.N. A study on solving the inverse kinematics of serial robots using artificial neural network and fuzzy neural network. In Proceedings of the 2019 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), New Orleans, LA, USA, 23–26 June 2019; pp. 1–6. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Lopez-Franco, C.; Hernandez-Barragan, J.; Alanis, A.Y.; Arana-Daniel, N. A soft computing approach for inverse kinematics of robot manipulators. Eng. Appl. Artif. Intell. 2018, 74, 104–120. [Google Scholar] [CrossRef]







| Reference | Robot Model | Analytical Solution | Accuracy | |
|---|---|---|---|---|
| ANN | [16,20,22,23,24,25,27,28,30] | Low-DoF or 6-DoF decoupled | Yes | low to extremely high |
| RNN | [18,21] | 6-DoF decoupled | Yes | fair to extremely high |
| RFB | [17,19] | 6-DoF decoupled | Yes | fair to high |
| GAN | [26] | Low-DoF | Yes | high |
| Our work | 6-DoF general robot | No | extremely high |
| Joint Number | a (mm) | (°) | d (mm) | |
|---|---|---|---|---|
| 1 | 0 | 267 | ||
| 2 | 289.5 | 0 | 0 | |
| 3 | 77.5 | 0 | ||
| 4 | 0 | 90 | 343.5 | |
| 5 | 76 | 0 | ||
| 6 | 0 | 0 | 97 |
| Joint Number | Goal Range | After Dividing |
|---|---|---|
| 1 | (0, 360°) | (0, 180°) (180, 360°) |
| 2 | (0, 90°) | (0, 60°) (60, 90°) |
| 3 | (−180, −90°) | (−180, −120°) (−120, −90°) |
| 4 | (0, 180°) | (0, 60°) (60, 120°) (120, 180°) |
| 5 | (0, 180°) | (0, 45°) (45, 90°) (90, 120°) (120, 180°) |
| 6 | (0, 360°) | (0, 180°) (180, 360°) |
| No. | 1 | 2 | 3 |
| HL No. | 6 | 20 | 30 |
| Hidden unit | 35 | 35 | 35 |
| AF in HL | Relu | Relu | Relu |
| AF in OL | softmax | softmax | softmax |
| Trainset | 576,000 | 960,000 | 768,000 |
| Optimizor | Adams | Adams | Adams |
| Features | Simple MLP | MLP with residual block | MLP with residual block and batch normalization |
| NN 1 | NN 2 | NN 3 | Overall Classification System | |
|---|---|---|---|---|
| Train set | 94.50% | 97.87% | 98.53% | N/A |
| Test set | 93.60% | 95.40% | 96.25% | 99.50% |
| No | x (m) | y (m) | z (m) | (rad) | (rad) | (rad) | |
|---|---|---|---|---|---|---|---|
| Goal Pose | 1 | −0.64142 | 0.22652 | 0.22762 | −0.10588 | −2.08249 | 2.34062 |
| 2 | 0.45064 | 0.15015 | 0.63200 | −2.54416 | −0.76447 | −2.30342 | |
| 3 | 0.19978 | 0.55744 | 0.51288 | −1.06619 | −1.83045 | 2.78188 | |
| 4 | 0.33833 | 0.42766 | 0.28287 | 0.40171 | −3.01724 | −0.99056 | |
| 5 | −0.24216 | 0.39147 | −0.17398 | 1.78176 | −2.12424 | 2.17019 | |
| No | |||||||
| Exact Solution | 1 | 160.46907 | 37.91946 | −135.87082 | 18.62891 | 39.46047 | 112.83264 |
| 2 | 24.29447 | 11.89334 | −153.69625 | 53.15470 | 8.58257 | 182.38461 | |
| 3 | 64.38381 | 14.31783 | −145.74087 | 54.39600 | 75.48167 | 120.27973 | |
| 4 | 50.64234 | 30.28887 | −156.69763 | 4.48408 | 132.64058 | 153.73039 | |
| 5 | 117.71272 | 57.93731 | −121.66049 | 15.36286 | 120.12755 | 320.55779 | |
| Initial Solution | 1 | 160.44294 | 37.90550 | −135.93878 | 18.59329 | 39.40203 | 112.92553 |
| 2 | 24.26964 | 11.93607 | −153.77572 | 53.15427 | 8.66457 | 182.47650 | |
| 3 | 64.36072 | 14.37610 | −145.80470 | 54.32014 | 75.51120 | 120.29442 | |
| 4 | 50.57437 | 30.29154 | −156.75669 | 4.56464 | 132.62676 | 153.75462 | |
| 5 | 117.75096 | 58.00550 | −121.67093 | 15.17564 | 120.30039 | 320.64783 | |
| Optimized Solution | 1 | 160.46905 | 37.91945 | −135.87089 | 18.62888 | 39.46041 | 112.83273 |
| 2 | 24.29433 | 11.89359 | −153.69672 | 53.15470 | 8.58306 | 182.38515 | |
| 3 | 64.38376 | 14.31797 | −145.74103 | 54.39582 | 75.48174 | 120.27977 | |
| 4 | 50.64217 | 30.28888 | −156.69777 | 4.48428 | 132.64055 | 153.73045 | |
| 5 | 117.71276 | 57.93739 | −121.66051 | 15.36263 | 120.12776 | 320.55790 |
| (m) | (m) | (m) | |
| mean absolute error | 0.0004 | 0.0005 | 0.0005 |
| minimum absolute error | 6 × | 3.6 × | 1.9 × |
| maximum absolute error | 0.014059 | 0.007147 | 0.007430 |
| (°) | (°) | (°) | |
| mean absolute error | 0.1344 | 0.0812 | 0.1687 |
| minimum absolute error | 6.241 × | 1.8 × | 3.946 × |
| maximum absolute error | 4.5682 | 2.0621 | 4.3986 |
| (m) | (m) | (m) | |
| mean absolute error | 5.461 | 5.462 | 5.884 |
| min absolute error | 1.612 | 5.875 | 3.483 |
| max absolute error | 9.998 | 9.994 | 9.998 |
| (°) | (°) | (°) | |
| mean absolute error | 1.868 | 1.233 | 2.572 |
| min absolute error | 1.209 | 2.025 | 1.059 |
| max absolute error | 5.7 | 2.1 | 6.3 |
| Sample No. | True Label | Classification System Output | Initial Solution Error ( Norm) | Criterion () |
|---|---|---|---|---|
| 73 | 3 | 11 | 9.6 × | 1.67 × |
| 345 | 14 | 22 | 1.005 × | 1.36 × |
| 372 | 15 | 111 | 1.318 × | 6.87 × |
| 381 | 16 | 8 and 15 | 3.3 × | 1.26 × |
| 610 | 25 | 73 and 121 | 4.07 × | 1.18 × |
| 1723 | 69 | 70 | 2.5 × | 8.15 × |
| 1836 | 74 | 82 | 2.58 × | 8.84 × |
| 1849 | 74 | 76 | 4.92 × | 9.45 × |
| 2112 | 85 | 87 | 3.7 × | 3.65 × |
| 2200 | 88 | 86 | 2.153 × | 6.03 × |
| 2480 | 100 | 148 | 2.07 × | 2.99 × |
| 2649 | 106 | 105 | 1 × | 5.44 × |
| 3019 | 121 | 122 | 1.3 × | 9.81 × |
| 3156 | 127 | 31 | 7 × | 4.65 × |
| 3233 | 130 | 178 | 1.347 × | 1.43 × |
| 3235 | 130 | 122 | 1.3 × | 9.81 × |
| 3246 | 130 | 122 | 4.801 × | 9.81 × |
| 3333 | 134 | 182 and 190 | 4.4 × | 1.28 × |
| 3352 | 135 | 143 | 1.007 × | 7.36 × |
| 3478 | 140 | 139 | 1.58 × | 5.41 × |
| 3514 | 141 | 189 | 4 × | 1.44 × |
| 3536 | 142 | 190 | 5.13 × | 6.36 × |
| 4052 | 163 | 67 | 2.6 × | 1.30 × |
| 4403 | 177 | 179 | 6.4 × | 9.00 × |
| Error for Position | Error for Orientation | Time on Initial Solution | Time on Optimization | Total | |
|---|---|---|---|---|---|
| NR | 0.001 mm (max) | 0.01° (max) | 0.0159 s | 0.0059 s | 0.0218 s |
| GA | 0.0037 mm (max) | N/A | N/A | N/A | 0.28 s |
| EF | 0.0054 mm (mean) | 1.1154° (mean) | 0.0075 s | 0.2775 s | 0.285 s |
| Total Steps | Run Time (s) | Time/Solution (s) | |||
|---|---|---|---|---|---|
| Test 01 | 53 | 18927 | 23780 | 481.52 | 0.1003 |
| Test 02 | 74 | 18293 | 23167 | 475.345 | 0.099 |
| Test 03 | 79 | 18423 | 23302 | 476.243 | 0.0992 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Zou, T.; Jiang, X. A Neural Network Based Approach to Inverse Kinematics Problem for General Six-Axis Robots. Sensors 2022, 22, 8909. https://doi.org/10.3390/s22228909
Lu J, Zou T, Jiang X. A Neural Network Based Approach to Inverse Kinematics Problem for General Six-Axis Robots. Sensors. 2022; 22(22):8909. https://doi.org/10.3390/s22228909
Chicago/Turabian StyleLu, Jiaoyang, Ting Zou, and Xianta Jiang. 2022. "A Neural Network Based Approach to Inverse Kinematics Problem for General Six-Axis Robots" Sensors 22, no. 22: 8909. https://doi.org/10.3390/s22228909
APA StyleLu, J., Zou, T., & Jiang, X. (2022). A Neural Network Based Approach to Inverse Kinematics Problem for General Six-Axis Robots. Sensors, 22(22), 8909. https://doi.org/10.3390/s22228909








