Design of Fractional Order Odd-Harmonics Repetitive Controller for Discrete-Time Linear Systems with Experimental Validations
Abstract
:1. Introduction
- An internal model with half-cycle delay representing odd-harmonic periodic signals is used to provide faster transient response.
- An optimization-based design methodology is developed to obtain the fractional order stabilizing controller.
- The fractional order stabilizing controller is realizable since the fractional part of the controller is approximated by using a stable and causal IIR filter.
2. Problem Statement and Preliminaries
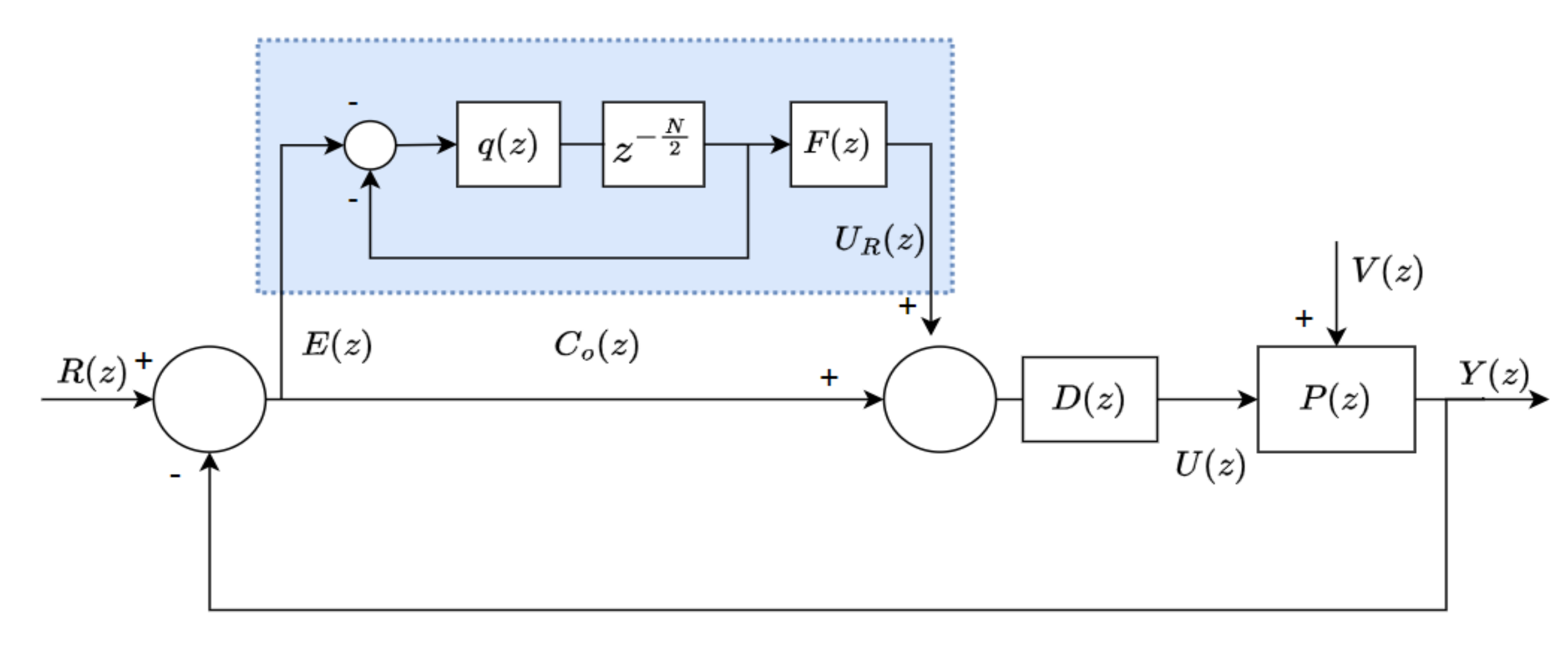
2.1. Repetitive Control Problem
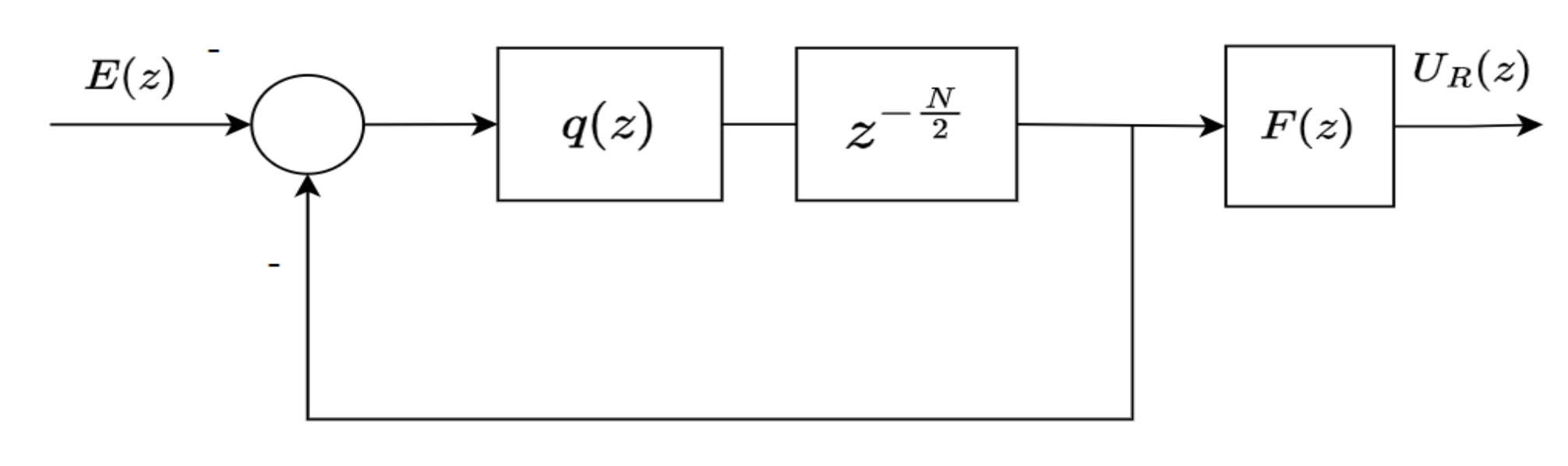
2.2. General Repetitive Controller
3. Proposed Method
3.1. Controller Structure
3.2. Stability Analysis
- –
- (C1): is stable.
- –
- (C2): is stable.
- –
- (C3): , which also can be expressed as
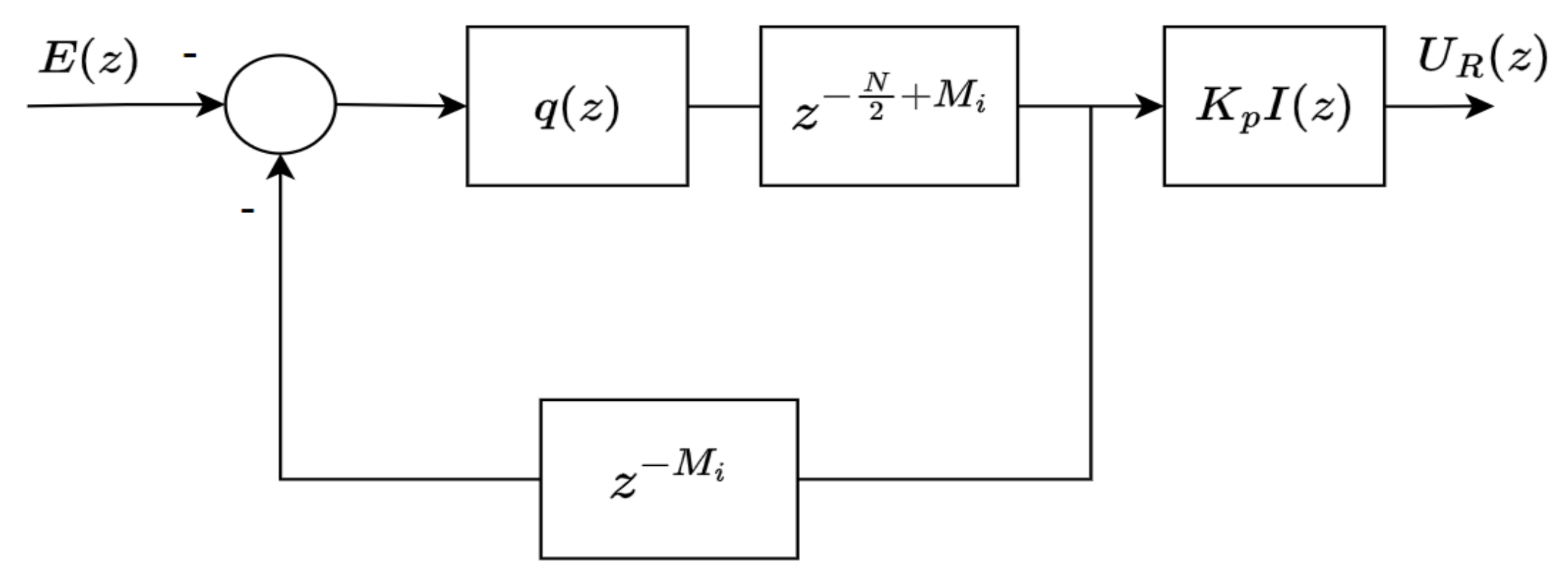
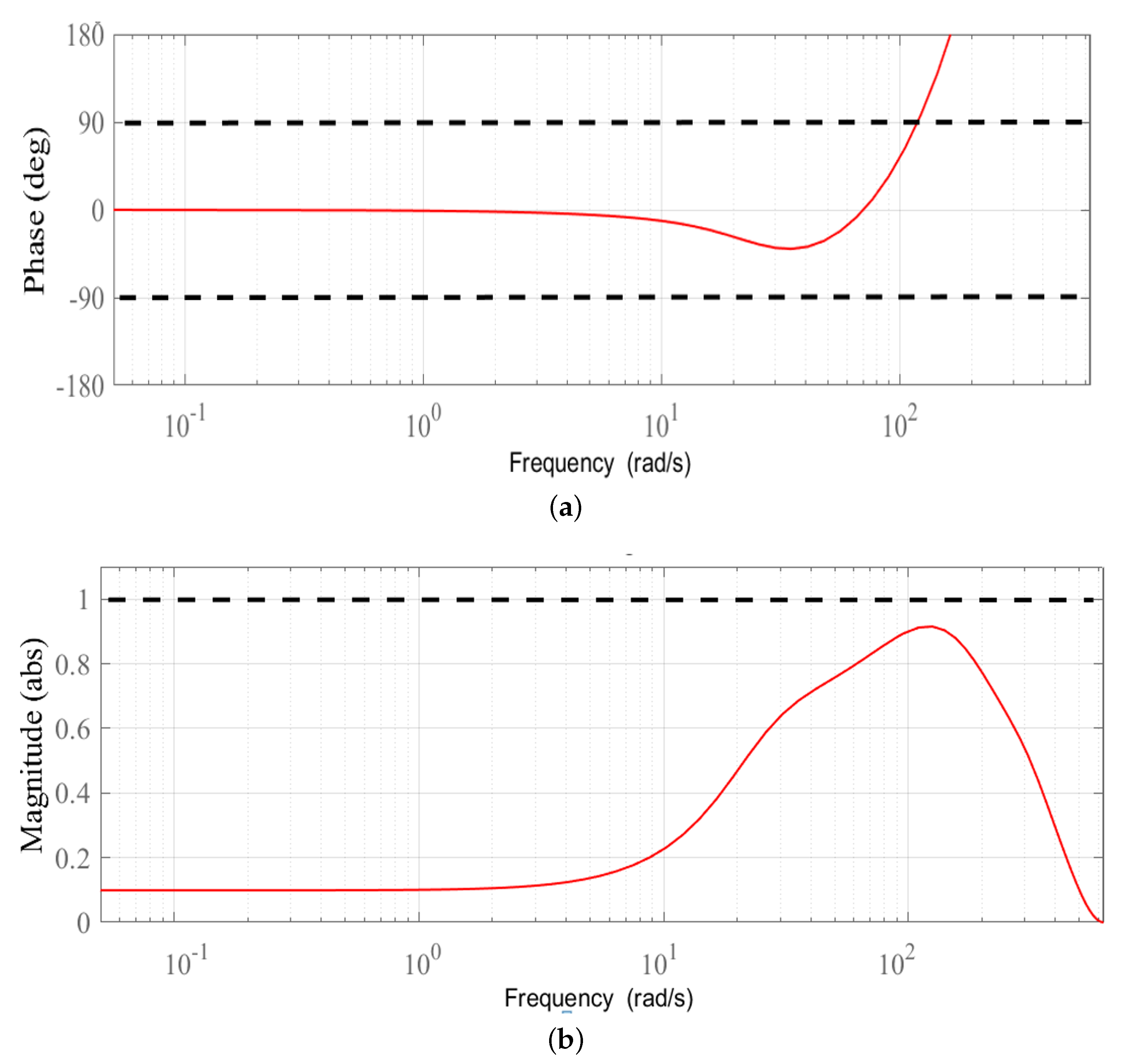
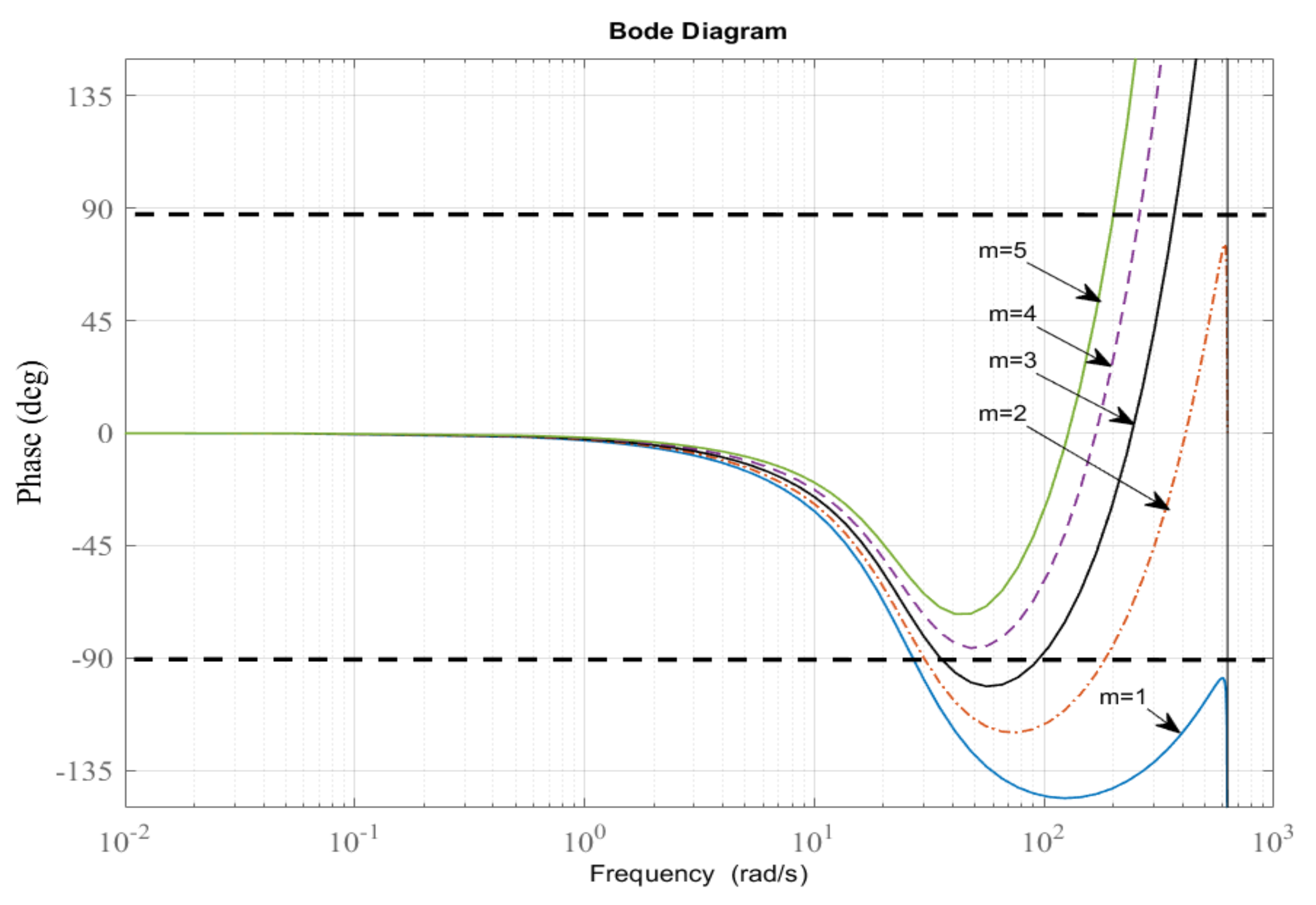
3.3. Fractional Order Stabilizing Controller
3.4. Realization of the Controller
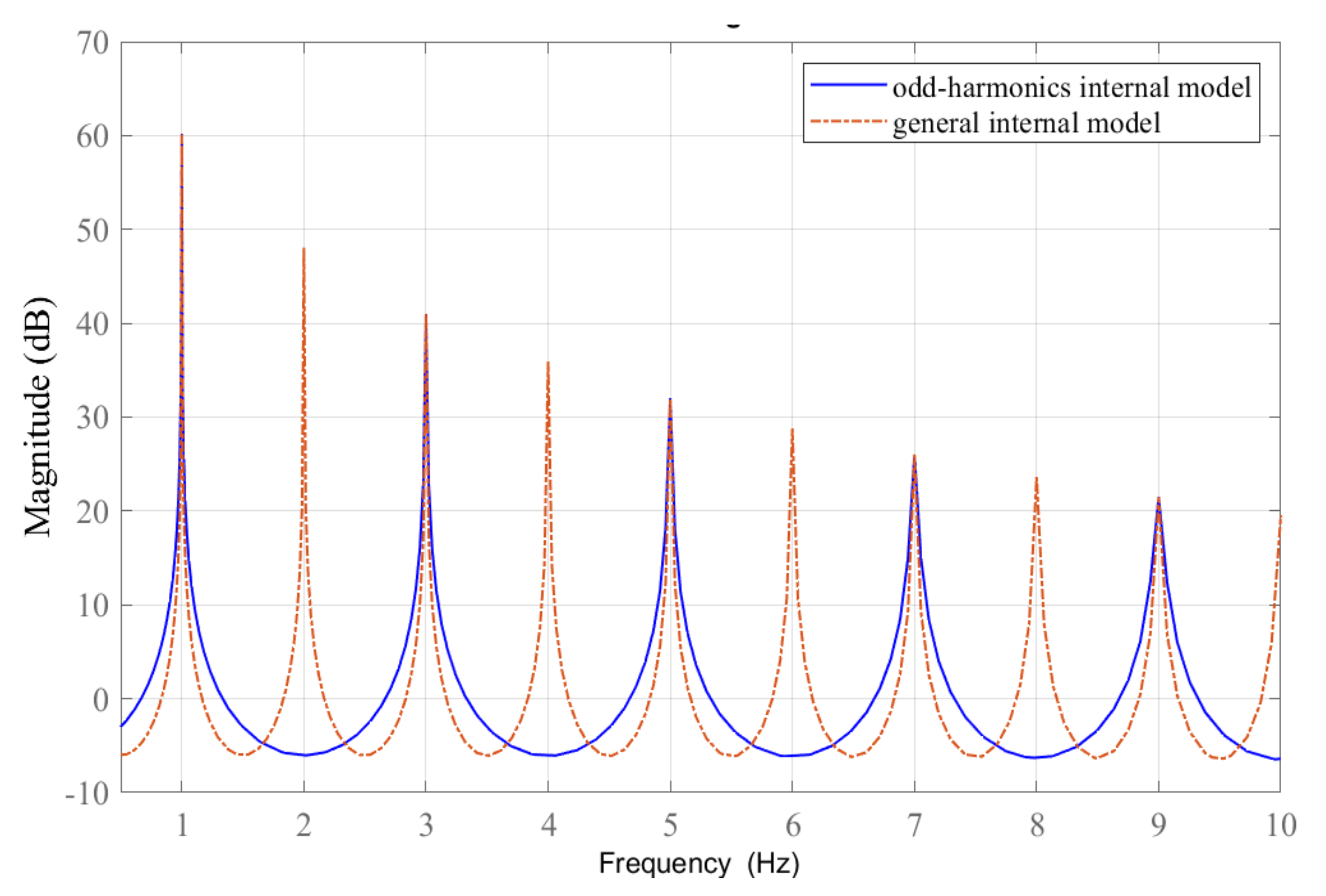
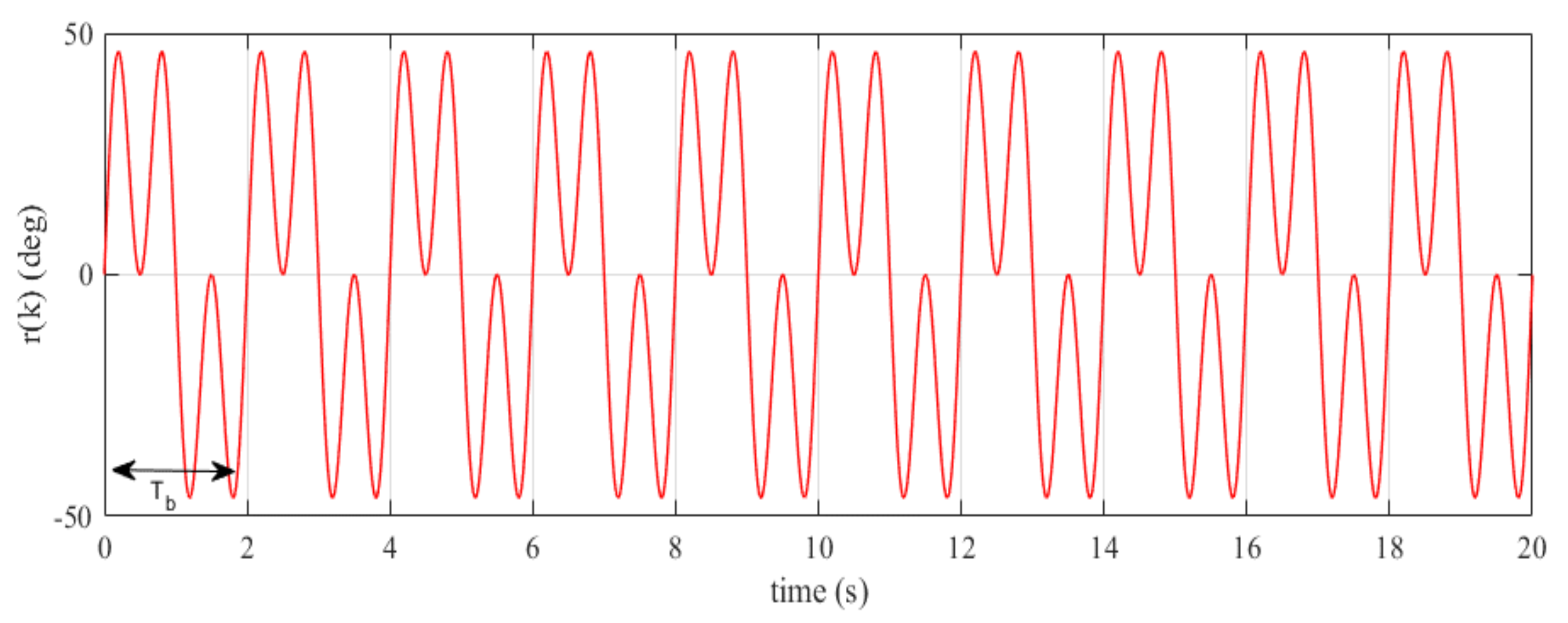
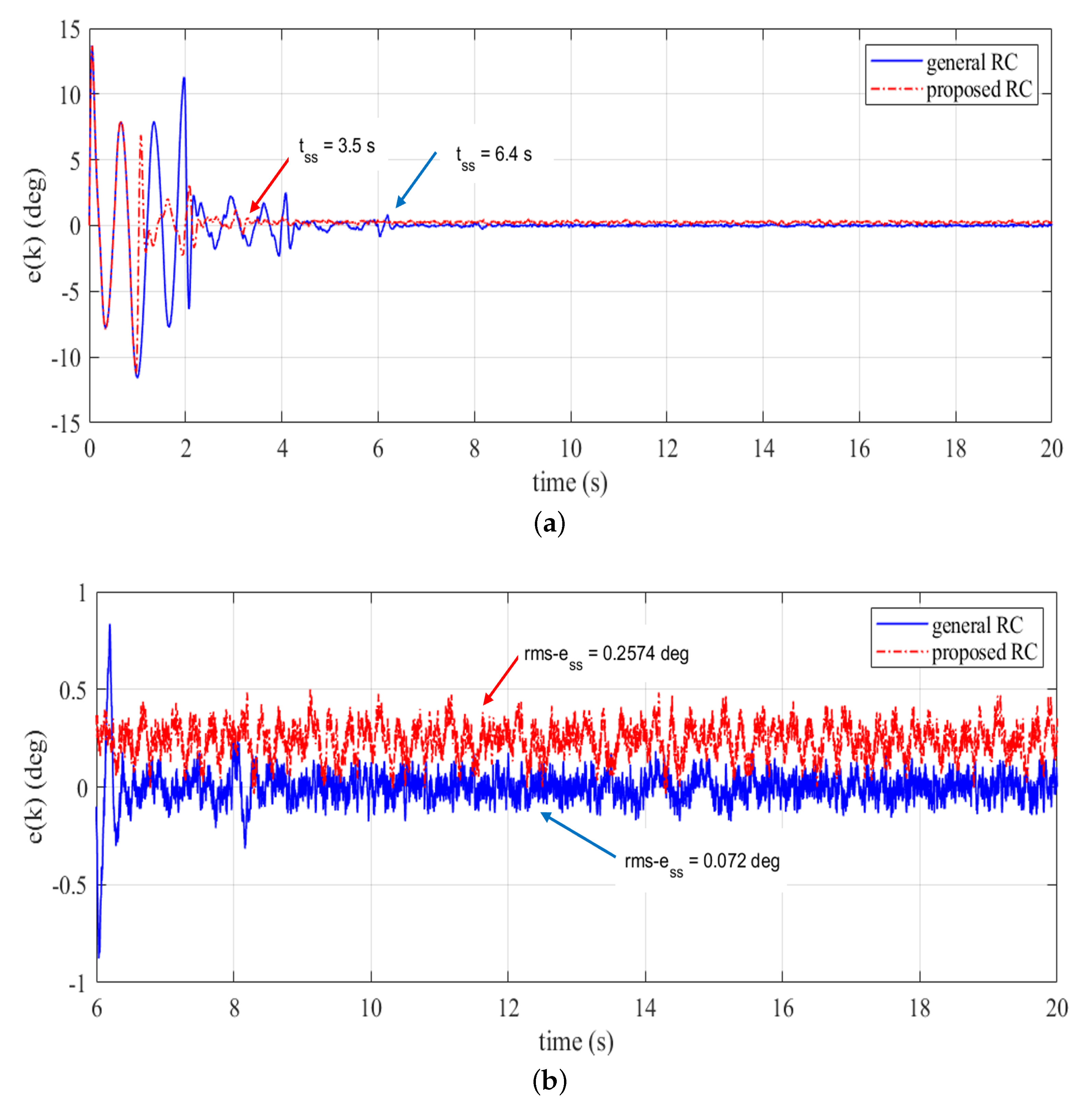
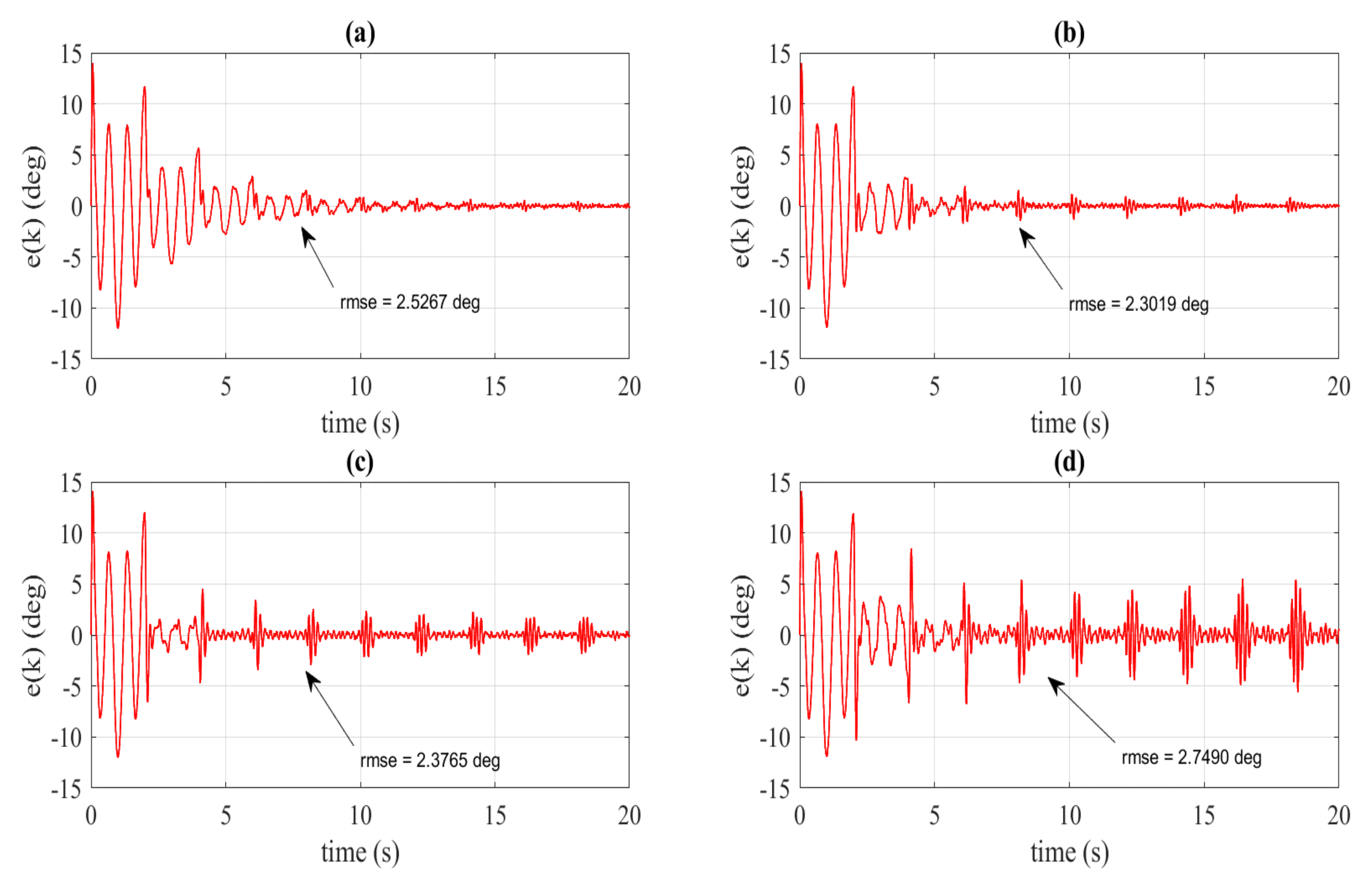
4. Simulation Results
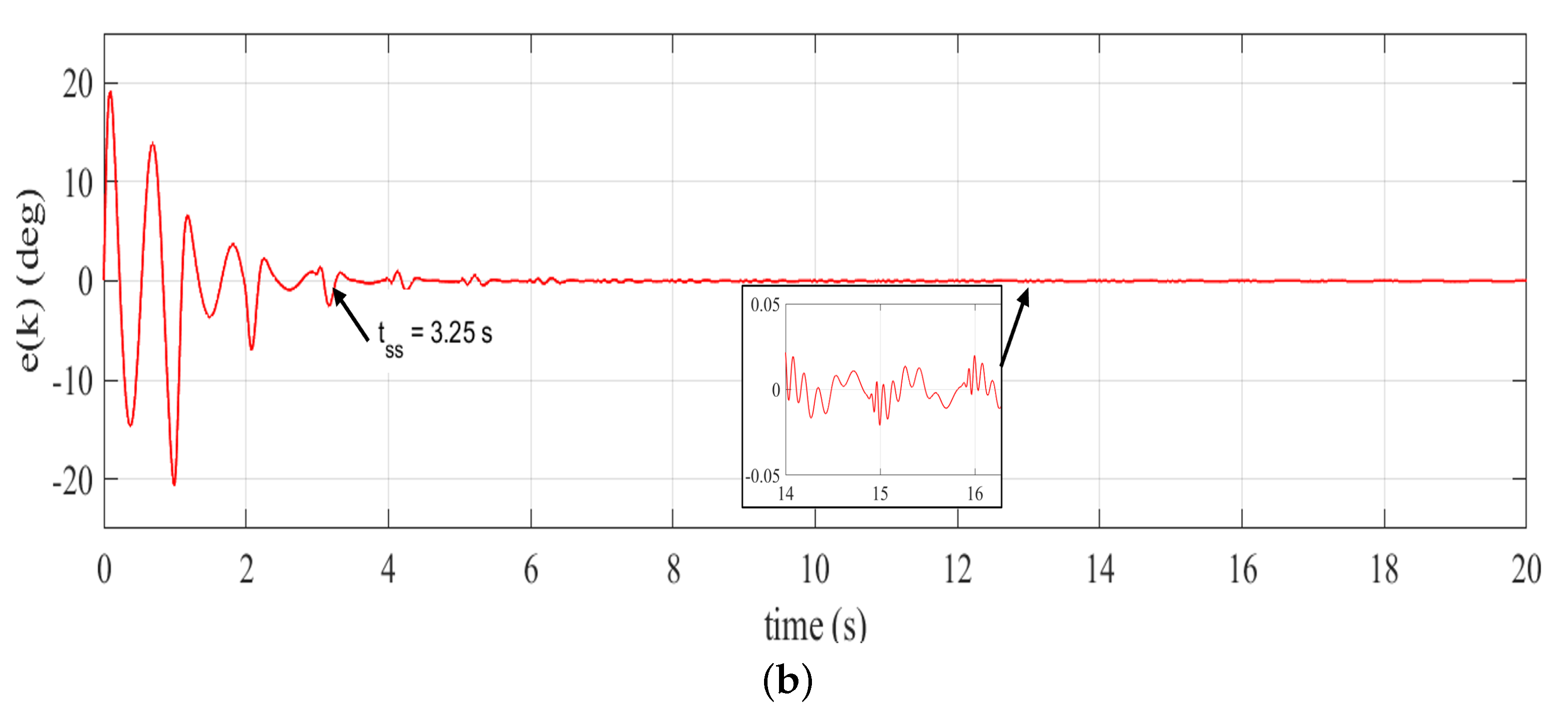
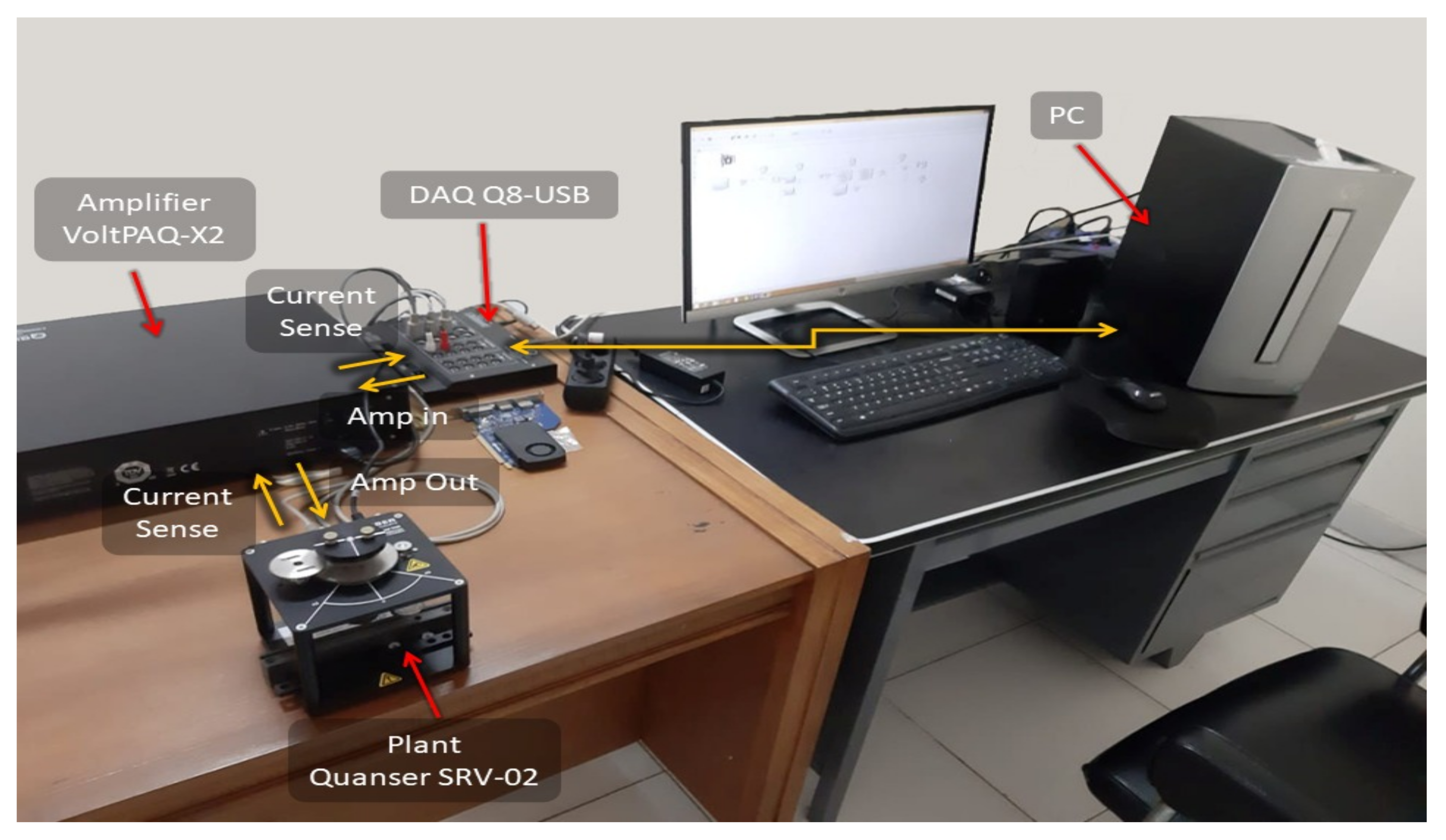
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Inoue, T.; Nakano, M.; Iwai, S. High accuracy control of a proton synchrotron magnet power supply. In Proceedings of the 8th world congress IFAC, Kyoto, Japan, 24–28 August 1981; pp. 3137–3142. [Google Scholar]
- Moore, K.L.; Chen, Y. Iterative Learning Control Approach to a Diffusion Control Problem in an Irrigation Application. In Proceedings of the International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 1329–1334. [Google Scholar]
- Dai, X.; Li, G.; Zhou, X. Iterative Learning Control of Dam-river Channel Irrigation Systems. J. Guangxi Norm. Univ. Nat. Sci. Ed. 2018, 36, 53–60. [Google Scholar]
- Yao, Q.; Jahanshahi, H.; Bekiros, S.; Mihalache, S.F.; Alotaibi, N.D. Gain-Scheduled Sliding-Mode-Type Iterative Learning Control Design for Mechanical Systems. Mathematics 2022, 10, 3005. [Google Scholar] [CrossRef]
- Huo, X.; Wang, M.; Liu, K.Z.; Tong, X. Attenuation of position-dependent periodic disturbance for rotary machines by improved spatial repetitive control with frequency alignment. IEEE/ASME Trans. Mechatronics 2020, 25, 339–348. [Google Scholar] [CrossRef]
- Ma, W.; Ouyang, S.; Zhang, J.; Xu, W. Control strategy based on H∞ repetitive controller with active damping for islanded microgrid. IEEE Access 2019, 162157–162168. [Google Scholar] [CrossRef]
- Coral-Enriquez, H.; Cortes-Romero, J.; Dorado-Rojas, S.A. Rejection of varying-frequency periodic load disturbances in wind turbines through active disturbance rejection-based control. Renew. Energy 2019, 141, 217–235. [Google Scholar] [CrossRef]
- Pandove, G.; Singh, M. Robust Repetitive Control Design for a Three-Phase Four Wire Shunt Active Power Filter. IEEE Trans. Ind. Inform. 2019, 15, 2810–2818. [Google Scholar] [CrossRef]
- Zheng, L.; Jiang, F.; Song, J.; Gao, Y.; Tian, M. A Discrete-Time Repetitive Sliding Mode Control for Voltage Source Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1553–1566. [Google Scholar] [CrossRef]
- Page, A.P.; Freeman, C.T. Point-to-point repetitive control of functional electrical stimulation for drop-foot. Control Eng. Pract. 2020, 96, 1–10. [Google Scholar] [CrossRef]
- Ott, L.; Nageotte, F.; Zanne, P.; de Mathelin, M. Simultaneous physiological motion cancellation and depth adaptation in flexible endoscopy. IEEE Trans. Biomed. Eng. 2009, 56, 2322–2326. [Google Scholar]
- Francis, B.A.; Wonham, W.M. The internal model principle for linear multivariable regulators. Appl. Math. Optim. 1975, 2, 170–194. [Google Scholar] [CrossRef]
- Han, B.; Jo, S.-W.; Kim, M.; Dung, N.A.; Lai, J.-S. Improved Odd-Harmonic Repetitive Control Scheme for Ćuk-Derived Inverter. IEEE Trans. Power Electron. 2022, 37, 1496–1508. [Google Scholar] [CrossRef]
- Zhou, K.; Low, K.-S.; Wang, D.; Luo, F.-L.; Zhang, B.; Wang, Y. Zero-phase odd-harmonic repetitive controller for a single-phase PWM inverter. IEEE Trans. Power Electron. 2006, 21, 193–201. [Google Scholar] [CrossRef]
- Cui, P.; Xu, H.; Liu, Z.; Han, B.; Li, H. Harmonic Current Suppression of Magnetically Suspended Rotor System via Odd-Harmonic Fractional RC. IEEE Sens. J. 2019, 19, 4812–4819. [Google Scholar] [CrossRef]
- Cui, P.; Zhang, G. Modified Repetitive Control for Odd-Harmonic Current Suppression in Magnetically Suspended Rotor Systems. IEEE Trans. Ind. Electron. 2019, 66, 8008–8018. [Google Scholar] [CrossRef]
- Li, L.; Aphale, S.S.; Zhu, L. Enhanced Odd-Harmonic Repetitive Control of Nanopositioning Stages Using Spectrum-Selection Filtering Scheme for High-Speed Raster Scanning. IEEE Trans. Autom. Sci. Eng. 2021, 18, 1087–1096. [Google Scholar] [CrossRef]
- Jeng, J.-T.; Hsu, T.-Y.; Lu, C.-C. Odd-Harmonic Characteristics of the Field-Modulated GMR Magnetometer. IEEE Trans. Magn. 2011, 47, 3538–3541. [Google Scholar] [CrossRef]
- Cai, K.; Deng, Z.; Peng, C.; Li, K. Suppression of Harmonic Vibration in Magnetically Suspended Centrifugal Compressor Using Zero-Phase Odd-Harmonic Repetitive Controller. IEEE Trans. Ind. Electron. 2020, 67, 7789–7797. [Google Scholar] [CrossRef]
- Grino, R.; Costa-Castello, R. Digital repetitive plug-in controller for odd-harmonic periodic references and disturbances. Automatica 2005, 41, 153–157. [Google Scholar] [CrossRef]
- Tomizuka, M. Zero phase error tracking algorithm for digital control. Trans. ASME J. Dyn. Syst. Meas. Contr. 1987, 109, 65–68. [Google Scholar] [CrossRef]
- Tomizuka, M.; Tsao, T.-C.; Chew, K.-K. Analysis and synthesis of discrete-time repetitive controllers. Trans. ASME J. Dyn. Syst. Meas. Contr. 1989, 111, 353–358. [Google Scholar] [CrossRef]
- Cosner, C.; Anwar, G.; Tomizuka, M. Plug in repetitive control for industrial robotic manipulators. In Proceedings of the ICRA, Cincinnati, OH, USA, 13–18 May 1990; Volume 3, pp. 1970–1975. [Google Scholar]
- Zhang, B.; Wang, D.; Zhou, K.; Wang, Y. Linear Phase Lead Compensation Repetitive Control of a CVCF PWM Inverter. IEEE Trans. Ind. Electron. 2008, 55, 1595–1602. [Google Scholar] [CrossRef]
- Hillerstrom, G.; Sternby, J. Application of repetitive control to a peristaltic pump. In Proceedings of the American Control Conference, Francisco, CA, USA, 2–4 June 1993; pp. 136–141. [Google Scholar]
- Ledwich, G.F.; Bolton, A. Repetitive and periodic controller design. Proc. Inst. Elect. Eng. Control Theory App. 1993, 140, 19–24. [Google Scholar] [CrossRef]
- Kurniawan, E.; Cao, Z.; Mahendra, O.; Wardoyo, R. A survey on robust Repetitive Control and applications. In Proceedings of the 2014 IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 28–30 November 2014; pp. 524–529. [Google Scholar]
- Zhang, B.; Zhou, K.; Ye, Y.; Wang, D. Design of linear phase lead repetitive control for CVCF PWM DC-AC converters. In Proceedings of the American Control Conference, Portland, Oregon, 8–10 June 2005; Volume 2, pp. 1154–1159. [Google Scholar]
- Kurniawan, E.; Harno, H.G.; Wijonarko, S.; Widiyatmoko, B.; Bayuwati, D.; Purwowibowo, P.; Maftukhah, T. Variable-structure repetitive control for discrete-time linear systems with multiple-period exogenous signals. Int. J. Appl. Math. Comp. Sci. 2020, 30, 207–218. [Google Scholar]
- Kurniawan, E.; Afandi, M.I.; Suryadi. Repetitive control system for tracking and rejection of multiple periodic signals. In Proceedings of the 2017 International Conference on Robotics, Automation and Sciences (ICORAS), Melaka, Malaysia, 27–29 November 2017. [Google Scholar]
- Thiran, J.P. Recursive digital filters with maximally flat group delay. IEEE Trans. Circuit Theory 1971, 18, 659–664. [Google Scholar] [CrossRef] [Green Version]
- Laakso, T.; Valimaki, V. Splitting the Unit Delay. IEEE Signal Process. Mag. 1996, 13, 30–60. [Google Scholar] [CrossRef]
- Kurniawan, E. Robust Repetitive Control and Applications. Ph.D. Thesis, Swinburne University of Technology, Melbourne, Austrilia, 2013. [Google Scholar]



| Stabilizing Controller | rmse (deg)-General RC | rmse (deg)-OHRC |
|---|---|---|
| 2.189 | 1.599 | |
| 2.207 | 1.605 | |
| 2.224 | 1.616 | |
| 2.247 | 1.656 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurniawan, E.; Prakosa, J.A.; Wang, H.; Wijonarko, S.; Maftukhah, T.; Purwowibowo, P.; Septanto, H.; Pratiwi, E.B.; Rustandi, D. Design of Fractional Order Odd-Harmonics Repetitive Controller for Discrete-Time Linear Systems with Experimental Validations. Sensors 2022, 22, 8873. https://doi.org/10.3390/s22228873
Kurniawan E, Prakosa JA, Wang H, Wijonarko S, Maftukhah T, Purwowibowo P, Septanto H, Pratiwi EB, Rustandi D. Design of Fractional Order Odd-Harmonics Repetitive Controller for Discrete-Time Linear Systems with Experimental Validations. Sensors. 2022; 22(22):8873. https://doi.org/10.3390/s22228873
Chicago/Turabian StyleKurniawan, Edi, Jalu A. Prakosa, Hai Wang, Sensus Wijonarko, Tatik Maftukhah, Purwowibowo Purwowibowo, Harry Septanto, Enggar B. Pratiwi, and Dadang Rustandi. 2022. "Design of Fractional Order Odd-Harmonics Repetitive Controller for Discrete-Time Linear Systems with Experimental Validations" Sensors 22, no. 22: 8873. https://doi.org/10.3390/s22228873
APA StyleKurniawan, E., Prakosa, J. A., Wang, H., Wijonarko, S., Maftukhah, T., Purwowibowo, P., Septanto, H., Pratiwi, E. B., & Rustandi, D. (2022). Design of Fractional Order Odd-Harmonics Repetitive Controller for Discrete-Time Linear Systems with Experimental Validations. Sensors, 22(22), 8873. https://doi.org/10.3390/s22228873








