Investigation of High-Resolution Distributed Fiber Sensing System Embedded in Flexible Silicone Carpet for 2D Pressure Mapping
Abstract
:1. Introduction
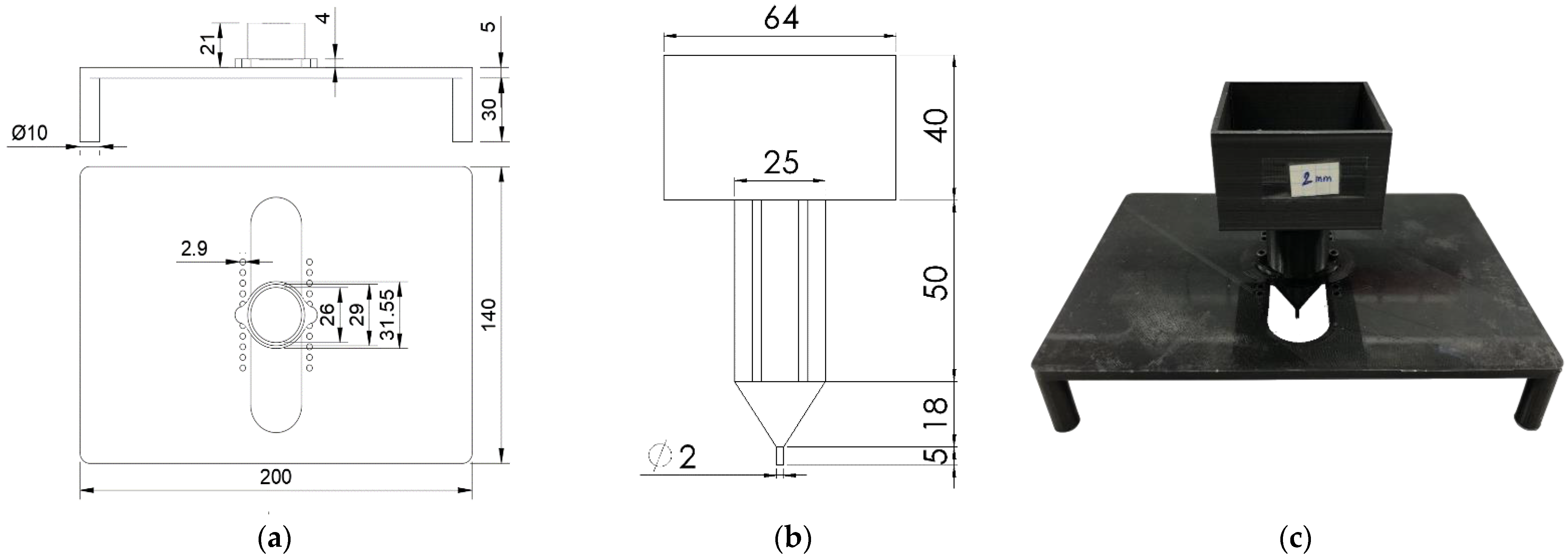
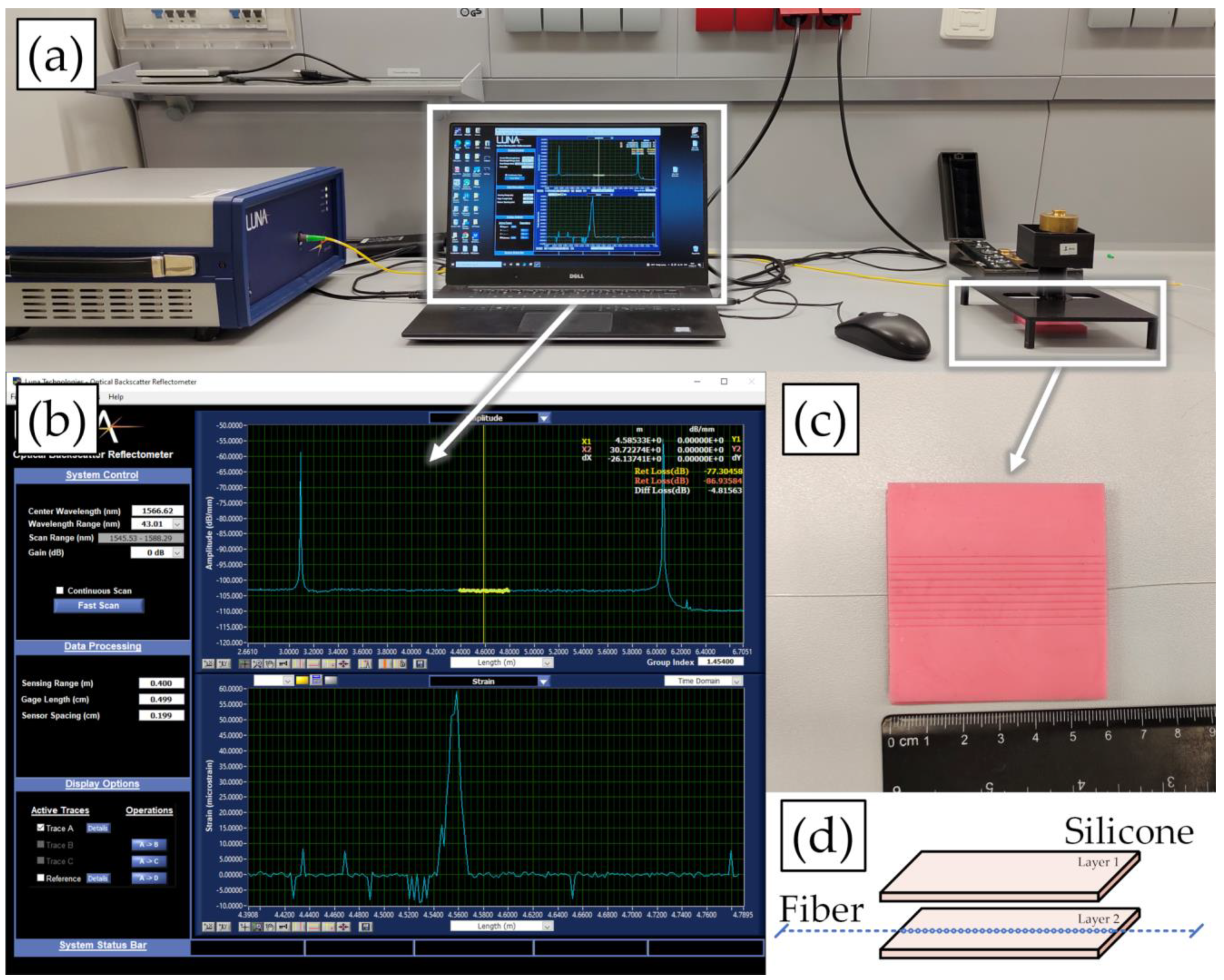
2. Experimental Setup
2.1. Materials
2.2. Methodology
- Fiber sandwiched between silicone layers with no cut groove;
- Fiber sandwiched between silicone layers with a cut groove;
- Fiber embedded in the silicone.
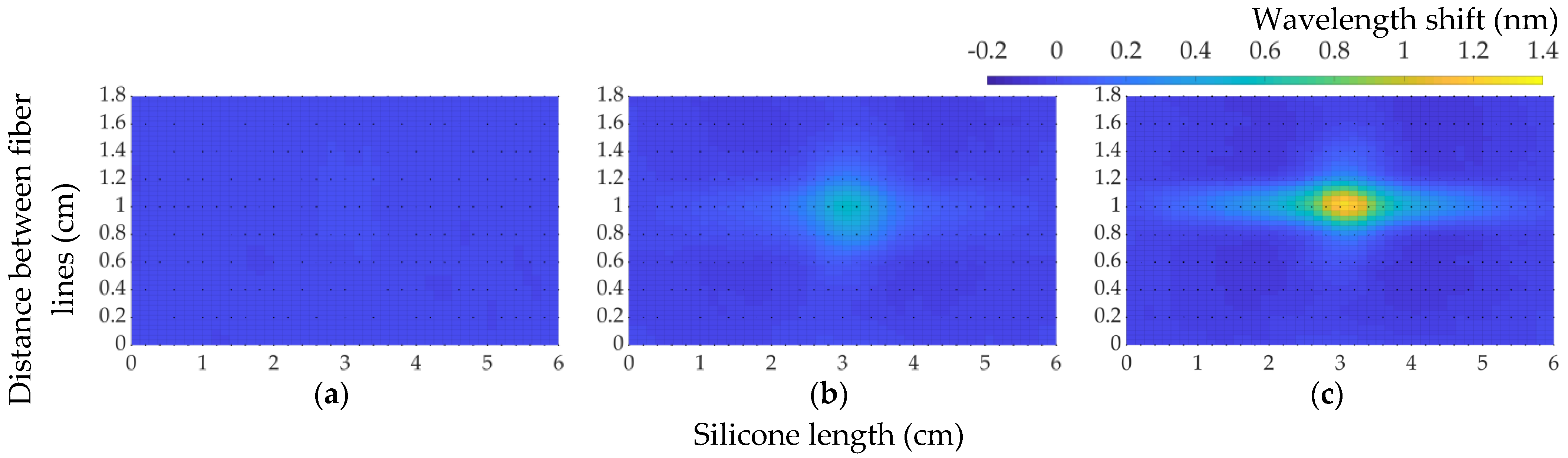
3. Results and Discussion
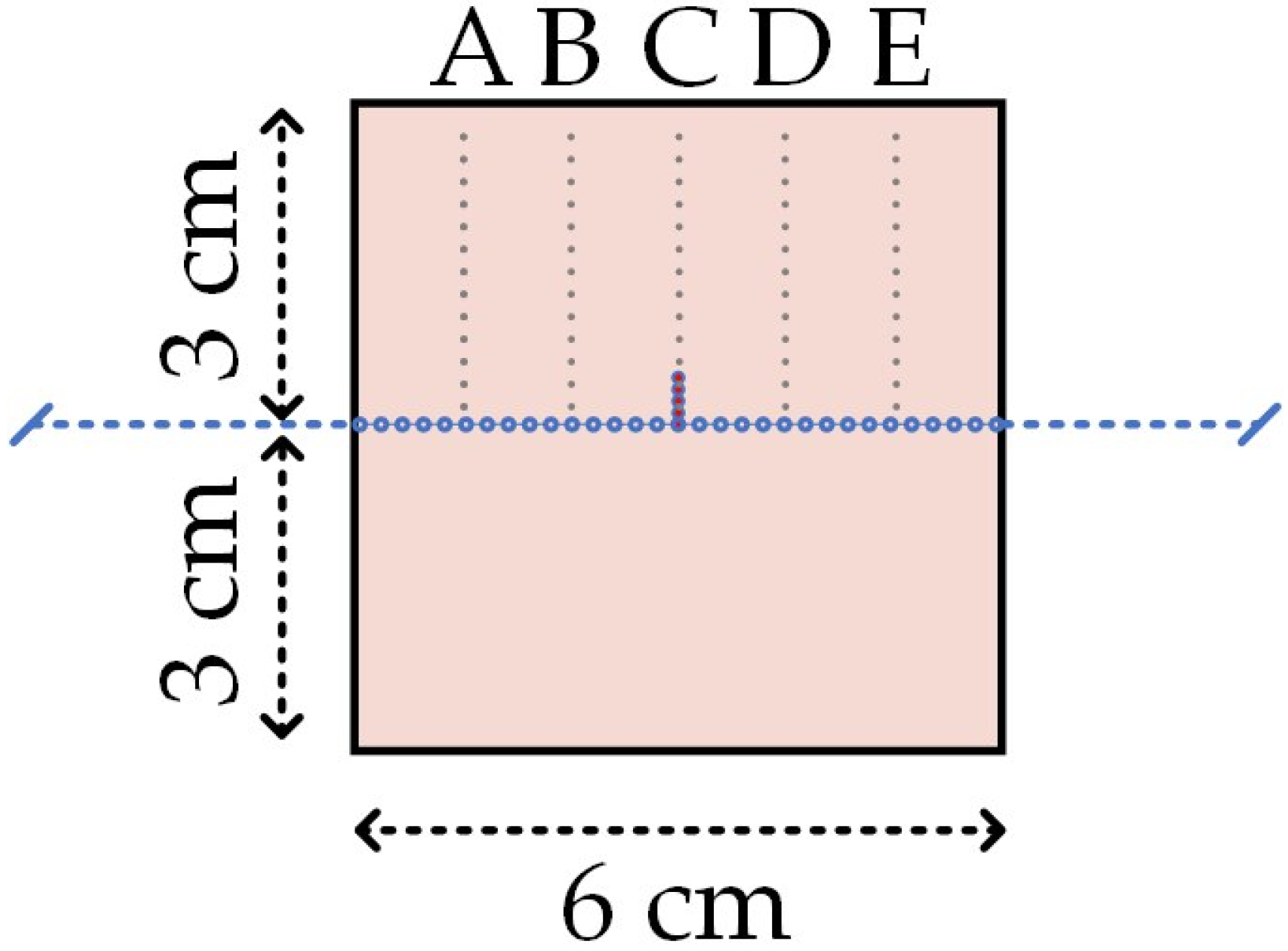
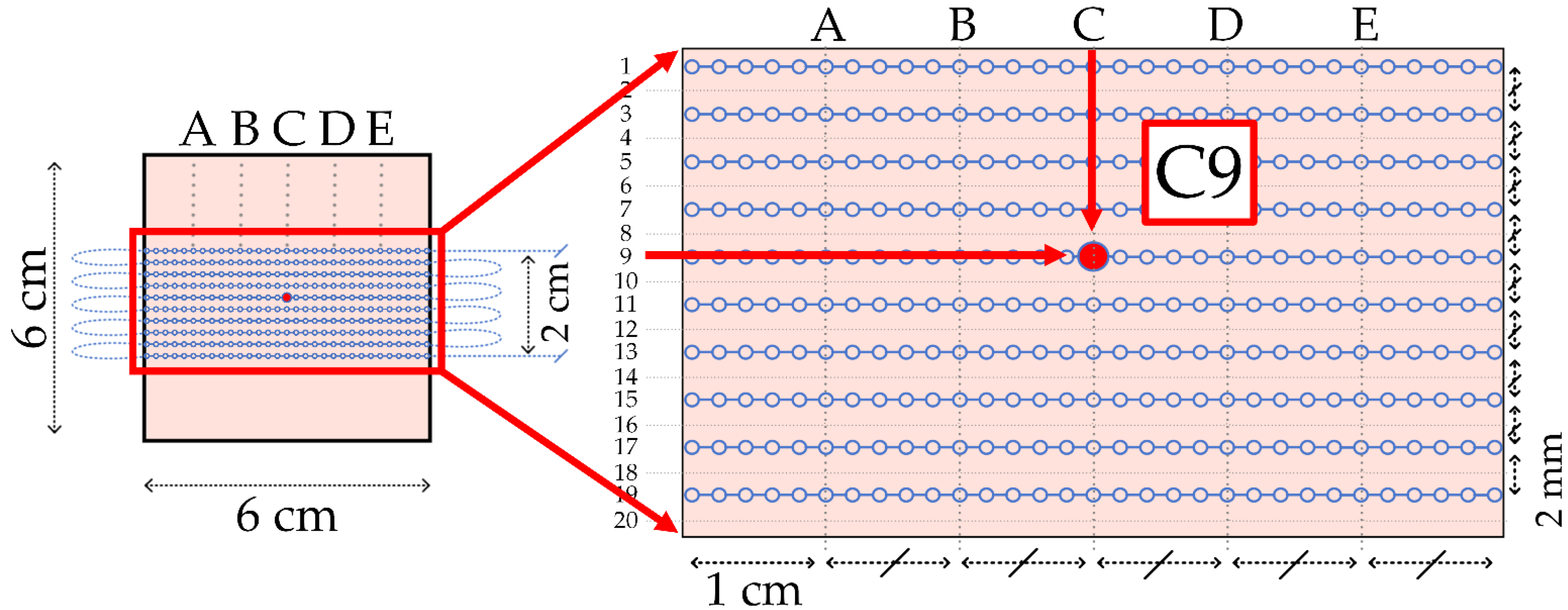
3.1. Calibration
3.2. The Sandwiched Fiber with Cut Silicone Prototype
3.3. The Prortype of Fiber Embedding in the Silicone Material
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tosi, D.; Schena, E.; Molardi, C.; Korganbayev, S. Fiber optic sensors for sub-centimeter spatially resolved measurements: Review and biomedical applications. Opt. Fiber Technol. 2018, 43, 6–19. [Google Scholar] [CrossRef]
- Udd, E.; Spillman, W. Fiber Optic Sensors: An Introduction for Engineers and Scientists; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Krohn, D.A.; MacDougall, T.; Mendez, A. Fiber Optic Sensors: Fundamentals and Applications; SPIE Press: Bellingham, WA, USA, 2014. [Google Scholar]
- Erdogan, T. Fiber Grating Spectra. J. Light. Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef] [Green Version]
- Rao, Y. Recent progress in applications of in-fibre Bragg grating sensors. Opt. Lasers Eng. 1999, 31, 297–324. [Google Scholar] [CrossRef]
- Li, C.; Tang, J.; Cheng, C.; Cai, L.; Yang, M. FBG Arrays for quasi-distributed sensing: A review. Photon. Sens. 2021, 11, 91–108. [Google Scholar] [CrossRef]
- Lindner, E.; Hartung, A.; Hoh, D.; Chojetzki, C.; Schuster, K.; Bierlich, J.; Rothhardt, M. Trends and future of fiber Bragg grating sensing technologies: Tailored draw tower gratings (DTGs). In Optical Sensing and Detection III; International Society for Optics and Photonics: San Diego, CA, USA, 2014; p. 91410X. [Google Scholar]
- Bao, X.; Chen, L. Recent progress in distributed fiber optic sensors. Sensors 2012, 12, 8601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Froggatt, M.; Moore, J. High-spatial-resolution distributed strain measurement in optical fiber with Rayleigh scatter. Appl. Opt. 1998, 37, 1735–1740. [Google Scholar] [CrossRef] [PubMed]
- Kreger, S.T.; Rahim, N.A.A.; Garg, N.; Klute, S.M.; Metrey, D.R.; Beaty, N.; Jeans, J.W.; Gamber, R. Optical frequency domain reflectometry: Principles and applications in fiber optic sensing. In Proceedings of the SPIE Commercial + Scientific Sensing and Imaging, Baltimore, MD, USA, 17–21 April 2016; Volume 9852, p. 98520T. [Google Scholar]
- OBR 4600 Optical Backscatter Reflectometer TM. Available online: https://lunainc.com/product/obr-4600 (accessed on 11 November 2022).
- Soller, B.J.; Gifford, D.K.; Wolfe, M.S.; Froggatt, M.E. High resolution optical frequency domain reflectometry for characterization of components and assemblies. Opt. Express 2005, 13, 666–674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schena, E.; Tosi, D.; Saccomandi, P.; Lewis, E.; Kim, T. Fiber optic sensors for temperature monitoring during thermal treatments: An overview. Sensors 2016, 16, 1144. [Google Scholar] [CrossRef] [PubMed]
- Ashikbayeva, Z.; Aitkulov, A.; Jelbuldina, M.; Issatayeva, A.; Beisenova, A.; Molardi, C.; Saccomandi, P.; Blanc, W.; Inglezakis, V.; Tosi, D. Distributed 2D temperature sensing during nanoparticles assisted laser ablation by means of high-scattering fiber sensors. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Beisenova, A.; Issatayeva, A.; Sovetov, S.; Korganbayev, S.; Jelbuldina, M.; Ashikbayeva, Z.; Blanc, W.; Schena, E.; Sales, S.; Molardi, C.; et al. Multi-fiber distributed thermal profiling of minimally invasive thermal ablation with scattering-level multiplexing in MgO-Doped fibers. Biomed. Opt. Express 2019, 10, 1282–1296. [Google Scholar] [CrossRef] [PubMed]
- Issatayeva, A.; Amantayeva, A.; Blanc, W.; Tosi, D.; Molardi, C. Design and analysis of a fiber-optic sensing system for shape reconstruction of a minimally invasive surgical needle. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Parent, F.; Loranger, S.; Mandal, K.K.; Iezzi, V.L.; Lapointe, J.; Boisvert, J.-S.; Baiad, M.D.; Kadoury, S.; Kashyap, R. Enhancement of accuracy in shape sensing of surgical needles using optical frequency domain reflectometry in optical fibers. Biomed. Opt. Express 2017, 8, 2210–2221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miller, G.A.; Askins, C.G.; Friebele, E.J. Shape Sensing Using Distributed Fiber Optic Strain Measurements. In Proceedings of the Second European Workshop on Optical Fibre Sensors, Santander, Spain, 7–9 June 2004; SPIE: Washington, WA, USA, 2004; Volume 5502, p. 528. [Google Scholar]
- Liu, H.; Farvardin, A.; Pedram, S.A.; Iordachita, I.; Taylor, R.H.; Armand, M. Large Deflection Shape Sensing of a Continuum Manipulator for Minimally-Invasive Surgery. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 27–29 June 2015; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2015; Volume 2015, pp. 201–206. [Google Scholar]
- Gonenc, B.; Chae, J.; Gehlbach, P.; Taylor, R.H.; Iordachita, I. Towards robot-assisted retinal vein cannulation: A motorized force-sensing microneedle integrated with a handheld micromanipulator. Sensors 2017, 17, 2195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandal, K.; Parent, F.; Martel, S.; Kashyap, R.; Kadoury, S. Vessel-based registration of an optical shape sensing catheter for MR navigation. Int. J. Comput. Assist. Radiol. Surg. 2016, 11, 1025–1034. [Google Scholar] [CrossRef] [PubMed]
- Roriz, P.; Carvalho, L.; Frazão, O.; Santos, J.L.; Simões, J.A. From conventional sensors to fibre optic sensors for strain and force measurements in biomechanics applications: A review. J. Biomech. 2014, 47, 1251–1261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsiokos, D.; Kanellos, G.T.; Papaioannou, G.; Pissadakis, S. Fiber Optic-Based Pressure Sensing Surface for Skin Health Management in Prosthetic and Rehabilitation Interventions. In Biomedical Engineering; Hudak, R., Penhaker, M., Majernik, J., Eds.; IntechOpen: Rijeka, Italy, 2012. [Google Scholar]
- Massari, L.; Fransvea, G.; D’Abbraccio, J.; Filosa, M.; Terruso, G.; Aliperta, A.; D’Alesio, G.; Zaltieri, M.; Schena, E.; Palermo, E.; et al. Functional mimicry of Ruffini receptors with fibre Bragg gratings and deep neural networks enables a bio-inspired large-area tactile-sensitive skin. Nat. Mach. Intell. 2022, 4, 425–435. [Google Scholar] [CrossRef]
- Kanellos, G.T.; Papaioannou, G.; Tsiokos, D.; Mitrogiannis, C.; Nianios, G.; Pleros, N. Two dimensional polymer-embedded quasi-distributed FBG pressure sensor for biomedical applications. Opt. Express 2009, 18, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Luis, E.; Pan, H.M.; Sing, S.L.; Bastola, A.K.; Goh, G.D.; Goh, G.L.; Tan, H.K.J.; Bajpai, R.; Song, J.; Yeong, W.Y. Silicone 3D printing: Process optimization, product biocompatibility, and reliability of silicone meniscus implants. 3D Print. Addit. Manuf. 2019, 6, 319–332. [Google Scholar] [CrossRef]
- Gent, A.N. On the relation between indentation hardness and Young’s modulus. Rubber Chem. Technol. 1958, 31, 896–906. [Google Scholar] [CrossRef]






| Center Wavelength (nm) | Wavelength Range (nm) | Sensing Range (m) | Gage Length (cm) | Sensor Spacing (cm) | Spatial Resolution (cm) |
|---|---|---|---|---|---|
| 1566.62 | 43.01 | 0.5 1 | 0.5 | 0.2 | 0.1 |
| Coordinates/Wavelength Shift (nm) | “A” | “C” | “E” |
|---|---|---|---|
| “5” | 0.98 | 1.33 | 1.1 |
| “9” | 1.1 | 1.2 | 1.2 |
| “15” | 1.11 | 1.38 | 1.36 |
| Mean, | 1.195 | ||
| Standard deviation, | 0.1296 | ||
| Variance, | 0.0168 | ||
| Min | 0.98 | ||
| Max | 1.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katrenova, Z.; Alisherov, S.; Abdol, T.; Yergibay, M.; Kappassov, Z.; Tosi, D.; Molardi, C. Investigation of High-Resolution Distributed Fiber Sensing System Embedded in Flexible Silicone Carpet for 2D Pressure Mapping. Sensors 2022, 22, 8800. https://doi.org/10.3390/s22228800
Katrenova Z, Alisherov S, Abdol T, Yergibay M, Kappassov Z, Tosi D, Molardi C. Investigation of High-Resolution Distributed Fiber Sensing System Embedded in Flexible Silicone Carpet for 2D Pressure Mapping. Sensors. 2022; 22(22):8800. https://doi.org/10.3390/s22228800
Chicago/Turabian StyleKatrenova, Zhanerke, Shakhrizat Alisherov, Turar Abdol, Madina Yergibay, Zhanat Kappassov, Daniele Tosi, and Carlo Molardi. 2022. "Investigation of High-Resolution Distributed Fiber Sensing System Embedded in Flexible Silicone Carpet for 2D Pressure Mapping" Sensors 22, no. 22: 8800. https://doi.org/10.3390/s22228800
APA StyleKatrenova, Z., Alisherov, S., Abdol, T., Yergibay, M., Kappassov, Z., Tosi, D., & Molardi, C. (2022). Investigation of High-Resolution Distributed Fiber Sensing System Embedded in Flexible Silicone Carpet for 2D Pressure Mapping. Sensors, 22(22), 8800. https://doi.org/10.3390/s22228800










