Parkinson’s Disease Wearable Gait Analysis: Kinematic and Dynamic Markers for Diagnosis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Data Analysis
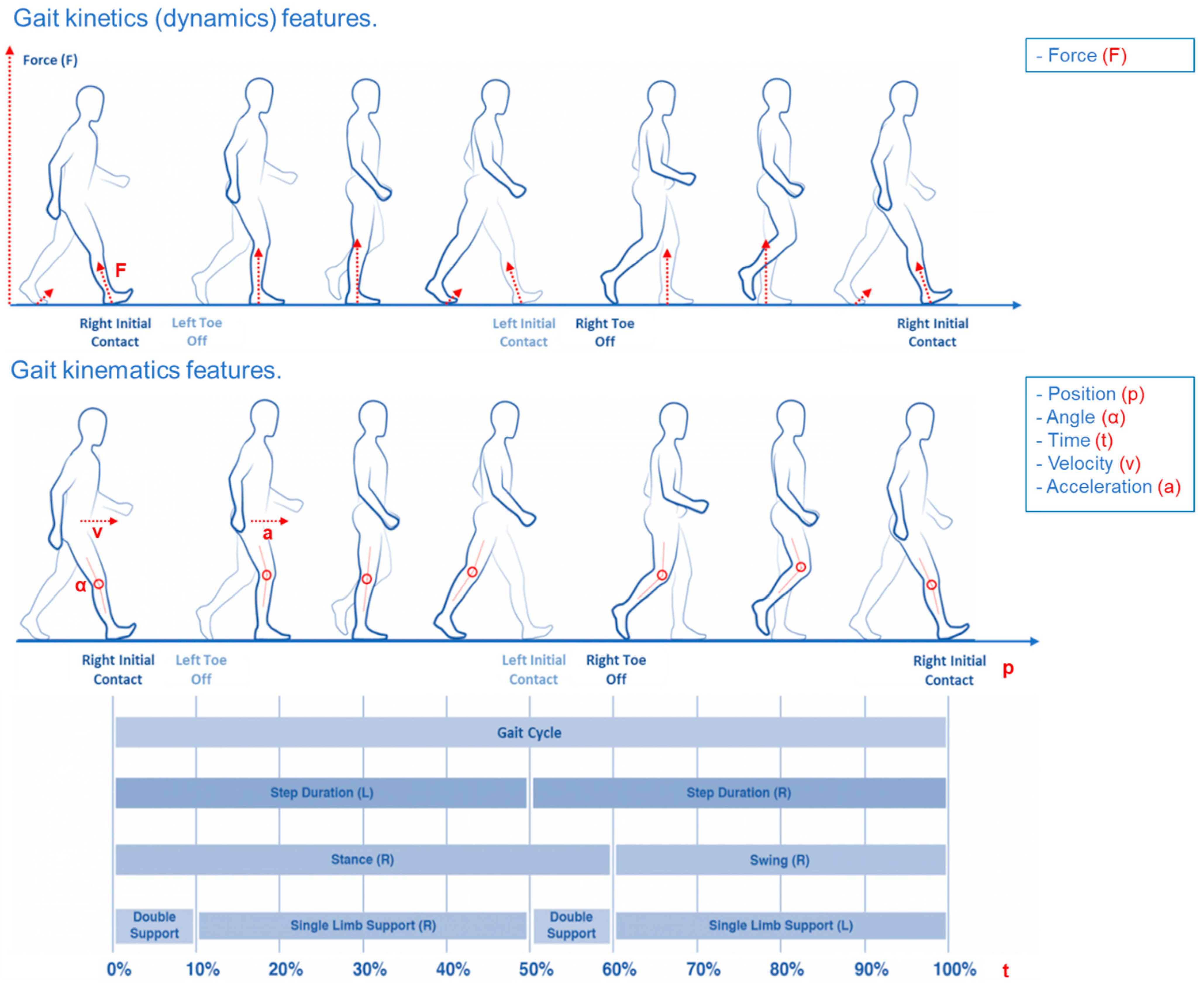
- Right and Left Stance, expressed both in seconds and as percentage of the stride length;
- Right and Left Swing, expressed both in seconds and as percentage of the stride length;
- Double Limb Supports, expressed both in seconds and as percentage of the stride length
- Right and Left Single Limb Supports, expressed both in seconds and as percentage of the stride length;
- Right and Left Step Duration, expressed both in seconds and as percentage of the stride length;
- Gait velocity expressed in m/s
- Time up and go test expressed in seconds
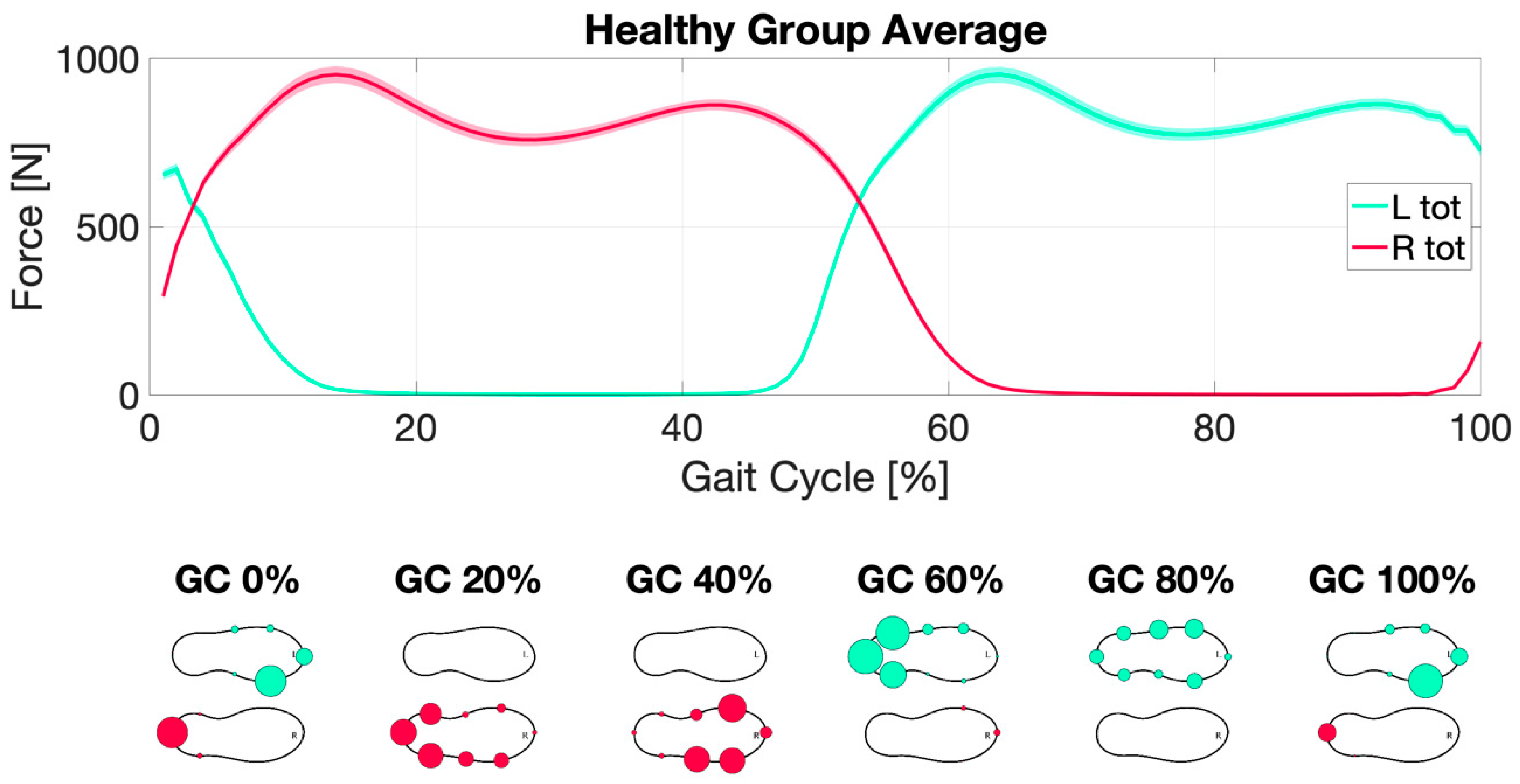
2.3. Dynamic Analysis
2.4. Kinematic Analysis
- Right and Left Stance, expressed both in seconds and as percentage of the stride length;
- Right and Left Swing, expressed both in seconds and as percentage of the stride length;
- Double Limb Supports, expressed both in seconds and as percentage of the stride length;
- Gait velocity expressed in m/s
- Time up and go test expressed in seconds
3. Results
3.1. Kinematic Analysis
- -
- Standard deviation (SD) left and right SWING absolute and percentage value
- -
- Standard deviation (SD) left and right STANCE percentage value
- -
- Standard deviation (SD) DOUBLE SUPPORT percentage value
- -
- Interquartile range (IQR) left and right SWING absolute and percentage value
- -
- Interquartile range (IQR) left and right STANCE absolute and percentage value
- -
- Interquartile range (IQR) DOUBLE SUPPORT percentage value
ROC Analysis
3.2. Dynamic Analysis
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bloem, B.R.; Okun, M.S.; Klein, C. Parkinson’s disease. Lancet 2021, 397, 2284–2303. [Google Scholar] [CrossRef]
- Poewe, W.; Seppi, K.; Tanner, C.M.; Halliday, G.M.; Brundin, P.; Volkmann, J.; Schrag, A.E.; Lang, A.E. Parkinson disease. Nat. Rev. Dis. Primers 2017, 3, 17013. [Google Scholar] [CrossRef] [PubMed]
- Gibb, W.R.G.; Lees, A.J. The relevance of the Lewy body to the pathogenesis of idiopathic Parkinson’s disease. J. Neurol. Neurosurg. Psychiatry 1988, 51, 745–752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rizzo, G.; Copetti, M.; Arcuti, S.; Martino, D.; Fontana, A.; Logroscino, G. Accuracy of clinical diagnosis of Parkinson disease A systematic review and meta-analysis. Neurology 2016, 91, e479–e489. [Google Scholar] [CrossRef]
- Sanchez-Ferro, A.; Elshehabi, M.; Godinho, C.; Salkovic, D.; Hobert, M.A.; Domingos, J.; van Uem, J.M.; Ferreira, J.J.; Maetzler, W. New methods for the assessment of Parkinson’s disease (2005 to 2015): A systematic review. Mov. Disord. Off. J. Mov. Disord. Soc. 2016, 31, 1283–1292. [Google Scholar] [CrossRef] [Green Version]
- Anand, V.; Bilal, E.; Ho, B.; Rice, J.J. Towards motor evaluation of Parkinson’s Disease Patients using wearable inertial sensors. AMIA Annu. Symp. Proc. AMIA Symp. 2020, 2020, 203–212. [Google Scholar]
- Stamatakis, J.; Ambroise, J.; Cremers, J.; Sharei, H.; Delvaux, V.; Macq, B.; Garraux, G. Finger tapping clinimetric score prediction in Parkinson’s disease using low-cost accelerometers. Comput. Intell. Neurosci. 2013, 2013, 717853. [Google Scholar] [CrossRef]
- Summa, S.; Tosi, J.; Taffoni, F.; Di Biase, L.; Marano, M.; Rizzo, A.C.; Tombini, M.; Di Pino, G.; Formica, D. Assessing Bradykinesia in Parkinson’s Disease Using Gyroscope Signals. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1556–1561. [Google Scholar]
- Di Biase, L.; Summa, S.; Tosi, J.; Taffoni, F.; Marano, M.; Cascio Rizzo, A.; Vecchio, F.; Formica, D.; Di Lazzaro, V.; Di Pino, G.; et al. Quantitative Analysis of Bradykinesia and Rigidity in Parkinson’s Disease. Front. Neurol. 2018, 9, 121. [Google Scholar] [CrossRef] [Green Version]
- Endo, T.; Okuno, R.; Yokoe, M.; Akazawa, K.; Sakoda, S. A novel method for systematic analysis of rigidity in Parkinson’s disease. Mov. Disord. Off. J. Mov. Disord. Soc. 2009, 24, 2218–2224. [Google Scholar] [CrossRef]
- Kwon, Y.; Park, S.H.; Kim, J.W.; Ho, Y.; Jeon, H.M.; Bang, M.J.; Koh, S.B.; Kim, J.H.; Eom, G.M. Quantitative evaluation of parkinsonian rigidity during intra-operative deep brain stimulation. Bio-Med. Mater. Eng. 2014, 24, 2273–2281. [Google Scholar] [CrossRef] [Green Version]
- Raiano, L.; Di Pino, G.; Di Biase, L.; Tombini, M.; Tagliamonte, N.L.; Formica, D. PDMeter: A Wrist Wearable Device for an at-home Assessment of the Parkinson’s Disease Rigidity. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1325–1333. [Google Scholar] [CrossRef] [PubMed]
- Deuschl, G.; Krack, P.; Lauk, M.; Timmer, J. Clinical neurophysiology of tremor. J. Clin. Neurophysiol. 1996, 13, 110–121. [Google Scholar] [CrossRef] [PubMed]
- Di Pino, G.; Formica, D.; Melgari, J.-M.; Taffoni, F.; Salomone, G.; di Biase, L.; Caimo, E.; Vernieri, F.; Guglielmelli, E. Neurophysiological bases of tremors and accelerometric parameters analysis. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; pp. 1820–1825. [Google Scholar]
- Di Biase, L.; Brittain, J.S.; Shah, S.A.; Pedrosa, D.J.; Cagnan, H.; Mathy, A.; Chen, C.C.; Martin-Rodriguez, J.F.; Mir, P.; Timmerman, L.; et al. Tremor stability index: A new tool for differential diagnosis in tremor syndromes. Brain J. Neurol. 2017, 140, 1977–1986. [Google Scholar] [CrossRef]
- Di Biase, L.; Brittain, J.-s.; Peter, B.; Di LAZZARO, V.; Shah, S.A. Methods and System for Characterising Tremors. Patent WO/2018/134579, 26 July 2018. [Google Scholar]
- Moore, S.T.; MacDougall, H.G.; Gracies, J.M.; Cohen, H.S.; Ondo, W.G. Long-term monitoring of gait in Parkinson’s disease. Gait Posture 2007, 26, 200–207. [Google Scholar] [CrossRef] [PubMed]
- Schlachetzki, J.C.M.; Barth, J.; Marxreiter, F.; Gossler, J.; Kohl, Z.; Reinfelder, S.; Gassner, H.; Aminian, K.; Eskofier, B.M.; Winkler, J.; et al. Wearable sensors objectively measure gait parameters in Parkinson’s disease. PLoS ONE 2017, 12, e0183989. [Google Scholar] [CrossRef]
- Tosi, J.; Summa, S.; Taffoni, F.; Biase, L.d.; Marano, M.; Rizzo, A.C.; Tombini, M.; Schena, E.; Formica, D.; Pino, G.D. Feature Extraction in Sit-to-Stand Task Using M-IMU Sensors and Evaluatiton in Parkinson’s Disease. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–6. [Google Scholar]
- Suppa, A.; Kita, A.; Leodori, G.; Zampogna, A.; Nicolini, E.; Lorenzi, P.; Rao, R.; Irrera, F. L-DOPA and freezing of gait in Parkinson’s disease: Objective assessment through a wearable wireless system. Front. Neurol. 2017, 8, 406. [Google Scholar] [CrossRef] [PubMed]
- Di Biase, L.; Di Santo, A.; Caminiti, M.L.; De Liso, A.; Shah, S.A.; Ricci, L.; Di Lazzaro, V. Gait analysis in Parkinson’s disease: An overview of the most accurate markers for diagnosis and symptoms monitoring. Sensors 2020, 20, 3529. [Google Scholar] [CrossRef]
- Di Biase, L.; Raiano, L.; Caminiti, M.L.; Pecoraro, P.M.; Di Lazzaroo, V. Artificial intelligence in Parkinson’s disease—Symptoms identification and monitoring. In Augmenting Neurological Disorder Prediction and Rehabilitation Using Artificial Intelligence; Elsevier: Amsterdam, The Netherlands, 2022; pp. 35–52. [Google Scholar]
- Di Biase, L.; Tinkhauser, G.; Martin Moraud, E.; Caminiti, M.L.; Pecoraro, P.M.; Di Lazzaro, V. Adaptive, personalized closed-loop therapy for Parkinson’s disease: Biochemical, neurophysiological, and wearable sensing systems. Expert Rev. Neurother. 2021, 21, 1371–1388. [Google Scholar] [CrossRef]
- Dicharry, J. Kinematics and kinetics of gait: From lab to clinic. Clin. Sports Med. 2010, 29, 347–364. [Google Scholar] [CrossRef]
- Webster, J.B.; Darter, B.J. Principles of Normal and Pathologic Gait. In Atlas of Orthoses and Assistive Devices; Elsevier: Amsterdam, The Netherlands, 2019; pp. 49–62.e1. [Google Scholar]
- Sica, M.; Tedesco, S.; Crowe, C.; Kenny, L.; Moore, K.; Timmons, S.; Barton, J.; O’Flynn, B.; Komaris, D.-S. Continuous home monitoring of Parkinson’s disease using inertial sensors: A systematic review. PLoS ONE 2021, 16, e0246528. [Google Scholar] [CrossRef]
- Schaafsma, J.D.; Giladi, N.; Balash, Y.; Bartels, A.L.; Gurevich, T.; Hausdorff, J.M. Gait dynamics in Parkinson’s disease: Relationship to Parkinsonian features, falls and response to levodopa. J. Neurol. Sci. 2003, 212, 47–53. [Google Scholar] [CrossRef]
- Blin, O.; Ferrandez, A.M.; Pailhous, J.; Serratrice, G. Dopa-sensitive and dopa-resistant gait parameters in Parkinson’s disease. J. Neurol. Sci. 1991, 103, 51–54. [Google Scholar] [CrossRef]
- Del Olmo, M.F.; Cudeiro, J. Temporal variability of gait in Parkinson disease: Effects of a rehabilitation programme based on rhythmic sound cues. Parkinsonism Relat. Disord. 2005, 11, 25–33. [Google Scholar] [CrossRef] [PubMed]
- Frenkel-Toledo, S.; Giladi, N.; Peretz, C.; Herman, T.; Gruendlinger, L.; Hausdorff, J.M. Treadmill walking as an external pacemaker to improve gait rhythm and stability in Parkinson’s disease. Mov. Disord. Off. J. Mov. Disord. Soc. 2005, 20, 1109–1114. [Google Scholar] [CrossRef]
- Pieruccini-Faria, F.; Montero-Odasso, M.; Hausdorff, J.M. Gait variability and fall risk in older adults: The role of cognitive function. In Falls and Cognition in Older Persons; Springer: Berlin/Heidelberg, Germany, 2020; pp. 107–138. [Google Scholar]
- Hausdorff, J.M.; Rios, D.A.; Edelberg, H.K. Gait variability and fall risk in community-living older adults: A 1-year prospective study. Arch. Phys. Med. Rehabil. 2001, 82, 1050–1056. [Google Scholar] [CrossRef]
- Maki, B.E. Gait changes in older adults: Predictors of falls or indicators of fear. J. Am. Geriatr. Soc. 1997, 45, 313–320. [Google Scholar] [CrossRef] [PubMed]
- Baltadjieva, R.; Giladi, N.; Gruendlinger, L.; Peretz, C.; Hausdorff, J.M. Marked alterations in the gait timing and rhythmicity of patients with de novo Parkinson’s disease. Eur. J. Neurosci. 2006, 24, 1815–1820. [Google Scholar] [CrossRef]
- Su, B.; Song, R.; Guo, L.; Yen, C.-W. Characterizing gait asymmetry via frequency sub-band components of the ground reaction force. Biomed. Signal Process. Control 2015, 18, 56–60. [Google Scholar] [CrossRef]
- Yogev, G.; Giladi, N.; Peretz, C.; Springer, S.; Simon, E.S.; Hausdorff, J.M. Dual tasking, gait rhythmicity, and Parkinson’s disease: Which aspects of gait are attention demanding? Eur. J. Neurosci. 2005, 22, 1248–1256. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Lowenthal, J.; Herman, T.; Gruendlinger, L.; Peretz, C.; Giladi, N. Rhythmic auditory stimulation modulates gait variability in Parkinson’s disease. Eur. J. Neurosci. 2007, 26, 2369–2375. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Lertratanakul, A.; Cudkowicz, M.E.; Peterson, A.L.; Kaliton, D.; Goldberger, A.L. Dynamic markers of altered gait rhythm in amyotrophic lateral sclerosis. J. Appl. Physiol. 2000, 88, 2045–2053. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gelb, D.J.; Oliver, E.; Gilman, S. Diagnostic criteria for Parkinson disease. Arch. Neurol. 1999, 56, 33–39. [Google Scholar] [CrossRef]
- Hoehn, M.M.; Yahr, M.D. Parkinsonism onset, progression, and mortality. Neurology 1967, 17, 427. [Google Scholar] [CrossRef] [Green Version]
- Fahn, S.; Elton, R.; UPDRS Development Committee. Recent Developments in Parkinson’s Disease; Macmillan Health Care Information: Folorham Park, NJ, USA, 1987; Volume 2, pp. 153–163, 293–304. [Google Scholar]
- Hausdorff, J.M.; Ladin, Z.; Wei, J.Y. Footswitch system for measurement of the temporal parameters of gait. J. Biomech. 1995, 28, 347–351. [Google Scholar] [CrossRef]
- Son, M.; Han, S.H.; Lyoo, C.H.; Lim, J.; Jeon, J.; Hong, K.-B.; Park, H. The effect of levodopa on bilateral coordination and gait asymmetry in Parkinson’s disease using inertial sensor. NPJ Parkinson’s Dis. 2021, 7, 42. [Google Scholar] [CrossRef] [PubMed]
- Blin, O.; Ferrandez, A.M.; Serratrice, G. Quantitative analysis of gait in Parkinson patients: Increased variability of stride length. J. Neurol. Sci. 1990, 98, 91–97. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Cudkowicz, M.E.; Firtion, R.; Wei, J.Y.; Goldberger, A.L. Gait variability and basal ganglia disorders: Stride-to-stride variations of gait cycle timing in Parkinson’s disease and Huntington’s disease. Mov. Disord. Off. J. Mov. Disord. Soc. 1998, 13, 428–437. [Google Scholar] [CrossRef] [PubMed]
- Gabell, A.; Nayak, U.S. The effect of age on variability in gait. J. Gerontol. 1984, 39, 662–666. [Google Scholar] [CrossRef]
- Hausdorff, J.M.; Mitchell, S.L.; Firtion, R.; Peng, C.K.; Cudkowicz, M.E.; Wei, J.Y.; Goldberger, A.L. Altered fractal dynamics of gait: Reduced stride-interval correlations with aging and Huntington’s disease. J. Appl. Physiol. 1997, 82, 262–269. [Google Scholar] [CrossRef]
- Hollman, J.H.; Von Arb, H.M.; Budreck, A.M.; Muehlemann, A.; Ness, D.K. Treadmill walking alters stride time dynamics in Parkinson’s disease. Gait Posture 2020, 77, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Yamasaki, M.; Sasaki, T.; Torii, M. Sex difference in the pattern of lower limb movement during treadmill walking. Eur. J. Appl. Physiol. Occup. Physiol. 1991, 62, 99–103. [Google Scholar] [CrossRef] [PubMed]
- Frenkel-Toledo, S.; Giladi, N.; Peretz, C.; Herman, T.; Gruendlinger, L.; Hausdorff, J.M. Effect of gait speed on gait rhythmicity in Parkinson’s disease: Variability of stride time and swing time respond differently. J. Neuroeng. Rehabil. 2005, 2, 23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malatesta, D.; Simar, D.; Dauvilliers, Y.; Candau, R.; Borrani, F.; Prefaut, C.; Caillaud, C. Energy cost of walking and gait instability in healthy 65- and 80-yr-olds. J. Appl. Physiol. 2003, 95, 2248–2256. [Google Scholar] [CrossRef] [Green Version]
- Grabiner, P.C.; Biswas, S.T.; Grabiner, M.D. Age-related changes in spatial and temporal gait variables. Arch. Phys. Med. Rehabil. 2001, 82, 31–35. [Google Scholar] [CrossRef]
- Alam, M.N.; Garg, A.; Munia, T.T.K.; Fazel-Rezai, R.; Tavakolian, K. Vertical ground reaction force marker for Parkinson’s disease. PLoS ONE 2017, 12, e0175951. [Google Scholar] [CrossRef]




| Ref | Cohort | Dataset | Data Source | Group | Subjects Number | Gender | Age (m ± SD) | Hoehn and Yahr (m ± SD) | UPDRS (m ± SD) |
|---|---|---|---|---|---|---|---|---|---|
| [36] | 1 | 1 | Movement Disorders Unit at the Tel-Aviv Sourasky Medical Center | PD | 29 | 69% male | 71 ± 8 | 2.3 ± 0.4 | 33 ± 12 |
| HS | 18 | 56% male | 72 ± 7 | ||||||
| [37] | 2 | 1 | Movement Disorders Unit at the Tel Aviv Sourasky Medical Center | PD | 29 | 55% male | 67 ± 9 | 2.4 ± 0.4 | 25 ± 8 |
| HS | 25 | 46% male | 65 ± 7 | ||||||
| [30] | 3 | 1 | Movement Disorders Unit at the Tel-Aviv Sourasky Medical Center. | PD | 35 | 63% male | 62 ± 9 | 2.1 ± 0.2 | 36 ± 11 |
| HS | 29 | 62% male | 58 ± 7 | ||||||
| [38] | 4 | 2 | Neurology Outpatient Clinic at Massachusetts General Hospital. | PD | 15 | 67% male | 67 ± 11 | 2.8 ± 0.9 | |
| HS | 16 | 13% male | 39 ± 19 |
| First Dataset Cohort 1-2-3 | Second Dataset Cohort 4 |
|---|---|
| Type of Data Available | |
|
|
| Data Manipulation | |
Kinematic Analysis:
| Kinematic Analysis:
|
Dynamic Analysis:
| Dynamic Analysis:
|
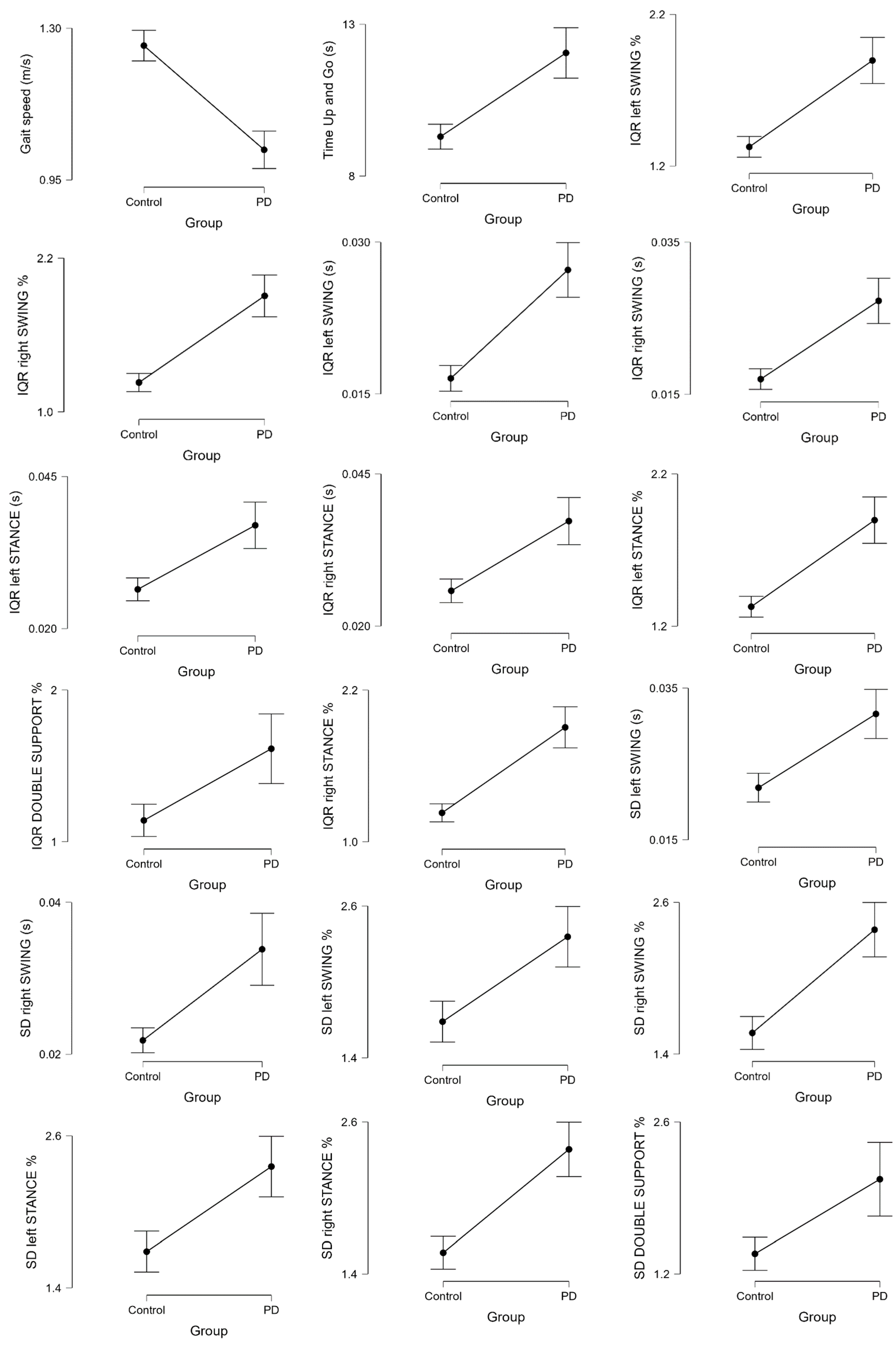
| Variables | Group | N | Average | Standard Deviation | t | df | p Value | ||
|---|---|---|---|---|---|---|---|---|---|
| Kinematic | central tendency indices | Gait Speed (m/s) | HS | 88 | 1.260 | 0.166 | 8.278 | 194 | <0.001 * |
| PD | 108 | 1.019 | 0.227 | ||||||
| Time Up and Go (s) | HS | 62 | 9.300 | 1.604 | −5.187 | 150 | <0.001 * | ||
| PD | 90 | 12.056 | 3.962 | ||||||
| Ave left SWING | HS | 88 | 0.442 | 0.040 | 0.361 | 194 | 0.719 | ||
| PD | 108 | 0.439 | 0.046 | ||||||
| Ave right SWING | HS | 88 | 0.443 | 0.041 | 1.158 | 194 | 0.248 | ||
| PD | 108 | 0.435 | 0.047 | ||||||
| Ave left SWING % | HS | 88 | 41.804 | 3.143 | 1.951 | 194 | 0.053 | ||
| PD | 108 | 40.781 | 4.018 | ||||||
| Ave right SWING % | HS | 88 | 41.916 | 3.488 | 2.682 | 194 | 0.008 | ||
| PD | 108 | 40.395 | 4.284 | ||||||
| Ave left STANCE | HS | 88 | 0.618 | 0.071 | −2.127 | 194 | 0.035 | ||
| PD | 108 | 0.646 | 0.109 | ||||||
| Ave right STANCE | HS | 88 | 0.616 | 0.074 | −2.431 | 194 | 0.016 | ||
| PD | 108 | 0.650 | 0.109 | ||||||
| Ave left STANCE % | HS | 88 | 58.196 | 3.143 | −1.951 | 194 | 0.053 | ||
| PD | 108 | 59.219 | 4.018 | ||||||
| Ave right STANCE % | HS | 88 | 58.084 | 3.488 | −2.682 | 194 | 0.008 | ||
| PD | 108 | 59.605 | 4.284 | ||||||
| Ave DOUBLE SUPPORT | HS | 88 | 0.115 | 0.095 | −1.106 | 194 | 0.270 | ||
| PD | 108 | 0.133 | 0.120 | ||||||
| Ave DOUBLE SUPPORT % | HS | 88 | 10.681 | 8.528 | −0.808 | 194 | 0.420 | ||
| PD | 108 | 11.734 | 9.492 | ||||||
| Med left SWING | HS | 88 | 0.441 | 0.040 | 0.123 | 194 | 0.902 | ||
| PD | 108 | 0.440 | 0.048 | ||||||
| Med right SWING | HS | 88 | 0.442 | 0.041 | 0.963 | 194 | 0.337 | ||
| PD | 108 | 0.436 | 0.047 | ||||||
| Med left SWING % | HS | 88 | 41.999 | 3.195 | 1.844 | 194 | 0.067 | ||
| PD | 108 | 41.029 | 4.003 | ||||||
| Med right SWING % | HS | 88 | 42.064 | 3.487 | 2.502 | 194 | 0.013 | ||
| PD | 108 | 40.655 | 4.240 | ||||||
| Med left STANCE | HS | 88 | 0.611 | 0.069 | −2.043 | 194 | 0.042 | ||
| PD | 108 | 0.638 | 0.106 | ||||||
| Med right STANCE | HS | 88 | 0.611 | 0.073 | −2.303 | 194 | 0.022 | ||
| PD | 108 | 0.642 | 0.106 | ||||||
| Med left STANCE % | HS | 88 | 58.001 | 3.195 | −1.844 | 194 | 0.067 | ||
| PD | 108 | 58.971 | 4.003 | ||||||
| Med right STANCE % | HS | 88 | 57.936 | 3.487 | −2.502 | 194 | 0.013 | ||
| PD | 108 | 59.345 | 4.240 | ||||||
| Med DOUBLE SUPPORT | HS | 88 | 0.113 | 0.094 | −0.943 | 194 | 0.347 | ||
| PD | 108 | 0.127 | 0.110 | ||||||
| Med DOUBLE SUPPORT% | HS | 88 | 10.483 | 8.518 | −0.742 | 194 | 0.459 | ||
| PD | 108 | 11.441 | 9.368 | ||||||
| dispersion indices | SD left SWING | HS | 88 | 0.022 | 0.009 | −4.851 | 194 | <0.001 * | |
| PD | 108 | 0.032 | 0.017 | ||||||
| SD right SWING | HS | 88 | 0.022 | 0.008 | −4.357 | 194 | <0.001 * | ||
| PD | 108 | 0.034 | 0.025 | ||||||
| SD left SWING % | HS | 88 | 1.686 | 0.762 | −4.400 | 194 | <0.001 * | ||
| PD | 108 | 2.357 | 1.254 | ||||||
| SD right SWING % | HS | 88 | 1.568 | 0.613 | −6.093 | 194 | <0.001 * | ||
| PD | 108 | 2.383 | 1.127 | ||||||
| SD left STANCE | HS | 88 | 0.035 | 0.016 | −1.640 | 194 | 0.103 | ||
| PD | 108 | 0.065 | 0.170 | ||||||
| SD right STANCE | HS | 88 | 0.033 | 0.014 | −1.736 | 194 | 0.084 | ||
| PD | 108 | 0.058 | 0.135 | ||||||
| SD left STANCE % | HS | 88 | 1.686 | 0.762 | −4.400 | 194 | <0.001 * | ||
| PD | 108 | 2.357 | 1.254 | ||||||
| SD right STANCE % | HS | 88 | 1.568 | 0.613 | −6.093 | 194 | <0.001 * | ||
| PD | 108 | 2.383 | 1.127 | ||||||
| SD DOUBLE SUPPORT | HS | 88 | 0.019 | 0.015 | −1.441 | 194 | 0.151 | ||
| PD | 108 | 0.045 | 0.171 | ||||||
| SD DOUBLE SUPPORT % | HS | 88 | 1.386 | 0.718 | −3.396 | 194 | <0.001 * | ||
| PD | 108 | 2.072 | 1.780 | ||||||
| IQR left SWING | HS | 88 | 0.017 | 0.006 | −6.651 | 194 | <0.001 * | ||
| PD | 108 | 0.027 | 0.014 | ||||||
| IQR right SWING | HS | 88 | 0.017 | 0.006 | −5.821 | 194 | <0.001 * | ||
| PD | 108 | 0.027 | 0.016 | ||||||
| IQR left SWING % | HS | 88 | 1.326 | 0.323 | −6.279 | 194 | <0.001 * | ||
| PD | 108 | 1.896 | 0.799 | ||||||
| IQR right SWING % | HS | 88 | 1.229 | 0.337 | −7.009 | 194 | <0.001 * | ||
| PD | 108 | 1.905 | 0.852 | ||||||
| IQR left STANCE | HS | 88 | 0.026 | 0.009 | −4.577 | 194 | <0.001 * | ||
| PD | 108 | 0.037 | 0.020 | ||||||
| IQR right STANCE | HS | 88 | 0.026 | 0.009 | −4.902 | 194 | <0.001 * | ||
| PD | 108 | 0.037 | 0.020 | ||||||
| IQR left STANCE % | HS | 88 | 1.326 | 0.323 | −6.279 | 194 | <0.001 * | ||
| PD | 108 | 1.896 | 0.799 | ||||||
| IQR right STANCE % | HS | 88 | 1.229 | 0.337 | −7.009 | 194 | <0.001 * | ||
| PD | 108 | 1.905 | 0.852 | ||||||
| IQR DOUBLE SUPPORT | HS | 88 | 0.013 | 0.008 | −2.875 | 194 | 0.004 | ||
| PD | 108 | 0.018 | 0.014 | ||||||
| IQR_DOUBLE_SUPPORT % | HS | 88 | 1.141 | 0.502 | −3.446 | 194 | <0.001 * | ||
| PD | 108 | 1.613 | 1.203 | ||||||
| Variables | AUC | Standard Error | p Value | Lower Limit | Upper Limit |
|---|---|---|---|---|---|
| Gait Speed (m/s) | 0.200 | 0.035 | <0.001 * | 0.130 | 0.269 |
| Time Up and Go (s) | 0.801 | 0.036 | <0.001 * | 0.730 | 0.872 |
| SD left SWING | 0.682 | 0.044 | <0.001 * | 0.595 | 0.768 |
| SD right SWING | 0.703 | 0.043 | <0.001 * | 0.620 | 0.787 |
| SD left SWING % | 0.674 | 0.045 | <0.001 * | 0.585 | 0.763 |
| SD right SWING % | 0.740 | 0.041 | <0.001 * | 0.660 | 0.819 |
| SD left STANCE % | 0.674 | 0.045 | <0.001 * | 0.585 | 0.763 |
| SD right STANCE % | 0.740 | 0.041 | <0.001 * | 0.660 | 0.819 |
| SD DOUBLE SUPPORT% | 0.643 | 0.039 | <0.001 * | 0.566 | 0.720 |
| IQR left SWING | 0.778 | 0.037 | <0.001 * | 0.704 | 0.851 |
| IQR right SWING | 0.733 | 0.041 | <0.001 * | 0.654 | 0.813 |
| IQR left SWING % | 0.776 | 0.037 | <0.001 * | 0.703 | 0.848 |
| IQR right SWING % | 0.820 | 0.034 | <0.001 * | 0.754 | 0.886 |
| IQR left STANCE | 0.639 | 0.045 | 0.0036 | 0.551 | 0.727 |
| IQR right STANCE | 0.667 | 0.044 | <0.001 * | 0.580 | 0.754 |
| IQR left STANCE % | 0.776 | 0.037 | <0.001 * | 0.703 | 0.848 |
| IQR right STANCE % | 0.820 | 0.034 | <0.001 * | 0.754 | 0.886 |
| IQR DOUBLE SUPPORT % | 0.634 | 0.040 | 0.0012 | 0.556 | 0.712 |
| Variables | Group | N | Average | Standard Deviation | t | df | p Value | ||
|---|---|---|---|---|---|---|---|---|---|
| dynamic | central tendency indices | Ave Force left | HS | 88 | 372.346 | 181.982 | −0.813 | 194 | 0.417 |
| PD | 108 | 392.385 | 162.683 | ||||||
| Ave Force right | HS | 88 | 369.036 | 181.877 | −1.044 | 194 | 0.298 | ||
| PD | 108 | 394.455 | 158.804 | ||||||
| Med Force left | HS | 88 | 467.395 | 235.065 | −0.537 | 194 | 0.592 | ||
| PD | 108 | 484.518 | 210.938 | ||||||
| Med Force right | HS | 88 | 459.291 | 235.530 | −1.025 | 194 | 0.307 | ||
| PD | 108 | 491.887 | 209.364 | ||||||
| dispersion indices | SD Force left | HS | 88 | 324.871 | 160.322 | −0.561 | 194 | 0.576 | |
| PD | 108 | 336.977 | 141.656 | ||||||
| SD Force right | HS | 88 | 324.106 | 160.490 | −0.608 | 194 | 0.544 | ||
| PD | 108 | 337.011 | 136.732 | ||||||
| IQR Force left | HS | 88 | 671.779 | 332.736 | −0.764 | 194 | 0.446 | ||
| PD | 108 | 706.230 | 297.570 | ||||||
| IQR Force right | HS | 88 | 671.246 | 332.261 | −0.877 | 194 | 0.382 | ||
| PD | 108 | 710.175 | 288.892 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
di Biase, L.; Raiano, L.; Caminiti, M.L.; Pecoraro, P.M.; Di Lazzaro, V. Parkinson’s Disease Wearable Gait Analysis: Kinematic and Dynamic Markers for Diagnosis. Sensors 2022, 22, 8773. https://doi.org/10.3390/s22228773
di Biase L, Raiano L, Caminiti ML, Pecoraro PM, Di Lazzaro V. Parkinson’s Disease Wearable Gait Analysis: Kinematic and Dynamic Markers for Diagnosis. Sensors. 2022; 22(22):8773. https://doi.org/10.3390/s22228773
Chicago/Turabian Styledi Biase, Lazzaro, Luigi Raiano, Maria Letizia Caminiti, Pasquale Maria Pecoraro, and Vincenzo Di Lazzaro. 2022. "Parkinson’s Disease Wearable Gait Analysis: Kinematic and Dynamic Markers for Diagnosis" Sensors 22, no. 22: 8773. https://doi.org/10.3390/s22228773
APA Styledi Biase, L., Raiano, L., Caminiti, M. L., Pecoraro, P. M., & Di Lazzaro, V. (2022). Parkinson’s Disease Wearable Gait Analysis: Kinematic and Dynamic Markers for Diagnosis. Sensors, 22(22), 8773. https://doi.org/10.3390/s22228773









