Integrated Gradient-Based Continuous Wavelet Transform for Bearing Fault Diagnosis
Abstract
:1. Introduction
2. Framework of the Proposed IG-CWT
2.1. Continuous Wavelet Transform
2.2. IG-Based Frequency Range Selection
3. Experimental Results and Discussion
3.1. PU Dataset
3.2. MFPT Datasets
3.3. JNU Bearing Dataset
3.4. CWRU Bearing Dataset
3.5. Discussion
4. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, Y.; Kim, C.H.; Kim, J.M. A Novel Hybrid Deep Learning Method for Fault Diagnosis of Rotating Machinery Based on Extended WDCNN and Long Short-Term Memory. Sensors 2021, 21, 6614. [Google Scholar] [CrossRef] [PubMed]
- Xie, T.; Huang, X.; Choi, S.K. Intelligent Mechanical Fault Diagnosis Using Multisensor Fusion and Convolution Neural Network. IEEE Trans. Ind. Inform. 2022, 18, 3213–3223. [Google Scholar] [CrossRef]
- Zhao, K.; Jiang, H.; Wu, Z.; Lu, T. A Novel Transfer Learning Fault Diagnosis Method Based on Manifold Embedded Distribution Alignment with A Little Labeled Data. J. Intell. Manuf. 2020, 33, 151–165. [Google Scholar] [CrossRef]
- Li, T.; Zhao, Z.; Sun, C.; Cheng, L.; Chen, X.; Yan, R.; Gao, R.X. WaveletKernelNet: An Interpretable Deep Neural Network for Industrial Intelligent Diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 2302–2312. [Google Scholar] [CrossRef]
- Bai, X.; Wang, X.; Liu, X.L.; Liu, Q.; Song, J.K.; Sebe, N.; Kim, B. Explainable Deep Learning for Efficient and Robust Pattern Recognition: A Survey of Recent Developments. Pattern Recognit. 2021, 120, 108102. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, L.; Li, X. A Generative Adversarial Network Based Deep Learning Method for Low-quality Defect Image Reconstruction and Recognition. IEEE Trans. Ind. Inform. 2020, 17, 3231–3240. [Google Scholar] [CrossRef]
- Neupane, D.; Seok, J. Bearing Fault Detection and Diagnosis Using Case Western Reserve University Dataset with Deep Learning Approaches: A Review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Thoppil, N.M.; Vasu, V.; Rao, C.S.P. Deep Learning Algorithms for Machinery Health Prognostics Using Time-Series Data: A Review. J. Vib. Eng. Technol. 2021, 9, 1123–1145. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; He, D.; Qu, Y. Unsupervised Rotating Machinery Fault Diagnosis Method Based on Integrated SAE–DBN and A Binary Processor. J. Intell. Manuf. 2020, 31, 1899–1916. [Google Scholar] [CrossRef]
- He, Z.Y.; Shao, H.D.; Jing, L.; Chang, J.S.; Yang, Y. Transfer Fault Diagnosis of Bearing Installed in Different Machines Using Enhanced Deep Auto-encoder. Measurement 2020, 152, 107393. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.Y.; Gao, L.; Zhang, Y.Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- He, J.J.; Wu, P.; Tong, Y.Z.; Zhang, X.J.; Lei, M.Z.; Gao, J.F. Bearing Fault Diagnosis via Improved One-Dimensional Multi-Scale Dilated CNN. Sensors 2021, 21, 7319. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.G.; Karimi, H.R.; Gelman, L. A Fuzzy Fusion Rotating Machinery Fault Diagnosis Framework Based on The Enhancement Deep Convolutional Neural Networks. Sensors 2022, 22, 671. [Google Scholar] [CrossRef] [PubMed]
- Shao, S.Y.; McAleer, S.; Yan, R.Q.; Baldi, P. Highly Accurate Machine Fault Diagnosis Using Deep Transfer Learning. IEEE Trans. Ind. Inform. 2019, 15, 2446–2455. [Google Scholar] [CrossRef]
- Cheng, Y.W.; Lin, M.X.; Wu, J.; Zhu, H.P.; Shao, X.Y. Intelligent Fault Diagnosis of Rotating Machinery Based on Continuous Wavelet Transform-Local Binary Convolutional Neural Network. Knowl. Based Syst. 2021, 216, 106796. [Google Scholar] [CrossRef]
- Fang, H.R.; Deng, J.; Zhao, B.; Shi, Y.; Zhou, J.Y.; Shao, S.Y. LEFE-Net: A Lightweight Efficient Feature Extraction Network with Strong Robustness for Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 3513311. [Google Scholar] [CrossRef]
- Ji, M.Y.; Peng, G.L.; He, J.; Liu, S.H.; Chen, Z.; Li, S.J. A Two-Stage, Intelligent Bearing-Fault-Diagnosis Method Using Order-Tracking and A One-Dimensional Convolutional Neural Network with Variable Speeds. Sensors 2021, 21, 675. [Google Scholar] [CrossRef]
- Bertocco, M.; Fort, A.; Landi, E.; Mugnaini, M.; Parri, L.; Peruzzi, G.; Pozzebon, A. Roller Bearing Failures Classification with Low Computational Cost Embedded Machine Learning. In Proceedings of the 2022 IEEE International Workshop on Metrology for Automotive (MetroAutomotive), Moden, Italy, 4–6 July 2022; pp. 12–17. [Google Scholar]
- Gao, Y.; Gao, L.; Li, X.; Cao, S. A Hierarchical Training-Convolutional Neural Network for Imbalanced Fault Diagnosis in Complex Equipment. IEEE Trans. Ind. Inform. 2022, 18, 8138–8145. [Google Scholar] [CrossRef]
- Gangsar, P.; Tiwari, R. Signal Based Condition Monitoring Techniques for Fault Detection and Diagnosis of Induction Motors: A State-of-the-Art Review. Mech. Syst. Signal Process. 2020, 144, 106908. [Google Scholar] [CrossRef]
- Wang, Y.S.; Liu, N.N.; Guo, H.; Wang, X.L. An Engine-Fault-Diagnosis System Based on Sound Intensity Analysis and Wavelet Packet Pre-Processing Neural Network. Eng. Appl. Artif. Intell. 2020, 94, 103765. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L. A New Reinforcement Learning Based Learning Rate Scheduler for Convolutional Neural Network in Fault Classification. IEEE Trans. Ind. Electron. 2021, 68, 12890–12900. [Google Scholar] [CrossRef]
- Zhang, K.; Tang, B.P.; Deng, L.; Liu, X.L. A Hybrid Attention Improved Resnet Based Fault Diagnosis Method of Wind Turbines Gearbox. Measurement 2021, 179, 109491. [Google Scholar] [CrossRef]
- Chen, Z.H.; Cen, J.; Xiong, J.B. Rolling Bearing Fault Diagnosis Using Time-Frequency Analysis and Deep Transfer Convolutional Neural Network. IEEE Access 2020, 8, 150248–150261. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Peng, G.L.; Chen, Y.H.; Gao, H.J. A Convolutional Neural Network Based on A Capsule Network with Strong Generalization for Bearing Fault Diagnosis. Neurocomputing 2019, 323, 62–75. [Google Scholar] [CrossRef]
- Pandhare, V.; Singh, J.; Lee, J. Convolutional Neural Network Based Rolling-Element Bearing Fault Diagnosis for Naturally Occurring and Progressing Defects Using Time-Frequency Domain Features. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Paris), Paris, France, 2–5 May 2019; pp. 320–326. [Google Scholar]
- Stepanov, A. Polynomial, Neural Network, and Spline Wavelet Models for Continuous Wavelet Transform of Signals. Sensors 2021, 21, 6416. [Google Scholar] [CrossRef]
- Qin, X.W.; Li, Q.L.; Dong, X.G.; Lv, S.Q. The Fault Diagnosis of Rolling Bearing Based on Ensemble Empirical Mode Decomposition and Random Forest. Shock. Vib. 2017, 2017, 2623081. [Google Scholar] [CrossRef] [Green Version]
- Arrieta, A.B.; Diaz-Rodriguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Garcia, S.; Gil-Lopez, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, Taxonomies, Opportunities and Challenges Toward Responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.R.; Kim, S.; Park, I.; Eo, T.; Hwang, D. Relevance-CAM: Your Model Already Knows Where to Look. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14939–14948. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q.Q. Axiomatic Attribution for Deep Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3319–3328. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–7 December 2017. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int. J. Comput. Vis. 2020, 128, 336–359. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.L.; Su, H.; Zhang, B.; Hu, X.L. Learning Reliable Visual Saliency for Model Explanations. IEEE Trans. Multimed. 2020, 22, 1796–1807. [Google Scholar] [CrossRef]
- Kenny, E.M.; Ford, C.; Quinn, M.; Keane, M.T. Explaining Black-Box Classifiers Using Post-Hoc Explanations-by-Example: The Effect of Explanations and Error-Rates in XAI User Studies. Artif. Intell. 2021, 294, 103459. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, Y.; Pan, W.J.; Chen, J.Y.; Qian, L.P.; Wu, Y. Visualizing Deep Learning-Based Radio Modulation Classifier. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 47–58. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.M. Bearing Fault Diagnosis Using Grad-CAM and Acoustic Emission Signals. Appl. Sci. 2020, 10, 2050. [Google Scholar] [CrossRef] [Green Version]
- Grezmak, J.; Wang, P.; Sun, C.; Gao, R.X. Explainable Convolutional Neural Network for Gearbox Fault Diagnosis. In Proceedings of the 26th CIRP Conference on Life Cycle Engineering (LCE), West Lafayette, IN, USA, 7–9 May 2019; pp. 476–481. [Google Scholar]
- Smilkov, D.; Thorat, N.; Kim, B.; Viégas, F.; Wattenberg, M. Smoothgrad: Removing Noise by Adding Noise. arXiv 2017, arXiv:1706.03825. [Google Scholar]
- Zhao, M.H.; Kang, M.S.; Tang, B.P.; Pecht, M. Multiple Wavelet Coefficients Fusion in Deep Residual Networks for Fault Diagnosis. IEEE Trans. Ind. Electron. 2019, 66, 4696–4706. [Google Scholar] [CrossRef]
- Amirtaha, T.; Hansen, M. Time-Frequency Distribution of Seismocardiographic Signals: A Comparative Study. Bioengineering 2017, 4, 32. [Google Scholar]
- Shao, S.Y.; Yan, R.Q.; Lu, Y.D.; Wang, P.; Gao, R.X. DCNN-Based Multi-Signal Induction Motor Fault Diagnosis. IEEE Trans. Instrum. Meas. 2020, 69, 2658–2669. [Google Scholar] [CrossRef]
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition Monitoring of Bearing Damage in Electromechanical Drive Systems by Using Motor Current Signals of Electric Motors: A Benchmark Data Set for Data-Driven Classification. In Proceedings of the European Conference of the Prognostics and Health Management Society, Bilbao, Spain, 6 July 2016. [Google Scholar]
- Zhao, Z.B.; Li, T.F.; Wu, J.Y.; Sun, C.; Wang, S.B.; Yan, R.Q.; Chen, X.F. Deep Learning Algorithms for Rotating Machinery Intelligent Diagnosis: An Open Source Benchmark Study. ISA Trans. 2020, 107, 224–255. [Google Scholar] [CrossRef]
- Bechhoefer, E. Machinery Failure Prevention Technology (MFPT) Datasets. 2013. Available online: https://mfpt.org/fault-datasets (accessed on 28 July 2022).
- Case Western Reserve University Bearing Data Center. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 2 November 2022).








| λ | AlexNet | ResNet18 | VGG16 | |||
|---|---|---|---|---|---|---|
| (kHz) | Acc (%) | (kHz) | Acc (%) | (kHz) | Acc (%) | |
| 1 | 0.4–9.9 | 97.67 ± 0.17 | 0.6–10.1 | 98.41 ± 0.35 | 0.2–10.1 | 97.20 ± 0.20 |
| 0.7 | 0.4–10.2 | 97.89 ± 0.25 | 0.6–10.3 | 98.42 ± 0.19 | 0.2–10.3 | 97.51 ± 0.12 |
| 0.6 | 0.4–10.5 | 98.13 ± 0.21 | 0.4–11.5 | 98.90 ± 0.19 | 0.2–11.2 | 97.82 ± 0.31 |
| 0.5 | 0.4–11.1 | 98.29 ± 0.25 | 0.4–12.9 | 99.18 ± 0.37 | 0.3–12.0 | 97.81 ± 0.23 |
| 0.4 | 0.4–11.2 | 98.28 ± 0.10 | 0.4–13.2 | 99.17 ± 0.35 | 0.3–12.9 | 97.98 ± 0.14 |
| 0.35 | 0.4–12.2 | 98.46 ± 0.27 | 0.4–15.3 | 99.38 ± 0.31 | 0.2–16.6 | 98.67 ± 0.26 |
| 0.3 | 0.4–12.3 | 98.51 ± 0.28 | 0.4–17.0 | 99.54 ± 0.17 | 0.2–19.0 | 98.53 ± 0.28 |
| 0.25 | 0.2–16.8 | 98.61 ± 0.32 | 0.2–17.4 | 99.52 ± 0.21 | 0.2–19.1 | 98.58 ± 0.12 |
| 0.2 | 0.2–25.1 | 98.42 ± 0.15 | 0.2–22.8 | 99.23 ± 0.21 | 0.2–23.6 | 98.25 ± 0.14 |
| λ | AlexNet | ResNet18 | VGG16 | |||
|---|---|---|---|---|---|---|
| (kHz) | Acc (%) | (kHz) | Acc (%) | (kHz) | Acc (%) | |
| 1 | 1.0–18.7 | 89.04 ± 0.33 | 0.7–17.0 | 92.23 ± 0.45 | 1.1–17.7 | 92.23 ± 0.23 |
| 0.7 | 0.9–18.8 | 89.21 ± 0.25 | 0.5–17.4 | 92.24 ± 0.17 | 0.8–18,7 | 92.31 ± 0.34 |
| 0.6 | 0.9–19.0 | 89.12 ± 0.21 | 0.5–17.7 | 92.22 ± 0.23 | 0.7–18.7 | 92.69 ± 0.21 |
| 0.5 | 0.7–19.3 | 90.41 ± 0.31 | 0.5–17.9 | 92.32 ± 0.27 | 0.7–18.7 | 92.69 ± 0.21 |
| 0.4 | 0.5–19.4 | 91.32 ± 0.10 | 0.5–18.1 | 92.99 ± 0.35 | 0.5–18.9 | 93.45 ± 0.14 |
| 0.35 | 0.5–19.4 | 91.32 ± 0.10 | 0.5–18.3 | 93.38 ± 0.23 | 0.5–18.9 | 93.45 ± 0.14 |
| 0.3 | 0.4–20.0 | 91.87 ± 0.32 | 0.4–20.5 | 94.00 ± 0.12 | 0.5–19.1 | 94.52 ± 0.24 |
| 0.25 | 0.4–20.0 | 91.87 ± 0.32 | 0.4–20.5 | 94.00 ± 0.12 | 0.5–19.4 | 93.33 ± 0.22 |
| 0.2 | 0.2–22.1 | 91.32 ± 0.37 | 0.3–21.5 | 91.67 ± 0.43 | 0.5–23.1 | 91.21 ± 0.25 |
| λ | AlexNet | ResNet18 | VGG16 | |||
|---|---|---|---|---|---|---|
| (kHz) | Acc (%) | (kHz) | Acc (%) | (kHz) | Acc (%) | |
| 1 | 0.4–1.1 | 97.25 ± 0.17 | 0.3–3.3 | 99.14 ± 0.25 | 0.3–2.9 | 97.51 ± 0.22 |
| 0.7 | 0.3–1.6 | 97.50 ± 0.08 | 0.3–5.0 | 99.25 ± 0.12 | 0.3–3.2 | 97.85 ± 0.32 |
| 0.6 | 0.3–4.2 | 97.43 ± 0.21 | 0.3–5.8 | 99.31 ± 0.18 | 0.3–5.1 | 98.36 ± 0.26 |
| 0.5 | 0.3–7.8 | 98.19 ± 0.15 | 0.3–7.7 | 99.18 ± 0.37 | 0.3–8.2 | 98.41 ± 0.13 |
| 0.4 | 0.3–8.0 | 98.28 ± 0.26 | 0.3–8.1 | 99.22 ± 0.25 | 0.3–8.5 | 98.45 ± 0.24 |
| 0.35 | 0.3–8.2 | 98.46 ± 0.19 | 0.3–9.0 | 99.74 ± 0.12 | 0.3–8.7 | 98.56 ± 0.18 |
| 0.3 | 0.3–8.8 | 98.71 ± 0.23 | 0.3–10.3 | 99.49 ± 0.27 | 0.3–9.3 | 99.05 ± 0.15 |
| 0.25 | 0.3–9.9 | 98.42 ± 0.30 | 0.2–11.4 | 99.48 ± 0.22 | 0.2–10.3 | 98.78 ± 0.27 |
| 0.2 | 0.2–21.1 | 98.21 ± 0.15 | 0.2–22.8 | 99.23 ± 0.31 | 0.2–19.9 | 98.25 ± 0.28 |
| λ | AlexNet | ResNet18 | VGG16 | |||
|---|---|---|---|---|---|---|
| (kHz) | Acc (%) | (kHz) | Acc (%) | (kHz) | Acc (%) | |
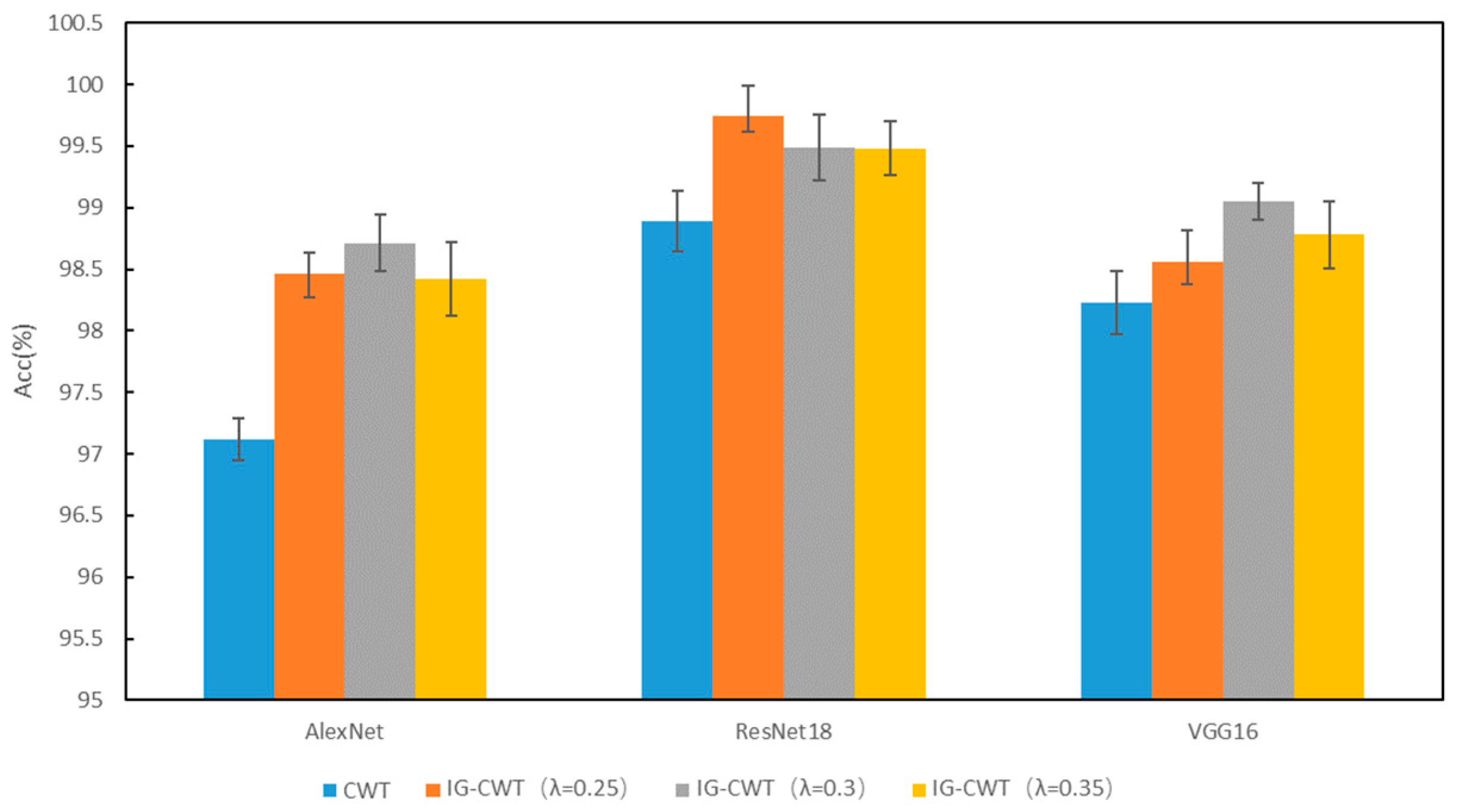
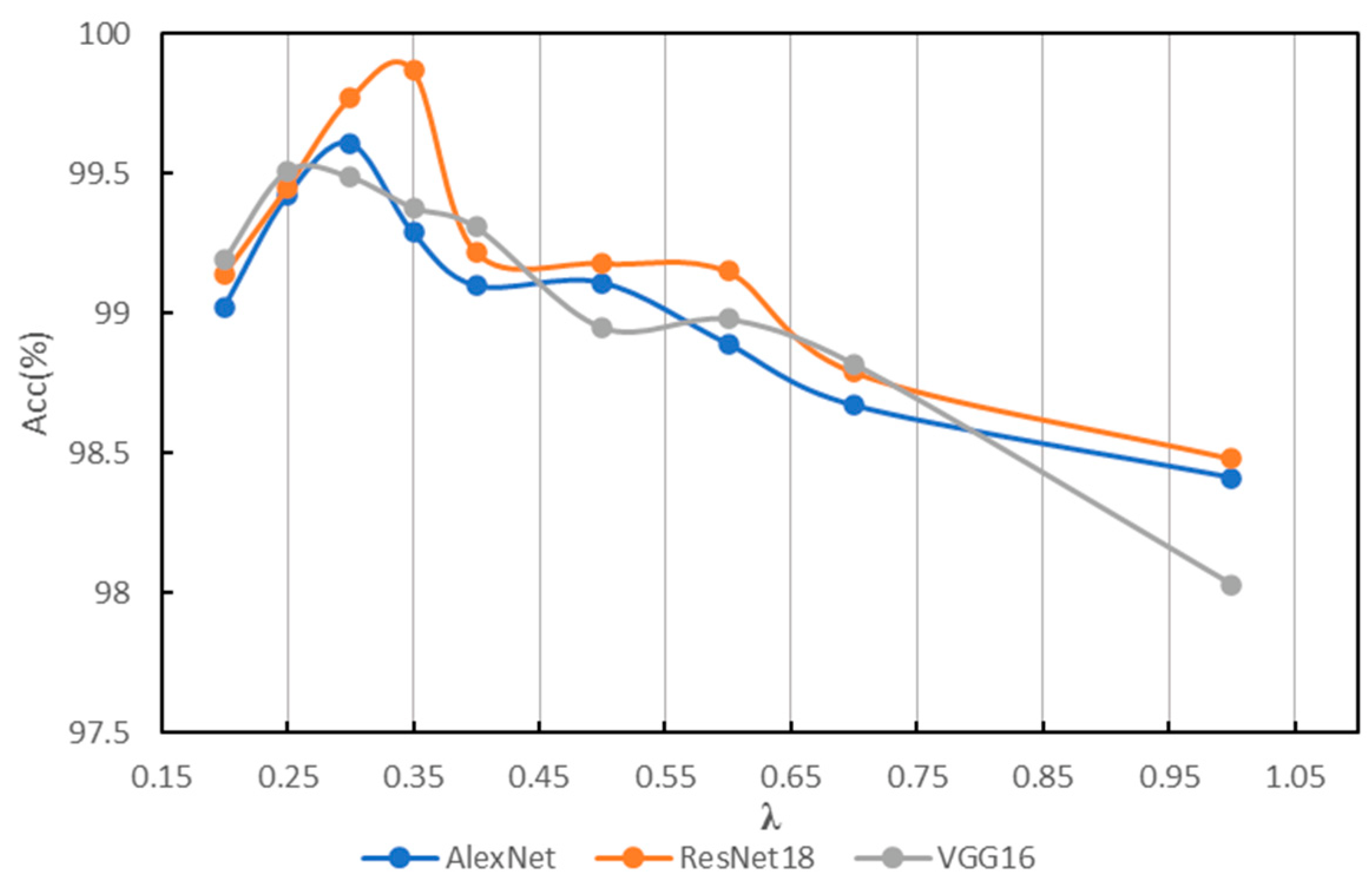
| 1 | 0.2–2.3 | 98.41 ± 0.12 | 0.3–2.4 | 98.48 ± 0.21 | 0.2–2.2 | 98.03 ± 0.34 |
| 0.7 | 0.2–3.0 | 98.67 ± 0.21 | 0.2–2.9 | 98.79 ± 0.16 | 0.2–2.8 | 98.82 ± 0.15 |
| 0.6 | 0.2–3.4 | 98.89 ± 0.14 | 0.2–3.4 | 99.15 ± 0.14 | 0.2–3.3 | 98.98 ± 0.21 |
| 0.5 | 0.1–3.8 | 99.11 ± 0.18 | 0.2–3.7 | 99.18 ± 0.12 | 0.2–3.5 | 98.95 ± 0.11 |
| 0.4 | 0.1–3.9 | 99.10 ± 0.19 | 0.1–4.0 | 99.22 ± 0.21 | 0.1–3.9 | 99.31 ± 0.15 |
| 0.35 | 0.1–4.2 | 99.29 ± 0.21 | 0.1–4.6 | 99.87 ± 0.20 | 0.1–4.2 | 99.38 ± 0.18 |
| 0.3 | 0.1–4.5 | 99.61 ± 0.09 | 0.1–4.7 | 99.77 ± 0.11 | 0.1–4.5 | 99.49 ± 0.17 |
| 0.25 | 0.1–4.8 | 99.42 ± 0.13 | 0.1–5.0 | 99.45 ± 0.24 | 0.1–4.6 | 99.51 ± 0.18 |
| 0.2 | 0.0–5.2 | 99.02 ± 0.24 | 0.0–5.4 | 99.14 ± 0.16 | 0.0–5.1 | 99.19 ± 0.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Li, X.; Gao, Y.; Gao, L. Integrated Gradient-Based Continuous Wavelet Transform for Bearing Fault Diagnosis. Sensors 2022, 22, 8760. https://doi.org/10.3390/s22228760
Du J, Li X, Gao Y, Gao L. Integrated Gradient-Based Continuous Wavelet Transform for Bearing Fault Diagnosis. Sensors. 2022; 22(22):8760. https://doi.org/10.3390/s22228760
Chicago/Turabian StyleDu, Junfei, Xinyu Li, Yiping Gao, and Liang Gao. 2022. "Integrated Gradient-Based Continuous Wavelet Transform for Bearing Fault Diagnosis" Sensors 22, no. 22: 8760. https://doi.org/10.3390/s22228760
APA StyleDu, J., Li, X., Gao, Y., & Gao, L. (2022). Integrated Gradient-Based Continuous Wavelet Transform for Bearing Fault Diagnosis. Sensors, 22(22), 8760. https://doi.org/10.3390/s22228760







