Spread Spectrum Modulation with Grassmannian Constellations for Mobile Multiple Access Underwater Acoustic Channels
Abstract
1. Introduction
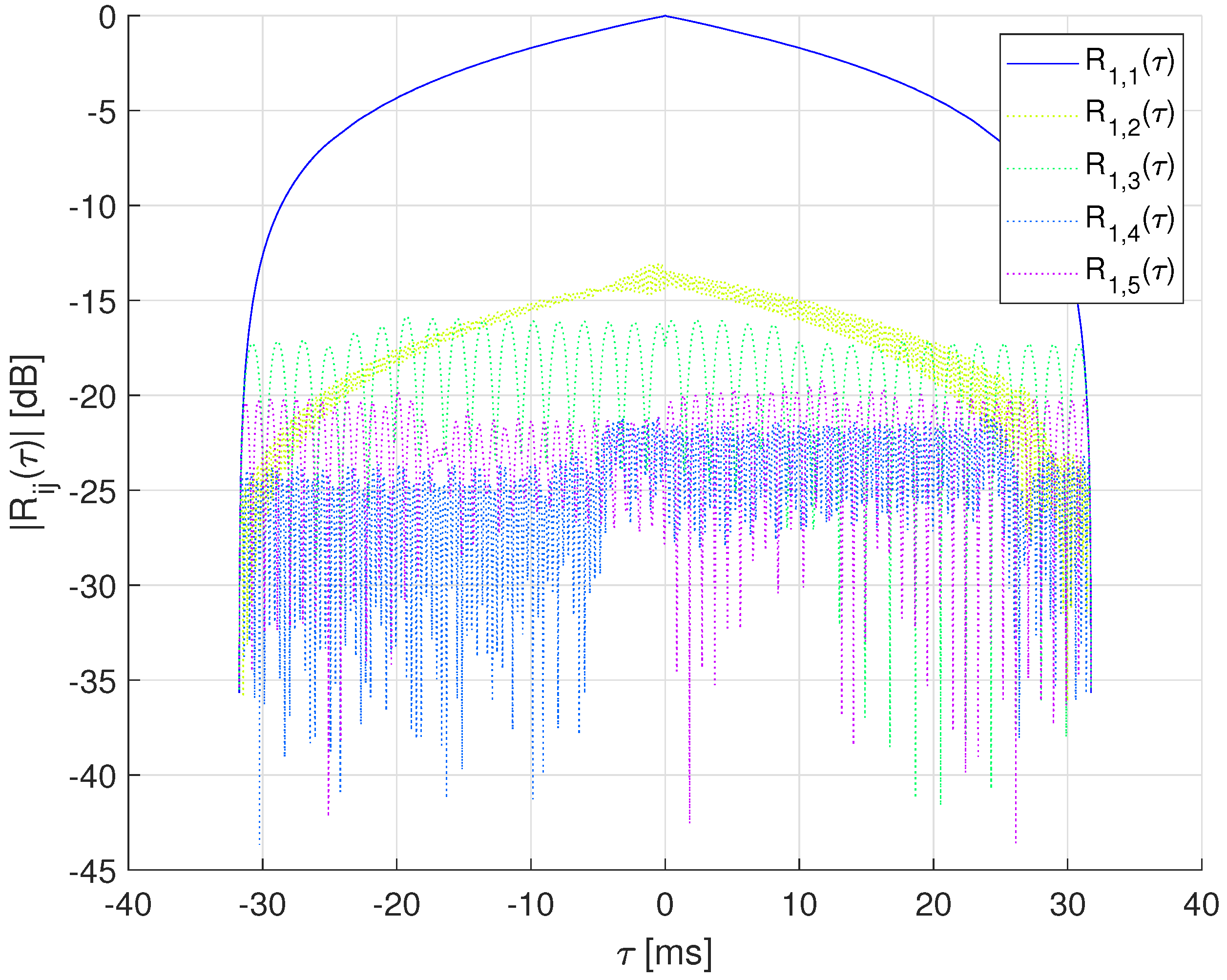
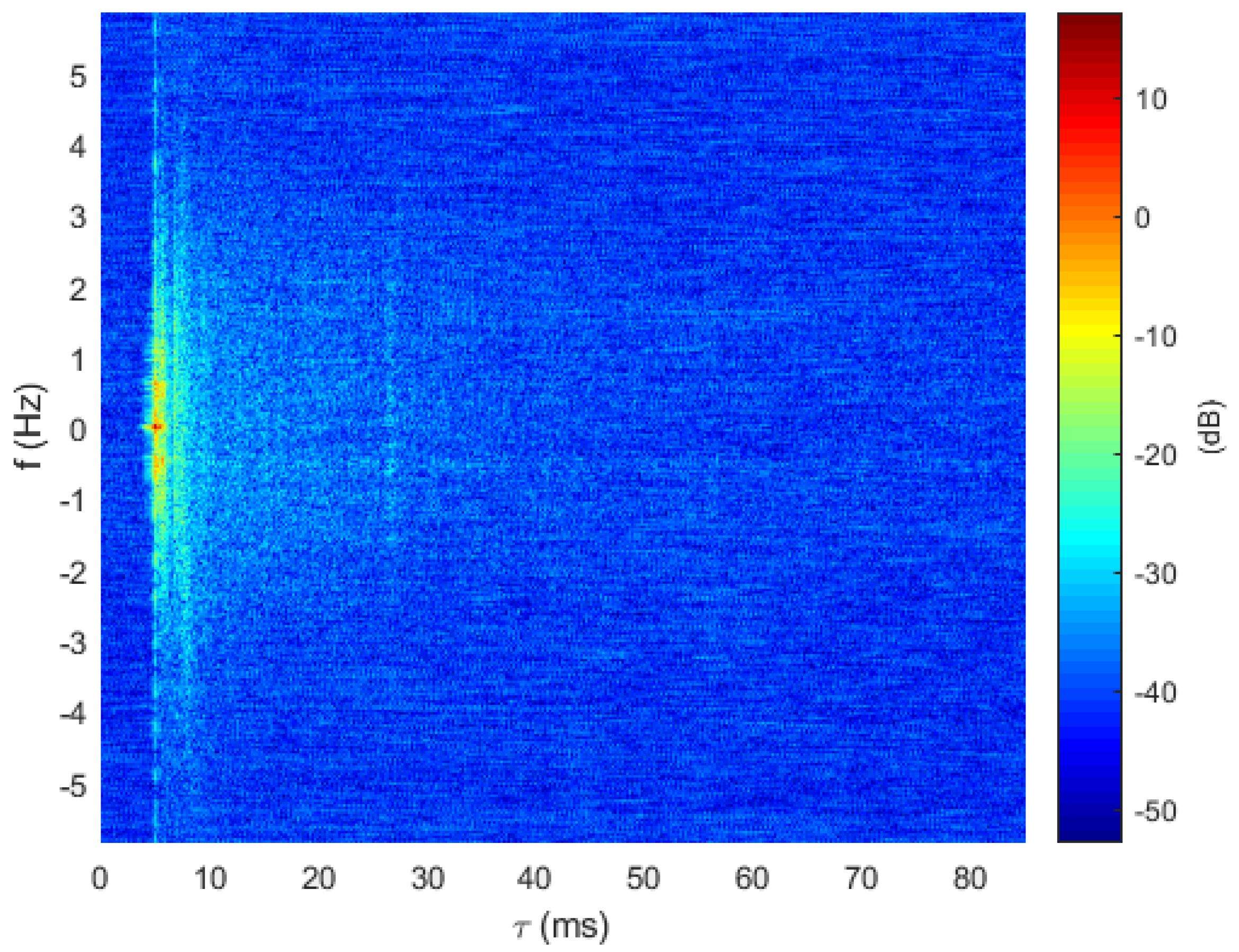
- The implementation of Doppler shift estimation and frame synchronization processes at the receiver side for more realistic communication and a comparison of the MU-HFM spreading sequence against Pseudo-Noise (PN) sequence as preamble for Doppler shift estimation.
2. System Model
2.1. Mathematical Notations
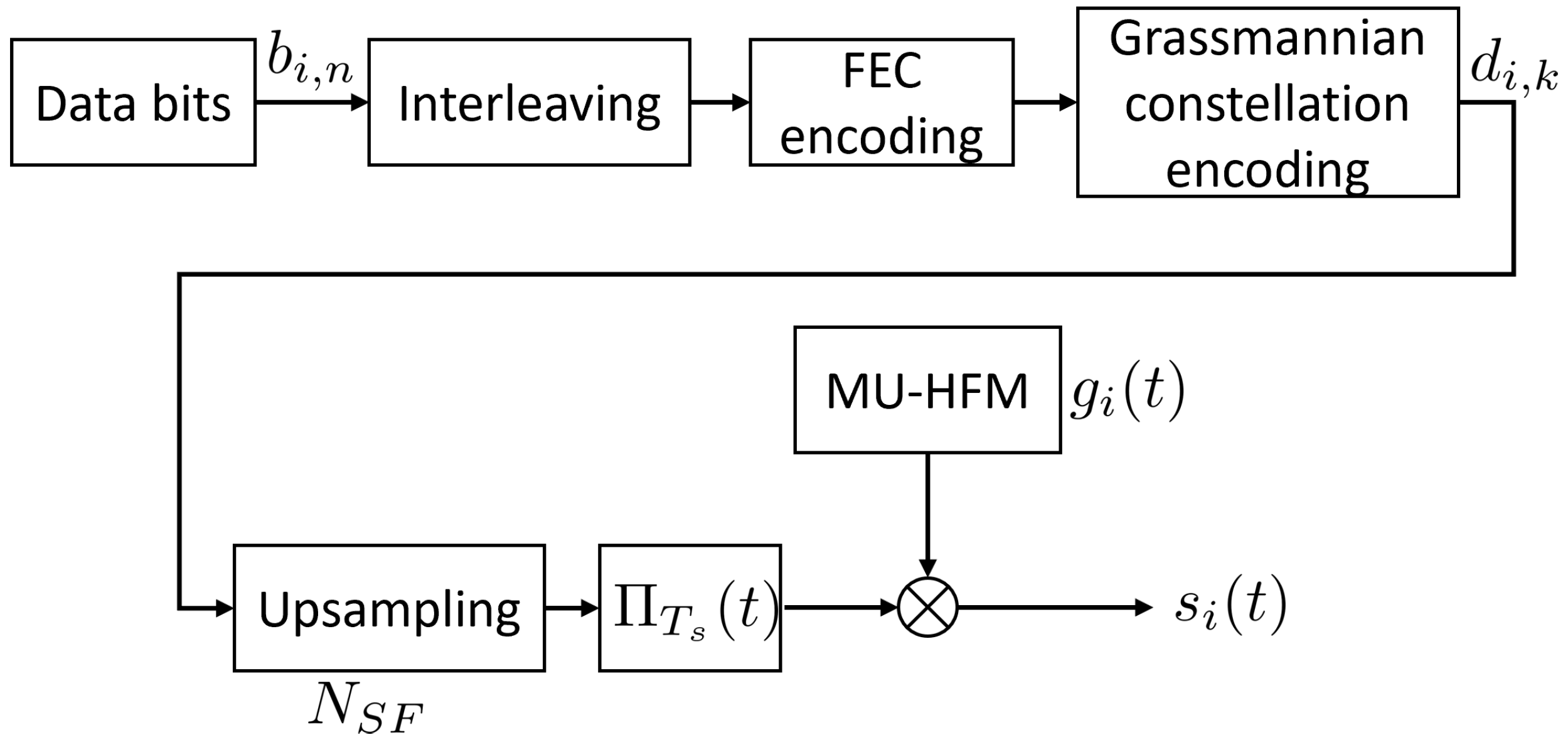
2.2. Transmitter
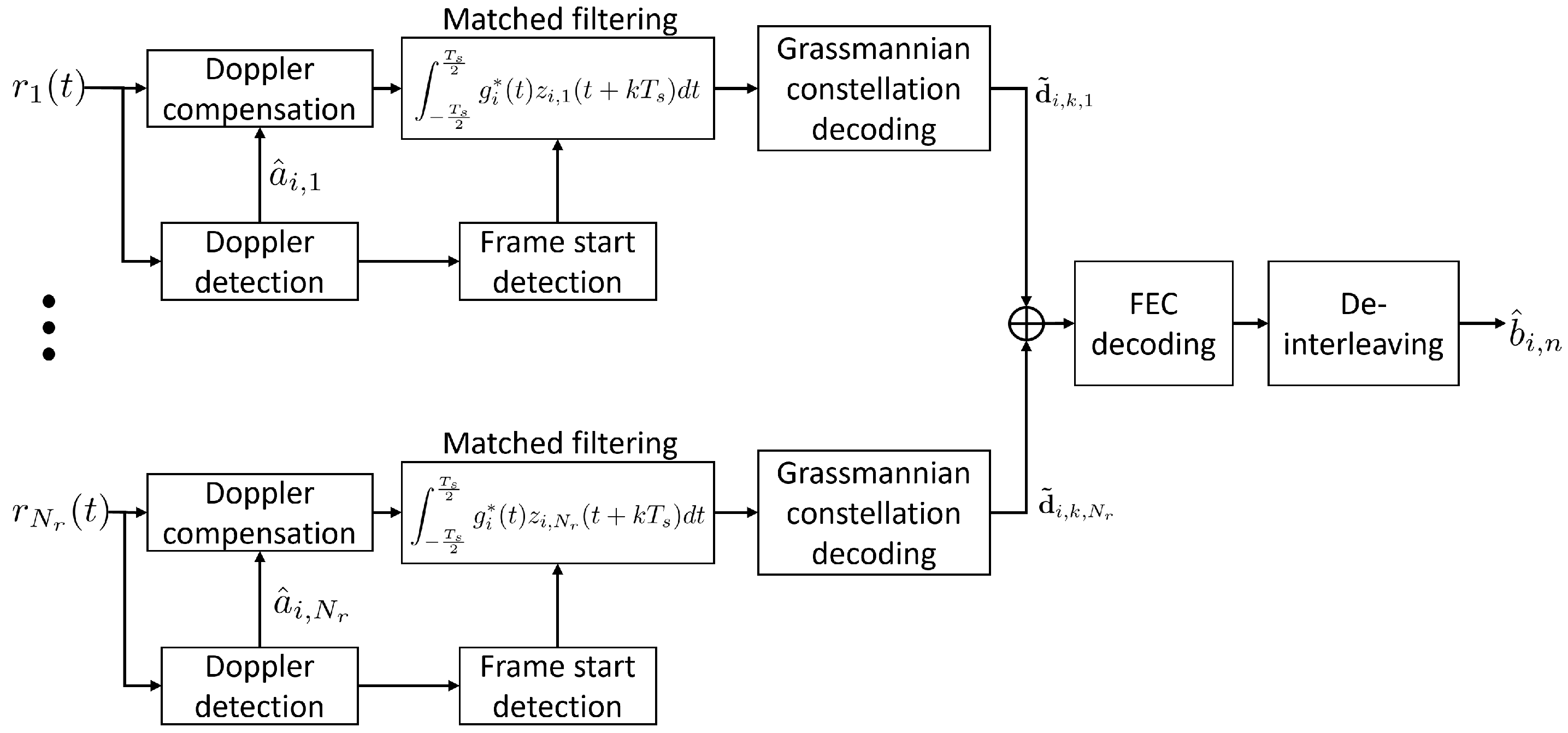
2.3. Receiver Architecture
3. Grassmannian Constellations
3.1. Transmitter Modulation Scheme Design
3.2. Receiver Demodulation Scheme Design
4. Results and Discussion
4.1. Watermark Replay Channel
4.2. Performance Metrics
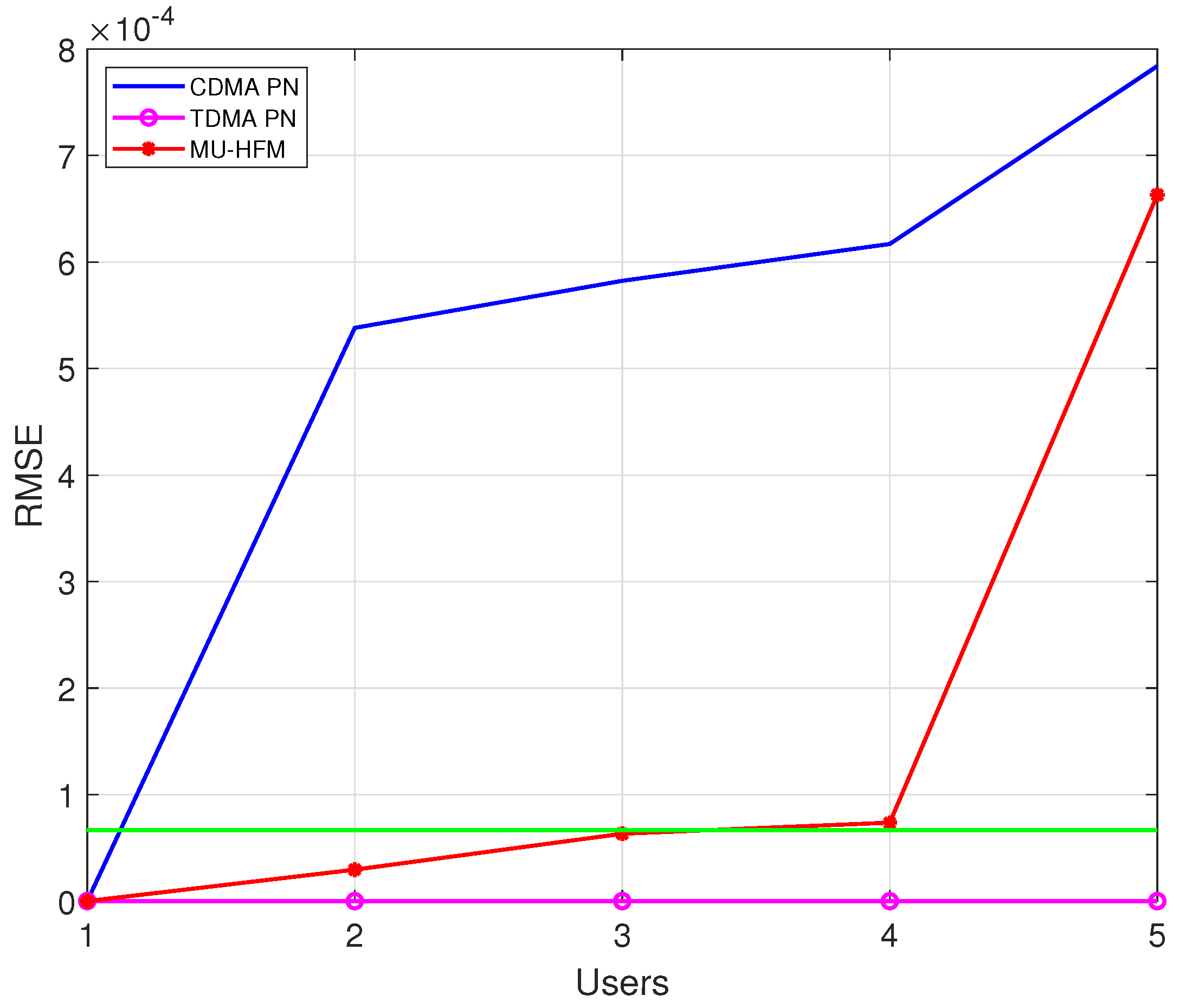
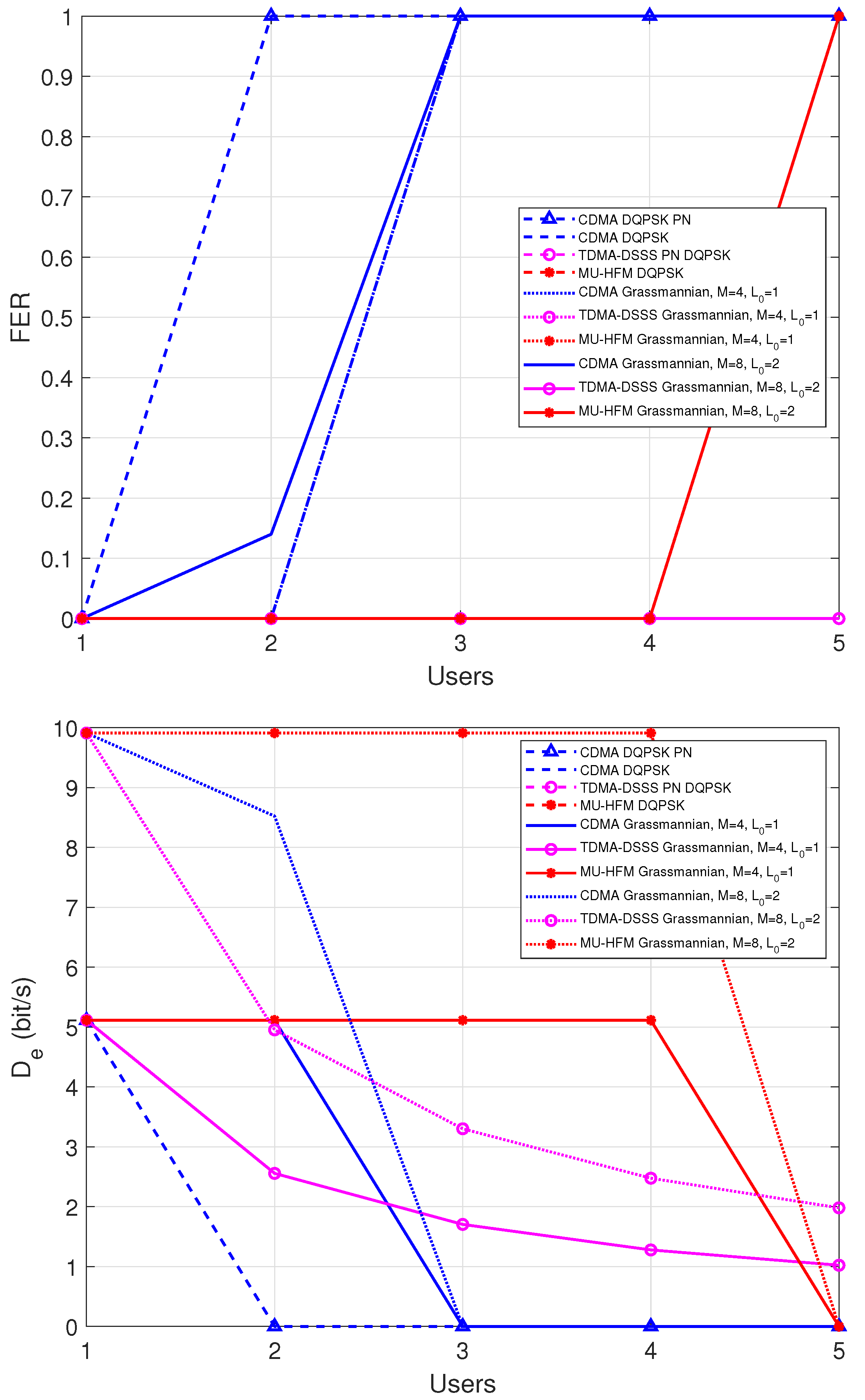
4.3. Performance Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| AUV | Autonomous Underwater Vehicle |
| AWGN | Additive White Gaussian Noise |
| BER | Bit Error Rate |
| CP | Cyclic Prefix |
| CDMA | Code-Division Multiple Access |
| CIR | Channel Impulse Response |
| CSI | Channel State Information |
| CSMA | Carrier Sense Multiple Access |
| PSK | Phase Shift Keying |
| DFE | Decision Feedback Equalizer |
| DPSK | Differential Phase Shift Keying |
| DBPSK | Differential Binary Phase Shift Keying |
| DQPSK | Differential Quaternary Phase Shift Keying |
| DSSS | Direct Sequence Spread Spectrum |
| FDMA | Frequency Divsion Multiple Access |
| FEC | Forward Error Correction |
| FER | Frame Error Rate |
| FFT | Fast Fourier Transform |
| FSK | Frequency Shift Keying |
| HFM | Hyperbolically Frequency Modulation |
| ISI | Inter Symbol Interference |
| MC-CDMA | Multi-Carrier Code-Division Multiple Access |
| MLS | Maximal Length Sequence |
| CSS | Chirp Spread Spectrum |
| LFM | Linear Frequency Modulation |
| MU-CSS | MultiUser Chirp Spread Spectrum |
| MU-HFM | MultiUser Hyperbolically Frequency Modulation |
| MU-MIMO | multiuser Multiple-Input Multiple-Output |
| OFDM | Orthogonal Frequency Division Multiplex |
| PN | Pseudo-Noise |
| PPC | Passive Phase Conjugation |
| QAM | Quadrature Amplitude Modulation |
| R_c | FEC rate |
| RMS | Root Mean Square |
| SIMO | Single Input Multiple Output |
| SISO | Single Input Single Output |
| SINR | Signal-to-Interference-plus-Noise Ratio |
| SNR | Signal-to-Noise Ratio |
| SRRC | Square Root Raised Cosine |
| TDMA | Time-Division Multiple Access |
| UAC | Underwater Acoustic channel |
| UWA | Underwater Acoustic |
| Watermark | underWater AcousTic channEl Replay benchMARK |
| VTRM | Virtual Time Reversal Mirror |
| FrFT | Fractional Fourier Transform |
| RMSE | Root Mean Square Error |
Appendix A. Calculation of γi,k,p, ηi,k,p and wi,k,p
Appendix B. Definition of the Bijective Mapping ϕl for the Cube-Split Modulation
References
- Stojanovic, M.; Preisig, J. Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Stojanovic, M.; Beaujean, P.P.J. Acoustic Communication. In Springer Handbook of Ocean Engineering; Dhanak, M.R., Xiros, N.I., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 359–386. [Google Scholar] [CrossRef]
- Stojanovic, M.; Freitag, L.; Johnson, M. Channel-estimation-based adaptive equalization of underwateracoustic signals. Oceans 1999, 2, 985–990. [Google Scholar] [CrossRef]
- Li, W.; Preisig, J.C. Estimation of Rapidly Time-Varying Sparse Channels. IEEE J. Ocean. Eng. 2007, 32, 927–939. [Google Scholar] [CrossRef]
- Roy, S.; Duman, T.M.; McDonald, V.; Proakis, J.G. High-Rate Communication for Underwater Acoustic Channels Using Multiple Transmitters and Space-Time Coding: Receiver Structures and Experimental Results. IEEE J. Ocean. Eng. 2007, 32, 663–688. [Google Scholar] [CrossRef]
- Yang, T.C. Spatially Multiplexed CDMA Multiuser Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2016, 41, 217–231. [Google Scholar] [CrossRef]
- Wang, K.; Chen, S.; Liu, C.; Liu, Y.; Xu, Y. Doppler estimation and timing synchronization of underwater acoustic communication based on hyperbolic frequency modulation signal. In Proceedings of the 2015 IEEE 12th International Conference on Networking, Sensing and Control, Taipei, Taiwan, 9–11 April 2015; pp. 75–80. [Google Scholar] [CrossRef]
- Wei, R.; Ma, X.; Zhao, S.; Yan, S. Doppler Estimation Based on Dual-HFM Signal and Speed Spectrum Scanning. IEEE Signal Process. Lett. 2020, 27, 1740–1744. [Google Scholar] [CrossRef]
- Peng, Y.; Song, C.; Qi, L.; Liu, P.; Dong, Y.; Yang, Y.; Zhang, B.; Qi, Z. JLHS: A Joint Linear Frequency Modulation and Hyperbolic Frequency Modulation Approach for Speed Measurement. IEEE Access 2020, 8, 205316–205326. [Google Scholar] [CrossRef]
- Sharif, B.S.; Neasham, J.; Hinton, O.R.; Adams, A.E. A computationally efficient Doppler compensation system for underwater acoustic communications. IEEE J. Ocean. Eng. 2000, 25, 52–61. [Google Scholar] [CrossRef]
- Otnes, R.; Asterjadhi, A.; Casari, P.; Goetz, M.; Husøy, T.; Nissen, I.; Rimstad, K.; Walree, P.v.; Zorzi, M. Underwater Acoustic Networking Techniques; Springer Briefs in Electrical and Computer Engineering; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Bernard, C.; Bouvet, P.J.; Pottier, A.; Forjonel, P. Multiple access acoustic communication in underwater mobile networks. In Proceedings of the 2021 5th Underwater Communications and Networking Conference (UComms), Virtual, 31 August–2 September 2021. [Google Scholar]
- Decurninge, A.; Guillaud, M. Cube-Split: Structured Quantizers on the Grassmannian of Lines. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Ngo, K.; Decurninge, A.; Guillaud, M.; Yang, S. Design and analysis of a practical codebook for non-coherent communications. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 1237–1241. [Google Scholar] [CrossRef]
- Beko, M.; Xavier, J.; Barroso, V.A.N. Noncoherent Communication in Multiple-Antenna Systems: Receiver Design and Codebook Construction. IEEE Trans. Signal Process. 2007, 55, 5703–5715. [Google Scholar] [CrossRef][Green Version]
- Tahir, B.; Schwarz, S.; Rupp, M. Constructing Grassmannian Frames by an Iterative Collision-Based Packing. IEEE Signal Process. Lett. 2019, 26, 1056–1060. [Google Scholar] [CrossRef]
- Van Walree, P.; Socheleau, F.X.; Otnes, R.; Jenserud, T. The Watermark Benchmark for Underwater Acoustic Modulation Schemes. IEEE J. Ocean. Eng. 2017, 42, 1007–1018. [Google Scholar] [CrossRef]
- Ralston, A. A First Course in Numerical Analysis; Dover Publications Inc.: Mineola, NY, USA, 2001. [Google Scholar]
- Lang, S. Introduction to Linear Algebra; Springer: New York, NY, USA, 1985. [Google Scholar]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Cho, S.E.; Song, H.C.; Hodgkiss, W.S. Multiuser acoustic communications with mobile users. J. Acoust. Soc. Am. 2013, 133, 880–890. [Google Scholar] [CrossRef] [PubMed]
- Stojanovic, M. Underwater Acoustic Communications: Design Considerations on the Physical Layer. In Proceedings of the 2008 Fifth Annual Conference on Wireless on Demand Network Systems and Services, Garmisch-Partenkirchen, Germany, 23–25 January 2008; pp. 1–10. [Google Scholar] [CrossRef]
- Bernard, C.; Bouvet, P.J.; Pottier, A.; Forjonel, P. Multiuser Chirp Spread Spectrum Transmission in an Underwater Acoustic Channel Applied to an AUV Fleet. Sensors 2020, 20, 1527. [Google Scholar] [CrossRef] [PubMed]
- Aval, Y.M.; Wilson, S.K.; Stojanovic, M. On the Average Achievable Rate of QPSK and DQPSK OFDM Over Rapidly Fading Channels. IEEE Access 2018, 6, 23659–23667. [Google Scholar] [CrossRef]
- Proakis, J.G.; Salehi, M. Digital Communications, 5th ed.; McGraw-Hill: Boston, MA, USA, 2008. [Google Scholar]
- Ngo, K.; Decurninge, A.; Guillaud, M.; Yang, S. Cube-Split: A Structured Grassmannian Constellation for Non-Coherent SIMO Communications. IEEE Trans. Wirel. Commun. 2020, 19, 1948–1964. [Google Scholar] [CrossRef]
- Gohary, R.H.; Davidson, T.N. Noncoherent MIMO Communication: Grassmannian Constellations and Efficient Detection. IEEE Trans. Inf. Theory 2009, 55, 1176–1205. [Google Scholar] [CrossRef]
- Stojanovic, M. Acoustic (Underwater) Communications. In Wiley Encyclopedia of Telecommunications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Bouvet, P.J.; Forjonel, P.; Auffret, Y. IROMI-LMAIR: An Innovative Network of Instrumental Platforms for Marine And Underwater Technologies; Sea Tech Week/Moqesm; Brest (Virtual), France, 13–15 October 2020. Available online: https://hal.archives-ouvertes.fr/hal-03022067 (accessed on 5 October 2022).
- van Walree, P.A. Channel Sounding for Acoustic Communications: Techniques and Shallow-Water Examples; Norwegian Defence Research Establishment: Kjeller, Norway, 2011. [Google Scholar]
- Thorp, W.H. Analytic Description of the Low-Frequency Attenuation Coefficient. Acoust. Soc. Am. J. 1967, 42, 270. [Google Scholar] [CrossRef]

| Symbol | Signification | Value |
|---|---|---|
| Center frequency | 27 kHz | |
| Sampling frequency | 96 kHz | |
| B | Signal bandwidth | 4 kHz |
| Transmission range | [65, 540] m | |
| Water depth | 10 m | |
| SNR | Signal to noise ratio | 10 dB |
| RMS channel delay spread [30] | [8.85, 26.49] ms | |
| RMS channel Doppler spread [30] | [0.85, 2.9] Hz |
| Symbol | Signification | Value |
|---|---|---|
| M | Grassmannian modulation order | 4, 8 |
| Number of local coordinates | 1, 2 | |
| Number of hydrophone receiving | 5 | |
| Number of symbols per frame | 200 | |
| Number of frames | 5000 | |
| FEC code type | Convolutive code | |
| FEC code generator | (133, 171)o | |
| FEC code rate | ||
| Guard interval time TDMA | 31.3 ms | |
| Chip duration | 0.25 ms | |
| , | Bounds of HFM signal | 6 kHz, 10 kHz |
| Pulse shaping filter roll-off factor | 0.25 | |
| Symbol duration | 31.75 ms | |
| Spreading factor | 127 | |
| Preamble duration | 63.75 ms | |
| Spreading factor for the preamble | 255 | |
| Guard interval time between the preamble and the message | 100 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernard, C.; Bouvet, P.-J.; Tomasi, B. Spread Spectrum Modulation with Grassmannian Constellations for Mobile Multiple Access Underwater Acoustic Channels. Sensors 2022, 22, 8518. https://doi.org/10.3390/s22218518
Bernard C, Bouvet P-J, Tomasi B. Spread Spectrum Modulation with Grassmannian Constellations for Mobile Multiple Access Underwater Acoustic Channels. Sensors. 2022; 22(21):8518. https://doi.org/10.3390/s22218518
Chicago/Turabian StyleBernard, Christophe, Pierre-Jean Bouvet, and Beatrice Tomasi. 2022. "Spread Spectrum Modulation with Grassmannian Constellations for Mobile Multiple Access Underwater Acoustic Channels" Sensors 22, no. 21: 8518. https://doi.org/10.3390/s22218518
APA StyleBernard, C., Bouvet, P.-J., & Tomasi, B. (2022). Spread Spectrum Modulation with Grassmannian Constellations for Mobile Multiple Access Underwater Acoustic Channels. Sensors, 22(21), 8518. https://doi.org/10.3390/s22218518







