3D Metrology Using One Camera with Rotating Anamorphic Lenses
Abstract
1. Introduction
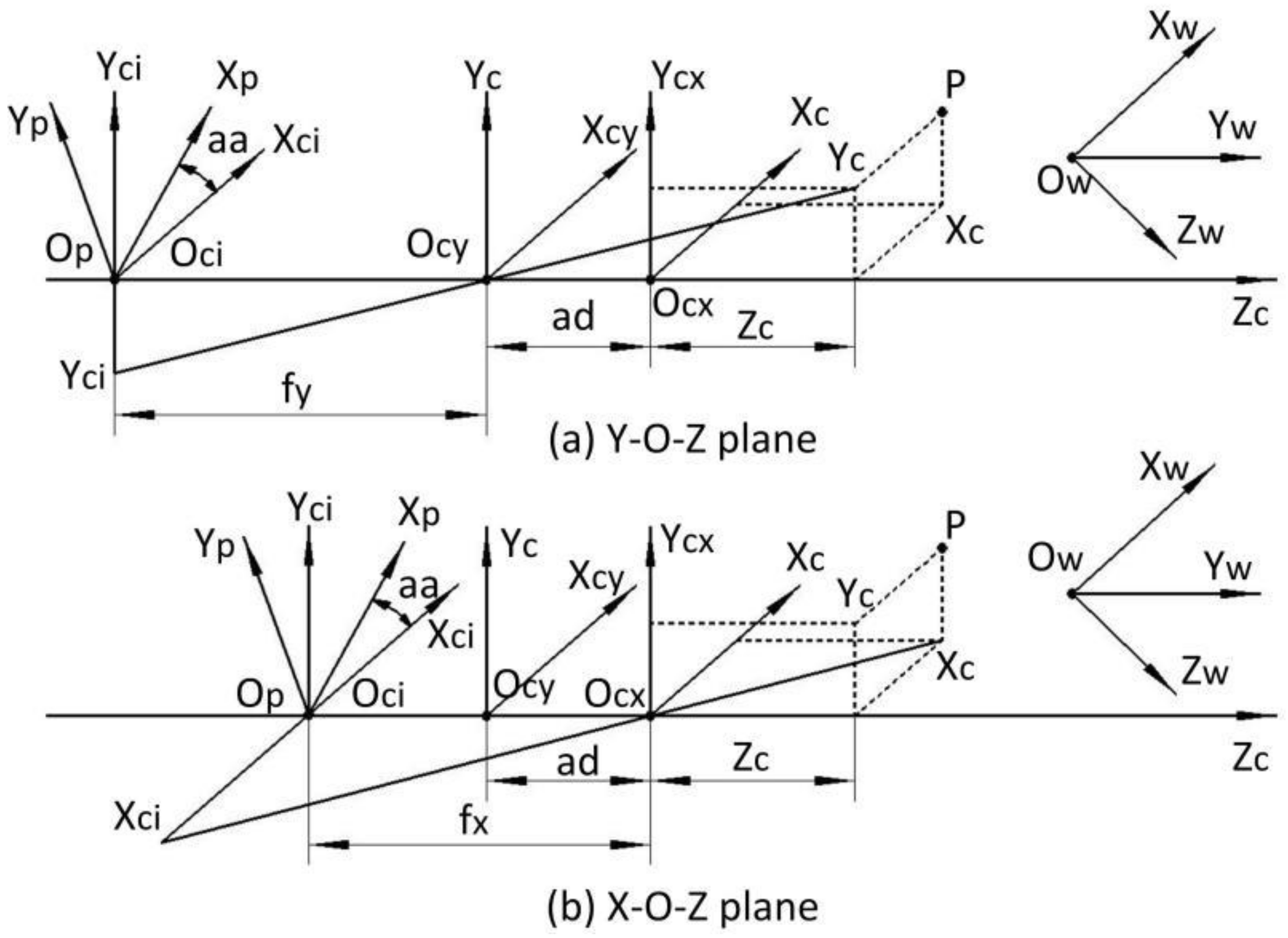
2. Anamorphic Imaging Model
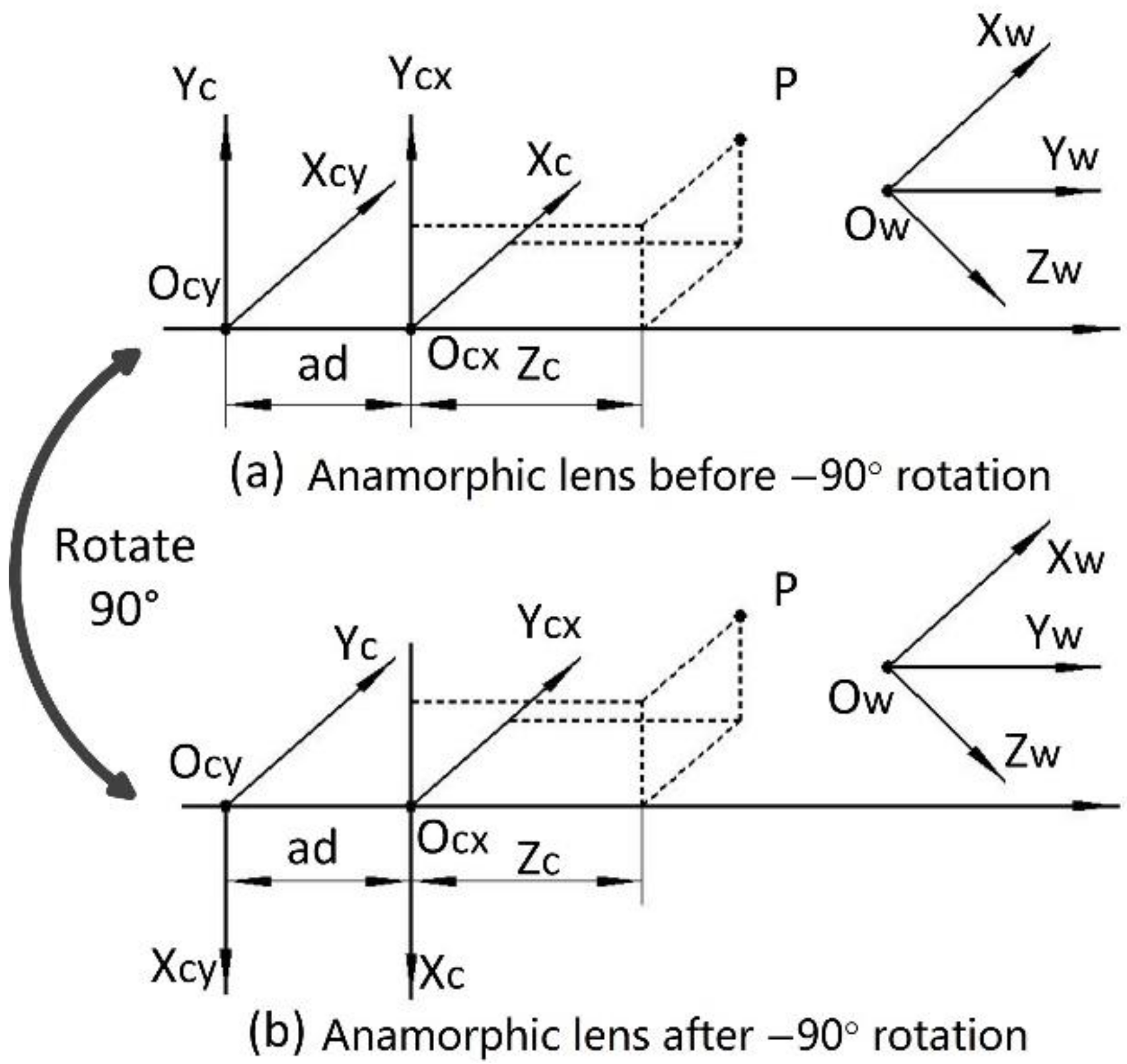
2.1. Anamorphic Imaging Model
2.2. Anamorphic Distortion Model
3. 3D Metrology Using Rotating Anamorphic Lenses
3.1. Description of 3D Metrology Using Rotating Anamorphic Lenses
3.2. Point Matching
3.3. Stereo Vision with Anamorphic Lenses
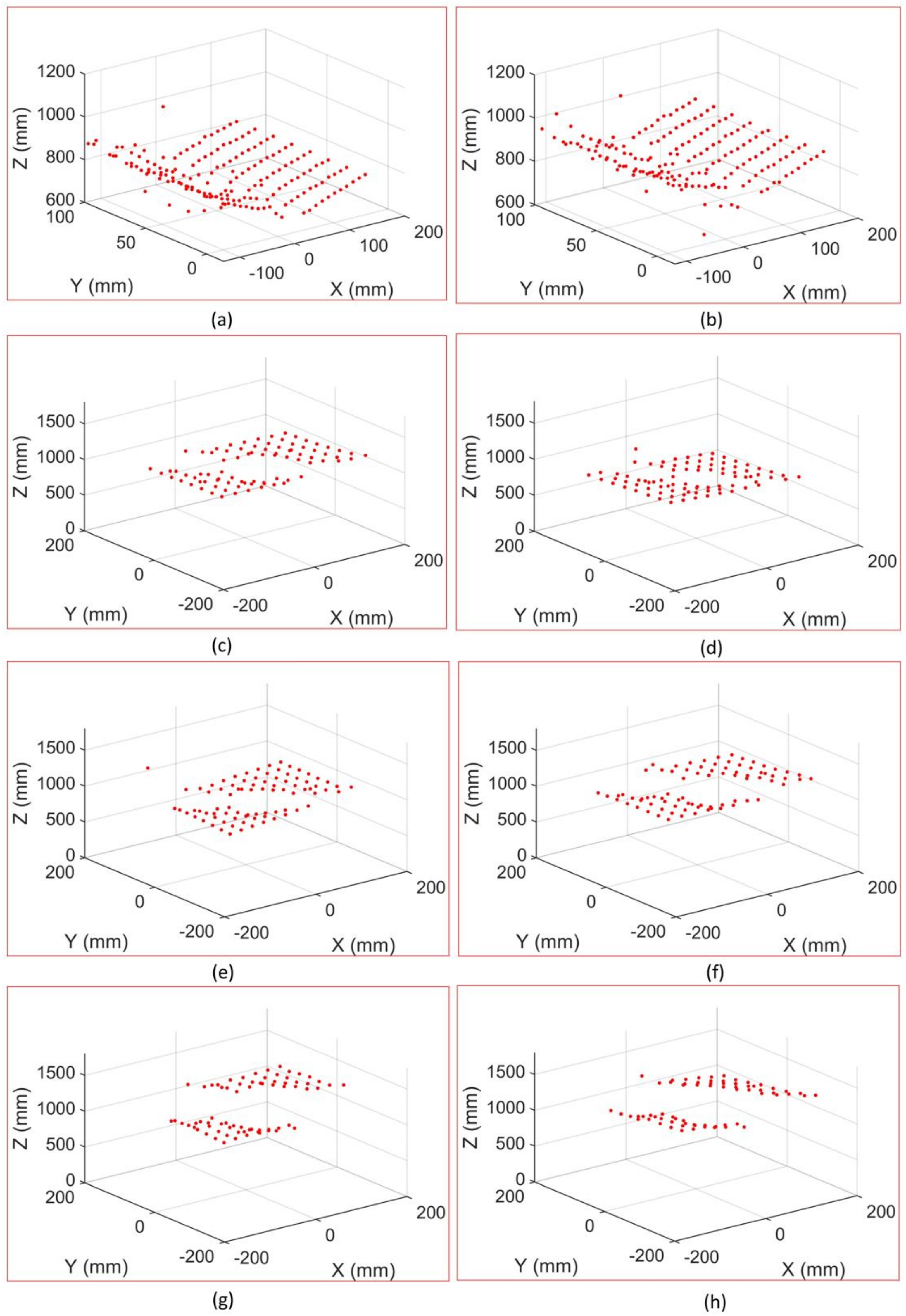
4. Experiments
4.1. Experiments
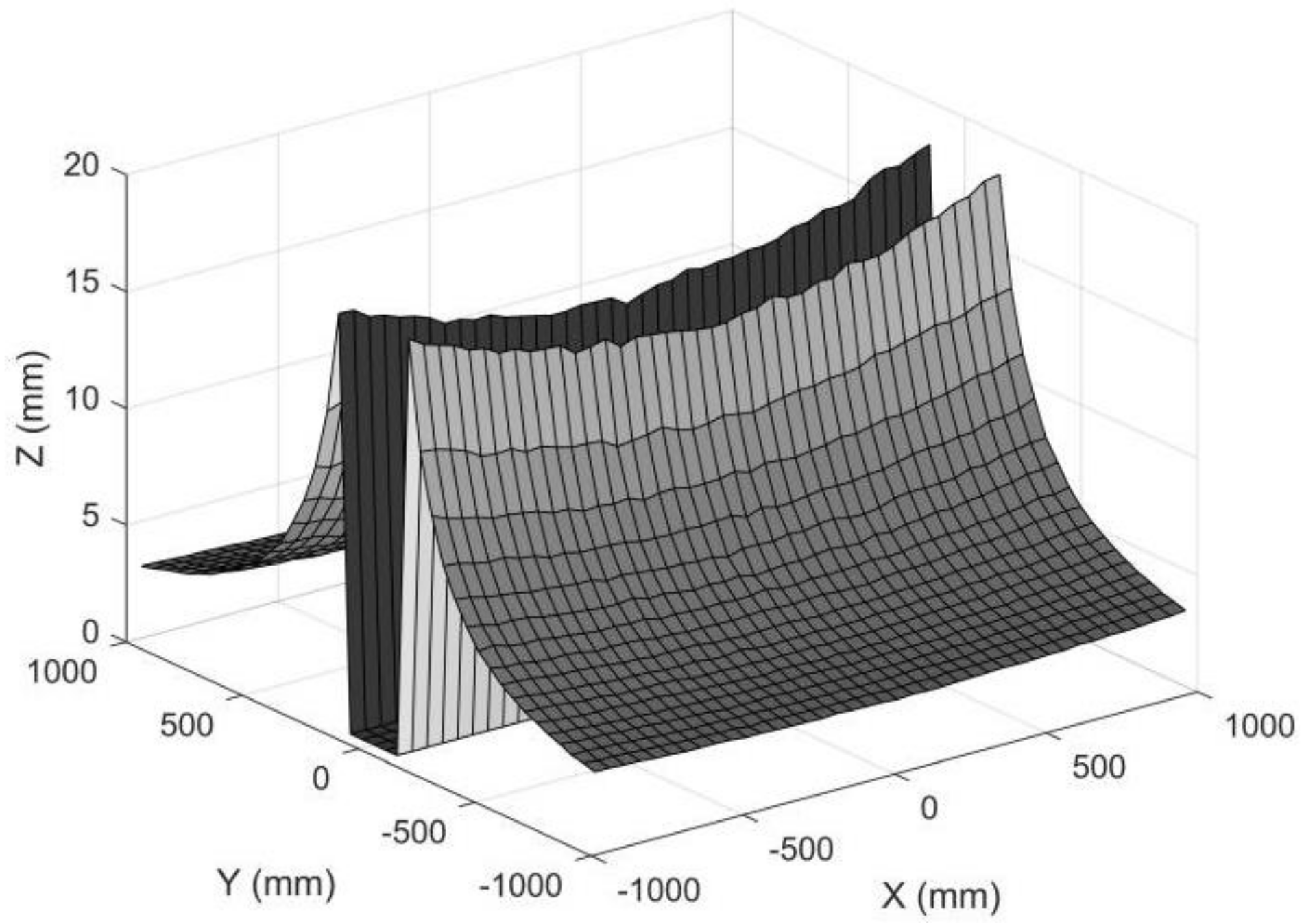
4.2. Accuracy Analysis
4.2.1. Accuracy Analysis for a Point
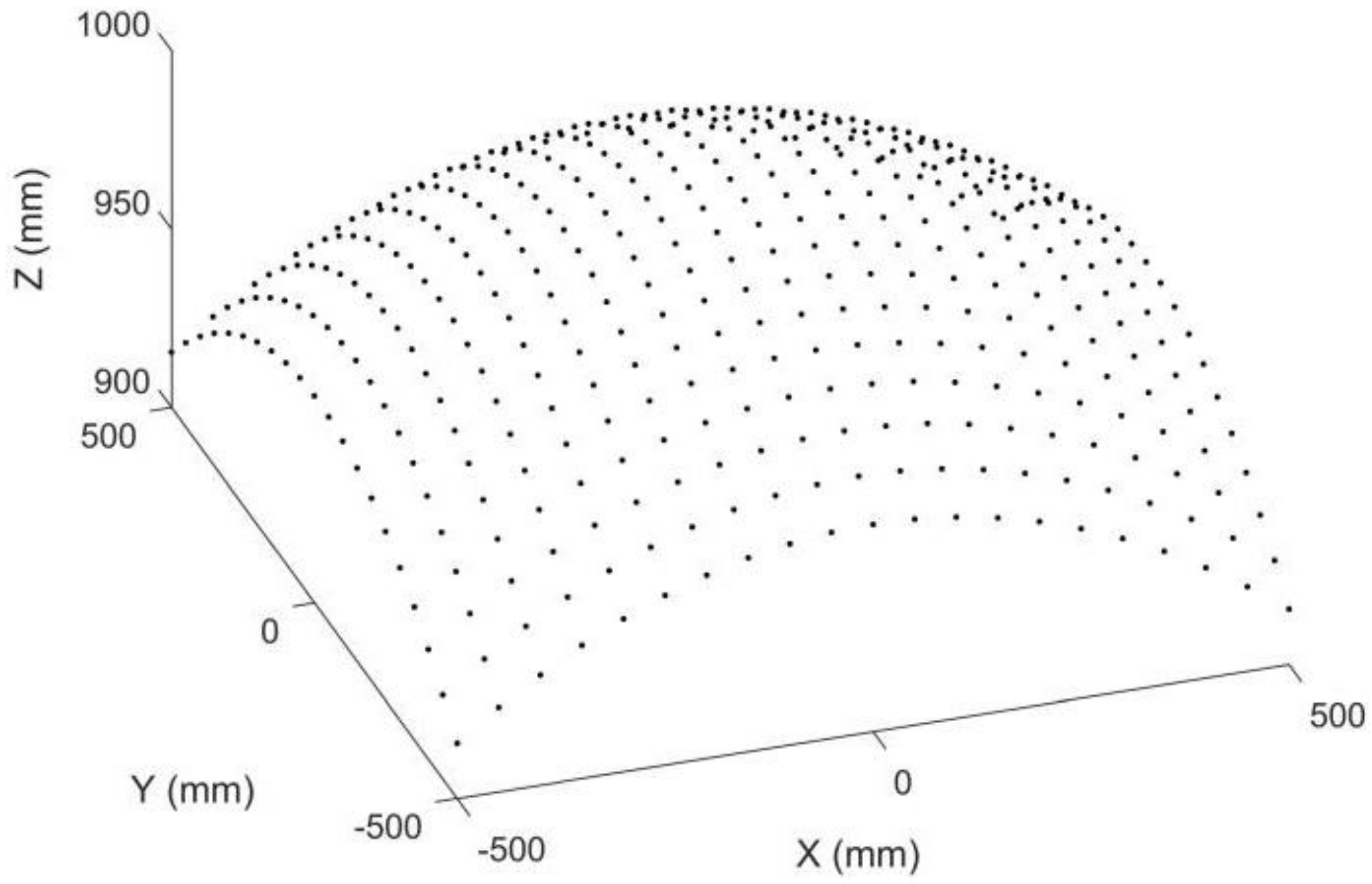
4.2.2. Accuracy Analysis for a Surface
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leach, R. Optical Measurement of Surface Topography; China Science Publishing & Media Ltd.: Beijing, China, 2012; pp. 154–196. [Google Scholar]
- Gaha, R.; Durupt, A.; Eynard, B. Towards the implementation of the Digital Twin in CMM inspection process: Opportunities, challenges and proposals. Procedia Manuf. 2021, 54, 216–221. [Google Scholar] [CrossRef]
- Sutton, M.A.; Li, N.; Joy, D.C.; Reynolds, A.P.; Li, X. Scanning electron microscopy for quantitative small and large deformation measurements part I: SEM imaging at magnifications from 200 to 10,000. Exp. Mech. 2007, 47, 775–787. [Google Scholar] [CrossRef]
- Harding, K. Challenges and opportunities for 3D optical metrology: What is needed today from an industry perspective. Two-Three-Dimens. Methods Insp. Metrol. VI 2008, 7066, 112–119. [Google Scholar]
- Marrugo, A.G.; Gao, F.; Zhang, S. State-of-the-art active optical techniques for three-dimensional surface metrology: A review. JOSA A 2020, 37, B60–B77. [Google Scholar] [CrossRef] [PubMed]
- Soid, S.N.; Zainal, Z.A. Spray and combustion characterization for internal combustion engines using optical measuring techniques—A review. Energy 2011, 36, 724–741. [Google Scholar] [CrossRef]
- O’Riordan, A.; Newe, T.; Dooly, G.; Toal, D. December. Stereo vision sensing: Review of existing systems. In Proceedings of the 2018 12th International Conference on Sensing Technology (ICST), Limerick, Ireland, 4–6 December 2018. [Google Scholar]
- Lazaros, N.; Sirakoulis, G.C.; Gasteratos, A. Review of stereo vision algorithms: From software to hardware. Int. J. Optomech. 2008, 2, 435–462. [Google Scholar] [CrossRef]
- Hussmann, S.; Ringbeck, T.; Hagebeuker, B. A performance review of 3D TOF vision systems in comparison to stereo vision systems. In Stereo Vision; Intechopen: London, UK, 2008. [Google Scholar]
- Zhang, S. High-speed 3D shape measurement with structured light methods: A review. Opt. Lasers Eng. 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Chen, M.; Tang, Y.; Zou, X.; Huang, Z.; Zhou, H.; Chen, S. 3D global mapping of large-scale un-structured orchard integrating eye-in-hand stereo vision and SLAM. Comput. Electron. Agric. 2021, 187, 106237. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, H.; Wang, H.; Zhang, Y. Fruit detection and positioning technology for a Camellia oleifera C. Abel orchard based on improved YOLOv4-tiny model and binocular stereo vision. Expert Syst. Appl. 2023, 211, 118573. [Google Scholar] [CrossRef]
- Navarro, A.V.; Navarro, A.V.; Garrido, C.A. Anamorphic Lens. US 9063321 B2, 23 June 2015. [Google Scholar]
- Lippman, D.H.; Teverovsky, D.S.; Bentley, J.L. Monte Carlo first-order design method for anamorphic cinema zoom lenses. Opt. Eng. 2021, 60, 051203. [Google Scholar] [CrossRef]
- Xu, C.; Song, W.; Wang, Y. Design of a miniature anamorphic lens with a freeform front group and an aspheric rear group. Opt. Eng. 2021, 60, 065104. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Ma, M.; Li, F.; Liu, H.; Cui, H. Camera calibration for anamorphic lenses with three-dimensional targets. Appl. Opt. 2020, 59, 324–332. [Google Scholar] [CrossRef] [PubMed]
- Dodoc, A. Anamorphic prime and zoom lenses. In Proceedings of the Zoom Lenses VI, SPIE, San Diego, CA, USA, 9 September 2019; Volume 11106, pp. 21–40. [Google Scholar]
- Zhang, J.; Chen, X.; Liu, H.; Li, F.; Sun, X. Thin lens aberrations for anamorphic lenses. Appl. Opt. 2019, 58, 182–188. [Google Scholar] [CrossRef] [PubMed]
- Soskind, M.; Soskind, Y.G. Propagation invariant laser beams for optical metrology applications. In Proceedings of the Modeling Aspects in Optical Metrology V, SPIE, Munich, Germany, 21 June 2015; Volume 9526, pp. 392–398. [Google Scholar]
- Ma, M.; Shao, H.; Zhang, J.; Wang, X.; Li, G. A Calibration Method of Anamorphic Lens Camera Based on Virtual 3D Target. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8 July 2019. [Google Scholar]
- Towers, C.E.; Towers, D.P.; Campbell, H.I. Three-dimensional particle imaging by wavefront sensing. Opt. Lett. 2006, 31, 1220–1222. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cao, Z.; Wang, K.; Wu, Q. Aspherical anamorphic lens for shaping laser diode beam. Opt. Commun. 2013, 305, 53–56. [Google Scholar] [CrossRef]
- Durko, H.L.; Barrett, H.H.; Furenlid, L.R. High-Resolution Anamorphic SPECT Imaging. IEEE Trans. Nucl. Sci. 2014, 61, 1126–1135. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Blais, F.; Beraldin, J.-A. Calibration of an anamorphic laser based 3-D range sensor. In Proceedings of the SPIE Videometrics V., San Diego, CA, USA, 27 July–1 August 1997; Volume 3174, pp. 113–122. [Google Scholar]
- Chen, X.; Zhang, J. High-precision anamorphic lens calibration with 3D and 2D calibration targets. Appl. Opt. 2022, 61, 6062–6075. [Google Scholar] [CrossRef] [PubMed]
- Yuan, S.; Sasian, J. Aberrations of anamorphic optical systems. II. Primary aberration theory for cylindrical anamorphic systems. Appl. Opt. 2009, 48, 2836–2841. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhang, J. Lens design for parallel cylindrical anamorphic attachments with finite object distance. Appl. Opt. 2022, 61, 4610–4619. [Google Scholar] [CrossRef] [PubMed]
- Jinkai, Z.; Chen, X. Paraxial lens design of anamorphic lenses with a fixed anamorphic ratio. OSA Contin. 2019, 2, 1430–1454. [Google Scholar]

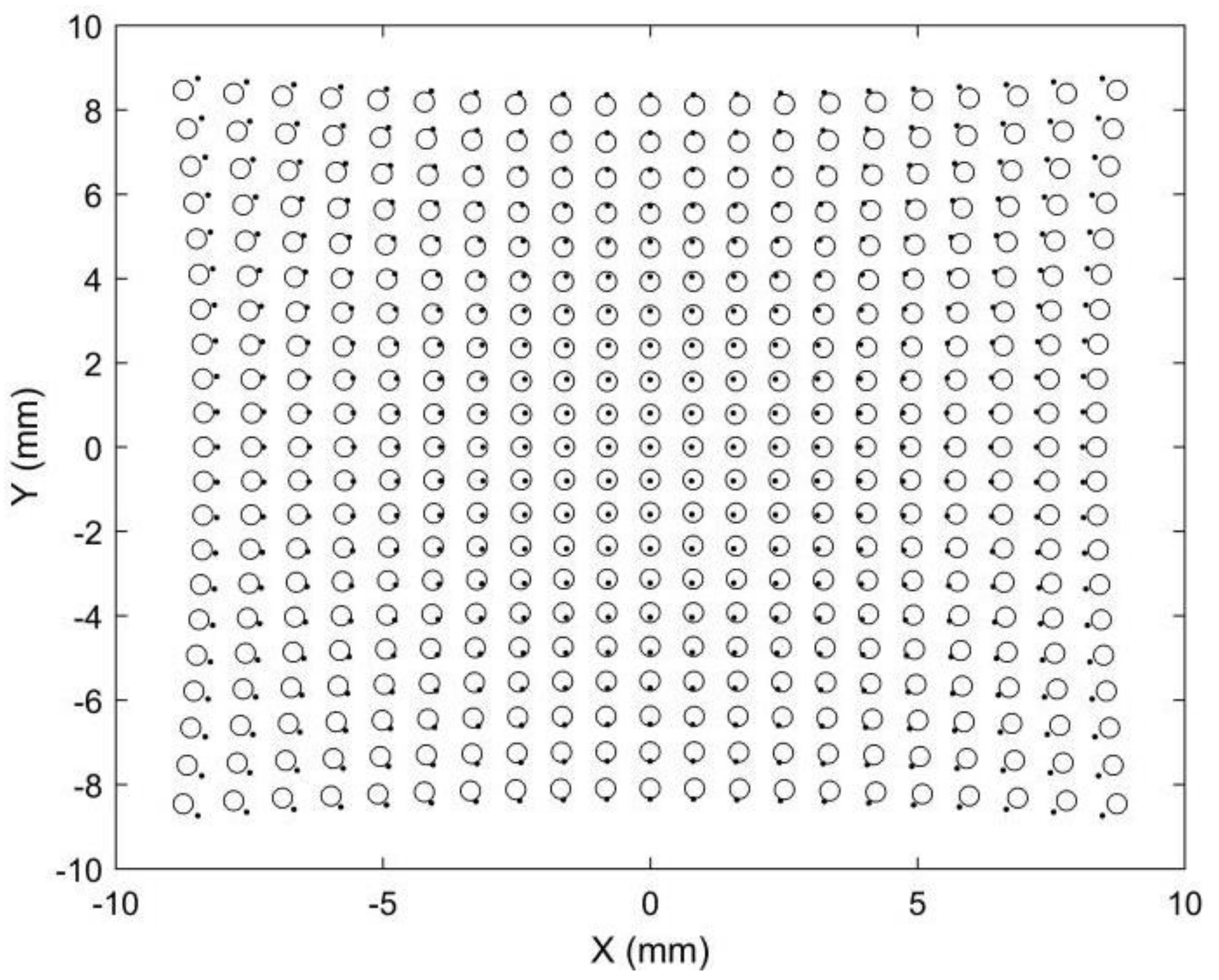
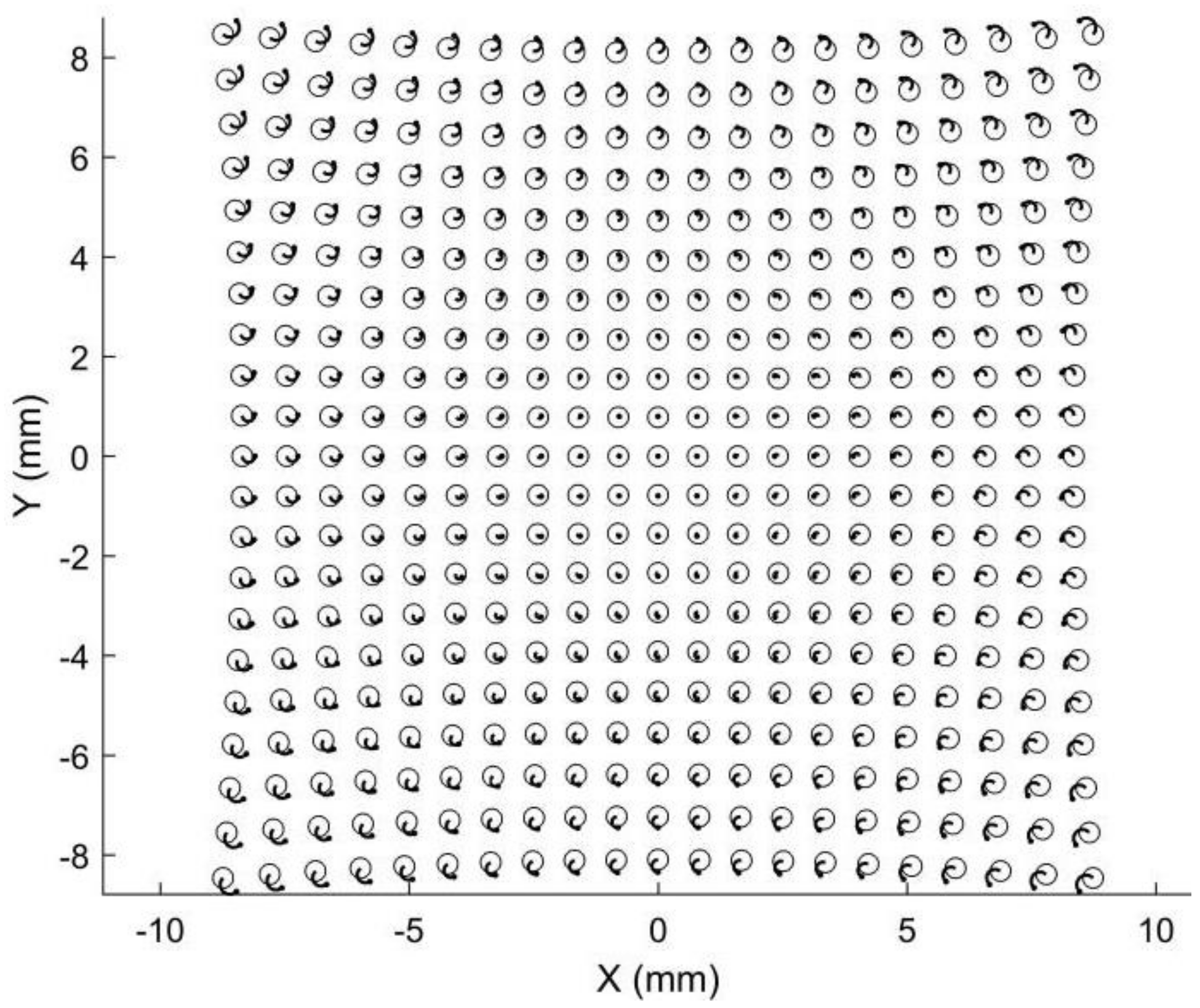








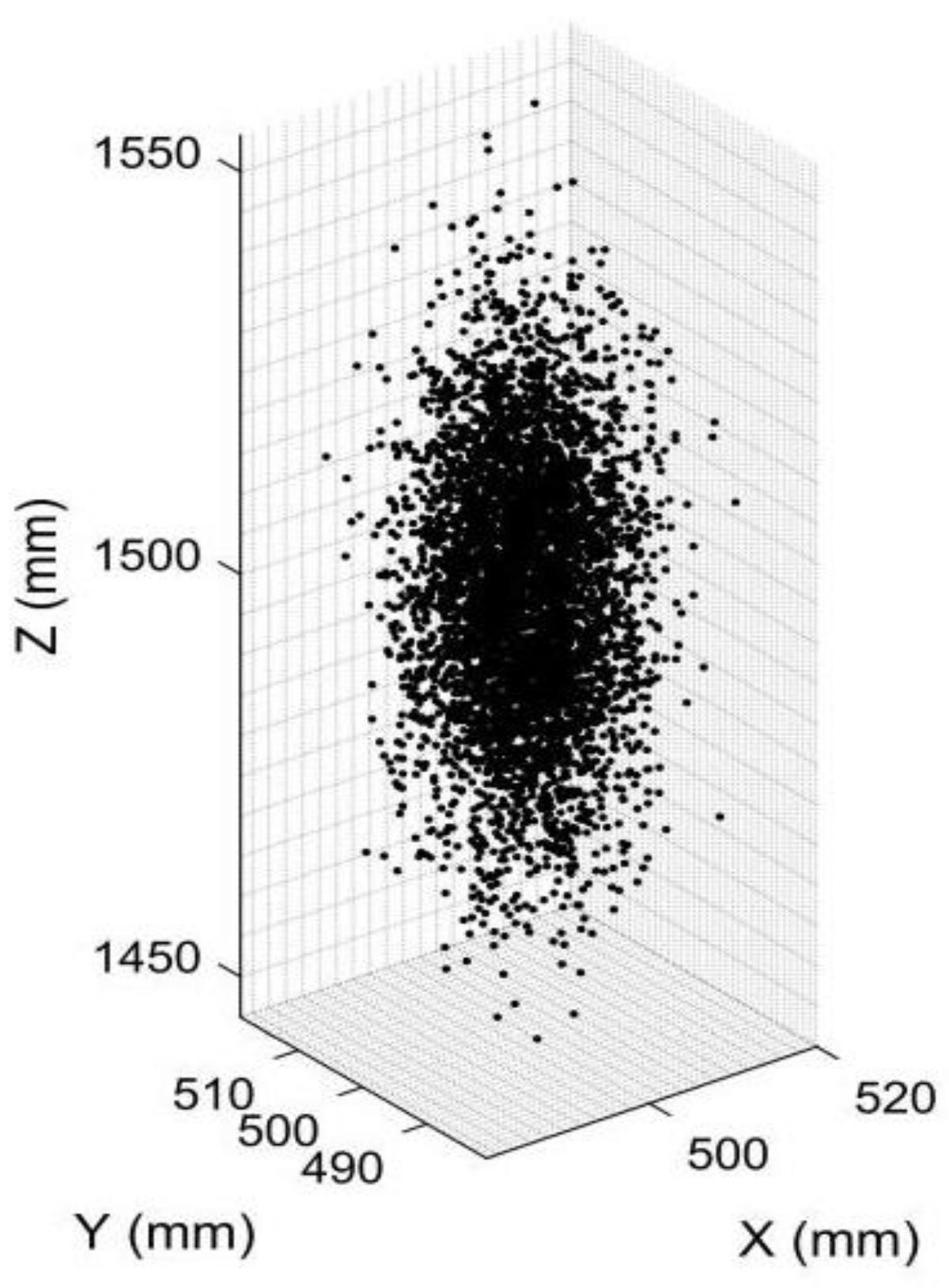
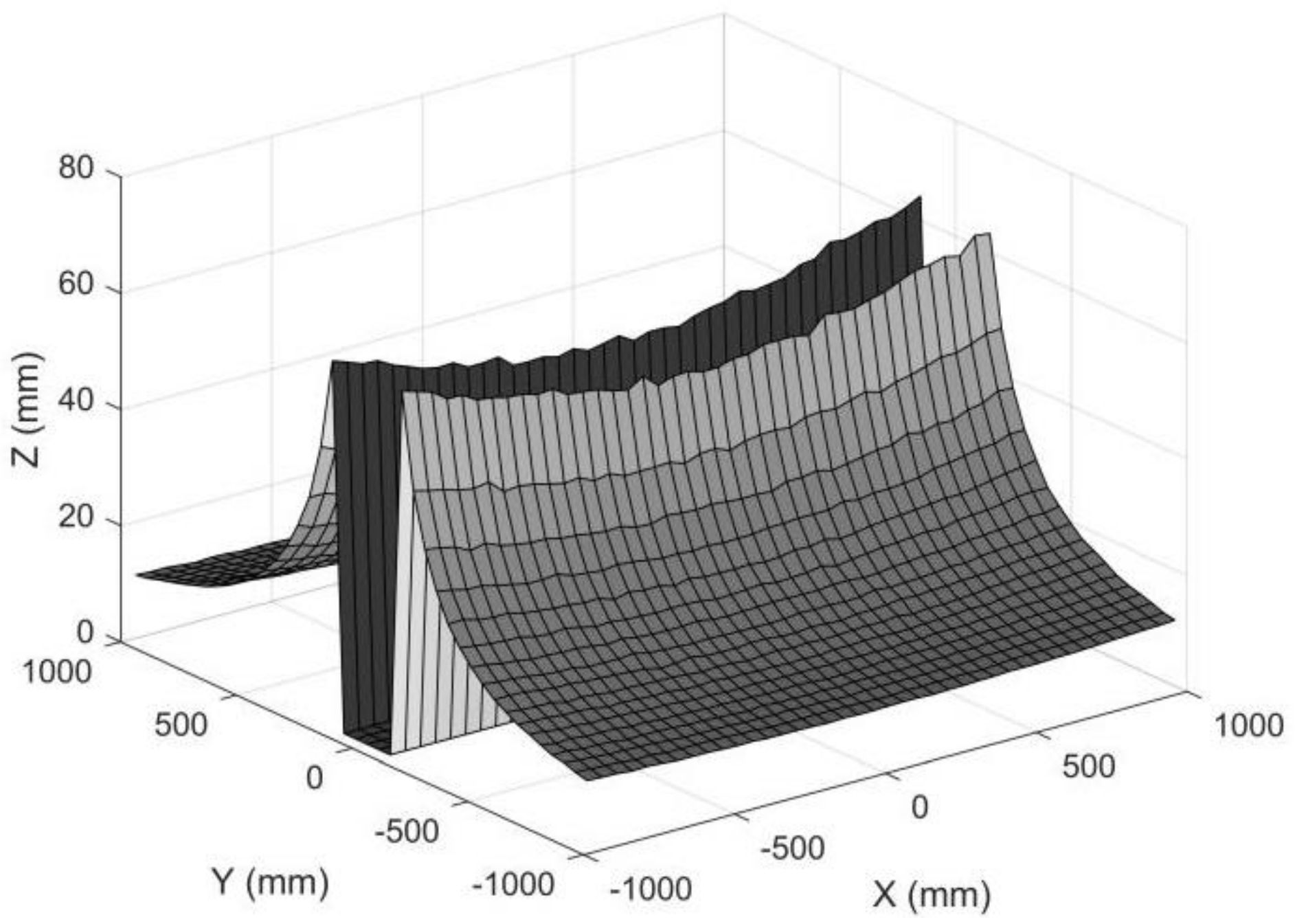
| e0 (mm) | e1 (mm) | e2 (mm) | T11 (mm) | T12 (mm) | T2 (mm) |
|---|---|---|---|---|---|
| 16.163062 | 30 | 40 | 4 | 4 | 4 |
| f (mm) | R11 (mm) | R12 (mm) | R13 (mm) | R21 (mm) | R22 (mm) |
| 16 | 155 | 156.4 | −857.6 | −174.8 | 124.5 |
| n1 | V1 | n2 | V2 | n3 | V3 |
| 1.516797 | 64.212351 | 1.672702 | 32.17888 | 1.516797 | 64.212351 |
| fx (mm) | fy (mm) | u0 (pixel) | v0 (pixel) | ad (mm) |
|---|---|---|---|---|
| 12.0520 | 16.1026 | 1.2790 × 103 | 1.0023 × 103 | 26.5516 |
| aa (°) | k1 | k2 | n1 | n2 |
| −0.5789 | 0.0304 | −2.7151 × 10−5 | 0.0183 | −3.3372 × 10−5 |
| m1 | m2 | x21 | x12 | x03 |
| −0.0155 | 1.277e-5 | 9.1986 × 10−5 | −0.0139 | 1.8928 × 10−5 |
| y30 | y21 | y12 | y03 | x20 |
| 1.6727 × 10−5 | 0.011 | 1.0611 × 10−4 | −0.0023 | 1.3802 × 10−4 |
| x11 | x02 | y20 | y11 | y02 |
| −4.7071 × 10−5 | 5.8709 × 10−5 | 9.3657 × 10−5 | −3.9944 × 10−4 | −2.9851 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Zhang, J.; Xi, J. 3D Metrology Using One Camera with Rotating Anamorphic Lenses. Sensors 2022, 22, 8407. https://doi.org/10.3390/s22218407
Chen X, Zhang J, Xi J. 3D Metrology Using One Camera with Rotating Anamorphic Lenses. Sensors. 2022; 22(21):8407. https://doi.org/10.3390/s22218407
Chicago/Turabian StyleChen, Xiaobo, Jinkai Zhang, and Juntong Xi. 2022. "3D Metrology Using One Camera with Rotating Anamorphic Lenses" Sensors 22, no. 21: 8407. https://doi.org/10.3390/s22218407
APA StyleChen, X., Zhang, J., & Xi, J. (2022). 3D Metrology Using One Camera with Rotating Anamorphic Lenses. Sensors, 22(21), 8407. https://doi.org/10.3390/s22218407