Study on Laser Parameter Measurement System Based on Cone-Arranged Fibers and CCD Camera
Abstract
:1. Introduction
2. Theoretical Model
2.1. Bend Fiber Transmission
- All-glass fiber is suitable for its high laser damage threshold due to low absorption and high-temperature resistance.
- Multimode fiber is more suitable than single-mode fiber because of its larger core diameter and higher laser damage tolerance threshold. The former has a higher duty cycle after the array is integrated, so the spot details the are more accessible [22].
2.2. Fiber-Homogenizer Model
3. Methods
3.1. Instrument Design
3.2. Computational Correction
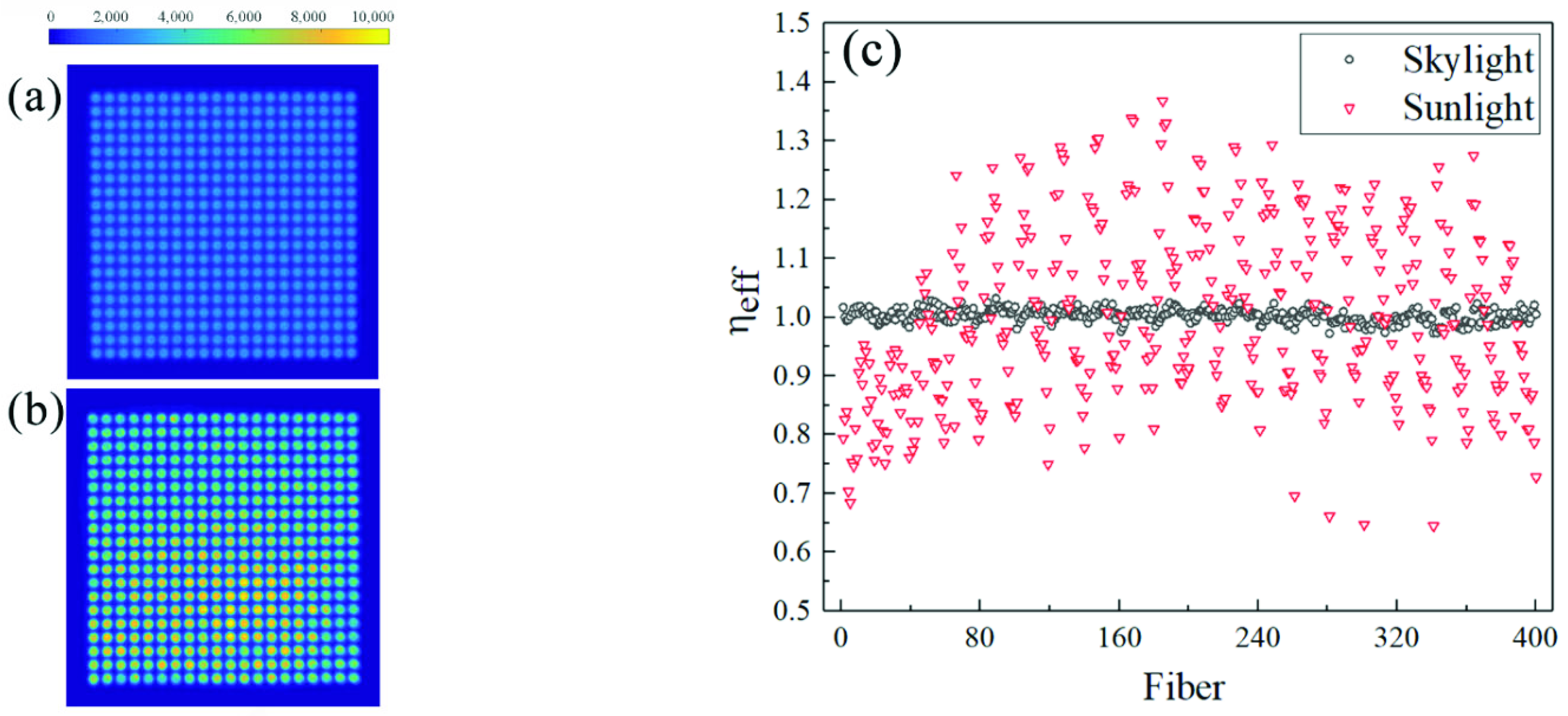
4. Results and Discussions
5. Conclusions
- The CCD camera can shoot large spots without the distortion caused by a large field of view for the cross−section spot is shrunk with high fidelity.
- The sampling resolution is higher and the design is simpler compared with the traditional array target.
- The allowed incident angle range is acceptable. The measurement of the total power and the power density distribution of the spots has high accuracy when the beam’s incident angle is between −8° and 8°.
- Measurement resolution can be improved further without the limitations of complex unit structure. For example, the hexagonal fiber layout will be an optimization direction for the higher fiber packing density than the square layout.
- When it is needed to focus on a larger angle, a fiber with higher NA should be considered. The system’s actual NA and the fiber’s theoretical NA are predicted to have a linear correlation, and the relevant theoretical discussion and experimental verification are worth studying.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaplan, A.F.H. Analysis and modeling of a high−power Yb: Fiber laser beam profile. Opt. Eng. 2011, 50, 054201. [Google Scholar] [CrossRef]
- Pan, S.; Ma, J.; Zhu, R.; Tu, B.; Zhou, W. Actual−time complex amplitude reconstruction method for beam quality M2 factor measurement. Opt. Express 2017, 25, 20142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, F.; Xie, Y.J.; Ji, Y.F.; Duan, L.H.; Ye, X.S. A compound detector array for the measurement of large area laser beam intensity distribution. In Proceedings of the 2nd International Symposium on Laser Interaction with Matter, Xi’an, China, 16 May 2013. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.B.; Shao, B.B.; Yang, P.L.; Tao, M.M. Near-Infrared Detecting Array for High Energy Laser Beam Diagnostics. Adv. Mater. Res. 2012, 571, 156–159. [Google Scholar] [CrossRef]
- Feng, G.B.; Yang, P.L.; Wang, Q.S.; Liu, F.H.; Ye, X.S. Intensity laser far-field spot intensity distribution measurement technology. High Power Laser Part. Beams 2013, 25, 1615–1619. (In Chinese) [Google Scholar] [CrossRef]
- Higgs, C.; Grey, P.C.; Mooney, J.G.; Hatch, R.E.; Carlson, R.R.; Murphy, D.V. Dynamic target board for ABL-ACT performance characterization. In Proceedings of the Airborne Laser Advanced Technology II, Orlando, FL, USA, 5 April 1999. [Google Scholar] [CrossRef]
- Raj, V.; Swapna, M.S.; Sankararaman, S. Unwrapping the laser beam quality through nonlinear time series and fractal analyses: A surrogate approach. Opt. Laser Technol. 2021, 140, 107029. [Google Scholar] [CrossRef]
- Ji, K.H.; Hou, T.R.; Li, J.B.; Meng, L.Q.; Han, Z.G.; Zhu, R.H. Fast measurement of the laser beam quality factor based on phase retrieval with a liquid lens. Appl. Opt. 2019, 58, 2765–2772. [Google Scholar] [CrossRef]
- Schmidt, O.A.; Schulze, C.; Flamm, D.; Brüning, R.; Kaiser, T.; Schröter, S.; Duparré, M. Actual-time determination of laser beam quality by modal decomposition. Opt. Express 2011, 19, 6741–6748. [Google Scholar] [CrossRef] [PubMed]
- Bonora, S.; Beydaghyan, G.; Haché, A.; Ashrit, P.V. Mid-IR laser beam quality measurement through vanadium dioxide optical switching. Opt. Lett. 2013, 38, 1554–1556. [Google Scholar] [CrossRef]
- Ke, Y.; Zeng, C.L.; Xie, P.Y.; Jiang, Q.S.; Liang, K.; Yang, Z.Y.; Zhao, M. Measurement system with high accuracy for laser beam quality. Appl. Opt. 2015, 54, 4876–4880. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.Y.; Xiao, Z.J.; Liang, X.; Bao, L. Study of zero position variation for an optical sight by using a CCD. J. Opt. Technol. 2019, 86, 374–378. [Google Scholar] [CrossRef]
- Nemoto, K.; Nayuki, T.; Fujii, T.; Goto, N.; Kanai, Y. Optimum control of the laser beam intensity profile with a deformable mirror. Appl. Opt. 1997, 36, 7689–7695. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Lee, M.; Park, J.; Lee, K.; Hwang, I. Solar tracking system for lighting fiber. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO)—Laser Science to Photonic Applications, San Jose, CA, USA, 8 June 2014. [Google Scholar] [CrossRef]
- Röpke, U.; Bartelt, H.; Unger, S.; Schuster, K.; Kobelke, J. Two-dimensional high-precision fiber waveguide arrays for coherent light propagation. Opt. Express 2007, 15, 6894–6899. [Google Scholar] [CrossRef] [PubMed]
- Heyvaert, S.; Ottevaere, H.; Kujawa, I.; Buczynski, R.; Raes, M.; Terryn, H.; Thienpont, H. Numerical characterization of an ultra-high NA coherent fiber bundle part I: Modal analysis. Opt. Express 2013, 21, 21991–22011. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Qin, L.A.; Hou, Z.H.; Guan, W.L.; Zhu, W.Y.; Zhang, S.L.; Tan, F.F. Optical fiber transmission characteristics in laser spot distribution measurement system. Acta Opt. 2021, 41, 146–152. (In Chinese) [Google Scholar] [CrossRef]
- Boechat, A.A.P.; Su, D.; Hall, D.R.; Jones, J.D.C. Bend loss in large core multimode optical fiber beam delivery systems. Appl. Opt. 1991, 30, 321–327. [Google Scholar] [CrossRef] [PubMed]
- Jeong, Y.; Sahu, J.K.; Payne, D.N.; Nilsson, J. Ytterbium-doped large-core fiber laser with 1.36 kW continuous-wave output power. Opt. Express 2004, 12, 6088–6092. [Google Scholar] [CrossRef] [PubMed]
- Yalin, A.P. High power fiber delivery for laser ignition applications. Opt. Express 2013, 21, A1102–A1112. [Google Scholar] [CrossRef] [PubMed]
- Pask, C.; Snyder, A.W. Multimode optical fibers: Interplay of absorption and radiation losses. Appl. Opt. 1976, 15, 1295–1298. [Google Scholar] [CrossRef] [PubMed]
- Velamuri, A.V.; Patel, K.; Sharma, I.; Gupta, S.S.; Gaikwad, S.; Krishnamurthy, P.K. Investigation of Planar and Helical Bend Losses in Single- and Few-Mode Optical Fibers. J. Light. Technol. 2019, 37, 3544–3556. [Google Scholar] [CrossRef]
- Donlagic, D. A low bending loss multimode fiber transmission system. Opt. Express 2009, 17, 22081–22095. [Google Scholar] [CrossRef] [PubMed]
- Goto, Y.; Nakajima, K.; Matsui, T.; Kurashima, T.; Yamamoto, F. Influence of Cladding Thickness on Transmission Loss and its Relationship with Multicore Fiber Structure. J. Light. Technol. 2015, 33, 4942–4949. [Google Scholar] [CrossRef]
- Haggans, C.W.; Singh, H.; Varner, W.F.; Wang, J. Narrow-Depressed Cladding Fiber Design for Minimization of Cladding Mode Losses in Azimuthally Asymmetric Fiber Bragg Gratings. J. Light. Technol. 1998, 16, 902–909. [Google Scholar] [CrossRef]
- Varghese, B.; Rajan, V.; Leeuwen, T.G.V.; Steenbergen, W. Evaluation of a multimode fiber optic low coherence interferometer for path length resolved Doppler measurements of diffuse light. Rev. Sci. Instrum. 2007, 78, 7664–7667. [Google Scholar] [CrossRef]
- Smith, R.C.G.; Sarangan, A.M.; Jiang, Z.; Marciante, J.R. Direct measurement of bend-induced mode deformation in large-mode-area fibers. Opt. Express 2012, 20, 4436–4443. [Google Scholar] [CrossRef] [Green Version]
- Gambling, W.A.; Payne, D.N.; Matsumura, H. Mode conversion coefficients in optical fibers. Appl. Opt. 1975, 14, 1538–1542. [Google Scholar] [CrossRef]
- Berrocal, E.; Meglinski, I.; Jermy, M. New model for light propagation in highly inhomogeneous polydisperse turbid media with applications in spray diagnostics. Opt. Express 2005, 13, 9181–9195. [Google Scholar] [CrossRef] [Green Version]
- Schermer, R.T. Mode scalability in bent optical fibers. Opt. Express 2007, 15, 15674–15701. [Google Scholar] [CrossRef]
- Pang, M.; Gao, X.; Rong, J. Technical requirements and uncertainty of far field laser spot centroid measurement using array detection method. Optik 2015, 126, 5881–5885. [Google Scholar] [CrossRef]
- Cheng, Y.L.; He, F.; Tan, F.F. Research on the laser spot restoration method of detector array target. Laser Infrared 2020, 50, 749–753. [Google Scholar] [CrossRef]
- Guan, W.L.; Tan, F.F.; Hou, Z.H. Research on Wide Angle Array Detection Technology for High Power Density Laser. Acta Opt. Sin. 2022, 42, 0214002. [Google Scholar] [CrossRef]

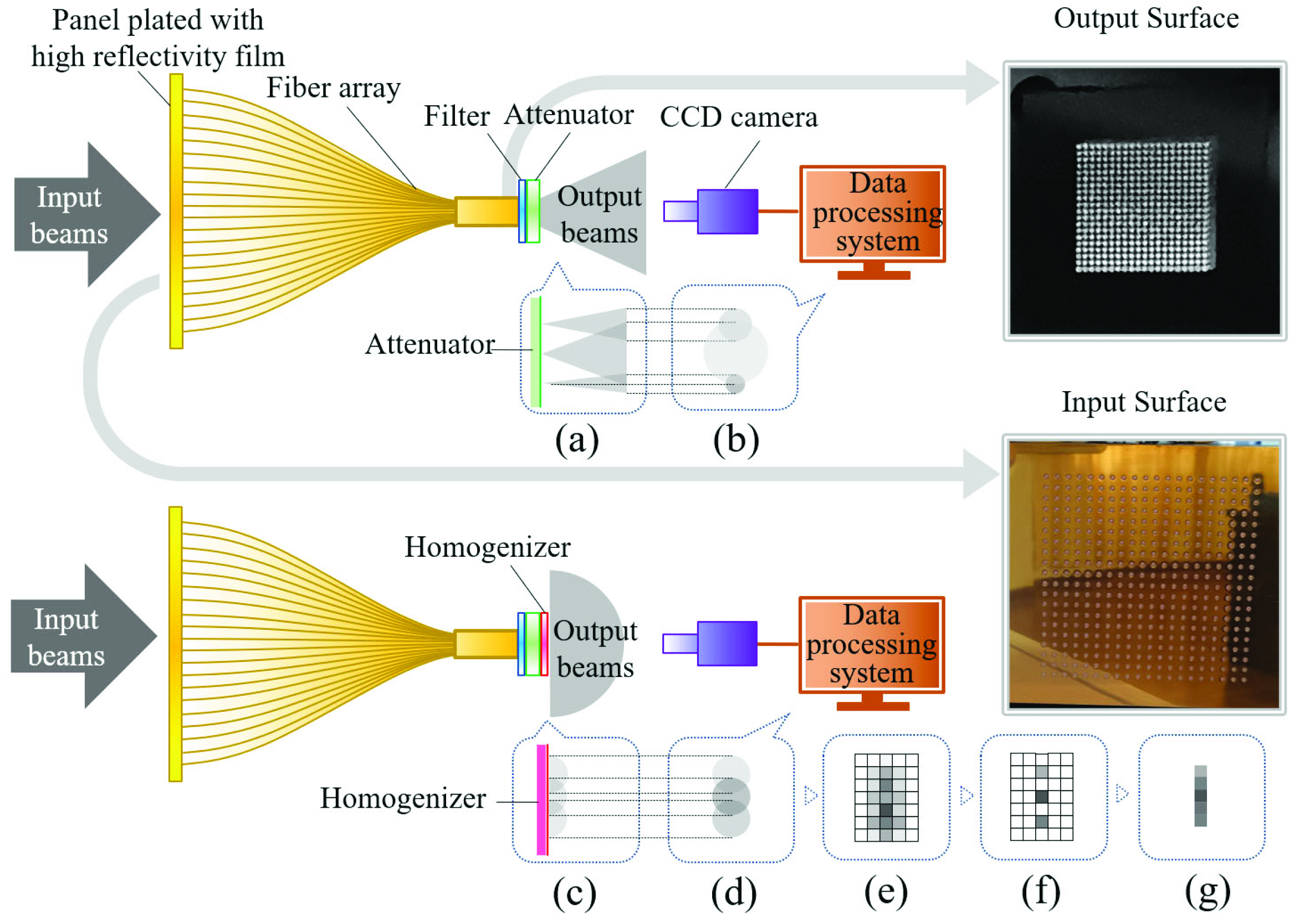



| Instrument | Feature | Specification |
|---|---|---|
| Laser | Wavelength | 1064 nm |
| Polarization | Linear | |
| Output power | 1~100 W, continuously adjustable | |
| Working mode | Continuous wave | |
| Diffuse reflection screen | Diffuse reflectance ratio | >99% |
| Material | Thermoplastic resin | |
| Filter | Central wavelength | 1064 nm |
| Bandwidth | 8 nm | |
| Attenuators | Type | Absorptive neutral density |
| Optical density (OD) | 2~5 | |
| Lenses | Focal for actual spot | 12 mm/F 1.4 |
| Focal for reduced spot (with extension ring) | 50 mm/F 1.4 | |
| CCD camera | Camera | Allied Vision Prosilica GT |
| Sensor | Sony ICX674ALG | |
| Pixels | 1936 (H) × 1456 (V) | |
| Pixel size with lens for actual spot | 121 μm (H) × 121 μm (V) | |
| Pixel size with lens for reduced spot | 5 μm (H) × 5 μm (V) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Qin, L.; Hou, Z.; Zhang, S.; Zhu, W.; Guan, W. Study on Laser Parameter Measurement System Based on Cone-Arranged Fibers and CCD Camera. Sensors 2022, 22, 7892. https://doi.org/10.3390/s22207892
Luo J, Qin L, Hou Z, Zhang S, Zhu W, Guan W. Study on Laser Parameter Measurement System Based on Cone-Arranged Fibers and CCD Camera. Sensors. 2022; 22(20):7892. https://doi.org/10.3390/s22207892
Chicago/Turabian StyleLuo, Jie, Laian Qin, Zaihong Hou, Silong Zhang, Wenyue Zhu, and Wenlu Guan. 2022. "Study on Laser Parameter Measurement System Based on Cone-Arranged Fibers and CCD Camera" Sensors 22, no. 20: 7892. https://doi.org/10.3390/s22207892
APA StyleLuo, J., Qin, L., Hou, Z., Zhang, S., Zhu, W., & Guan, W. (2022). Study on Laser Parameter Measurement System Based on Cone-Arranged Fibers and CCD Camera. Sensors, 22(20), 7892. https://doi.org/10.3390/s22207892





