Fiber Lateral Pressure Sensor Based on Vernier– Effect Improved Fabry–Perot Interferometer
Abstract
1. Introduction
2. Methodology
2.1. Principle
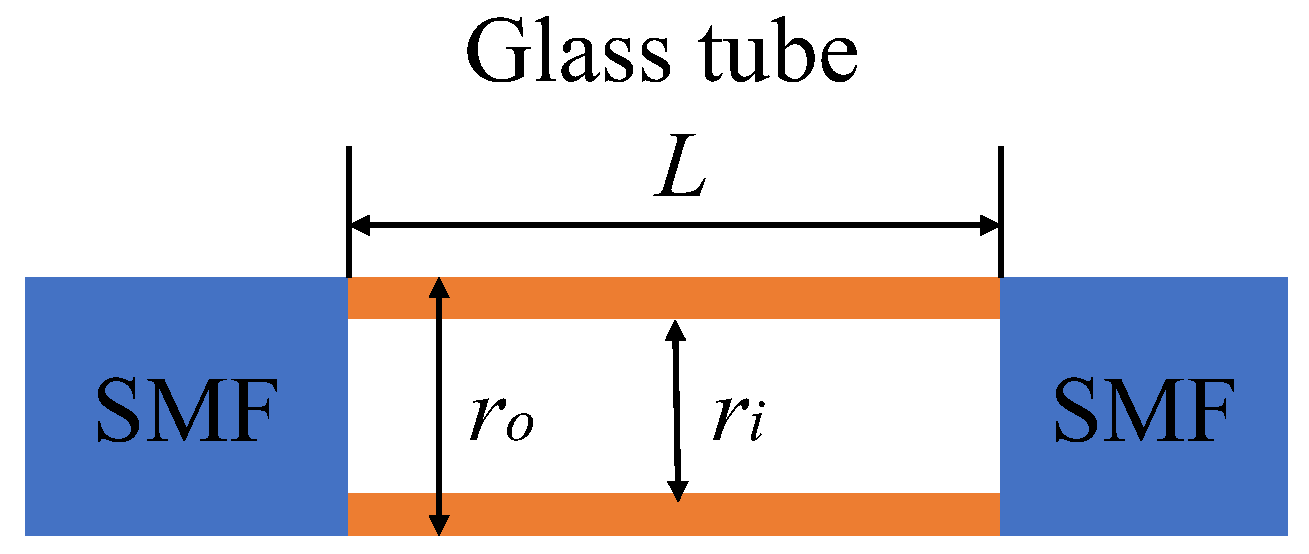
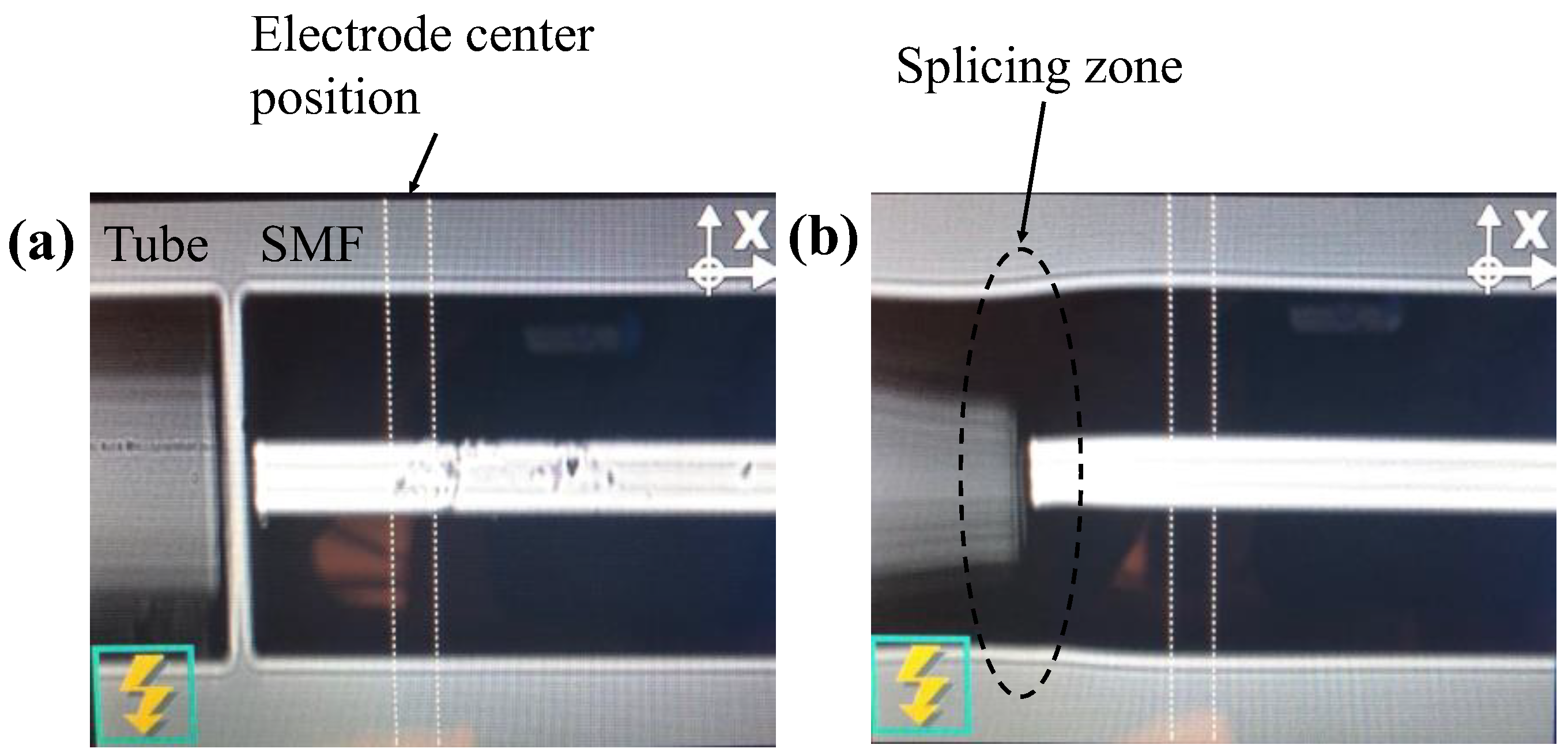
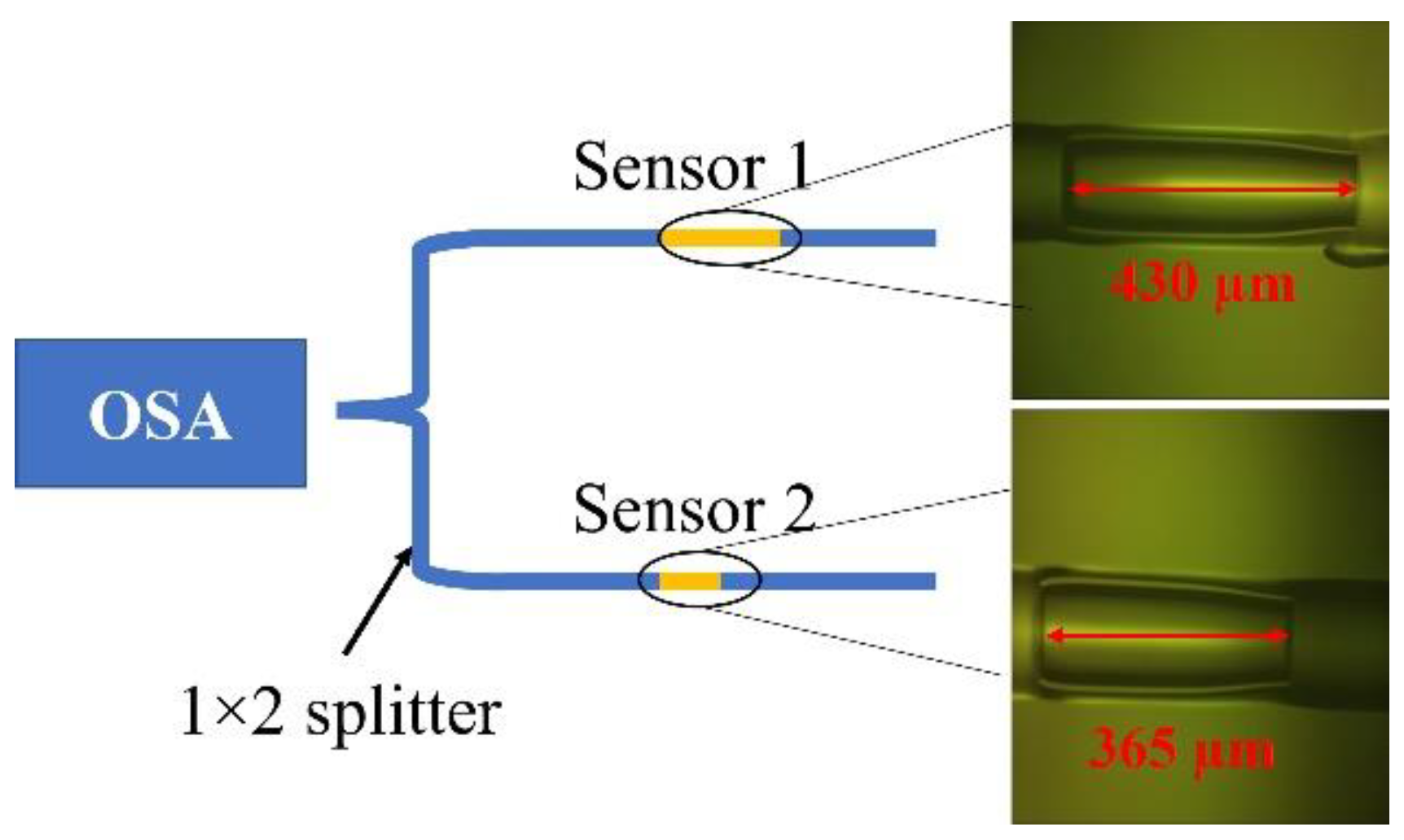
2.2. Fabrication
3. Experiments and Results
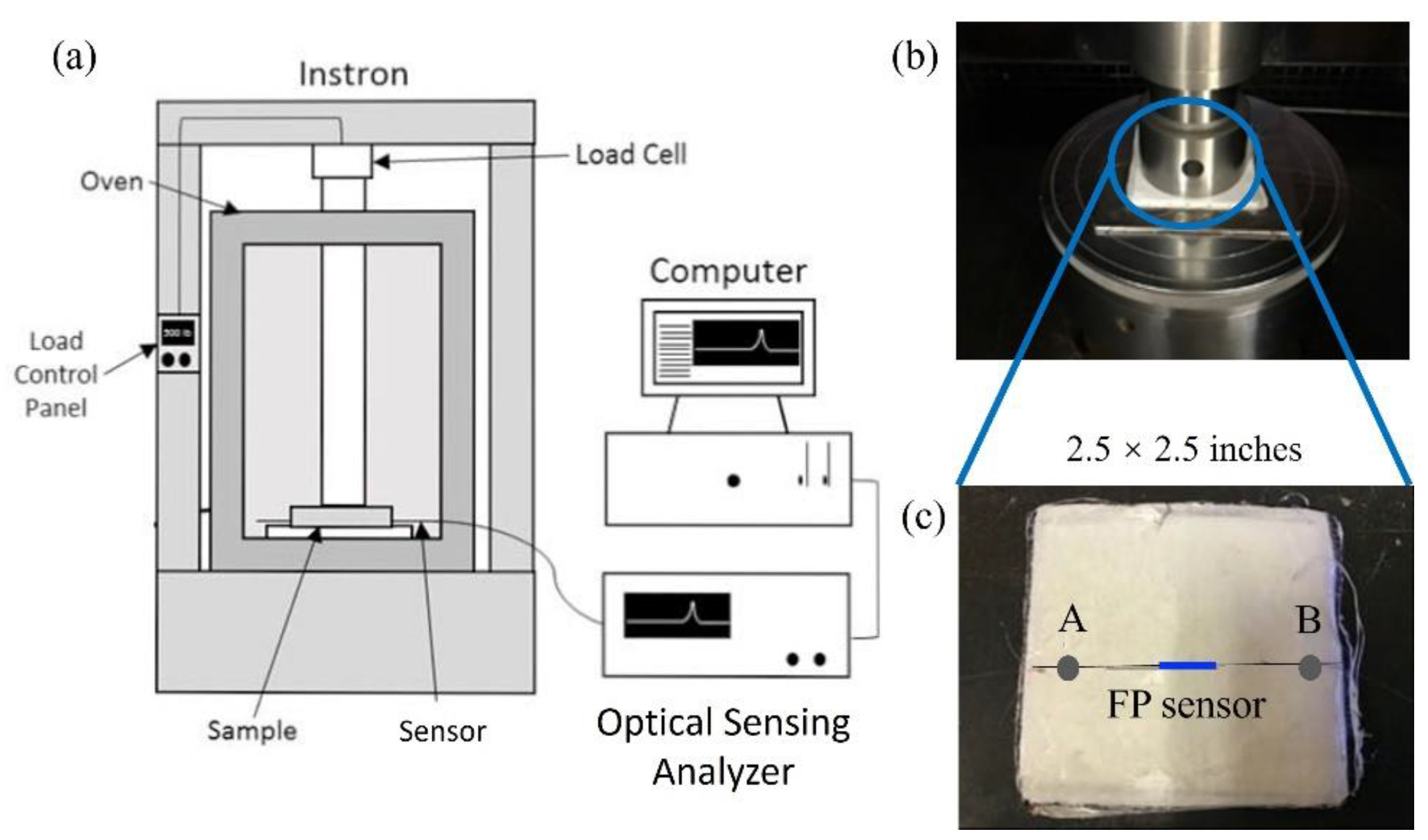
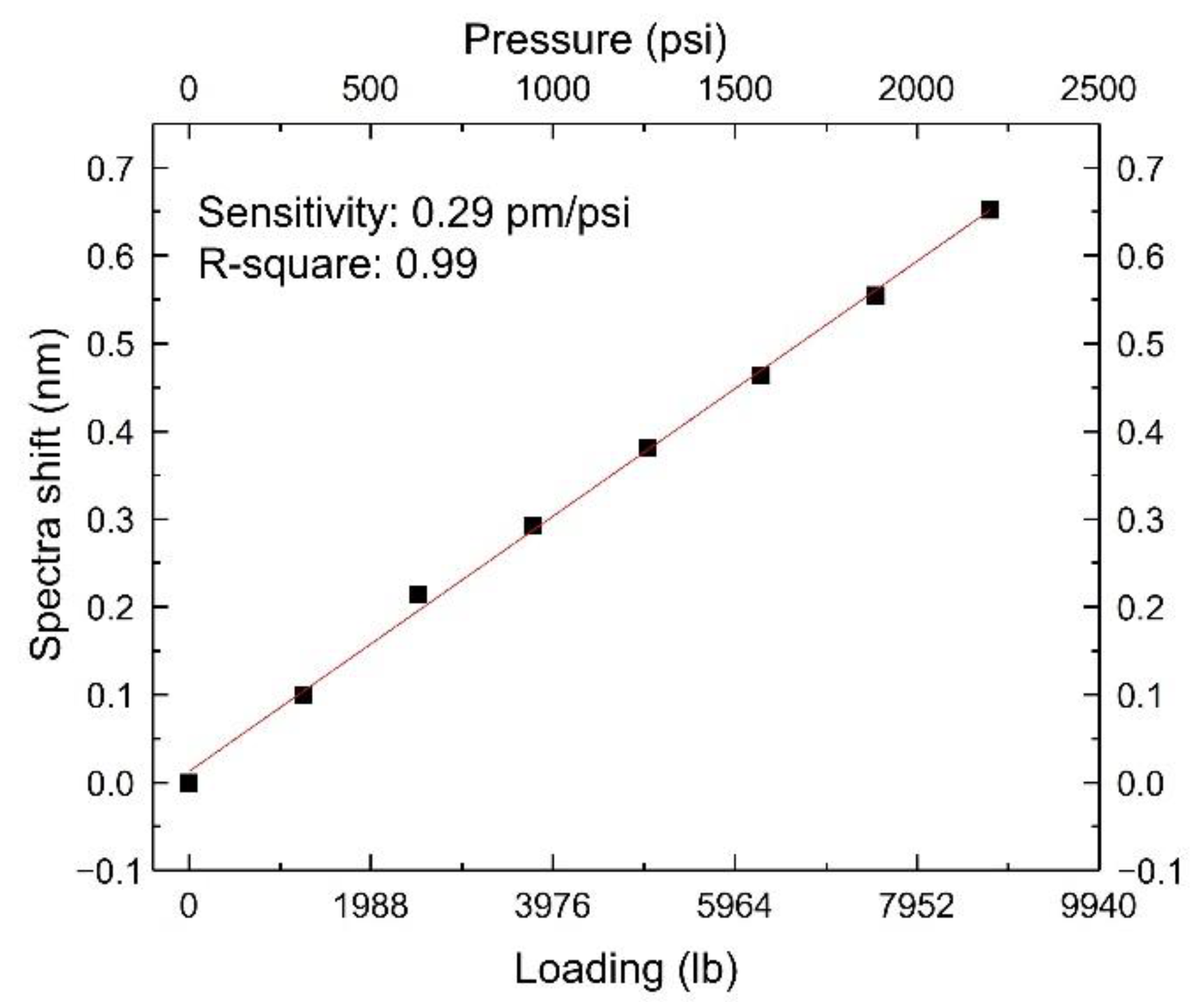
3.1. Pressure Test
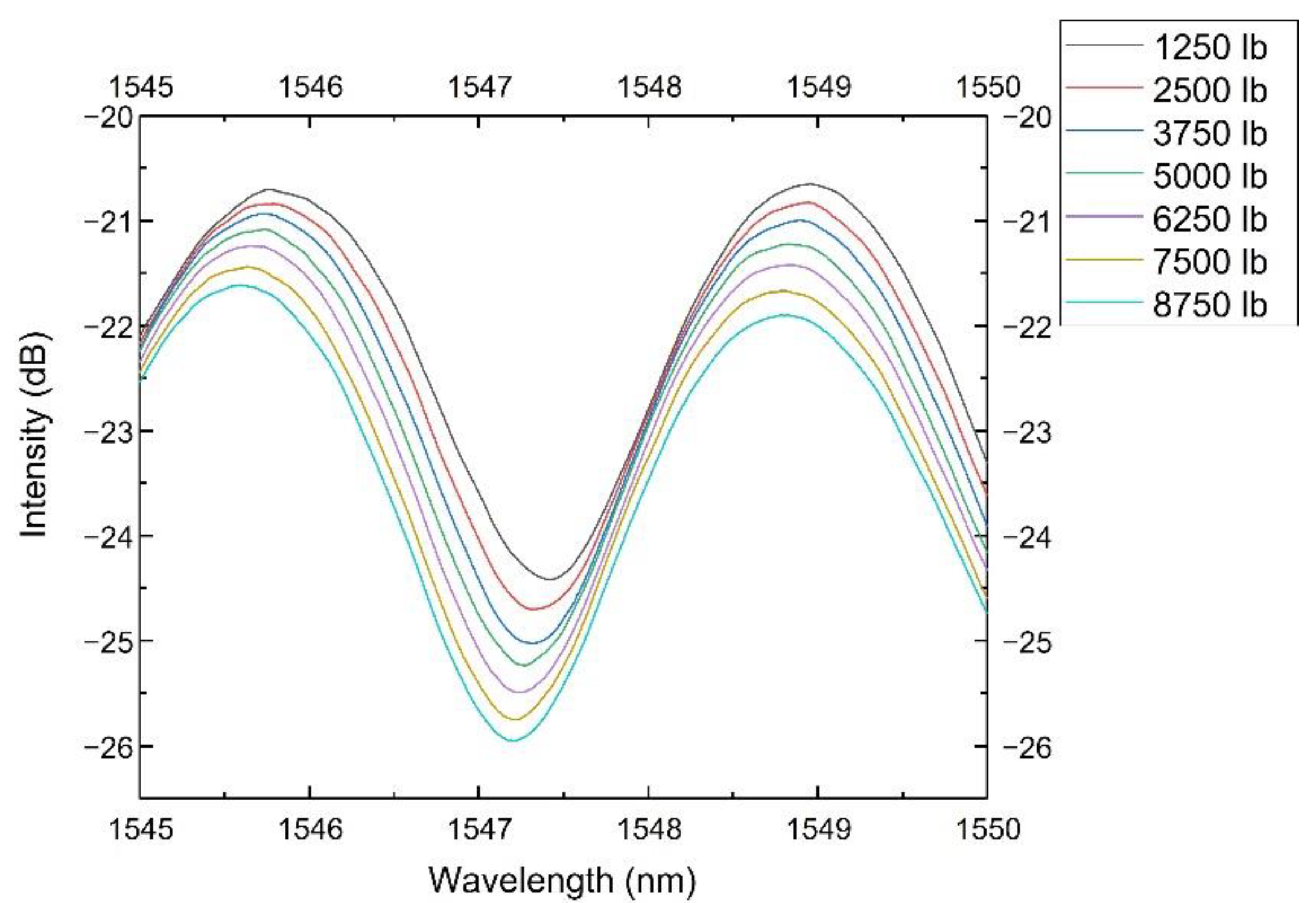
3.2. Results and Discussion
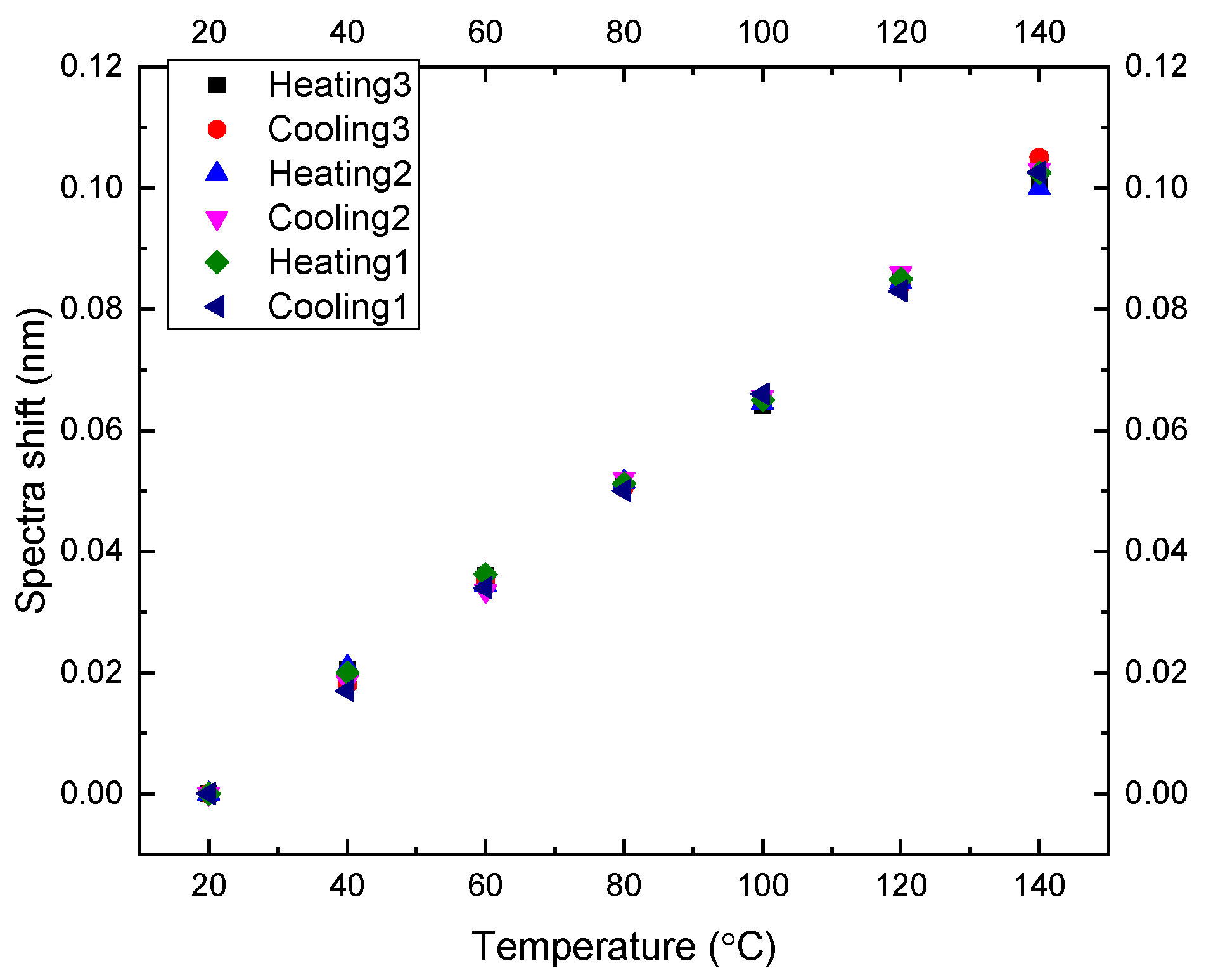
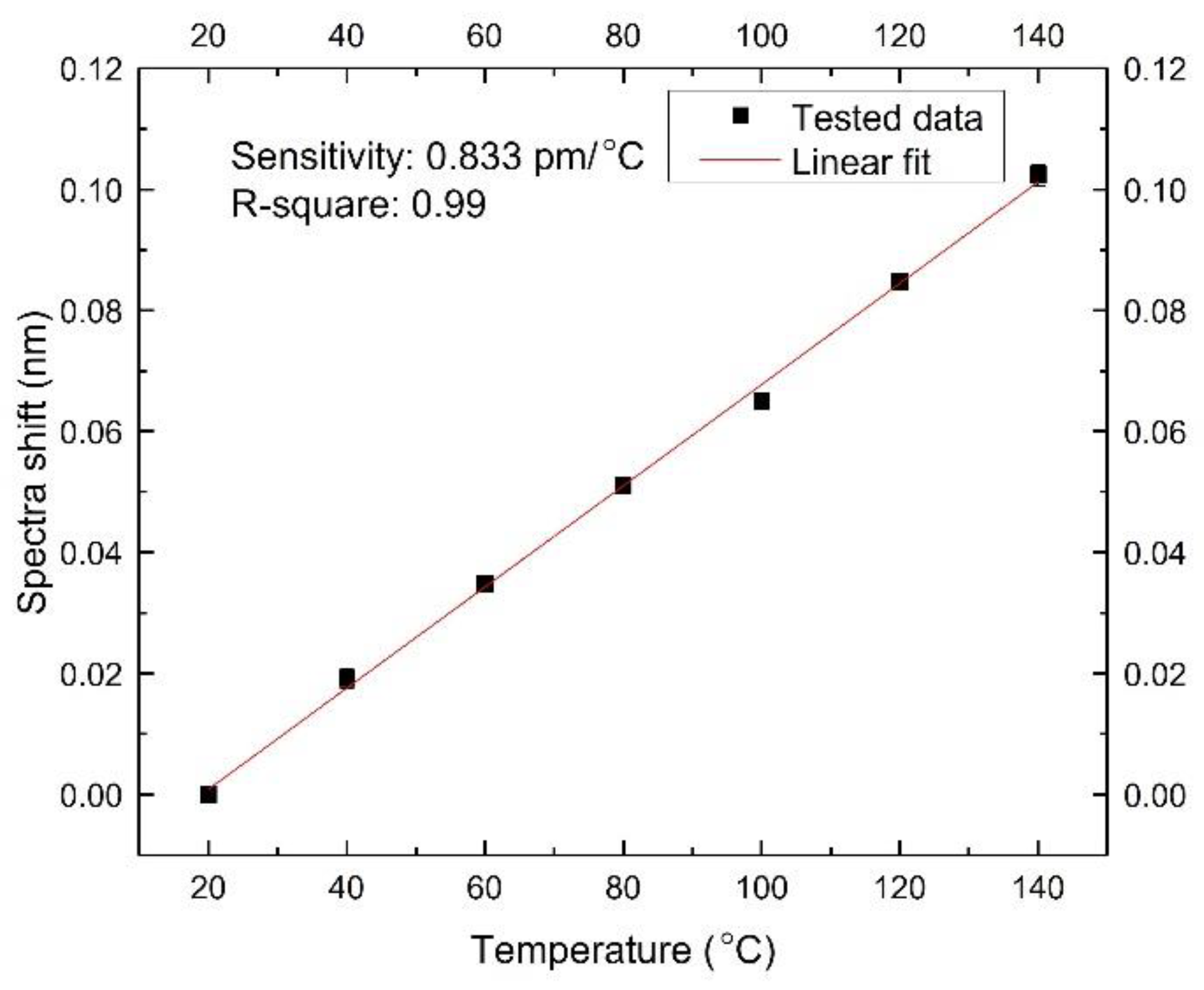
3.3. Temperature Test
4. Vernier Effect
5. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Chung, D.D. Composite Materials: Science and Applications; Springer Science & Business Media: Buffalo, NY, USA, 3 April 2010. [Google Scholar]
- Gay, D. Composite Materials: Design and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Biondi, A.M.; Zhou, J.; Guo, X.; Wu, R.; Tang, Q.; Gandhi, H.; Yu, T.; Gopalan, B.; Hanna, T.; Ivey, J.; et al. Pipeline structural health monitoring using distributed fiber optic sensing textile. Opt. Fiber Technol. 2022, 70, 102876. [Google Scholar] [CrossRef]
- Ramakrishnan, M.; Rajan, G.; Semenova, Y.; Farrell, G. Overview of fiber optic sensor technologies for strain/temperature sensing applications in composite materials. Sensors 2016, 16, 99. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.; Vinayaka, S.; Wang, J.; Gandhi, H.; Yu, T.; Zhou, J.; Guo, X.; Wang, X. Detection of ground motion induced pipe deformation using a sensing textile. In Proceedings of the 46th Annual Review of Progress in Quantitative Nondestructive Evaluation, Portland, OR, USA, 14–18 July 2019. [Google Scholar]
- Shivakumar, K.; Emmanwori, L. Mechanics of failure of composite laminates with an embedded fiber optic sensor. J. Compos. Mater. 2004, 38, 669–680. [Google Scholar] [CrossRef]
- Lu, P.; Lin, G.; Wang, X.; Chen, L.; Bao, X. Lateral stress detection using a tapered fiber mach–zehnder interferometer. IEEE Photon- Technol. Lett. 2012, 24, 2038–2041. [Google Scholar]
- Li, Y.; Song, Z.; Wei, J.; Hu, J. Fiber in-line Mach-Zehnder interferometer for simultaneous measurement of transverse loading and temperature based on multi-core fiber. Opt. Laser Technol. 2021, 143, 107354. [Google Scholar] [CrossRef]
- Zhang, S.; Cao, Z.; Xia, T.; Yang, C.; Liu, Z.; Li, Z. Lateral Force Sensing Based on Sagnac Interferometry Realized by a High-Birefringence Suspended-Core Fiber. J. Lightware Technol. 2022, 40, 3935–3941. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, B.; Zhao, L.; Hllah, R.; Mao, Y.; Ren, J.; Wang, T. Compact Optical Fiber Sensor Based on Silica Capillary Tube for Simultaneous High Temperature and Transverse Load Measurement. IEEE Photonics J. 2021, 14, 1–8. [Google Scholar] [CrossRef]
- Azevedo, A.; Coghe, F.; Teixeira-Dias, F. Behind Helmet Blunt Trauma: Matching Measurement to Injury Using Finite Element Modelling. In Advanced Materials for Defense; Springer: Cham, Switzerland, 2020; pp. 95–101. [Google Scholar]
- Tan, X.G.; Bagchi, A. Computational Analysis of Combat Helmet Protection Against Blunt Impact to Head. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: Salt Lake City, UT, USA, 2019; Volume 59407, p. V003T04A052. [Google Scholar]
- Guo, X.; Zhou, J.; Du, C.; Wang, X. Highly sensitive miniature all-silica fiber tip Fabry–Pérot pressure sensor. IEEE Photonics Technol. Lett. 2019, 31, 689–692. [Google Scholar] [CrossRef]
- Skotak, M.; Salib, J.; Misistia, A.; Cardenas, A.; Alay, E.; Chandra, N.; Kamimori, G. Factors contributing to increased blast overpressure inside modern ballistic helmets. Appl. Sci. 2020, 10, 7193. [Google Scholar] [CrossRef]
- Xu, M.; Reekie, L.; Chow, Y.; Dakin, J. Optical in-fibre grating high pressure sensor. Electron. Lett. 1993, 29, 398–399. [Google Scholar] [CrossRef]
- Wu, C.; Guan, B.-O.; Wang, Z.; Feng, X. Characterization of pressure response of Bragg gratings in grapefruit microstructured fibers. J. Lightware Technol. 2010, 28, 1392–1397. [Google Scholar]
- Liu, Z.; Tse, M.-L.V.; Wu, C.; Chen, D.; Lu, C.; Tam, H.Y. Intermodal coupling of supermodes in a twin-core photonic crystal fiber and its application as a pressure sensor. Opt. Express 2012, 20, 21749–21757. [Google Scholar] [CrossRef]
- Hu, G.; Chen, D.; Jiang, X. Side-hole two-core microstructured optical fiber for hydrostatic pressure sensing. Appl. Opt. 2012, 51, 4867–4872. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.Y.; Wu, C.; Tse, M.L.V.; Zhang, L.; Cheng, K.-C.D.; Tam, H.Y.; Guan, B.-O.; Lu, C. High pressure sensor based on photonic crystal fiber for downhole application. Appl. Opt. 2010, 49, 2639–2643. [Google Scholar] [CrossRef]
- Guo, X.; Wu, N.; Zhou, J.; Du, C.; Wang, X. Validation of an ultrasound transducer’s generation and receiving function on one single-mode fiber. Opt. Lasers Eng. 2019, 127, 105962. [Google Scholar] [CrossRef]
- Zhou, J.; Guo, X.; Du, C.; Lou, X.; Cao, C.; Wang, X. A fiber optic acoustic pyrometer for temperature monitoring in an exhaust pipe of a boiler. IEEE Photon.-Technol. Lett. 2019, 31, 1580–1583. [Google Scholar] [CrossRef]
- Liu, Q.; Peng, W. Fast interrogation of dynamic low-finesse Fabry-Perot interferometers: A review. Microw. Opt. Technol. Lett. 2021, 63, 2279–2291. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, Y.; Liu, T.; Sun, T.; Grattan, K.T. TDLAS Detection of Propane/Butane Gas Mixture by Using Reference Gas Absorption Cells and Partial Least Square Approach. IEEE Sens. J. 2018, 18, 8587–8596. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, W.; Xiao, H.; Wang, A. Self-calibrated interferometric/intensity-based optical fiber sensors. J. Lightware Technol. 2001, 19, 1495. [Google Scholar] [CrossRef]
- Wu, C.; Fu, H.Y.; Qureshi, K.; Guan, B.-O.; Tam, H.Y. High-pressure and high-temperature characteristics of a Fabry–Perot interferometer based on photonic crystal fiber. Opt. Lett. 2011, 36, 412–414. [Google Scholar] [CrossRef]
- Nan, T.; Liu, B.; Wu, Y.; Wang, J.; Mao, Y.; Zhao, L.; Sun, T.; Wang, J. Ultrasensitive strain sensor based on Vernier- effect improved parallel structured fiber-optic Fabry-Perot interferometer. Opt. Express 2019, 27, 17239–17250. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Tang, M.; Gao, F.; Zhu, B.; Zhao, Z.; Duan, L.; Fu, S.; Ouyang, J.; Wei, H.; Shum, P.P.; et al. Simplified hollow-core fiber-based Fabry–Perot interferometer with modified Vernier effect for highly sensitive high-temperature measurement. IEEE Photon. J. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Quan, M.; Tian, J.; Yao, Y. Ultra-high sensitivity Fabry–Perot interferometer gas refractive index fiber sensor based on photonic crystal fiber and Vernier effect. Opt. Lett. 2015, 40, 4891–4894. [Google Scholar] [CrossRef] [PubMed]
- La Notte, M.; Passaro, V.M. Ultra high sensitivity chemical photonic sensing by Mach–Zehnder interferometer enhanced Vernier-effect. Sens. Actuators B Chem. 2013, 176, 994–1007. [Google Scholar] [CrossRef]
- Liao, H.; Lu, P.; Fu, X.; Jiang, X.; Ni, W.; Liu, D.; Zhang, J. Sensitivity amplification of fiber-optic in-line Mach–Zehnder Interferometer sensors with modified Vernier-effect. Opt. Express 2017, 25, 26898–26909. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Chen, H.; Zhang, S.; Fu, H.; Luo, Z.; Zhang, L.; Zhao, M.; Xu, H.; Cai, Z. Tunable and selectable multipassband microwave photonic filter utilizing reflective and cascaded fiber Mach–Zehnder interferometers. J. Lightware Technol. 2017, 35, 2660–2668. [Google Scholar] [CrossRef]
- Claes, T.; Bogaerts, W.; Bienstman, P. Experimental characterization of a silicon photonic biosensor consisting of two cascaded ring resonators based on the Vernier-effect and introduction of a curve fitting method for an improved detection limit. Opt. Express 2010, 18, 22747–22761. [Google Scholar] [CrossRef]
- Li, S.; Wu, R.; Wang, H.; Chen, X.; Fu, P.; Fu, H.; Wang, Y.; Xu, H.; Cai, Z. Fiber-ring-based rf filtering for temperature and transversal loading measurement and interrogation. IEEE Sens. J. 2018, 18, 5794–5798. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Zhao, Y.; Jiang, J.; He, X.; Yang, W.; Zhu, Z.; Gao, W.; Li, L. Sensitivity-enhanced temperature sensor by hybrid cascaded configuration of a Sagnac loop and a FP cavity. Opt. Express 2017, 25, 33290–33296. [Google Scholar] [CrossRef]
- Nan, T.; Liu, B.; Wu, Y.; Wang, J.; Mao, Y.; Zhao, L.; Sun, T.; Wang, J.; Zhao, D. High-temperature fiber sensor based on two paralleled fiber-optic Fabry–Perot interferometers with ultrahigh sensitivity. Opt. Eng. 2020, 59, 027102. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, B.; Wu, J.; Zhao, L.; Sun, T.; Mao, Y.; Nan, T.; Wang, J. A transverse load sensor with ultra-sensitivity employing Vernier-effect improved parallel-structured fiber-optic Fabry-Perot interferometer. IEEE Access 2019, 7, 120297–120303. [Google Scholar] [CrossRef]
- Cui, X.L.; Zhang, H.; Wang, D.N. Parallel structured optical fiber in-line Fabry–Perot interferometers for high temperature sensing. Opt. Lett. 2020, 45, 726–729. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Wang, X.; Cooper, K.L.; Wang, A. Miniature all-silica fiber optic pressure and acoustic sensors. Opt. Lett. 2005, 30, 3269–3271. [Google Scholar] [CrossRef] [PubMed]


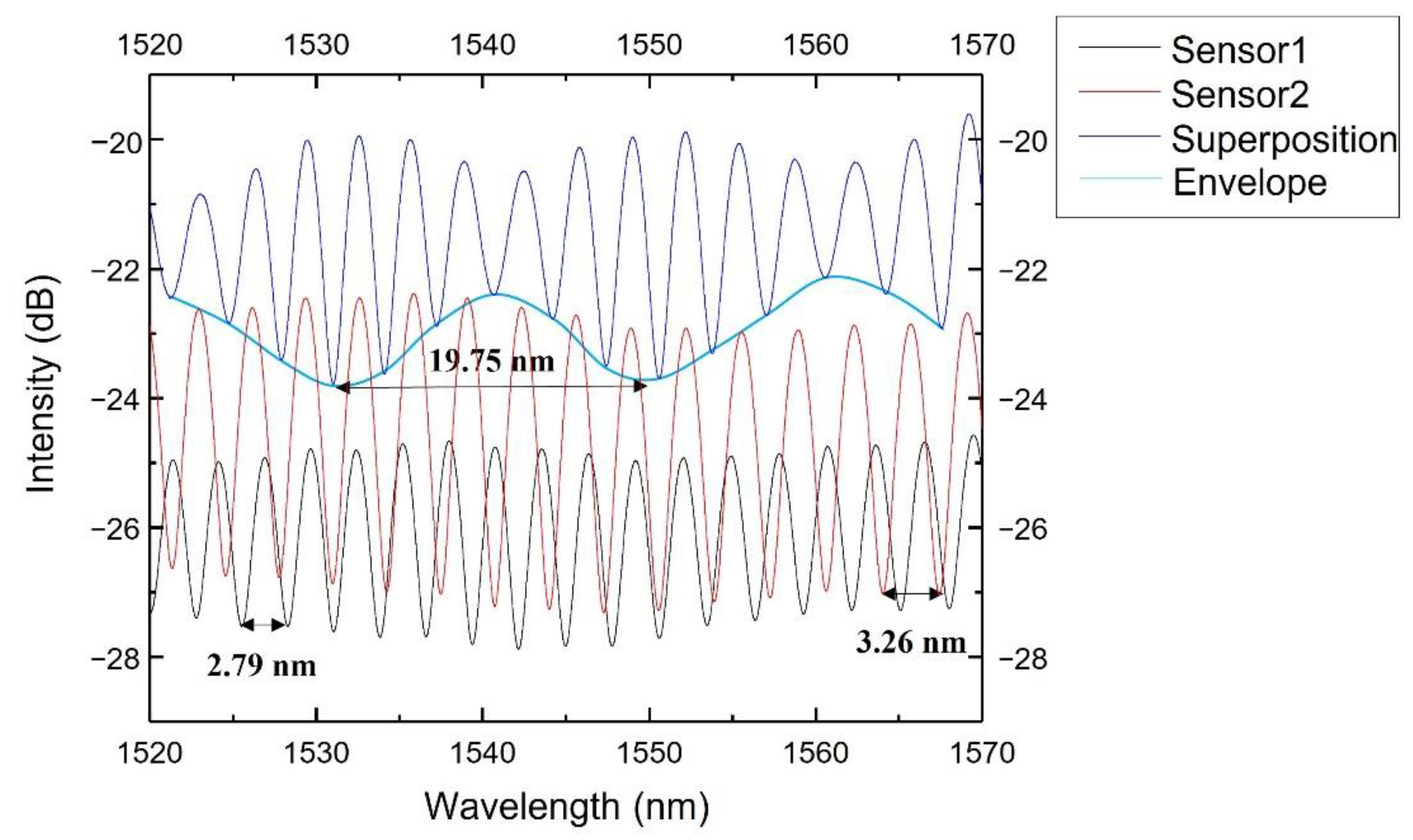

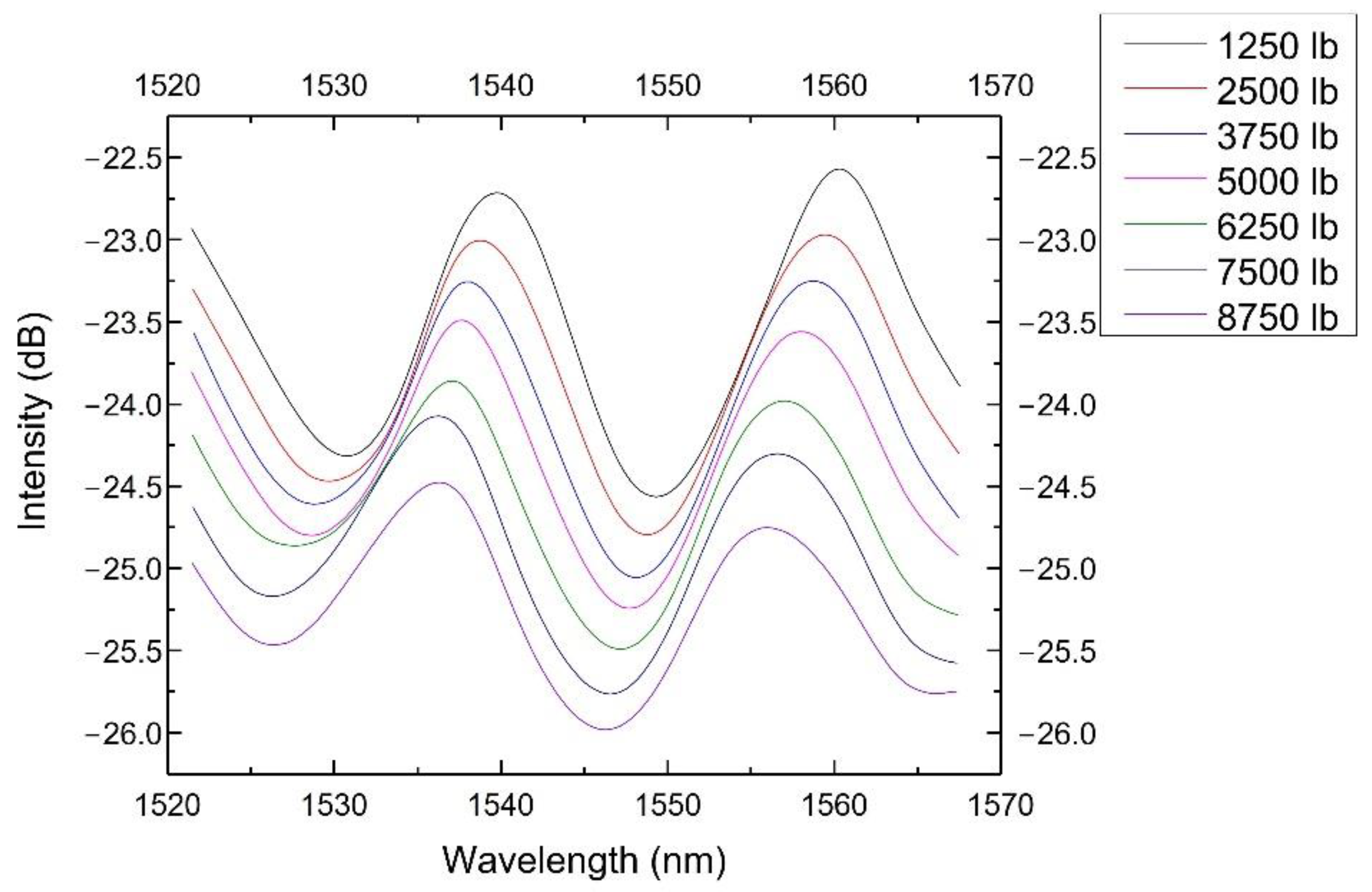
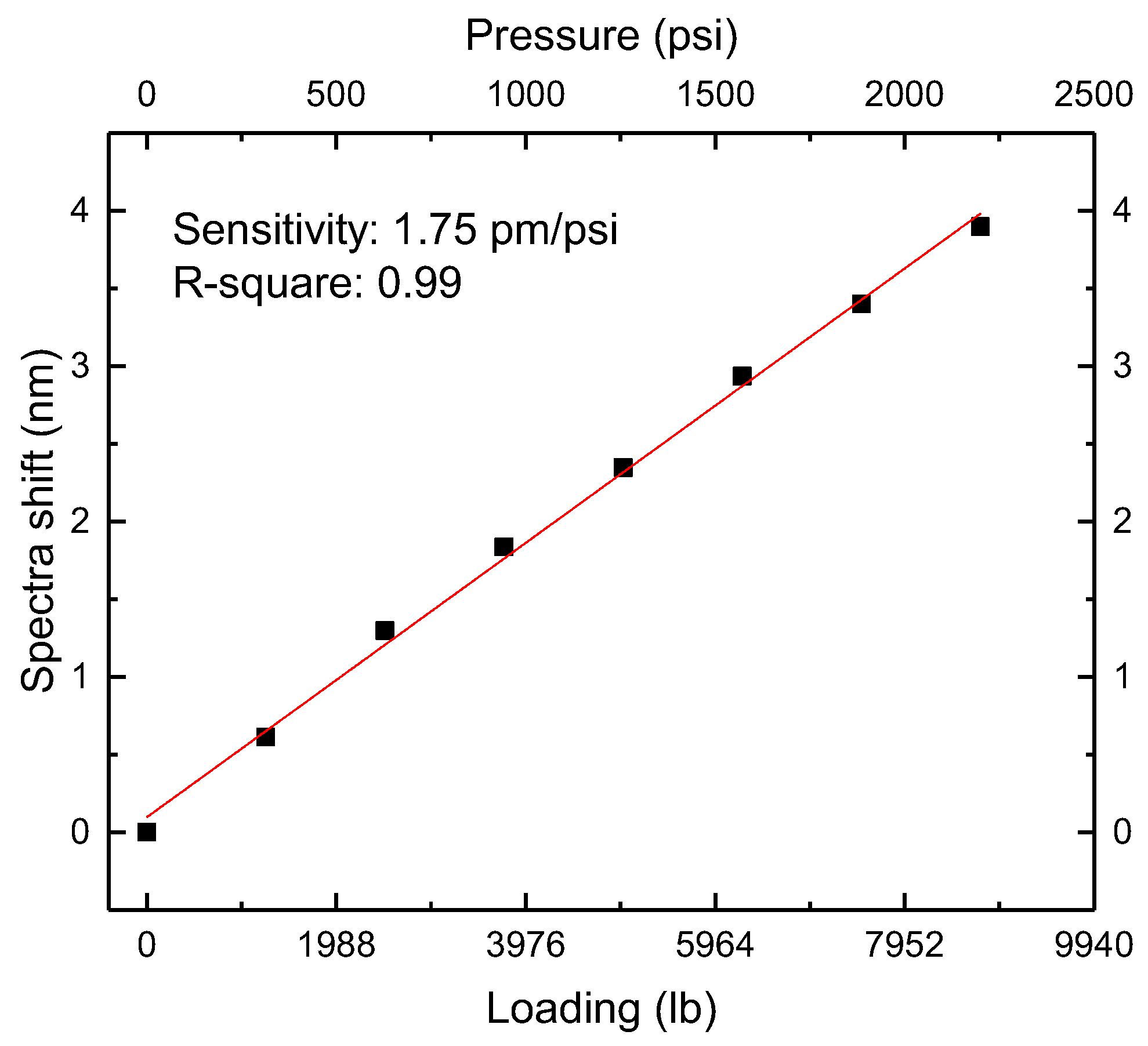
| Group | Sensitivity (pm/MPa) | Pressure Range (MPa) | Structure |
|---|---|---|---|
| C. Wu et al. [16] | 12.86 | 25 | FBG structure on a grapefruit micro-structured fiber |
| Z. Liu et al. [17] | 21 | 45 | A 20 cm twin-core photonic crystal fiber |
| G. Hu et al. [18] | 110.8 | 200 | An 8 cm side-hole two-core micro-structured optical fiber |
| H. Fu et al. [19] | 4210 | 20 | A 60 cm polarization-maintaining photonic crystal fiber was coiled circularly to a diameter of 1.8 cm |
| A. Wang et al. [24] | 15.5 | 40 | Two SMFs were fused inside a hollow silica glass tube |
| C. Wu et al. [25] | 2.8 | 400 | A 2.1 mm solid-core PCF to an SMF and the other end of the PCF was collapsed |
| Loading (lb) | Pressure (psi) |
|---|---|
| 1250 | 314.4 |
| 2500 | 628.8 |
| 3750 | 943.1 |
| 5000 | 1257.5 |
| 6250 | 1571.9 |
| 7500 | 1886.3 |
| 8750 | 2200.7 |
| FP Sensor | FBG Sensor | |
|---|---|---|
| Pressure sensitivity (pm/MPa) | 42.2 | 3.04 |
| Temperature sensitivity (pm/°C) | 0.833 | 12 |
| Temperature cross-sensitivity (MPa/°C) | 0.0197 | 3.95 |
| Loading (lb) | Single (nm) | FSR (nm) | M Value |
|---|---|---|---|
| 1250 | 0.10 | 0.61 | 6.10 |
| 2500 | 0.21 | 1.30 | 6.04 |
| 3750 | 0.29 | 1.83 | 6.25 |
| 5000 | 0.38 | 2.35 | 6.16 |
| 6250 | 0.46 | 2.93 | 6.32 |
| 7500 | 0.55 | 3.40 | 6.13 |
| 8750 | 0.65 | 3.90 | 5.97 |
| Std: 0.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Wu, R.; Zhou, J.; Biondi, A.; Cao, L.; Wang, X. Fiber Lateral Pressure Sensor Based on Vernier– Effect Improved Fabry–Perot Interferometer. Sensors 2022, 22, 7850. https://doi.org/10.3390/s22207850
Guo X, Wu R, Zhou J, Biondi A, Cao L, Wang X. Fiber Lateral Pressure Sensor Based on Vernier– Effect Improved Fabry–Perot Interferometer. Sensors. 2022; 22(20):7850. https://doi.org/10.3390/s22207850
Chicago/Turabian StyleGuo, Xu, Rui Wu, Jingcheng Zhou, Andres Biondi, Lidan Cao, and Xingwei Wang. 2022. "Fiber Lateral Pressure Sensor Based on Vernier– Effect Improved Fabry–Perot Interferometer" Sensors 22, no. 20: 7850. https://doi.org/10.3390/s22207850
APA StyleGuo, X., Wu, R., Zhou, J., Biondi, A., Cao, L., & Wang, X. (2022). Fiber Lateral Pressure Sensor Based on Vernier– Effect Improved Fabry–Perot Interferometer. Sensors, 22(20), 7850. https://doi.org/10.3390/s22207850







