Empirical Mode Decomposition-Based Feature Extraction for Environmental Sound Classification
Abstract
1. Introduction
2. Empirical Mode Decomposition-Teager–Kaiser Energy Operator (EMD-TKEO) Method
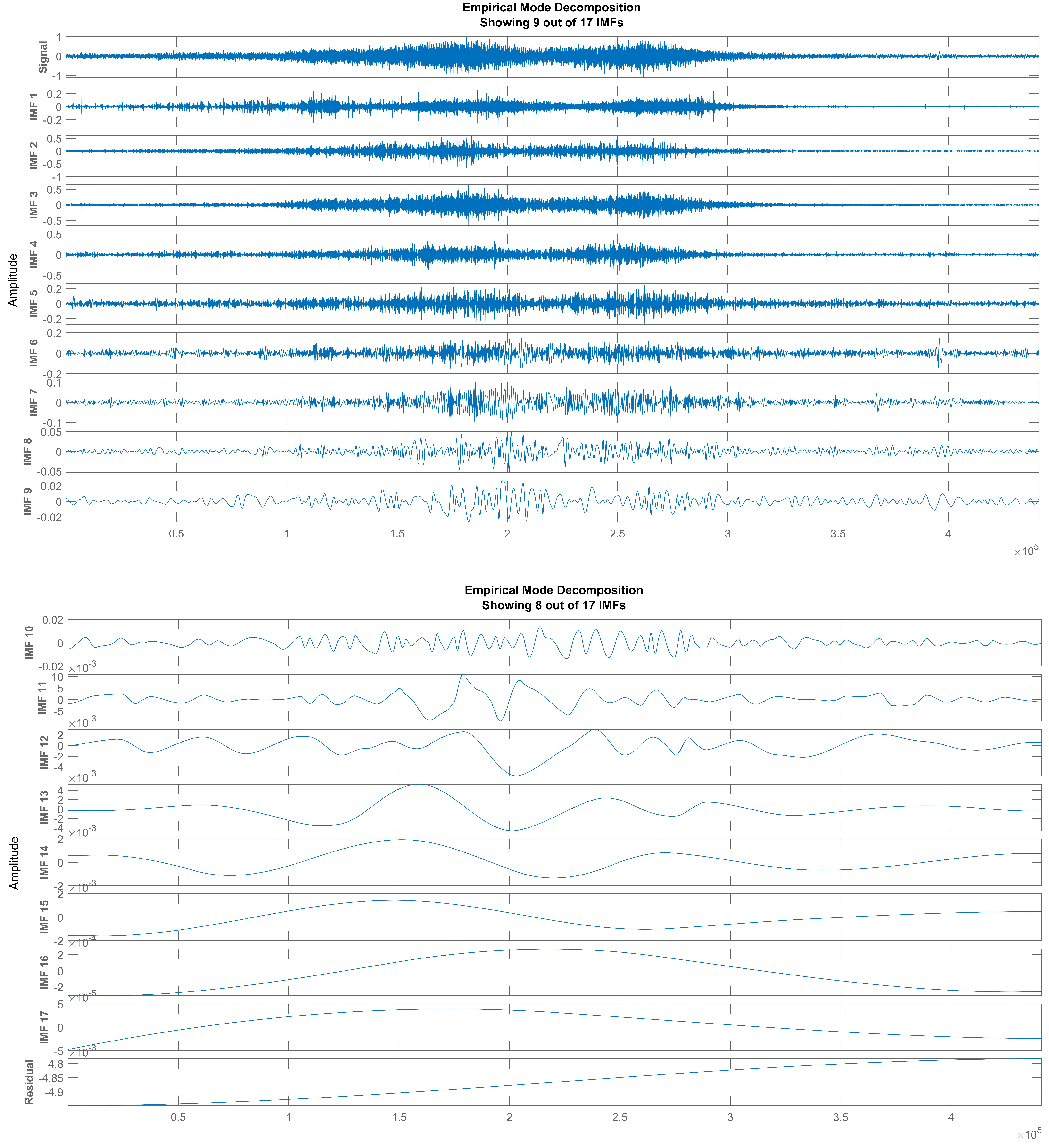
2.1. Empirical Mode Decomposition
2.2. Sifting Process for IMFs
- 1
- The number of extrema (maxima and minima) in a signal must be equal to the zero-crossing number or differ at most by one;
- 2
- The mean of the envelopes obtained through local maxima and local minima must be equal to zero at all times.
| Algorithm 1: Sifting process for intrinsic mode functions |
Input: a sound event signal Output: collection of IMFs
|
- 1
- The process terminates when the ; the last IMF, is either a monotonic function or function with only one extremum.
- 2
- The number of IMFs is subjected to stopping criteria, where the user terminates the sifting process after a particular number of IMFs have been created.
2.3. Teager–Kaiser Energy Operator (TKEO)
3. Feature Extraction
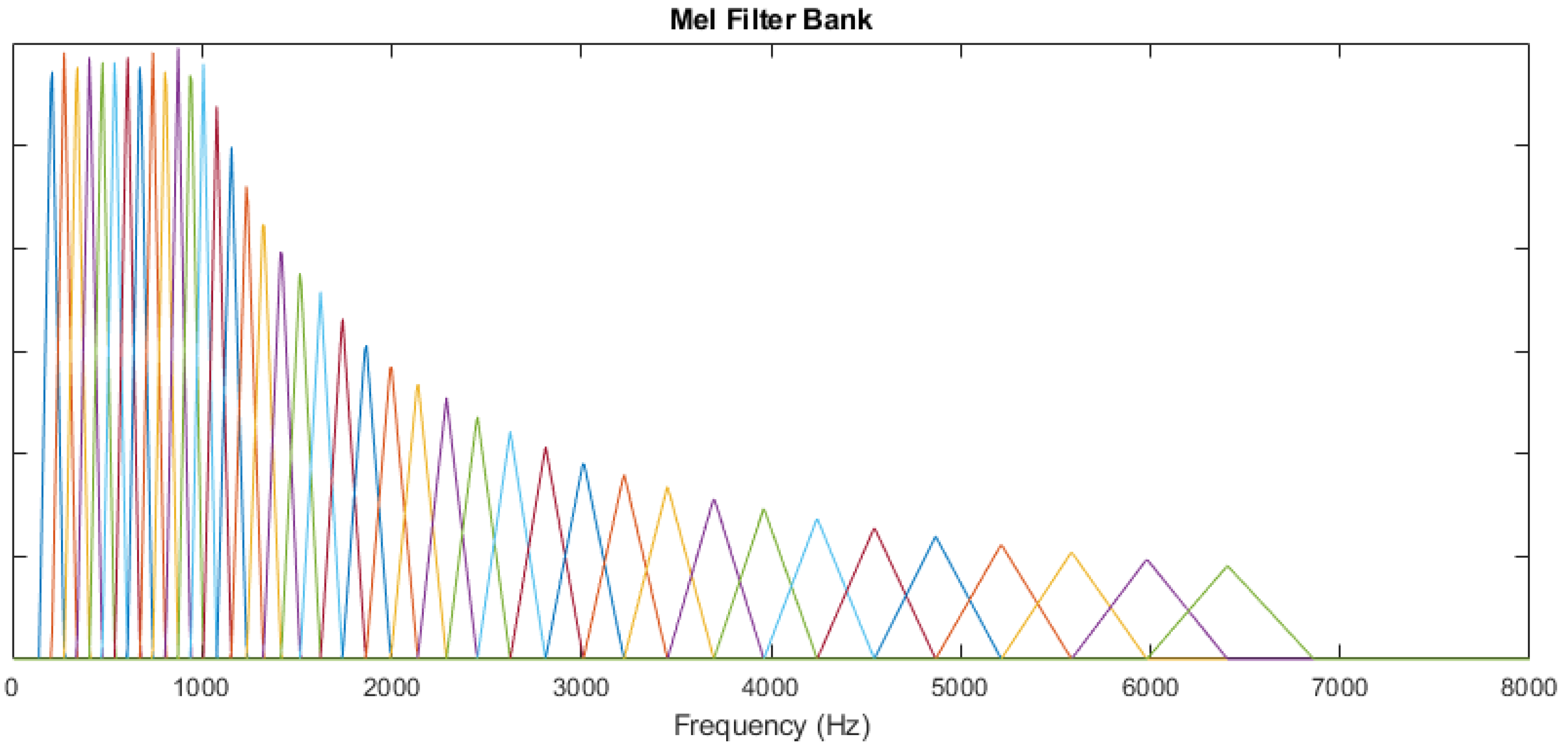
3.1. Mel Band Energies
- Number of Mel filters, F;
- Minimum frequency, ;
- Maximum frequency, .
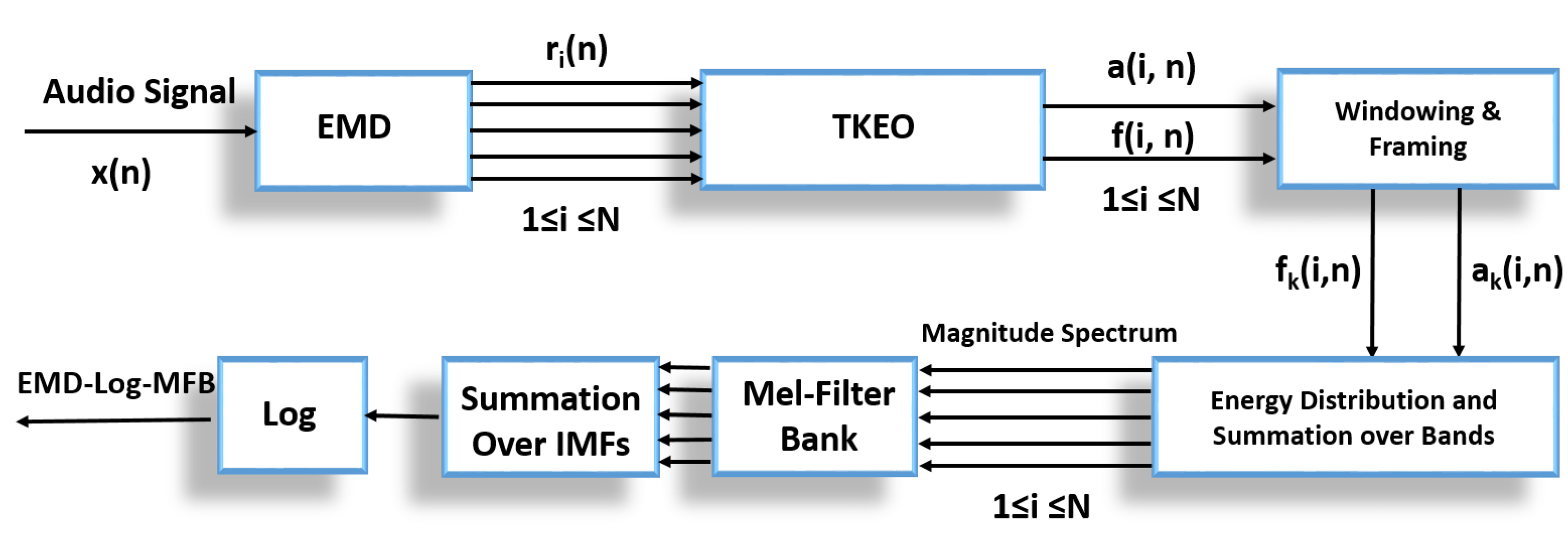
3.2. EMD-Mel Band Energies
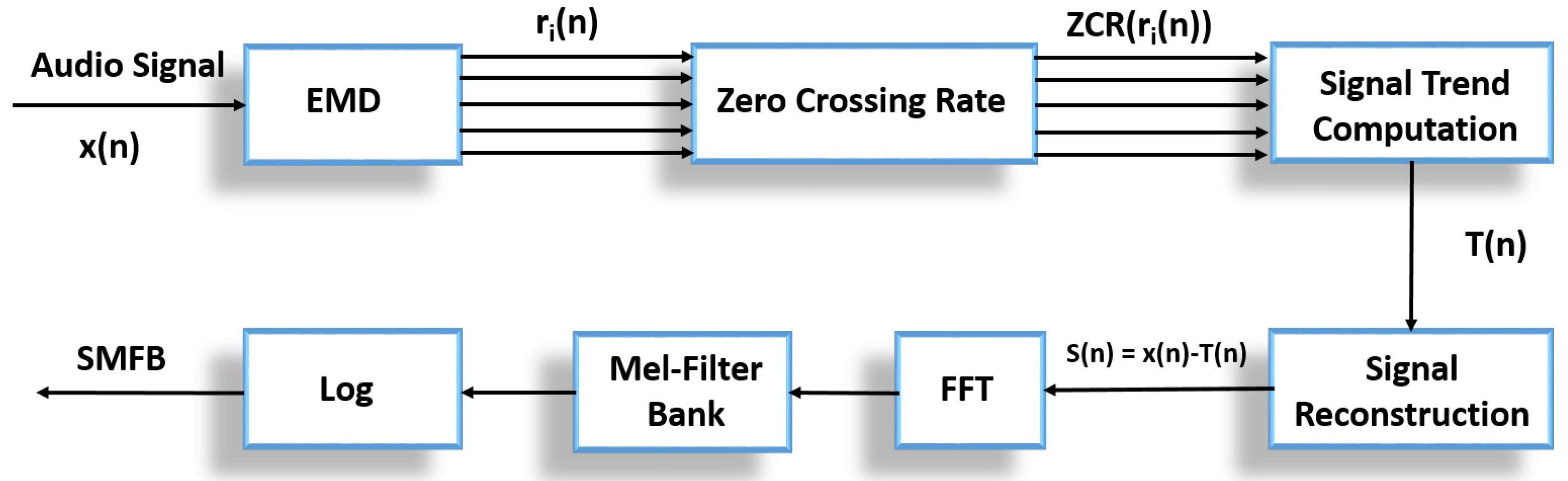
3.3. S-MBE
3.4. Features
4. Experimental Setup
4.1. Databases
4.1.1. Acoustic Scene Classification Dataset
4.1.2. Low-Complexity Acoustic Scene Classification Dataset
- Indoor scenes—indoor: airport, indoor shopping mall, and metro station;
- Outdoor scenes—pedestrian street, public square, a street with a medium level of traffic, and urban park;
- Transportation-related scenes—traveling by bus, traveling by tram, traveling by underground metro.
4.1.3. Urbansound8k
4.1.4. Custom Database
4.2. Classification Model
- Log-scaled Mel band energies were extracted for every dataset. For the Acoustic Scene Classification Dataset and Low-Complexity Acoustic Scene Classification Dataset, we extracted 40 Mel bands using an analysis frame of 40 ms with a 50% overlap. Similarly, the EMD-Log Mel band energies and log scaled S-MBEs were calculated for both datasets with similar characteristics, resulting in similar shape. The input shape is , trained for 200 epochs with a mini batch size of 16 and data shuffling between epochs. An Adam optimizer [55] is used for optimisation, with a learning rate of 0.001. Model performance is checked after each epoch on the validation set, and the best performing is chosen. The system was trained for 200 epochs with the Adam optimizer, with an initial learning rate of 0.001.
- For Urbansound8k, the log Mel band energies, EMD-log Mel band energies, and log scaled S-MBEs were extracted with 60 Mel bands; a window size of 1024 samples with a hop length of 512 samples is used. The input size for the CNN was and silent segments were discarded. The Urbansound dataset was trained using 10-fold cross validation. The network was trained for 300 epochs with the Adagrad optimizer [56].
- For the custom database, the log Mel band energies, EMD-log Mel band energies, and log scaled S-MBEs were extracted with 128 Mel bands with 50% overlap. The custom dataset was trained using seven-fold cross validation. The system was trained for 200 epochs with Adagrad optimizer, with an initial learning rate of 0.001.
- To evaluate the experimental results, this paper uses classification accuracy as a metric:where TN and TP are defined as the number of negative and positive examples that are classified successfully, respectively. FN and FP are the number of misclassified positive and negative examples, respectively. The evaluation metric is chosen according to the baseline system [46] to perform comparisons between the feature extraction methods under the same evaluation metrics.
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mesaros, A.; Heittola, T.; Benetos, E.; Foster, P.; Lagrange, M.; Virtanen, T.; Plumbley, M.D. Detection and classification of acoustic scenes and events: Outcome of the DCASE 2016 challenge. IEEE Trans. Audio Speech Lang. Process. 2017, 26, 379–393. [Google Scholar] [CrossRef]
- Plumbley, M.D.; Kroos, C.; Bello, J.P.; Richard, G.; Ellis, D.P.; Mesaros, A. (Eds.) Proceedings of the Detection and Classification of Acoustic Scenes and Events 2018 Workshop (DCASE2018); Tampere University of Technology: Tampere, Finland, 2018. [Google Scholar]
- Çakır, E.; Parascandolo, G.; Heittola, T.; Huttunen, H.; Virtanen, T. Convolutional Recurrent Neural Networks for Polyphonic Sound Event Detection. IEEE Trans. Audio Speech Lang. Process. 2017, 25, 1291–1303. [Google Scholar] [CrossRef]
- Cakir, E.; Heittola, T.; Huttunen, H.; Virtanen, T. Polyphonic sound event detection using multi label deep neural networks. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Hershey, S.; Chaudhuri, S.; Ellis, D.P.; Gemmeke, J.F.; Jansen, A.; Moore, R.C.; Plakal, M.; Platt, D.; Saurous, R.A.; Seybold, B.; et al. CNN architectures for large-scale audio classification. In Proceedings of the 2017 IEEE International Conference On Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 131–135. [Google Scholar]
- Zinemanas, P.; Cancela, P.; Rocamora, M. End-to-end convolutional neural networks for sound event detection in urban environments. In Proceedings of the 2019 24th Conference of Open Innovations Association (FRUCT), Moscow, Russia, 8–12 April 2019; pp. 533–539. [Google Scholar]
- Adavanne, S.; Parascandolo, G.; Pertilä, P.; Heittola, T.; Virtanen, T. Sound event detection in multichannel audio using spatial and harmonic features. arXiv 2017, arXiv:1706.02293. [Google Scholar]
- Sejdić, E.; Djurović, I.; Jiang, J. Time–frequency feature representation using energy concentration: An overview of recent advances. Digital Signal Process. 2009, 19, 153–183. [Google Scholar] [CrossRef]
- Griffin, D.; Lim, J. Signal estimation from modified short-time Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 236–243. [Google Scholar] [CrossRef]
- Portnoff, M. Time-frequency representation of digital signals and systems based on short-time Fourier analysis. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 55–69. [Google Scholar] [CrossRef]
- Shor, J.; Jansen, A.; Maor, R.; Lang, O.; Tuval, O.; Quitry, F.d.C.; Tagliasacchi, M.; Shavitt, I.; Emanuel, D.; Haviv, Y. Towards learning a universal non-semantic representation of speech. arXiv 2020, arXiv:2002.12764. [Google Scholar]
- Drossos, K.; Mimilakis, S.I.; Gharib, S.; Li, Y.; Virtanen, T. Sound event detection with depthwise separable and dilated convolutions. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6848–6856. [Google Scholar]
- Tsalera, E.; Papadakis, A.; Samarakou, M. Comparison of Pre-Trained CNNs for Audio Classification Using Transfer Learning. J. Sens. Actuator Netw. 2021, 10, 72. [Google Scholar] [CrossRef]
- Titchmarsh, E.C. Introduction to the Theory of Fourier Integrals; Clarendon Press Oxford: London, UK, 1948; Volume 2. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Ono, N.; Harada, N.; Kawaguchi, Y.; Mesaros, A.; Imoto, K.; Koizumi, Y.; Komatsu, T. (Eds.) In Proceedings of the Fifth Workshop on Detection and Classification of Acoustic Scenes and Events (DCASE 2020), Tokyo, Japan, 2–4 November 2020. [CrossRef]
- Mesaros, A.; Heittola, T.; Virtanen, T. Acoustic scene classification: An overview of DCASE 2017 challenge entries. In Proceedings of the 2018 16th International Workshop on Acoustic Signal Enhancement (IWAENC), Tokyo, Japan, 17–20 September 2018; pp. 411–415. [Google Scholar]
- Mesaros, A.; Heittola, T.; Virtanen, T. Assessment of human and machine performance in acoustic scene classification: Dcase 2016 case study. In Proceedings of the 2017 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, USA, 15–18 October 2017; pp. 319–323. [Google Scholar] [CrossRef]
- Stowell, D.; Giannoulis, D.; Benetos, E.; Lagrange, M.; Plumbley, M.D. Detection and classification of acoustic scenes and events. IEEE Trans. Multimed. 2015, 17, 1733–1746. [Google Scholar] [CrossRef]
- Ricker, N. The form and nature of seismic waves and the structure of seismograms. Geophysics 1940, 5, 348–366. [Google Scholar] [CrossRef]
- Wirsing, K. Time Frequency Analysis of Wavelet and Fourier Transform. In Wavelet Theory; IntechOpen: London, UK, 2020. [Google Scholar]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef]
- Morlet, J. Sampling theory and wave propagation. In Issues in Acoustic Signal—Image Processing and Recognition; Springer: Berlin/Heidelberg, Germany, 1983; pp. 233–261. [Google Scholar]
- Djordjević, V.; Stojanović, V.; Pršić, D.; Dubonjić, L.; Morato, M.M. Observer-based fault estimation in steer-by-wire vehicle. Eng. Today 2022, 1, 7–17. [Google Scholar]
- Xu, Z.; Li, X.; Stojanovic, V. Exponential stability of nonlinear state-dependent delayed impulsive systems with applications. Nonlinear Anal. Hybrid Syst. 2021, 42, 101088. [Google Scholar] [CrossRef]
- Khaldi, K.; Boudraa, A.O.; Komaty, A. Speech enhancement using empirical mode decomposition and the Teager–Kaiser energy operator. J. Acoust. Soc. Am. 2014, 135, 451–459. [Google Scholar] [CrossRef]
- Krishnan, P.T.; Joseph Raj, A.N.; Rajangam, V. Emotion classification from speech signal based on empirical mode decomposition and non-linear features. Complex Intell. Syst. 2021, 7, 1919–1934. [Google Scholar] [CrossRef]
- De La Cruz, C.; Santhanam, B. A joint EMD and Teager-Kaiser energy approach towards normal and nasal speech analysis. In Proceedings of the 2016 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2016; pp. 429–433. [Google Scholar]
- Kerkeni, L.; Serrestou, Y.; Raoof, K.; Mbarki, M.; Mahjoub, M.A.; Cleder, C. Automatic speech emotion recognition using an optimal combination of features based on EMD-TKEO. Speech Commun. 2019, 114, 22–35. [Google Scholar] [CrossRef]
- Jayalakshmy, S.; Sudha, G.F. GTCC-based BiLSTM deep-learning framework for respiratory sound classification using empirical mode decomposition. Neural Comput. Appl. 2021, 33, 17029–17040. [Google Scholar] [CrossRef]
- Maragos, P.; Kaiser, J.; Quatieri, T. Energy separation in signal modulations with application to speech analysis. IEEE Trans. Signal Process. 1993, 41, 3024–3051. [Google Scholar] [CrossRef]
- Potamianos, A.; Maragos, P. A comparison of the energy operator and the Hilbert transform approach to signal and speech demodulation. Signal Process. 1994, 37, 95–120. [Google Scholar] [CrossRef]
- Sharma, R.; Vignolo, L.; Schlotthauer, G.; Colominas, M.A.; Rufiner, H.L.; Prasanna, S. Empirical mode decomposition for adaptive AM-FM analysis of speech: A review. Speech Commun. 2017, 88, 39–64. [Google Scholar] [CrossRef]
- Sethu, V.; Ambikairajah, E.; Epps, J. Empirical mode decomposition based weighted frequency feature for speech-based emotion classification. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 12 May 2008; pp. 5017–5020. [Google Scholar]
- Kaiser, J. On a simple algorithm to calculate the ‘energy’ of a signal. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; Volume 1, pp. 381–384. [Google Scholar] [CrossRef]
- Boudraa, A.O.; Salzenstein, F. Teager–Kaiser energy methods for signal and image analysis: A review. Digital Signal Process. 2018, 78, 338–375. [Google Scholar] [CrossRef]
- Maragos, P.; Kaiser, J.F.; Quatieri, T.F. On amplitude and frequency demodulation using energy operators. IEEE Trans. Signal Process. 1993, 41, 1532–1550. [Google Scholar] [CrossRef]
- Kaiser, J.F. Some useful properties of Teager’s energy operators. In Proceedings of the 1993 IEEE International Conference On Acoustics, Speech, and Signal Processing, Minneapolis, MN, USA, 27–30 April 1993; Volume 3, pp. 149–152. [Google Scholar]
- Bouchikhi, A. AM-FM Signal Analysis by Teager Huang Transform: Application to Underwater Acoustics. Ph.D. Thesis, Université Rennes 1, Rennes, France, 2010. [Google Scholar]
- Maragos, P.; Kaiser, J.F.; Quatieri, T.F. On separating amplitude from frequency modulations using energy operators. In Proceedings of the 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ’92), San Francisco, CA, USA, 23–26 March 1992; Volume 92. [Google Scholar]
- Li, X.; Li, X.; Zheng, X.; Zhang, D. Emd-teo based speech emotion recognition. In Life System Modeling and Intelligent Computing; Springer: Berlin, Germany, 2010; pp. 180–189. [Google Scholar]
- Mesaros, A.; Heittola, T.; Virtanen, T. A multi-device dataset for urban acoustic scene classification. In Proceedings of the Detection and Classification of Acoustic Scenes and Events 2018 Workshop (DCASE2018), Surrey, UK, 19–20 November 2018; pp. 9–13. [Google Scholar]
- Kumari, S.; Roy, D.; Cartwright, M.; Bello, J.P.; Arora, A. EdgeLˆ 3: Compressing Lˆ 3-Net for Mote Scale Urban Noise Monitoring. In Proceedings of the 2019 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), Rio de Janeiro, Brazil, 24 May 2019; pp. 877–884. [Google Scholar]
- Salamon, J.; Bello, J.P. Unsupervised feature learning for urban sound classification. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 171–175. [Google Scholar]
- Piczak, K.J. Environmental sound classification with convolutional neural networks. In Proceedings of the 2015 IEEE 25th international workshop on machine learning for signal processing (MLSP), Boston, MA, USA, 17–20 September 2015; pp. 1–6. [Google Scholar]
- Font, F.; Roma, G.; Serra, X. Freesound Technical Demo. In Proceedings of the 21st ACM International Conference on Multimedia (MM ’13), New York, NY, USA, 21 October 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 411–412. [Google Scholar] [CrossRef]
- Ahmed, A.; Serrestou, Y.; Raoof, K.; Diouris, J.F. Sound event classification using neural networks and feature selection based methods. In Proceedings of the 2021 IEEE International Conference on Electro Information Technology (EIT), Mt. Pleasant, MI, USA, 14–15 May 2021; pp. 1–6. [Google Scholar]
- Sakashita, Y.; Aono, M. Acoustic scene classification by ensemble of spectrograms based on adaptive temporal divisions. In Proceedings of the Detection and Classification of Acoustic Scenes and Events, Surrey, UK, 19–20 November 2018. [Google Scholar]
- Dorfer, M.; Lehner, B.; Eghbal-zadeh, H.; Christop, H.; Fabian, P.; Gerhard, W. Acoustic scene classification with fully convolutional neural networks and I-vectors. In Proceedings of the Detection and Classification of Acoustic Scenes and Events, Surrey, UK, 19–20 November 2018. [Google Scholar]
- Guo, J.; Li, C.; Sun, Z.; Li, J.; Wang, P. A Deep Attention Model for Environmental Sound Classification from Multi-Feature Data. Appl. Sci. 2022, 12, 5988. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Zheng, J.; Cheng, J.; Yang, Y. Partly ensemble empirical mode decomposition: An improved noise-assisted method for eliminating mode mixing. Signal Process. 2014, 96, 362–374. [Google Scholar] [CrossRef]
- Xu, G.; Yang, Z.; Wang, S. Study on mode mixing problem of empirical mode decomposition. In Proceedings of the Joint International Information Technology, Mechanical and Electronic Engineering Conference, Xi’an, China, 4–5 October 2016; Volume 1, pp. 389–394. [Google Scholar]
- Gao, Y.; Ge, G.; Sheng, Z.; Sang, E. Analysis and solution to the mode mixing phenomenon in EMD. In Proceedings of the 2008 Congress on Image and Signal Processing, Sanya, Hainan, China, 27–30 May 2008; Volume 5, pp. 223–227. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Shen, W.C.; Chen, Y.H.; Wu, A.Y.A. Low-complexity sinusoidal-assisted EMD (SAEMD) algorithms for solving mode-mixing problems in HHT. Digital Signal Process. 2014, 24, 170–186. [Google Scholar] [CrossRef]
- Tang, B.; Dong, S.; Song, T. Method for eliminating mode mixing of empirical mode decomposition based on the revised blind source separation. Signal Process. 2012, 92, 248–258. [Google Scholar] [CrossRef]


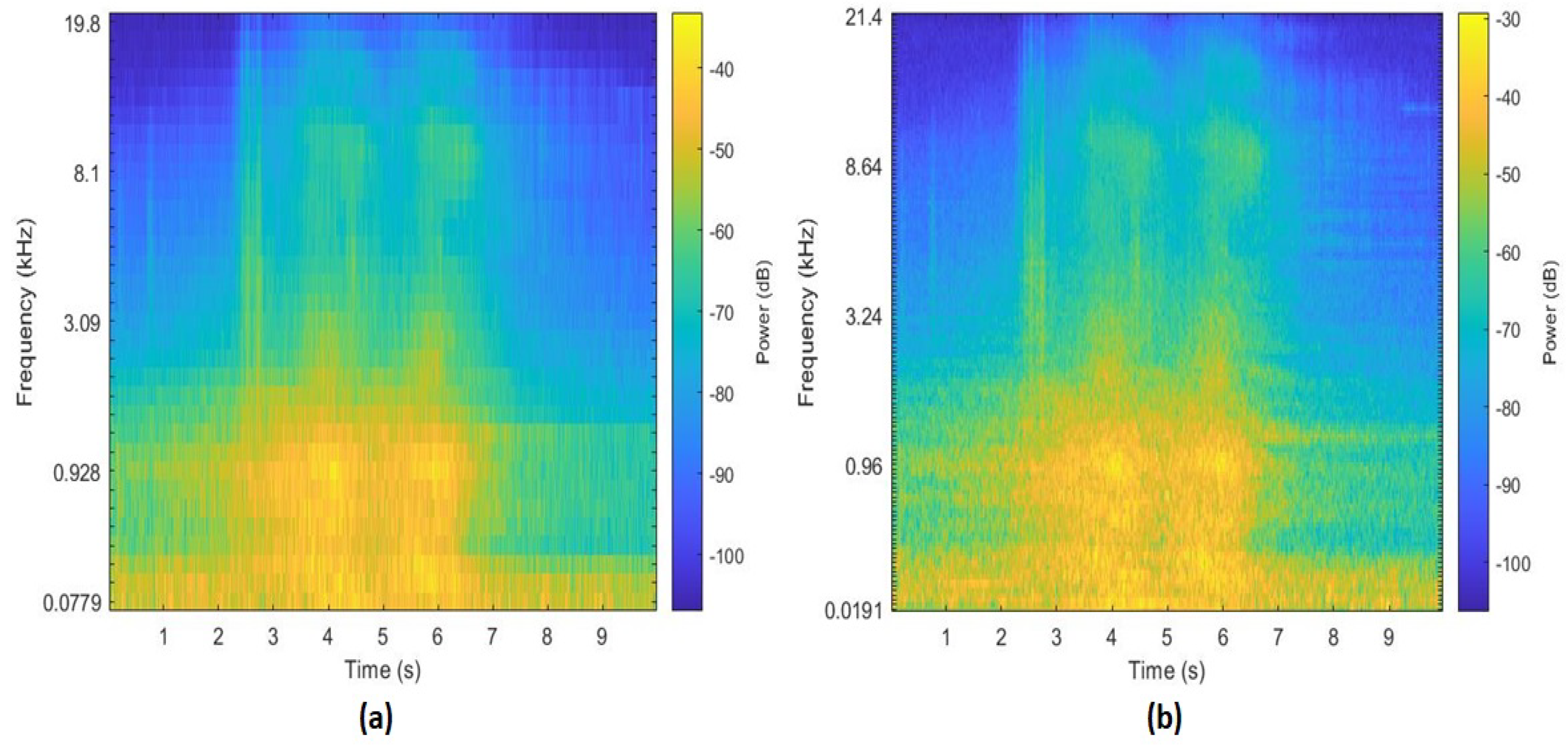
| Layers | Model Specifications | |
|---|---|---|
| CNN1 | CNN2 | |
| Layer 1 | Conv2D (32,(7,7)) | Conv2D (64,(4,4) ) |
| Relu, strides = 1 | tanh, strides = 1 | |
| MaxPool2D (5, 5) | MaxPool2D (2, 2), stride = 2 | |
| Dropout (0.3) | ||
| Batch normalisation | ||
| Layer 2 | Conv2D (64,(7,7)) | Conv2D (32,(4,4) ) |
| Relu, strides = 1 | tanh, strides = 1 | |
| MaxPool2D (4, 100) | MaxPool2D (2, 2), stride = 2 | |
| Dropout (0.3) | Dropout (0.2) | |
| Batch normalisation | ||
| Layer 3 | - | Conv2D (16,(4,4) ) |
| tanh, strides = 1 | ||
| MaxPool2D (2, 2), stride = 2 | ||
| Dropout (0.2) | ||
| Layer 4 | Dense (100) | 2 X Dense (400) |
| Activation = relu | Activation = tanh | |
| Dropout = 0.3 | ||
| Layer 5 | - | Dense (300) |
| Activation = tanh | ||
| Dropout = 0.2 | ||
| Layer 6 | Dense (classes, softmax) | |
| Features | Accuracy per Database | |||
|---|---|---|---|---|
| ASC Dataset | Low Complexity ASC | Urbansound8k | Custom | |
| FFT | 54.77% | 84.18% | 63.36% | 75.61% |
| EMD | 52.5% | 79.74% | 54.64% | 75.05% |
| SMB | 48.25% | 79.55% | 52.41% | 71.93% |
| FFT+EMD | 56.08% | 84.49% | 63.70% | 78.87% |
| FFT+EMD+SMB | 57.78% | 84.83% | 62.31% | 79.25% |
| Classes | Features | ||||
|---|---|---|---|---|---|
| FFT-MBE | EMD-MBE | SMBE | FFT + EMD | SMBE + FFT + EMD | |
| Airport | 53.90% | 40% | 37.36% | 40% | 55.094% |
| Bus | 52.89% | 82.23% | 40.9% | 63.22% | 76.033% |
| Metro | 60.53% | 32.18% | 34.1% | 51.34% | 57.85% |
| Metro Station | 57.14% | 42.85% | 52.5% | 54.44% | 54.44% |
| Park | 70.24% | 63.22% | 66.11% | 74.38% | 65.29% |
| Public Square | 42.12% | 44.9% | 33.33% | 47.22% | 49.07% |
| Shopping Mall | 56.27% | 64.87% | 55.91% | 59.50% | 62.72% |
| Street Pedestrian | 32.79% | 28.34% | 37.25% | 39.27% | 36.03% |
| Street Traffic | 75.61% | 72.76% | 72.76% | 76.83% | 80.08% |
| Tram | 46.74% | 54.4% | 50.96% | 55.17% | 41.37% |
| Classes | Features | ||||
|---|---|---|---|---|---|
| FFT-MBE | EMD-MBE | SMBE | FFT + EMD | SMBE + FFT + EMD | |
| Indoor | 78.72% | 77.87% | 73.01% | 81.34% | 78.72% |
| Outdoor | 81.67% | 76.80% | 84.54% | 80.54% | 82.29% |
| Transportation | 92.83% | 85.28% | 79.90% | 92.60% | 94.15% |
| Classes | Features | ||||
|---|---|---|---|---|---|
| FFT-MBE | EMD-MBE | SMBE | FFT + EMD MBE | SMBE + FFT + EMD-MBE | |
| air_conditioner | 39.2% | 41.5% | 30.6% | 44.9% | 43.1% |
| car_horn | 70.92% | 32.38% | 20.9% | 74.90% | 71.52% |
| children_playing | 70.4% | 50.5% | 55.6% | 66.5% | 61.4% |
| dog_bark | 71.3% | 63.6% | 66.1% | 69.4% | 64.2% |
| drilling | 60.3% | 60.7% | 54.6% | 65.6% | 64.1% |
| engine_idle | 51.49% | 51.54% | 40.3% | 52.26% | 58.61% |
| gun_shot | 84.60% | 52.80% | 24.2% | 76.54% | 70.82% |
| jack_hammer | 61.58% | 51.73% | 38.9% | 60.00% | 56.35% |
| siren | 69.18% | 73.35% | 66% | 77.14% | 72.80% |
| street_music | 78.3% | 57.7% | 62.3% | 72% | 73.7% |
| Classes | Features | ||||
|---|---|---|---|---|---|
| FFT-MBE | EMD-MBE | SMBE | FFT+EMD | SMBE + FFT + EMD | |
| Car Passing | 74.24% | 53.63% | 65.67% | 81.14% | 81.48% |
| Rain | 85.28% | 81.42% | 79.09% | 89.33% | 88.71% |
| Walking | 61.57% | 71.09% | 80.52% | 66.29% | 71.81% |
| Wind | 83.28% | 70.57% | 62.43% | 78.71% | 75% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.; Serrestou, Y.; Raoof, K.; Diouris, J.-F. Empirical Mode Decomposition-Based Feature Extraction for Environmental Sound Classification. Sensors 2022, 22, 7717. https://doi.org/10.3390/s22207717
Ahmed A, Serrestou Y, Raoof K, Diouris J-F. Empirical Mode Decomposition-Based Feature Extraction for Environmental Sound Classification. Sensors. 2022; 22(20):7717. https://doi.org/10.3390/s22207717
Chicago/Turabian StyleAhmed, Ammar, Youssef Serrestou, Kosai Raoof, and Jean-François Diouris. 2022. "Empirical Mode Decomposition-Based Feature Extraction for Environmental Sound Classification" Sensors 22, no. 20: 7717. https://doi.org/10.3390/s22207717
APA StyleAhmed, A., Serrestou, Y., Raoof, K., & Diouris, J.-F. (2022). Empirical Mode Decomposition-Based Feature Extraction for Environmental Sound Classification. Sensors, 22(20), 7717. https://doi.org/10.3390/s22207717







