Simple and Robust Deep Learning Approach for Fast Fluorescence Lifetime Imaging
Abstract
1. Introduction
2. Methods and Theory
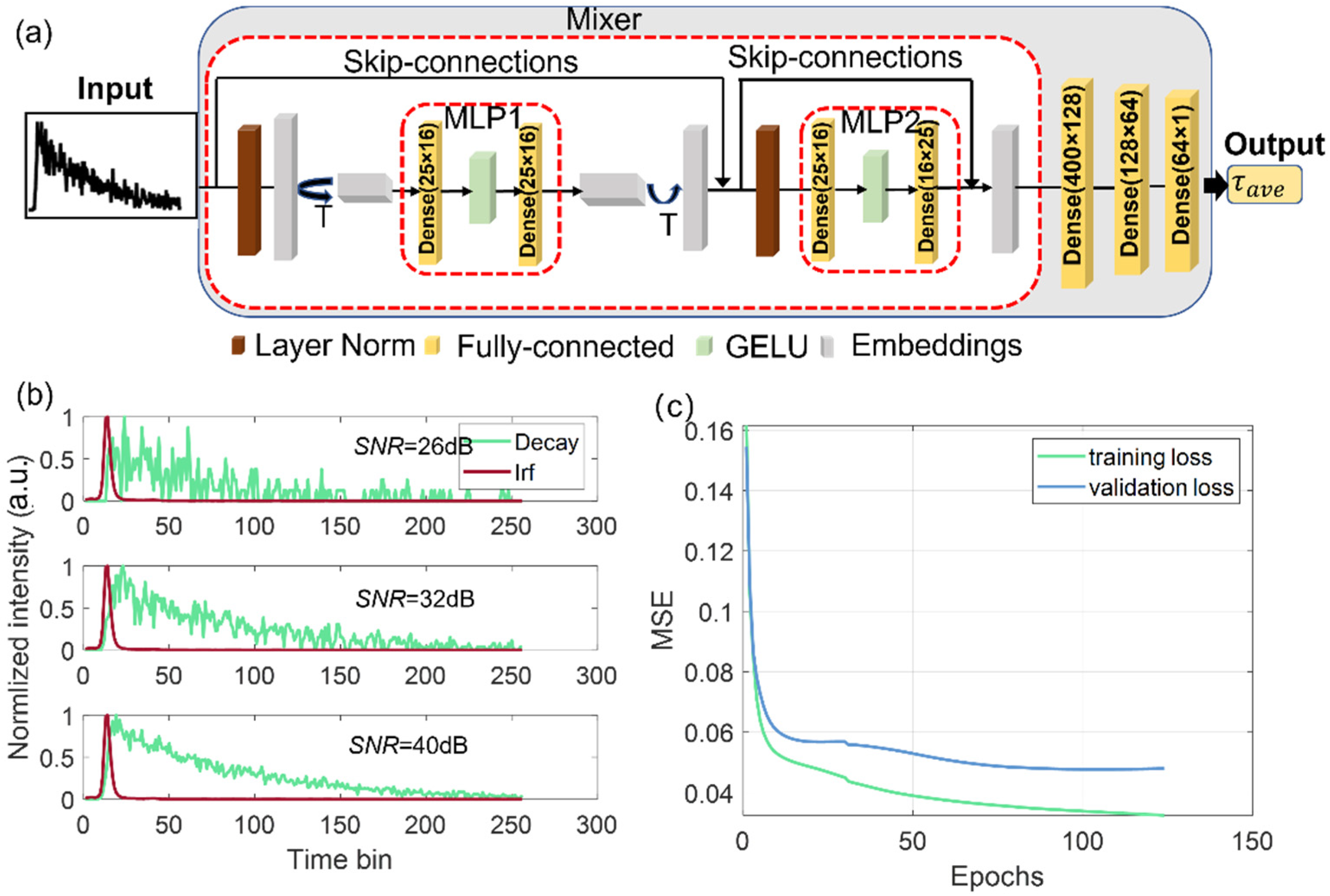
2.1. Architecture Design
2.2. Training Dataset Preparation
2.3. Training and Evaluation
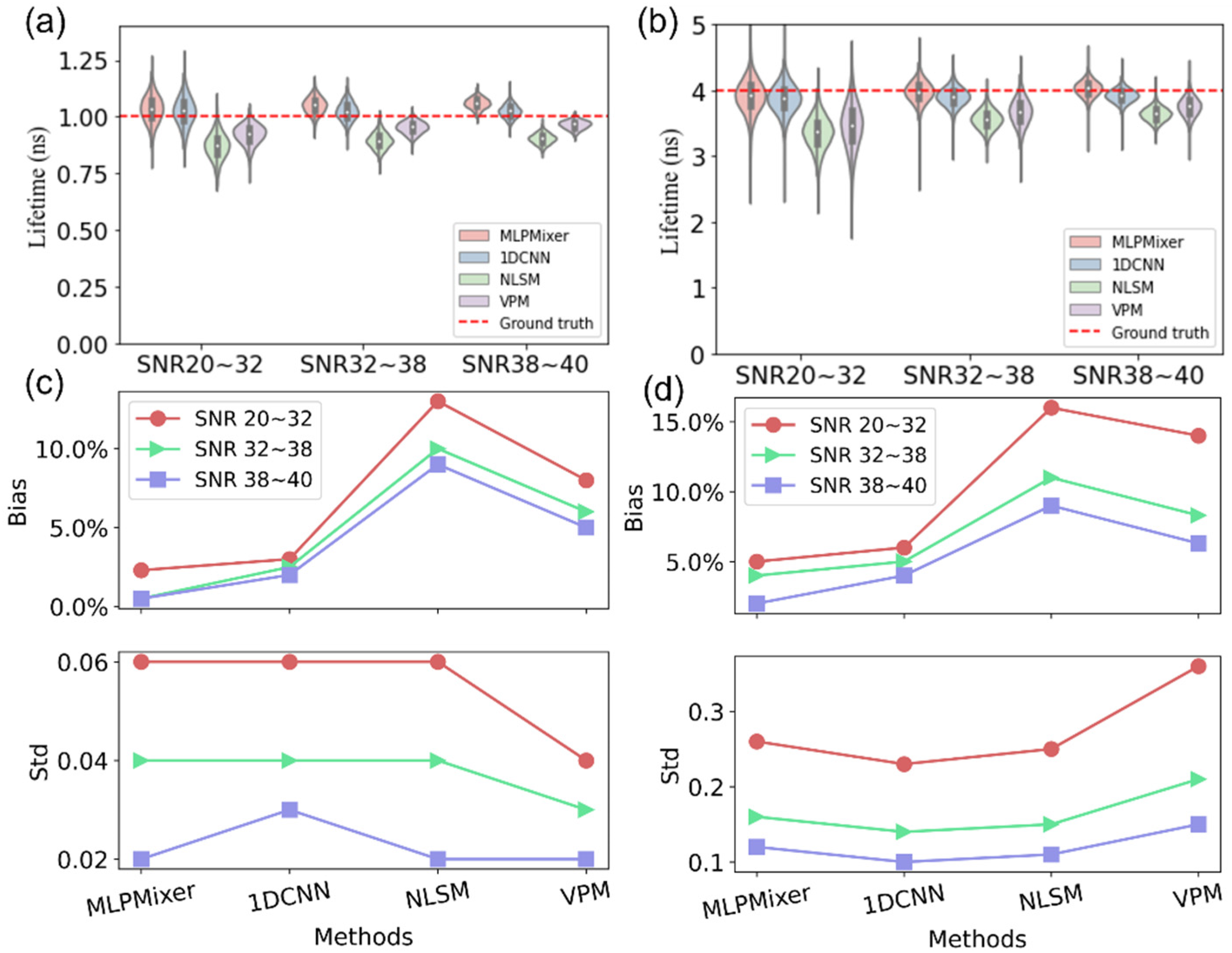
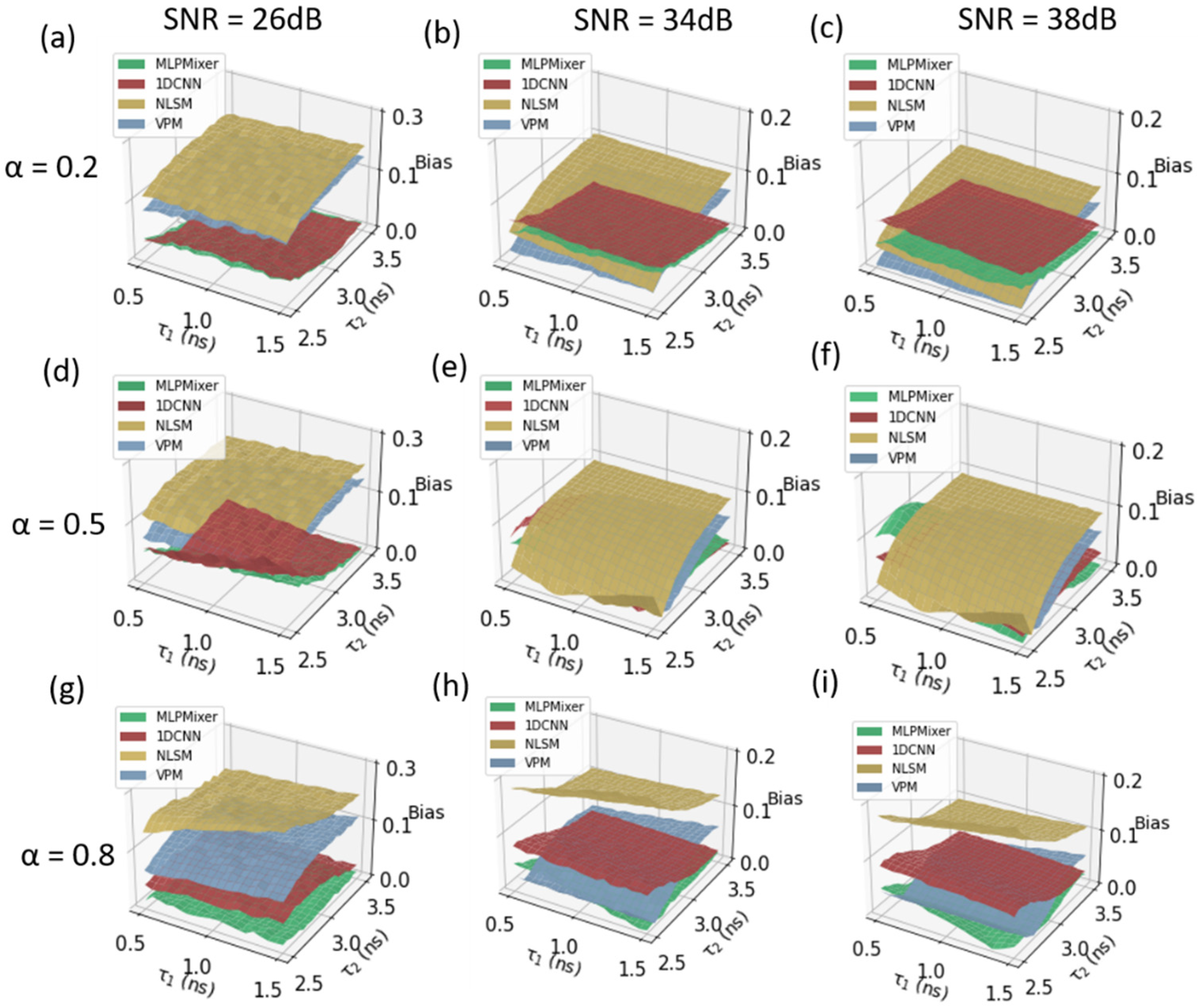
3. Simulation Results
4. Experimental Results and Discussion
4.1. Rhodamine 6G and Rhodamine B Solutions
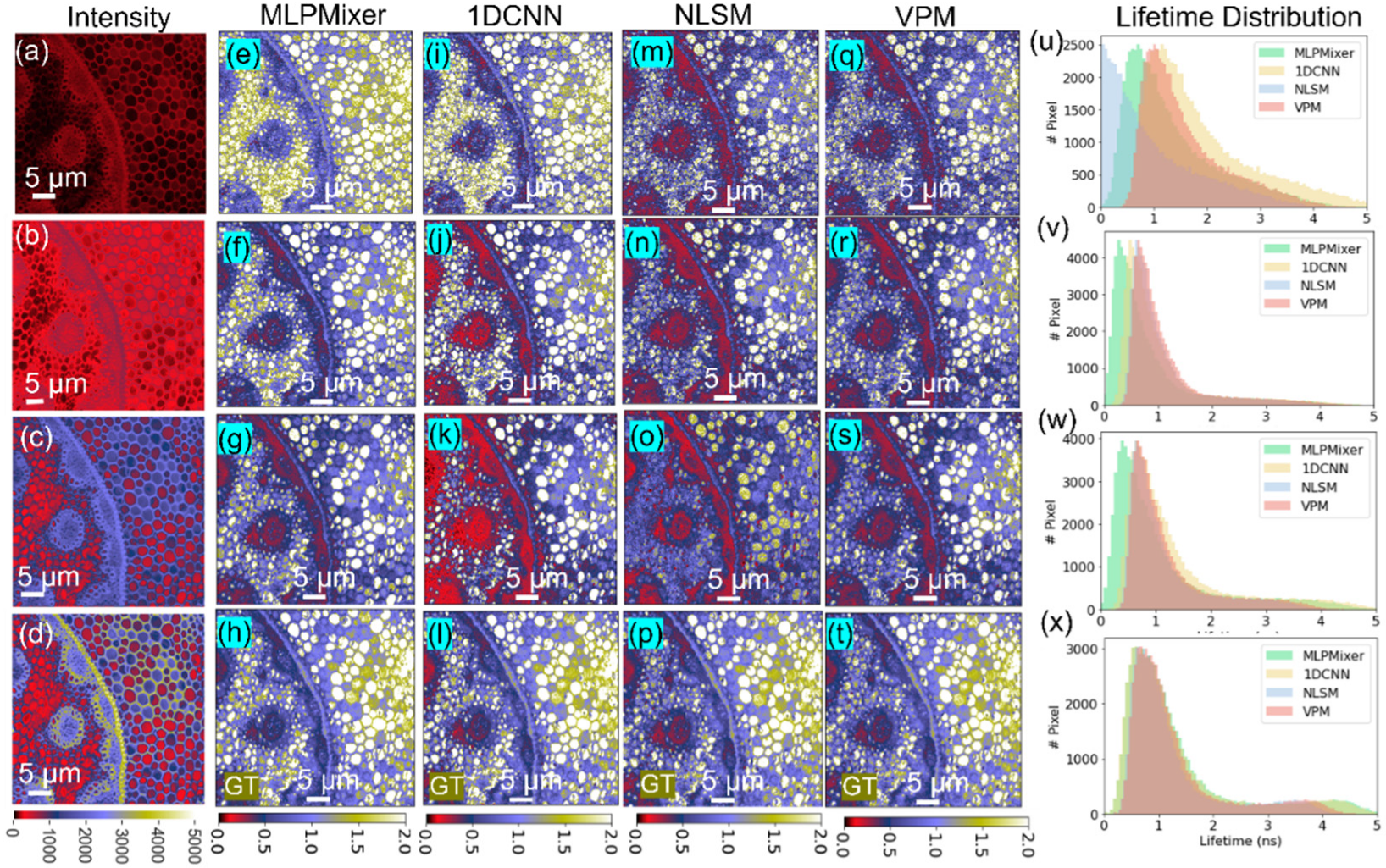
4.2. Convallaria majalis Cells
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berezin, M.Y.; Achilefu, S. Fluorescence Lifetime Measurements and Biological Imaging. Chem. Rev. 2010, 110, 2641–2684. [Google Scholar] [CrossRef] [PubMed]
- Suhling, F.; Sahlén, G.; Gorb, S.; Kalkman, V.J.; Dijkstra, K.-D.B.; van Tol, J. Order Odonata. In Thorp and Covich’s Freshwater Invertebrates; Elsevier: Amsterdam, The Netherlands, 2015; pp. 893–932. [Google Scholar]
- Ning, Y.; Cheng, S.; Wang, J.-X.; Liu, Y.-W.; Feng, W.; Li, F.; Zhang, J.-L. Fluorescence Lifetime Imaging of Upper Gastrointestinal PH in Vivo with a Lanthanide Based near-Infrared τ Probe. Chem. Sci. 2019, 10, 4227–4235. [Google Scholar] [CrossRef]
- Agronskaia, A.V.; Tertoolen, L.; Gerritsen, H.C. Fast Fluorescence Lifetime Imaging of Calcium in Living Cells. J. Biomed. Opt. 2004, 9, 1230. [Google Scholar] [CrossRef] [PubMed]
- Zheng, K.; Jensen, T.P.; Rusakov, D.A. Monitoring Intracellular Nanomolar Calcium Using Fluorescence Lifetime Imaging. Nat. Protoc. 2018, 13, 581–597. [Google Scholar] [CrossRef] [PubMed]
- Hosny, N.A.; Lee, D.A.; Knight, M.M. Single Photon Counting Fluorescence Lifetime Detection of Pericellular Oxygen Concentrations. J. Biomed. Opt. 2012, 17, 016007. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Peng, X.; Yang, Z.; Wang, J.; Fan, J.; He, Y.; Song, F.; Wang, B.; Sun, S.; Qu, J.; Qi, J.; et al. Fluorescence Ratiometry and Fluorescence Lifetime Imaging: Using a Single Molecular Sensor for Dual Mode Imaging of Cellular Viscosity. J. Am. Chem. Soc. 2011, 133, 6626–6635. [Google Scholar] [CrossRef]
- Loura, L. FRET in Membrane Biophysics: An Overview. Front. Physiol. 2011, 2, 82. [Google Scholar] [CrossRef] [PubMed]
- Bajar, B.; Wang, E.; Zhang, S.; Lin, M.; Chu, J. A Guide to Fluorescent Protein FRET Pairs. Sensors 2016, 16, 1488. [Google Scholar] [CrossRef] [PubMed]
- Lakowicz, J.R.; Szmacinski, H.; Nowaczyk, K.; Johnson, M.L. Fluorescence Lifetime Imaging of Calcium Using Quin-2. Cell Calcium 1992, 13, 131–147. [Google Scholar] [CrossRef]
- Yahav, G.; Gershanov, S.; Salmon-Divon, M.; Ben-Zvi, H.; Mircus, G.; Goldenberg-Cohen, N.; Fixler, D. Pathogen Detection Using Frequency Domain Fluorescent Lifetime Measurements. IEEE Trans. Biomed. Eng. 2018, 65, 2731–2741. [Google Scholar] [CrossRef] [PubMed]
- Becker, W. Advanced Time-Correlated Single Photon Counting Techniques; Springer Series in Chemical Physics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005; ISBN 978-3-540-26047-9. [Google Scholar]
- Peter, M.; Ameer-Beg, S.M. Imaging Molecular Interactions by Multiphoton FLIM. Biol. Cell 2004, 96, 231–236. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Natakorn, S.; Chen, Y.; Safar, M.; Cunningham, M.; Tian, J.; Li, D.D.-U. Investigations on Average Fluorescence Lifetimes for Visualizing Multi-Exponential Decays. Front. Phys. 2020, 8, 576862. [Google Scholar] [CrossRef]
- Periasamy, N. Analysis of Fluorescence Decay by the Nonlinear Least Squares Method. Biophys. J. 1988, 54, 961–967. [Google Scholar] [CrossRef]
- Bajzer, Ž.; Therneau, T.M.; Sharp, J.C.; Prendergast, F.G. Maximum Likelihood Method for the Analysis of Time-Resolved Fluorescence Decay Curves. Eur. Biophys. J. 1991, 20, 247–262. [Google Scholar] [CrossRef]
- Rowley, M.I.; Barber, P.R.; Coolen, A.C.C.; Vojnovic, B. Bayesian Analysis of Fluorescence Lifetime Imaging Data; Periasamy, A., König, K., So, P.T.C., Eds.; SPIE: San Francisco, CA, USA, 2011; p. 790325. [Google Scholar]
- Jo, J.A.; Fang, Q.; Marcu, L. Ultrafast Method for the Analysis of Fluorescence Lifetime Imaging Microscopy Data Based on the Laguerre Expansion Technique. IEEE J. Select. Top. Quantum Electron. 2005, 11, 835–845. [Google Scholar] [CrossRef]
- Stringari, C.; Cinquin, A.; Cinquin, O.; Digman, M.A.; Donovan, P.J.; Gratton, E. Phasor Approach to Fluorescence Lifetime Microscopy Distinguishes Different Metabolic States of Germ Cells in a Live Tissue. Proc. Natl. Acad. Sci. USA 2011, 108, 13582–13587. [Google Scholar] [CrossRef]
- Li, D.D.-U.; Arlt, J.; Tyndall, D.; Walker, R.; Richardson, J.; Stoppa, D.; Charbon, E.; Henderson, R.K. Video-Rate Fluorescence Lifetime Imaging Camera with CMOS Single-Photon Avalanche Diode Arrays and High-Speed Imaging Algorithm. J. Biomed. Opt. 2011, 16, 096012. [Google Scholar] [CrossRef]
- Redford, G.I.; Clegg, R.M. Polar Plot Representation for Frequency-Domain Analysis of Fluorescence Lifetimes. J. Fluoresc. 2005, 15, 805–815. [Google Scholar] [CrossRef]
- Clayton, A.H.A.; Hanley, Q.S.; Verveer, P.J. Graphical Representation and Multicomponent Analysis of Single-Frequency Fluorescence Lifetime Imaging Microscopy Data. J. Microsc. 2004, 213, 1–5. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing FPGA-Based Accelerator Design for Deep Convolutional Neural Networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; ACM: Monterey, CA, USA; pp. 161–170. [Google Scholar]
- Belthangady, C.; Royer, L.A. Applications, Promises, and Pitfalls of Deep Learning for Fluorescence Image Reconstruction. Nat. Methods 2019, 16, 1215–1225. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Nowotny, T.; Zhang, Y.; Yu, H.-Q.; Li, D.D.-U. Artificial Neural Network Approaches for Fluorescence Lifetime Imaging Techniques. Opt. Lett. 2016, 41, 2561. [Google Scholar] [CrossRef]
- Zickus, V.; Wu, M.-L.; Morimoto, K.; Kapitany, V.; Fatima, A.; Turpin, A.; Insall, R.; Whitelaw, J.; Machesky, L.; Bruschini, C.; et al. Fluorescence Lifetime Imaging with a Megapixel SPAD Camera and Neural Network Lifetime Estimation. Sci. Rep. 2020, 10, 20986. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.T.; Yao, R.; Sinsuebphon, N.; Rudkouskaya, A.; Un, N.; Mazurkiewicz, J.; Barroso, M.; Yan, P.; Intes, X. Fast Fit-Free Analysis of Fluorescence Lifetime Imaging via Deep Learning. Proc. Natl. Acad. Sci. USA 2019, 116, 24019–24030. [Google Scholar] [CrossRef]
- Zang, Z.; Xiao, D.; Wang, Q.; Li, Z.; Xie, W.; Chen, Y.; Li, D.D.U. Fast Analysis of Time-Domain Fluorescence Lifetime Imaging via Extreme Learning Machine. Sensors 2022, 22, 3758. [Google Scholar] [CrossRef]
- Chen, Y.-I.; Chang, Y.-J.; Liao, S.-C.; Nguyen, T.D.; Yang, J.; Kuo, Y.-A.; Hong, S.; Liu, Y.-L.; Rylander, H.G.; Santacruz, S.R.; et al. Generative Adversarial Network Enables Rapid and Robust Fluorescence Lifetime Image Analysis in Live Cells. Commun. Biol. 2022, 5, 18. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Chen, Y.; Li, D.D.-U. One-Dimensional Deep Learning Architecture for Fast Fluorescence Lifetime Imaging. IEEE J. Select. Top. Quantum Electron. 2021, 27, 1–10. [Google Scholar] [CrossRef]
- Tolstikhin, I.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Steiner, A.; Keysers, D.; Uszkoreit, J.; et al. MLP-Mixer: An All-MLP Architecture for Vision 2021. Adv. Neural Inf. Process. Syst. 2021, 34, 24261–24272. [Google Scholar]
- Zhang, Y.; Cuyt, A.; Lee, W.; Lo Bianco, G.; Wu, G.; Chen, Y.; Li, D.D.-U. Towards Unsupervised Fluorescence Lifetime Imaging Using Low Dimensional Variable Projection. Opt. Express 2016, 24, 26777. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs) 2020. arXiv 2020, arXiv:1606.08415. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition 2015. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Available online: http://pytorch.org/ (accessed on 27 October 2017).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization 2017. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Kristoffersen, A.S.; Erga, S.R.; Hamre, B.; Frette, Ø. Testing Fluorescence Lifetime Standards Using Two-Photon Excitation and Time-Domain Instrumentation: Rhodamine B, Coumarin 6 and Lucifer Yellow. J. Fluoresc. 2014, 24, 1015–1024. [Google Scholar] [CrossRef]
- Elder, A.D.; Frank, J.H.; Swartling, J.; Dai, X.; Kaminski, C.F. Calibration of a Wide-Field Frequency-Domain Fluorescence Lifetime Microscopy System Using Light Emitting Diodes as Light Sources. J. Microsc. 2006, 224, 166–180. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]

| Algorithm | Total Parameters | FLOPs | Total Training Time (s) | Inference Time |
|---|---|---|---|---|
| MLP-Mixer | 61,306 | 5.9 B | 1871.0 | 12.54 s |
| 1D-CNN | 17,409 | 5.4 B | 2270.65 | 34.06 s |
| Rhodamine B | SNR 26~32 | SNR 32~38 | SNR 38~44 | τ_REF (ns) | |
| MLP-Mixer | (ns) | 1.70 | 1.73 | 1.71 | 1.72 [37] |
| Std | 0.40 | 0.46 | 0.50 | ||
| Bias | 1.16% | 0.58% | 0.58% | ||
| (ns) | 1.68 | 1.65 | 1.69 | ||
| 1D-CNN | Std | 0.59 | 0.54 | 0.52 | |
| Bias | 2.33% | 4.07% | 1.74% | ||
| (ns) | 1.55 | 1.61 | 1.63 | ||
| NLSM | Std | 0.39 | 0.24 | 0.27 | |
| Bias | 9.88% | 6.40% | 5.32% | ||
| (ns) | 1.62 | 1.64 | 1.67 | ||
| VPM | Std | 0.52 | 0.47 | 0.45 | |
| Bias | 5.81% | 4.56% | 2.96% | ||
| Rhodamine 6G | SNR 26~32 | SNR 32~38 | SNR 38~44 | τ_REF (ns) | |
| MLP-Mixer | (ns) | 4.00 | 4.04 | 4.07 | 4.06 [38] |
| Std | 0.59 | 0.46 | 0.62 | ||
| Bias | 1.48% | 0.5% | 0.25% | ||
| (ns) | 4.22 | 3.93 | 3.94 | ||
| 1D-CNN | Std | 0.78 | 0.7 | 0.72 | |
| Bias | 3.94% | 3.20% | 2.95% | ||
| (ns) | 3.58 | 3.68 | 3.75 | ||
| NLSM | Std | 0.53 | 0.27 | 0.34 | |
| Bias | 11.82% | 9.36% | 7.64% | ||
| (ns) | 3.79 | 3.89 | 3.92 | ||
| VPM | Std | 0.87 | 0.61 | 0.48 | |
| Bias | 6.65% | 4.19% | 3.45% |
| Data | MLP-Mixer | 1D-CNN | NLSM | VPM |
|---|---|---|---|---|
| HPC | 0.98 | 0.95 | 0.94 | 0.95 |
| MPC | 0.96 | 0.94 | 0.91 | 0.94 |
| LPC | 0.95 | 0.93 | 0.81 | 0.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Li, Y.; Xiao, D.; Zang, Z.; Jiao, Z.; Chen, Y.; Li, D.D.U. Simple and Robust Deep Learning Approach for Fast Fluorescence Lifetime Imaging. Sensors 2022, 22, 7293. https://doi.org/10.3390/s22197293
Wang Q, Li Y, Xiao D, Zang Z, Jiao Z, Chen Y, Li DDU. Simple and Robust Deep Learning Approach for Fast Fluorescence Lifetime Imaging. Sensors. 2022; 22(19):7293. https://doi.org/10.3390/s22197293
Chicago/Turabian StyleWang, Quan, Yahui Li, Dong Xiao, Zhenya Zang, Zi’ao Jiao, Yu Chen, and David Day Uei Li. 2022. "Simple and Robust Deep Learning Approach for Fast Fluorescence Lifetime Imaging" Sensors 22, no. 19: 7293. https://doi.org/10.3390/s22197293
APA StyleWang, Q., Li, Y., Xiao, D., Zang, Z., Jiao, Z., Chen, Y., & Li, D. D. U. (2022). Simple and Robust Deep Learning Approach for Fast Fluorescence Lifetime Imaging. Sensors, 22(19), 7293. https://doi.org/10.3390/s22197293









