Heart Rate Variability Control Using a Biofeedback and Wearable System
Abstract
1. Introduction
2. Related Work
- We propose a model identification method via a transfer function for HRV focused on a specific population of individuals using the method of instrumental variables.
- We propose the design of an MRAC controller (Model Reference Adaptive Controller) using the estimated HRV model.
- We describe the design of light actuators to establish a conditioned reflex.
- We propose an experiment to validate the HRV model obtained through biofeedback.
3. Materials and Methods
- Age: 35–45 years.
- Weight: 80–95 kg.
- Height: 160–181 cm.
- Occupation firefighters and forest firefighters.
- No heart disease.
- Physically active.
3.1. System Modeling
3.1.1. Input Signal
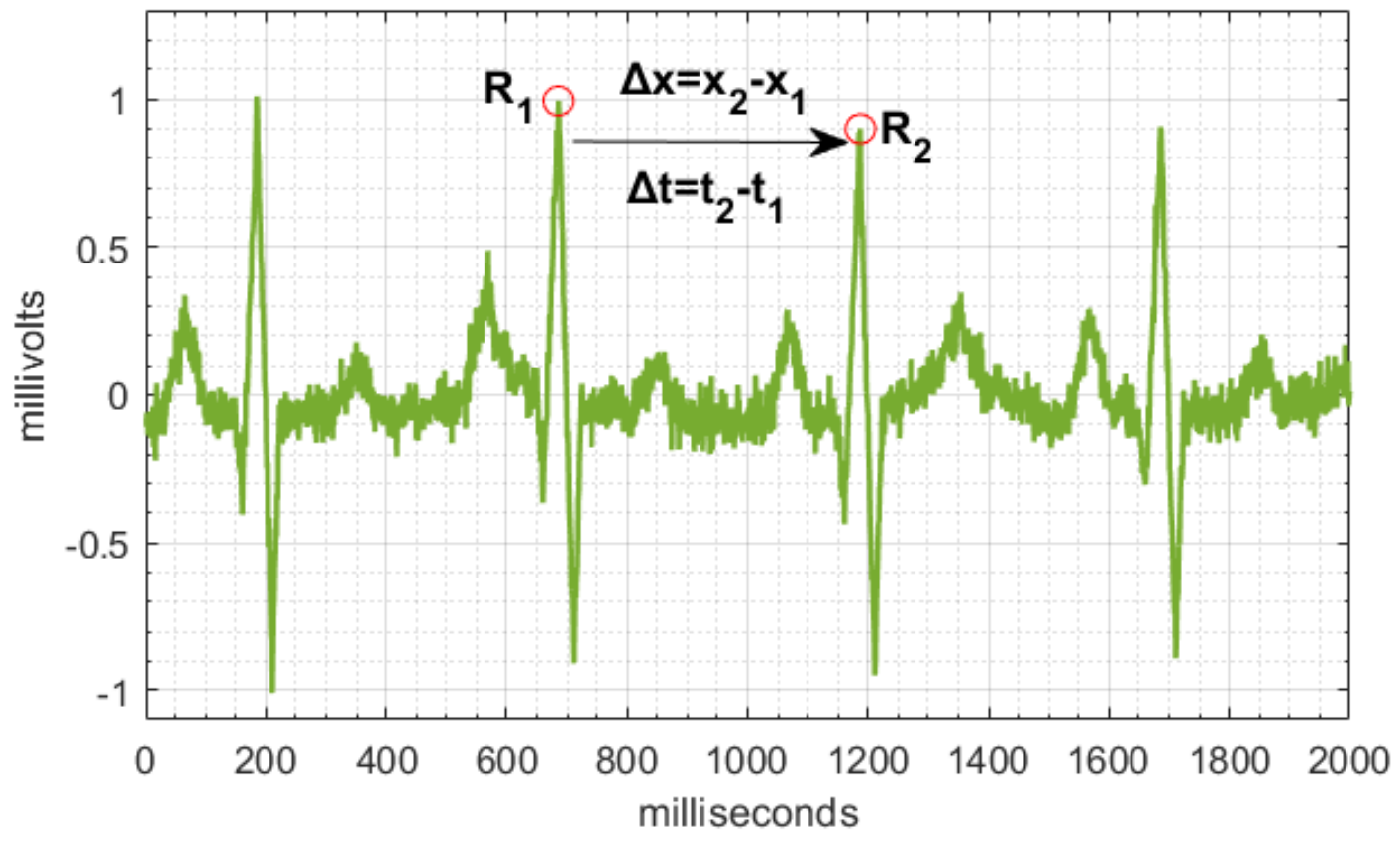
3.1.2. Output Signal
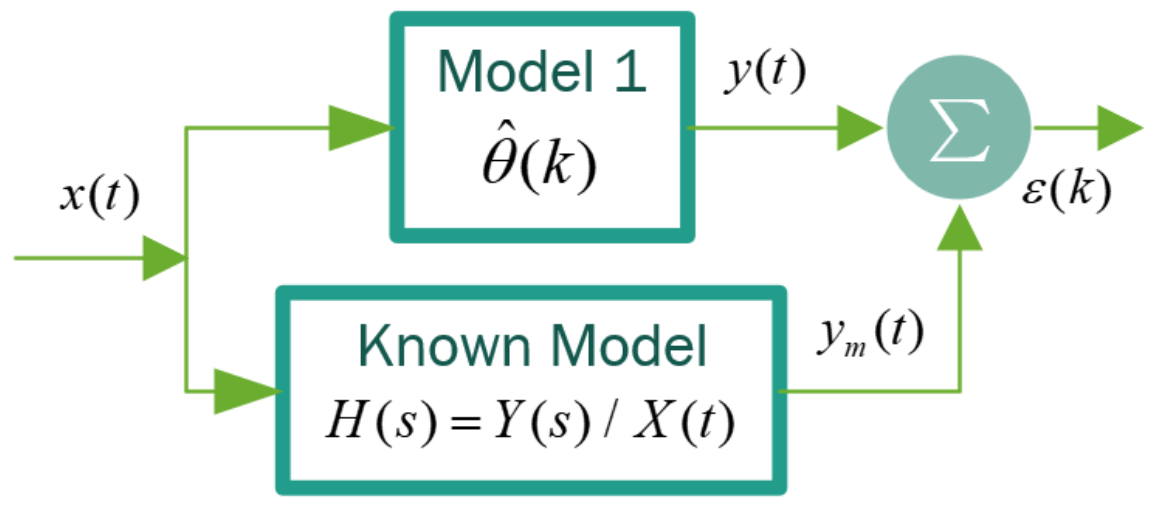
3.1.3. Identification Model
- Transfer function type 1:
- Transfer function type 2:
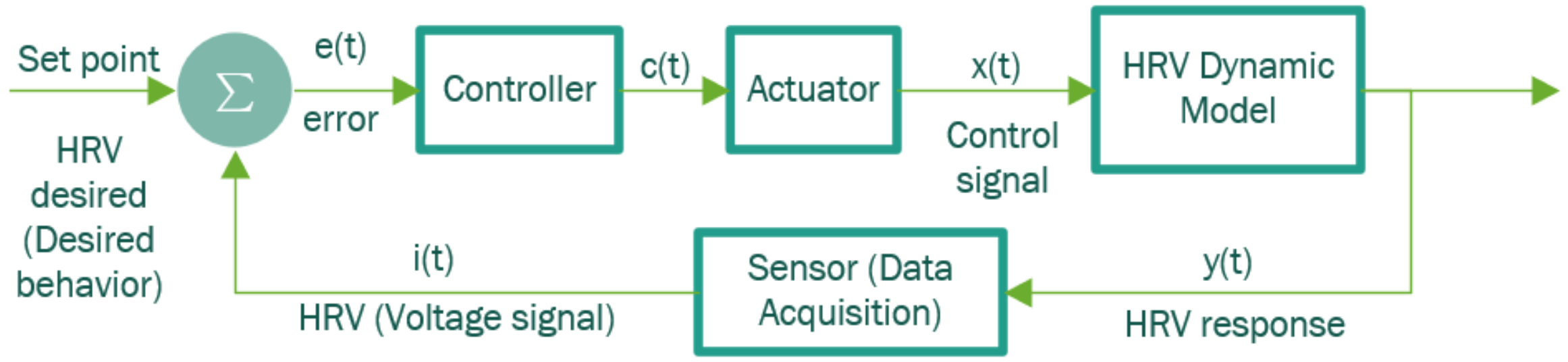
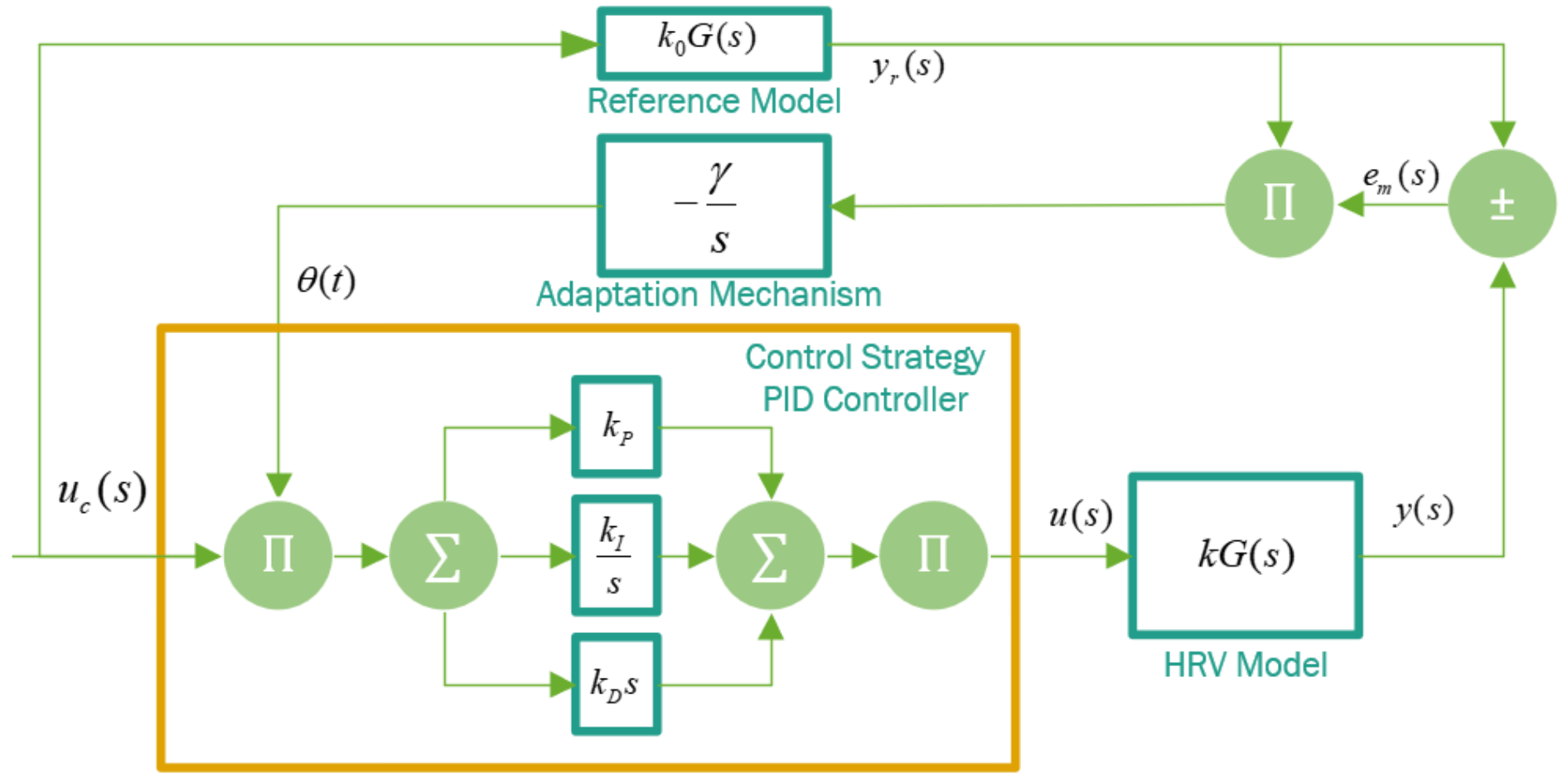
3.1.4. Controller Design
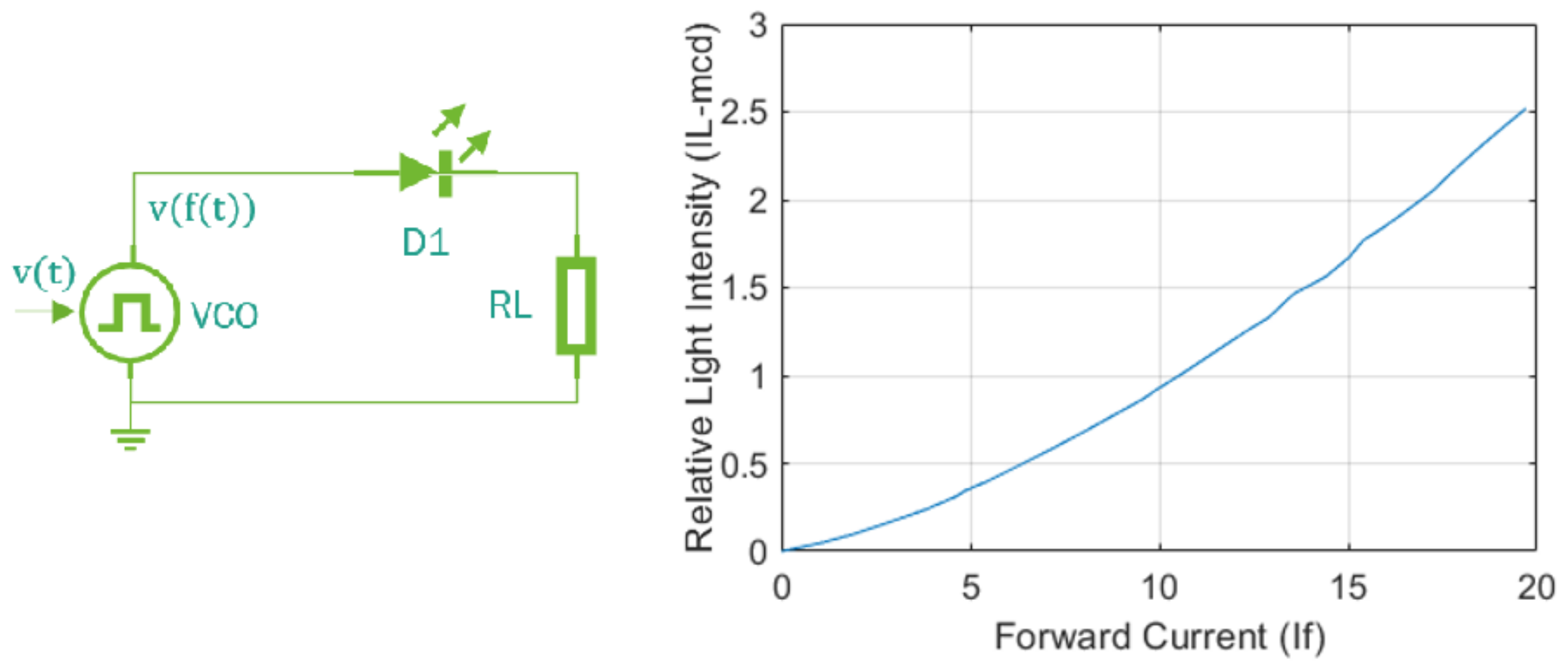
3.2. Actuator Design
4. Results
4.1. Experiment Design
- Maximum generated torque: 12.2 Nm.
- Maximum braking force: 36 N.
- Mass inertia: 8 Kg.
- Maximum power: 700 W.
- A: inertia output and generation of maximum effort in the least time.
- B: free run stage.
- C: controlled mode or activated HRV controller.
- D: free run stage.
4.2. Experimental Results
- Response as acceleration of heart rate mm/s.
- Response of heart rate as speed BPM.
- v Response of speed of the bicycle in km/h.
5. Analysis Result
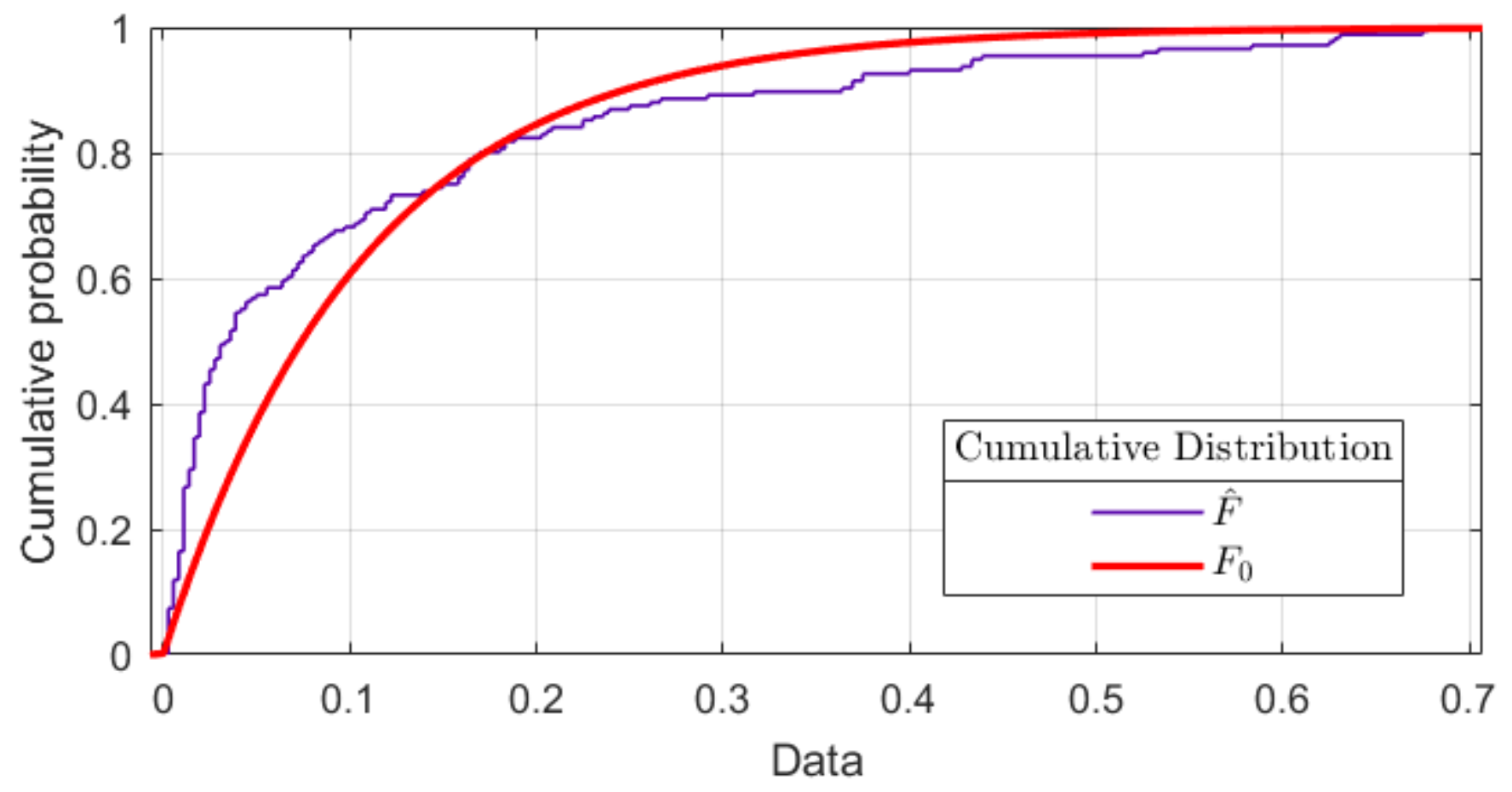
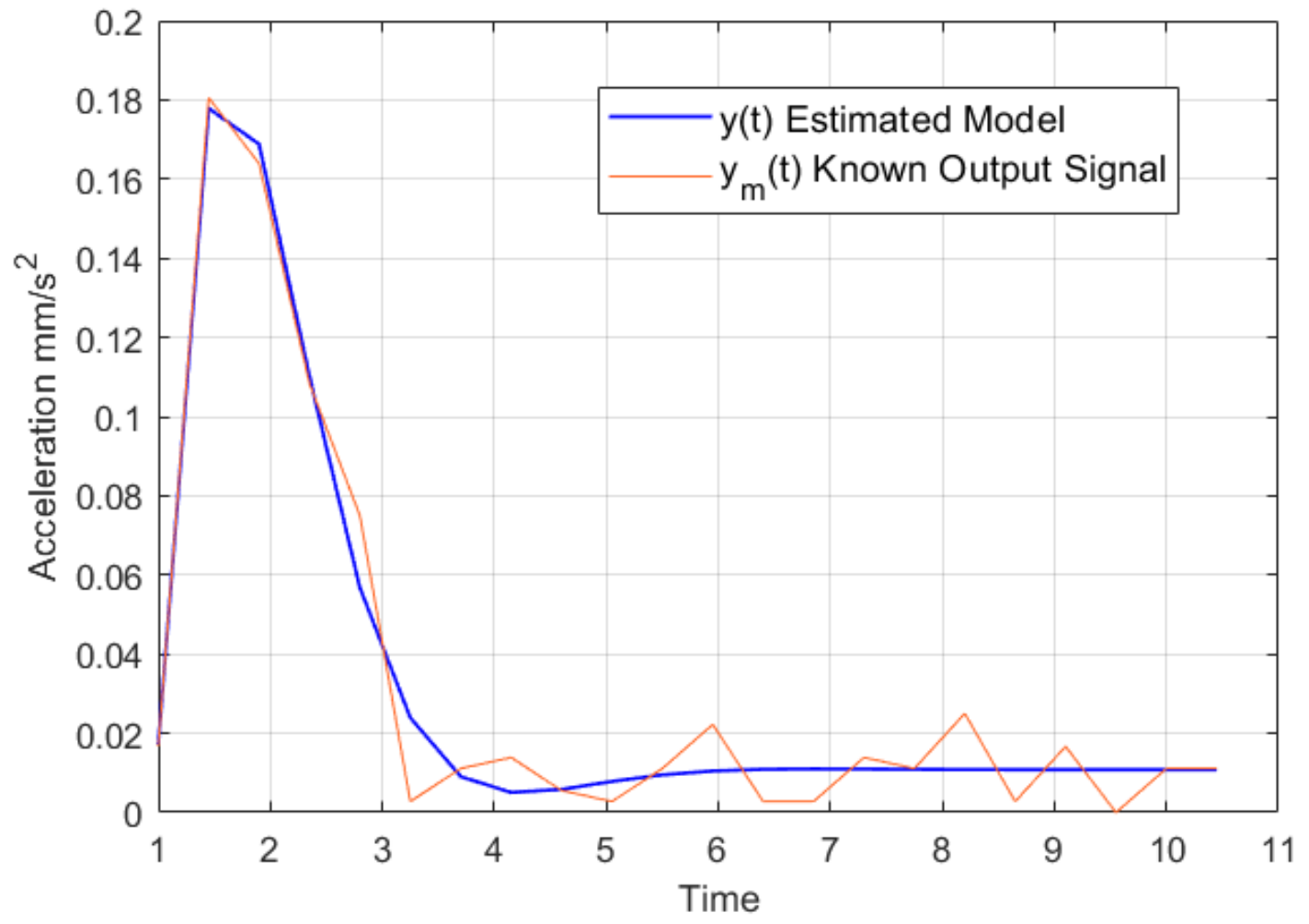
5.1. Model Analysis
5.2. Controller and Actuators Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Tiwari, R.; Kumar, R.; Malik, S.; Raj, T.; Kumar, P. Analysis of Heart Rate Variability and Implication of Different Factors on Heart Rate Variability. Curr. Cardiol. Rev. 2021, 17, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Lai, D.T.H.; Lee, W.S. Biofeedback Technologies for Wireless Body Area Networks. In Advanced Mechatronics and MEMS Devices II; Microsystems and Nanosystems; Springer: Cham, Switzerland, 2017; pp. 659–686. [Google Scholar] [CrossRef]
- Huang, J.; Liu, Y.; Peng, X. Recognition of driver’s mental workload based on physiological signals, a comparative study. Biomed. Signal Process. Control 2022, 71, 103094. [Google Scholar] [CrossRef]
- Shanks, J.; Abukar, Y.; Lever, N.A.; Pachen, M.; LeGrice, I.J.; Crossman, D.J.; Nogaret, A.; Paton, J.F.R.; Ramchandra, R. Reverse re-modelling chronic heart failure by reinstating heart rate variability. Basic Res. Cardiol. 2022, 117, 4. [Google Scholar] [CrossRef] [PubMed]
- Chalmers, T.; Hickey, B.A.; Newton, P.; Lin, C.T.; Sibbritt, D.; McLachlan, C.S.; Clifton-Bligh, R.; Morley, J.; Lal, S. Stress Watch: The Use of Heart Rate and Heart Rate Variability to Detect Stress: A Pilot Study Using Smart Watch Wearables. Sensors 2022, 22, 151. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhou, Y.; Zhao, C. Heart-rate analysis of healthy and insomnia groups with detrended fractal dimension feature in edge. Tsinghua Sci. Technol. 2022, 27, 325–332. [Google Scholar] [CrossRef]
- Hirten, R.P.; Danieletto, M.; Scheel, R.; Shervey, M.; Ji, J.; Hu, L.; Sauk, J.; Chang, L.; Arnrich, B.; Bottinger, E.; et al. Longitudinal Autonomic Nervous System Measures Correlate with Stress and Ulcerative Colitis Disease Activity and Predict Flare. Inflamm. Bowel Dis. 2021, 27, 1576–1584. [Google Scholar] [CrossRef] [PubMed]
- Oba, Y.; Hoshide, S.; Kabutoya, T.; Kario, K. Increased Resting Heart Rate on Electrocardiogram Relative to In-office Pulse Rate Indicates Cardiac Overload: The J-HOP Study. Am. J. Hypertens. 2018, 31, 1106–1112. [Google Scholar] [CrossRef]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA-The Instrumentation, Systems, and Automation Society: Research Triangle Park, NC, USA, 2006. [Google Scholar]
- Harrison, T.R.; Petersdorf, R.G.; Resnick, W.R.; Wilson, J.D.; Wintrobe, M.M.; Martin, J.B.; Thorn, G.W.; Fauci, A.S.; Adams, R.D.; Root, R.; et al. Harrison Principios de Medicina Interna, 19th ed.; McGRAW-Hill Interamericana Editores S.A. de C.V: Mexico City, Mexico, 2015; Volume 1. [Google Scholar]
- Jafarova, O.; Mazhirina, K.; Sokhadze, E.; Shtark, M. Self-regulation Strategies and Heart Rate Biofeedback Training. Appl. Psychophysiol. Biofeedback 2020, 45, 87–98. [Google Scholar] [CrossRef]
- Forte, G.; Troisi, G.; Pazzaglia, M.; Pascalis, V.D.; Casagrande, M. Heart Rate Variability and Pain: A Systematic Review. Brain Sci. 2022, 12, 153. [Google Scholar] [CrossRef]
- Wieling, W.; Thijs, R.D.; van Dijk, N.; Wilde, A.A.M.; Benditt, D.G.; van Dijk, J.G. Symptoms and signs of syncope: A review of the link between physiology and clinical clues. Brain 2009, 132, 2630–2642. [Google Scholar] [CrossRef]
- Windthorst, P.; Mazurak, N.; Kuske, M.; Hipp, A.; Giel, K.E.; Enck, P.; Nieß, A.; Zipfel, S.; Teufel, M. Heart rate variability biofeedback therapy and graded exercise training in management of chronic fatigue syndrome: An exploratory pilot study. J. Psychosom. Res. 2017, 93, 6–13. [Google Scholar] [CrossRef]
- Chen, S.T.; Lin, S.S.; Lan, C.W.; Hsu, H.Y. Design and Development of a Wearable Device for Heat Stroke Detection. Sensors 2017, 18, 17. [Google Scholar] [CrossRef]
- Niskanen, J.P.; Tarvainen, M.P.; Ranta-aho, P.O.; Karjalainen, P.A. Software for advanced HRV analysis. Comput. Methods Programs Biomed. 2004, 76, 73–81. [Google Scholar] [CrossRef]
- Yokoyama, K.; Hayashi, E.; Ito, H.; Kawahara, Y. Estimation of Heart Rate Variability from Heartrate Measured with Wristwatch-Type Heartrate Monitor. IEEJ Trans. Electron. Inf. Syst. 2022, 142, 46–54. [Google Scholar] [CrossRef]
- Carballo-Leyenda, B.; Gutiérrez-Arroyo, J.; García-Heras, F.; Sánchez-Collado, P.; Villa-Vicente, J.G.; Rodríguez-Marroyo, J.A. Influence of Personal Protective Equipment on Wildland Firefighters’ Physiological Response and Performance during the Pack Test. Int. J. Environ. Res. Public Health 2021, 18, 5050. [Google Scholar] [CrossRef]
- KIM, S.; KIM, D.H.; LEE, H.H.; LEE, J.Y. Frequency of firefighters’ heat-related illness and its association with removing personal protective equipment and working hours. Ind. Health 2019, 57, 370–380. [Google Scholar] [CrossRef]
- Halabicky, O.M.; Pinto-Martin, J.A.; Compton, P.; Liu, J. Early childhood lead exposure and adolescent heart rate variability: A longitudinal cohort study. Environ. Res. 2022, 205, 112551. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.J.; Kim, S.; Chung, W.H.; Park, K.A.; Kim, J.D.K.; Kim, D.; Kim, M.J.; Kim, K.; Jeon, H.J. Effect of Virtual Reality on Stress Reduction and Change of Physiological Parameters Including Heart Rate Variability in People With High Stress: An Open Randomized Crossover Trial. Front. Psychiatry 2021, 12, 614539. [Google Scholar] [CrossRef]
- Kim, S.; Zemon, V.; Lehrer, P.; McCraty, R.; Cavallo, M.M.; Raghavan, P.; Ginsberg, J.J.; Foley, F.W. Emotion regulation after acquired brain injury: A study of heart rate variability, attentional control, and psychophysiology. Brain Inj. 2019, 33, 1012–1020. [Google Scholar] [CrossRef]
- Kesavayuth, D.; Shangkhum, P.; Zikos, V. Building physical health: What is the role of mental health? Bull. Econ. Res. 2021, 74, 457–483. [Google Scholar] [CrossRef]
- Parak, J.; Salonen, M.; Myllymäki, T.; Korhonen, I. Comparison of Heart Rate Monitoring Accuracy between Chest Strap and Vest during Physical Training and Implications on Training Decisions. Sensors 2021, 21, 8411. [Google Scholar] [CrossRef]
- Ratajczak, E.; Hajnowski, M.; Stawicki, M.; Duch, W. Novel Methodological Tools for Behavioral Interventions: The Case of HRV-Biofeedback. Sham Control and Quantitative Physiology-Based Assessment of Training Quality and Fidelity. Sensors 2021, 21, 3670. [Google Scholar] [CrossRef]
- Asarcikli, L.D.; Hayiroglu, M.İ.; Osken, A.; Keskin, K.; Kolak, Z.; Aksu, T. Heart rate variability and cardiac autonomic functions in post-COVID period. J. Interv. Card. Electrophysiol. 2022, 63, 715–721. [Google Scholar] [CrossRef]
- Yousefian, P.; Shin, S.; Mousavi, A.S.; Kim, C.S.; Finegan, B.; McMurtry, M.S.; Mukkamala, R.; Jang, D.G.; Kwon, U.; Kim, Y.H.; et al. Physiological Association between Limb Ballistocardiogram and Arterial Blood Pressure Waveforms: A Mathematical Model-Based Analysis. Sci. Rep. 2019, 9, 5146. [Google Scholar] [CrossRef]
- Khoo, M.C.K. Physiological Control Systems: Analysis, Simulation, and Estimation, 2nd ed.; IEEE Press Series in Biomedical, Engineering; IEEE Press: Piscataway, NJ, USA; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Huang, Z.; Bauer, R.; Pan, Y.J. Closed-Loop Identification and Real-Time Control of a Micro Quadcopter. IEEE Trans. Ind. Electron. 2022, 69, 2855–2863. [Google Scholar] [CrossRef]
- Escobar, J.; Gallardo-Hernandez, A.G.; Gonzalez-Olvera, M.A. How to Deal with Parameter Estimation in Continuous-Time Stochastic Systems. Circuits Syst. Signal Process. 2021, 41, 2338–2357. [Google Scholar] [CrossRef]
- Atanasov, N.; Ichtev, A. Closed-Loop System Identification with Modifications of the Instrumental Variable Method. Informatica 2010, 21, 159–174. [Google Scholar] [CrossRef]
- Gilson, M.; Van den Hof, P. Instrumental variable methods for closed-loop system identification. Automatica 2005, 41, 241–249. [Google Scholar] [CrossRef]
- Bowman, T.; Gervasoni, E.; Arienti, C.; Lazzarini, S.G.; Negrini, S.; Crea, S.; Cattaneo, D.; Carrozza, M.C. Wearable Devices for Biofeedback Rehabilitation: A Systematic Review and Meta-Analysis to Design Application Rules and Estimate the Effectiveness on Balance and Gait Outcomes in Neurological Diseases. Sensors 2021, 21, 3444. [Google Scholar] [CrossRef] [PubMed]
- Giraldo-Pedroza, A.; Lee, W.C.C.; Lam, W.K.; Coman, R.; Alici, G. A Wearable Biofeedback Device to Increase Gait Swing Time Could Have Positive Effects on Gait among Older Adults. Sensors 2021, 22, 102. [Google Scholar] [CrossRef]
- Skvortsov, D.V.; Kaurkin, S.N.; Ivanova, G.E. A Study of Biofeedback Gait Training in Cerebral Stroke Patients in the Early Recovery Phase with Stance Phase as Target Parameter. Sensors 2021, 21, 7217. [Google Scholar] [CrossRef]
- Hughes, A.; Jorda, S. Applications of Biological and Physiological Signals in Commercial Video Gaming and Game Research: A Review. Front. Comput. Sci. 2021, 3, 557608. [Google Scholar] [CrossRef]
- Lan, K.C.; Li, C.W.; Cheung, Y. Slow Breathing Exercise with Multimodal Virtual Reality: A Feasibility Study. Sensors 2021, 21, 5462. [Google Scholar] [CrossRef]
- Schmid, P.M.; Bauer, C.M.; Ernst, M.J.; Sommer, B.; Lünenburger, L.; Weisenhorn, M. A Two Joint Neck Model to Identify Malposition of the Head Relative to the Thorax. Sensors 2021, 21, 3297. [Google Scholar] [CrossRef]
- Liparoti, M.; Lopez, E.T. Biofeedback in sport and education. J. Hum. Sport Exerc. 2021, 16, S922–S929. [Google Scholar] [CrossRef]
- Zhou, J.; Ho, V.; Javadi, B. New Internet of Medical Things for Home-Based Treatment of Anorectal Disorders. Sensors 2022, 22, 625. [Google Scholar] [CrossRef]
- Vasilyev, V.; Borisov, V.; Syskov, A. Biofeedback Methodology: A Narrative Review. In Proceedings of the 2019 International Multi-Conference on Engineering, Computer and Information Sciences (SIBIRCON), Novosibirsk, Russia, 21–27 October 2019; pp. 11–16. [Google Scholar] [CrossRef]
- Idrobo-Ávila, E.; Loaiza-Correa, H.; Muñoz-Bolaños, F.; van Noorden, L.; Vargas-Cañas, R. Development of a biofeedback system using harmonic musical intervals to control heart rate variability with a generative adversarial network. Biomed. Signal Process. Control 2022, 71, 103095. [Google Scholar] [CrossRef]
- Bouteraa, Y.; Ben Abdallah, I.; Ibrahim, A.; Ahanger, T.A. Development of an IoT-Based Solution Incorporating Biofeedback and Fuzzy Logic Control for Elbow Rehabilitation. Appl. Sci. 2020, 10, 7793. [Google Scholar] [CrossRef]
- Sho’ouri, N. Soft boundary-based neurofeedback training based on fuzzy similarity measures: A method for learning how to control EEG Signal features during neurofeedback training. J. Neurosci. Methods 2020, 343, 108805. [Google Scholar] [CrossRef]
- Argha, A.; Su, S.W.; Celler, B.G. Heart rate regulation during cycle-ergometer exercise via event-driven biofeedback. Med. Biol. Eng. Comput. 2017, 55, 483–492. [Google Scholar] [CrossRef][Green Version]
- Longobardo, G.S.; Gothe, B.; Goldman, M.D.; Cherniack, N.S. Sleep apnea considered as a control system instability. Respir. Physiol. 1982, 50, 311–333. [Google Scholar] [CrossRef]
- Minetti, A.E.; Boldrini, L.; Brusamolin, L.; Zamparo, P.; McKee, T. A feedback-controlled treadmill (treadmill-on-demand) and the spontaneous speed of walking and running in humans. J. Appl. Physiol. 2003, 95, 838–843. [Google Scholar] [CrossRef]
- Gu, F.; Niu, J.; Das, S.K.; He, Z. RunnerPal: A Runner Monitoring and Advisory System Based on Smart Devices. IEEE Trans. Serv. Comput. 2018, 11, 262–276. [Google Scholar] [CrossRef]
- Chang, A.M.; Scheer, F.A.J.L.; Czeisler, C.A.; Aeschbach, D. Direct Effects of Light on Alertness, Vigilance, and the Waking Electroencephalogram in Humans Depend on Prior Light History. Sleep 2013, 36, 1239–1246. [Google Scholar] [CrossRef]
- Lockley, S.W.; Evans, E.E.; Scheer, F.A.; Brainard, G.C.; Czeisler, C.A.; Aeschbach, D. Short-Wavelength Sensitivity for the Direct Effects of Light on Alertness, Vigilance, and the Waking Electroencephalogram in Humans. Sleep 2006, 29, 161–168. [Google Scholar] [CrossRef]
- Petrowski, K.; Buehrer, S.; Niedling, M.; Schmalbach, B. The effects of light exposure on the cortisol stress response in human males. Stress 2021, 24, 29–35. [Google Scholar] [CrossRef]
- Kompier, M. Studying Effects of Light on Stress Development and Evaluation of a Method to Reliably Measure (Day)Light to Study Its Effects on Stress in the Field. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2018. [Google Scholar]
- Lockley, S.W.; Brainard, G.C.; Czeisler, C.A. High Sensitivity of the Human Circadian Melatonin Rhythm to Resetting by Short Wavelength Light. J. Clin. Endocrinol. Metab. 2003, 88, 4502–4505. [Google Scholar] [CrossRef]
- Fernandes de Godoy, M.; Lima Gregório, M. Heart Rate Variability as a Marker of Homeostatic Level. In Physiology; Aslanidis, T., Nouris, C., Eds.; IntechOpen: London, UK, 2022; Volume 14. [Google Scholar] [CrossRef]
- Viera, E.; Kaschel, H.; Valencia, C. ECG processing algorithm in the QRS complex. In Proceedings of the 2021 IEEE International Conference on Automation/XXIV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Valparaiso, Chile, 22–26 March 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Crow, E.L.; Davis, F.A.; Maxfield, M.W. Statistics Manual: With Examples Taken from Ordnance Development; Dover Books on Advanced Mathematics; Dover: New York, NY, USA, 1960. [Google Scholar]
- Dupont, W.D. Statistical Modeling for Biomedical Researchers: A Simple Introduction to the Analysis of Complex Data, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Fleming, J.S. Interpreting the Electrocardiogram; Springer: Dordrecht, The Netherlands, 1980. [Google Scholar] [CrossRef]
- Pezzulo, G.; Rigoli, F.; Friston, K. Active Inference, homeostatic regulation and adaptive behavioural control. Prog. Neurobiol. 2015, 134, 17–35. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User; Prentice-Hall Information and System Sciences Series; Prentice-Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Sachit, S.; Vinod, B.R. MRAS Based Speed Control of DC Motor with Conventional PI Control—A Comparative Study. Int. J. Control Autom. Syst. 2022, 20, 1–12. [Google Scholar] [CrossRef]
- Kendall, K.E. The Effects of Light Spectra on Stress and Behavior. Master’s Thesis, University of Massachusetts Amherst, Amherst, MA, USA, 1982; p. 75. [Google Scholar]
- Kompier, M.; Smolders, K.; van Marken Lichtenbelt, W.; de Kort, Y. Effects of light transitions on measures of alertness, arousal and comfort. Physiol. Behav. 2020, 223, 112999. [Google Scholar] [CrossRef] [PubMed]
- Kompier, M.; Smolders, K.; de Kort, Y. A systematic literature review on the rationale for and effects of dynamic light scenarios. Build. Environ. 2020, 186, 107326. [Google Scholar] [CrossRef]


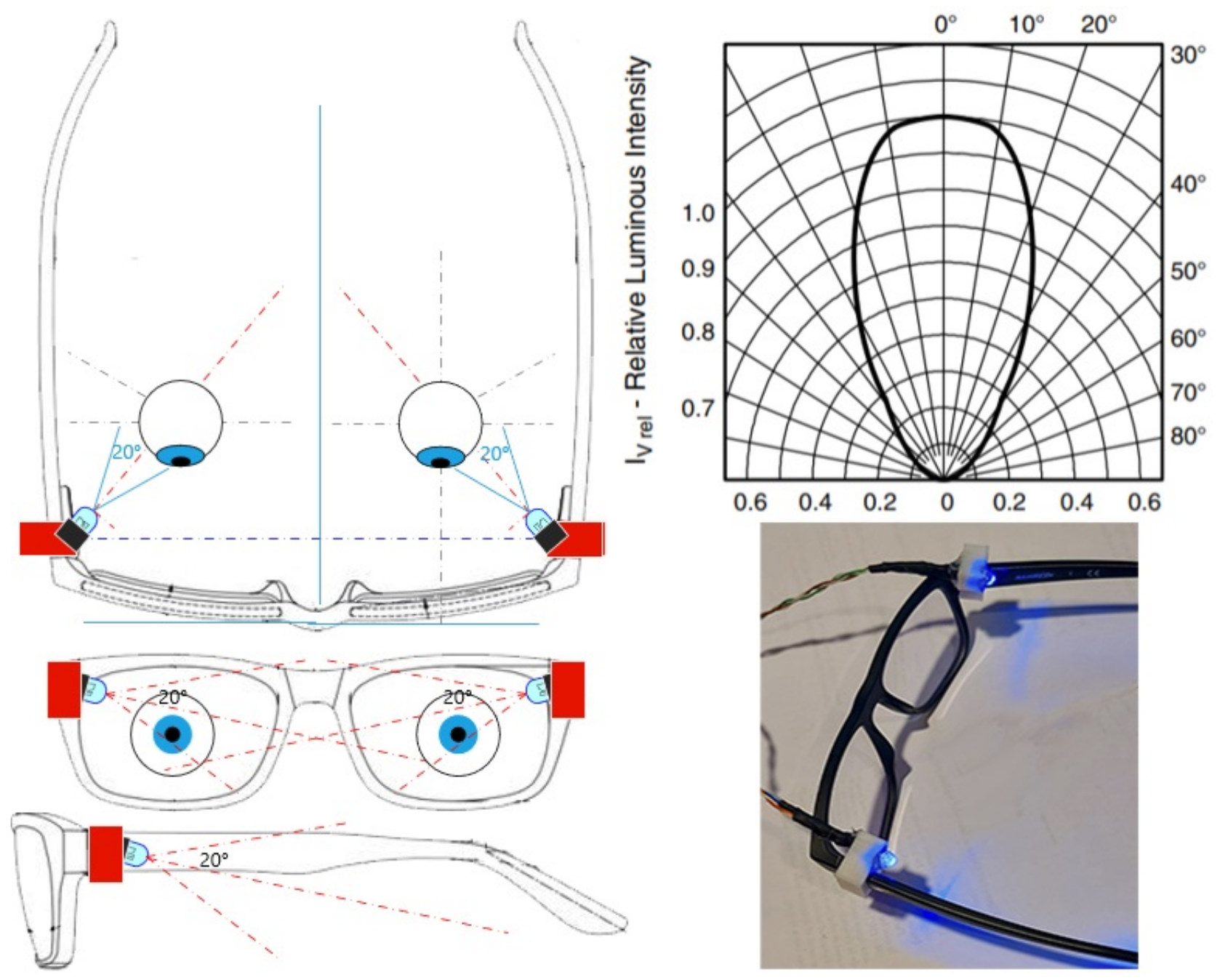
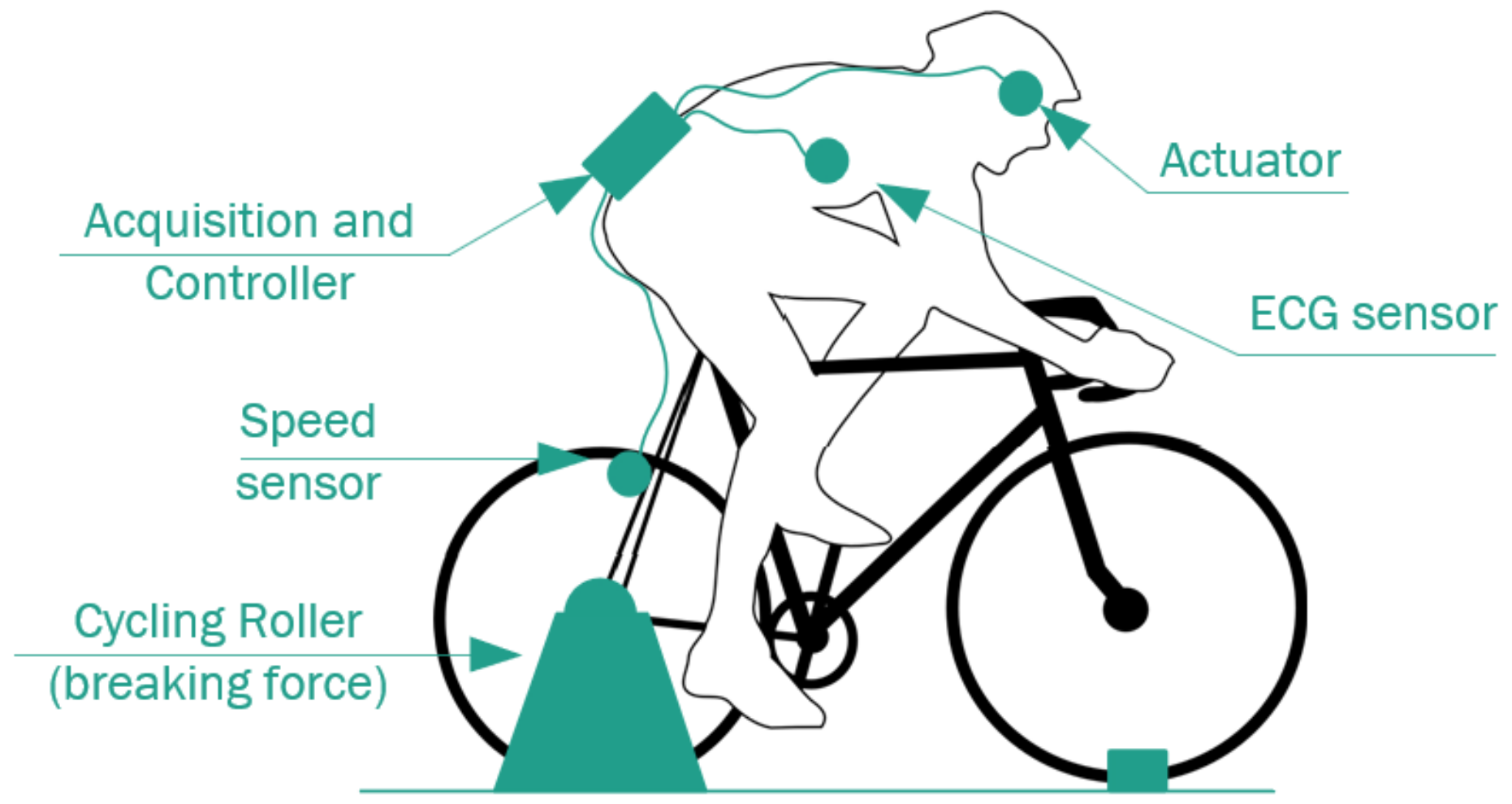
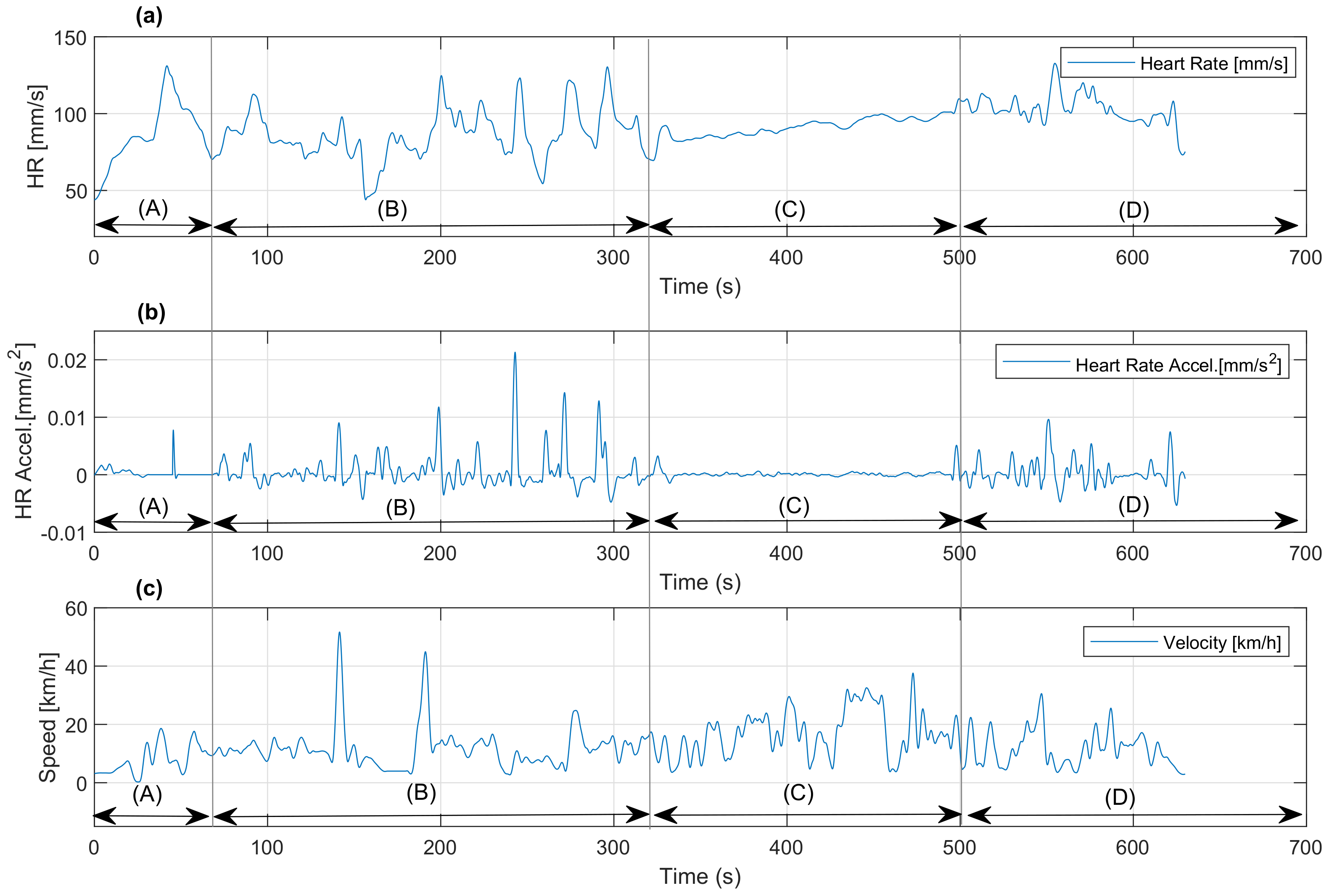


| Experimental Distribution | ||
|---|---|---|
| Parameter | Magnitud | Unit |
| 0.0323 | mm/s | |
| 0.04392 | mm/s | |
| 0.04378 | mm/s | |
| 0.04392 | mm/s | |
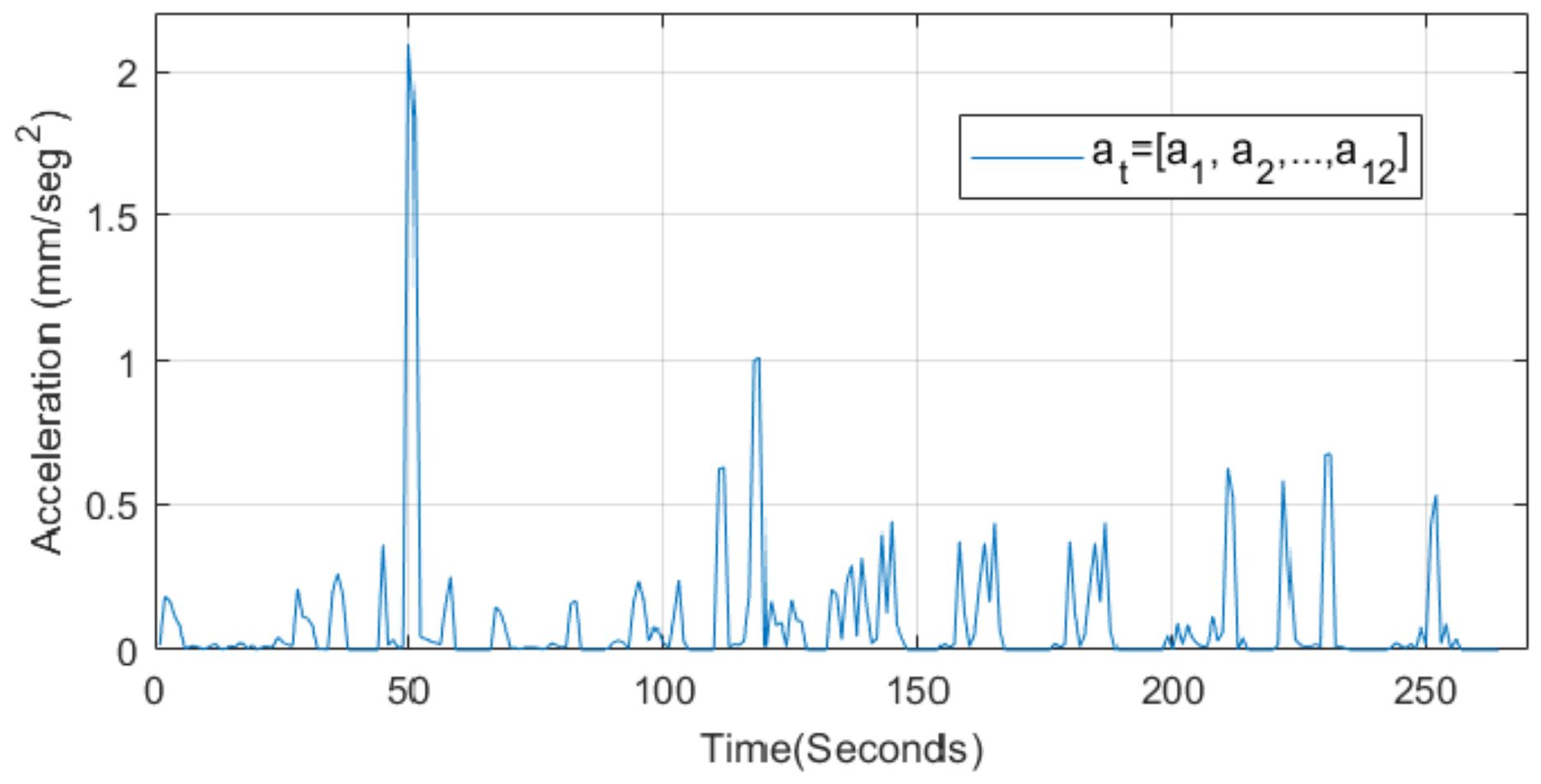
| Sample | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [s] | 1 | 11 | 5 | 15 | 5 | 6 | 3 | 2 | 11 | 7 | 5 | 10 |
| [s] | 6 | 16 | 9 | 18 | 9 | 10 | 9 | 6 | 15 | 11 | 10 | 16 |
| [s] | 5 | 5 | 4 | 3 | 4 | 4 | 6 | 4 | 4 | 4 | 5 | 6 |
| Adaptation Gain | Max Overshoot % | Settling Time | Rising Time |
|---|---|---|---|
| 0.1 | 20.7316 | 0.2801 | 0.0579 |
| 3.33 | 20.5850 | 0.279 | 0.0579 |
| 66 | 19.895 | 0.386 | 0.0580 |
| 9.95 | 18.944 | 0.388 | 0.0582 |
| 20 | 16.771 | 0.36 | 0.0588 |
| Stage | Description | Period S | Remarks |
|---|---|---|---|
| A | Step test | 68 | Initial movement from repose. |
| B | Free run | 252 | Freecycling, aiming to reach the max. HR. |
| C | Controller activated | 246 | Controlled cycling, aiming to increase. the speed while having the HR acceleration constant (control action). |
| D | Free Cycling | 64 | Freecycling, aiming to reach the max. HR. |
| Variable | Min | Max | Mean | Std. Dev. | Variance |
|---|---|---|---|---|---|
| HR Acceleration () [mm/s] | −0.0228 | 0.09119 | 0.0019 | 0.01032 | 0.000107 |
| HR () [BPM] | 43 | 131 | 91 | 15 | 211 |
| Speed () [km/h] | 2.2 | 29.6 | 12.8 | 4.8 | 22.7 |
| RMSE | R | Pearson | Spearman | Covariance |
|---|---|---|---|---|
| 0.0435 | 0.895 | 0.6203 | 0.9465 | 0.0180 |
| Section | Variable | Mean | Std. Dev. | Var | Vdc |
|---|---|---|---|---|---|
| B | Acceleration HR [mm/s] | 0.000691 | 0.003087 | 0.000010 | 0.022161 |
| B | HR [BPM] | 88 | 15 | 238 | 2821 |
| B | Speed [km/h] | 27.4 | 8.2 | 66.4 | 877.3 |
| C | Acceleration HR [mm/s] | 0.000063 | 0.000223 | 0.000000050 | 0.001171 |
| C | HR [BPM] | 94 | 6 | 30 | 1756 |
| C | Speed [km/h] | 41.2 | 10.7 | 115 | 771 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viera, E.; Kaschel, H.; Valencia, C. Heart Rate Variability Control Using a Biofeedback and Wearable System. Sensors 2022, 22, 7153. https://doi.org/10.3390/s22197153
Viera E, Kaschel H, Valencia C. Heart Rate Variability Control Using a Biofeedback and Wearable System. Sensors. 2022; 22(19):7153. https://doi.org/10.3390/s22197153
Chicago/Turabian StyleViera, Eduardo, Hector Kaschel, and Claudio Valencia. 2022. "Heart Rate Variability Control Using a Biofeedback and Wearable System" Sensors 22, no. 19: 7153. https://doi.org/10.3390/s22197153
APA StyleViera, E., Kaschel, H., & Valencia, C. (2022). Heart Rate Variability Control Using a Biofeedback and Wearable System. Sensors, 22(19), 7153. https://doi.org/10.3390/s22197153






