Noise-Adaptive Non-Blind Image Deblurring
Abstract
:1. Introduction
2. Regularized Deconvolution
2.1. Tikhonov Regularization
Wiener Regularization
2.2. Optimal Regularization Parameter—MSE Approach
- 1.
- Take an image
- 2.
- Design a blur kernel; blur the image; add noise
- 3.
- Perform regularized deconvolution using different values of
- 4.
- For each value of , calculate the mean squared error (MSE) between the deblurred image and the original one
2.3. Common Artifacts in Image Deblurring
3. Deblurring with Deep Learning
- 1.
- Perform regularized deconvolution of the blurred image
- 2.
- Pass the deconvolved image through a deep neural network to remove residual artifacts.
3.1. Known Input Noise
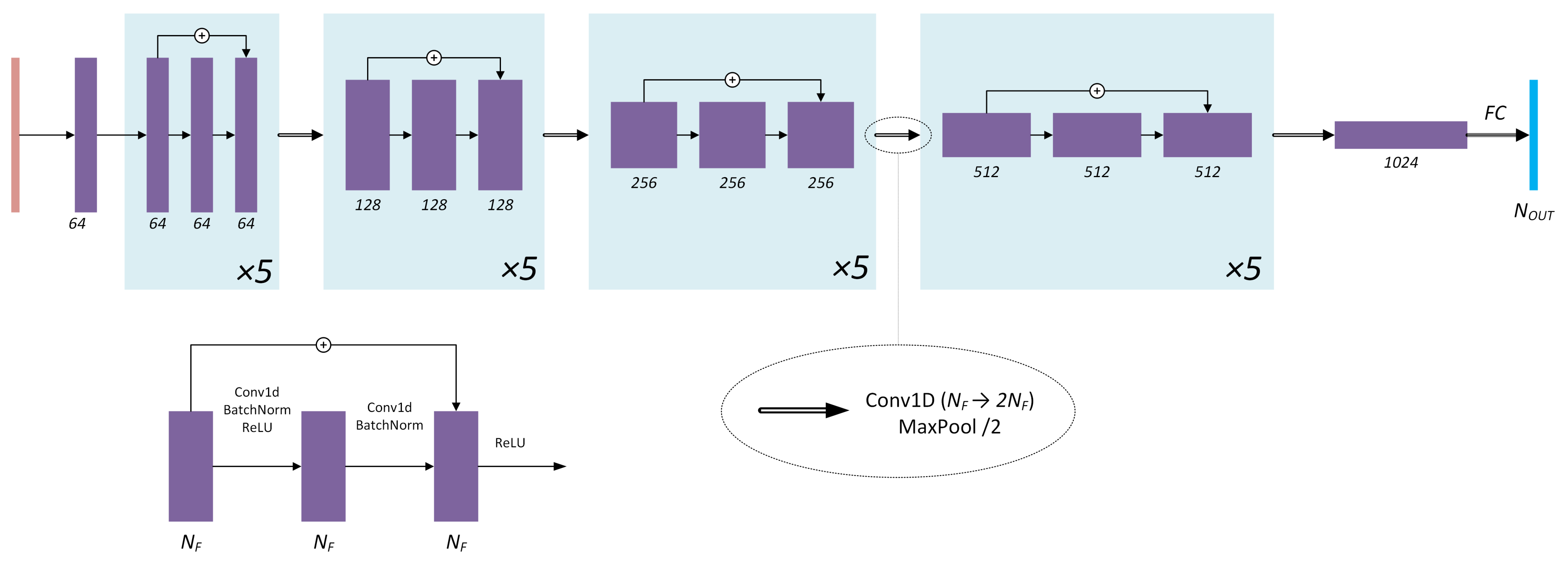
3.1.1. Neural Network Architectures
Uniform Width CNN
U-Net
3.1.2. Joint Parameter Optimization
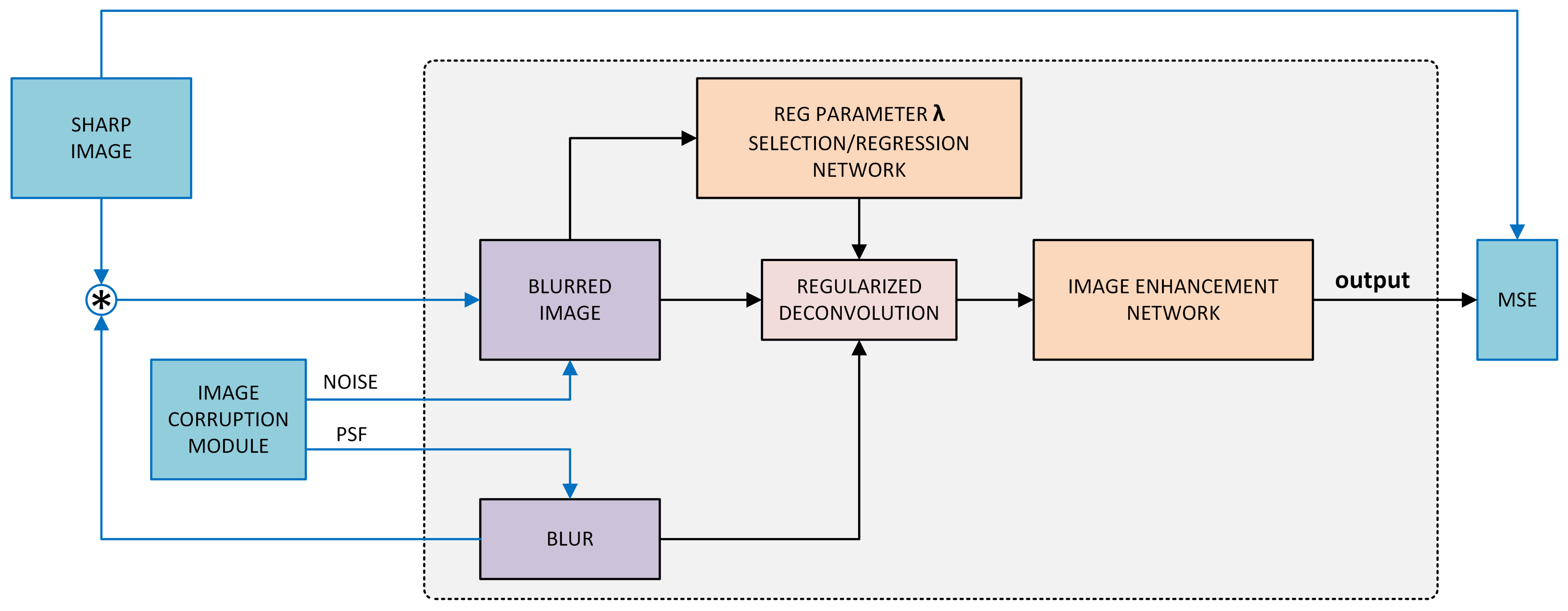
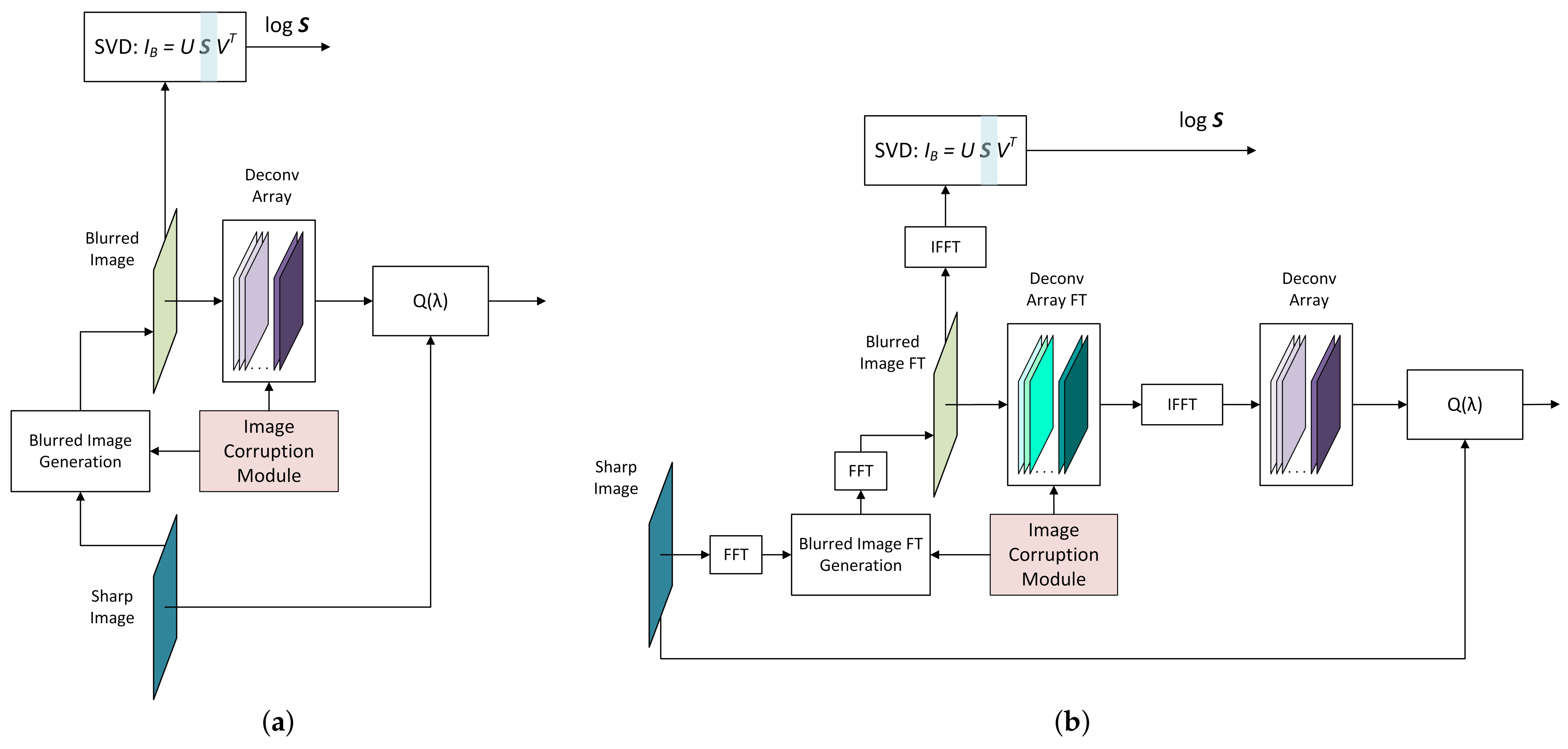
3.2. Noise-Adaptive Deblurring
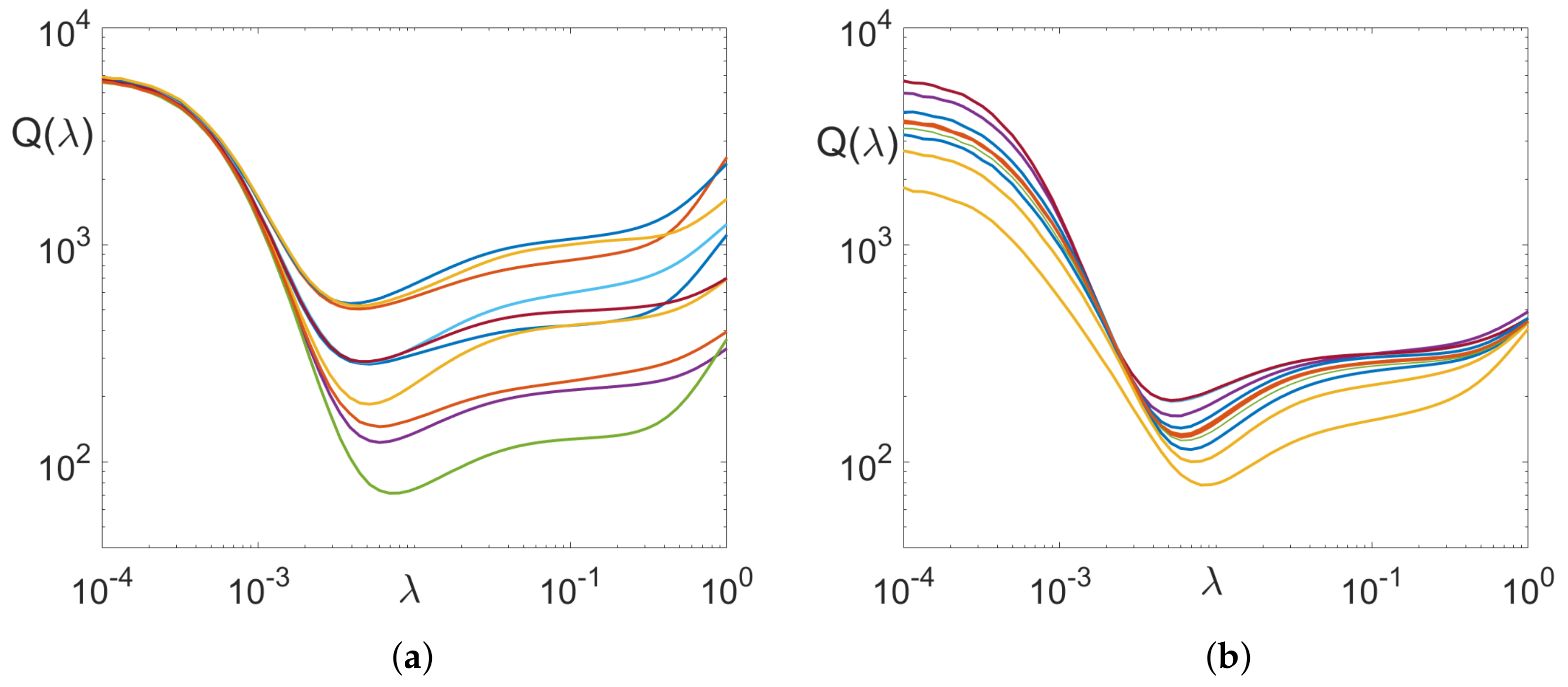
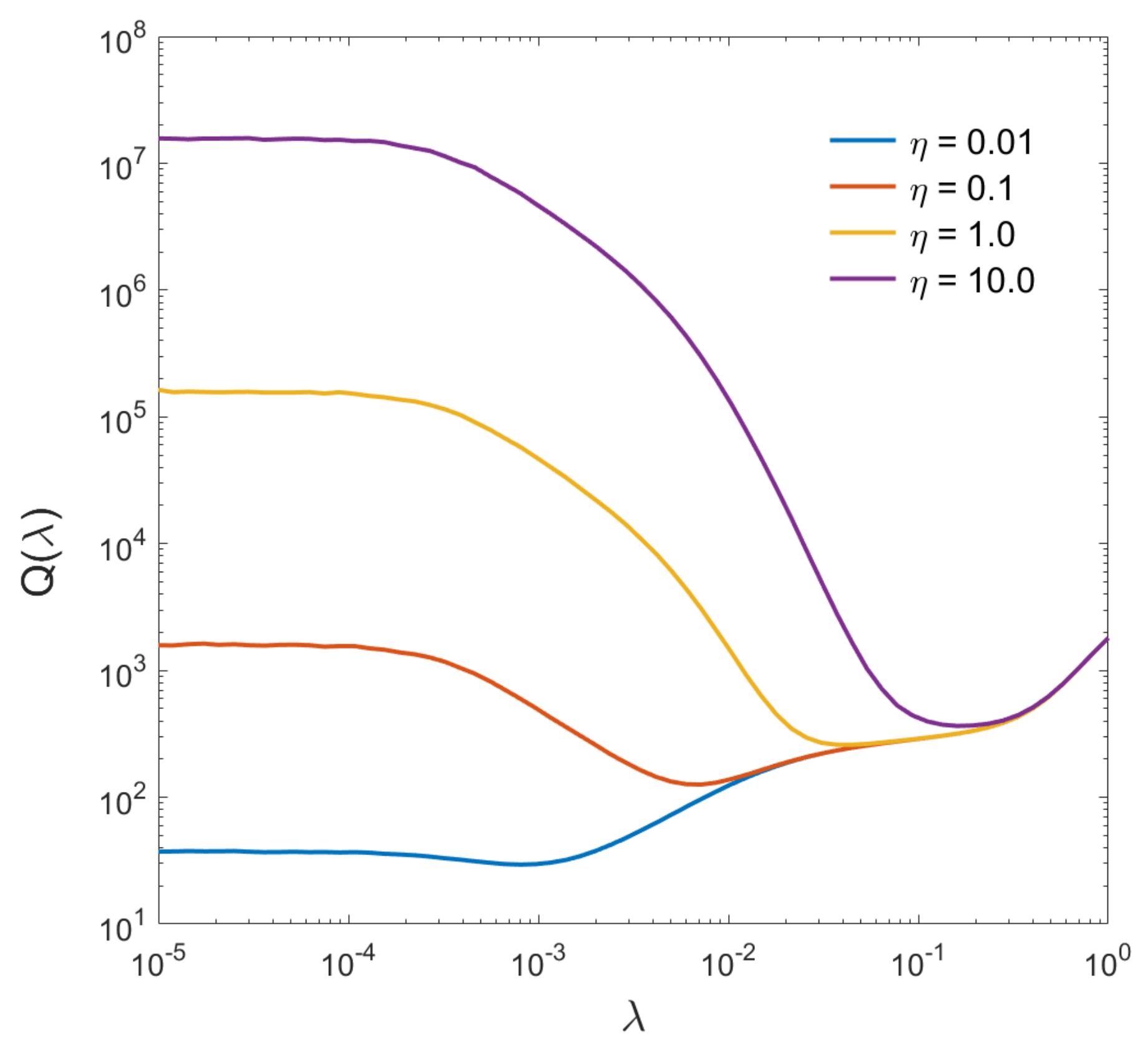
3.2.1. Deblurring Error for Varying Noise
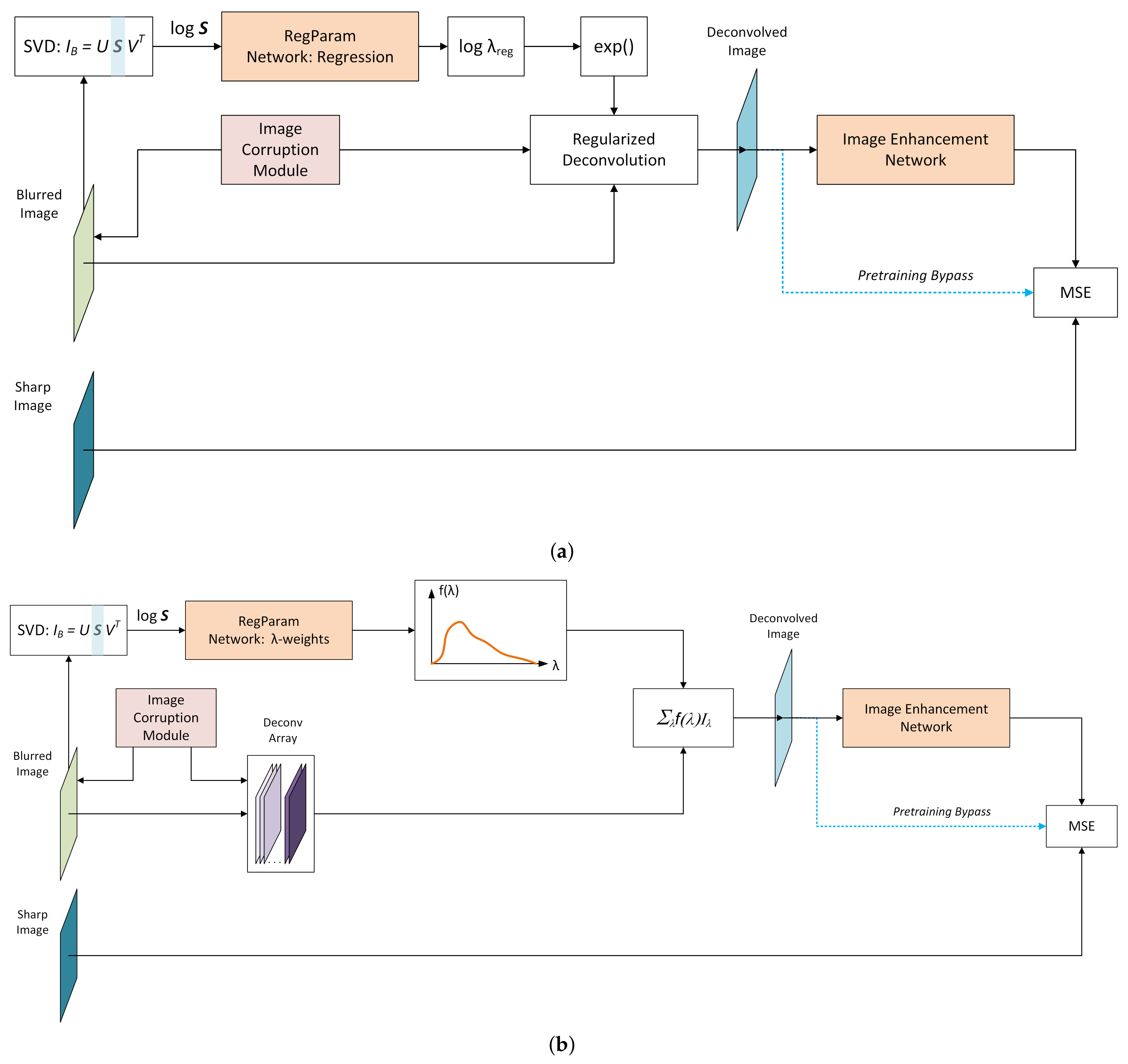
3.2.2. The General Idea
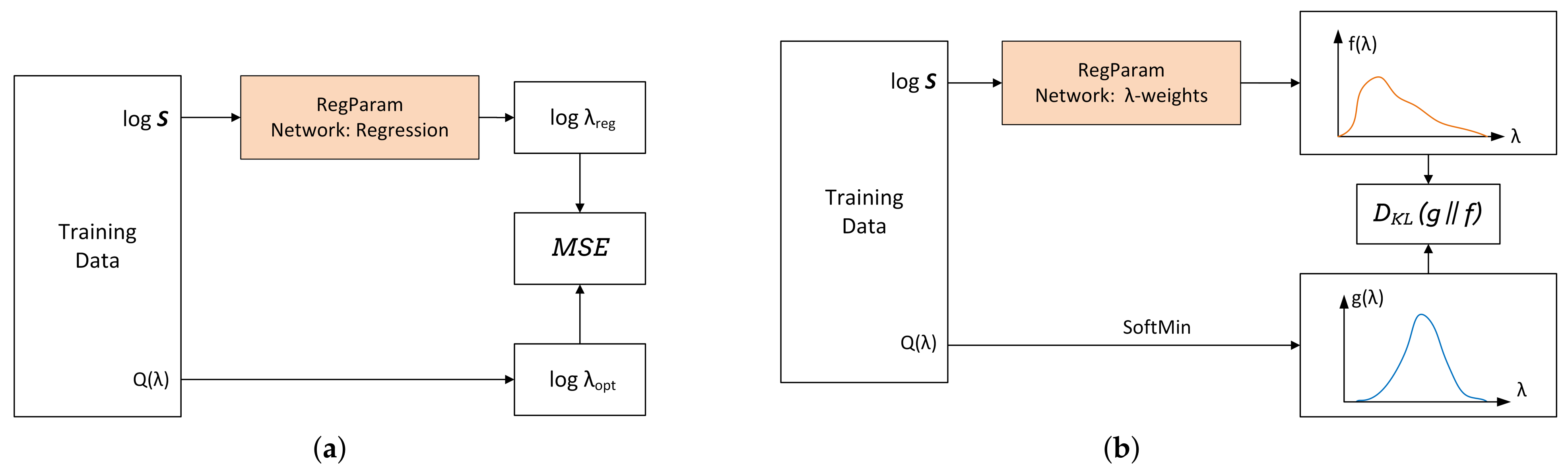
3.2.3. RegParam Network Architecture
- 1.
- Direct regression of
- 2.
- Selection of from a set of values.
3.2.4. RegParamNet Training Schemes
Training Data Generation
RegParamNet Modes
4. Experiments
4.1. Known Input Noise
4.1.1. Training
4.1.2. Quality Metrics
4.1.3. Results
4.1.4. Joint Parameter Optimization
4.2. Noise-Adaptive Deblurring
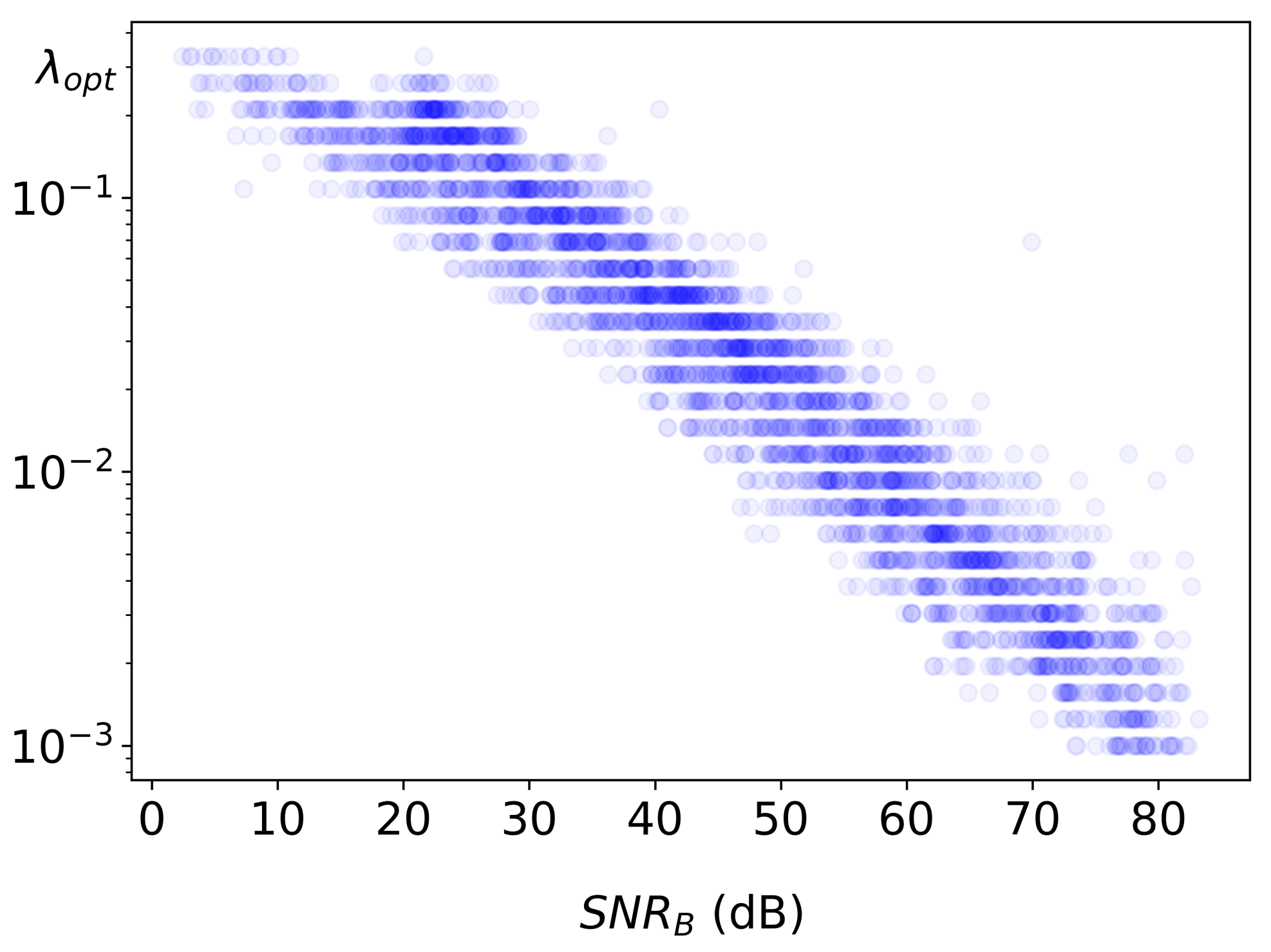
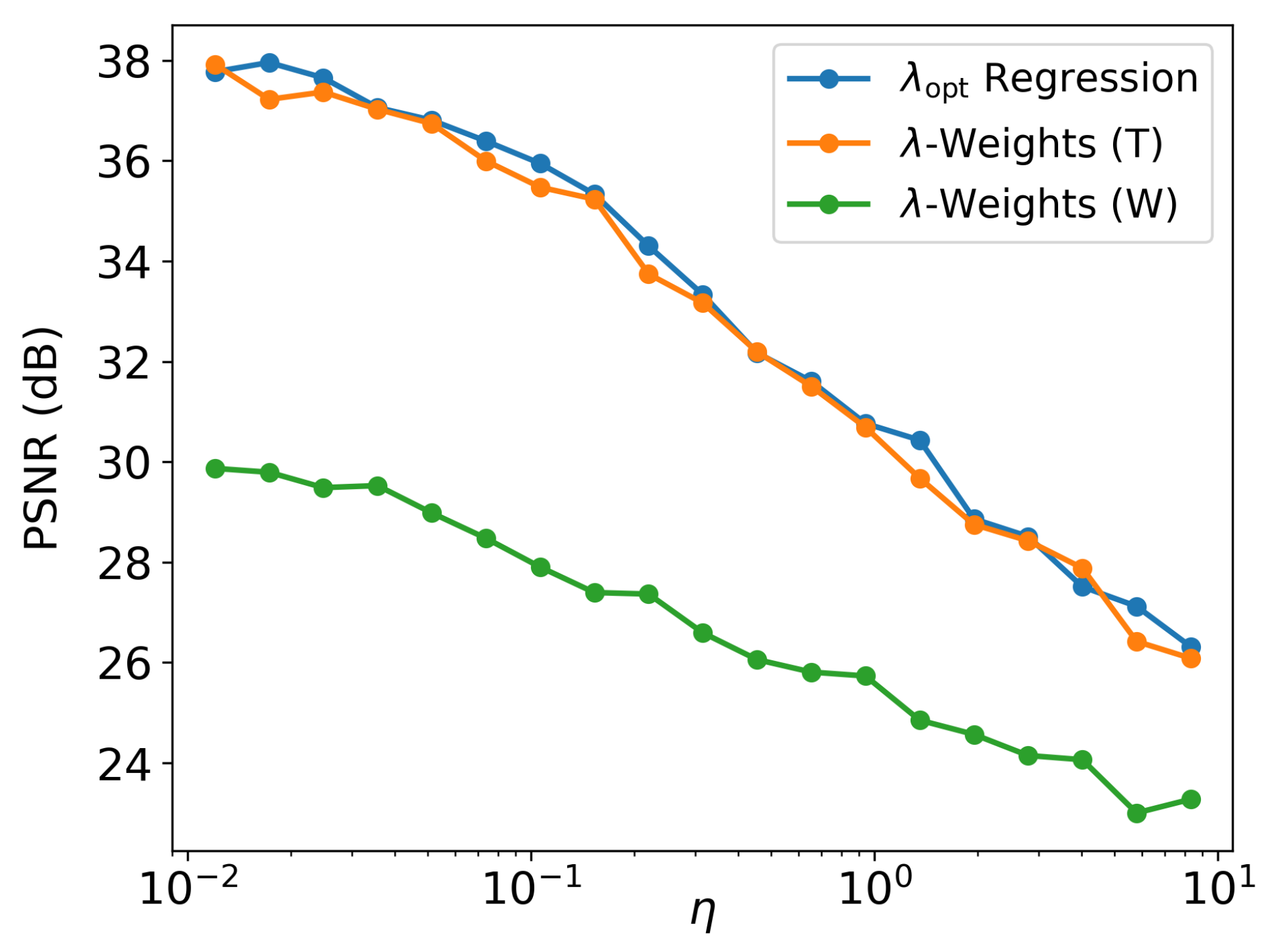
4.2.1. RegParamNet Training
Direct Regression
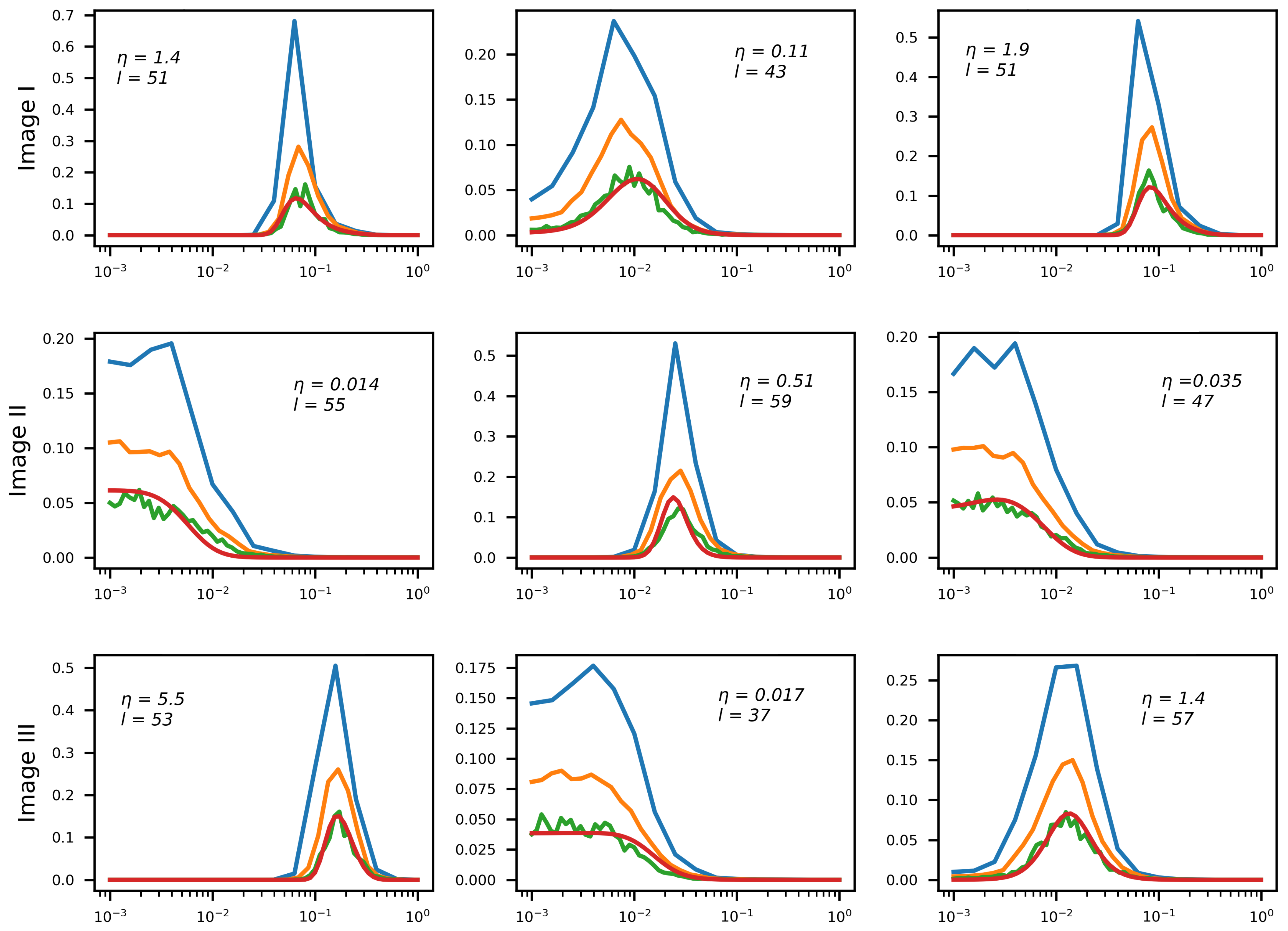
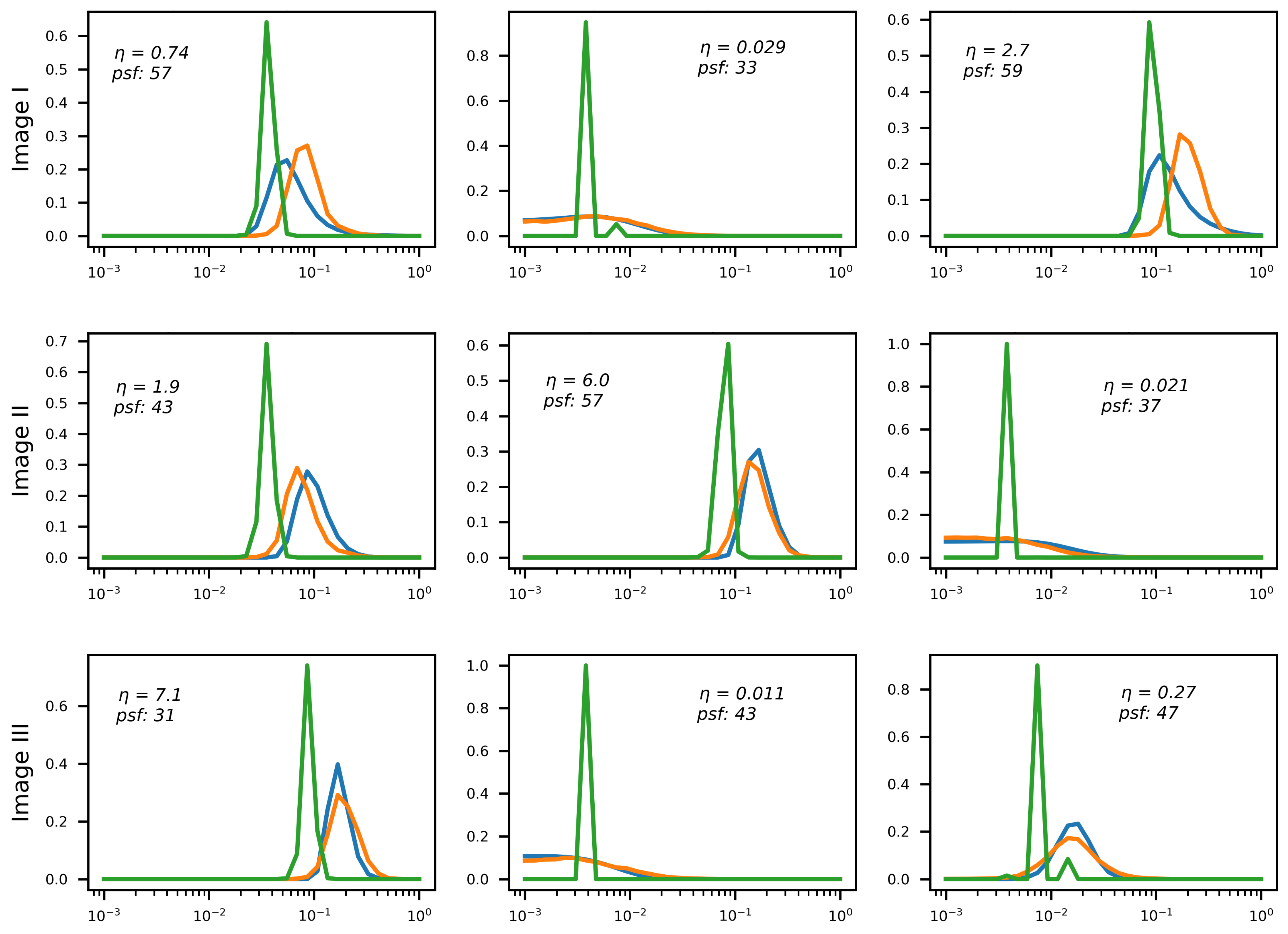
-Weight Array Generation
4.2.2. End-to-End System Training
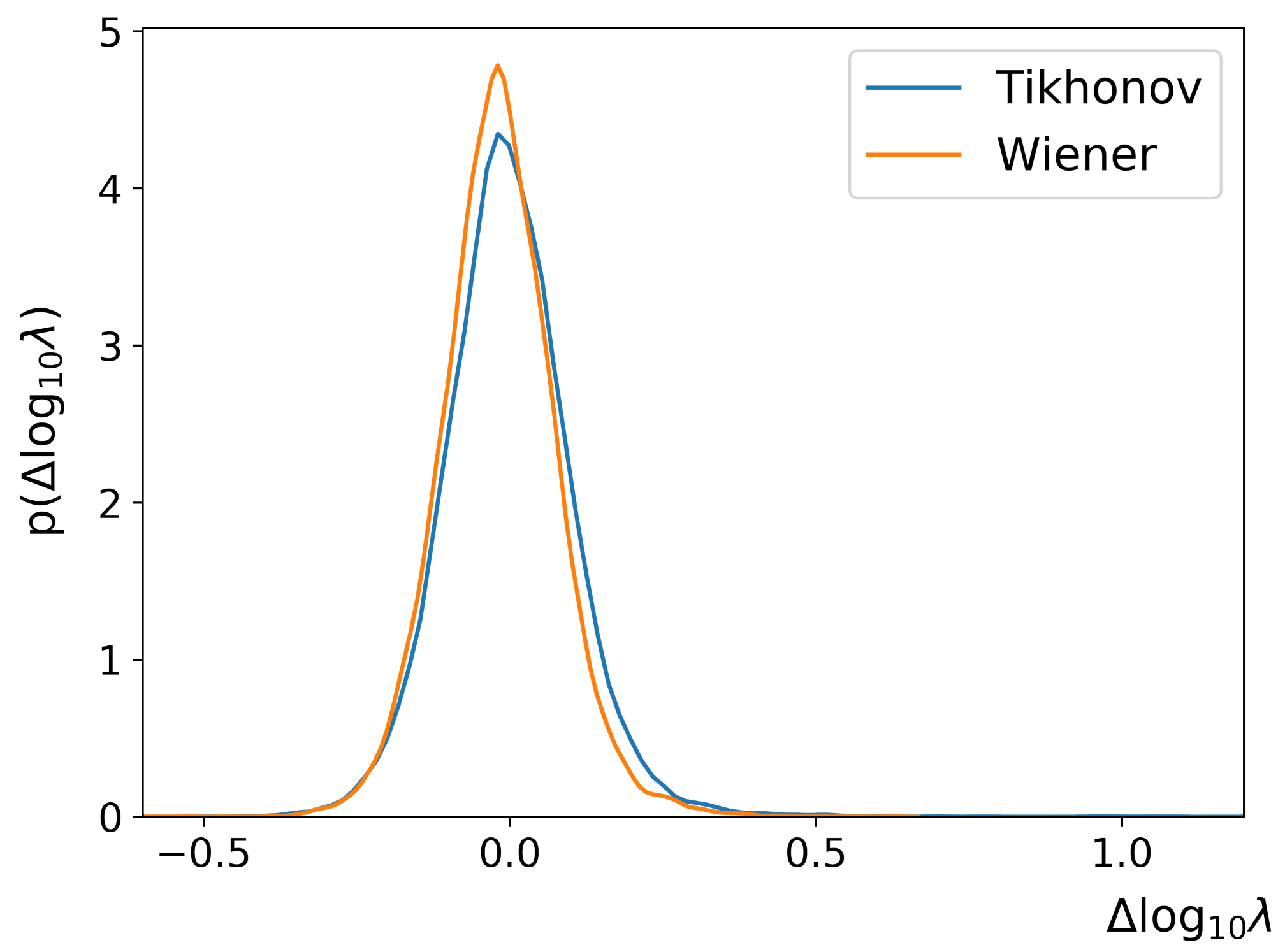
4.2.3. Results: Statistics
- (a)
- RD output before E2E training
- (b)
- RD output after E2E training
- (c)
- IEN output before E2E training
- (d)
- IEN output after E2E training
4.2.4. Results: Images
4.2.5. Results: Comparison to Other Approaches
- Gaussian kernel with spatial standard deviation equal to 1.6 and noise (denoted as GaussianA; in the proposed method)
- Gaussian kernel with spatial standard deviation equal to 3 and noise (denoted as GaussianB; in the proposed method)
- Gaussian kernel with spatial standard deviation equal to 5 and noise (denoted as GaussianC; in the proposed method)
- Square kernel with a side size of 19 and noise of (denoted as SquareA)
- Square kernel with a side size of 13 and noise of (denoted as SquareB; in the proposed method)
- Gaussian kernel with spatial standard deviation equal to 3 and noise (denoted as GaussianD)
- Gaussian kernel with spatial standard deviation equal to 5 and noise (denoted as GaussianE)
- Square kernel with a side size of 19 and noise of (denoted as SquareC)
- Square kernel with a side size of 13 and noise of (denoted as SquareD)
5. Summary
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 1D/2D | One-Dimensional / Two-Dimensional |
| ADAS | Advanced Driver Assistance System(s) |
| AV | Autonomous Vehicle |
| BDD | Berkeley Deep Drive |
| BSD | Berkeley Segmentation Dataset |
| CNN/DNN | Convolutional Neural Network / Deep Neural Network |
| DSLR | Digital Single-Lens Reflex (camera) |
| E2E | End-to-End |
| FC | Fully Connected (layer) |
| GCV | Generalized Cross-Validation |
| ICM | Image Corruption Module |
| IEN | Image Enhancement Network |
| ISP | Image Signal Processing/Processor |
| MAP | Maximum A Posteriori (estimation) |
| MSE | Mean Squared Error |
| PSF | Point Spread Function |
| PSNR | Peak Signal-to-Noise Ratio |
| RD | Regularized Deconvolution |
| ReLU | Rectified Linear Unit |
| RMS | Root Mean Square |
| SGD | Stochastic Gradient Descent |
| SNR | Signal-to-Noise Ratio |
| SSIM | Structural Similarity |
| SVD | Singular Value Decomposition |
| UW | Uniform Width |
References
- Nakamura, J. Image Sensors and Signal Processing for Digital Still Cameras; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Janai, J.; Güney, F.; Behl, A.; Geiger, A. Computer vision for autonomous vehicles: Problems, datasets and state-of-the-art. arXiv 2017, arXiv:1704.05519. [Google Scholar]
- Pei, Y.; Huang, Y.; Zou, Q.; Zhang, X.; Wang, S. Effects of Image Degradation and Degradation Removal to CNN-based Image Classification. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 1239–1253. [Google Scholar]
- Hege, E.K.; Jefferies, S.M.; Lloyd-Hart, M. Computing and telescopes at the frontiers of optical astronomy. Comput. Sci. Eng. 2003, 5, 42–51. [Google Scholar] [CrossRef]
- Sage, D.; Donati, L.; Soulez, F.; Fortun, D.; Schmit, G.; Seitz, A.; Guiet, R.; Vonesch, C.; Unser, M. DeconvolutionLab2: An open-source software for deconvolution microscopy. Methods 2017, 115, 28–41. [Google Scholar] [CrossRef]
- Maître, H. From Photon to Pixel: The Digital Camera Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Lee, H.C. Review of image-blur models in a photographic system using the principles of optics. Opt. Eng. 1990, 29, 405–422. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Yang, J.; Yu, J. A theoretical analysis of camera response functions in image deblurring. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 333–346. [Google Scholar]
- Hansen, P.C.; Nagy, J.G.; O’Leary, D.P. Deblurring Images: Matrices, Spectra, and Filtering; SIAM: Philadelphia, PA, USA, 2006; Volume 3. [Google Scholar]
- Harris, J.L. Image evaluation and restoration. JOSA 1966, 56, 569–574. [Google Scholar] [CrossRef]
- Richardson, W.H. Bayesian-based iterative method of image restoration. JOSA 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Lucy, L.B. An iterative technique for the rectification of observed distributions. Astron. J. 1974, 79, 745. [Google Scholar] [CrossRef]
- Mustaniemi, J.; Kannala, J.; Särkkä, S.; Matas, J.; Heikkila, J. Gyroscope-Aided Motion Deblurring with Deep Networks. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; IEEE: New York, NY, USA, 2019; pp. 1914–1922. [Google Scholar]
- Wang, R.; Tao, D. Recent progress in image deblurring. arXiv 2014, arXiv:1409.6838. [Google Scholar]
- McCann, M.T.; Jin, K.H.; Unser, M. Convolutional neural networks for inverse problems in imaging: A review. IEEE Signal Process. Mag. 2017, 34, 85–95. [Google Scholar] [CrossRef]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef]
- Schuler, C.J.; Hirsch, M.; Harmeling, S.; Schölkopf, B. Learning to deblur. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 1439–1451. [Google Scholar] [CrossRef]
- Zhang, K.; Ren, W.; Luo, W.; Lai, W.S.; Stenger, B.; Yang, M.H.; Li, H. Deep image deblurring: A survey. Int. J. Comput. Vis. 2022, 130, 2103–2130. [Google Scholar] [CrossRef]
- Nah, S.; Son, S.; Lee, S.; Timofte, R.; Lee, K.M. NTIRE 2021 challenge on image deblurring. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 149–165. [Google Scholar]
- Ren, W.; Zhang, J.; Ma, L.; Pan, J.; Cao, X.; Zuo, W.; Liu, W.; Yang, M.H. Deep non-blind deconvolution via generalized low-rank approximation. In Proceedings of the Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 297–307. [Google Scholar]
- Vasu, S.; Reddy Maligireddy, V.; Rajagopalan, A. Non-blind deblurring: Handling kernel uncertainty with CNNs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3272–3281. [Google Scholar]
- Hosseini, M.S.; Plataniotis, K.N. Convolutional Deblurring for Natural Imaging. IEEE Trans. Image Process. 2019, 29, 250–264. [Google Scholar] [CrossRef]
- Xu, L.; Ren, J.S.; Liu, C.; Jia, J. Deep convolutional neural network for image deconvolution. In Proceedings of the Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1790–1798. [Google Scholar]
- Wang, R.; Tao, D. Training very deep CNNs for general non-blind deconvolution. IEEE Trans. Image Process. 2018, 27, 2897–2910. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Wiener, N. The Interpolation, Extrapolation and Smoothing of Stationary Time Series; MIT: Cambridge, MA, USA, 1942. [Google Scholar]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Springer Science & Business Media: Berlin, Germany, 1996; Volume 375. [Google Scholar]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Hansen, P.C. The L-curve and its use in the numerical treatment of inverse problems. In Computational Inverse Problems in Electrocardiology; WIT Press: Southampton, UK, 1999; pp. 119–142. [Google Scholar]
- Liu, R.; Jia, J. Reducing boundary artifacts in image deconvolution. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; IEEE: New York, NY, USA, 2008; pp. 505–508. [Google Scholar]
- Reeves, S.J. Fast image restoration without boundary artifacts. IEEE Trans. Image Process. 2005, 14, 1448–1453. [Google Scholar] [CrossRef]
- Sorel, M. Removing boundary artifacts for real-time iterated shrinkage deconvolution. IEEE Trans. Image Process. 2011, 21, 2329–2334. [Google Scholar] [CrossRef]
- Yuan, L.; Sun, J.; Quan, L.; Shum, H.Y. Progressive inter-scale and intra-scale non-blind image deconvolution. ACM Trans. Graph. (TOG) 2008, 27, 1–10. [Google Scholar] [CrossRef]
- Lee, J.H.; Ho, Y.S. High-quality non-blind image deconvolution with adaptive regularization. J. Vis. Commun. Image Represent. 2011, 22, 653–663. [Google Scholar] [CrossRef]
- Mosleh, A.; Langlois, J.P.; Green, P. Image deconvolution ringing artifact detection and removal via PSF frequency analysis. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 247–262. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Lucas, A.; Iliadis, M.; Molina, R.; Katsaggelos, A.K. Using deep neural networks for inverse problems in imaging: Beyond analytical methods. IEEE Signal Process. Mag. 2018, 35, 20–36. [Google Scholar] [CrossRef]
- Schmidt, U.; Schelten, K.; Roth, S. Bayesian deblurring with integrated noise estimation. In Proceedings of the 24th IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2011), Colorado Springs, CO, USA, 20–25 June 2011; IEEE: New York, NY, USA, 2011; pp. 2625–2632. [Google Scholar]
- Meer, P.; Jolion, J.M.; Rosenfeld, A. A fast parallel algorithm for blind estimation of noise variance. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 216–223. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, W.; Lin, W. Adaptive median filter based on SNR estimation of single image. In Proceedings of the 2012 International Conference on Computer Science and Service System, Nanjing, China, 11–13 August 2012; IEEE: New York, NY, USA, 2012; pp. 246–249. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- MacKay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Yu, F.; Xian, W.; Chen, Y.; Liu, F.; Liao, M.; Madhavan, V.; Darrell, T. BDD100K: A Diverse Driving Video Database with Scalable Annotation Tooling. arXiv 2018, arXiv:1805.04687. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Nice, France, 2019; pp. 8024–8035. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Liu, Y.; Wang, J.; Cho, S.; Finkelstein, A.; Rusinkiewicz, S. A no-reference metric for evaluating the quality of motion deblurring. ACM Trans. Graph. 2013, 32, 175. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Schuler, C.J.; Christopher Burger, H.; Harmeling, S.; Scholkopf, B. A machine learning approach for non-blind image deconvolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1067–1074. [Google Scholar]
- Son, H.; Lee, S. Fast non-blind deconvolution via regularized residual networks with long/short skip-connections. In Proceedings of the 2017 IEEE International Conference on Computational Photography (ICCP), Stanford, CA, USA, 12–14 May 2017; IEEE: New York, NY, USA, 2017; pp. 1–10. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A Database of Human Segmented Natural Images and its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics. In Proceedings of the 8th International Conference on Computer Vision, Vancouver, BC, Canada, 9–12 July 2001; Volume 2, pp. 416–423. [Google Scholar]
- Levin, A.; Weiss, Y.; Durand, F.; Freeman, W.T. Understanding and evaluating blind deconvolution algorithms. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 22–24 June 2009; IEEE: New York, NY, USA, 2009; pp. 1964–1971. [Google Scholar]
- Romano, Y.; Elad, M.; Milanfar, P. The little engine that could: Regularization by denoising (RED). SIAM J. Imaging Sci. 2017, 10, 1804–1844. [Google Scholar] [CrossRef]
- Kim, J.; Kwon Lee, J.; Mu Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 19–23 June 2018; pp. 4510–4520. [Google Scholar]
- Wang, E.; Davis, J.J.; Zhao, R.; Ng, H.C.; Niu, X.; Luk, W.; Cheung, P.Y.; Constantinides, G.A. Deep Neural Network Approximation for Custom Hardware: Where We’ve Been, Where We’re Going. ACM Comput. Surv. (CSUR) 2019, 52, 1–39. [Google Scholar] [CrossRef]






| Deblurring Configuration | PSNR [dB]/SSIM |
|---|---|
| Initial: Tikhonov Deconvolution | 30.13 ± 3.04/0.926 ± 0.025 |
| Initial + UW-64 | 34.11 ±3.14/0.964 ± 0.015 |
| Initial + UW-128 | 34.46 ± 3.55/0.968 ± 0.016 |
| Initial + residual U-Net | 35.65 ± 3.95/0.974 ± 0.015 |
| Deblurring Configuration | PSNR [dB]/SSIM |
|---|---|
| Tikhonov Deconvolution | 30.13 ± 3.04/0.926 ± 0.024 |
| Tikhonov Deconvolution (after joint training) | 27.66 ± 1.46/0.818 ± 0.014 |
| Initial + residual U-Net | 35.65 ± 3.95/0.974 ± 0.015 |
| Initial + residual U-Net: Jointly Trained | 36.90 ± 3.93/0.980 ± 0.012 |
| RegParamNet | RD before E2E | RD after E2E | IEN before E2E | IEN after E2E |
|---|---|---|---|---|
| Configuration | PSNR [dB]/SSIM | PSNR [dB]/SSIM | PSNR [dB]/SSIM | PSNR [dB]/SSIM |
| -Weights (T) | 31.67 ± 4.35/0.76 ± 0.18 | 31.67 ± 4.34/0.932 ± 0.054 | 32.0 ± 5.0/0.94 ± 0.056 | |
| Regression (T) | 28.58 ± 4.74/0.875 ± 0.09 | 28.0 ± 5.0/0.80 ± 0.14 | 32.84 ± 5.0/0.94 ± 0.053 | 33.0 ± 5.0/0.94 ± 0.054 |
| -Weights (W) | 25.16 ± 3.23/0.734 ± 0.107 | 25.17 ± 3.0/0.742 ± 0.10 | 27.49 ± 3.1/0.865 ± 0.064 | 27.54 ± 3.19/0.87 ± 0.064 |
| Test | DBCNN [24] | MLP [50] | Son et al. [51] | NANBD | NANBD* (BDD Set) |
|---|---|---|---|---|---|
| Configuration | PSNR [dB]/SSIM | PSNR [dB]/SSIM | PSNR [dB]/SSIM | PSNR [dB]/SSIM | PSNR [dB]/SSIM |
| GaussianA | 28.47/0.8790 | 27.16/0.8645 | 23.18/0.7347 | 29.51/0.8732 | 36.45/0.9744 |
| GaussianB | 25.34/0.7811 | 24.48/0.7766 | 22.88/0.6814 | 29.14/0.865 | 34.97/0.9608 |
| GaussianC | 22.79/0.7194 | 22.31/0.6752 | 22.17/0.659 | 28.57/0.85 | 33.62/0.95 |
| GaussianD | - | - | - | 21.99/0.5477 | 27.92/0.803 |
| GaussianE | - | - | - | 25.14/0.7222 | 29.99/0.8876 |
| SquareA | 22.90/0.7078 | 22.81/0.6975 | 17.74/0.4139 | 28.57/0.8432 | 34.99/0.9637 |
| SquareB | 24.01/0.7564 | 23.52/0.7375 | 19.29/0.4788 | 28.91/0.8589 | 34.45/0.956 |
| SquareC | - | - | - | 21.52/0.7127 | 29.99/0.8866 |
| SquareD | - | - | - | 24.92/0.519 | 27.61/0.8032 |
| MotionA | 27.93/0.8795 | 26.73/08448 | 27.15/0.8525 | 30.65/0.8912 | 36.27/0.9748 |
| MotionB | 25.50/0.8009 | 24.77/0.7726 | 24.49/0.7378 | 29.34/ 0.8819 | 35.85/0.9716 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slutsky, M. Noise-Adaptive Non-Blind Image Deblurring. Sensors 2022, 22, 6923. https://doi.org/10.3390/s22186923
Slutsky M. Noise-Adaptive Non-Blind Image Deblurring. Sensors. 2022; 22(18):6923. https://doi.org/10.3390/s22186923
Chicago/Turabian StyleSlutsky, Michael. 2022. "Noise-Adaptive Non-Blind Image Deblurring" Sensors 22, no. 18: 6923. https://doi.org/10.3390/s22186923
APA StyleSlutsky, M. (2022). Noise-Adaptive Non-Blind Image Deblurring. Sensors, 22(18), 6923. https://doi.org/10.3390/s22186923





