Strip-Type Embeddable Shape Sensor Based on Fiber Optics for In Situ Composite Consolidation Monitoring
Abstract
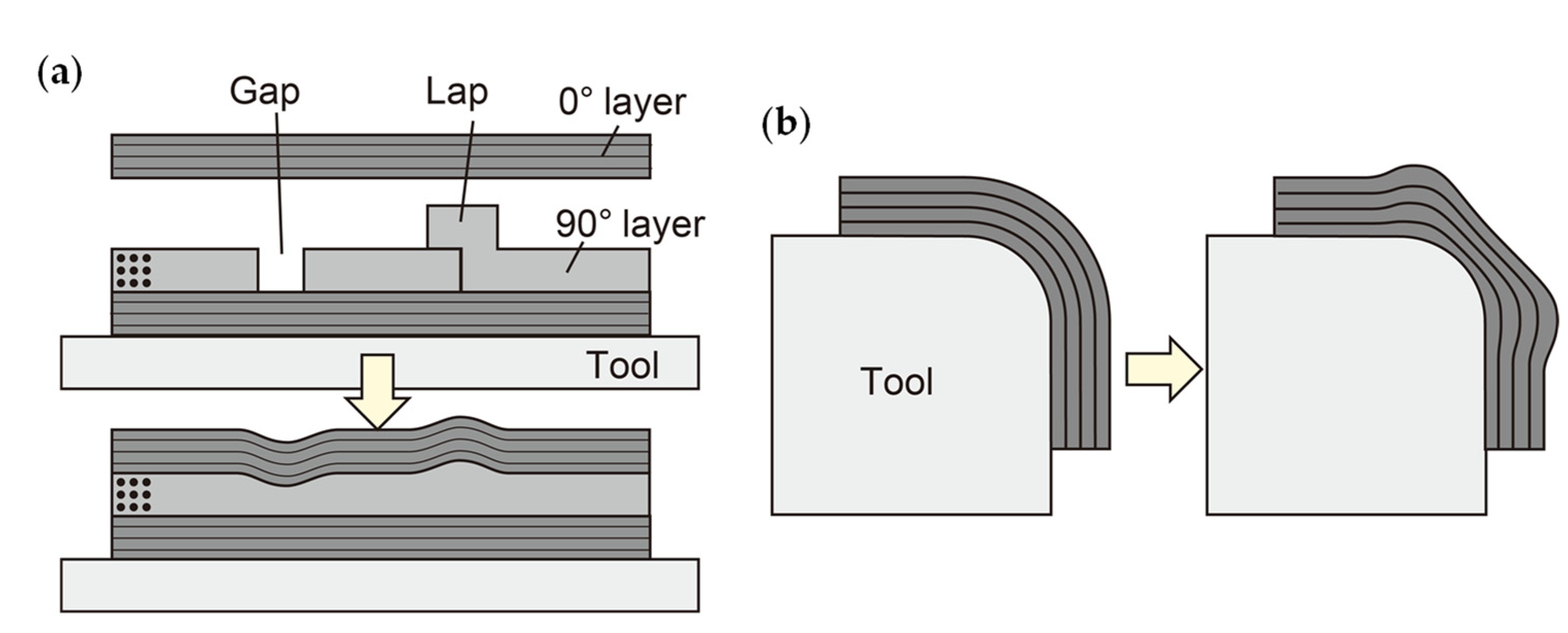
:1. Introduction
2. Strip-Type Embeddable Shape Sensor Based on Fiber Optics
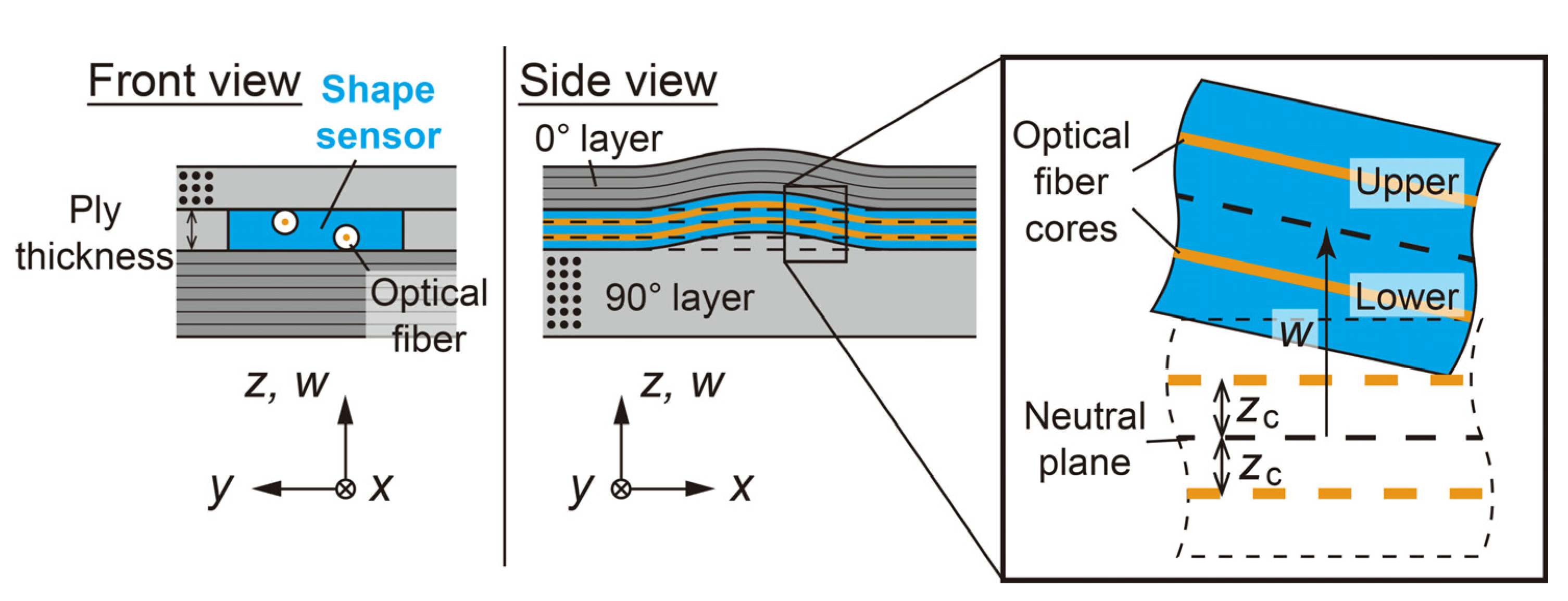
2.1. Basic Concept
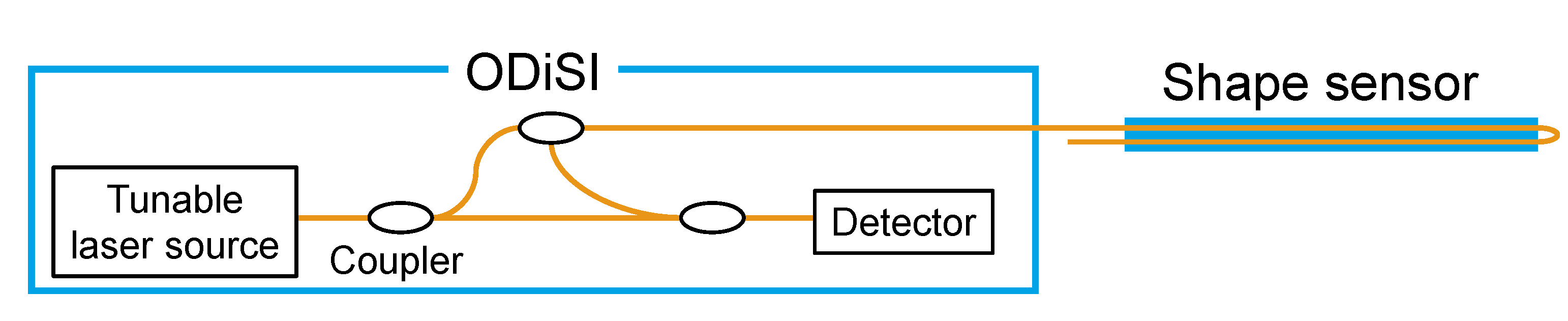
2.2. Measurement System
2.3. Sensor Fabrication
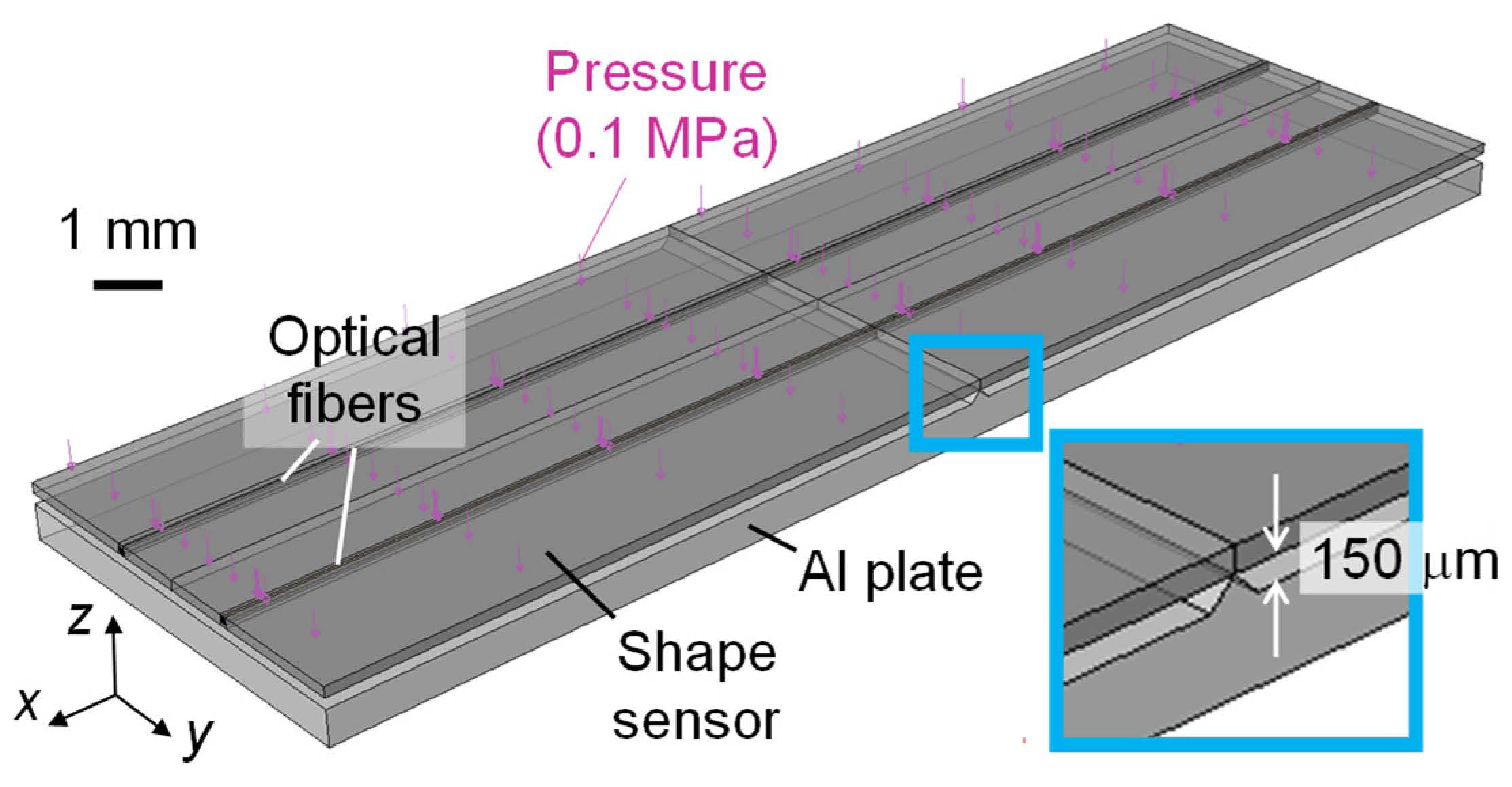
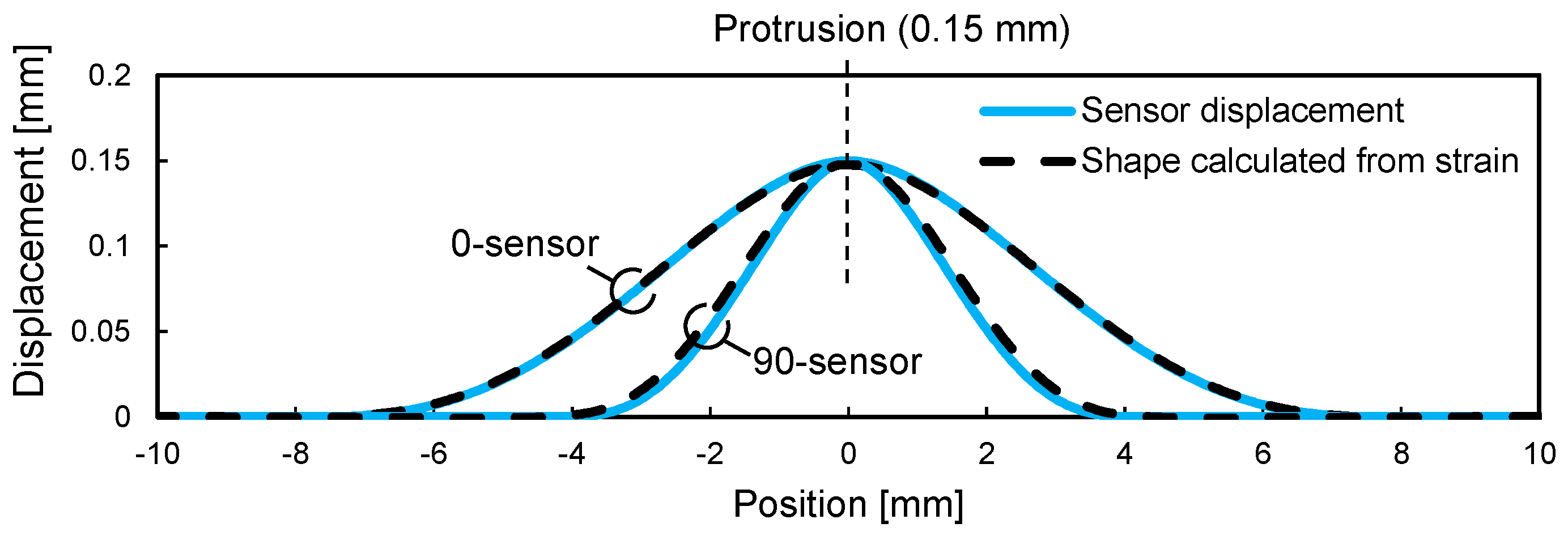
2.4. Finite Element Analysis for Sensor Response Evaluation
3. Sensor Response Evaluation Test
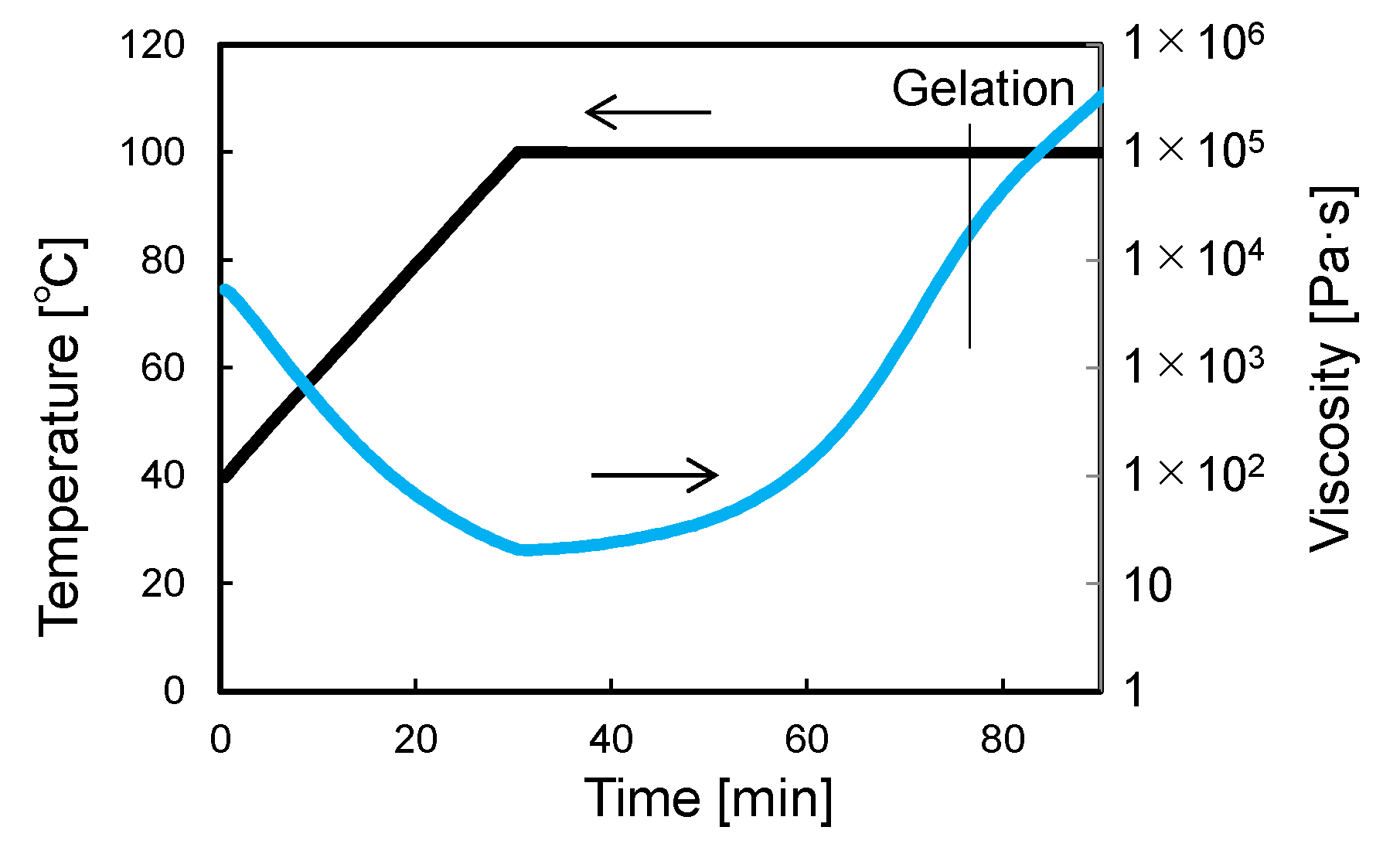
3.1. Materials and Methods
3.2. Results
4. Consolidation Monitoring of Composite Gap/Lap
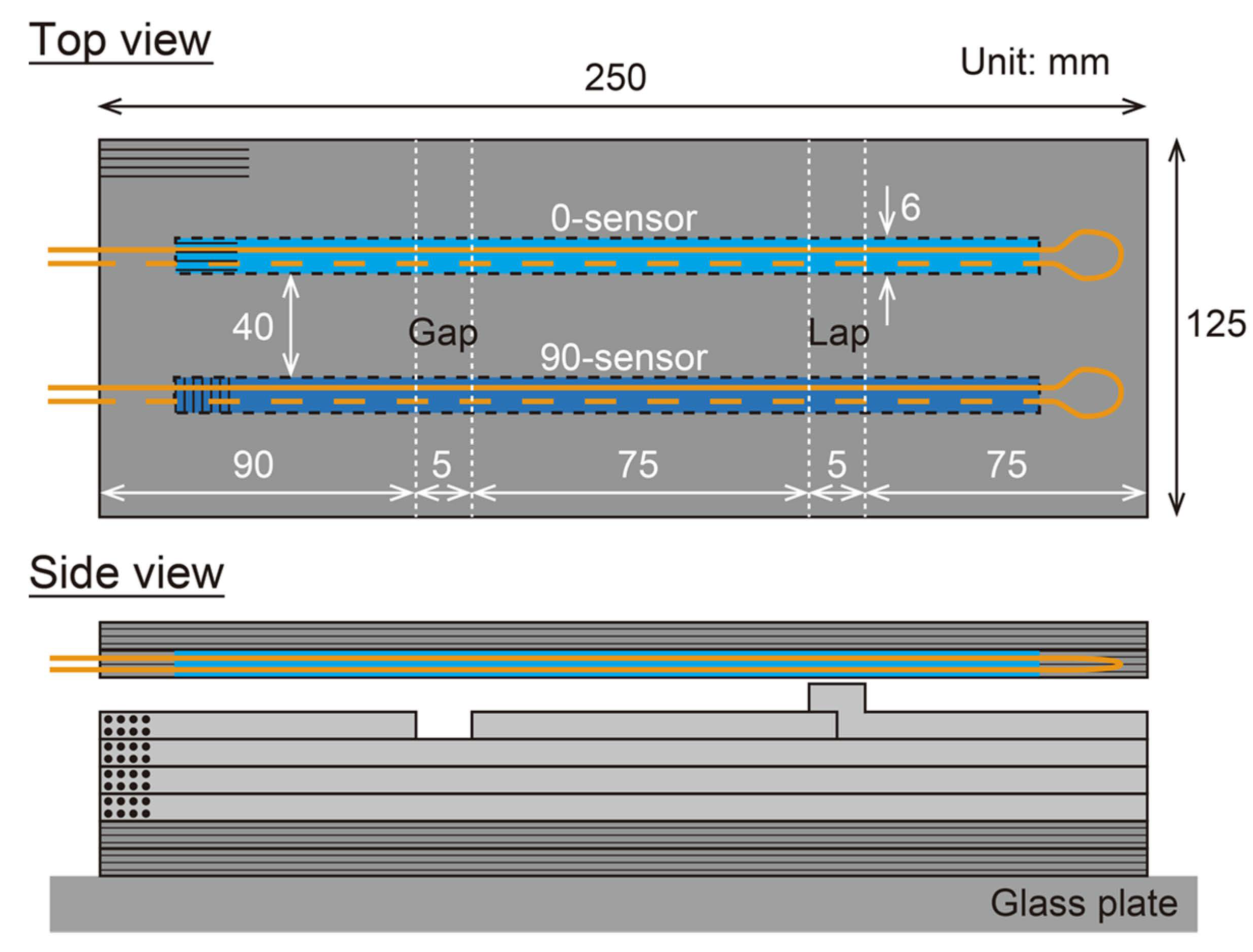
4.1. Materials and Methods
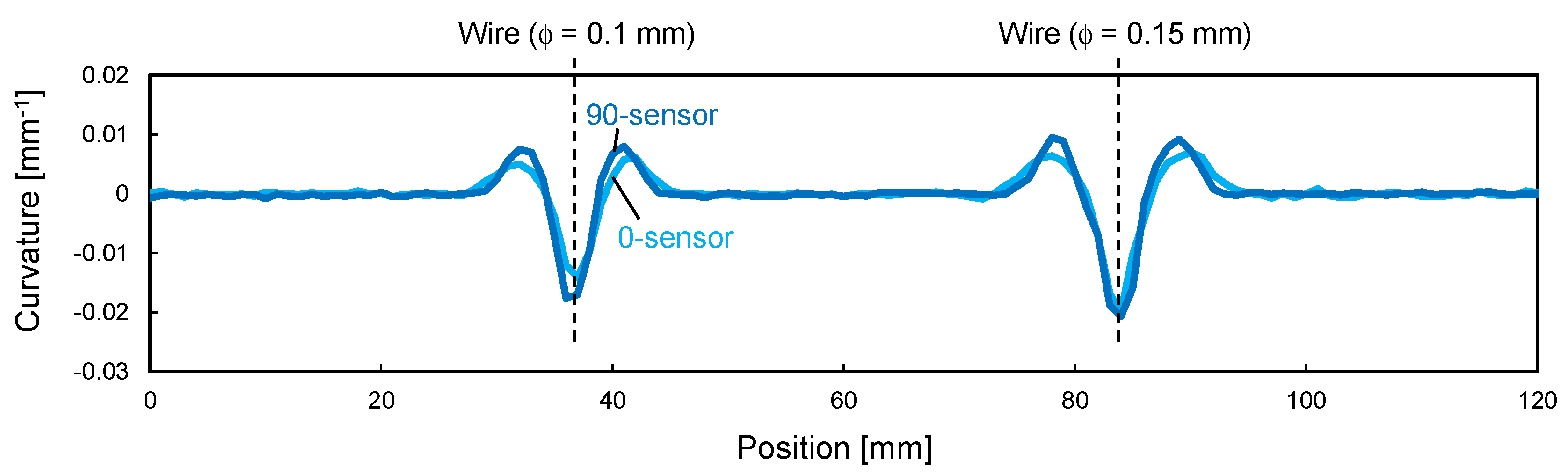
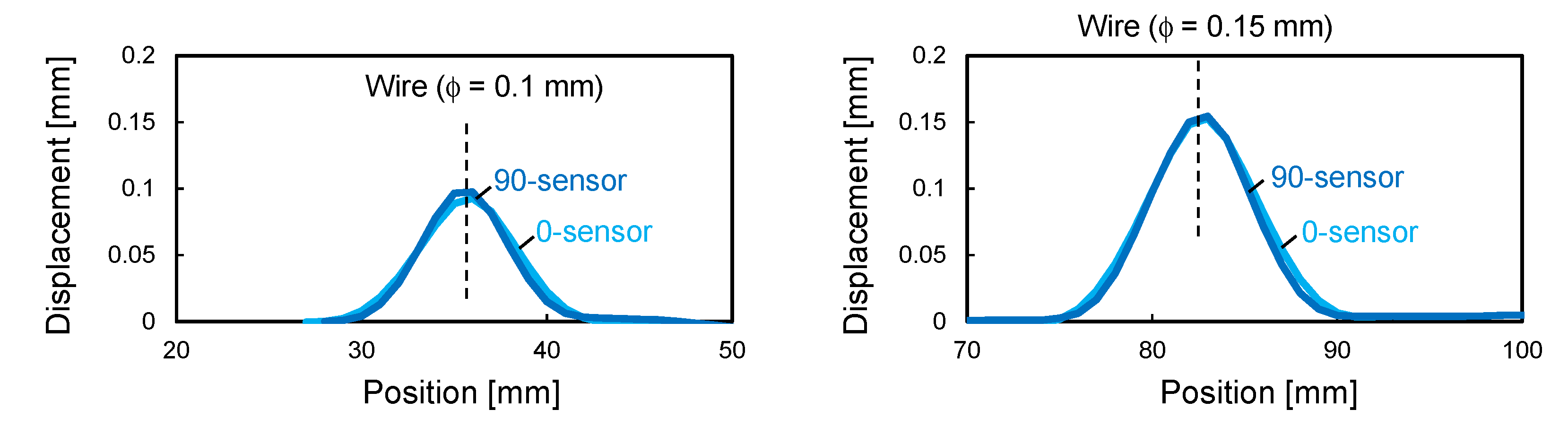
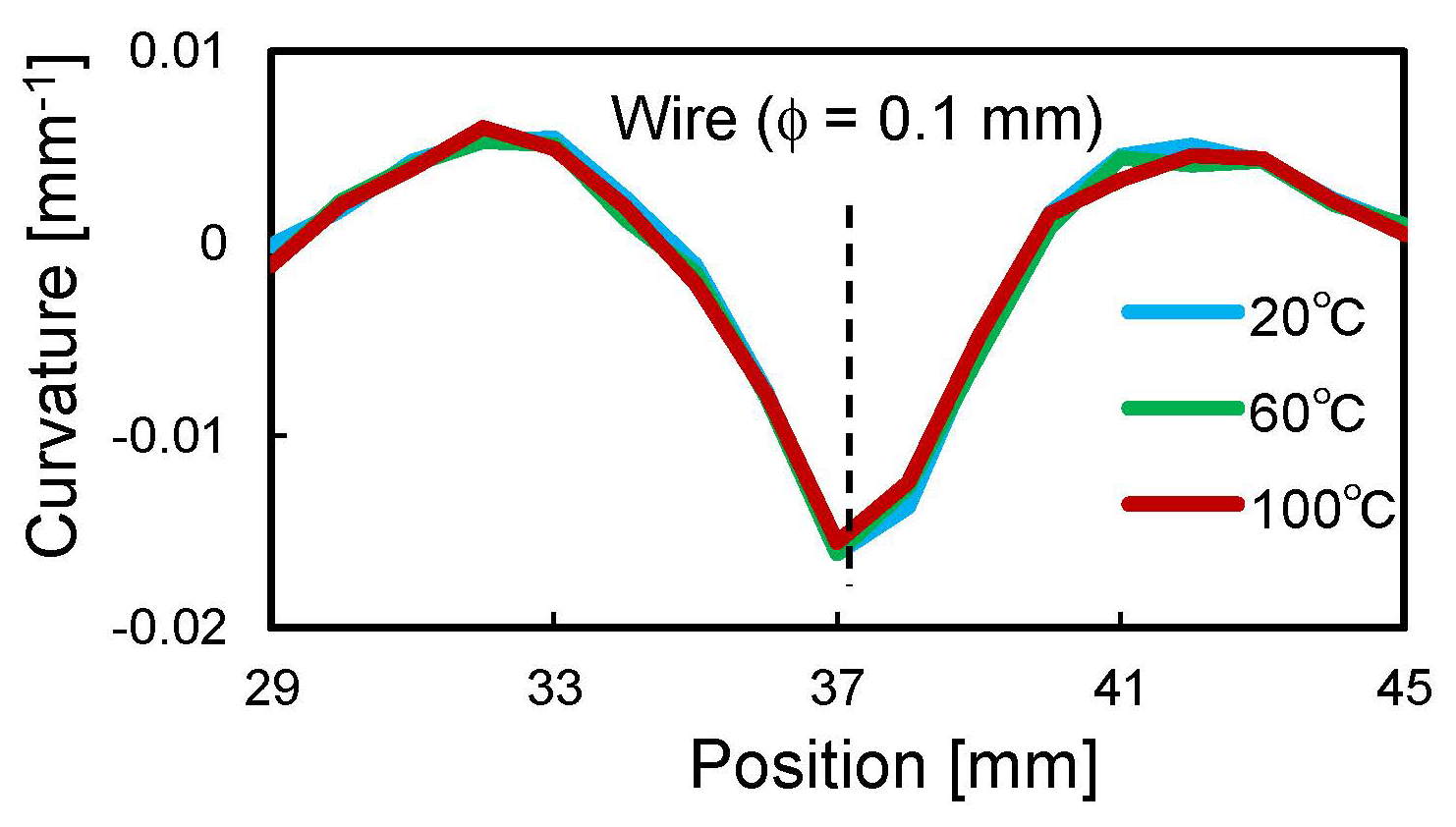
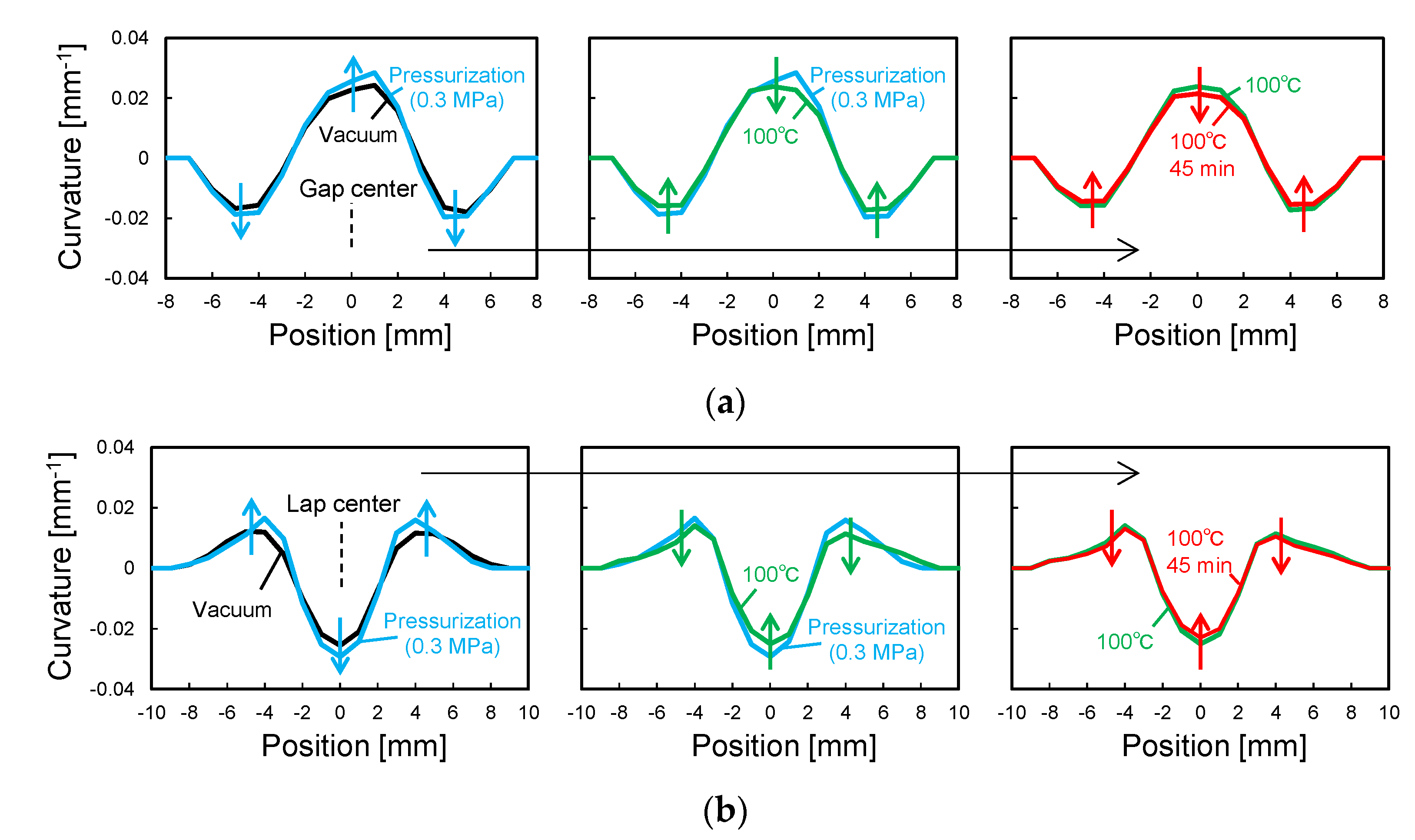
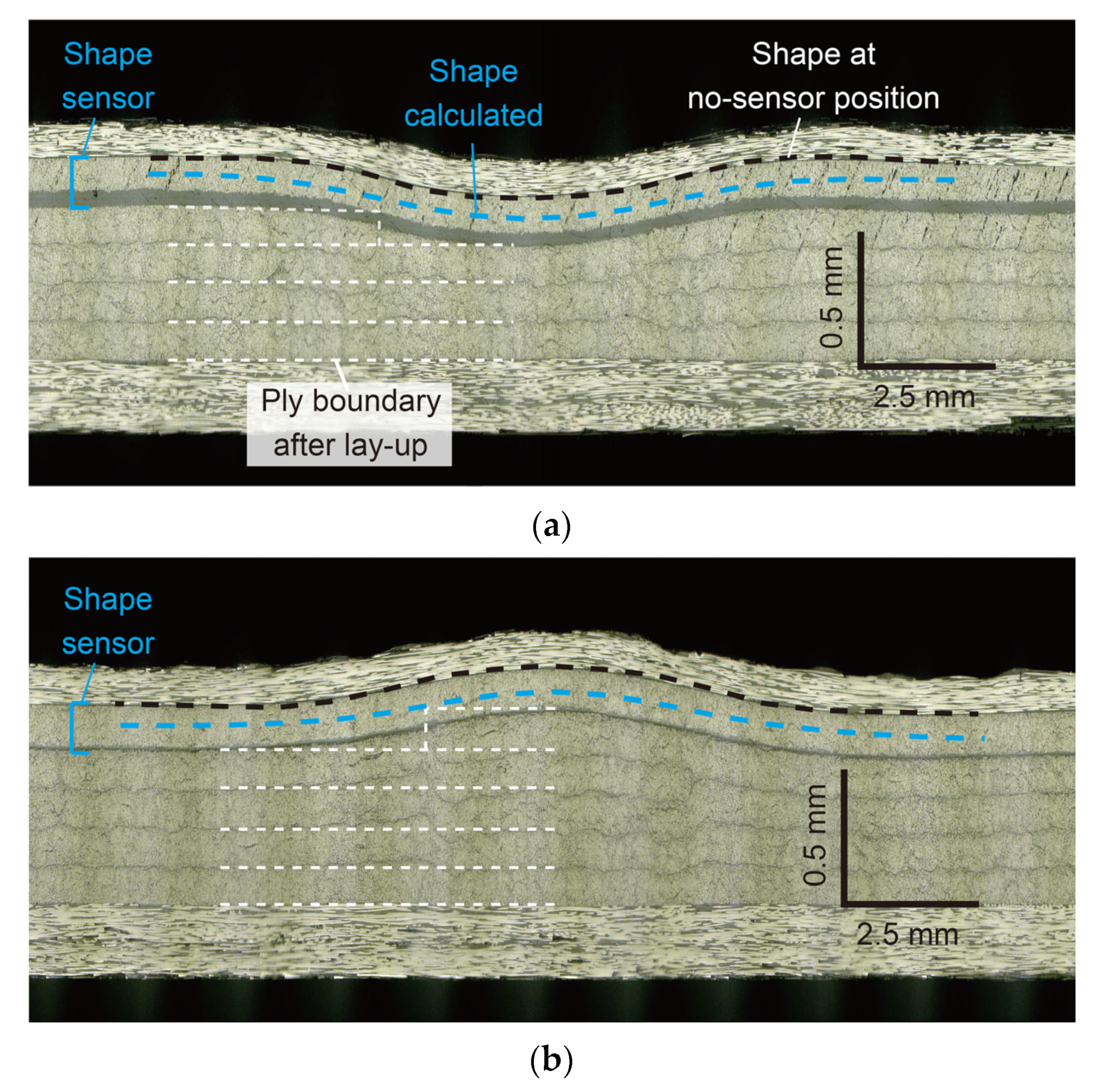
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jones, R.M. Design of Composite Structures; Bull Ridge Publishing: Blacksburg, VA, USA, 2015. [Google Scholar]
- Clyne, T.W.; Hull, D. An Introduction to Composite Materials; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Li, X.; Hallett, S.R.; Wisnom, M.R. Modelling the effect of gaps and overlaps in automated fibre placement (AFP)-manufactured laminates. Sci. Eng. Compos. Mater. 2015, 22, 115–129. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Vijayachandran, A.A.; Davidson, P.; Call, D.; Lee, D.; Waas, A.M. Effect of automated fiber placement (AFP) manufacturing signature on mechanical performance of composite structures. Compos. Struct. 2019, 228, 111335. [Google Scholar] [CrossRef]
- Xu, X.; Jones, M.I.; Ali, H.; Wisnom, M.R.; Hallett, S.R. Effect of out-of-plane wrinkles in curved multi-directional carbon/epoxy laminates. Compos. Sci. Technol. 2020, 197, 108282. [Google Scholar] [CrossRef]
- Naderi, M.; Ji, M.; Liyanage, S.; Palliyaguru, U.; Soghrati, S.; Iyyer, N.; Seneviratned, W.; Phan, N. Experimental and numerical analysis of wrinkles influence on damage mechanisms and strength of L-Shape cross-ply composite beams. Compos. Sci. Technol. 2022, 223, 109420. [Google Scholar] [CrossRef]
- Hubert, P.; Poursartip, A. Aspects of the compaction of composite angle laminates: An experimental investigation. J. Compos. Mater. 2001, 35, 2–26. [Google Scholar] [CrossRef]
- Netzel, C.; Mordasini, A.; Schubert, J.; Allen, T.; Battley, M.; Hickey CM, D.; Hubert, P.; Bickerton, S. An experimental study of defect evolution in corners by autoclave processing of prepreg material. Compos. Part A Appl. Sci. Manuf. 2021, 144, 106348. [Google Scholar] [CrossRef]
- Chava, S.; Namilae, S. Continuous evolution of processing induced residual stresses in composites: An in-situ approach. Compos. Part A Appl. Sci. Manuf. 2021, 145, 106368. [Google Scholar] [CrossRef]
- Hubert, P.; Kratz, J. Tool interface pressure during the forming of model composite corners. Compos. Part A Appl. Sci. Manuf. 2021, 151, 106639. [Google Scholar] [CrossRef]
- Hubert, P.; Vaziri, R.; Poursartip, A. A two-dimensional flow model for the process simulation of complex shape composite laminates. Int. J. Numer. Methods Eng. 1999, 44, 1–26. [Google Scholar] [CrossRef]
- Belnoue, J.P.H.; Mesogitis, T.; Nixon-Pearson, O.J.; Kratz, J.; Ivanov, D.S.; Partridge, I.K.; Potter, K.D.; Hallett, S.R. Understanding and predicting defect formation in automated fibre placement pre-preg laminates. Compos. Part A Appl. Sci. Manuf. 2017, 102, 196–206. [Google Scholar] [CrossRef]
- Belnoue, J.H.; Nixon-Pearson, O.J.; Thompson, A.J.; Ivanov, D.S.; Potter, K.D.; Hallett, S.R. Consolidation-driven defect generation in thick composite parts. J. Manuf. Sci Eng. 2018, 140, 071006. [Google Scholar] [CrossRef]
- Levy, A.; Hubert, P. Vacuum-bagged composite laminate forming processes: Predicting thickness deviation in complex shapes. Compos. Part A Appl. Sci. Manuf. 2019, 126, 105568. [Google Scholar] [CrossRef]
- Kermani, N.N.; Gargitter, V.; Simacek, P.; Advani, S.G. Gap filling mechanisms during the thin ply Automated Tape Placement process. Compos. Part A Appl. Sci. Manuf. 2021, 147, 106454. [Google Scholar] [CrossRef]
- Simacek, P.; Kermani, N.N.; Gargitter, V.; Advani, S.G. Role of resin percolation in gap filling mechanisms during the thin ply thermosetting automated tape placement process. Compos. Part A Appl. Sci. Manuf. 2022, 152, 106677. [Google Scholar] [CrossRef]
- Kratz, J.; Galvez-Hernandez, P.; Pickard, L.R.; Belnoue, J.; Potter, K. Lab-based in-situ micro-CT observation of gaps in prepreg laminates during consolidation and cure. Compos. Part A Appl. Sci. Manuf. 2021, 140, 106180. [Google Scholar] [CrossRef]
- Luyckx, G.; Voet, E.; Lammens, N.; Degrieck, J. Strain measurements of composite laminates with embedded fibre Bragg gratings: Criticism and opportunities for research. Sensors 2010, 11, 384–408. [Google Scholar] [CrossRef]
- Di Sante, R. Fibre optic sensors for structural health monitoring of aircraft composite structures: Recent advances and applications. Sensors 2015, 15, 18666–18713. [Google Scholar] [CrossRef]
- Ramakrishnan, M.; Rajan, G.; Semenova, Y.; Farrell, G. Overview of fiber optic sensor technologies for strain/temperature sensing applications in composite materials. Sensors 2016, 16, 99. [Google Scholar] [CrossRef]
- Minakuchi, S. In situ characterization of direction-dependent cure-induced shrinkage in thermoset composite laminates with fiber-optic sensors embedded in through-thickness and in-plane directions. J. Compos. Mater. 2015, 49, 1021–1034. [Google Scholar] [CrossRef]
- Hu, H.; Li, S.; Wang, J.; Zu, L.; Cao, D.; Zhong, Y. Monitoring the gelation and effective chemical shrinkage of composite curing process with a novel FBG approach. Compos. Struct. 2017, 176, 187–194. [Google Scholar] [CrossRef]
- Prussak, R.; Stefaniak, D.; Hühne, C.; Sinapius, M. Evaluation of residual stress development in FRP-metal hybrids using fiber Bragg grating sensors. Prod. Eng. 2018, 12, 259–267. [Google Scholar] [CrossRef]
- Amanzadeh, M.; Aminossadati, S.M.; Kizil, M.S.; Rakić, A.D. Recent developments in fibre optic shape sensing. Measurement 2018, 128, 119–137. [Google Scholar] [CrossRef]
- Floris, I.; Adam, J.M.; Calderón, P.A.; Sales, S. Fiber optic shape sensors: A comprehensive review. Opt. Lasers Eng. 2021, 139, 106508. [Google Scholar] [CrossRef]
- Soller, B.J.; Wolfe, M.; Froggatt, M.E. Polarization resolved measurement of Rayleigh backscatter in fiber-optic components. In Proceedings of the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 6 March 2005; Optica Publishing Group: Washington, DC, USA, 2005; p. NWD3. [Google Scholar]
- Soller, B.J.; Gifford, D.K.; Wolfe, M.S.; Froggatt, M.E. High resolution optical frequency domain reflectometry for characterization of components and assemblies. Opt. Express 2005, 13, 666–674. [Google Scholar] [CrossRef] [Green Version]




| T700S/2592 Unidirectional | Cladding and Core | Polyimide Coating | Aluminum | |
|---|---|---|---|---|
| Elastic moduli (GPa) | ||||
| E11 | 135 | 73.1 | 1.5 | 70 |
| E22 | 8.5 | |||
| G12 | 4.8 | |||
| G23 | 2.7 | |||
| Poisson’s ratios | ||||
| ν12 | 0.34 | 0.16 | 0.25 | 0.35 |
| ν23 | 0.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minakuchi, S.; Niwa, S.; Takeda, N. Strip-Type Embeddable Shape Sensor Based on Fiber Optics for In Situ Composite Consolidation Monitoring. Sensors 2022, 22, 6604. https://doi.org/10.3390/s22176604
Minakuchi S, Niwa S, Takeda N. Strip-Type Embeddable Shape Sensor Based on Fiber Optics for In Situ Composite Consolidation Monitoring. Sensors. 2022; 22(17):6604. https://doi.org/10.3390/s22176604
Chicago/Turabian StyleMinakuchi, Shu, Shoma Niwa, and Nobuo Takeda. 2022. "Strip-Type Embeddable Shape Sensor Based on Fiber Optics for In Situ Composite Consolidation Monitoring" Sensors 22, no. 17: 6604. https://doi.org/10.3390/s22176604
APA StyleMinakuchi, S., Niwa, S., & Takeda, N. (2022). Strip-Type Embeddable Shape Sensor Based on Fiber Optics for In Situ Composite Consolidation Monitoring. Sensors, 22(17), 6604. https://doi.org/10.3390/s22176604






