Capped Linex Metric Twin Support Vector Machine for Robust Classification
Abstract
1. Introduction
2. Related Work
2.1. Linex-SVM
2.2. TSVM
3. Main Contribution
3.1. Capped Linex Loss Function
3.2. Capped Linex Twin Support Vector Machine
| Algorithm 1 Iterative algorithm to solve Linex-CTSVM |
| Input: Training data and ; Parameters and . Establish matrixs . Initialize and . Let Iterative Let k = k + 1 and go to step 2, until convergence stops. Output: Optimal solution and . |
3.3. Bayes Rule
3.4. Computational Complexity Analysis
4. Experimental Results and Discussions
4.1. Experimental Setup
4.1.1. Evaluation Criteria
4.1.2. Parameters Selection
- SVM and LSSVM:the kernel parameter .
- C-SVM: the regularization parameter c, the kernel parameter .
- NPSVM and TBSVM: the regularization parameters , , and , the kernel parameter .
- Linex-SVM: the regularization parameter c, a parameter a of the linex loss, the kernel parameter .
- Linex-TSVM: the regularization parameter , , , , a parameter a of the linex loss, the parameters , , , and the kernel parameter .where ; , , , ; . The experimental parameters are selected by ten cross-validation methods, and the test accuracy is the average of 10 clusters of results in each dataset.
4.1.3. Description of the Datasets
4.2. Experimental Results on the Employed Datasets without Outliers
4.3. Experimental Results on the Employed Datasets with Outliers
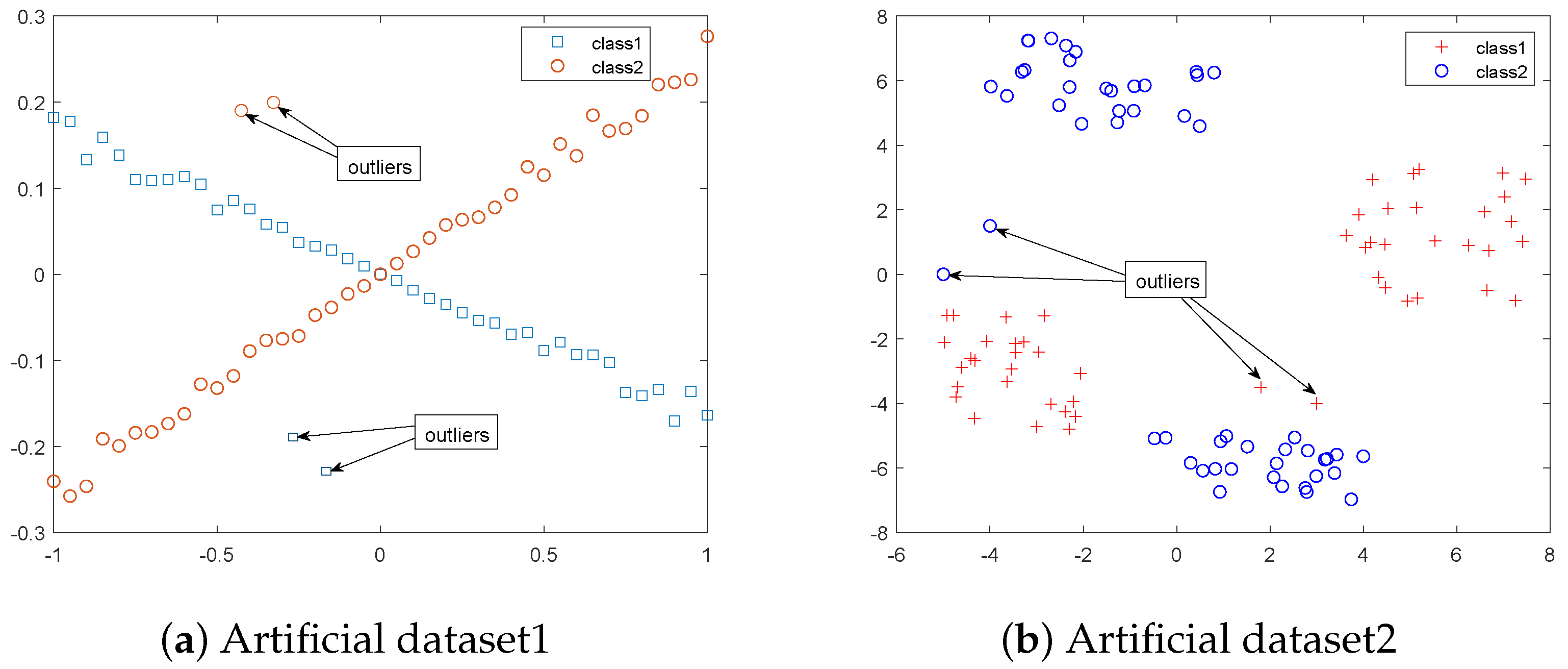
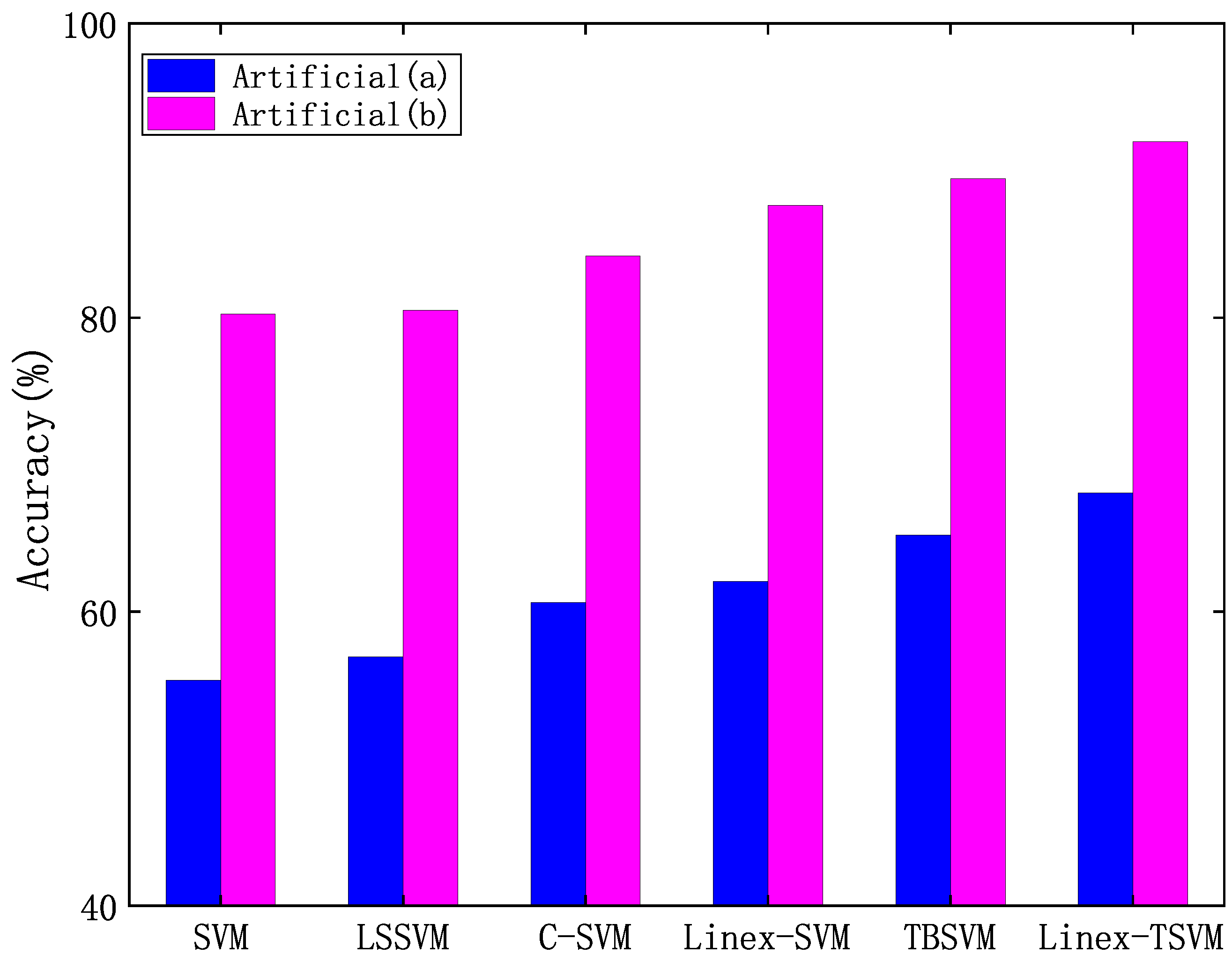
4.3.1. Experimental Results on Artificial Dataset with Outliers
4.3.2. Experimental Results on UCI Dataset with Outliers
4.4. Analysis for the Convergence
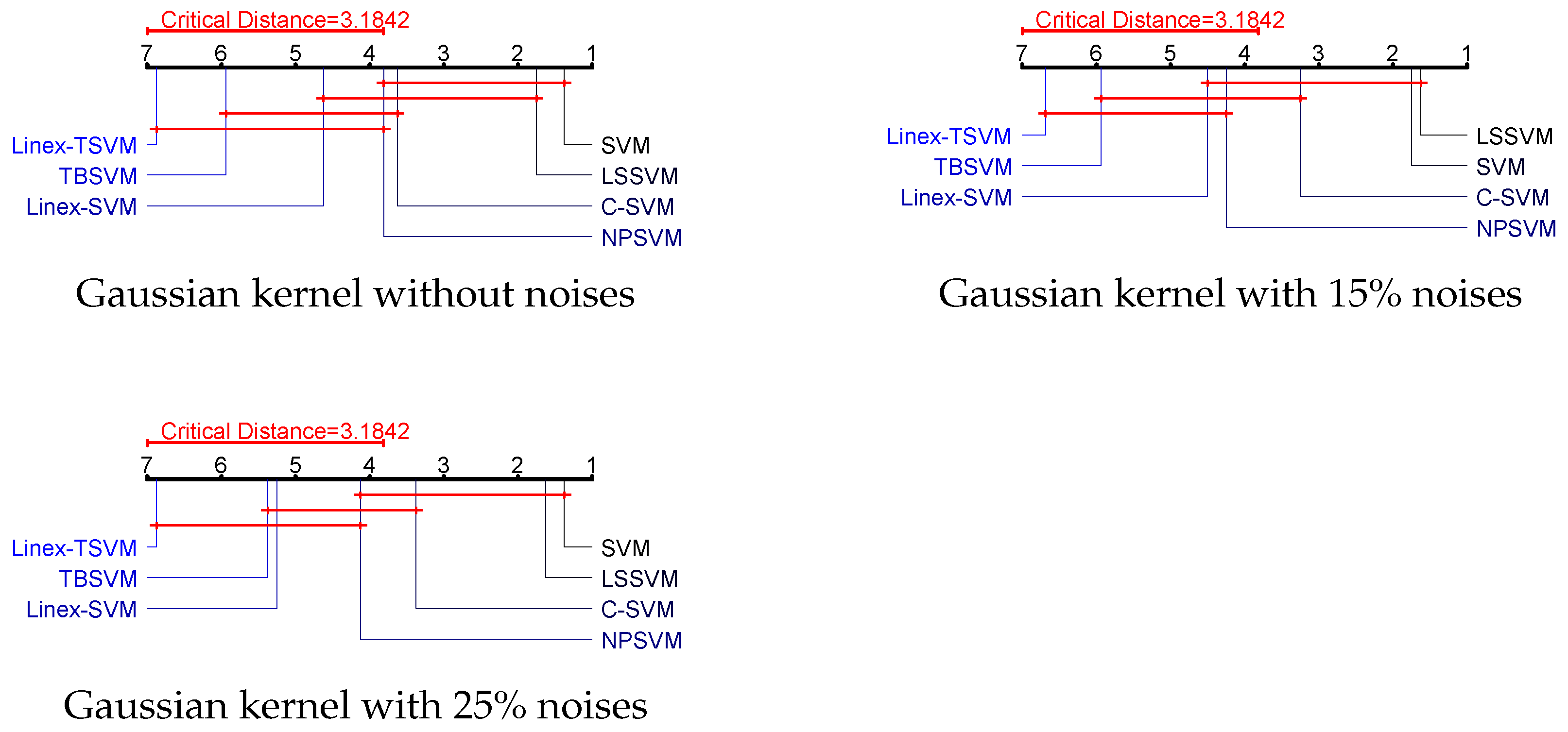
4.5. Statistical Analysis
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Brown, M.P.; Grundy, W.N.; Lin, D.; Cristianini, N.; Sugnet, C.W.; Furey, T.S.; Haussler, D. Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc. Natl. Acad. Sci. USA 2000, 97, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Cheng, B.; Shang, Z.; Liu, G. Scattering transform and LSPTSVM based fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2018, 104, 55–170. [Google Scholar] [CrossRef]
- Goh, K.S.; Chang, E.Y.; Li, B. Using one-class and two-class SVMs for multiclass image annotation. IEEE Trans. Knowl. Data Eng. 2005, 17, 1333–1346. [Google Scholar] [CrossRef]
- Bi, J.; Zhang, T. Support vector classification with input data uncertainty. In Proceedings of the Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 13–18 December 2004. [Google Scholar]
- Saunders, C.; Gammerman, A.; Vovk, V. Ridge regression learning algorithm in dual variables. In Proceedings of the 15th International Conference on Machine Learning, ICML’98, Madison, WI, USA, 24–27 July 1998. [Google Scholar]
- Suykens, J.A.K.; Vewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Q.; Li, D.; Tian, Y. Linex support vector machine for large-scale classification. IEEE Access 2019, 7, 70319–70331. [Google Scholar] [CrossRef]
- Khemchani, R.; Chra, S. Twin support vector machines for pattern classification. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 905–910. [Google Scholar]
- Gao, S.; Ye, Q.; Ye, N. 1-Norm least squares twin support vector machines. Neurocomputing 2011, 74, 3590–3597. [Google Scholar] [CrossRef]
- Ye, Q.; Zhao, H.; Li, Z.; Yang, X.; Gao, S.; Yin, T.; Ye, N. L1-Norm distance minimization-based fast robust twin support vector k-plane clustering. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 4494–4503. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Ye, Q.; Zhang, T.A.; Yu, D.J.; Yuan, X.; Xu, Y.; Fu, L. Least squares twin bounded support vector machines based on L1-norm distance metric for classification. Pattern Recognit. 2018, 74, 434–447. [Google Scholar] [CrossRef]
- Wu, M.J.; Liu, J.X.; Gao, Y.L.; Kong, X.Z.; Feng, C.M. Feature selection and clustering via robust graph-laplacian PCA based on capped L1-norm. In Proceedings of the 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Kansas City, MO, USA, 13–16 November 2017; pp. 1741–1745. [Google Scholar]
- Zhang, C.; Wang, Z. Linex-RSVM:ramp linex support vector machine. Procedia Comput. Sci. 2022, 199, 524–531. [Google Scholar] [CrossRef]
- Kinyanjui, J.K.; Korir, B.C. Bayesian Estimation of Parameters of Weibull Distribution Using Linex Error Loss Function. Int. J. Stat. Probab. 2020, 9, 1–38. [Google Scholar] [CrossRef][Green Version]
- Zou, G. Admissible estimation for finite population under the LINEX loss function. J. Stat. Plan. Inference 1997, 61, 373–384. [Google Scholar] [CrossRef]
- Hwang, L.C. Second order optimal approximation in a particular exponential family under asymmetric linex loss. Stat. Probab. Lett. 2018, 137, 283–291. [Google Scholar] [CrossRef]
- Wang, C.; Ye, Q.; Luo, P.; Ye, N.; Fu, L. Robust capped L1-norm twin support vector machine. Neural Netw. 2019, 114, 47–59. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Luo, M.; Li, Z.; Nie, F.; Zhang, H.; Liu, J.; Zheng, Q. Large-scale robust semisupervised classification. IEEE Trans. Cybern. 2018, 49, 907–917. [Google Scholar] [CrossRef] [PubMed]
- Nie, F.; Huang, Y.; Wang, X.; Huang, H. New primal SVM solver with linear computational cost for big data classifications. In Proceedings of the 31st International Conference on International Conference on Machine Learning, Bejing, China, 22–24 June 2014; Volume 32, pp. 505–513. [Google Scholar]
- Nie, F.; Huo, Z.; Huang, H. Joint capped norms minimization for robust matrix recovery. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017. [Google Scholar]
- Zhao, M.; Chow, T.W.; Zhang, H.; Li, Y. Rolling fault diagnosis via robust semi-supervised model with capped L2,1-norm regularization. In Proceedings of the IEEE International Conference on Industrial Technology, Toronto, ON, Canada, 22–25 March 2017; pp. 1064–1069. [Google Scholar]
- Nie, F.; Wang, X.; Huang, H. Multiclass capped Lp-norm SVM for robust classifications. In Proceedings of the 32th AAAI Conference on Artificial Intelligence, Palo Alto, CA, USA, 4–9 February 2017. [Google Scholar]
- Ahmadi, J.; Doostparast, M.; Parsian, A. Estimation and prediction in a two-parameter exponential distribution based on k-record values under LINEX loss function. Commun.-Stat. Theory Methods 2005, 34, 795–805. [Google Scholar] [CrossRef]
- Pandey, B.N.; Dwividi, N.; Pulastya, B. Comparison between Bayesian and maximum likelihood estimation of the scale parameter in Weibull distribution with known shape under linex loss function. J. Sci. Res. 2011, 55, 163–172. [Google Scholar]
- Demar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–3. [Google Scholar]




| Datasets | Samples | Attributes | Datasets | Samples | Attributes |
|---|---|---|---|---|---|
| Australian | 690 | 14 | Spect | 267 | 45 |
| Pima | 768 | 8 | German | 1000 | 24 |
| Sonar | 198 | 60 | Vote | 432 | 16 |
| CMC | 1140 | 9 | codrna | 59,535 | 9 |
| SVM | LSSVM | C-SVM | NPSVM | Linex-SVM | TBSVM | Linex-TSVM | |
|---|---|---|---|---|---|---|---|
| Datasets | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) |
| Times (s) | Times (s) | Times (s) | Times (s) | Times (s) | Times (s) | Times (s) | |
| Australian | 82.06 ± 0.63 | 82.75 ± 1.52 | 83.24 ± 3.39 | 83.96 ± 2.53 | 83.68 ± 1.63 | 84.05 ± 1.14 | 84.12 ± 0.42 |
| 1.905 | 1.108 | 1.241 | 2.037 | 2.644 | 2.358 | 4.535 | |
| Vote | 89.52 ± 0.73 | 90.12 ± 1.17 | 93.62 ± 1.53 | 94.03 ± 1.87 | 94.29 ± 0.97 | 95.02 ± 1.34 | 95.24 ± 1.05 |
| 0.943 | 0.793 | 1.832 | 1.834 | 1.846 | 1.115 | 2.062 | |
| German | 70.60 ± 1.74 | 71.35 ± 0.21 | 72.11 ± 3.22 | 73.26 ± 1.26 | 73.20 ± 2.86 | 75.61 ± 0.87 | 75.85 ± 0.21 |
| 2.286 | 1.719 | 2.303 | 3.421 | 4.672 | 3.719 | 9.695 | |
| Spect | 78.08 ± 1.62 | 77.94 ± 1.53 | 79.42 ± 5.25 | 80.11 ± 0.41 | 80.52 ± 2.34 | 80.77 ± 1.09 | 82.12 ± 1.01 |
| 0.639 | 0.945 | 1.347 | 2.014 | 1.739 | 1.235 | 1.438 | |
| CMC | 55.13 ± 3.62 | 56.42 ± 2.79 | 57.52 ± 1.52 | 56.33 ± 3.15 | 57.17 ± 0.76 | 61.12 ± 5.71 | 60.97 ± 0.62 |
| 1.441 | 1.367 | 2.980 | 3.286 | 5.862 | 3.744 | 8.328 | |
| Pima | 73.42 ± 0.72 | 72.79 ± 1.24 | 74.21 ± 1.03 | 73.48 ± 1.64 | 74.63 ± 1.69 | 75.58 ± 0.66 | 75.79 ± 1.31 |
| 1.117 | 1.036 | 1.125 | 2.185 | 2.092 | 1.626 | 5.032 | |
| Sonar | 63.54 ± 2.54 | 63.62 ± 2.34 | 65.39 ± 0.69 | 64.13 ± 0.68 | 64.37 ± 1.42 | 65.63 ± 2.16 | 66.50 ± 0.68 |
| 0.350 | 0.137 | 0.659 | 0.517 | 0.813 | 0.534 | 0.913 | |
| codrna | 82.14 ± 1.73 | 80.01 ± 2.61 | 83.62 ± 0.11 | 85.43 ± 2.24 | 86.10 ± 0.62 | 85.43 ± 3.11 | 88.73 ± 3.40 |
| 50.947 | 43.400 | 49.203 | 51.229 | 70.562 | 66.548 | 59.914 |
| SVM | LSSVM | C-SVM | NPSVM | Linex-SVM | TBSVM | Linex-TSVM | |
|---|---|---|---|---|---|---|---|
| Datasets | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) |
| Times (s) | Times (s) | Times (s) | Times (s) | Times (s) | Times (s) | Times (s) | |
| Australian | 81.61 ± 0.82 | 81.51 ± 0.83 | 82.44 ± 2.60 | 81.27 ± 1.39 | 83.11 ± 1.45 | 83.61 ± 1.07 | 83.83 ± 0.31 |
| 1.866 | 1.154 | 1.346 | 1.302 | 2.842 | 2.775 | 4.279 | |
| Vote | 88.77 ± 0.63 | 89.25 ± 1.38 | 93.07 ± 1.63 | 93.60 ± 2.95 | 92.35 ± 1.68 | 93.27 ± 2.17 | 94.29 ± 1.01 |
| 1.193 | 0.810 | 1.893 | 1.027 | 1.088 | 1.607 | 2.034 | |
| German | 68.22 ± 0.89 | 69.15 ± 2.41 | 70.84 ± 2.41 | 74.30 ± 2.26 | 71.66 ± 2.50 | 73.14 ± 1.21 | 73.91 ± 0.82 |
| 2.876 | 2.274 | 2.507 | 2.460 | 4.339 | 3.105 | 9.148 | |
| Spect | 77.29 ± 1.87 | 77.91 ± 0.88 | 78.48 ± 3.57 | 78.51 ± 3.11 | 78.75 ± 1.35 | 79.06 ± 4.62 | 81.73 ± 0.94 |
| 1.519 | 0.988 | 1.830 | 1.616 | 1.613 | 1.012 | 1.910 | |
| CMC | 54.74 ± 3.30 | 53.20 ± 2.79 | 54.59 ± 2.24 | 58.03 ± 0.87 | 57.74 ± 1.17 | 59.91 ± 0.13 | 59.91 ± 0.75 |
| 1.441 | 1.367 | 2.980 | 4.339 | 5.862 | 3.744 | 8.215 | |
| Pima | 70.42 ± 0.72 | 71.79 ± 1.24 | 72.21 ± 1.03 | 71.82 ± 0.14 | 72.70 ± 1.69 | 73.92 ± 0.66 | 73.53 ± 1.31 |
| 1.535 | 1.239 | 1.599 | 3.700 | 2.272 | 1.803 | 5.118 | |
| Sonar | 62.93 ± 2.54 | 62.71 ± 2.34 | 63.06 ± 1.19 | 63.14 ± 3.01 | 63.27 ± 1.42 | 63.85 ± 1.13 | 64.50 ± 4.95 |
| 1.184 | 0.917 | 0.726 | 1.715 | 1.476 | 1.244 | 1.619 | |
| Codrna | 80.67 ± 2.67 | 81.44 ± 3.61 | 81.61 ± 1.02 | 82.35 ± 1.11 | 84.29 ± 0.90 | 86.77 ± 1.30 | 87.54 ± 0.34 |
| 54.302 | 46.169 | 50.495 | 62.376 | 55.482 | 61.517 | 58.455 |
| SVM | LSSVM | C-SVM | NPSVM | Linex-SVM | TBSVM | Linex-TSVM | |
|---|---|---|---|---|---|---|---|
| Datasets | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) | ACC ± S (%) |
| Times (s) | Times (s) | Times (s) | Times (s) | Times (s) | Times (s) | Times (s) | |
| Australian | 78.83 ± 1.27 | 78.75 ± 1.52 | 79.24 ± 3.39 | 79.14 ± 1.67 | 80.68 ± 1.63 | 82.05 ± 1.14 | 81.18 ± 3.74 |
| 1.365 | 1.233 | 1.490 | 1.910 | 2.076 | 2.851 | 4.648 | |
| Vote | 87.69 ± 1.07 | 88.05 ± 0.98 | 89.13 ± 1.39 | 88.28 ± 2.38 | 90.71 ± 0.88 | 91.01 ± 2.59 | 92.62 ± 3.37 |
| 1.053 | 0.928 | 1.634 | 1.667 | 2.069 | 1.942 | 2.143 | |
| German | 68.83 ± 1.21 | 68.04 ± 0.80 | 69.71 ± 2.36 | 70.35 ± 1.64 | 70.14 ± 2.84 | 69.79 ± 3.54 | 72.30 ± 0.99 |
| 2.922 | 2.421 | 2.665 | 5.196 | 4.904 | 3.454 | 8.615 | |
| Spect | 75.81 ± 1.17 | 75.93 ± 0.81 | 77.64 ± 1.53 | 76.04 ± 1.30 | 78.60 ± 2.09 | 80.19 ± 3.77 | 81.15 ± 3.06 |
| 0.703 | 0.914 | 0.998 | 1.632 | 1.143 | 1.447 | 1.519 | |
| CMC | 52.13 ± 3.62 | 53.42 ± 2.79 | 54.52 ± 1.52 | 54.86 ± 0.88 | 55.17 ± 0.76 | 56.91 ± 0.13 | 57.79 ± 3.50 |
| 2.951 | 2.566 | 3.291 | 5.157 | 4.017 | 4.521 | 8.693 | |
| Pima | 70.42 ± 0.72 | 71.79 ± 1.24 | 72.16 ± 1.03 | 73.25 ± 3.67 | 73.70 ± 1.69 | 72.43 ± 2.41 | 73.92 ± 0.93 |
| 1.785 | 1.355 | 1.936 | 1.902 | 2.084 | 2.741 | 5.375 | |
| Sonar | 60.24 ± 4.95 | 60.50 ± 0.36 | 61.73 ± 1.06 | 62.88 ± 2.78 | 62.99 ± 1.12 | 62.87 ± 0.94 | 63.25 ± 0.35 |
| 0.861 | 0.352 | 0.886 | 1.749 | 1.347 | 1.365 | 1.698 | |
| codrna | 79.14 ± 1.91 | 78.01 ± 2.76 | 79.65 ± 3.08 | 82.20 ± 5.29 | 83.52 ± 1.63 | 86.14 ± 2.30 | 86.87 ± 1.49 |
| 58.147 | 54.990 | 53.892 | 68.956 | 70.108 | 69.560 | 71.928 |
| SVM | LSSVM | C-SVM | NPSVM | Linex-SVM | TBSVM | Linex-TSVM | |
|---|---|---|---|---|---|---|---|
| Avg.ACC 0% | 74.31 | 74.38 | 76.14 | 76.34 | 76.76 | 77.90 | 78.67 |
| Avg.rank 0% | 6.63 | 6.25 | 4.38 | 4.25 | 3.38 | 2.00 | 1.13 |
| Avg.ACC 10% | 73.08 | 73.37 | 74.54 | 75.38 | 75.48 | 76.69 | 77.41 |
| Avg.rank 10% | 6.38 | 6.25 | 4.13 | 3.88 | 3.50 | 1.94 | 1.31 |
| Avg.ACC 25% | 71.64 | 71.81 | 72.97 | 73.38 | 74.44 | 75.17 | 76.14 |
| Avg.rank 25% | 6.63 | 6.38 | 4.63 | 4.00 | 2.88 | 2.38 | 1.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yu, G.; Ma, J. Capped Linex Metric Twin Support Vector Machine for Robust Classification. Sensors 2022, 22, 6583. https://doi.org/10.3390/s22176583
Wang Y, Yu G, Ma J. Capped Linex Metric Twin Support Vector Machine for Robust Classification. Sensors. 2022; 22(17):6583. https://doi.org/10.3390/s22176583
Chicago/Turabian StyleWang, Yifan, Guolin Yu, and Jun Ma. 2022. "Capped Linex Metric Twin Support Vector Machine for Robust Classification" Sensors 22, no. 17: 6583. https://doi.org/10.3390/s22176583
APA StyleWang, Y., Yu, G., & Ma, J. (2022). Capped Linex Metric Twin Support Vector Machine for Robust Classification. Sensors, 22(17), 6583. https://doi.org/10.3390/s22176583





