A Study of Optimizing Lamb Wave Acoustic Mass Sensors’ Performance through Adjustment of the Transduction Electrode Metallization Ratio
Abstract
:1. Introduction
2. Theoretical Background
3. System Overview and Simulation Methodology
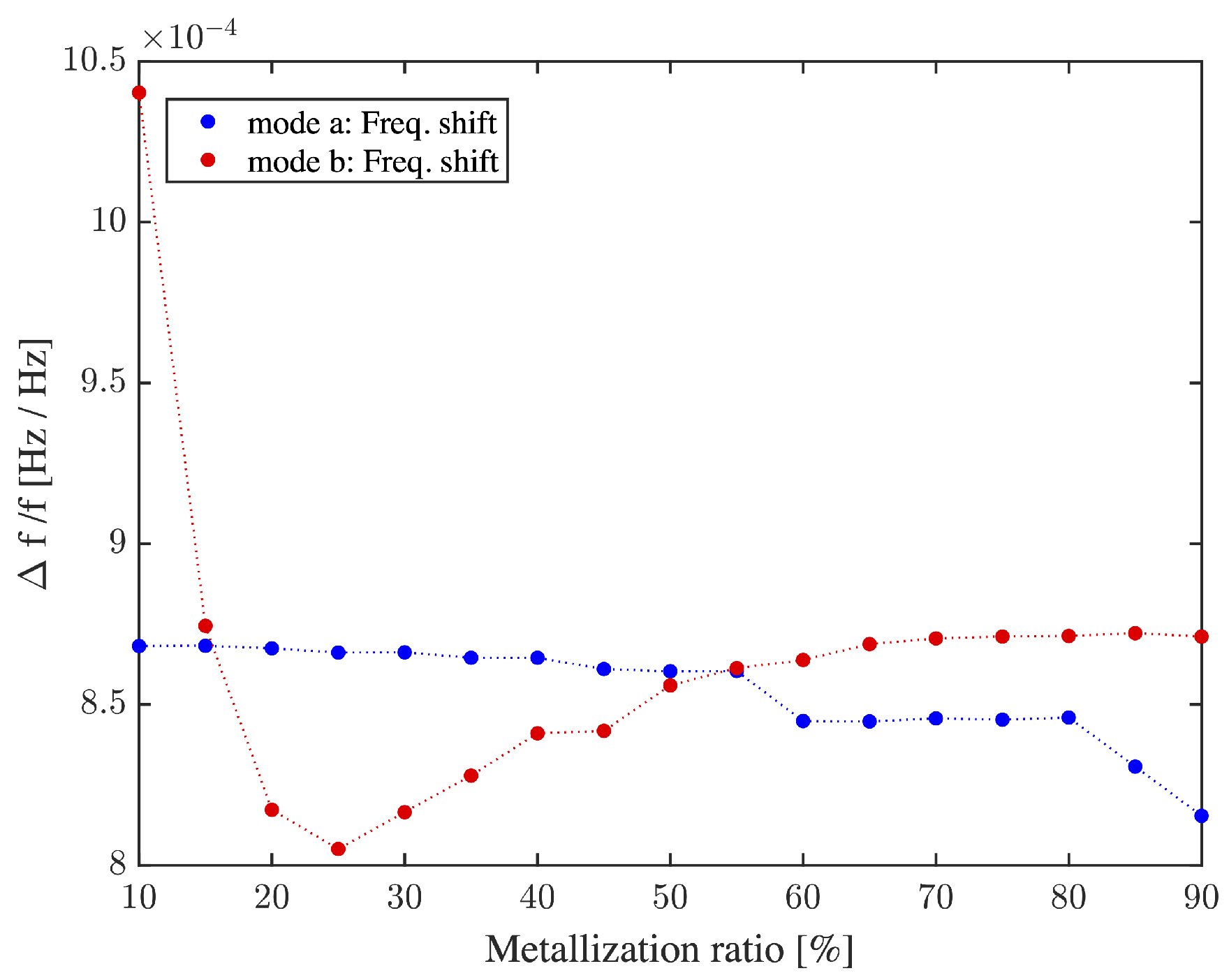
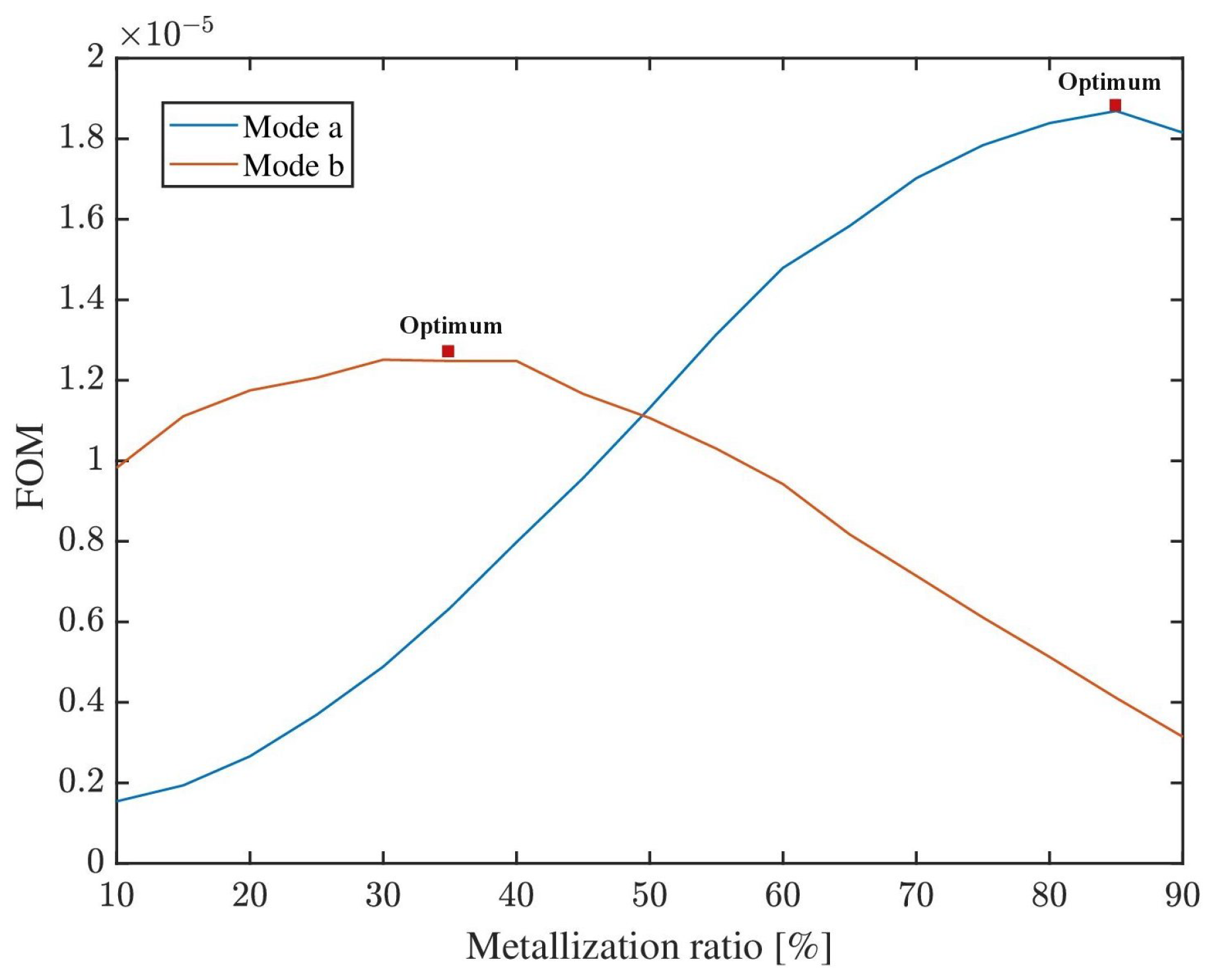
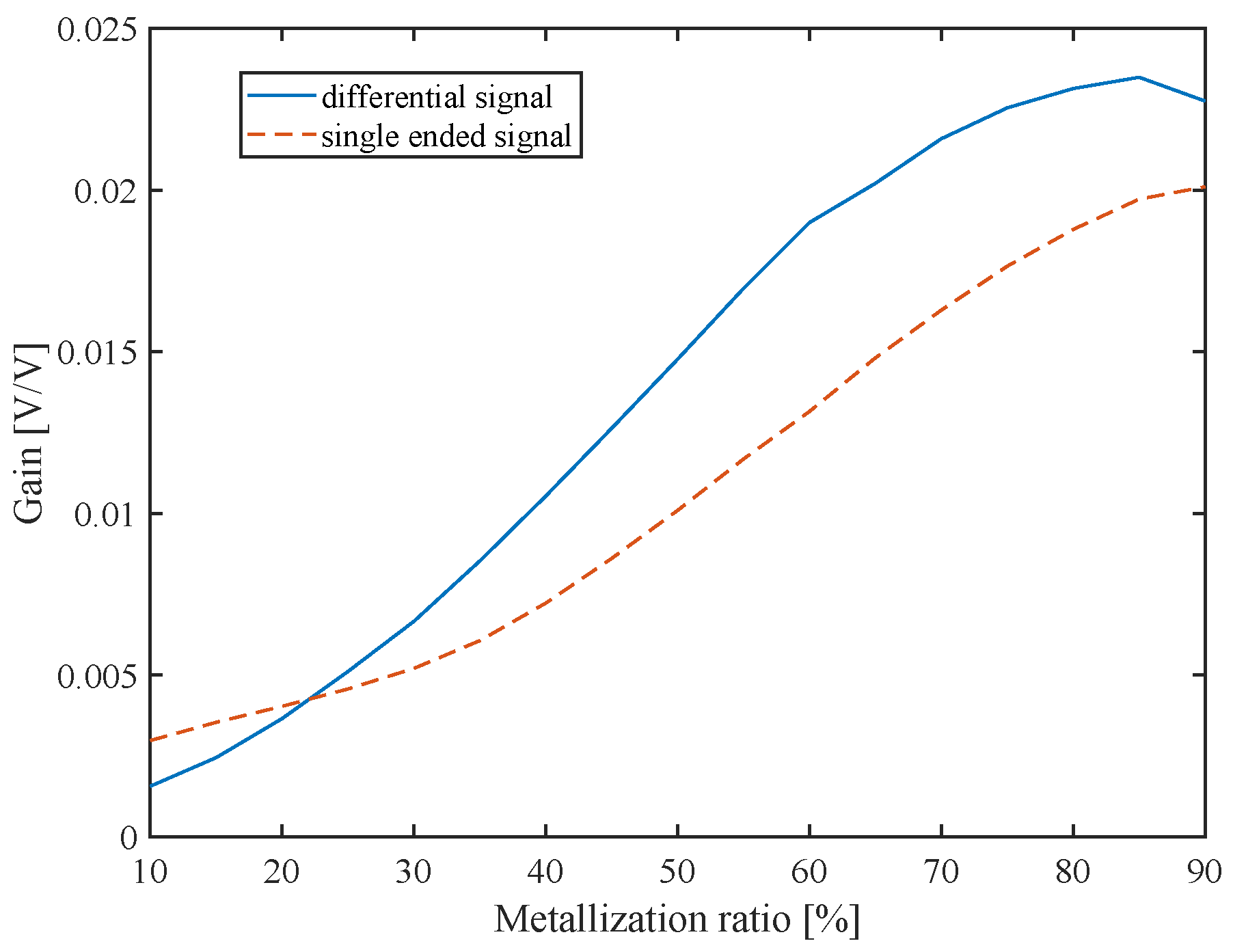
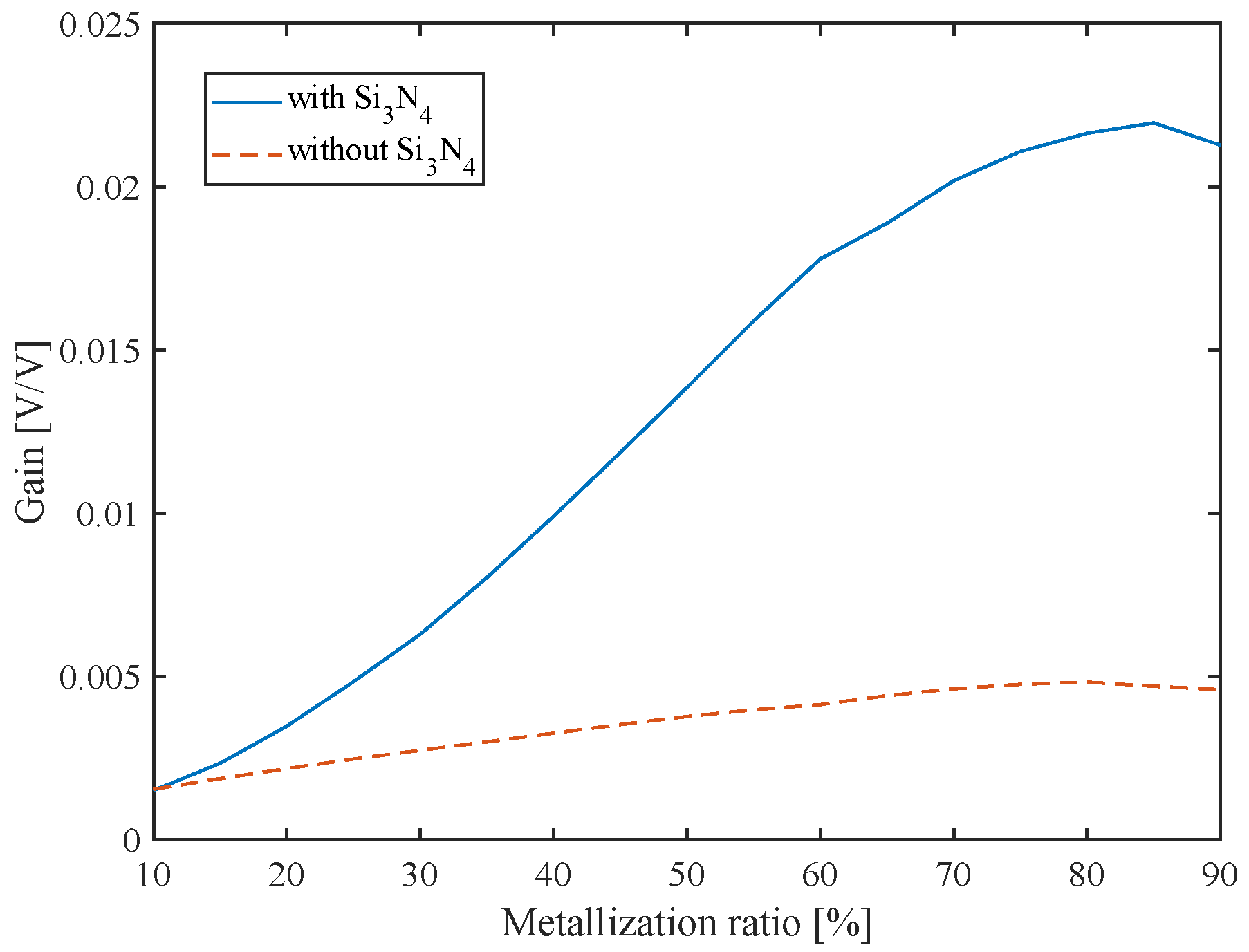
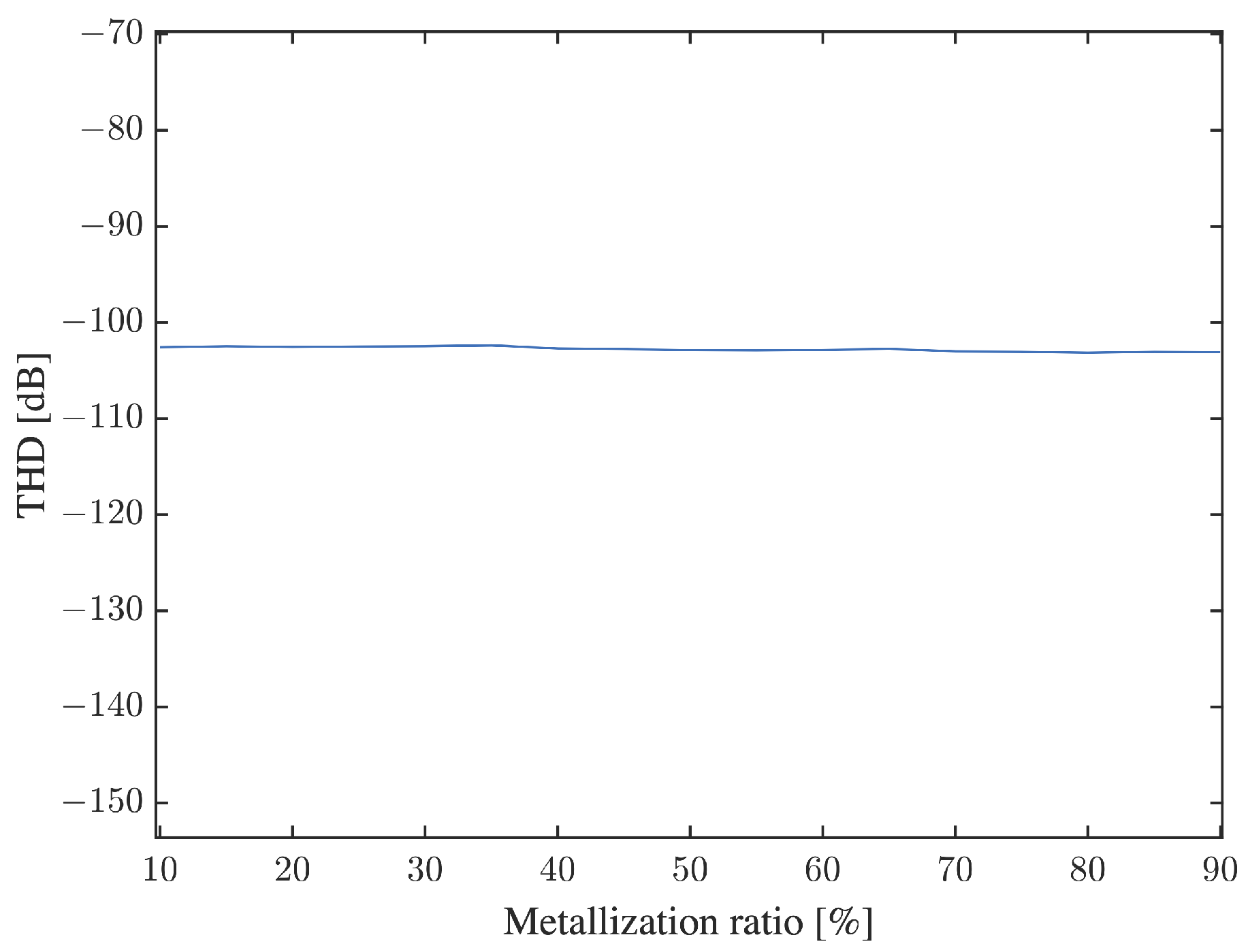
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, H.S.; Chung, G.S. Surface acoustic wave humidity sensor based on polycrystalline AlN thin film coated with sol-gel derived nanocrystalline zinc oxide film. Sens. Actuators Chem. 2010, 148, 347–352. [Google Scholar] [CrossRef]
- Lee, C.Y.; Shen, C.C.; Lee, S.J.; Chiu, C.W.; Lin, H.T. Real-time microscopic monitoring of temperature and strain on the surface of magnesium hydrogen storage tank by high temperature resistant flexible integrated microsensor. Int. J. Hydrogen. Energy 2022, 47, 12815–12821. [Google Scholar] [CrossRef]
- Piro, L.; Lamanna, L.; Guido, F.; Balena, A.; Mariello, M.; Rizzi, F.; De Vittorio, M. Flexible SAW Microfluidic Devices as Wearable pH Sensors Based on ZnO Nanoparticles. Nanomaterials 2021, 11, 1479. [Google Scholar] [CrossRef]
- Choujaa, A.; Tirole, N.; Bonjour, C.; Martin, G.; Hauden, D.; Blind, P.; Cachard, A.; Pommier, C. AlN/silicon Lamb-wave microsensors for pressure and gravimetric measurements. Sens. Actuators Phys. 1995, 46, 179–182. [Google Scholar] [CrossRef]
- Zhan, G.; Wang, W.; Sun, H.; Hou, Y.; Feng, L. Auto-CSC: A Transfer Learning Based Automatic Cell Segmentation and Count Framework. Cyborg Bionic Syst. 2022, 2022, 9842349. [Google Scholar] [CrossRef]
- Sakaguchi, K.; Akimoto, K.; Takaira, M.; Tanaka, R.i.; Shimizu, T.; Umezu, S. Cell-Based Microfluidic Device Utilizing Cell Sheet Technology. Cyborg Bionic Syst. 2022, 2022, 9758187. [Google Scholar] [CrossRef]
- Oda, H.; Kihara, K.; Morimoto, Y.; Takeuchi, S. Cell-based biohybrid sensor device for chemical source direction estimation. Cyborg Bionic Syst. 2021, 2021, 8907148. [Google Scholar] [CrossRef]
- Akiyama, Y. Design of temperature-responsive cell culture surfaces for cell sheet engineering. Cyborg Bionic Syst. 2021, 2021, 5738457. [Google Scholar] [CrossRef]
- Fu, Y.; Luo, J.; Nguyen, N.; Walton, A.; Flewitt, A.; Zu, X.; Li, Y.; McHale, G.; Matthews, A.; Iborra, E.; et al. Advances in piezoelectric thin films for acoustic biosensors, acoustofluidics and lab-on-chip applications. Prog. Mater. Sci. 2017, 89, 31–91. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Wei, X.; Xue, Y.; Wan, H.; Wang, P. Recent advances in acoustic wave biosensors for the detection of disease-related biomarkers: A review. Anal. Chim. Acta 2021, 1164, 338321. [Google Scholar] [CrossRef]
- Chang, H.W.; Shih, J.S. Surface acoustic wave immunosensors based on immobilized C60-proteins. Sens. Actuators B Chem. 2007, 121, 522–529. [Google Scholar] [CrossRef]
- Luo, J.; Luo, P.; Xie, M.; Du, K.; Zhao, B.; Pan, F.; Fan, P.; Zeng, F.; Zhang, D.; Zheng, Z.; et al. A new type of glucose biosensor based on surface acoustic wave resonator using Mn-doped ZnO multilayer structure. Biosens. Bioelectron. 2013, 49, 512–518. [Google Scholar] [CrossRef] [PubMed]
- Trivedi, S.; Nemade, H.B. Finite element simulation of Love wave resonator for DNA detection. Int. J. Adv. Eng. Sci. Appl. Math. 2015, 7, 210–218. [Google Scholar] [CrossRef]
- Tigli, O.; Bivona, L.; Berg, P.; Zaghloul, M. Fabrication and Characterization of a Surface-Acoustic-Wave Biosensor in CMOS Technology for Cancer Biomarker Detection. Biomed. Circuits Syst. IEEE Trans. 2010, 4, 62–73. [Google Scholar] [CrossRef]
- Tamarin, O.; Rube, M.; Lachaud, J.L.; Raimbault, V.; Rebière, D.; Dejous, C. Mobile Acoustic Wave Platform Deployment in the Amazon River: Impact of the Water Sample on the Love Wave Sensor Response. Sensors 2020, 20, 72. [Google Scholar] [CrossRef]
- Storey, M.V.; Van der Gaag, B.; Burns, B.P. Advances in on-line drinking water quality monitoring and early warning systems. Water Res. 2011, 45, 741–747. [Google Scholar] [CrossRef] [PubMed]
- Pohanka, M. Overview of Piezoelectric Biosensors, Immunosensors and DNA Sensors and Their Applications. Materials 2018, 11, 448. [Google Scholar] [CrossRef] [PubMed]
- Hossain, M.Z.; Shimizu, N. Covalent Immobilization of Gold Nanoparticles on Graphene. J. Phys. Chem. C 2019, 123, 3512–3516. [Google Scholar] [CrossRef]
- Huang, Y.; Kannan, P.; Zhang, L.; Chen, T.; Kim, D.H. Concave gold nanoparticle-based highly sensitive electrochemical IgG immunobiosensor for the detection of antibody–antigen interactions. RSC Adv. 2015, 5, 58478–58484. [Google Scholar] [CrossRef]
- Tang, D.; Yuan, R.; Chai, Y.; Zhong, X.; Liu, Y.; Dai, J.; Zhang, L. Novel potentiometric immunosensor for hepatitis B surface antigen using a gold nanoparticle-based biomolecular immobilization method. Anal. Biochem. 2004, 333, 345–350. [Google Scholar] [CrossRef]
- Pantazis, A.K.; Konstantinidis, G.; Gizeli, E. Characterization of a GaN Lamb-Wave Sensor for Liquid-Based Mass Sensing Applications. IEEE Sens. J. 2014, 14, 908–911. [Google Scholar] [CrossRef]
- Aslam, M.Z.; Jeoti, V.; Manzoor, S.; Hanif, M.; Junaid, M. An aluminium nitride based multilayer structure for Love mode surface acoustic wave devices. Semicond. Sci. Technol. 2020, 35, 115007. [Google Scholar] [CrossRef]
- Fu, Y.; Luo, J.; Du, X.; Flewitt, A.; Li, Y.; Markx, G.; Walton, A.; Milne, W. Recent developments on ZnO films for acoustic wave based bio-sensing and microfluidic applications: A review. Sens. Actuators B Chem. 2010, 143, 606–619. [Google Scholar] [CrossRef]
- Skinner, J.; Cardinale, G.; Talin, A.; Brocato, R. Effect of critical dimension variation on SAW correlator energy. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 497–501. [Google Scholar] [CrossRef]
- Kuznetsova, I.; Smirnov, A.; Plekhanova, Y.V.; Reshetilov, A.; Wang, G.J. Effect of the Aperture of an Interdigital Transducer on the Characteristics of Its Output Signal in a Piezoelectric Plate. Bull. Russ. Acad. Sci. Phys. 2020, 84, 644–647. [Google Scholar] [CrossRef]
- Zou, J.; Lin, C.M.; Lam, C.S.; Pisano, A.P. Transducer design for AlN Lamb wave resonators. J. Appl. Phys. 2017, 121, 154502. [Google Scholar] [CrossRef]
- Caliendo, C.; Hamidullah, M. Guided acoustic wave sensors for liquid environments. J. Phys. D Appl. Phys. 2019, 52, 153001. [Google Scholar] [CrossRef]
- Wenzel, S.; White, R. A multisensor employing an ultrasonic Lamb-wave oscillator. IEEE Trans. Electron Devices 1988, 35, 735–743. [Google Scholar] [CrossRef]
- Kong, H.; Li, C.; Guo, Z.; Zhang, W.; Yao, J.; Zhu, H.; Yan, R.; Wang, L.; Li, J.; Wei, W.; et al. Sensitivity improved with Parylene-C passivized on Lamb wave sensor for aPTT measurement through monitoring whole blood reaction. Sens. Actuators B Chem. 2019, 285, 479–486. [Google Scholar] [CrossRef]
- Nam, J.; Jang, W.S.; Kim, J.; Lee, H.; Lim, C.S. Lamb wave-based molecular diagnosis using DNA hydrogel formation by rolling circle amplification (RCA) process. Biosens. Bioelectron. 2019, 142, 111496. [Google Scholar] [CrossRef]
- Kuznetsova, I.E.; Anisimkin, V.I.; Gubin, S.P.; Tkachev, S.V.; Kolesov, V.V.; Kashin, V.V.; Zaitsev, B.D.; Shikhabudinov, A.M.; Verona, E.; Sun, S. Super high sensitive plate acoustic wave humidity sensor based on graphene oxide film. Ultrasonics 2017, 81, 135–139. [Google Scholar] [CrossRef] [PubMed]
- Yule, L.; Zaghari, B.; Harris, N.; Hill, M. Modelling and validation of a guided acoustic wave temperature monitoring system. Sensors 2021, 21, 7390. [Google Scholar] [CrossRef]
- Caliendo, C.; Hamidullah, M. Pressure sensing with zero group velocity lamb modes in self-supported a-SiC/c-ZnO membranes. J. Phys. D Appl. Phys. 2018, 51, 385102. [Google Scholar] [CrossRef]
- Salim, Z.T.; Hashim, U.; Arshad, M.; Fakhri, M.A.; Salim, E.T. Frequency-based detection of female Aedes mosquito using surface acoustic wave technology: Early prevention of dengue fever. Microelectron. Eng. 2017, 179, 83–90. [Google Scholar] [CrossRef]
- Zhang, F.; Li, S.; Cao, K.; Wang, P.; Su, Y.; Zhu, X.; Wan, Y. A Microfluidic Love-Wave Biosensing Device for PSA Detection Based on an Aptamer Beacon Probe. Sensors 2015, 15, 13839–13850. [Google Scholar] [CrossRef]
- Kishor, R.; Gao, F.; Sreejith, S.; Feng, X.; Seah, Y.P.; Wang, Z.; Stuparu, M.C.; Lim, T.T.; Chen, X.; Zheng, Y. Photoacoustic induced surface acoustic wave sensor for concurrent opto-mechanical microfluidic sensing of dyes and plasmonic nanoparticles. RSC Adv. 2016, 6, 50238–50244. [Google Scholar] [CrossRef]
- Duhamel, R.; Robert, L.; Jia, H.; Li, F.; Lardet-Vieudrin, F.; Manceau, J.F.; Bastien, F. Sensitivity of a Lamb wave sensor with 2 μm AlN membrane. Ultrasonics 2006, 44, e893–e897. [Google Scholar] [CrossRef]
- Zamora, I.; Ledesma, E.; Uranga, A.; Barniol, N. Monolithic Single PMUT-on-CMOS Ultrasound System With +17 dB SNR for Imaging Applications. IEEE Access 2020, 8, 142785–142794. [Google Scholar] [CrossRef]
- Malik, A.F.; Jeoti, V.; Fawzy, M.; Iqbal, A.; Aslam, Z.; Pandian, M.S.; Marigo, E. Estimation of SAW velocity and coupling coefficient in multilayered piezo-substrates AlN/SiO2/Si. In Proceedings of the 2016 6th International Conference on Intelligent and Advanced Systems (ICIAS), Kuala Lumpur, Malaysia, 15–17 August 2016; pp. 1–5. [Google Scholar]
- Wingqvist, G.; Arapan, L.; Yantchev, V.; Katardjiev, I. A micromachined thermally compensated thin film Lamb wave resonator for frequency control and sensing applications. J. Micromech. Microeng. 2009, 19, 035018. [Google Scholar] [CrossRef]
- Wu, J.; Zhu, Z. Sensitivity of Lamb wave sensors in liquid sensing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 71–72. [Google Scholar]
- Pantazis, A.K.; Gizeli, E.; Konstantinidis, G. A high frequency GaN Lamb-wave sensor device. Appl. Phys. Lett. 2010, 96, 194103. [Google Scholar] [CrossRef]
- Han, K.; Yuan, Y.J. Mass Sensitivity Evaluation and Device Design of a LOVE Wave Device for Bond Rupture Biosensors Using the Finite Element Method. IEEE Sens. J. 2014, 14, 2601–2608. [Google Scholar] [CrossRef]
- Yantchev, V.; Katardjiev, I. Thin film Lamb wave resonators in frequency control and sensing applications: A review. J. Micromech. Microeng. 2013, 23, 043001. [Google Scholar] [CrossRef]
- Viktrov, I. Rayleigh and Lamb Waves: Physical Theory and Applications; Springer: New York, NY, USA, 1967; Chapter II. [Google Scholar]
- Lin, C.M.; Yantchev, V.; Zou, J.; Chen, Y.Y.; Pisano, A.P. Micromachined One-Port Aluminum Nitride Lamb Wave Resonators Utilizing the Lowest-Order Symmetric Mode. J. Microelectromech. Syst. 2014, 23, 78–91. [Google Scholar] [CrossRef]
- Wohltjen, H. Mechanism of operation and design considerations for surface acoustic wave device vapour sensors. Sens. Actuators 1984, 5, 307–325. [Google Scholar] [CrossRef]
- Nakamura, H.; Nakanishi, H.; Tsurunari, T.; Matsunami, K.; Iwasaki, Y. 6E-1 A Small-Sized SAW Duplexer on a SiO2/IDT/LiNbO3 Structure for Wideband CDMA Application. In Proceedings of the 2007 IEEE Ultrasonics Symposium Proceedings, New York, NY, USA, 28–31 October 2007; pp. 488–491. [Google Scholar]
- Caliendo, C.; Giovine, E.; Hamidullah, M. Design and fabrication of zero-group-velocity Lamb wave resonator onto silicon nitride/aluminum nitride suspended membrane. AIP Conf. Proc. 2018, 1990, 020013. [Google Scholar]
- Dieulesaint, E.; Royer, D. Elastic Waves in Solids: Applications to Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Awai, I.; Zhang, Y. Overlap integral calculation of resonator coupling. In Proceedings of the 2006 12th International Symposium on Antenna Technology and Applied Electromagnetics and Canadian Radio Sciences Conference, Montreal, QC, Canada, 17–19 July 2006; pp. 1–4. [Google Scholar]
- Davis, B.; Dulbecco, R.; Eiser, H.; Ginsberg, H. Microbiology: Including Immunology and Molecular Genetics, Harper and Row; Harper & Row: Manhattan, NY, USA, 1980; p. 19802. [Google Scholar]
- Zou, J.; Lin, C.M.; Gao, A.; Pisano, A.P. The Multi-Mode Resonance in AlN Lamb Wave Resonators. J. Microelectromech. Syst. 2018, 27, 973–984. [Google Scholar] [CrossRef]
- Weser, R.; Winkler, A.; Weihnacht, M.; Menzel, S.; Schmidt, H. The complexity of surface acoustic wave fields used for microfluidic applications. Ultrasonics 2020, 106, 106160. [Google Scholar] [CrossRef]
- Wang, Z.; Cheeke, J.D.N.; Jen, C.K. Sensitivity analysis for Love mode acoustic gravimetric sensors. Appl. Phys. Lett. 1994, 64, 2940–2942. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Z. Design and Fabrication of ZnO-Based SAW Sensor Using Low Power Homo-Buffer Layer for Enhanced Humidity Sensing. IEEE Sens. J. 2021, 21, 7428–7433. [Google Scholar] [CrossRef]
- Powell, D.A.; Kalantar-zadeh, K.; Wlodarski, W. Numerical calculation of SAW sensitivity: Application to ZnO/LiTaO3 transducers. Sens. Actuators A Phys. 2004, 115, 456–461. [Google Scholar] [CrossRef]
- Lan, J.W.; Huang, I.Y.; Lin, Y.C.; Lin, C.Y.; Chen, J.L.; Hsieh, C.H. Development of an FPW Biosensor with Low Insertion Loss and High Fabrication Yield for Detection of Carcinoembryonic Antigen. Sensors 2016, 16, 1729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reusch, M.; Holc, K.; Lebedev, V.; Kurz, N.; Žukauskaitė, A.; Ambacher, O. Temperature Cross-Sensitivity of AlN-Based Flexural Plate Wave Sensors. IEEE Sens. J. 2018, 18, 7810–7818. [Google Scholar] [CrossRef]
- Liu, M.; Li, J.; Ma, J.; Wang, C. Design and fabrication of a MEMS Lamb wave device based on ZnO thin film. J. Semicond. 2011, 32, 044006. [Google Scholar] [CrossRef]
- Li, F.; Wu, Y.H.; Manceau, J.F.; Bastien, F. Multi-parameter sensing in liquid using a lamb wave based microsensor. In Proceedings of the 2008 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications, Nanjing, China, 5–8 December 2008; pp. 320–323. [Google Scholar]
- Lu, X.; Lee, C.M.; Wu, S.Y.; Ho, H.P.; Lau, K.M. GaN-Based S0-Wave Sensors on Silicon for Chemical and Biological Sensing in Liquid Environments. IEEE Sens. J. 2013, 13, 1245–1251. [Google Scholar] [CrossRef]
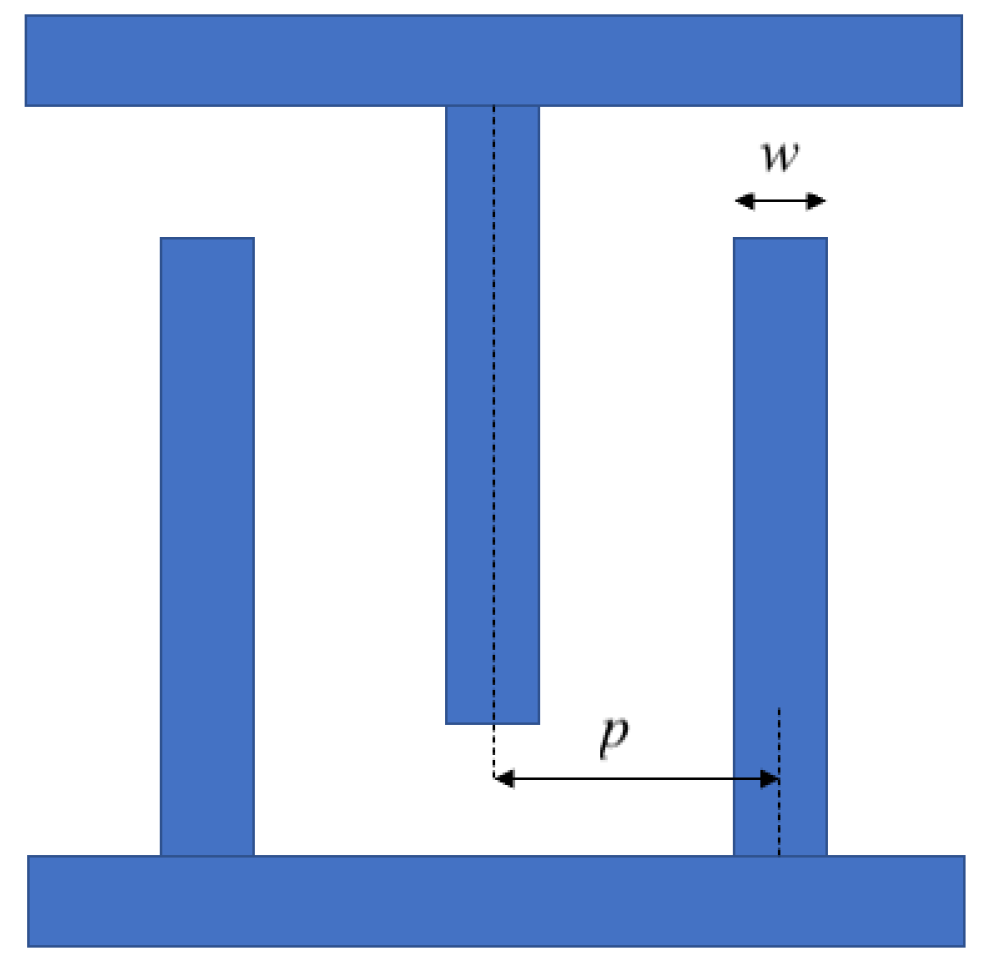
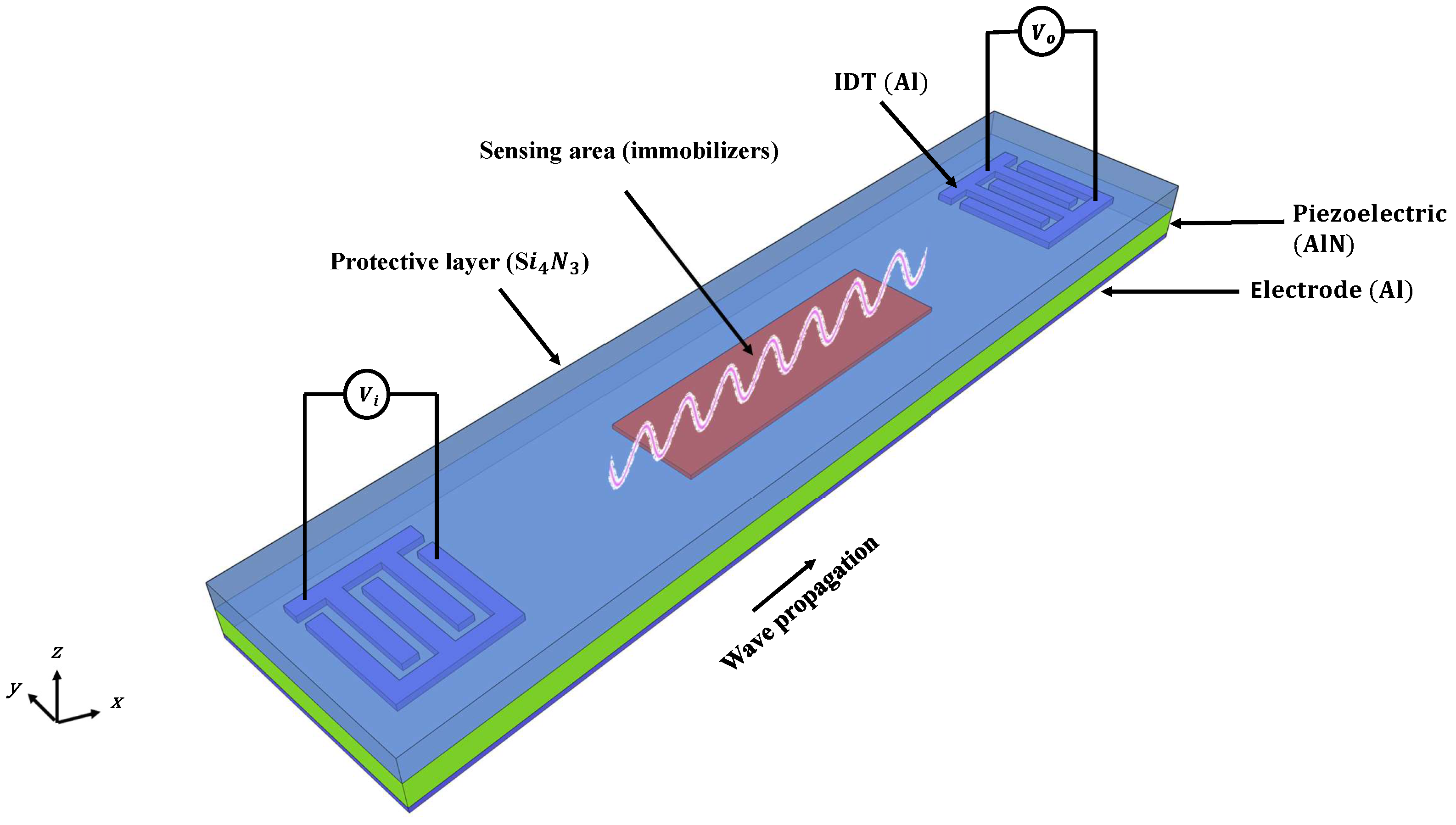
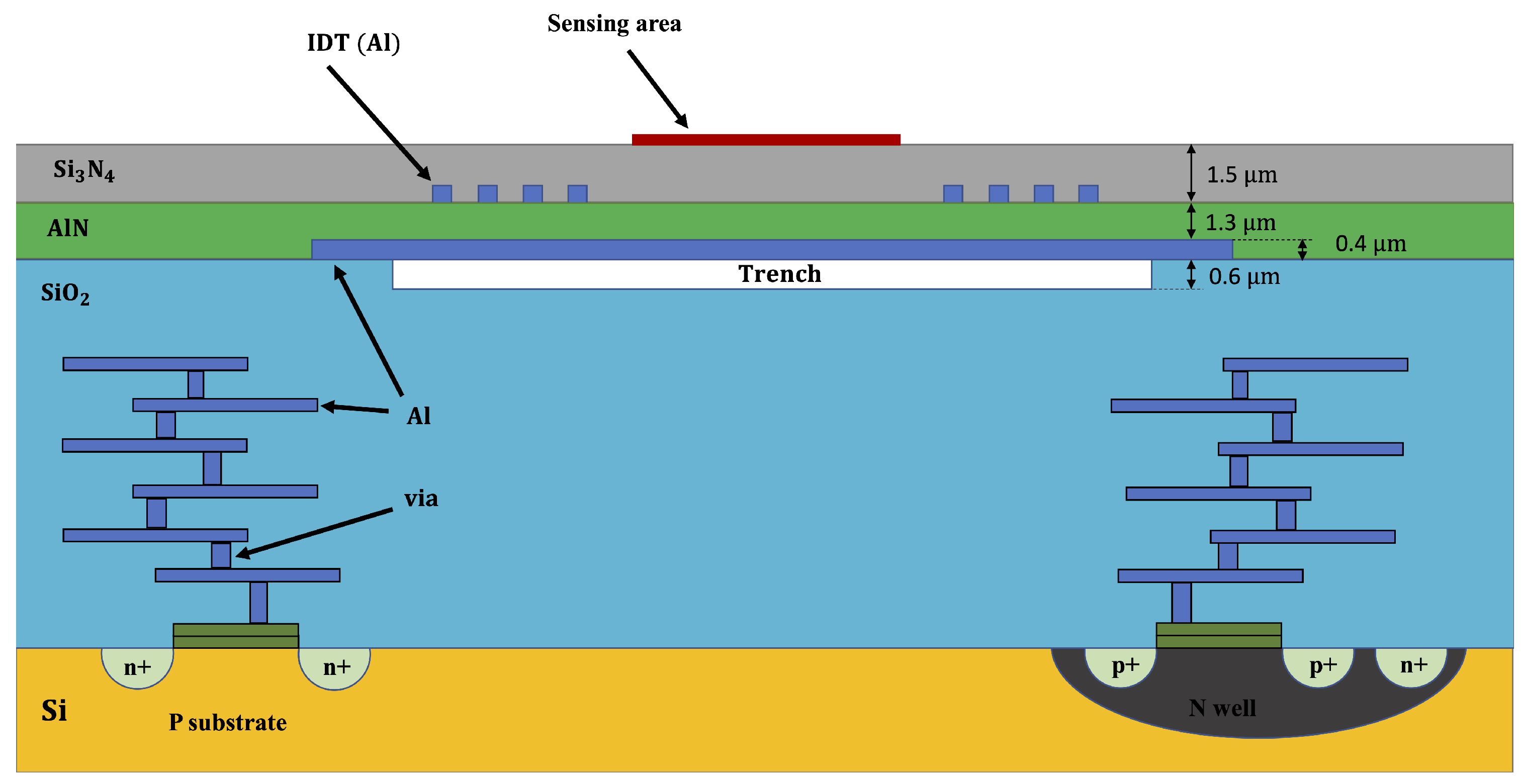


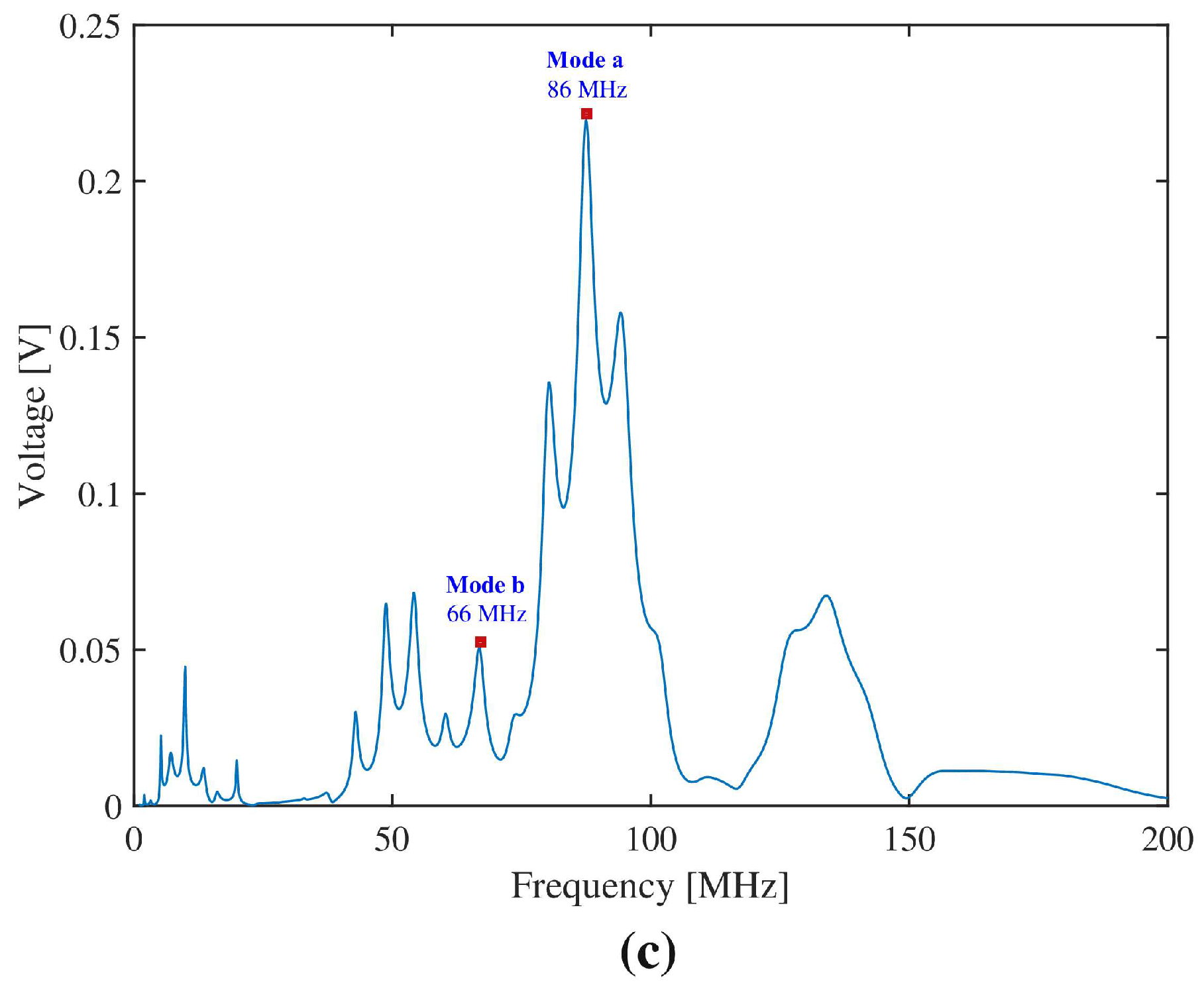





| Symbol | AlN | Unit | |
|---|---|---|---|
| Stiffness constants | 345 | [N/m] | |
| 125 | |||
| 120 | |||
| 395 | |||
| 118 | |||
| 110 | |||
| Dielectric constants | 8.0 | [F/N] | |
| 9.5 | |||
| Piezo constants | −0.48 | [C/m] | |
| −0.58 | |||
| 1.55 | |||
| Mass density | 3260 | [Kg/m] |
| Biosensor Type | [cm/g] | IL [dB] | FOM (/IL) | Piezoelectric Material | Reference |
|---|---|---|---|---|---|
| SAW | 2.6–121.7 | 25–55 | 1.196 | ZnO | [56] |
| SAW | - | 52.5–53.25 | - | ZnO/quartz | [56] |
| SAW | 70 | - | - | ZnO/LiTaO3 | [57] |
| FPW | 60.16–70.06 | 36.04 | 1.944 | ZnO | [58] |
| LW | 160–240 | - | - | AlN | [59] |
| LW | 91.65 | 18.53 | 4.946 | ZnO | [60] |
| LW(A0) | 175.8 | 45 | 3.907 | AlN | [61] |
| LW(A0 & S0) | 174–272 | 20–38 | 13.6 | GaN | [62] |
| LW (Min IL) | 114 | 26.74 | 4.263 | AlN | This work |
| LW (Max ) | 140 | 66.02 | 2.12 | AlN | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholami, F.; Shih, A.; Robichaud, A.; Cicek, P.-V. A Study of Optimizing Lamb Wave Acoustic Mass Sensors’ Performance through Adjustment of the Transduction Electrode Metallization Ratio. Sensors 2022, 22, 6428. https://doi.org/10.3390/s22176428
Gholami F, Shih A, Robichaud A, Cicek P-V. A Study of Optimizing Lamb Wave Acoustic Mass Sensors’ Performance through Adjustment of the Transduction Electrode Metallization Ratio. Sensors. 2022; 22(17):6428. https://doi.org/10.3390/s22176428
Chicago/Turabian StyleGholami, Fatemeh, Andy Shih, Alexandre Robichaud, and Paul-Vahe Cicek. 2022. "A Study of Optimizing Lamb Wave Acoustic Mass Sensors’ Performance through Adjustment of the Transduction Electrode Metallization Ratio" Sensors 22, no. 17: 6428. https://doi.org/10.3390/s22176428
APA StyleGholami, F., Shih, A., Robichaud, A., & Cicek, P.-V. (2022). A Study of Optimizing Lamb Wave Acoustic Mass Sensors’ Performance through Adjustment of the Transduction Electrode Metallization Ratio. Sensors, 22(17), 6428. https://doi.org/10.3390/s22176428







