Fault Identification in Membrane Structures Using the Hilbert Transforms
Abstract
:1. Introduction
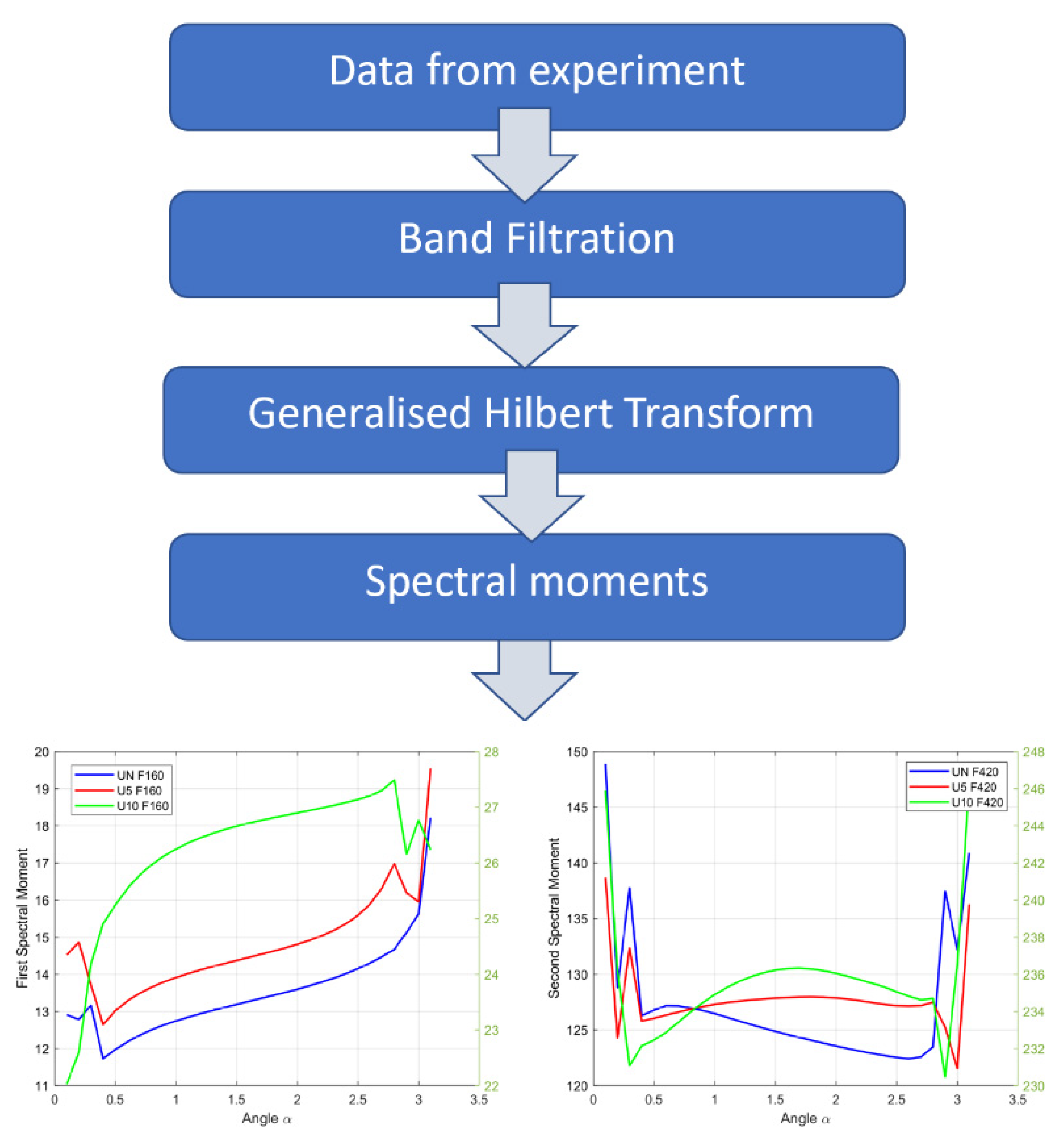
2. Presentation of the Hilbert Transforms and Spectral Moments
2.1. Classical Hilbert Transform
2.2. The Generalized Hilbert Transform
2.3. The Fractional Hilbert Transform
2.4. Spectral Moments
3. The Membrane Structures and the Experimental Setup
3.1. Membrane Structures
3.2. Test Stand
4. Application of the Transforms and Spectral Moments to the Experimental Data
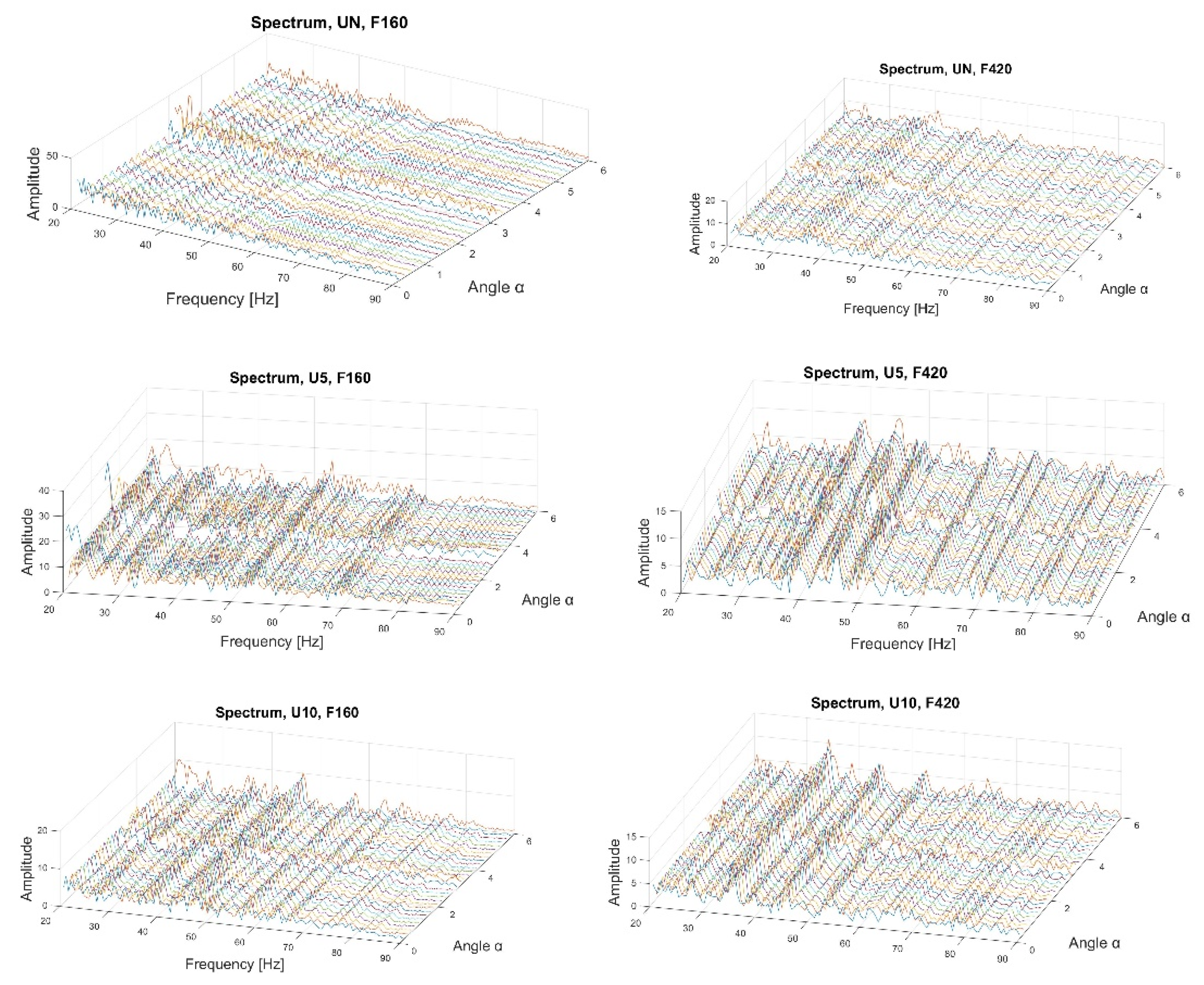
4.1. Applications of the Fractional Hilbert Transform
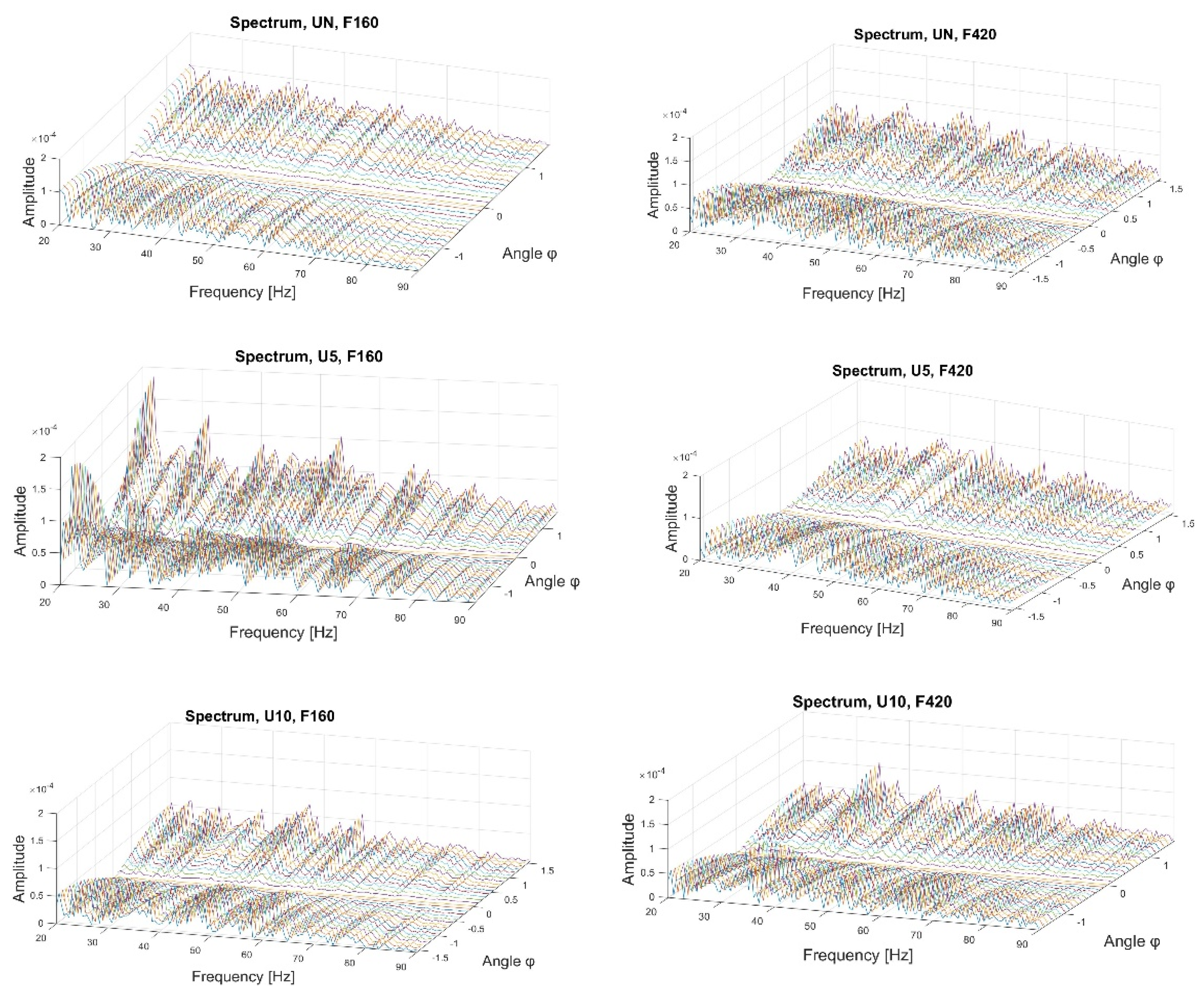
4.2. Application of the Generalized Hilbert Transform
4.3. Application of Spectral Moments with the Fractional Hilbert Transform
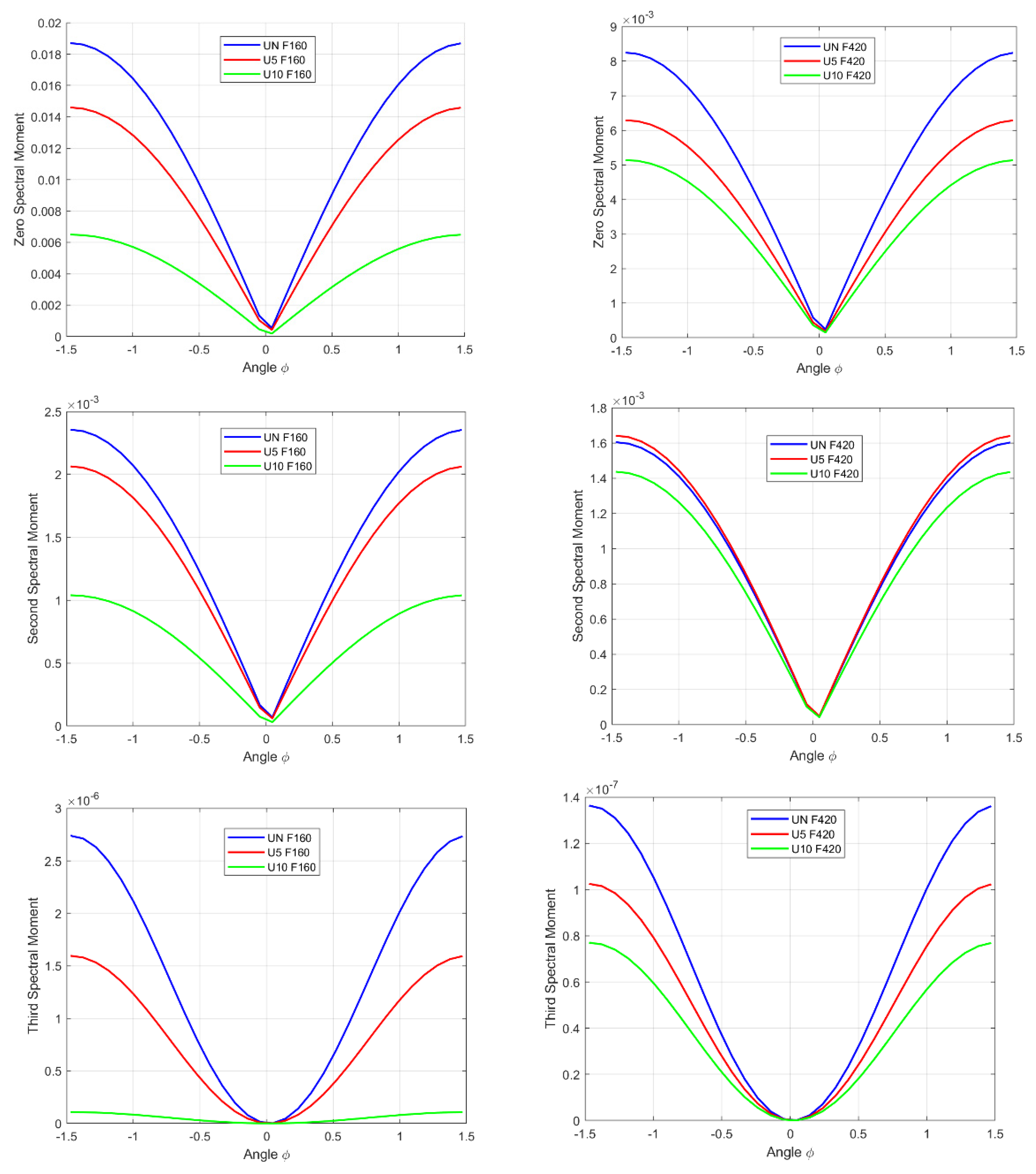
4.4. Application of Spectral Moments with the Generalized Hilbert Transform
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Radkowski, S.; Jasinski, M. Use of condition monitoring in the proactive maintenance strategy. In Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Lei, Y. Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery; W. Butterworth-Heinemann: Amsterdam, The Netherlands, 2017; ISBN 9780128115350. [Google Scholar]
- Dybała, J. Vibrodiagnostics of gearboxes using NBV-based classifier: A pattern recognition approach. Mech. Syst. Signal Process. 2013, 38, 5–22. [Google Scholar] [CrossRef]
- Gryllias, K.; Moschini, S.; Antoni, J. Application of Cyclo-Non-Stationary Indicators for Bearing Monitoring under Varying Operating Conditions. J. Eng. Gas Turbines Power 2018, 140, 012501. [Google Scholar] [CrossRef]
- Mączak, J. Local meshing plane analysis as a source of information about the gear quality. Mech. Syst. Signal Process. 2013, 38, 154–164. [Google Scholar] [CrossRef]
- Gałęzia, A. Teager-Kaiser energetic trajectory for machine diagnosis purposes. J. Vibroeng. 2017, 19, 1014–1025. [Google Scholar] [CrossRef]
- Gałęzia, A.; Gumiński, R.; Jasiński, M.; Mączak, J. Application of energy operators for detection of failures in gearboxes. Mech. Res. Commun. 2017, 82, 3–8. [Google Scholar] [CrossRef]
- Radkowski, S.; Gontarz, S. Diagnostic Model of Hysteresis for Condition Monitoring of Large Construction Structures; W. Lecture Notes in Mechanical Engineering: Hong Kong, China, 2015; pp. 611–623. [Google Scholar]
- Orłowska, A.; Kołakowski, P.; Holnicki-Szulc, J. Detecting delamination zones in composites by embedded electrical grid and thermographic methods. Smart Mater. Struct. 2011, 20, 105009. [Google Scholar] [CrossRef]
- Gałęzia, A. Utilization of components of signals from high frequency range in condition monitoring of bearings. Diagnostyka 2010, 3, 35–44. [Google Scholar]
- Gontarz, S.; Szulim, P.; Seńko, J.; Dybała, J. Use of magnetic monitoring of vehicles for proactive strategy development. Transp. Res. Part C Emerg. Technol. 2015, 52, 102–115. [Google Scholar] [CrossRef]
- Radkowski, S.; Guminski, R. Impact of vibroacoustic diagnostics on certainty of reliability assessment. In Engineering Asset Lifecycle Management, Proceedings of the 4th World Congress on Engineering Asset Management (WCEAM 2009), Athens, Greece, 28–30 September 2009; Springer: Cham, Switzerland, 2009; pp. 574–582. [Google Scholar]
- Gontarz, S.; Mączak, J.; Szulim, P. Online monitoring of steel constructions using passive methods. In Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2015; Volume 19, pp. 625–635. [Google Scholar] [CrossRef]
- Gontarz, S.; Gumiński, R. The use of magnetic phenomena and Bayesian updating in the risk assessment of structural damage. In Mathematical and Numerical Approaches; Awrejcewicz, J., Kaźmierczak, M., Mrozowski, J., Olejnik, P., Eds.; Wydawnictwo Politechniki Łódzkiej: Łódź, Poland, 2015; pp. 223–234. [Google Scholar]
- Sofer, M.; Cienciala, J.; Fusek, M.; Pavlicek, P.; Moravec, R. Damage Analysis of Composite CFRP Tubes Using Acoustic Emission Monitoring and Pattern Recognition Approach. Materials 2021, 14, 786. [Google Scholar] [CrossRef] [PubMed]
- Zima, B.; Kędra, R. Detection and size estimation of crack in plate based on guided wave propagation. Mech. Syst. Signal Process. 2020, 142, 1–19. [Google Scholar] [CrossRef]
- Zima, B.; Rucka, M. The paper presents results of the comprehensive theoretical and experimental investigation of crack detection in metallic plate using guided wave propagation. The main aim of the paper is to develop the novel method which would allow for linear crack size. Arch. Civ. Mech. Eng. 2016, 16, 387–396. [Google Scholar] [CrossRef]
- Feldman, M. Hilbert Transform Applications in Mechanical Vibration; Wiley: New York, NY, USA, 2011; ISBN 9780470978276. [Google Scholar]
- Brandt, A. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures; Wiley: New York, NY, USA, 2011; ISBN 9780470746448. [Google Scholar]
- Randall, R.B. Vibration-Based Condition Monitoring: Industrial, Aerospace and Automotive Applications; Wiley: New York, NY, USA, 2010; ISBN 9780470977668. [Google Scholar]
- Waszczuk-Młyńska, A.; Radkowski, S. Circular membrane with a centrally-located opening—analytical model using parameterisation of the non-empty torus. Z. Angew. Math. Mech. 2019, 99, e201800167. [Google Scholar] [CrossRef]
- Collacott, R.A. Mechanical Fault Diagnosis and Condition Monitoring; Springer: Berlin/Heidelberg, Germany, 1977; ISBN 978-94-009-5725-1. [Google Scholar]
- Rivola, A. Applications of Higher Order Spectra to the Machine Condition Monitoring; University of Bologna: Bologna, Italy, 2000; pp. 2–4. [Google Scholar]
- Szabatin, J. Przetwarzanie Sygnałów; Wydawnictwo Naukowe Uniwersytetu Mikołaja Kopernika: Toruń, Poland, 2003; ISBN 9788362773091. [Google Scholar]
- Zayed, A.I. Hilbert transform associated with the fractional Fourier transform. IEEE Signal Process. Lett. 1998, 5, 206–208. [Google Scholar] [CrossRef]
- Gabor, D. Theory of Communication. J. Inst. Electr. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef]
- Venkitaraman, A.; Seelamantula, C.S. Fractional Hilbert transform extensions and associated analytic signal construction. Signal Process. 2014, 94, 359–372. [Google Scholar] [CrossRef]
- Boltezar, M.; Strancar, B.; Kuhelj, A. Identification of transverse crack location in flexural vibrations of free-free beams. J. Sound Vib. 1998, 211, 729–734. [Google Scholar] [CrossRef]
- Waszczuk-Młyńska, A.; Radkowski, S. About a certain way of the membrane kinetic energy transformation into electric energy. Adv. Intell. Syst. Comput. 2015, 352, 303–312. [Google Scholar] [CrossRef]
- Sarkar, S.; Mukherjee, K.; Ray, A. Symbolic analysis of time series signals using generalized hilbert transform. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 5422–5427. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waszczuk-Młyńska, A.; Gałęzia, A.; Stanisław, R. Fault Identification in Membrane Structures Using the Hilbert Transforms. Sensors 2022, 22, 6224. https://doi.org/10.3390/s22166224
Waszczuk-Młyńska A, Gałęzia A, Stanisław R. Fault Identification in Membrane Structures Using the Hilbert Transforms. Sensors. 2022; 22(16):6224. https://doi.org/10.3390/s22166224
Chicago/Turabian StyleWaszczuk-Młyńska, Aleksandra, Adam Gałęzia, and Radkowski Stanisław. 2022. "Fault Identification in Membrane Structures Using the Hilbert Transforms" Sensors 22, no. 16: 6224. https://doi.org/10.3390/s22166224
APA StyleWaszczuk-Młyńska, A., Gałęzia, A., & Stanisław, R. (2022). Fault Identification in Membrane Structures Using the Hilbert Transforms. Sensors, 22(16), 6224. https://doi.org/10.3390/s22166224





