1. Introduction
For several decades, heart rate variability (HRV) has been a researched field because of its ability to evaluate the autonomic nervous system (ANS) noninvasively, presenting itself as a potential tool for the prognosis, diagnosis and monitoring of diseases, mainly in the clinical environment [
1,
2,
3,
4,
5,
6,
7]. HRV is defined as the changes in the duration of the beat-to-beat interval, which is calculated from R-wave detections in electrocardiographic (ECG) signals. Alternatively, variability in pulse rate (PRV) can be derived from pulse photoplethysmography (PPG). This signal can be recorded at various locations on the body, making it of interest for wearable devices. Despite pulse rate variability being different from HRV, it can be used as a surrogate in many practical situations [
8,
9].
The exponential growth of wearable devices able to record ECG and/or PPG signals has opened up a new horizon for HRV, allowing massive monitoring at a relatively low cost. The accessibility of a large variety of designs has made them an everyday use tool, allowing non-invasive health monitoring in the general population. In this context, assessing the state of the ANS during daily life has become a very attractive objective in the field of health and well-being. However, obtaining reliable variability measurements from wearable devices is challenging. Wearable devices are worn throughout the day in constantly changing conditions, and motion artifacts are very frequent. In addition, comfortability is relevant when deciding the place of recording of a wearable device, in contrast to the clinical settings, where the signal quality is usually more relevant. All this leads to an overall low signal quality compared to clinical monitoring scenarios, downgrading the performance of the traditional HRV methods. Most devices only measure the mean heart rate (MHR), which is very robust to data loss in stationary conditions but less powerful for ANS assessment than HRV. Although changes in the MHR are mainly induced by the ANS, it cannot be considered a measure of autonomic function [
10,
11,
12]. Despite studies that criticize the added value of HRV with respect to MHR [
13], there are scenarios in which an alteration of ANS function produces changes in HRV but not in MHR, such as in depressed patients with respect to controls [
14] or in exercise contexts [
15].
Acquisition technology has made a qualitative leap that has surpassed traditional HRV preprocessing methods to some extent. In a few years, the challenge has shifted from dealing with casual artifacts to being forced to forego a large part of the total recording time. The proliferation of health applications of wearable devices makes it necessary to investigate the degradation of HRV metrics in the presence of incomplete recordings, as well as new methods that allow robust analysis under adverse conditions.
1.1. Related Work
Artifacts have been a concern since the beginning of HRV studies, as they can appear even in the most controlled environments. Most of the works in the literature focus on artifacts of small duration, which are often treated in the same way as ectopic beats [
16,
17,
18,
19,
20,
21,
22]. In general, methods are divided between those that simply remove outliers in beat detections—both false positives and false negatives—and those that interpolate them based on accepted proximal values (gap-filling methods) [
16]. Correction methods are mandatory since errors representing less than 0.1% of the detections may cause variations of up to 50% in some HRV metrics [
16].
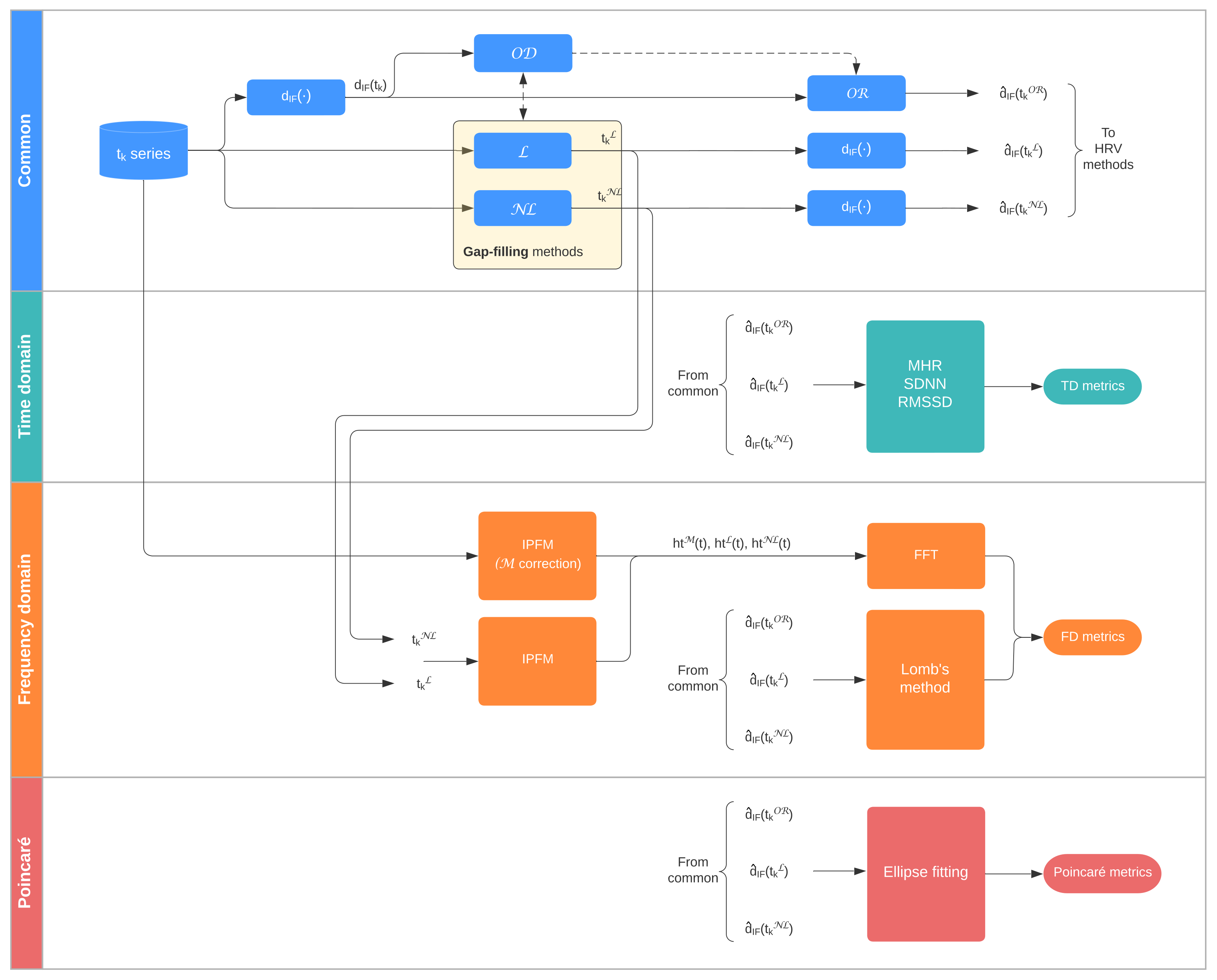
Some gap-filling methods generate evenly-spaced interpolations. The beat event series is not available with these methods, so time-domain metrics or Poincaré plots cannot be assessed. Mateo and Laguna proposed an IPFM-model based corrector for ectopic beats on the heart timing signal [
17], a continuous signal, assuming that autonomic modulation can be modeled using a band-limited signal. Meanwhile, McNames et al. used an impulse rejection filter on the instantaneous heart rate signal—evenly sampled—on the basis that nonpathological artifacts are of small duration and large amplitude [
18]. Lee and Yu detected and corrected outliers in the tachogram using cubic splines [
19].
On the other hand, some studies obtain a corrected unevenly-sampled inter-beat interval (IBI) series, allowing the assessment of time-domain metrics and Poincaré plots. Begum et al. used k-nearest neighbors in the IBI series [
20], while Al Osman et al. used a combination of cubic and nonlinear predictive interpolation methods [
21]. An interesting aspect of the latter is the use of simulation to introduce artifacts in order to compare errors. Giles and Draper compared different interpolation methods of the IBI series, including cubic splines [
22].
Although the previous methods may work for isolated outliers, they have not been evaluated for longer artifact segments. Baek and Shin studied the degradation of temporal and frequency metrics in response to an increase in missing IBI data, obtained by simulation, although they do not provide any correction method [
23]. The simulation randomly removes samples from the tachogram in an increasing manner, over a fairly wide range, from 5 to 285 intervals, in 5 min recordings. Morelli et al. developed one of the first studies to investigate the effect of large heartbeat losses, from the perspective of wearable devices [
24]. Their simulation method for missing detections is based on a two-state Markov chain, simulating losses of 30%, 50% and 70% of IBIs. This is one of the most complete studies on artifact correction applied to wearables, including temporal and frequency metrics and Poincaré plots. Benchekroun et al. used filtering and gap filling using a Gaussian distribution in IBI series with 5% to 35% simulated missing beats [
25]. HRV metrics were derived from corrected series and used as features for a stress/relax classification. Classification results were compared with other gap-filling approaches (linear, spline, and pchip). Nevertheless, no separate metric results were reported. Królak et al. proposed a gap-filling algorithm tested with bursts of up to seven missing beats [
26]. They reported that cubic interpolation can in some cases result in lower errors for long gaps. Finally, some works address artifact correction in the detection stage, using methods such as adaptive filtering, wavelet transform or feature extraction of the cardiac signal [
27,
28]. These approaches are beyond the scope of this paper, as they are signal specific, and many wearables do not allow exporting cardiac signals but event series. In addition, they can be used in conjunction with event series correction.
1.2. Aims of the Study
There is still much to be known about the degradation of HRV metrics in scenarios with large missing data. To the authors’ knowledge, there is no study that provides insight into how correction methods behave under different types of losses that can occur in a real case: bursts and scattered missing beats. There is also no conclusion on the maximum burst size to discard a segment for further analysis. The same is true for scattered missing beats. In this work, the degradation of different HRV metrics—in the time domain and frequency domain and Poincaré plots—is evaluated in missing data scenarios. A missing data simulation protocol has been developed for this purpose. In addition, a method to attenuate the effect of missing data in HRV metrics has been proposed and compared to existing methods in the literature. Then, these methods have been applied to analyze PRV derived from Apple Watch. This work aims to contribute to HRV/PRV analysis by proposing guidelines to select the best correction method for each studied metric and missing data scenario and to provide conclusions about when to discard a segment for further analysis depending on the quantity and distribution of missing data.
4. Discussion
An analysis of the degradation of some of the most important HRV metrics due to data loss has been presented. A simulation study has been designed to test the influence of missing beats depending on whether they are distributed scattered or in bursts. Correction methods have been tested with both simulation and experimental data, recorded with a commercial wearable. Note that, in contrast to the simulation dataset, PRV was compared to the HRV in the case of the Apple Watch dataset. Thus, the error results obtained for the simulation dataset should not be compared with those obtained for the Apple Watch dataset. Nevertheless, correction methods within the same dataset can still be compared. In the following, a discussion of the best correction method for each metric is given, as well as the maximum acceptable missing beats for a relative error less than 20% in the third quartile. A summary is shown in
Table 13.
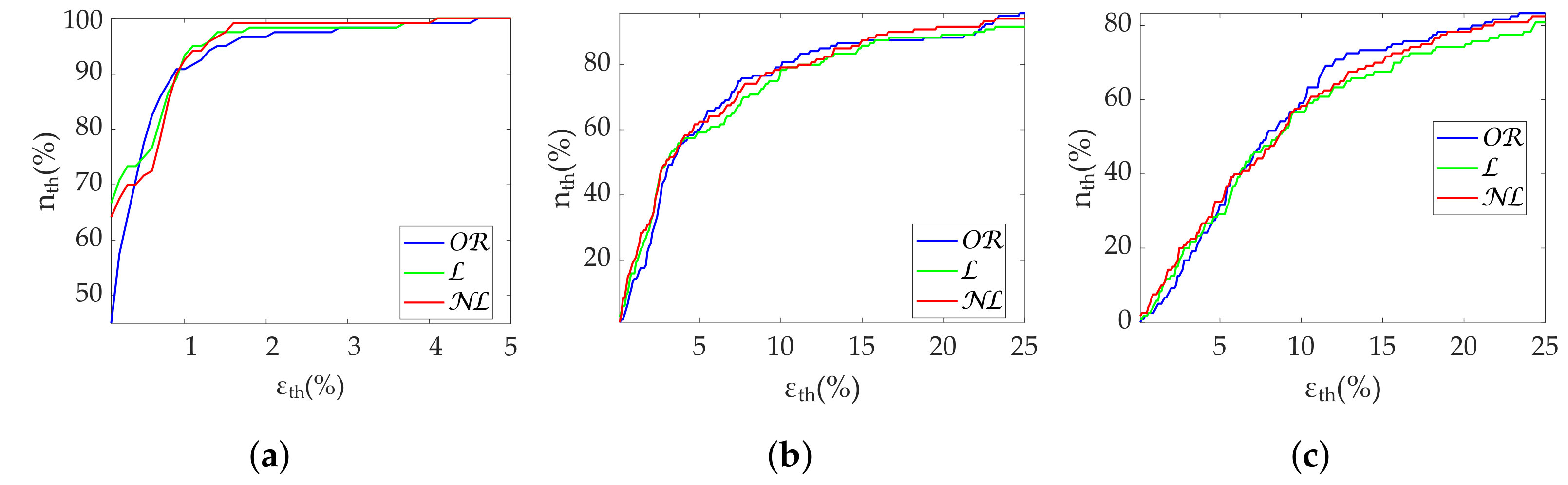
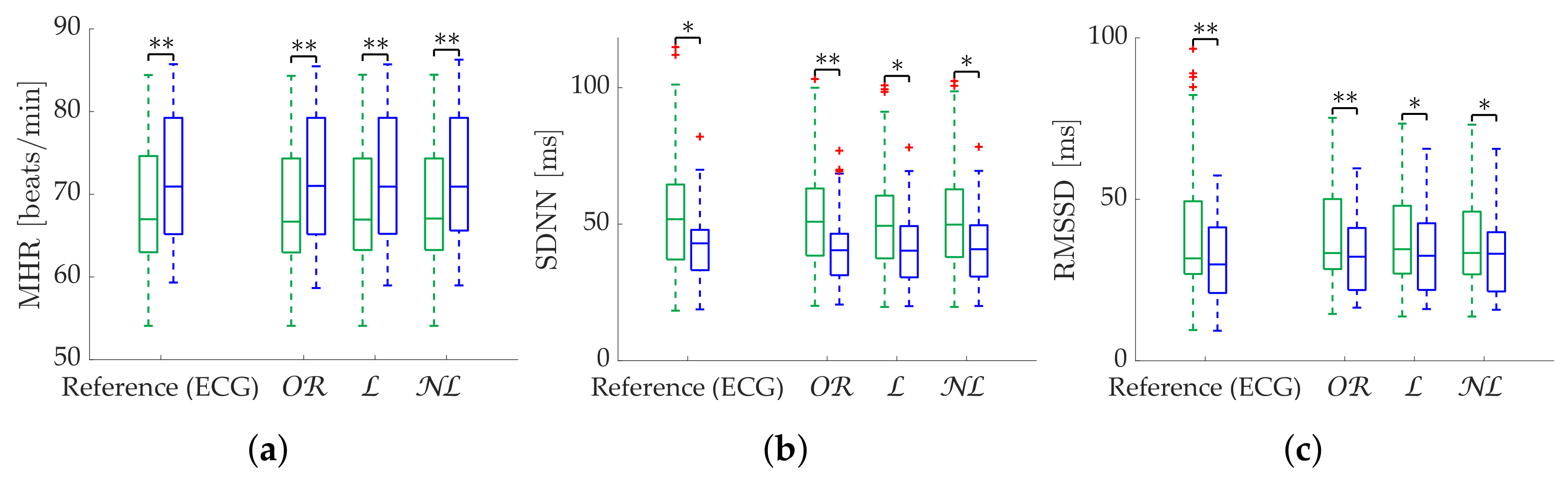
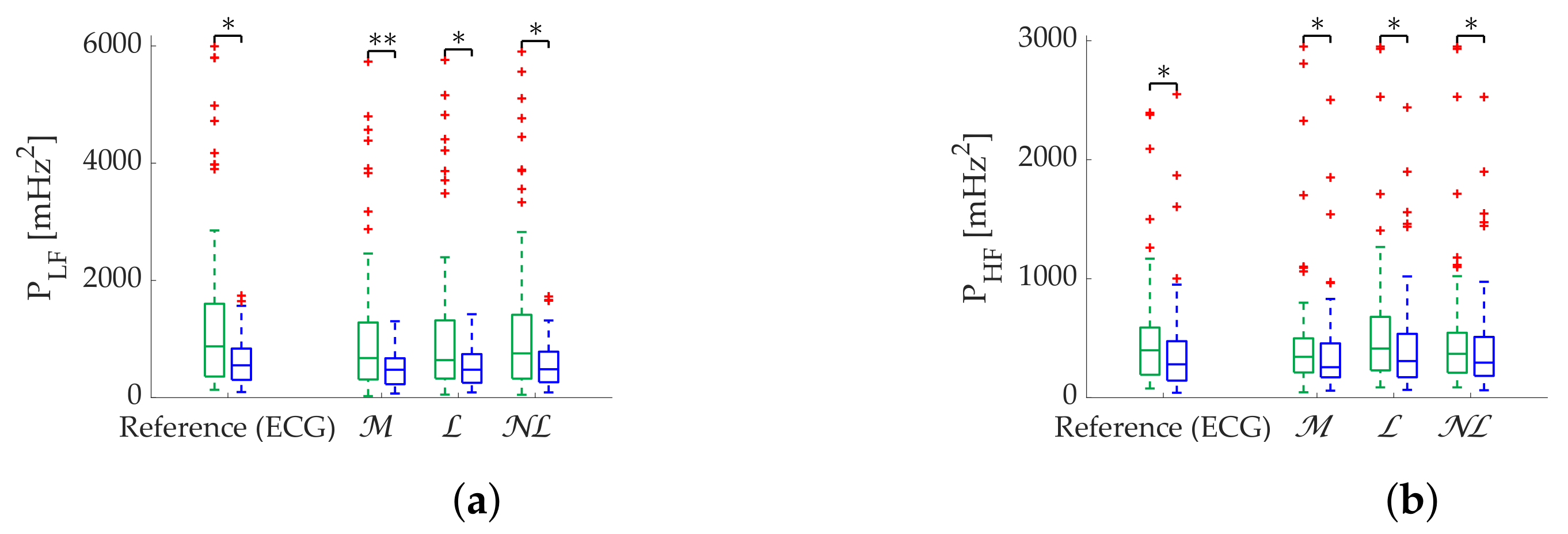
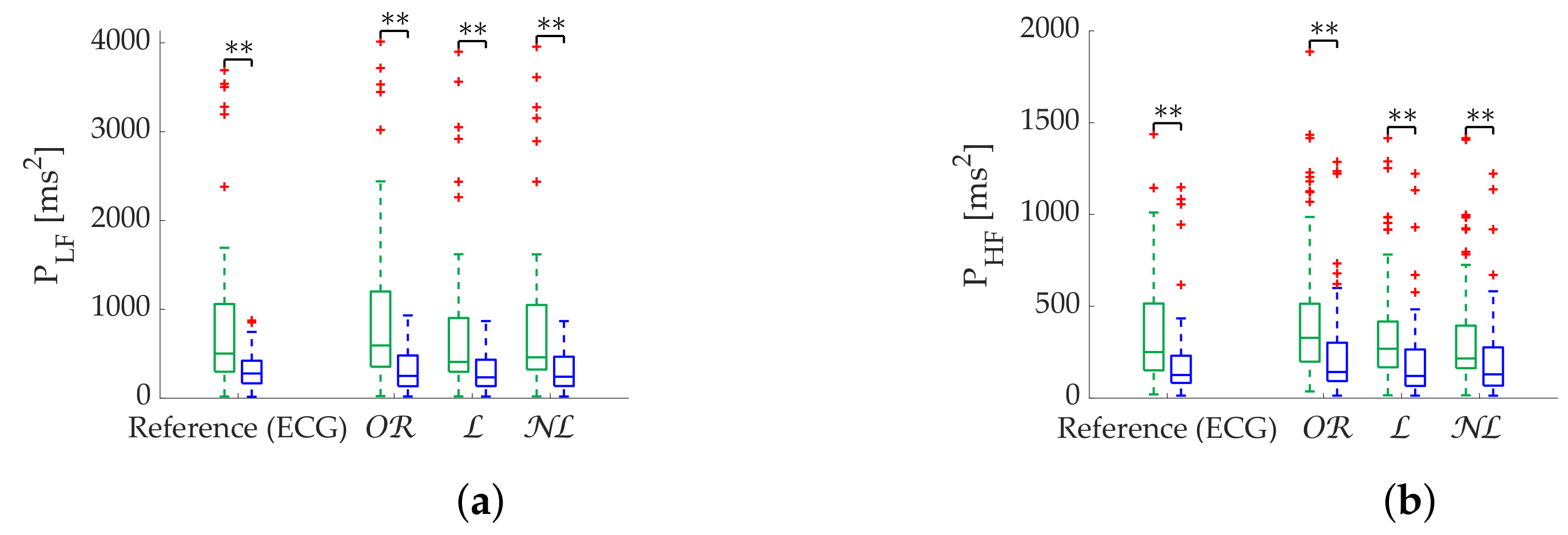
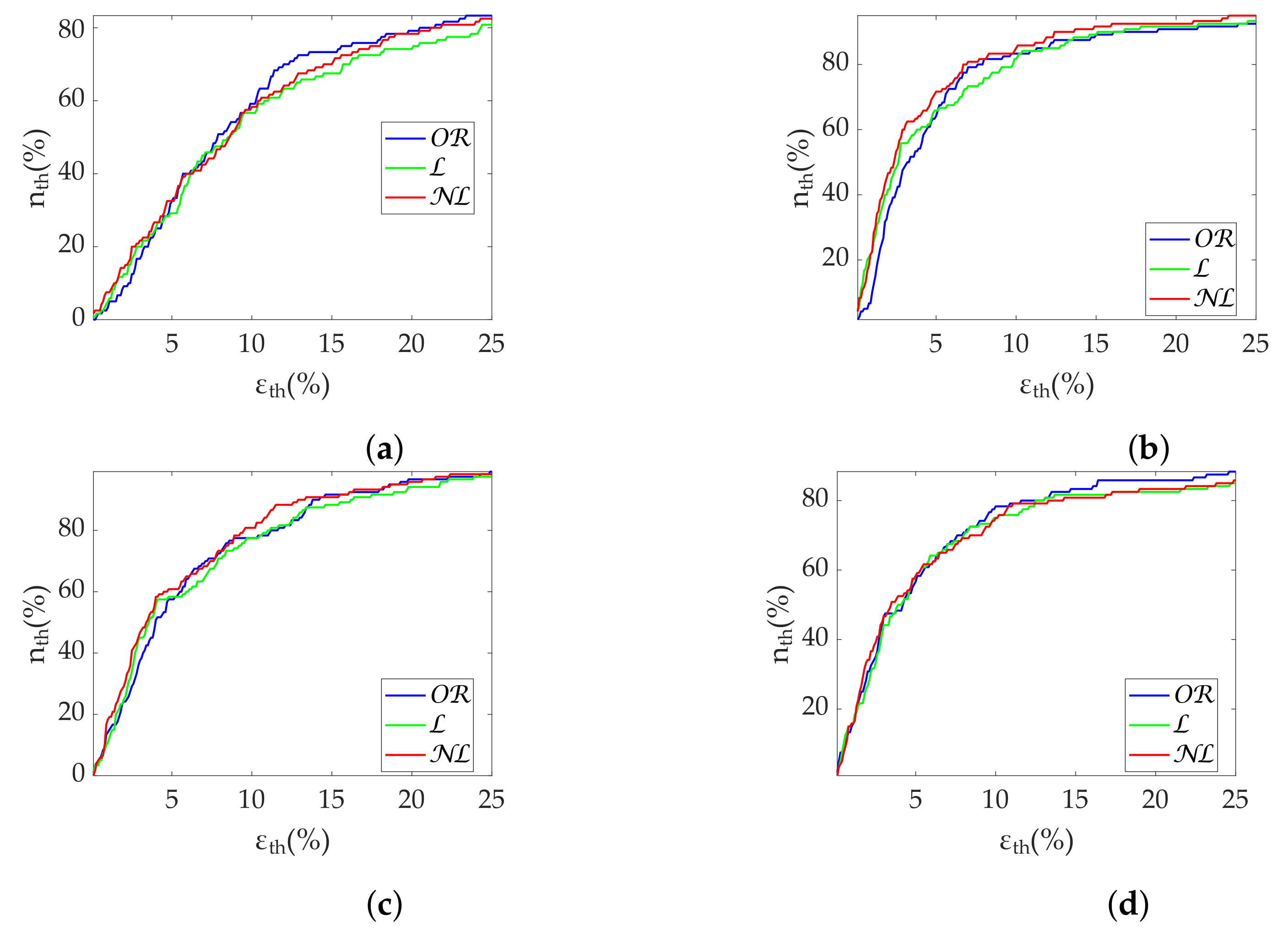
Regarding time-domain metrics, noticeable differences are only found in the relative error results of the simulation. is the best option in case of applications where MHR is the only interesting metric, as it is the best correction method both with bursts and scattered missing beats. is also the best-performing method for SDNN with scattered losses. is a reliable correction for SDNN and RMSSD in datasets with burst predominance, while RMSSD should be computed using with scattered missing beats. The robustness of MHR using both and gap filling supports the idea that the number of missing beats is well approximated by these methods. Gap-filling degradation with bursts of missing beats is easily explained by the lack of information as the correction moves away from the edges of the burst. Phenomena such as respiratory sinus arrhythmia also cannot be inferred in large bursts. MHR proved to be a very robust metric in missing data scenarios, assuming a worst-case maximum deviation of 0.7 beats per minute. Although not shown in our results, MHR was able to withstand losses in bursts of up to one minute without the median error exceeding 1 beat per minute. However, it is not easy to establish a threshold for which it is preferable to reject the segment. This will rather depend on the stationarity of the data. Because of the metric’s robustness, in periods where variations are expected, the rate of these changes should be a more dominant factor than metric degradation in the segment rejection decision. The case of scattered losses can be more complex, as depending on the distribution, it can be complicated for an outlier detection method to correctly work. This is magnified in cases with large respiratory sinus arrhythmia oscillations. Segment rejection is encouraged when computing RMSSD with >25% missing beats, as the third quartile error is around 20%. In any case, attempting to correct segments with more than 35% missing beats or a 20 s burst is not considered adequate.
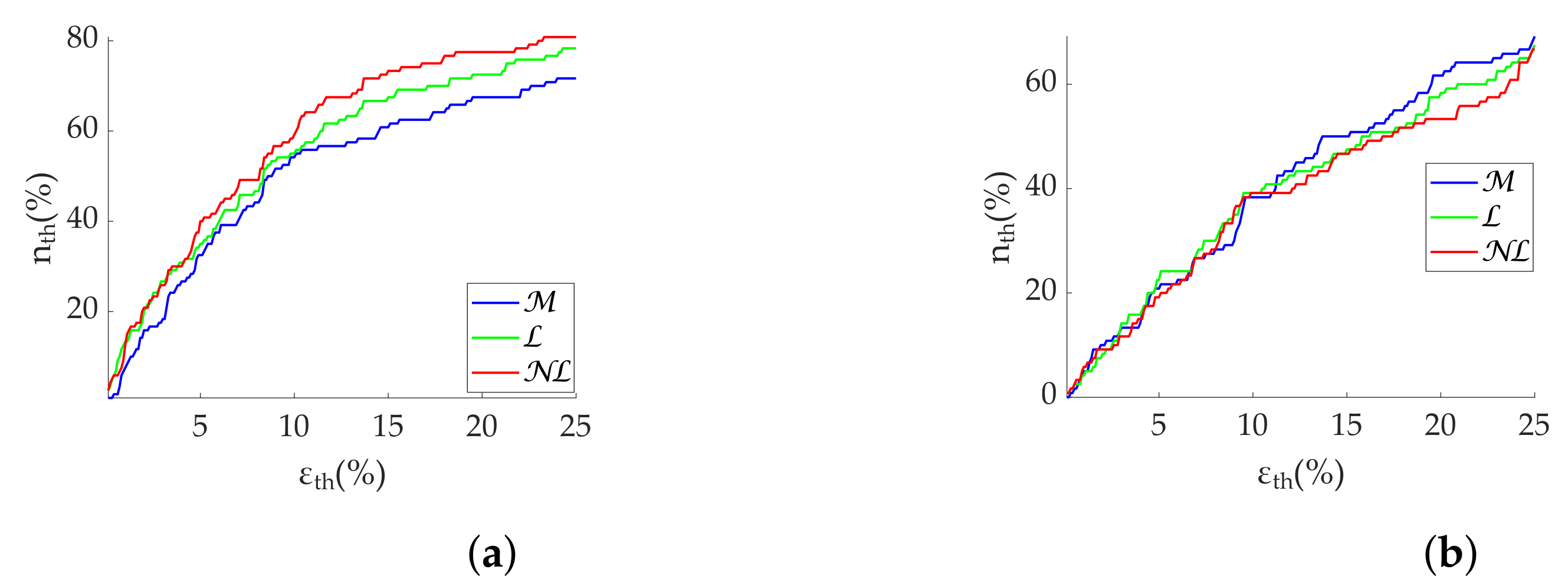
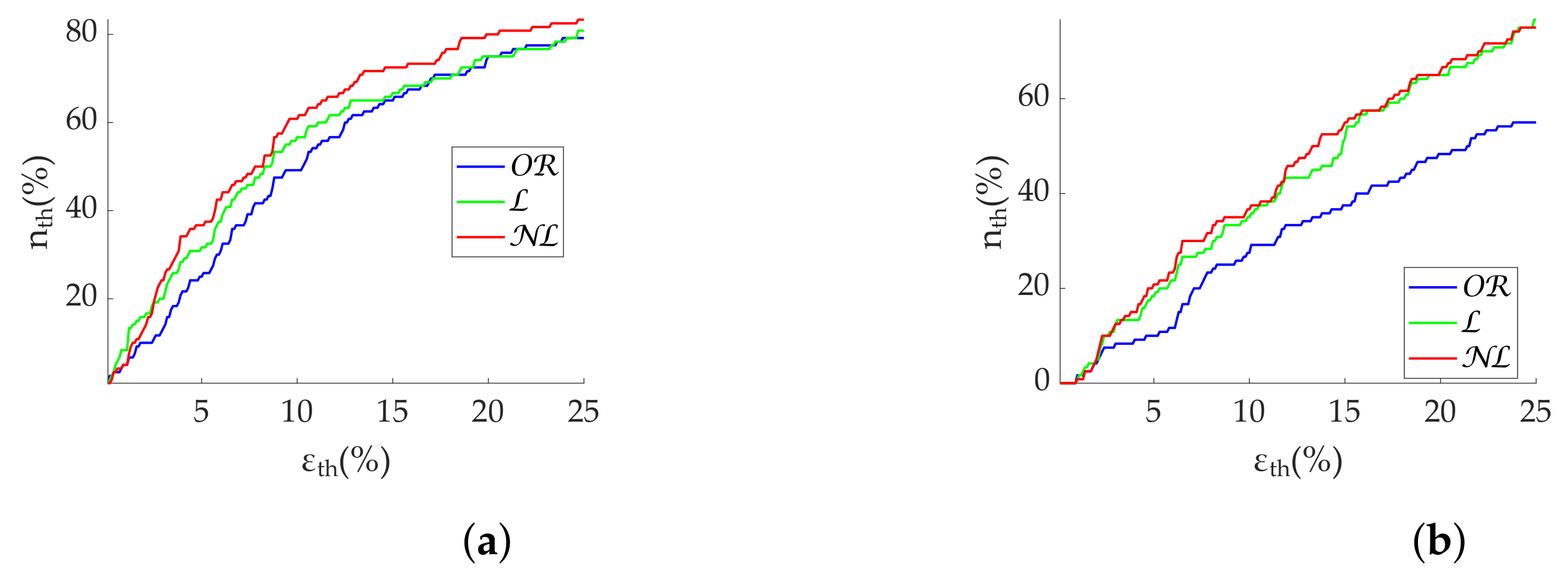
Regarding frequency metrics calculated via FFT, gap-filling methods show a clear advantage in terms of error and state discrimination. was the best correction method for datasets with scattered missing beats predominance. In datasets with burst predominance, performed better for , while obtained better results for . The third quartile of error is greater than 20% in case of segments with more than 25% scattered missing beats, suggesting that those segments should be discarded for analysis. In the case of , segments with more than 15% missing beats should also be discarded. Discarding segments is suggested when analyzing missing data in bursts longer than 10 s.
In regards to Lomb’s method,
obtained the best results for scattered missing beats. In datasets with burst predominance,
obtained the best results for
, while
obtained the best results for
. Segment rejection for
analysis is suggested with more than 25% scattered missing beats. In case of
analysis, rejection is suggested with more than 15% missing beats. Segments should be discarded for bursts longer than 10 s as well. Although Lomb’s method allows its use without gap filling—in fact, with no interpolation at all—it deteriorates rapidly in the absence of the whole series (
case). This is explained due to the phenomenon of the over-oscillation of the spectrum as samples are discarded, whose effect is limited when calculating the power by integrating [
39], but still causes a degradation of the metrics.
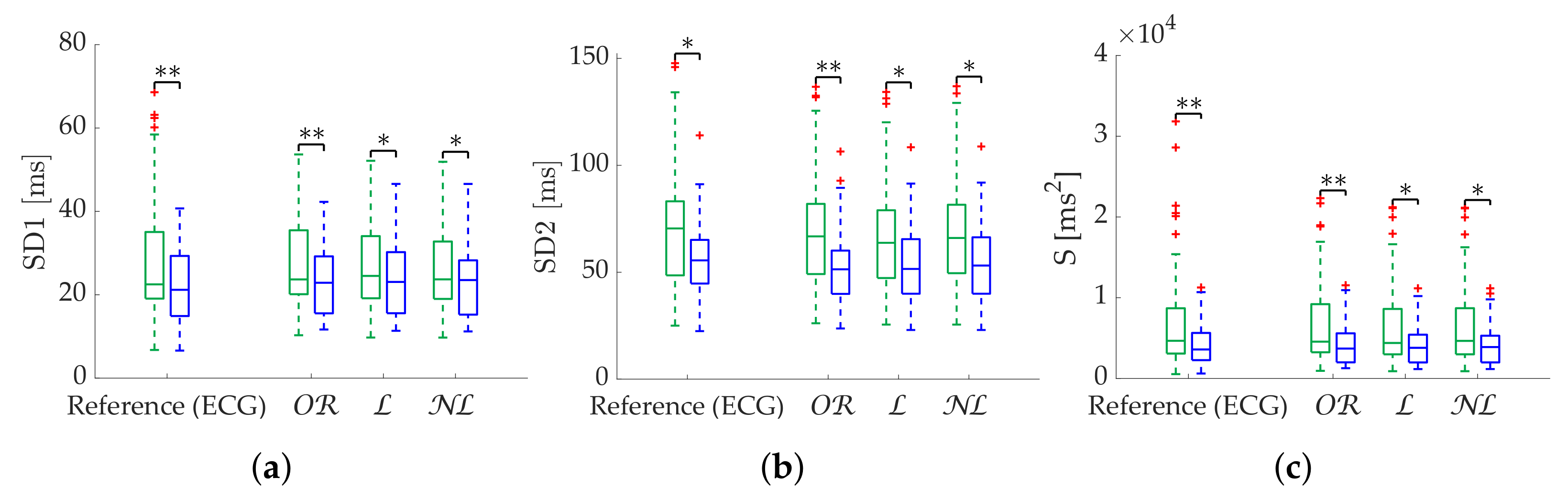
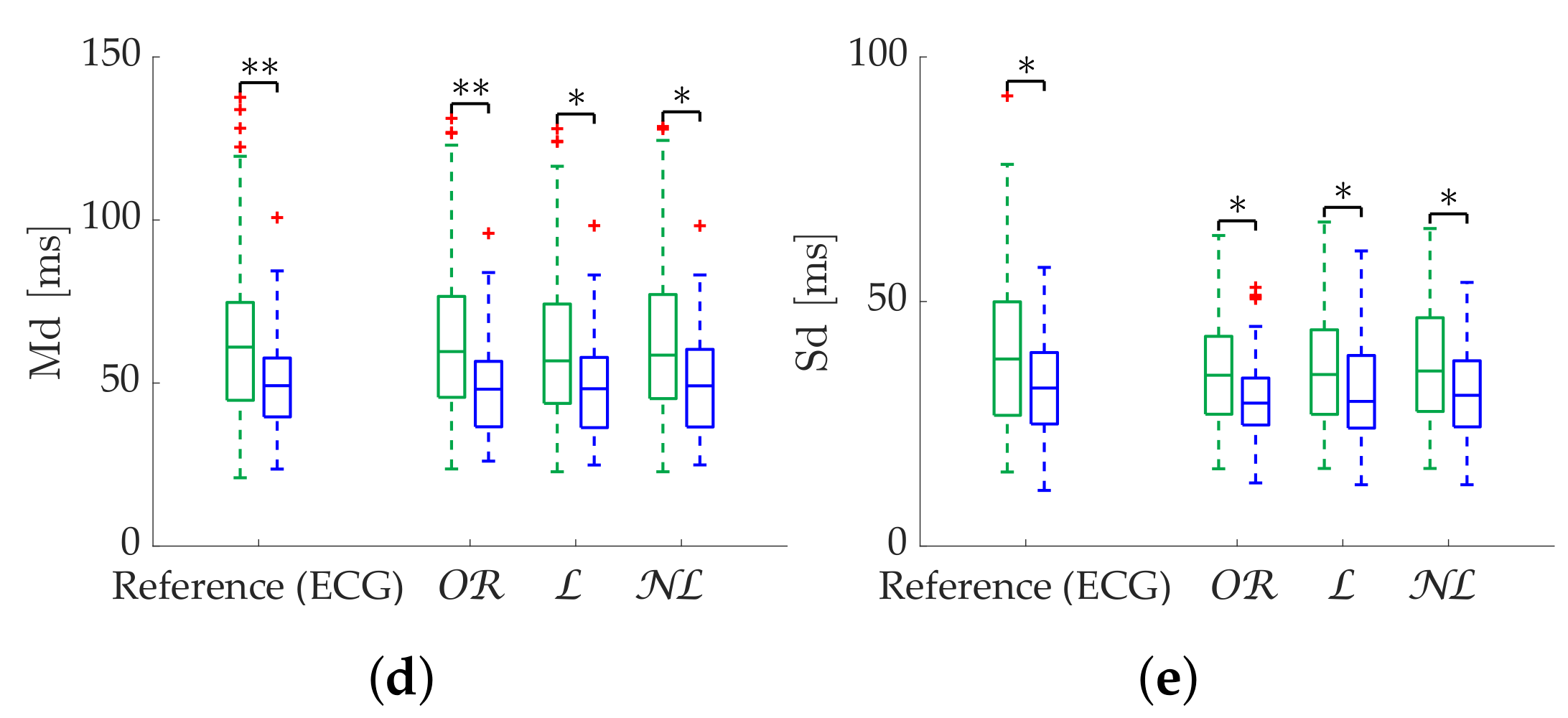
In the case of Poincaré metrics, obtained better results in the case of scattered losses for most metrics, in terms of both error and discrimination between states. obtained the best results when analyzing specifically SD1 up to 25% of missing beats, while obtained better results with more than 25% missing beats. However, the third quartile error is greater than 20% in this case, and segment rejection is suggested. As in the case of time-domain metrics, the criterion for rejecting a segment should prioritize the expected stationarity, given the robustness of the metrics with correction methods. obtained the best results in the case of bursts for all metrics.
The proposed gap-filling method, especially in its non-linear version, has been demonstrated to be a very effective correction method. In [
24], the difference between correcting the interval series, as is the case with most of the methods in the literature, and correcting the event series, i.e., the beat-occurrence timestamps, was shown. Correcting the interval series involves shifting the timestamps of subsequent beats to address the interval correction. This ultimately means forgoing the reference provided by the subsequent, well-detected beats. Instead, the proposed method corrects the event series without this shifting by adding a variable number of beats, taking into account the budget of seconds to be filled in. Larger gaps require a greater number of filling beats to obtain IBIs in accordance with the adjacent intervals to the gap. In [
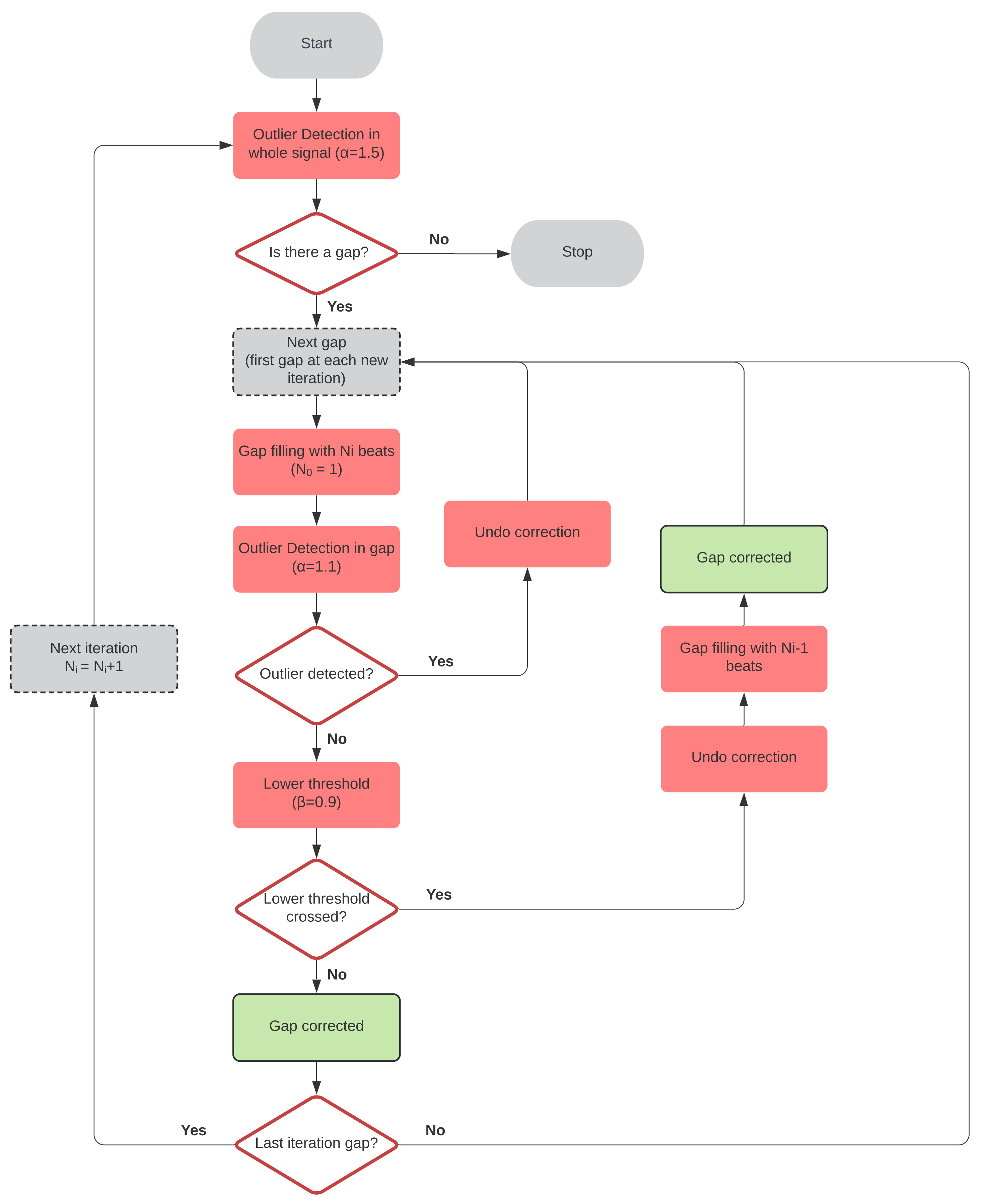
24], it is shown that event correction yields more accurate results than interval series correction. Besides, a novel aspect of the proposed gap-filling method lies in the way in which the correction of each segment is approached. The proposed method is a segment-based iterative algorithm instead of a gap-based one. The use of this kind of algorithm aims to cope with two major problems of event series gap filling: distinguishing outliers at high loss rates and the lack of knowledge of the number of missing beats per gap. Thus, it starts by solving simple gaps before those involving more than one beat. This is an improvement over the majority of gap-filling methods in the literature, where each gap is corrected before moving on to the next one, missing the advantage of solving the shorter gaps first.
It should be noted that the best method is not necessarily the one with the lowest error. Depending on the application, especially working with devices with limited computational capacity and/or which are battery-operated, a method with acceptable results is interesting if it means an improvement in computation time and overall processing load.
Limitations
Regarding the limitations of this work, it is important to note that this research only focuses on data losses—false negatives in beat detections—and not on general errors—a combination of false positives and false negatives. The presence of false positives has a deleterious impact when trying to obtain the most accurate metrics. This type of error introduces an additional variable: the baseline from which to infer false negatives could be lost. In addition to a previous artifact detection stage, a false beat detection rejection stage should be implemented before applying the presented methods to deal with missing data. If the number of false beat detections is not very high, a moving-average-based algorithm may be enough. This concept is of paramount importance when dealing with wearable devices, especially those that monitor 24/7, since beat detections can be unreliable a high percentage of the time, and therefore for any further processing.
Another limitation is the monotonicity of Hermite polynomials. As this interpolation eliminates relative maxima and minima within the burst, it should be taken into account in cases with long bursts and high variability, such as in cases with strong respiratory sinus arrhythmia. Despite this, it performs better than other traditional interpolation methods in the literature, such as cubic splines, which present convergence problems by introducing unwanted oscillations. Further work should be done to address this, for example, by introducing estimated stationary points before interpolating. In addition, interpolation methods that do not impose monotonicity while limiting overshooting should also be investigated.
In addition, in contrast to the simulation database, respiratory frequencies have not been tested for the Apple Watch database. Therefore, the use of classical frequency bands may result in an incorrect evaluation of the frequency metrics in some cases, and their behavior may differ from that seen in simulation [
34]. However, data presentation in medians and quartiles should limit the effect of these outliers in the results.