Influence of Sea Level Anomaly on Underwater Gravity Gradient Measurements
Abstract
:1. Introduction
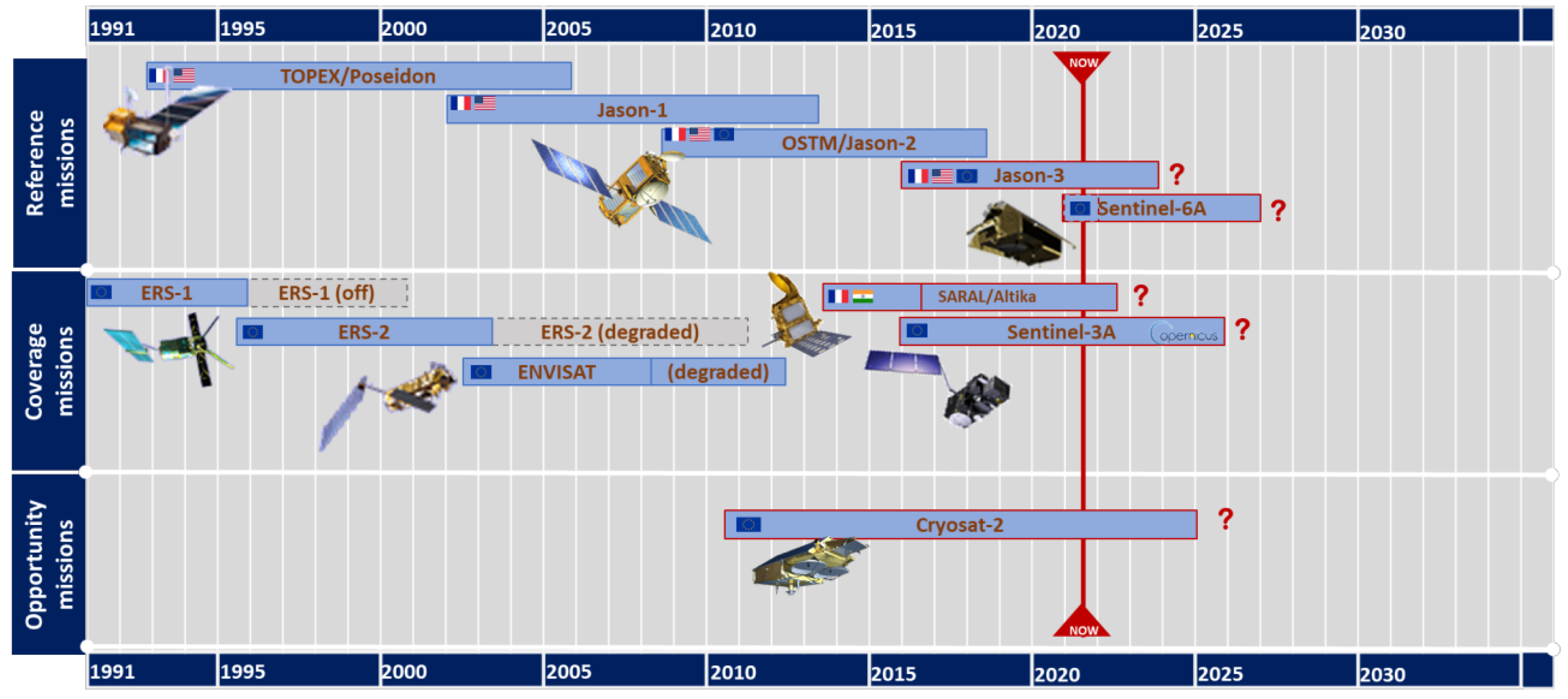
2. Data and Methods
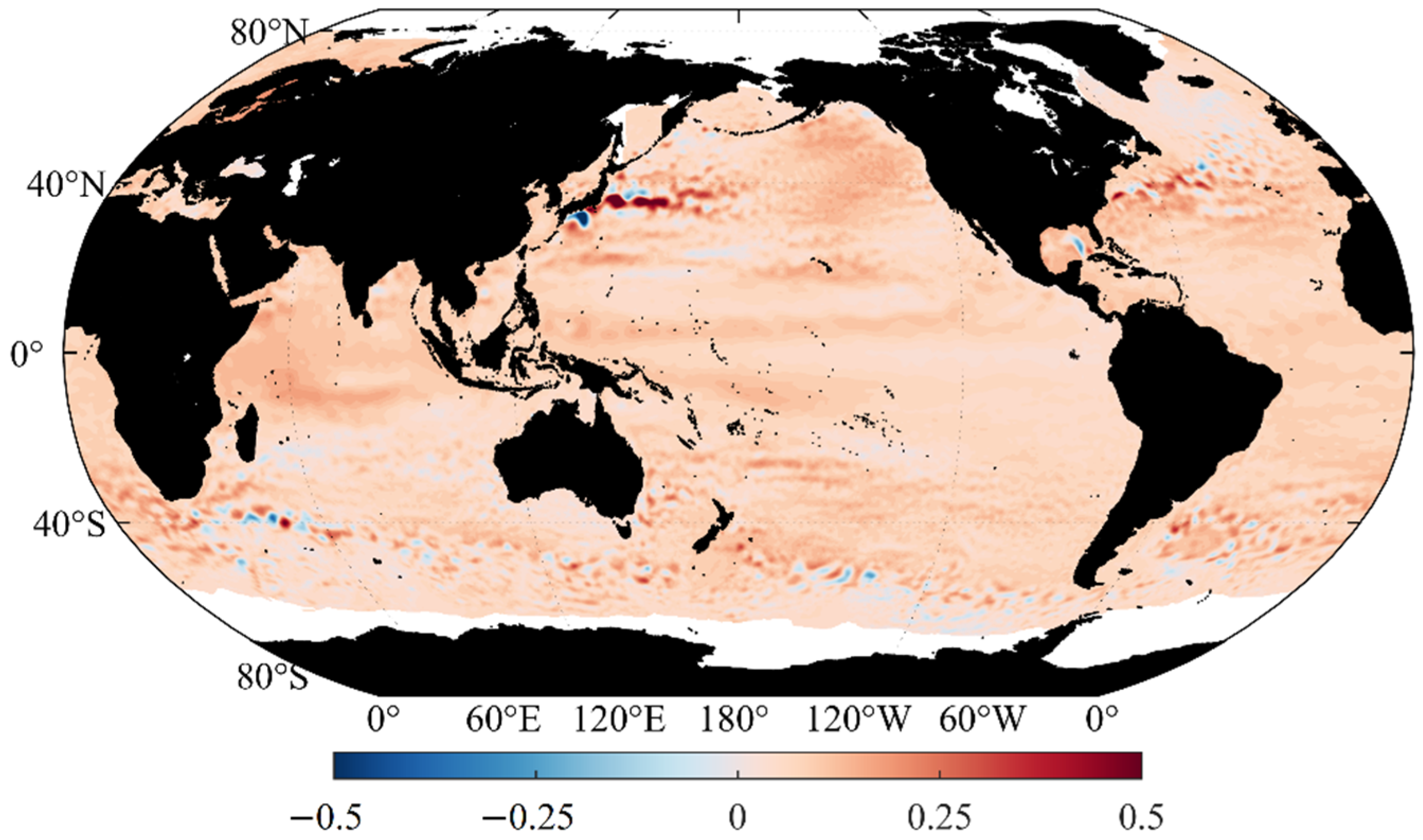
3. Spatial and Temporal Distribution of Sea Level Anomalies
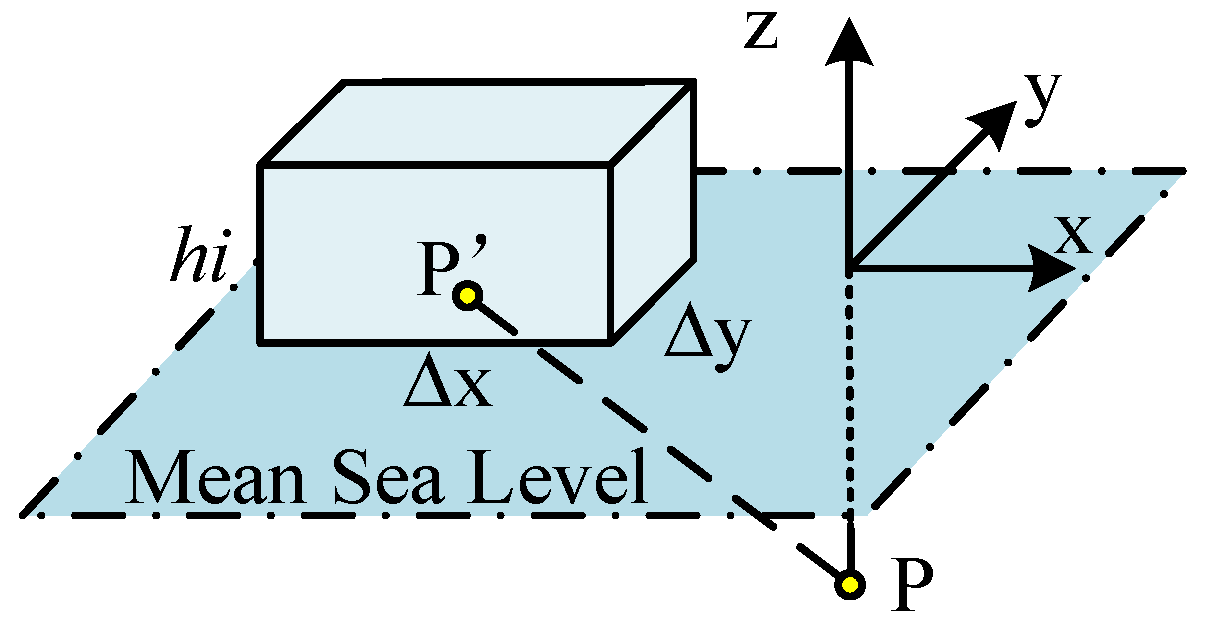
4. Simulation Calculation of Gravity Gradient
5. Experimental Results and Analysis
6. Conclusions
- (1)
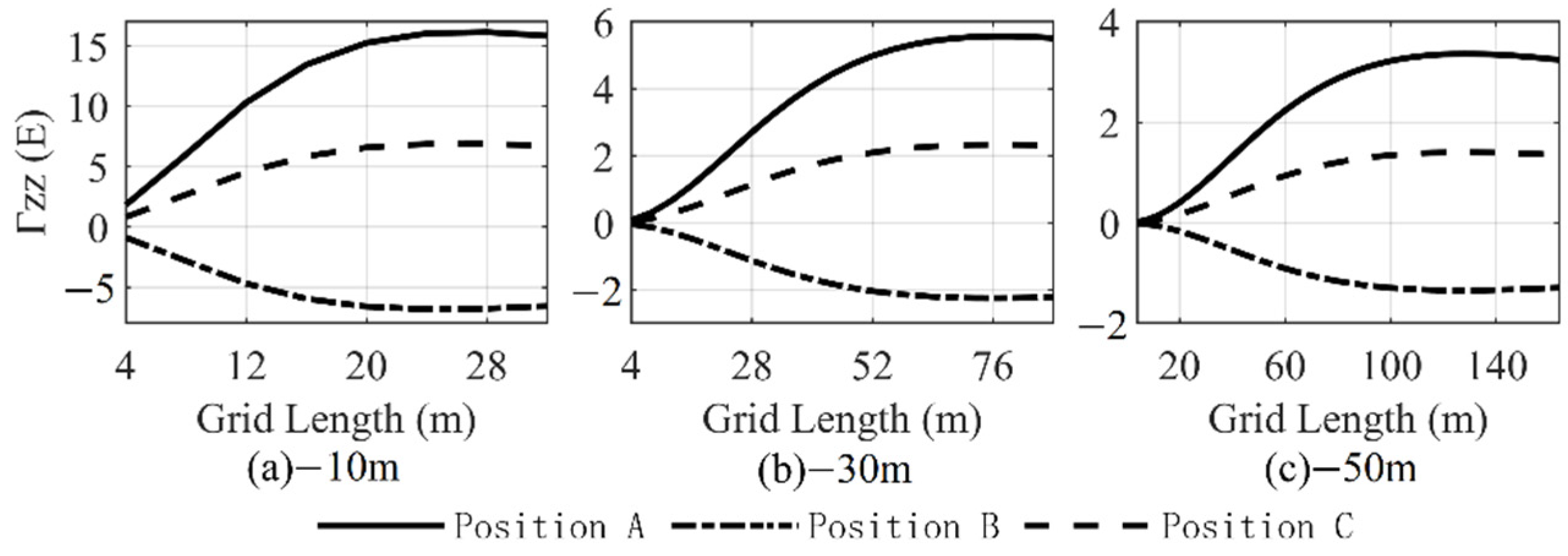
- The gravity gradient forward modeling results are related to the integration range, and the selection of the integration range is related to the calculation height (depth). Therefore, to obtain relatively accurate forward modeling results, different integration ranges need to be considered when calculating at different heights (depths).
- (2)
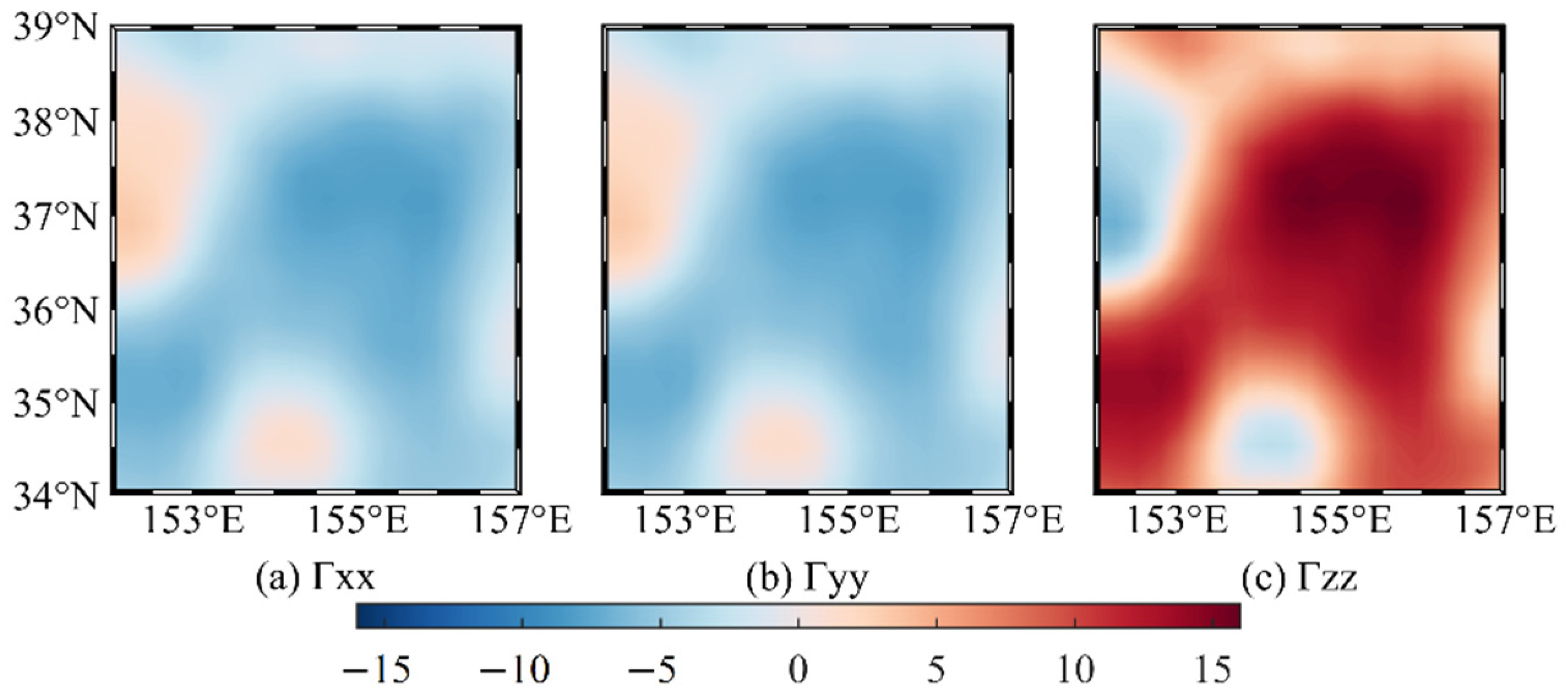
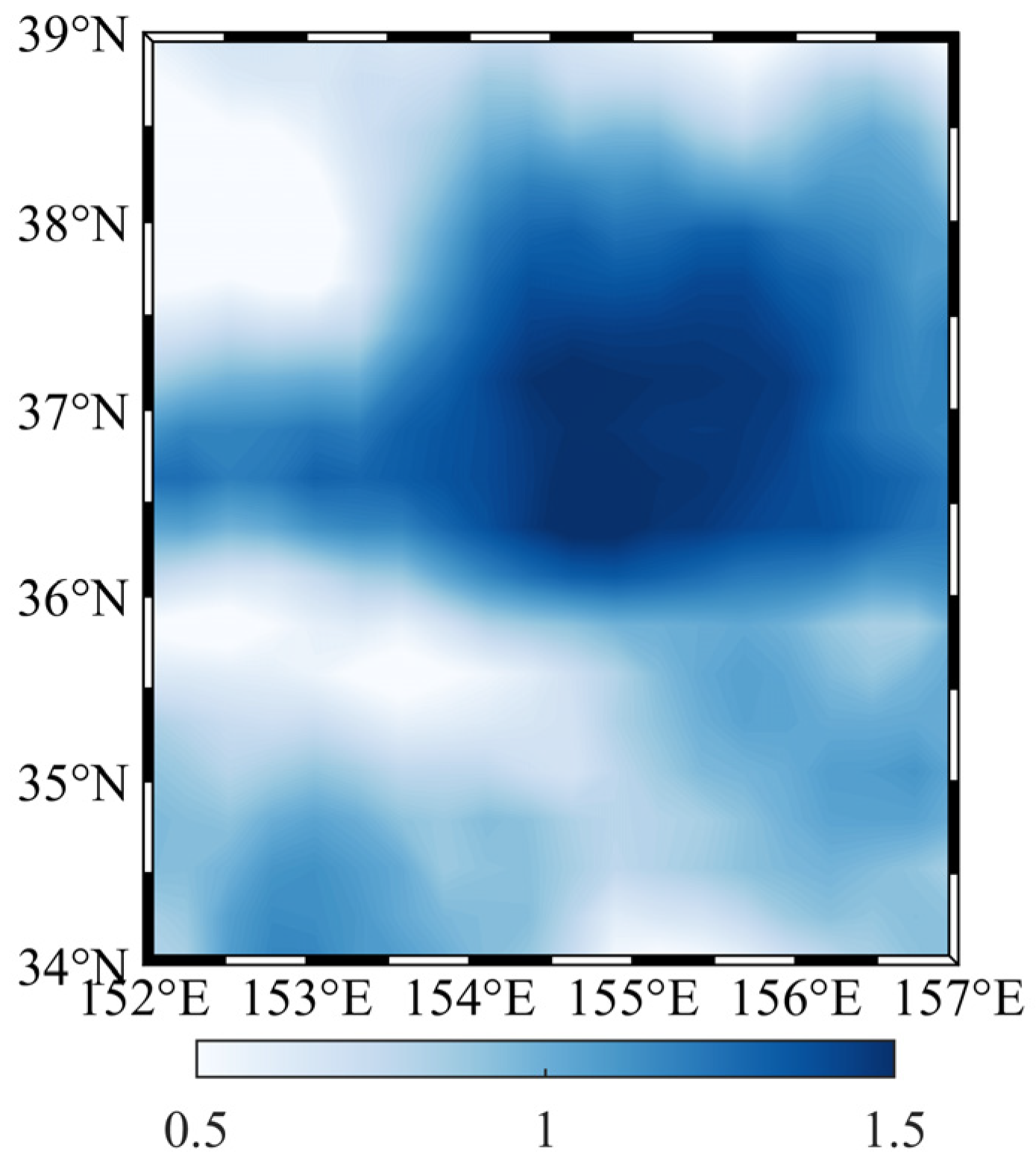
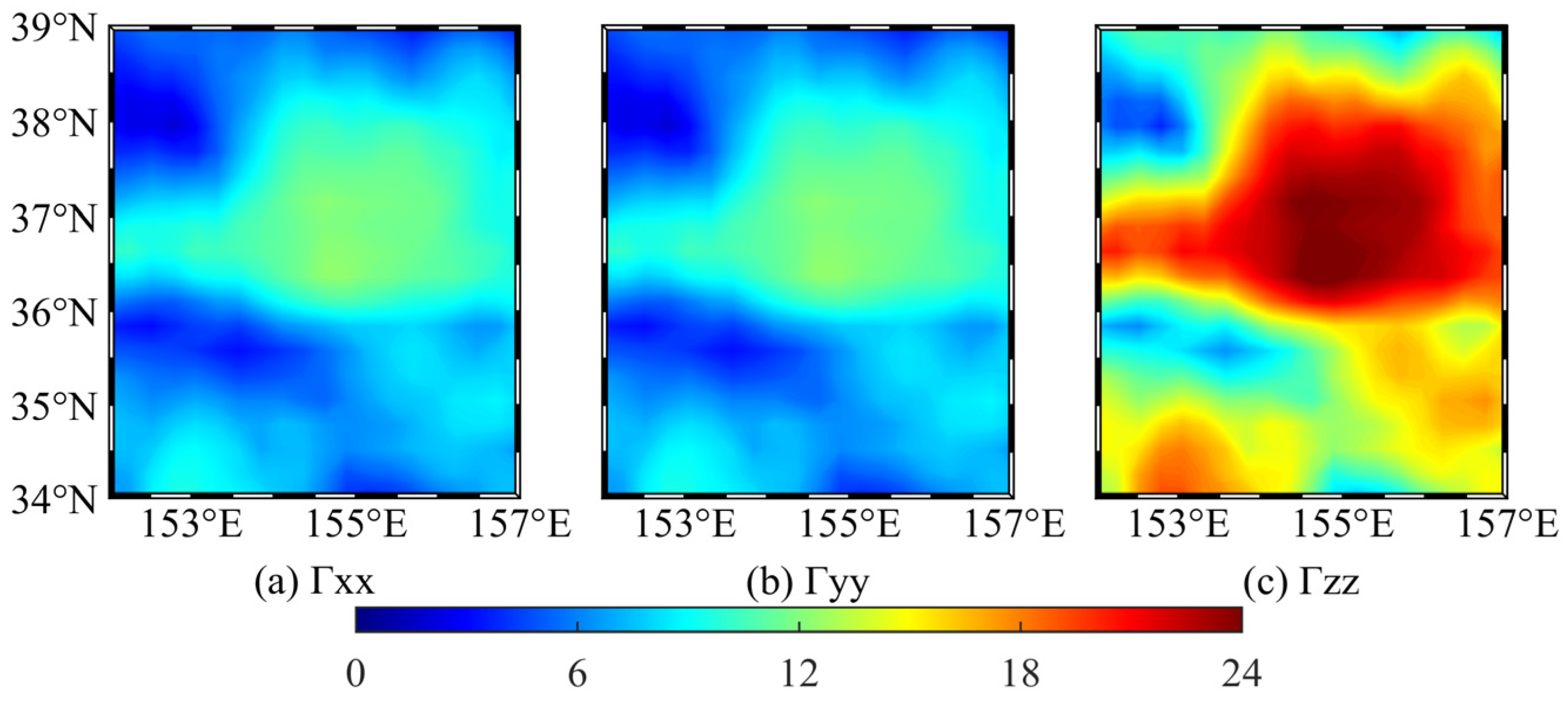
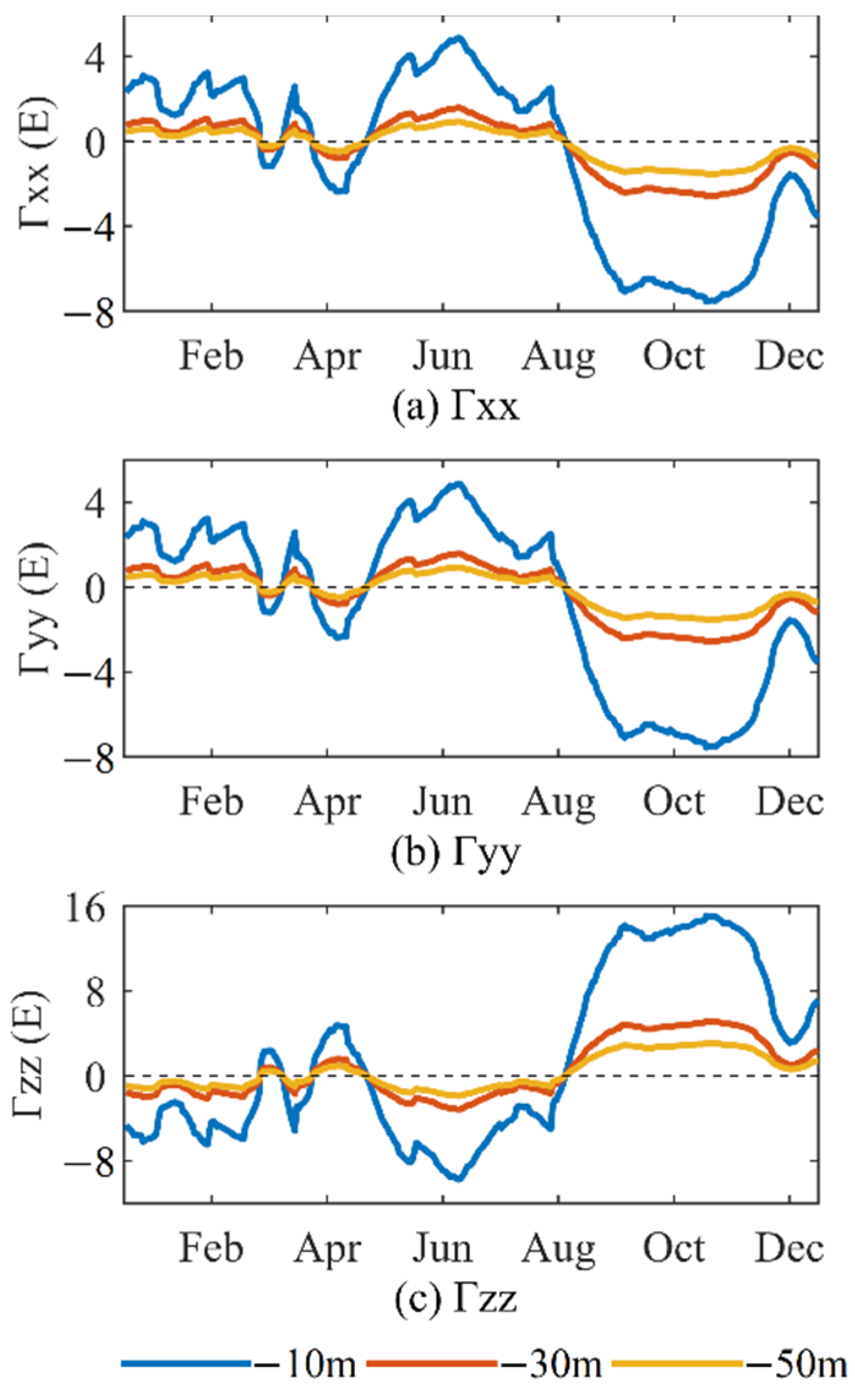
- Based on the measurement accuracy of the gravity gradiometer 1 E, within 50 m below the mean sea level, sea level anomalies at local positions will significantly affect the underwater gravity gradient measurements, with a maximum contribution exceeding 10 E and the maximum difference between different locations exceeding 20 E. Moreover, the change of the sea level anomalies with time will significantly impact the underwater gravity gradient measurements, with the maximum change value exceeding 20 E, and the impact will accordingly change with the seasonal change of the sea level anomalies. Therefore, underwater carriers need to consider the disturbing gravity gradient caused by sea level anomalies when using gravity gradient for underwater detection and navigation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, L.; Tian, X.; Ma, J.; Tian, J. Underwater Object Detection Based on Gravity Gradient. IEEE Geosci. Remote Sens. Lett. 2010, 7, 362–365. [Google Scholar]
- Zhu, L. Gradient Modeling with Gravity and DEM; The Ohio State University: Columbus, OH, USA, 2007. [Google Scholar]
- Zhu, L.; Jekeli, C. Gravity gradient modeling using gravity and DEM. J. Geod. 2009, 83, 557–567. [Google Scholar] [CrossRef]
- Richeson, J.A. Gravity Gradiometer Aided Inertial Navigation within Non-GNSS Environments; University of Maryland: College Park, MD, USA, 2008. [Google Scholar]
- Heath, P.; Greenhalgh, S.; Direen, N. Modelling Gravity and Magnetic Gradient Tensor Responses for Exploration within the Regolith. Explor. Geophys. 2005, 36, 357–364. [Google Scholar] [CrossRef]
- Liu, J.; Liu, L.; Liang, X.; Ye, Z.; Su, X. Base on measured gravity anomaly and terrain data to determine the gravity gradient. Chin. J. Geophys. 2013, 56, 2245–2256. [Google Scholar]
- Wu, L.; Ma, J.; Zhou, Y.; Tian, J. Modelling Full-tensor Gravity Gradient Maps for Gravity Matching Navigation. J. Syst. Simul. 2009, 21, 7037–7041. [Google Scholar]
- Yan, Z.; Ma, J.; Tian, J.; Xiong, L. Impact of waves on detection of high-precision underwater gravity gradient. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2013, 41, 121–124. [Google Scholar]
- Tapley, B.D.; Ries, J.C.; Davis, G.W.; Eanes, R.J.; Schutz, B.E.; Shum, C.K.; Watkins, M.M.; Marshall, J.A.; Nerem, R.S.; Putney, B.H.; et al. Precision orbit determination for TOPEX/POSEIDON. J. Geophys. Res. Ocean. 1994, 99, 24383–24404. [Google Scholar] [CrossRef]
- Stammer, D.; Wunsch, C. Preliminary assessment of the accuracy and precision of TOPEX/POSEIDON altimeter data with respect to the large-scale ocean circulation. J. Geophys. Res. 1994, 99, 24584–24604. [Google Scholar] [CrossRef]
- Maximenko, N.; Niiler, P.; Centurioni, L.; Rio, M.; Melnichenko, O.; Chambers, D.; Zlotnicki, V.; Galperin, B. Mean Dynamic Topography of the Ocean Derived from Satellite and Drifting Buoy Data Using Three Different Techniques. J. Atmos. Ocean. Technol. 2009, 26, 1910–1919. [Google Scholar] [CrossRef]
- Losch, M.; Schröter, J. Estimating the circulation from hydrography and satellite altimetry in the Southern Ocean: Limitations imposed by the current geoid models. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2004, 51, 1131–1143. [Google Scholar] [CrossRef] [Green Version]
- Niiler, P.P.; Maximenko, N.A.; McWilliams, J.C. Dynamically balanced absolute sea level of the global ocean derived from near-surface velocity observations. Geophys. Res. Lett. 2003, 30, 2164. [Google Scholar] [CrossRef] [Green Version]
- Sandwell, D.T.; Smith, W.H.F. Marine gravity anomaly from Geosat and ERS 1 satellite altimetry. J. Geophys. Res. Solid Earth 1997, 102, 10039–10054. [Google Scholar] [CrossRef] [Green Version]
- Taburet, G.; Mertz, F.; Legeais, J.F. Product User Guide and Specification (Sea Level); Copernicus Climate Change Service: Reading, UK, 2021. [Google Scholar]
- Yang, J.; Jekeli, C.; Liu, L. Seafloor topography estimation from gravity gradients using simulated annealing. J. Geophys. Res. Solid Earth 2018, 123, 6958–6975. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geod. 2000, 74, 552–560. [Google Scholar] [CrossRef]
- Jekeli, C. Extent and resolution requirements for the residual terrain effect in gravity gradiometry. Geophys. J. Int. 2013, 195, 211–221. [Google Scholar] [CrossRef]
- Xian, P.; Ji, B.; Liu, B. The influence of the mass of crew on gravity gradient detection in submarine. Hydrogr. Surv. Charting 2021, 41, 32–36. [Google Scholar]
- Zhou, L.; Xiong, Z.; Yang, W.; Tang, B.; Peng, W.; Wang, Y.; Xu, P.; Wang, J.; Zhan, M. Measurement of Local Gravity via a Cold Atom Interferometer. Chin. Phys. Lett. 2011, 28, 13701. [Google Scholar] [CrossRef]
- Zhou, M.; Mao, D.; Yao, H.; Deng, X.; Luo, J.; Hu, Z.; Duan, X. Operating an atom-interferometry-based gravity gradiometer by the dual-fringe-locking method. Phys. Rev. A 2014, 90, 023617. [Google Scholar]
- Wang, P.; Li, R.; Yan, H.; Wang, J.; Zhan, M. Demonstration of a Sagnac-Type Cold Atom Interferometer with Stimulated Raman Transitions. Chin. Phys. Lett. 2007, 24, 27. [Google Scholar]
- Yu, N.; Kohel, J.M.; Kellogg, J.R.; Maleki, L. Development of an atom-interferometer gravity gradiometer for gravity measurement from space. Appl. Phys. B 2006, 84, 647–652. [Google Scholar] [CrossRef]
- Moody, M.; Paik, H.J.; Canavan, E. Three-axis superconducting gravity gradiometer for sensitive gravity experiments. Rev. Sci. Instrum. 2002, 73, 3957–3974. [Google Scholar] [CrossRef]
- McGuirk, J.M.; Bouyer, P.; Haritos, K.G.; Kasevich, M.A.; Snadden, M.J. Measurement of the Earth’s Gravity Gradient with an Atom Interferometer-Based Gravity Gradiometer. Phys. Rev. Lett. 1998, 81, 971–974. [Google Scholar]

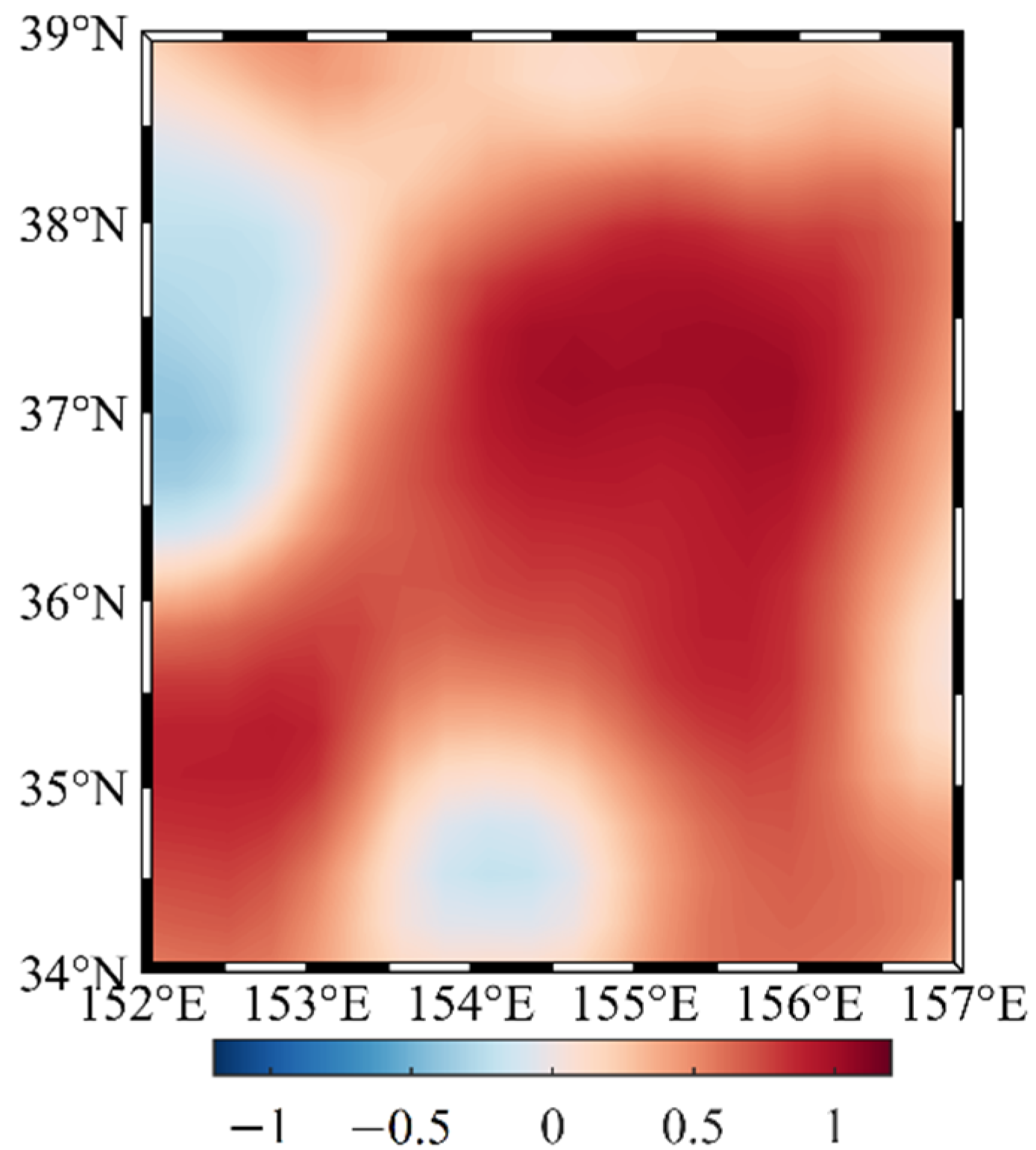
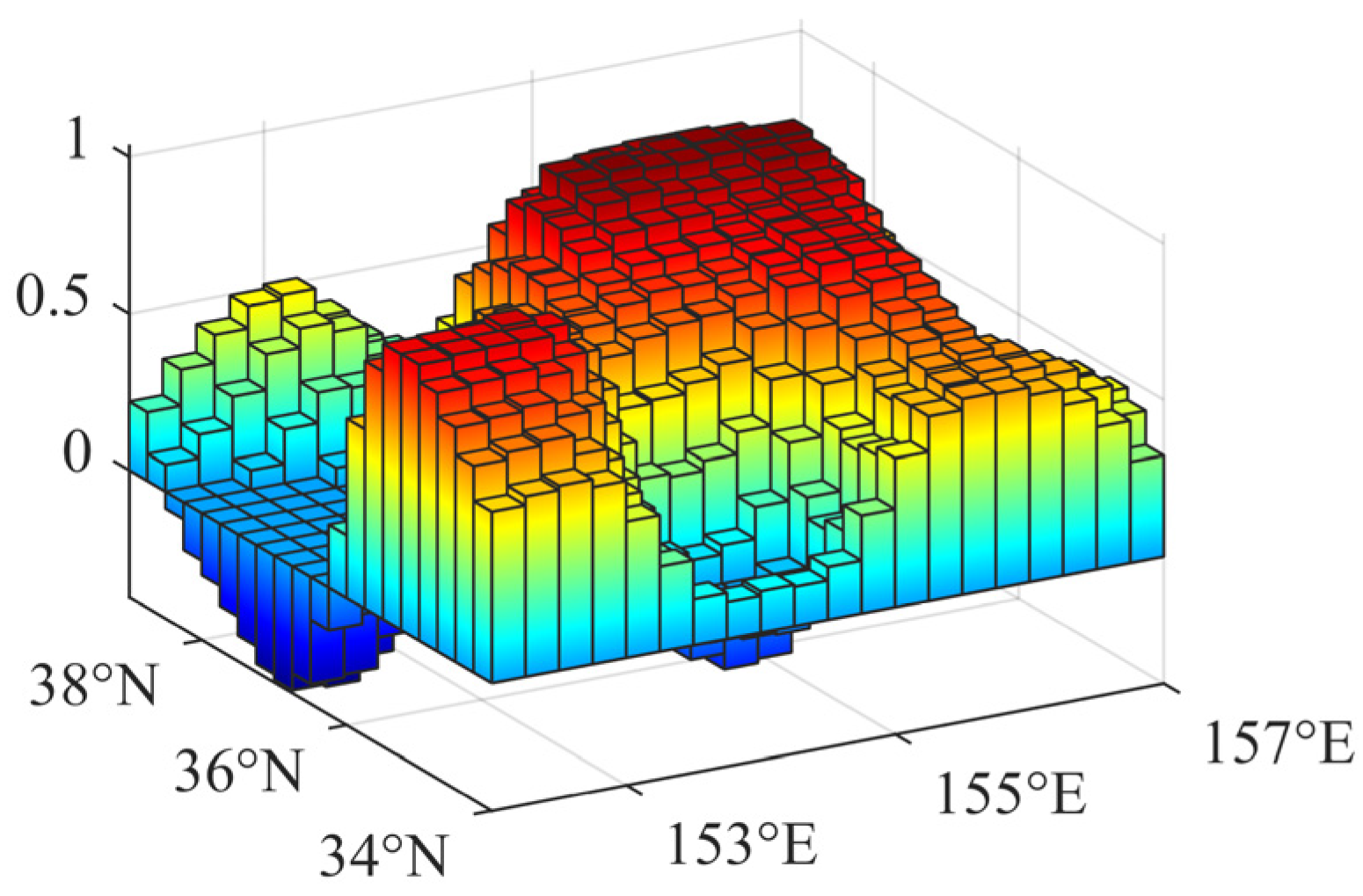
| Lat. and Lon. | Resolution | Number of Grids | Max (m) | Min (m) | STD (m) | Mean (m) |
|---|---|---|---|---|---|---|
| 34° N–39° N 152° E–157° E | 0.25° × 0.25° | 400 | 1.0347 | −0.4070 | 0.3537 | 0.4768 |
| Side Length of Integration Area (m) | Vertical Gravity Gradient at 10 m below Mean Sea Level (E) | ||
|---|---|---|---|
| Position A | Position B | Position C | |
| 4 | 1.821 | −0.874 | 0.819 |
| 8 | 6.008 | −2.813 | 2.675 |
| 12 | 10.305 | −4.687 | 4.537 |
| 16 | 13.446 | −5.952 | 5.858 |
| 20 | 15.258 | −6.603 | 6.588 |
| 24 | 16.038 | −6.818 | 6.874 |
| 28 | 16.140 | −6.765 | 6.878 |
| 32 | 15.838 | −6.566 | 6.719 |
| Side Length of Integration Area (m) | Vertical Gravity Gradient at 30 m below Mean Sea Level (E) | ||
|---|---|---|---|
| Position A | Position B | Position C | |
| 44 | 4.441 | −1.823 | 1.876 |
| 48 | 4.738 | −1.939 | 1.999 |
| 52 | 4.981 | −2.033 | 2.099 |
| 56 | 5.174 | −2.106 | 2.178 |
| 60 | 5.322 | −2.161 | 2.238 |
| 64 | 5.430 | −2.200 | 2.281 |
| 68 | 5.503 | −2.226 | 2.310 |
| 72 | 5.547 | −2.239 | 2.327 |
| Side Length of Integration Area (m) | Vertical Gravity Gradient at 50 m below Mean Sea Level (E) | ||
|---|---|---|---|
| Position A | Position B | Position C | |
| 84 | 2.966 | −1.194 | 1.242 |
| 88 | 3.045 | −1.224 | 1.275 |
| 92 | 3.113 | −1.251 | 1.303 |
| 96 | 3.172 | −1.273 | 1.327 |
| 100 | 3.220 | −1.292 | 1.347 |
| 104 | 3.262 | −1.307 | 1.364 |
| 108 | 3.295 | −1.319 | 1.377 |
| 112 | 3.320 | −1.328 | 1.387 |
| Depths | Statistics | Max | Min | Mean | STD | Range |
|---|---|---|---|---|---|---|
| 10 m | Γxx | 3.409 | −8.019 | −3.754 | 2.777 | 11.428 |
| Γyy | 3.409 | −8.019 | −3.754 | 2.777 | 11.428 | |
| Γzz | 16.038 | −6.817 | 7.509 | 5.554 | 22.855 | |
| 30 m | Γxx | 1.113 | −2.751 | −1.275 | 0.945 | 3.864 |
| Γyy | 1.113 | −2.752 | −1.275 | 0.945 | 3.865 | |
| Γzz | 5.503 | −2.226 | 2.550 | 1.890 | 7.729 | |
| 50 m | Γxx | 0.659 | −1.646 | −0.761 | 0.564 | 2.305 |
| Γyy | 0.660 | −1.648 | −0.762 | 0.565 | 2.308 | |
| Γzz | 3.295 | −1.319 | 1.524 | 1.129 | 4.614 |
| Depths | Statistics | Max | Min | Mean | STD | Range |
|---|---|---|---|---|---|---|
| 10 m | Γxx | −1.941 | −12.428 | −7.678 | 2.401 | 10.486 |
| Γyy | −1.942 | −12.428 | −7.679 | 2.401 | 10.487 | |
| Γzz | 24.856 | 3.883 | 15.357 | 4.803 | 20.973 | |
| 30 m | Γxx | −0.637 | −4.166 | −2.591 | 0.807 | 3.529 |
| Γyy | −0.637 | −4.167 | −2.591 | 0.807 | 3.530 | |
| Γzz | 8.333 | 1.274 | 5.182 | 1.614 | 7.059 | |
| 50 m | Γxx | −0.378 | −2.481 | −1.545 | 0.481 | 2.104 |
| Γyy | −0.378 | −2.484 | −1.547 | 0.482 | 2.106 | |
| Γzz | 4.966 | 0.756 | 3.092 | 0.963 | 4.210 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xian, P.; Ji, B.; Bian, S.; Liu, B. Influence of Sea Level Anomaly on Underwater Gravity Gradient Measurements. Sensors 2022, 22, 5758. https://doi.org/10.3390/s22155758
Xian P, Ji B, Bian S, Liu B. Influence of Sea Level Anomaly on Underwater Gravity Gradient Measurements. Sensors. 2022; 22(15):5758. https://doi.org/10.3390/s22155758
Chicago/Turabian StyleXian, Pengfei, Bing Ji, Shaofeng Bian, and Bei Liu. 2022. "Influence of Sea Level Anomaly on Underwater Gravity Gradient Measurements" Sensors 22, no. 15: 5758. https://doi.org/10.3390/s22155758
APA StyleXian, P., Ji, B., Bian, S., & Liu, B. (2022). Influence of Sea Level Anomaly on Underwater Gravity Gradient Measurements. Sensors, 22(15), 5758. https://doi.org/10.3390/s22155758






