Zero Moment Line—Universal Stability Parameter for Multi-Contact Systems in Three Dimensions
Abstract
:1. Introduction
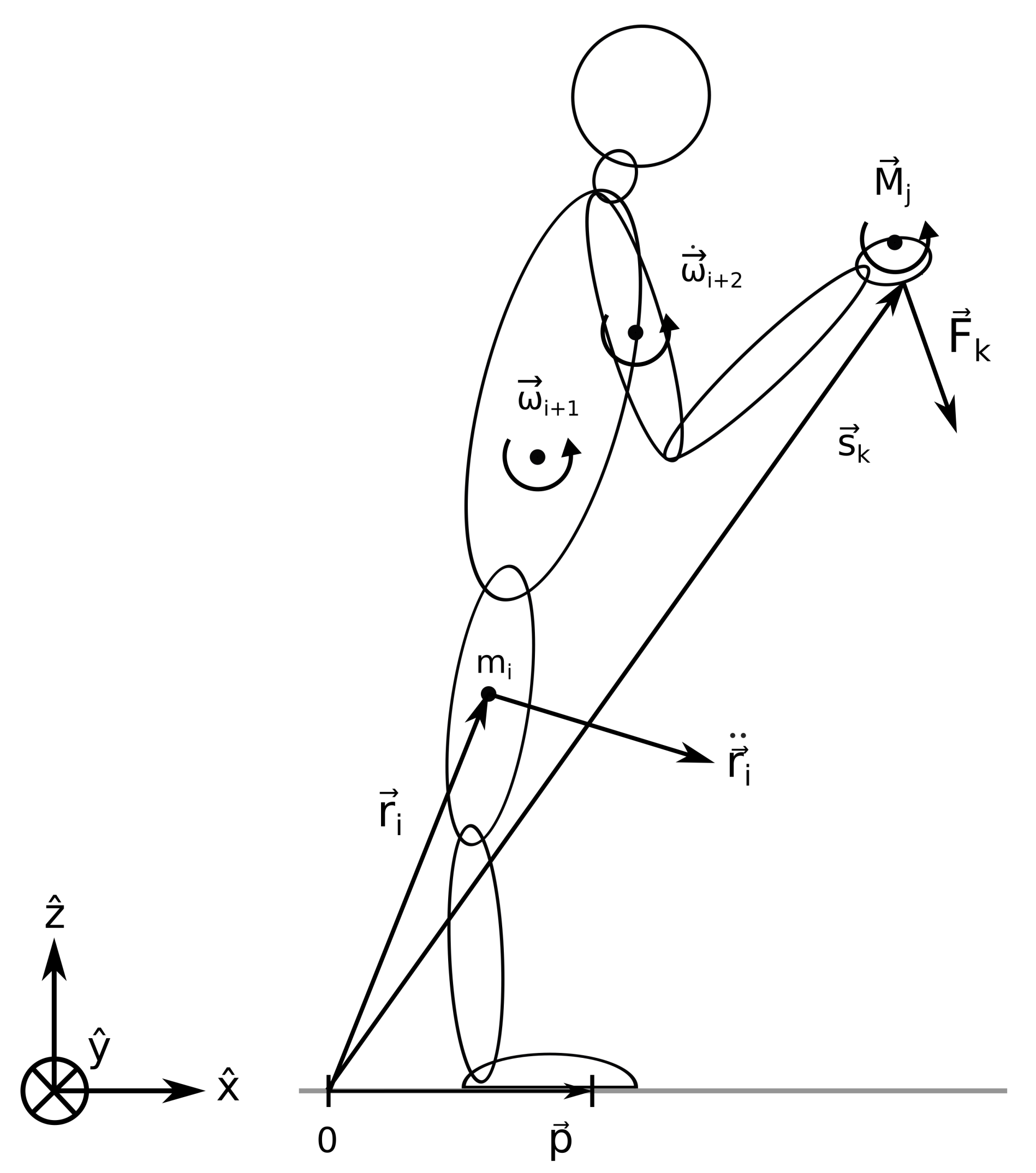
2. Methods
2.1. The Zero Moment Point
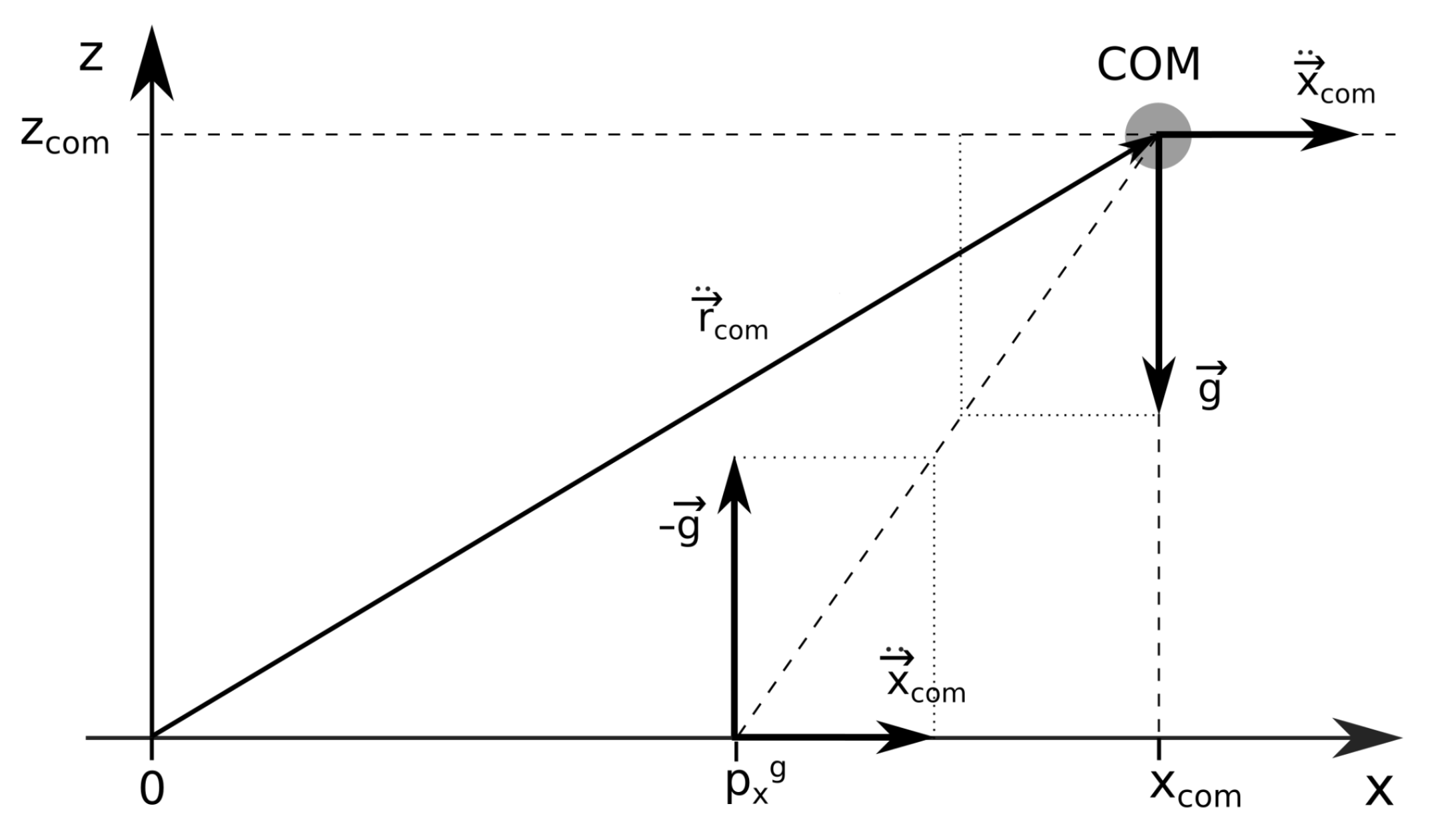
2.1.1. The Standard Definition
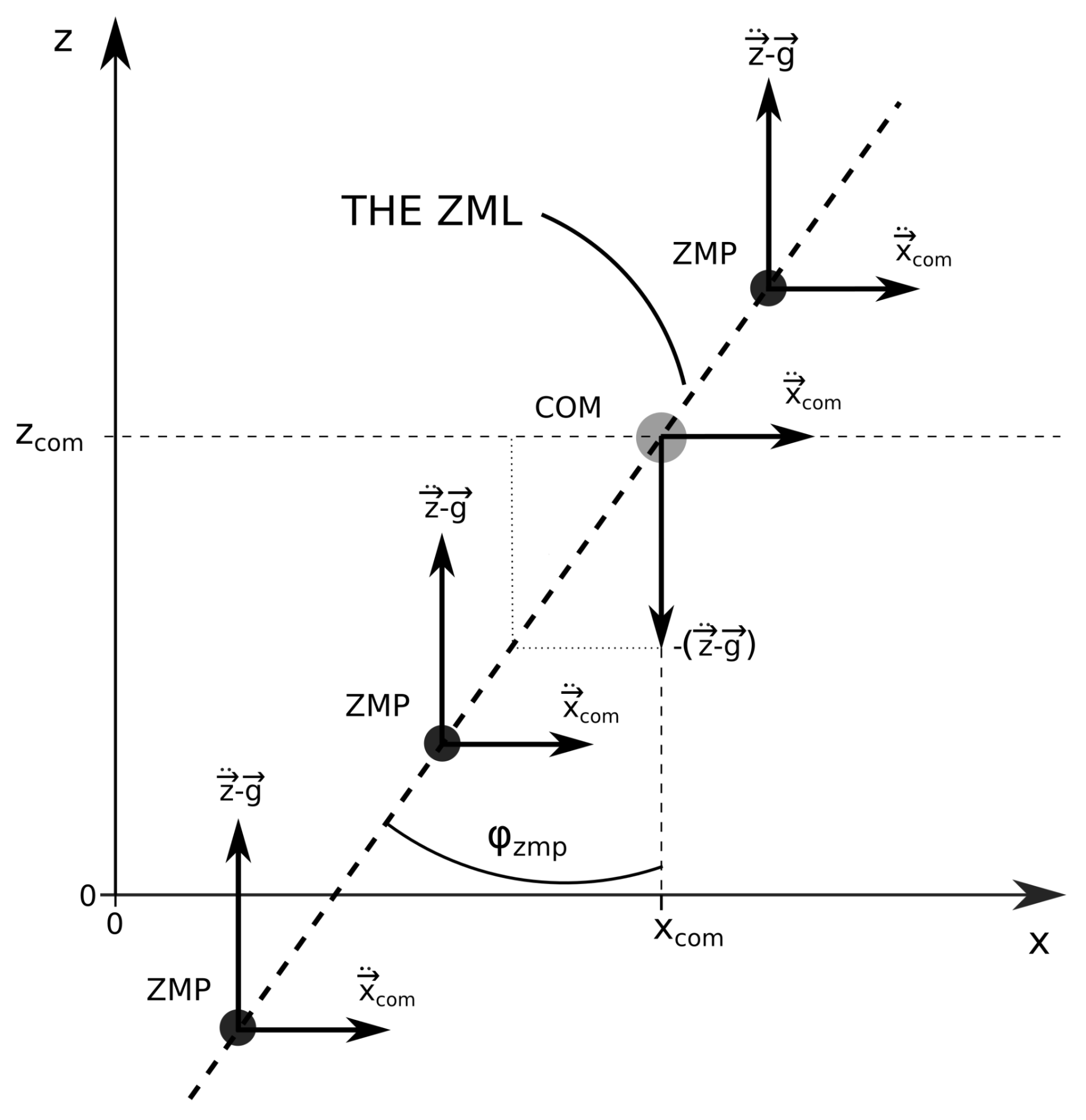
2.1.2. The Line Definition
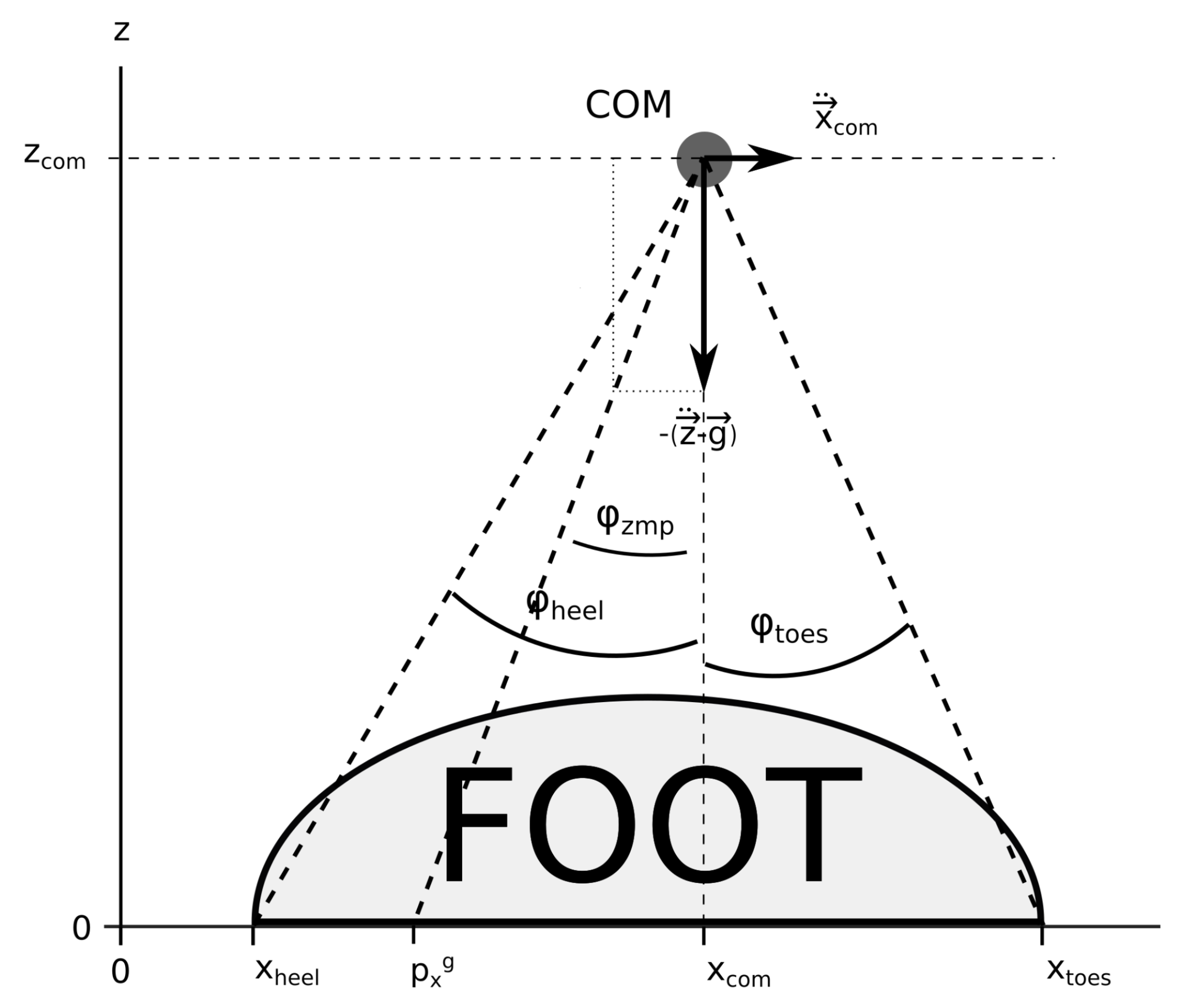
2.1.3. The Angular Definition
2.2. Stability and the Support Polygon
3. Results—Application of the Line Definition
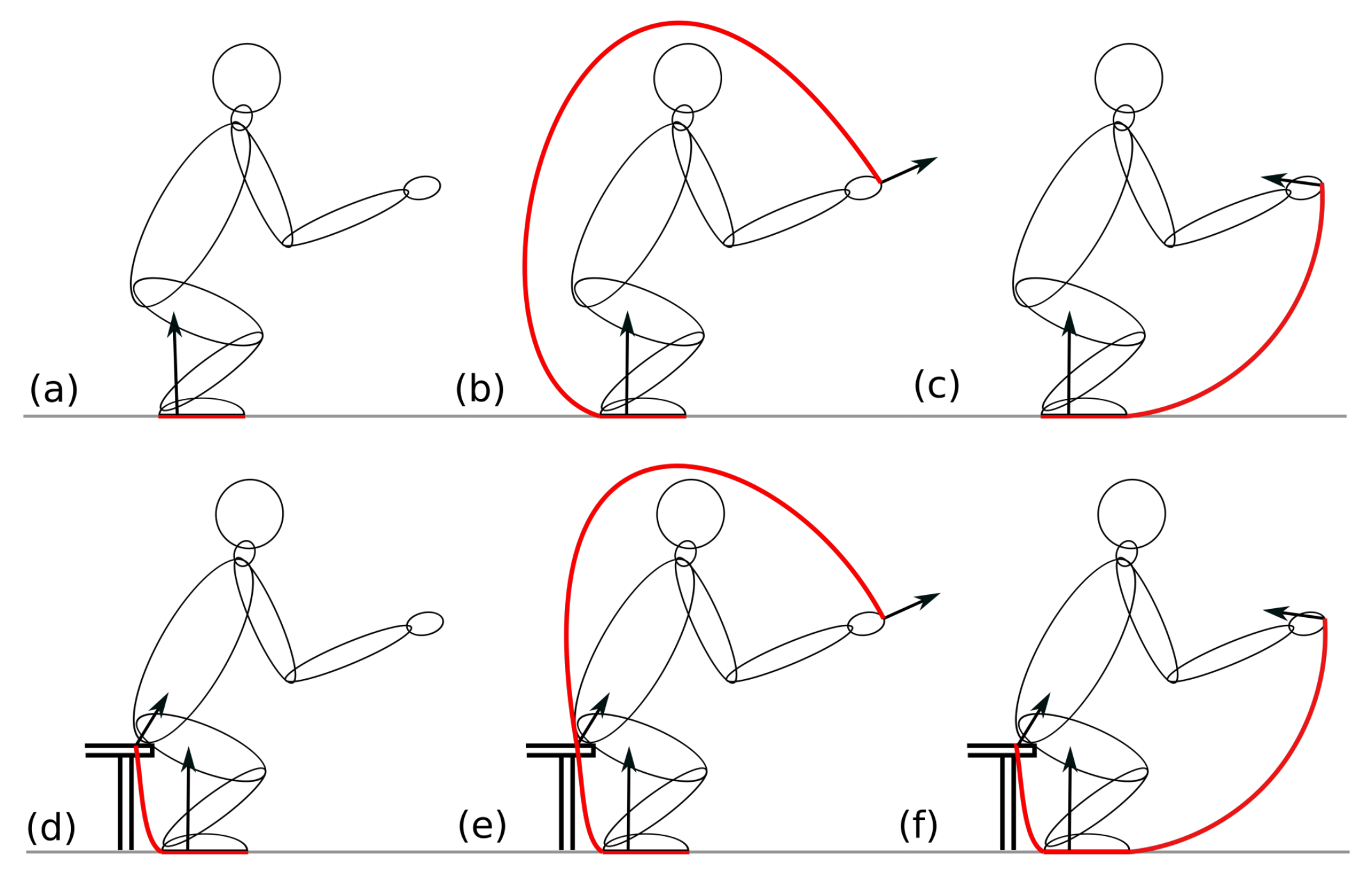
3.1. Standing Up with Help
3.2. Two Approaches for Treating a Balanced System
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ZMP | Zero moment point |
| ZML | Zero moment line |
| COM | Center of mass |
| SP | Support polygon |
Appendix A
References
- Atkeson, C.G.; Hale, J.G.; Pollick, F.; Riley, M.; Kotosaka, S.; Schaul, S.; Shibata, T.; Tevatia, G.; Ude, A.; Vijayakumar, S.; et al. Using humanoid robots to study human behavior. IEEE Intell. Syst. Their Appl. 2000, 15, 46–56. [Google Scholar] [CrossRef] [Green Version]
- Shin, D.; Sardellitti, I.; Park, Y.L.; Khatib, O.; Cutkosky, M. Design and Control of a Bio-inspired Human-friendly Robot. Int. J. Robot. Res. 2010, 29, 571–584. [Google Scholar] [CrossRef] [Green Version]
- Petrič, T.; Žlajpah, L.; Garofalo, G.; Ott, C. Walking Control Using Adaptive Oscillators Combined with Dynamic Movement Primitives. In Proceedings of the 22nd International Workshop on Robotics in Alpe-Adria-Danube Region, Portoroz, Slovenia, 11–13 September 2013. [Google Scholar]
- Ijspeert, A.J. Central pattern generators for locomotion control in animals and robots: A review. Neural Netw. 2008, 21, 642–653. [Google Scholar] [CrossRef] [PubMed]
- Righetti, L.; Ijspeert, A. Programmable central pattern generators: An application to biped locomotion control. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, (ICRA 2006), Orlando, FL, USA, 15–19 May 2006; Volume 2006, pp. 1585–1590. [Google Scholar] [CrossRef] [Green Version]
- Dadashzadeh, B.; Vejdani, H.R.; Hurst, J. From template to anchor: A novel control strategy for spring-mass running of bipedal robots. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2566–2571. [Google Scholar] [CrossRef]
- Liu, G.H.; Chen, M.Z.; Chen, Y. When joggers meet robots: The past, present, and future of research on humanoid robots. Bio-Des. Manuf. 2019, 2, 108–118. [Google Scholar] [CrossRef]
- Hosoda, K.; Sakaguchi, Y.; Takayama, H.; Takuma, T. Pneumatic-driven jumping robot with anthropomorphic muscular skeleton structure. Auton. Robot. 2010, 28, 307–316. [Google Scholar] [CrossRef]
- Nagasaka, K.; Kuroki, Y.; Suzuki, S.; Itoh, Y.; Yamaguchi, J. Integrated motion control for walking, jumping and running on a small bipedal entertainment robot. In Proceedings of the IEEE International Conference on Robotics and Automation, (Proceedings, ICRA ’04), New Orleans, LA, USA, 26 April–1 May 2004; Volume 4, pp. 3189–3194. [Google Scholar] [CrossRef]
- Nashihin, D.; Dimas Pristovani, R.; Sandi Marta, B.; Dewanto, R.S.; Pramadihanto, D. Multivariable Control for Jumping Mechanism of T-FLoW Humanoid Robot. In Proceedings of the 2018 International Electronics Symposium on Engineering Technology and Applications (IES-ETA), Bali, Indonesia, 29–30 October 2018; pp. 260–265. [Google Scholar] [CrossRef]
- Petrič, T.; Gams, A.; Babič, J.; Žlajpah, L. Reflexive stability control framework for humanoid robots. Auton. Robot. 2013, 34, 347–361. [Google Scholar] [CrossRef]
- Vukobratovič, M.; Juričić, D. Contribution to the synthesis of biped gait. IEEE Trans.-Bio-Med. Eng. 1969, 16, 1–6. [Google Scholar] [CrossRef]
- Vukobratovič, M.; Borovac, B. Zero-Moment Point—Thirty Five Years of its Life. Int. J. Hum. Robot. 2004, 1, 157–173. [Google Scholar] [CrossRef]
- Goswami, A. Postural Stability of Biped Robots and the Foot-Rotation Indicator (FRI) Point. Int. J. Robot. Res. 1999, 18, 523–533. [Google Scholar] [CrossRef]
- Sardain, P.; Bessonnet, G. Gait Analysis of a Human Walker wearing Robot Feet as Shoes. In Proceedings of the 2001 IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001. [Google Scholar]
- Sugihara, T.; Nakamura, Y.; Inoue, H. Real-time humanoid motion generation through ZMP manipulation based on inverted pendulum control. In Proceedings of the Proceedings 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 2, pp. 1404–1409. [Google Scholar] [CrossRef]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Fujiwara, K.; Harada, K.; Yokoi, K.; Hirukawa, H. Resolved Momentum Control: Humanoid Motion Planning Based on the Linear and Angular Momentum. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), Las Vegas, NV, USA, 27–31 October 2003; Volume 2, pp. 1644–1650. [Google Scholar] [CrossRef]
- Sardain, P.; Bessonnet, G. Forces acting on a biped robot. Center of pressure-zero moment point. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2004, 34, 630–637. [Google Scholar] [CrossRef]
- Baskoro, A.S.; Priyono, M.G. Design of humanoid robot stable walking using inverse kinematics and zero moment point. In Proceedings of the 2016 International Electronics Symposium (IES), Denpasar, Indonesia, 29–30 September 2016; pp. 335–339. [Google Scholar] [CrossRef]
- Pristovani, R.D.; Henfri, B.E.; Sanggar, D.; Dadet, P. Walking strategy model based on zero moment point with single inverted pendulum approach in “T-FLoW” humanoid robot. In Proceedings of the 2017 2nd International conferences on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 1–2 November 2017; pp. 217–222. [Google Scholar] [CrossRef]
- Mummolo, C.; Mangialardi, L.; Kim, J.H. Numerical Estimation of Balanced and Falling States for Constrained Legged Systems. J. Nonlinear Sci. 2017, 27, 1291–1323. [Google Scholar] [CrossRef]
- Kim, J.H. Multi-Axis Force-Torque Sensors for Measuring Zero-Moment Point in Humanoid Robots: A Review. IEEE Sens. J. 2020, 20, 1126–1141. [Google Scholar] [CrossRef]
- Harada, K.; Kajita, S.; Kaneko, K.; Hirukawa, H. Dynamics and balance of a humanoid robot during manipulation tasks. IEEE Trans. Robot. 2006, 22, 568–575. [Google Scholar] [CrossRef]
- Cisneros, R.; Yokoi, K.; Yoshida, E. Yaw moment compensation by using full body motion. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 119–125. [Google Scholar] [CrossRef]
- Dai, H.; Valenzuela, A.; Tedrake, R. Whole-body motion planning with centroidal dynamics and full kinematics. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; pp. 295–302. [Google Scholar] [CrossRef]
- Audren, H.; Vaillant, J.; Kheddar, A.; Escande, A.; Kaneko, K.; Yoshida, E. Model preview control in multi-contact motion-application to a humanoid robot. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4030–4035. [Google Scholar] [CrossRef] [Green Version]
- Henze, B.; Ott, C.; Roa, M.A. Posture and balance control for humanoid robots in multi-contact scenarios based on Model Predictive Control. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 3253–3258. [Google Scholar] [CrossRef]
- Harada, K.; Hirukawa, H.; Kanehiro, F.; Fujiwara, K.; Kaneko, K.; Kajita, S.; Nakamura, M. Dynamical balance of a humanoid robot grasping an environment. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No.04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 2, pp. 1167–1173. [Google Scholar] [CrossRef] [Green Version]
- Hirukawa, H.; Hattori, S.; Harada, K.; Kajita, S.; Kaneko, K.; Kanehiro, F.; Fujiwara, K.; Morisawa, M. A universal stability criterion of the foot contact of legged robots-adios ZMP. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, (ICRA 2006), Orlando, FL, USA, 15–19 May 2006; pp. 1976–1983. [Google Scholar] [CrossRef]
- Yu, Z.; Ming, C.L.; Dinesh, M.; Albertus, H.A.; Chee-Meng, C. A Walking Pattern Generator for Biped Robots on Uneven Terrains. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010. [Google Scholar]
- Sentis, L.; Park, J.; Khatib, O. Compliant Control of Multicontact and Center-of-Mass Behaviors in Humanoid Robots. IEEE Trans. Robot. 2010, 26, 483–501. [Google Scholar] [CrossRef] [Green Version]
- Nikolic, M.; Borovac, B.; Raković, M. Dynamic balance preservation and prevention of sliding for humanoid robots in the presence of multiple spatial contacts. Multibody Syst. Dyn. 2018, 42, 197–218. [Google Scholar] [CrossRef]
- Caron, S.; Pham, Q.C.; Nakamura, Y. Stability of Surface Contacts for Humanoid Robots: Closed-Form Formulae of the Contact Wrench Cone for Rectangular Support Areas. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; Volume 2015. [Google Scholar] [CrossRef] [Green Version]
- Caron, S.; Pham, Q.C.; Nakamura, Y. Leveraging Cone Double Description for Multi-contact Stability of Humanoids with Applications to Statics and Dynamics. In Proceedings of the Robotics: Science and Systems (RSS), Roma, Italy, July 16-17 2015. [Google Scholar] [CrossRef]
- Caron, S.; Kheddar, A. Multi-contact walking pattern generation based on model preview control of 3D COM accelerations. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; pp. 550–557. [Google Scholar] [CrossRef] [Green Version]
- Audren, H.; Kheddar, A.; Gergondet, P. Stability polygons reshaping and morphing for smooth multi-contact transitions and force control of humanoid robots. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; pp. 1037–1044. [Google Scholar] [CrossRef] [Green Version]
- Caron, S.; Pham, Q.C.; Nakamura, Y. ZMP Support Areas for Multi-contact Mobility Under Frictional Constraints. IEEE Trans. Robot. 2017, 33, 67–80. [Google Scholar] [CrossRef] [Green Version]
- Mummolo, C.; Peng, W.Z.; Gonzalez, C.; Kim, J.H. Contact-Dependent Balance Stability of Biped Robots. J. Mech. Robot. 2018, 10, 021009. [Google Scholar] [CrossRef] [Green Version]
- Bouyarmane, K.; Caron, S.; Escande, A.; Kheddar, A. Multi-contact Motion Planning and Control. In Humanoid Robotics: A Reference; Goswami, A., Vadakkepat, P., Eds.; Springer Nature: Berlin/Heidelberg, Germany, 2018; pp. 1763–1804. [Google Scholar] [CrossRef]
- Morisawa, M.; Benallegue, M.; Cisneros, R.; Kumagai, I.; Escande, A.; Kaneko, K.; Kanehiro, F. Multi-Contact Stabilization of a Humanoid Robot for Realizing Dynamic Contact Transitions on Non-coplanar Surfaces. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 2252–2258. [Google Scholar] [CrossRef]
- Brecelj, T.; Petrič, T. Angular Dependency of the Zero Moment Point. Adv. Serv. Ind. Robot. 2021, 102, 135–144. [Google Scholar]
- Brecelj, T.; Petrič, T. Application of the Angular Dependency of the Zero Moment Point. In Proceedings of the 8th International Conference on Electrical, Electronics and Computing Engineering IcETRAN 2021 and 65th National Conference on Electronics, Telecommunication, Computing, Automatic Control and Nuclear Engineering ETRAN 2021, Bijeljina, Bosnia and Herzegovina, 8–10 September 2021; pp. 591–596. [Google Scholar]
- Kajita, S.; Tani, K. Study of dynamic biped locomotion on rugged terrain-derivation and application of the linear inverted pendulum mode. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; Volume 2, pp. 1405–1411. [Google Scholar] [CrossRef]
- Force Plates. Available online: http://www.btsbioengineering.com/products/infini-t-force-platform/ (accessed on 2 June 2022).
- Force Sensors. Available online: https://www.ati-ia.com/products/ft/ft_models.aspx?id=Nano25 (accessed on 2 June 2022).
- OptiTrack. Available online: https://optitrack.com/ (accessed on 2 June 2022).
- Motive. Available online: https://optitrack.com/software/motive/ (accessed on 2 June 2022).




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brecelj, T.; Petrič, T. Zero Moment Line—Universal Stability Parameter for Multi-Contact Systems in Three Dimensions. Sensors 2022, 22, 5656. https://doi.org/10.3390/s22155656
Brecelj T, Petrič T. Zero Moment Line—Universal Stability Parameter for Multi-Contact Systems in Three Dimensions. Sensors. 2022; 22(15):5656. https://doi.org/10.3390/s22155656
Chicago/Turabian StyleBrecelj, Tilen, and Tadej Petrič. 2022. "Zero Moment Line—Universal Stability Parameter for Multi-Contact Systems in Three Dimensions" Sensors 22, no. 15: 5656. https://doi.org/10.3390/s22155656
APA StyleBrecelj, T., & Petrič, T. (2022). Zero Moment Line—Universal Stability Parameter for Multi-Contact Systems in Three Dimensions. Sensors, 22(15), 5656. https://doi.org/10.3390/s22155656





