Reconfigurable Security Architecture (RESA) Based on PUF for FPGA-Based IoT Devices
Abstract
:1. Introduction
Research Goal Summary
- The authentication procedure based on PUF shall have enough CRPs for IoT product lifetimes. This approach shall not increase the size of the PUF circuit on the chip.
- The solution shall be compatible with modular system designs on FPGAs (as discussed in Section 2.1).
- The solution shall have resiliency against machine learning attacks.
- The proposed solution shall follow the initial promise of PUFs to provide a lightweight security solution without cryptographic primitives.
2. Background and Related Work
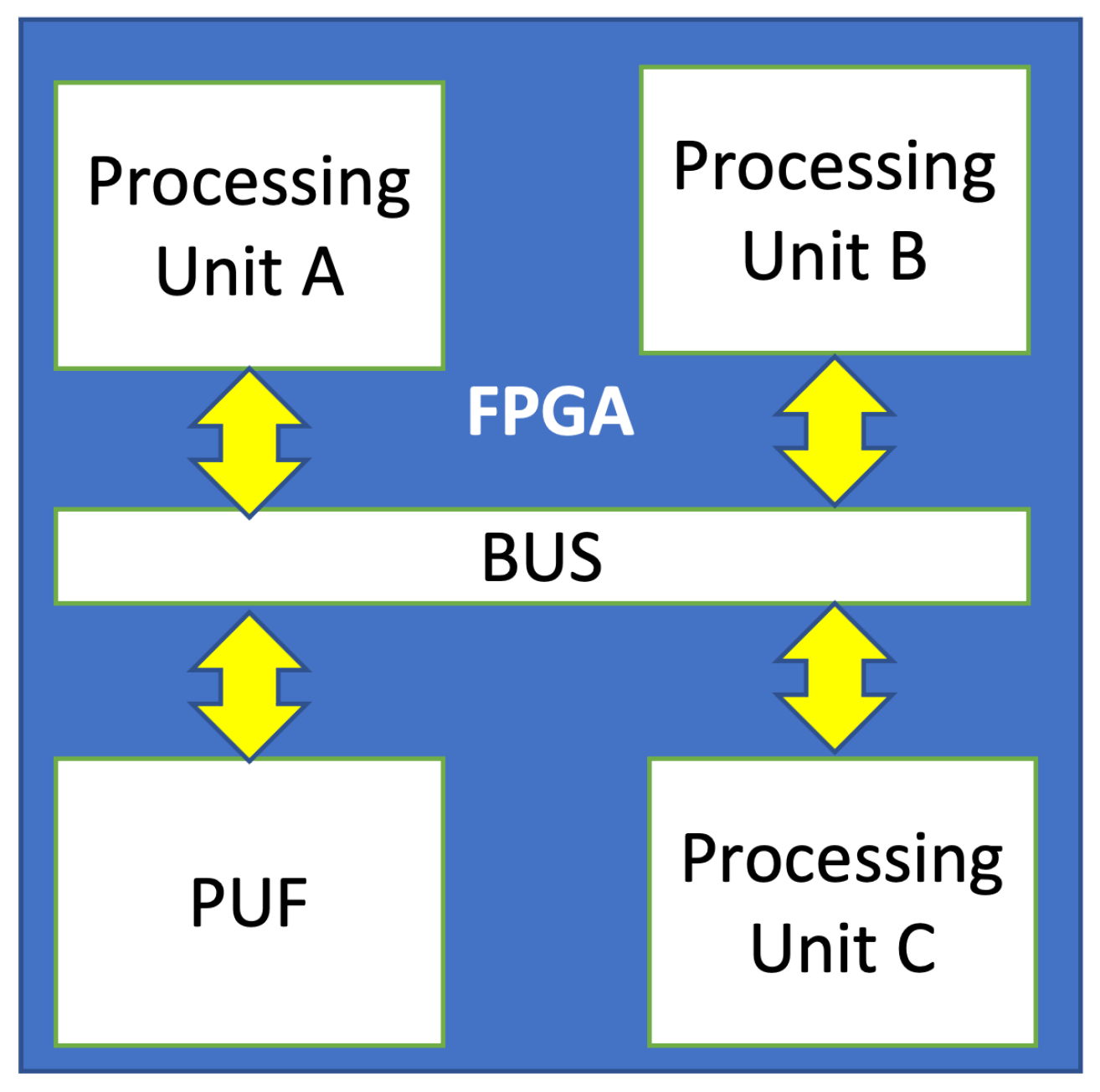
2.1. FPGAs in IoT Devices
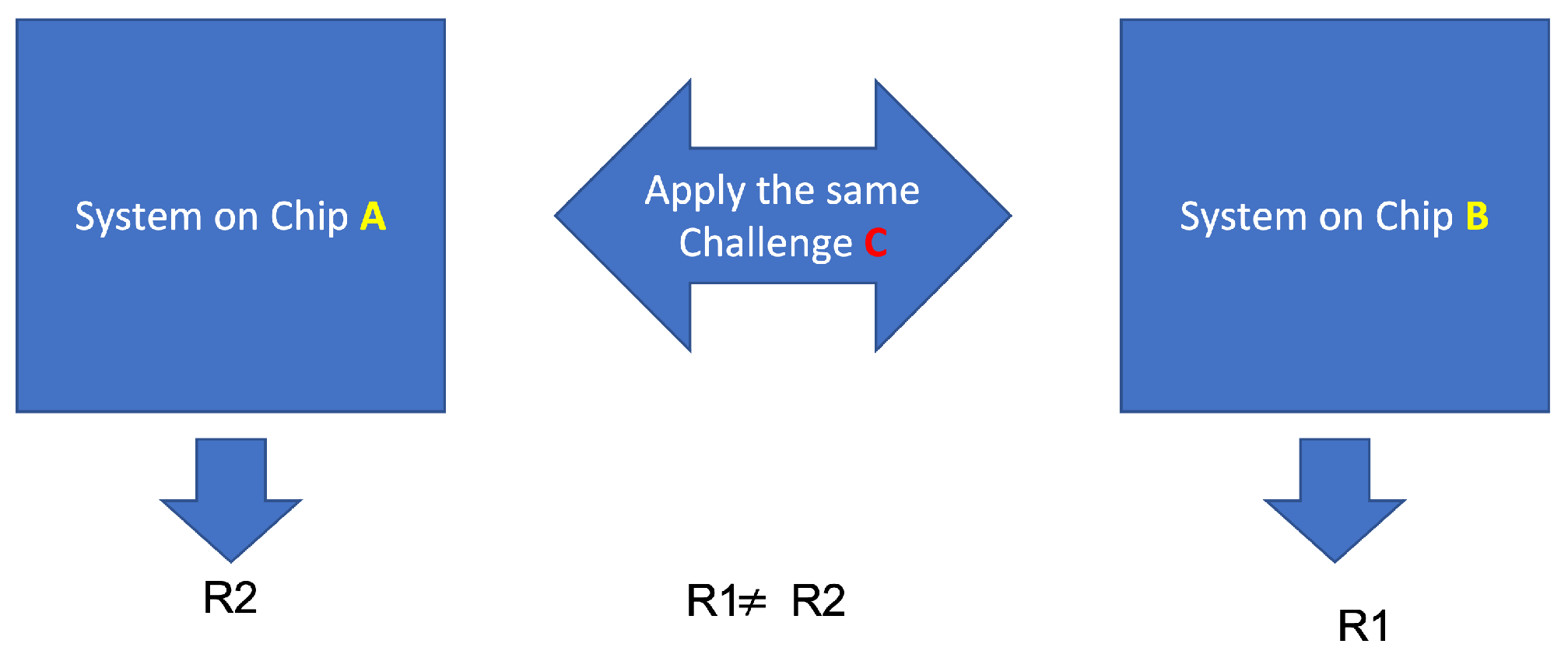
2.2. What Is a PUF?
2.3. PUF Architecture Selection
2.4. PUF Applications
2.5. PUF Attack Overview
2.6. PUF Resiliency against ML Attacks
2.7. CRPs vs. Lifetime
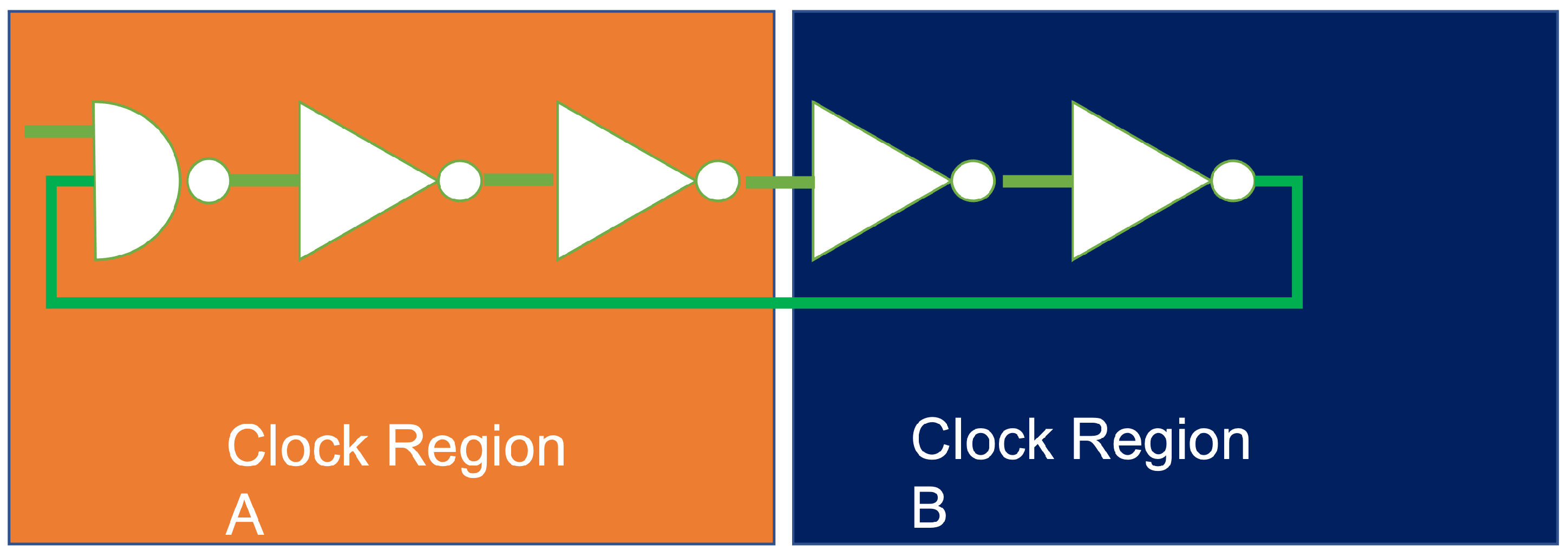
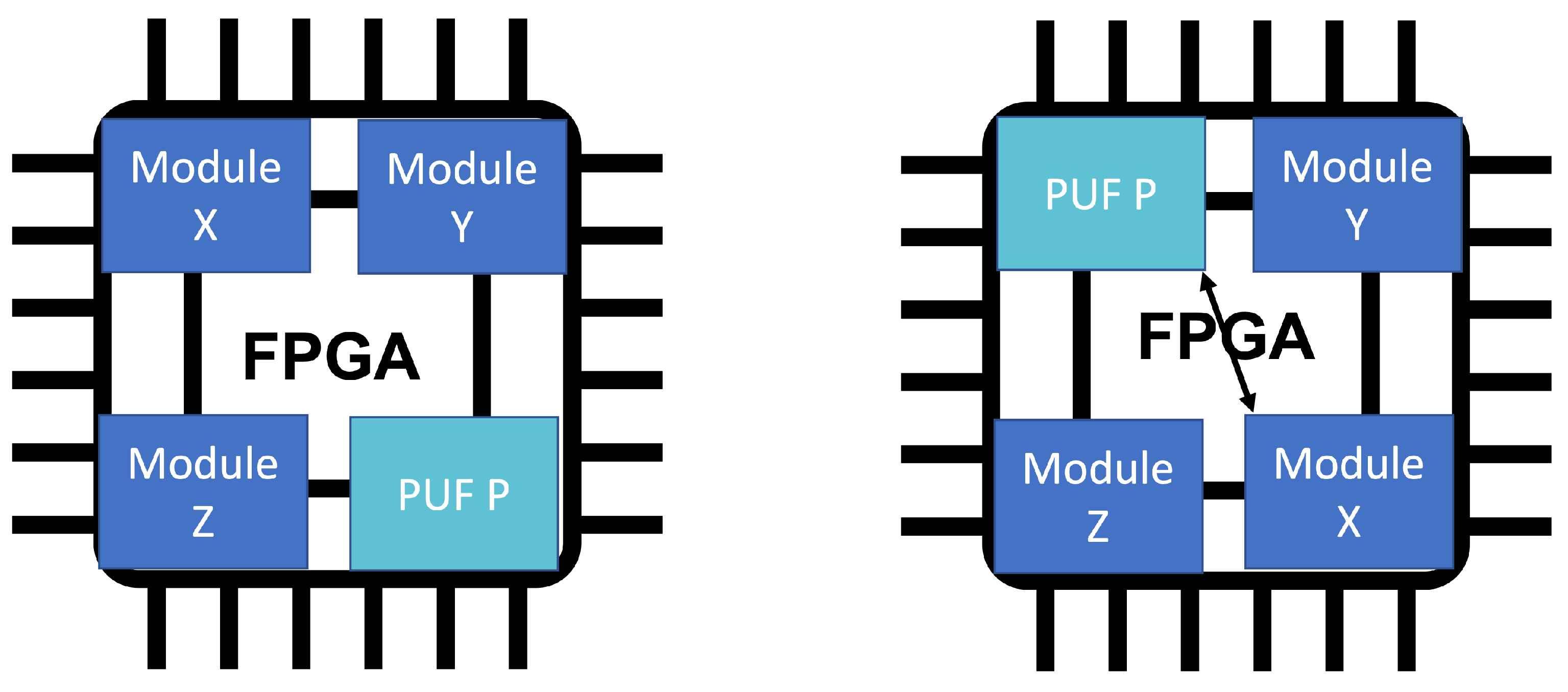
3. Extended Spatial PUF
4. The RESA PUF Protocols
4.1. Underlying Assumptions and Notation
4.2. A Straightforward Solution
- Research on ML attacks continuously reduces the numbers of CRPs required to accurately model a PUF [25]. Hence, once a threshold is set in practice, there is no guarantee that this threshold will remain secure in the future.
- If we select the threshold to a low value, we would lose many of the available CRPs and would thereby greatly reduce the operational lifetimes of the devices.
- An attacker may query the device on certain placements to model the PUF independently of genuine authentication requests by the server. While the impact of such a scenario could be reduced by time gating mechanisms, the attacker would still be able to perform some queries and thereby bypass the threshold.
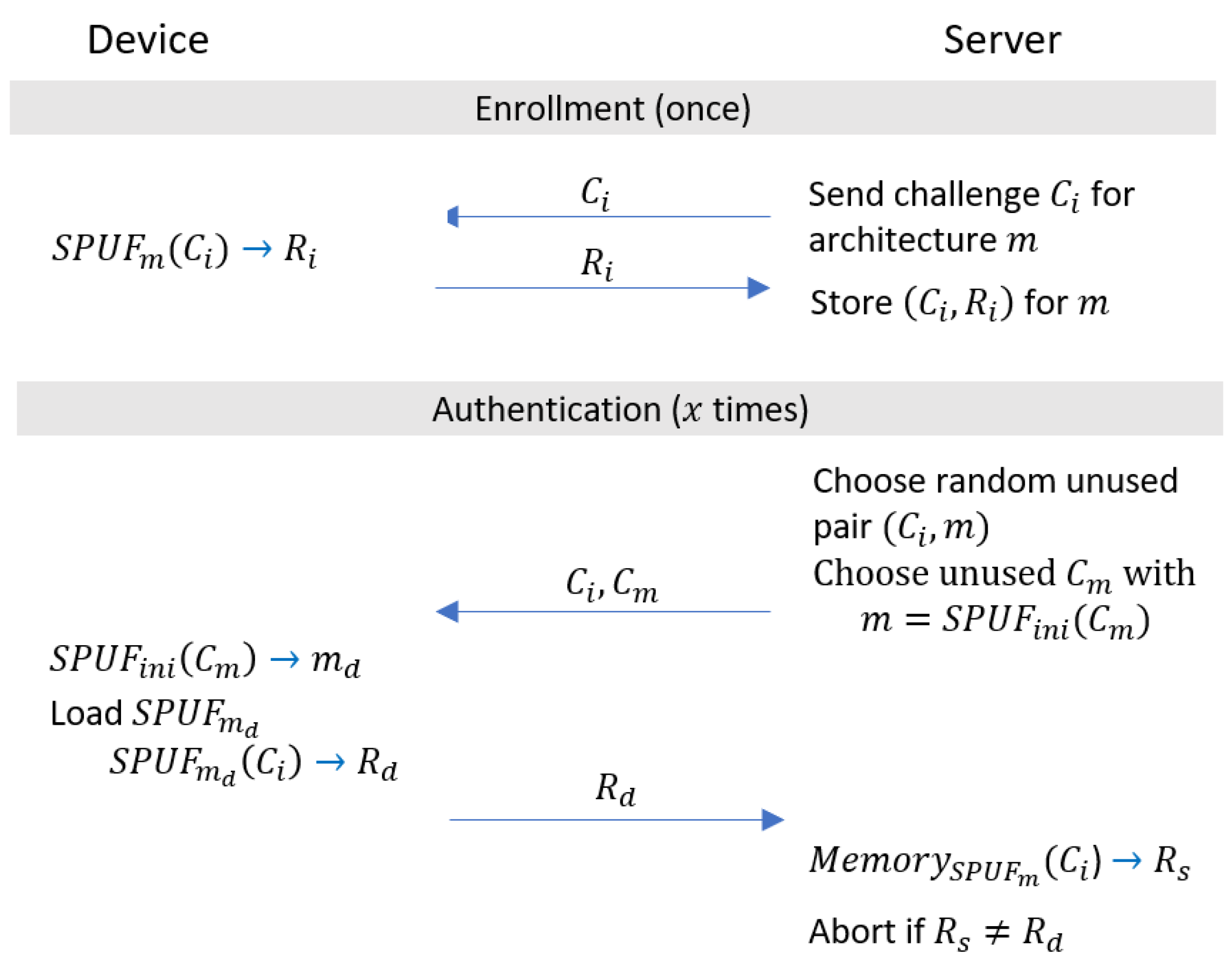
4.3. RESA-P Authentication Protocol
- Encrypting the placement: Not possible, since we want to avoid cryptographic functions, which may become insecure over time.
- Fixing an order during enrollment: Not possible, since the order (e.g., a seed of a PRNG or sequential list of placements) is confidential and needs to be stored in a dedicated secure memory, which may not be available on low resource devices.
4.3.1. Enrollment Phase
4.3.2. Authentication Phase
4.3.3. Security Proof
4.3.4. Re-Using CRPs
4.4. RESA-PC Authentication Protocol
- The challenge of the CRP is communicated in the open;
- There can only be possible CRPs, which the attacker can infer by observing the challenges communicated by the server.
4.4.1. Enrollment Phase
4.4.2. Authentication Phase
4.4.3. Security Proof
4.4.4. Re-Using CRPs
5. Evaluation
5.1. Test Strategy
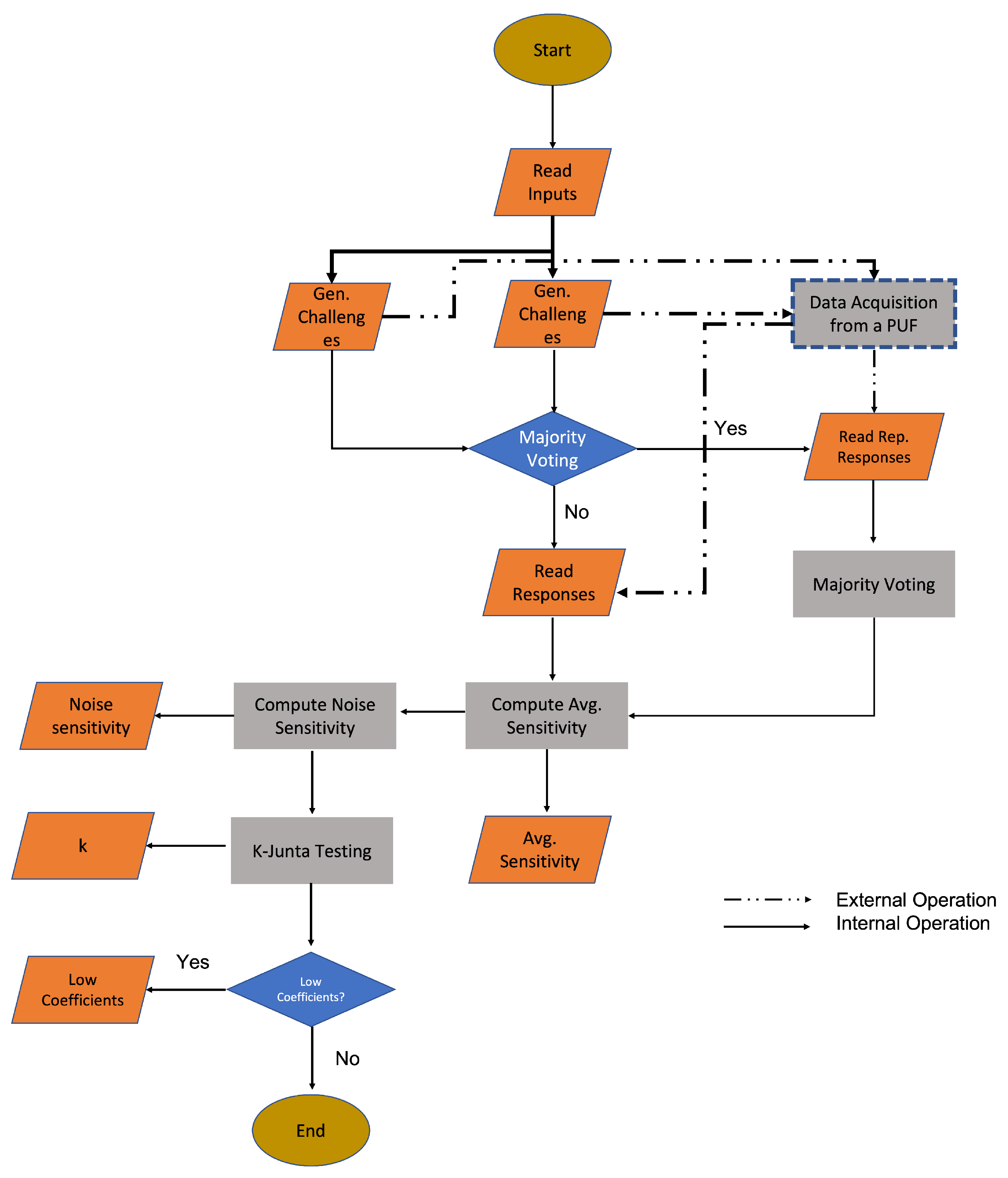
5.2. PUFmeter Testing Procedure
5.3. PUFmeter Validation
5.4. Evaluating the RESA PUF Authentication Protocol
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Maes, R. Physically Unclonable Functions: Constructions, Properties and Applications (Fysisch Onkloonbare Functies: Constructies, Eigenschappen en Toepassingen). Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2012. [Google Scholar]
- Merli, D. Attacking and Protecting Ring Oscillator Physical Unclonable Functions and Code-Offset Fuzzy Extractors. Ph.D. Thesis, Technische Universität München, München, Germany, 2014. [Google Scholar]
- An akumar, N.N.; Hashmi, M.S.; Tehranipoor, M. FPGA-Based Physical Unclonable Functions: A Comprehensive Overview of Theory and Architectures; Elsevier: Amsterdam, The Netherlands, 2021; pp. 175–194. [Google Scholar]
- Shamsoshoara, A.; Korenda, A.; Afghah, F.; Zeadally, S. A survey on physical unclonable function (PUF)-based security solutions for Internet of Things. Comput. Netw. J. 2020, 183, 107593. [Google Scholar] [CrossRef]
- Burger, A.; Cichiwskyj, C.; Schmeißer, S.; Schiele, G. The Elastic Internet of Things—A platform for self-integrating and self-adaptive IoT-systems with support for embedded adaptive hardware. In Future Generation Computer Systems; Elsevier: Amsterdam, The Netherlands, 2020; pp. 607–619. [Google Scholar]
- Babaei, A.; Schiele, G. Spatial reconfigurable physical unclonable functions for the internet of things. In Proceedings of the International Conference on Security, Privacy and Anonymity in Computation, Communication and Storage, Guangzhou, China, 18–20 December 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 312–321. [Google Scholar]
- Xilinx. Partial Reconfiguration, Vivado Design Suit User Guide. UG909 (v2020.1) February 2022. Available online: https://docs.xilinx.com/v/u/2020.1-English/ug909-vivado-partial-reconfiguration (accessed on 20 June 2022).
- Rührmair, U.; Sehnke, F.; Sölter, J.; Dror, G.; Devadas, S.; Schmidhuber, J. Modeling attacks on physical unclonable functions. In Proceedings of the 17th ACM Conference on Computer and Communications Security, Chicago, IL, USA, 4–8 October 2010; pp. 237–249. [Google Scholar]
- Babaei, A.; Schiele, G. Physical unclonable functions in the internet of things: State of the art and open challenges. Sensors 2019, 19, 3208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cristina, A.-G.; Iluminada, B. Calibration of Ring Oscillator PUF and TRNG. In Proceedings of the 2020 European Conference on Circuit Theory and Design (ECCTD), Sofia, Bulgaria, 7–10 September 2020; pp. 1–4. [Google Scholar]
- Mahshid, D.; Sattar, M.; Javad, M. A Ring Oscillator-Based PUF With Enhanced Challenge-Response Pairs. Can. J. Electr. Comput. Eng. 2016, 39, 174–180. [Google Scholar]
- Dodis, Y.; Reyzin, L.; Smith, A. Fuzzy Extractors: How to Generate Strong Keys from Biometrics and Other Noisy Data. In Advances in Cryptology—EUROCRYPT 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 523–540. [Google Scholar]
- Becker, G.T. The gap between promise and reality: On the insecurity of xor arbiter pufs. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 535–555. [Google Scholar]
- Standaert, F.X. Introduction to side-channel attacks. In Secure Integrated Circuits and Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 27–42. [Google Scholar]
- Ganji, F. On the Learnability of Physically Unclonable Functions; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Mahmoud, A.; Rührmair, U.; Majzoobi, M.; Koushanfar, F. Combined modeling and side channel attacks on strong pufs. IACR Cryptol. ePrint Arch. 2013, 632, 2013. [Google Scholar]
- Kumar, R.; Burleson, W. Hybrid modeling attacks on current-based pufs. In Proceedings of the 2014 IEEE 32nd International Conference on Computer Design (ICCD), Seoul, Korea, 19–22 October 2014; pp. 493–496. [Google Scholar]
- Xu, X.; Burleson, W. Hybrid side-channel/machine-learning attacks on pufs: A new threat? In Proceedings of the Conference on Design, Automation & Test in Europe, Dresden, Germany, 24–28 March 2014; p. 349. [Google Scholar]
- Katzenbeisser, S.; Kocabaş, Ü.; Van Der Leest, V.; Sadeghi, A.-R.; Schrijen, G.-J.; Wachsmann, C. Recyclable pufs: Logically reconfigurable pufs. J. Cryptogr. Eng. 2011, 1, 177. [Google Scholar] [CrossRef]
- Jin, Y.; Xin, W.; Sun, H.; Chen, Z. Puf-based rfid authentication protocol against secret key leakage. In Proceedings of the Asia-Pacific Web Conference, Kunming, China, 11–13 April 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 318–329. [Google Scholar]
- Kocabaş, Ü.; Peter, A.; Katzenbeisser, S.; Sadeghi, A.-R. Converse puf-based authentication. In Proceedings of the International Conference on Trust and Trustworthy Computing, Vienna, Austria, 13–15 June 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 142–158. [Google Scholar]
- Ganji, F.; Tajik, S.; Stauss, P.; Seifert, J.-P.; Forte, D.; Tehranipoor, M. Rock’n’roll PUFs: Crafting Provably Secure PUFs from Less Secure Ones. In Proceedings of the 8th International Workshop on Security Proofs for Embedded Systems, Atlanta GA, USA, 24 August 2019; pp. 33–48. [Google Scholar]
- Yu, M.-D.; Hiller, M.; Delvaux, J.; Sowell, R.; Devadas, S.; Verbauwhede, I. A lockdown technique to prevent machine learning on pufs for lightweight authentication. IEEE Trans. Multi-Scale Comput. Syst. 2016, 2, 146–159. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Li, G.; Ma, H.; Al-Sarawi, S.F.; Kavehei, O.; Abbott, D.; Ranasinghe, D.C. Obfuscated challenge-response: A secure lightweight authentication mechanism for puf-based pervasive devices. In Proceedings of the 2016 IEEE International Conference on Pervasive Computing and Communication Workshops (PerCom Workshops), Sydney, NSW, Australia, 14–18 March 2016; pp. 1–6. [Google Scholar]
- Ganji, F.; Forte, D.; Seifert, J.P. PUFmeter A Property Testing Tool for Assessing the Robustness of Physically Unclonable Functions to Machine Learning Attacks. IEEE Access 2019, 7, 122513–122521. [Google Scholar] [CrossRef]
- Linial, N.; Mansour, Y.; Nisan, N. Constant Depth Circuits, Fourier Transform, and Learnability. J. ACM 1993, 40, 607. [Google Scholar] [CrossRef]


| Region AB | Region AD | Region ABDE | Region BE | Region BC | Region BCEF | Region CF | Region EF | Region DE | |
|---|---|---|---|---|---|---|---|---|---|
| Distance from Opt. Value | 5% | 3% | 4.5% | 6% | 8% | 2% | 7% | 3.5% | 4% |
| Region A | Region B | Region C | Region D | Region E | Region F | Region AB | |
| Region A | |||||||
| Region B | 1% | ||||||
| Region C | 0% | 2% | |||||
| Region D | 8% | 8% | 2% | ||||
| Region E | 4% | 3% | 1% | 6% | |||
| Region F | 1% | 5% | 1% | 5% | 3% | ||
| Region AB | 6% | 7% | 5% | 3% | 2% | 4% | |
| Region AD | 5% | 3% | 1% | 4% | 7% | 2% | 6% |
| Region ABDE | 7% | 4% | 8% | 2% | 5% | 1% | 3% |
| Region BE | 2% | 3% | 5% | 0% | 4% | 7% | 1% |
| Region BC | 1% | 1% | 7% | 9% | 4% | 5% | 5% |
| Region BCEF | 4% | 4% | 9% | 4% | 2% | 8% | 3% |
| Region CF | 8% | 5% | 3% | 2% | 4% | 1% | 5% |
| Region EF | 3% | 7% | 8% | 2% | 6% | 8% | 5% |
| Region DE | 4% | 2% | 0% | 7% | 8% | 5% | 6% |
| Region AD | Region ABDE | Region BE | Region BC | Region BCEF | Region CF | Region EF | |
| Region AD | |||||||
| Region ABDE | 7% | ||||||
| Region BE | 3% | 6% | |||||
| Region BC | 7% | 3% | 9% | ||||
| Region BCEF | 6% | 8% | 1% | 6% | |||
| Region CF | 3% | 2% | 1% | 7% | 5% | ||
| Region EF | 6% | 5% | 4% | 8% | 3% | 9% | |
| Region DE | 7% | 4% | 1% | 8% | 5% | 6% | 1% |
| Metrics & Techniques | Description | Interpretation | Theoretical Bound |
|---|---|---|---|
| Average sensitivity (p) | Average influence of challenge bits on the responses (over all challenge bits) | Smaller values correlate to higher probability of learning | |
| Noise Sensitivity () | Total impact of flipping bits (with probability ) on the responses | Smaller values correlate to higher probability of learning | |
| K-junta Testing (k) | Number of influential bits | Smaller values correlate to higher probability of learning | |
| LMN Algorithm | Finding a small portion of the Fourier spectral determining the responses | Fewer and smaller coefficients correlate to higher probability of learning | N/A |
| Average Sensitivity | Noise Sensitivity | K-Junta Determinant Variables | Coefficients | Conclusion |
|---|---|---|---|---|
| 5.694882 | 0.1961122 | 2 | 0.73529, 0.32353 | PUF is vulnerable to K-junta Testing |
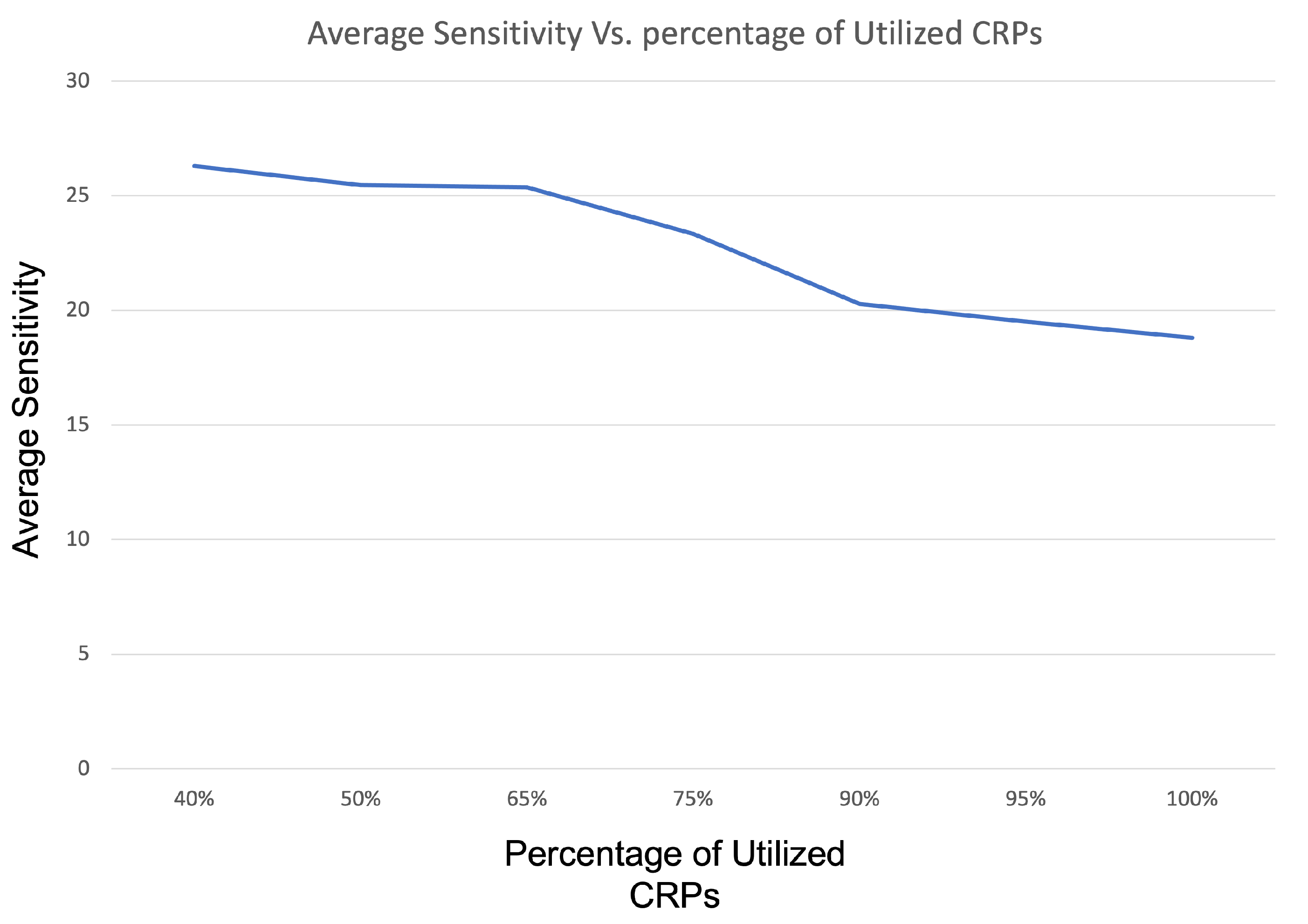
| Percentage CRP | Number of CRPs | Average Sensitivity | Noise Sensitivity | K-Junta Determinant Variable |
|---|---|---|---|---|
| 40 | 19,508 | 26.292 | 0.24544 | 13 |
| 50 | 24,384 | 25.455 | 0.24151 | 13 |
| 65 | 31,700 | 25.367 | 0.24539 | 12 |
| 75 | 36,576 | 23.337 | 0.24661 | 13 |
| 90 | 43,892 | 20.284 | 0.2467 | 13 |
| 95 | 46,330 | 19.496 | 0.24738 | 13 |
| 100 | 48,768 | 18.804 | 0.24701 | 13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babaei, A.; Schiele, G.; Zohner, M. Reconfigurable Security Architecture (RESA) Based on PUF for FPGA-Based IoT Devices. Sensors 2022, 22, 5577. https://doi.org/10.3390/s22155577
Babaei A, Schiele G, Zohner M. Reconfigurable Security Architecture (RESA) Based on PUF for FPGA-Based IoT Devices. Sensors. 2022; 22(15):5577. https://doi.org/10.3390/s22155577
Chicago/Turabian StyleBabaei, Armin, Gregor Schiele, and Michael Zohner. 2022. "Reconfigurable Security Architecture (RESA) Based on PUF for FPGA-Based IoT Devices" Sensors 22, no. 15: 5577. https://doi.org/10.3390/s22155577
APA StyleBabaei, A., Schiele, G., & Zohner, M. (2022). Reconfigurable Security Architecture (RESA) Based on PUF for FPGA-Based IoT Devices. Sensors, 22(15), 5577. https://doi.org/10.3390/s22155577







