1. Introduction
Currently, there has been a growing interest in monitoring marine ecosystems for scientific research, military applications, and commercial exploitation [
1]. The UWSN is the most effective method of monitoring the marine environment. In principle, the UWSN is a wireless communication network comprised of tens or hundreds of battery-powered sensor nodes [
2]. Unlike wireless connections between ground sensors, the underwater channel has a high latency and low bandwidth, which uses a lot of power. In addition, changing or recharging a battery in UWSNs is far more complex than in ground WSNs. That is why the current security algorithms struggle with power usage [
3]. Due to the constrained resources, the sensor nodes suffer from an energy consumption problem [
4]. Therefore, almost all of the existing research and technology on UWSNs is focused on power savings at the expense of security and capability.
Security is one of the key elements in the design of the UWSNs’ protocol and mechanism. As a result of their low cost and proximity to the events they monitor, sensor nodes are prime targets for malicious attacks of many kinds. In addition, the public communication channel makes it possible for any device to participate in the flow of information. Therefore, an attacker might easily control the sensors and unsecured UWSN communication lines. The research available on UWSNs focuses on self-organization, communication, flexibility, low power consumption, and adaptability. Unfortunately, the current studies have a lot of limitations when it comes to how well UWSNs can resist security threats, because resources are very limited, and the security situation is usually server-based because of certain data and communication sites [
5].
In the context of security, authentication is necessary. Global WSN authentication solutions, such as public-based RSA [
6] and Blom’s symmetric matrix multiplication algorithm [
7], have been presented, but they do not work for UWSNs because of their increased computational and communicational complexity. As a result, UWSNs require the development of an authentication system based on signatures [
8].
A digital signature is a common solution for ensuring data authenticity in UWSNs. However, traditional digital signature schemes are based on expensive scaler point multiplication of the ECC, hyperelliptic curve devisor multiplication, and bilinear pairing operations, limiting their transmission to resource-limited devices such as sensors and IoT devices. An alternate solution to the problem is to utilize an offline/online signature, where the signature process is divided into online and offline phases. The offline phase performs computationally intensive tasks, while the online phase produces the signature on the message in real time. When installed on UWSNs, the gateway can simplify the online signature to generate authentic messages. Reducing the communication bandwidth and computation time is the key to the actual use of an online/offline signature technique. However, ensuring both the security and effectiveness of an online/offline approach in the real world remains a challenge. This is the main focus of the current paper.
1.1. Motivation and Contributions
The computation time and communication overhead are inversely related to the hardness of the underlying security concerns that must be spent on signature formation. Traditional signature techniques such as RSA and bilinear pairing, both of which are based on sub-exponential issues, need a significant amount of computation time and communication overhead and are not suitable for devices that have limited resources. Elliptic curve cryptography (ECC) is utilized instead. Their fundamental issue is a fully exponential one, and it is possible to generate their signatures in a significantly shorter amount of time.
However, it is still challenging to find a cryptographic solution that is appropriate for UWSNs. There are hardly any articles that concentrate on the cryptographic security and privacy for UWSNs [
9,
10,
11,
12,
13,
14]. However, bilinear pairing with elliptic curves is used to apply authenticity in various environments [
15]. Since HEC has a higher efficiency and a shorter key length than ECC, bilinear pairing, and RSA, it is often regarded as the most compact and effective form of cryptographic mechanisms. In the proposed work, we focused on proposing a new security solution for UWSNs devices by dividing our algorithm into online and offline phases to further reduce the computational time and communication bandwidth during the device operation. The contributions to this paper are as follows:
Firstly, we propose a new certificateless online/offline signature scheme based on a hyperelliptic curve cryptosystem for underwater wireless sensor networks.
Secondly, we present the generic syntax of the proposed certificateless online/offline signature scheme for underwater wireless sensor networks.
Thirdly, we provide the mathematical construction for the proposed certificateless online/offline signature scheme for underwater wireless sensor networks. The construction is actually an extension of the syntax. The designed approach offers the security necessity of unforgeability against both type one and type two adversaries, an antireplay attack.
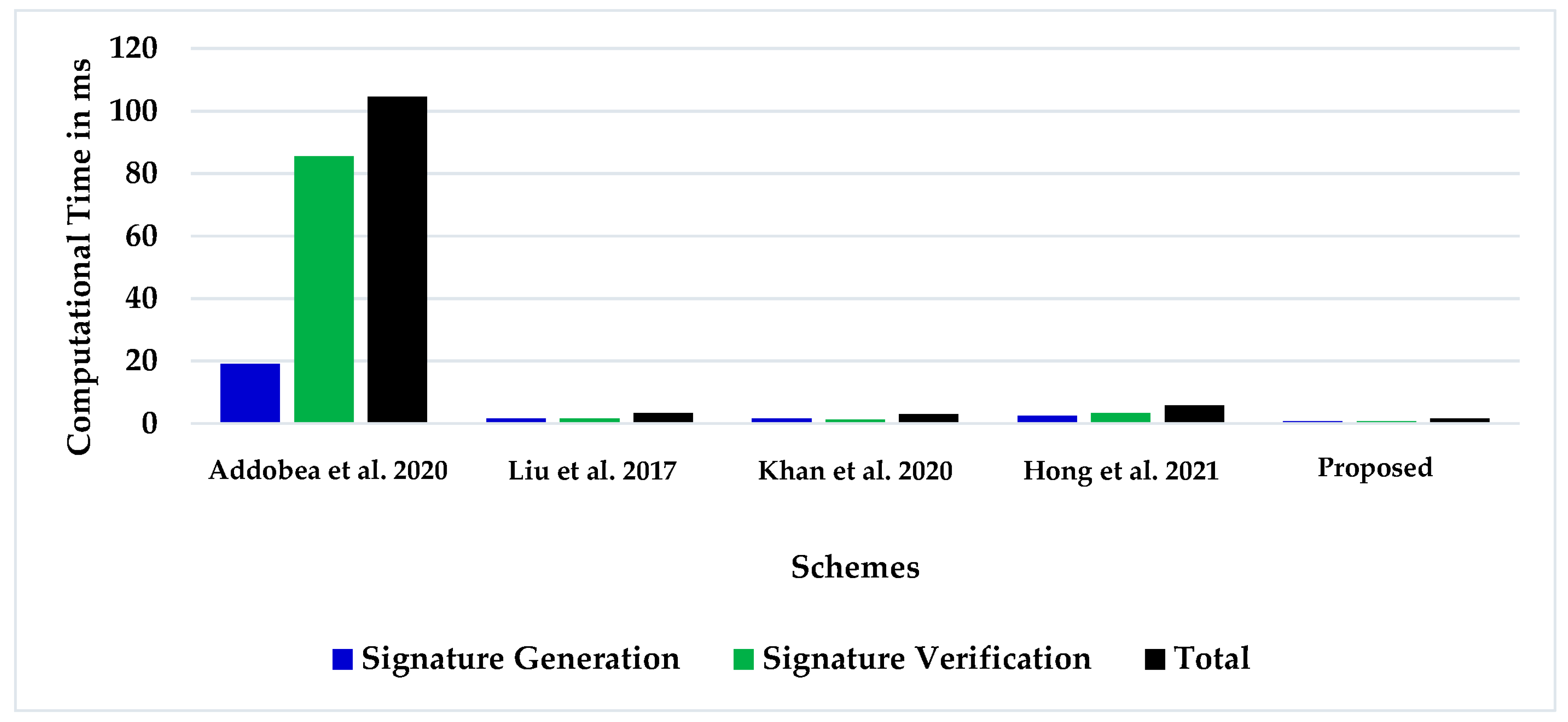
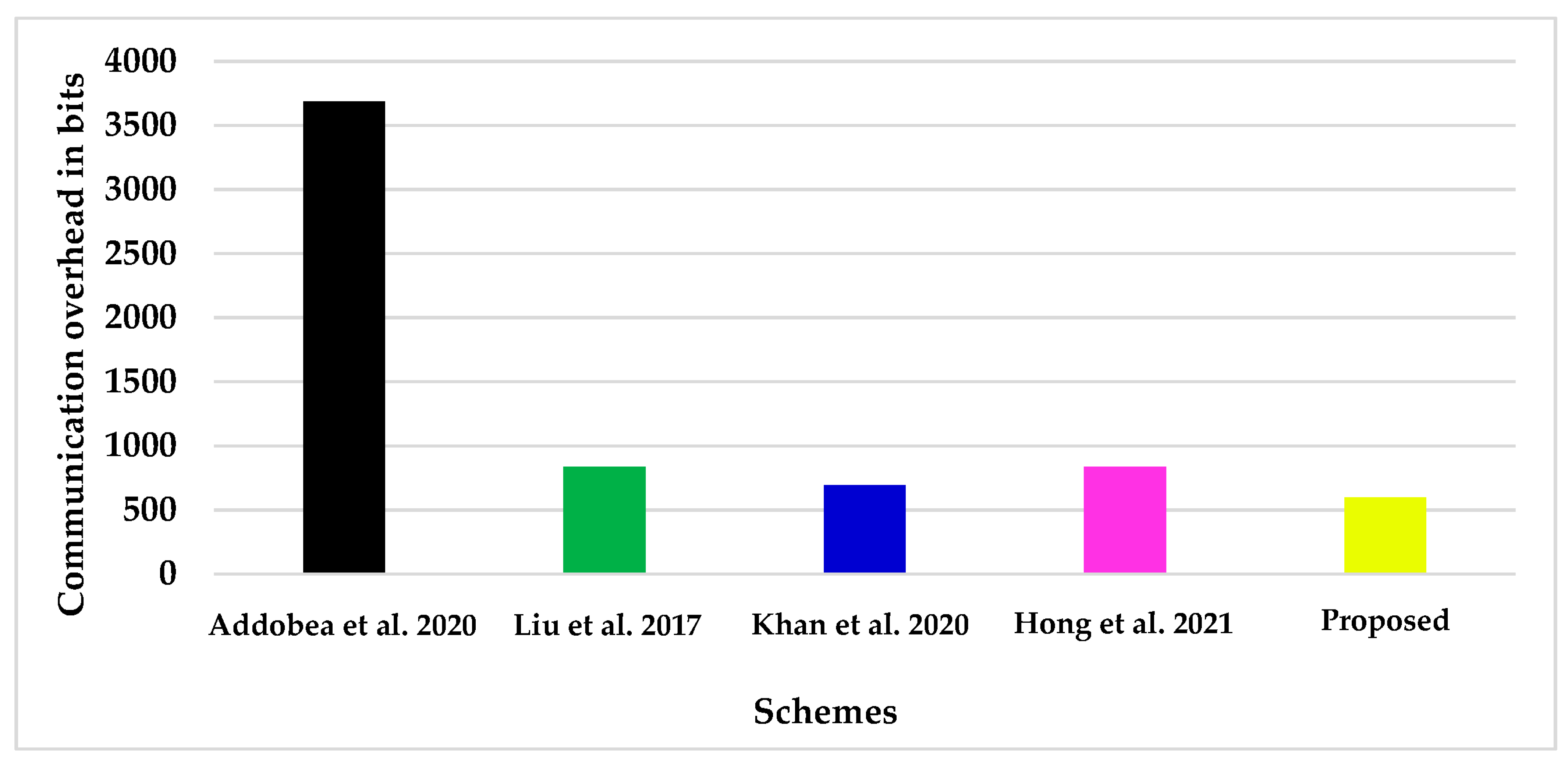
Finally, we compared the computational and communicational overhead of our proposed method with earlier certificateless online and offline signature solutions. According to the findings, the proposed strategy uses significantly fewer computing and communication resources than earlier solutions.
1.2. Paper Organization
In the upcoming section (i.e.,
Section 2), we will review the existing literature.
Section 3 presents our proposed network and the construction of an online/offline signature for UWSNs.
Section 4, presents the deployment of the proposed scheme on UWSNs.
Section 5 presents the formal security analysis and
Section 6 added the performance analysis.
Section 7 is a review of our contributions while
Section 8 concludes the research.
2. Related Works
Related studies have been presented to secure the UWSNs in recent years [
9,
10,
11,
12,
13,
14]. Unfortunately, the present key management and cryptographic solutions have some common problems, including computational and communicational complexity and the expansion of ciphertext [
4]. Therefore, in the proposed approach, we considered an online/offline signature with a lightweight hyperelliptic curve cryptosystem to reduce the computational and communicational complexities for UWSN communications.
Table 1 summarizes the related works.
Evan, Goldreich, and Micali [
16] proposed the online/offline signature concept in 1990. The authors divided the signing algorithm into two phases: online and offline. In the absence of a message, heavier computations are transferred to the offline phase, while lighter computations are performed online. During the production process or whenever the device’s power is connected, offline action can be conducted on the background computation device. Shamir and Thuman [
17] refined the Trapdoor hash function-based online/offline signature technique in 2001. This improves the online efficiency. However, the technique increases the signature costs and has a trapdoor leak issue. In 2007, Chen [
18] created an online/offline signature system employing the dual trapdoor hash function. However, in normal situations, neither method works.
Recently, Liu et al. [
19] proposed an identity-based online/offline signature using the elliptic curve discrete logarithm problem (ECDLP). Addobea et al. [
20] proposed COOS for mobile health devices in 2020. This study aims to reduce the computational and communication resources required by mobile health devices. According to Xu and Zeng [
21], the propose scheme of Addobea et al. [
20] is unable to accomplish correctness, a key security property that should be provided by a signature scheme. In the same year, Khan et al. [
22] provided a new COOS solution for IoHT employing hyperelliptic curve discrete logarithm problem hardness (HCDLP). According to Hussain et al. [
23], the given approach of Khan et al. [
22] is insecure when subject to adaptive chosen message attacks. It has been proven that an adversary can fake a valid signature on a message by substituting their own public key in place of the one that is supposed to be used. An attribute-based online/offline signature system for mobile crowdsourcing was presented in 2021 by Hong et al. [
24]. Sadly, the authors did not present a mathematical or network model. The solution is theoretical.
Table 1.
Summary of the literature.
Table 1.
Summary of the literature.
| Authors Name & Reference No. | Advantages | Limitations |
|---|
| Liu et al. [19] | | |
| Addobea et al. [20] | | |
| Khan et al. [22] | | Insecure when subject to adaptive chosen message attacks [ 23]
|
| Hong et al. [24] | | |
The above schemes are based on sophisticated cryptographic methods, i.e., bilinear pairing and ECC, and thus combined with the high cost of computation and communication. These approaches are therefore not compatible with UWSNs equipped with minimal computation and communication resources. To construct an effective cryptographic solution for UWSNs that requires minimal computational resources, there is a critical need for a more concrete and efficient online/offline signature scheme. Our design scheme is based on the HCC, which is a generalized form of an elliptic curve.
3. Construction of the Proposed Scheme
3.1. Security Threats
In certificateless public key cryptography, two types of adversaries are considered i.e., type-1 () and type-2 ().
The certificateless signature scheme has a unique security concept in comparison to those used by traditional signature schemes. According to the definitions found in [
25], a certificateless signature scheme ought to take into account two distinct kinds of adversaries: a Type-I (
) adversary and a Type-II (
) adversary. The adversary
is meant to stand in for a typical threat posed by a third party against the certificateless signature scheme. This means that
does not have access to the master key, but it is able to request public keys and replace existing public keys with values of its choosing. The adversarial
is a representation of a malicious Key Generation Center (KGC) that is responsible for generating users’ partial private keys. It is permissible for the adversary
to have access to the master key, but they are not authorized to replace the target user’s public key.
3.2. Hyperelliptic Curve Cryptosystem (HEC)
Koblitz [
26] is the one who first introduced the hyperelliptic curve cryptosystem (HEC), which belongs to a class of algebraic curves. It is also possible to think of it as a more generalized version of the elliptic curves cryptosystem (ECC) [
27]. The HEC points, as opposed to ECC points, cannot be obtained from a group in any way [
28]. The additive Abelian group that can be generated from a devisor is the subject of computation by the HEC. In comparison to RSA, bilinear pairing, and ECC, the HEC’s parameter size is significantly smaller while maintaining the same level of security. This makes the HEC appealing to resource-constrained devices.
The curve whose genus value is 1 is typically referred to as the ECC curve.
Figure 1 [
29] illustrates a HEC that has a genus that is higher than 1. In a similar manner, the group order of the finite field (
.) for the (genus = 1) needed operands that were 160 bits long, which necessitated the need for at least
, where g is the genus of the curve over,
., which is the set of a finite field of order q. In a similar manner, the curve with a genus equal to two needed operands that were 80 bits long. In addition, the curves with a genus equal to three required operands were 54 bits in length [
30].
Let us assume that
is a finite field and that
is the algebraic closure of
. An HEC of a genus (
) over
is a set of solutions to the following equation of the curve in the form (
)
x .
If there are no pairs of (
)
x that satisfy the condition, then the curve in question is regarded to be nonsingular. In addition, the curve in question must be able to satisfy both the previously mentioned curve equation, as well as the subsequent given partial differential equation.
The polynomial [u] is a degree of and [u] is the monic polynomial of degree .
3.3. Complexity Assumptions
During the course of the investigation, we found it necessary to presume the following assumptions:
is a finite field with order , where
D is a divisor of a HEC, which is a finite sum of points;
D = HEC , where .
3.3.1. Definition 1. Hyperelliptic Curve Discrete Logarithm Problem (HCDLP)
We made the following supposition for HECDLP.
Let and ; then, finding from is called HCDLP.
3.3.2. Definition 2. Hyperelliptic Curve Computational Diffie-Hellman Problem (HCCDH)
For , we make the following suppositions.
Let and , ; then, finding from and from is called HCCDH.
3.4. Network Model
In
Figure 2, we present the proposed network model for the online/offline sig-nature scheme for the underwater wireless sensors network. The proposed network model consists of a Network Manager (NM), an Intermediate Getaway, Underwater Sensors, and Surface Users.
Network Manager (NM): It is the responsibility of the NM to establish a secure connection between all of the entities within the networks, and it is a third party that can be trusted.
Underwater Sensors: These are the sensors that sense the underwater environment and transmit data to the surface of the water.
A surface user is a device or a client that is interested in underwater sensors, such as an Internet of Things device or a client.
Intermediary Getaway: The intermediate getaway is a collection of nodes that act as a conduit for data and requests between different entities.
The NM is in charge of the registration process that takes place prior to the creation of communication links. The NM first registers the communication parties in order to facilitate secure communication. A great amount of processing power, memory, and computational capability are available on the intermediate gateway device. Sensors with limited resources collect data and pass it to the intermediary gateway, which then processes it. In the presence of a message, the intermediate gateway then goes through the process of signature generation on the message.
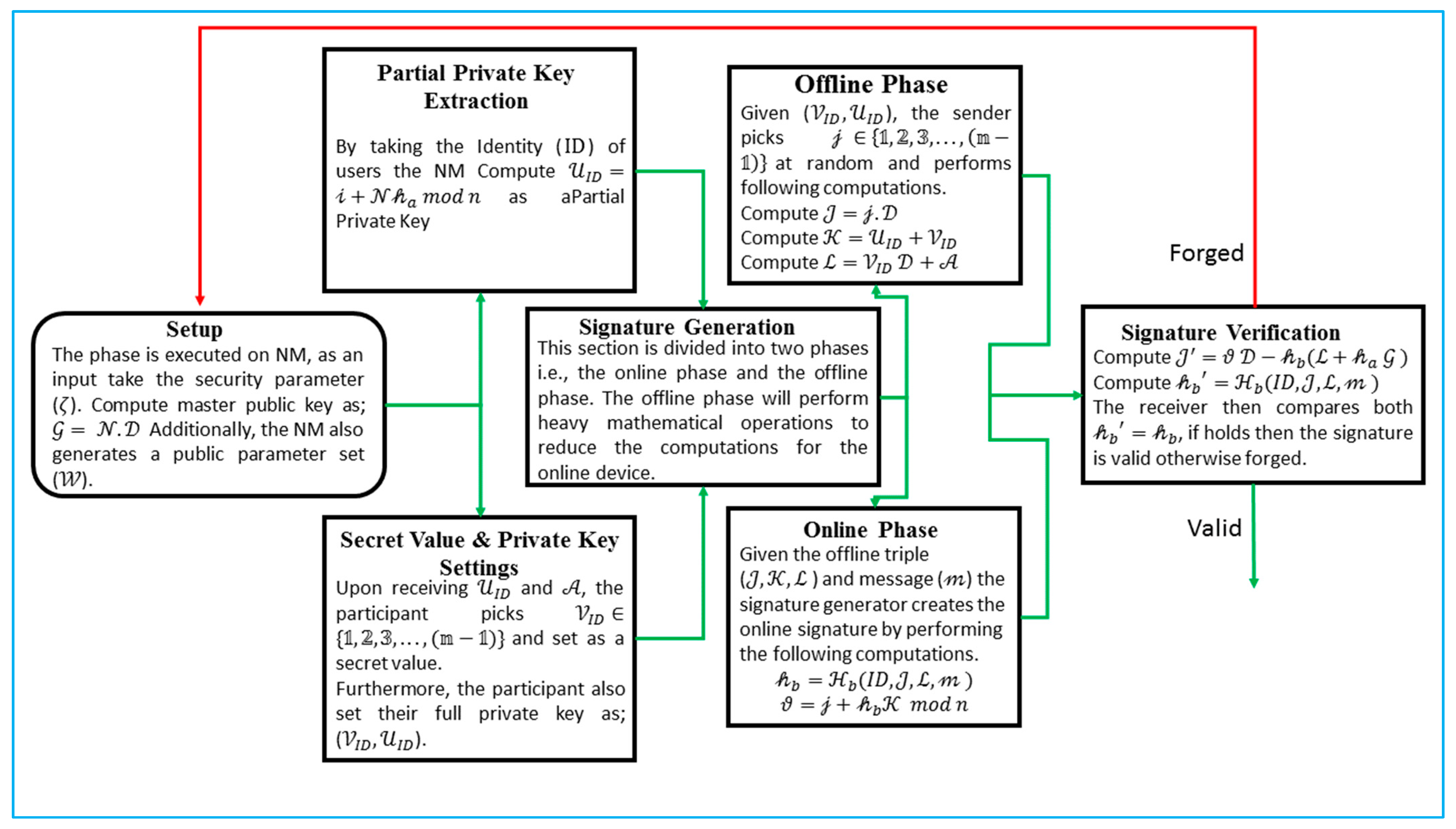
3.5. Proposed Online/Offline Signature Algorithm for UWSNs
The symbols that were used in the construction of the proposed online/offline signature algorithm are listed in
Table 2 of the following section. Additionally,
Figure 3 presents the flowchart of the proposed algorithm.
Setup: The phase is carried out on NM, it take the security parameter () as an input. In addition, the NM will carry out the following procedures in order to produce a public parameter set designated as “()”.
Select the genus () of HCC with the key size of 80 bits;
Select to compute the master public key as , where is a devisor of the hyperelliptic curve cryptosystem (HCC);
Choose two one-way hash functions ;
Finally, the NM advertise , } in the entire network while keeping the with itself.
Partial Private Key Extraction: By taking the identity () of users, the NM perform the following computations:
First pick ;
Compute ;
;
Compute .
The NM then send
and
to the participants. Upon receiving them, the participants can check the validity of the equation as
The partial private key is legitimate if the aforementioned equation is true; else, it is invalid.
Secret Value and Private Key Settings: Upon receiving and , the participants pick and set it as a secret value.
Furthermore, the participants also set their full private key as ().
Signature Generation: This section is divided into two phases, i.e., the online phase and the offline phase. The offline phase will perform heavy mathematical operations to reduce the computation for the online phase.
Offline Phase: Given (), the sender picks at random and performs the following computations.
The triple () is then assigned to the online phase.
Online Phase: Given the offline triple (
), fresh nonce (𝜏) and message (
), the signature generator creates an online signature by performing the following computations.
Finally, the sender computes the triple of () as a full signature.
Signature Verification: For an identity and message () with the computed signature triple () on , the receiver verifies the signature by performing the following operations:
Compute
Compute ;
Compute .
The receiver then compares both ; if it holds, then the signature is valid; otherwise, it is forged.
The consistency can be proved from the following equation.
4. Deployment of the Proposed Scheme
For deployment, we consider underwater sensors, and surface users want communication to share data. In this communication, there will be other entities like NM and the intermediate getaway. To make a connection and authentic sources of data, each entity will follow the following steps of the suggested online/offline signature.
Figure 4 shows the deployment of the proposed scheme.
4.1. Setup, Connectivity, and Keys Extraction
To connect devices, the NM as an input takes the security parameter (), and the KGC generates a public parameter set (). For this, the NM select a genus () of HCC with a key size of 80 bits, select compute the master public key as , where is a devisor of the hyperelliptic curve cryptosystem (HCC), and choose two one-way hash functions Finally, the NM advertise } in the entire network while keeping the with itself.
To contact the network, the underwater sensors and surface user send their identities () to NM. By taking the the NM first pick , compute , and compute The NM then send and to the underwater sensors and surface user as a partial private key. Upon receiving it, the users can check the validity of the equation as . If this equation holds, then the partial private key is valid; otherwise, it is invalid. Upon receiving and , the participant picks and set it as a secret value. Furthermore, the underwater sensors and surface user also set their full private key as ().
4.2. Signature Generation
In this step, the underwater sensors generate the signature on data. As we know, the underwater sensors have limited energy. This section is divided into two phases, i.e., the online phase and the offline phase of the signature. The offline phase will perform heavy mathematical operations to reduce the computations for the online device. The heir of the intermediate gateway performs the offline phase and underwater sensors online phase. The intermediate gateway picks at random, computes , computes and computes . The intermediate gateway then assigns the triple of () to underwater sensors.
The underwater sensors take the triplet () and data () and generate an online signature. For this, it calculates and . Finally, the underwater sensors compute the triple of () as a full signature and send it to the surface user.
4.3. Signature Verification
The surface user can verify the signature triple () on by computing , computing , and computing . The surface user then compares both ; If it holds, the signature is considered legitimate; if not, it is considered to be forged.
5. Security Analysis
5.1. Theorem 1
Definition 3. “Under the security assumptions of the random oracle model (ROM), an adversary () is unforgeable against the adaptive chosen message and identity attacks without knowledge of the partial private key and secret value.”
Proof. Assume () as a random HCDLP stance that outputs 𝓸. An algorithm () will perform the subsequent simulations for interacting with . □
Setup: In this phase, performs the following steps.
The sets the public key as and advertises } in the entire network.
For , the chooses at random as a challenging ID for this particular game, while represents the utmost number of the querying oracle.
The picks at random and sets , defines , and adds the triple of () to the .
Finally, the gives the global parameters set as }.
After that, the starts answering the queries from as
: The inputs (), and with that, the calls the . If the has the (), provides it to the . If not, the picks at random and adds () to the and response to the .
The inputs and with that, the calls the . If the already has the requested query, it simply returns back to the . If not, the picks at random and adds to the and response to the .
Partial Private Key Extraction Queries: Upon requesting the private key associated with , the first verifies if stays or not. The also maintains the
If the terminates the simulation and outputs an error.
If , the choose at random as of the secret value allied with . The picks and computes . If the () already exists, then the terminates the simulation and outputs an error. The process is termed the Event by . The then adds () and () to the To end with, the outputs and .
The probability of is the utmost , where represent the querying of the key extraction oracle.
Secret Value Extraction Queries:
If the terminates the simulation and outputs an error.
If , the searches () from the and responds to the allied secret value ().
Signature Generation Queries: Suppose a query for a signature with an identity and message ().
If the picks , at random and sets and computes , where . If already exists, terminates the simulation and outputs an error. The process is the Event .
Finally, the outputs the triple (,) as the signature. The probability of is utmost , where represents the querying of the signature generation oracle.
If , the signature is normal, as the has the partial private key and secret value. Thus, the can ordinarily perform the online signature generation.
Forgery: Let the generate a forgeable digital signature () on the message () for a given identity (), though is not submitted to the and and (,) is not a query to the .
If and , then the terminates the simulation and outputs an error. The process is termed the Event . The probability of is utmost , where represent the utmost number of querying the oracle.
If not, then according to the forking lemma [
19], another algorithm (
) exists that is able to produce two valid digital signatures
and
in a probabilistic polynomial time, where
while
remains the same due to
. Thus, the subsequent equations hold as
After the calculations, we obtain , then get and output as a solution for the HCDLP instance, respectively.
5.2. Theorem 2
Definition 4. There is an adversary () who is existentially unforgeable against the adaptive chosen message and identity attacks and has the knowledge of the partial private key/master secret key but does not have the participant’s secret value in the ROM under the security HCDLP assumptions.
Proof. Assume () as a random HCDLP stance that outputs 𝓸. An algorithm () will perform the subsequent simulations for interacting with . □
Setup: In this phase, performs the following steps.
The sets the public key as and advertises } in the entire network.
For , the chooses at random as a challenging ID for this particular game, while represents the utmost number of querying oracles.
Finally, the gives the global parameters set } and master secret key ().
After that, the starts answering the queries from as:
: The inputs (), and with that, the calls the . If the has the (), provides it to the . If not, the picks at random and adds () to the and response to the .
The inputs , and with that, the calls the . If the already has the requested query, it simply returns back to the . If not, the picks at random and adds to the and response to the .
Partial Private Key Extraction Queries: Upon requesting the private key associated with , the first verifies if stays or not. The also maintains the
If the sets and obtains () from . The then picks at random and computes and adds () to the list (), where represents the unknown secret value for the identity . To end with, the returns .
If , the finds () from the . The then chooses at random and computes and adds () to the list. To end with, the returns
Signature Generation Queries: Suppose a query for a signature with an identity and message ().
If the picks , at random and sets and finds () from and additionally, the also sets and computes , where . If already exists, terminates the simulation and outputs an error. The process is termed the Event .
Computes , where . If already exists, terminates the simulation and outputs an error. The process is termed the Event . Finally, the outputs the triple as the signature. The probability of is the utmost , where represents the querying of the signature generation oracle.
If , the signature is normal, as the has the partial private key and secret value. Thus, the can ordinarily perform the online signature generation.
Forgery: Let the generate a forgeable digital signature () on the message () for a given identity (), though is not submitted to the , and (,) is not query to the .
If and , then the terminates the simulation and outputs an error. The process is termed as the Event . The probability of is not less than , where represent the utmost number of querying oracles.
If not, then according to the forking lemma [
19], another algorithm (
) exists that is able to produce two valid digital signatures
and
in a probabilistic polynomial time, where
and
remain the same. Thus, the subsequent equations hold as:
After the calculations, we obtain , then get and output as a solution for the HCDLP instance, respectively.
5.3. Theorem 3
Definition 5. If the NM impersonates an authentic participant in order to forge the signature and has knowledge of the participant’s partial private key and secret value (an alternate secret value that is not real), we can demonstrate to the mediator that the NM is dishonest.
Proof. According to the above two theorems, the proposed scheme is unforgeable against both malicious type-1 and type-2 adversaries. The process is split into two steps, i.e., forging the private key and signing the message. □
Forging the Private Key: Let be the identity of the participant, and () is the respective private key. The NM simulates the participant to generate a signature in two possible ways:
By knowing the participant’s secret value .
By replacing the participant’s secret value . As we know that the is picked at random from the , it is infeasible of the NM to obtain the .
Thus, the NM has to pick a secret value for the participants to produce another private key using the identity ID. The procedure is mentioned below.
The NM picks for the replacement of the participant’s secret value.
The NM picks at random and computes and . Let , satisfy and produce a private key ().
Signing message: After forging the participant private key (), the NM executes the signature generation algorithm. The triple () on the message is for a given identity (ID) of the participant. The participant can run the signature generation algorithm twice to make sure that () is forged by the NM or an adversary conspired with the NM. Let the participant produce two signatures, () and (), and submit the () and () to the intermediary trusted authority.
Note: Here, ,. If the NM aims to make then the NM needs to satisfy . Furthermore, the NM also needs to know the value , but the NM does not know about . Thus, according to the HCDLP, it is infeasible for the NM to obtain and . Hence, .
Now, if the above three signatures are valid, then the in the triple () and () are the same. We obtain in (). Hence, () definitely is forged by the NM or an adversary conspired with the NM.