Physics of Composites for Low-Frequency Magnetoelectric Devices
Abstract
:1. Introduction
2. Longitudinal and Bending Modes
2.1. Symmetric ME Structure
2.1.1. Resonance Mode
2.1.2. Quasi-Static Mode
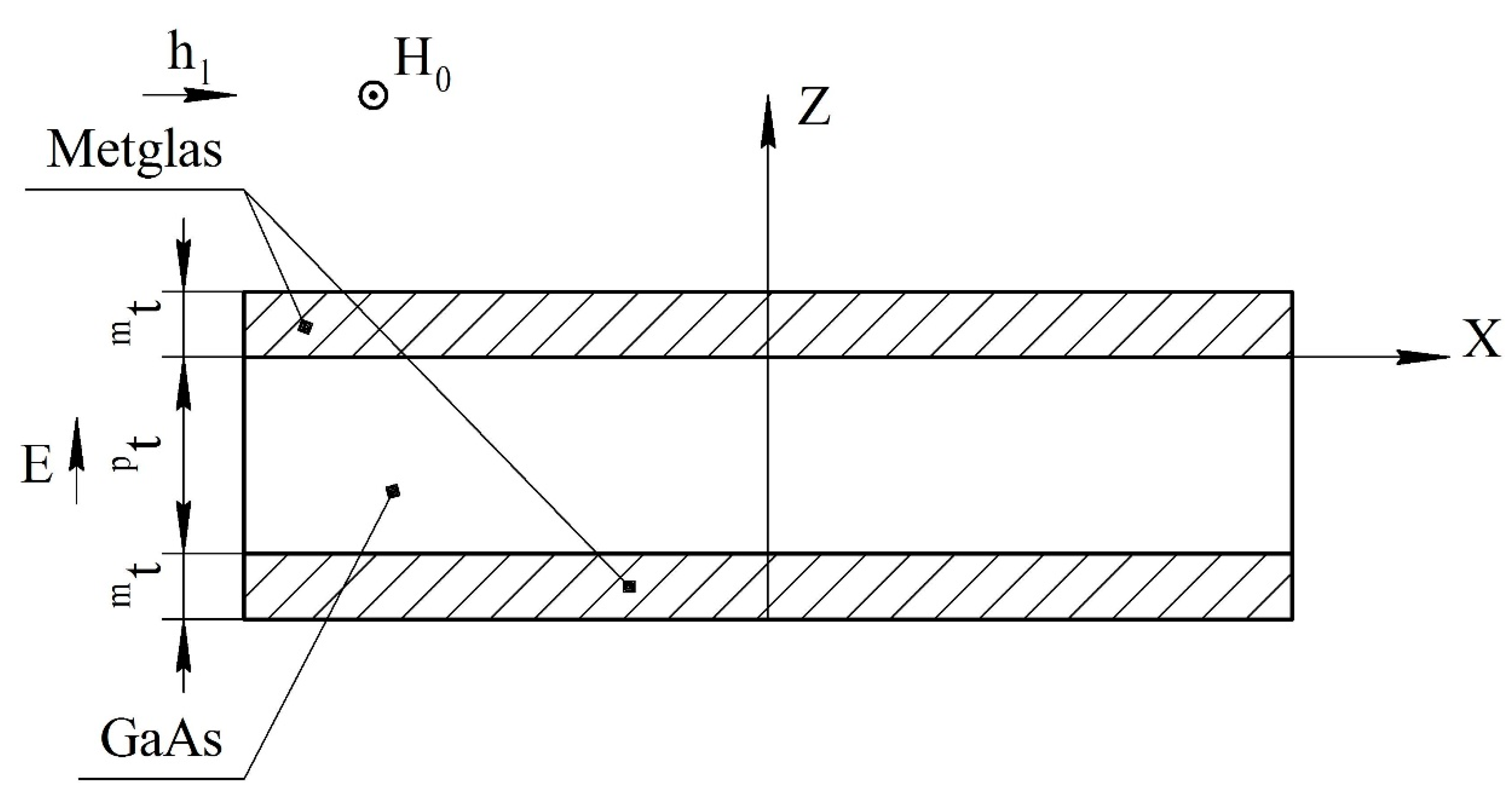
2.2. Asymmetric ME Structure
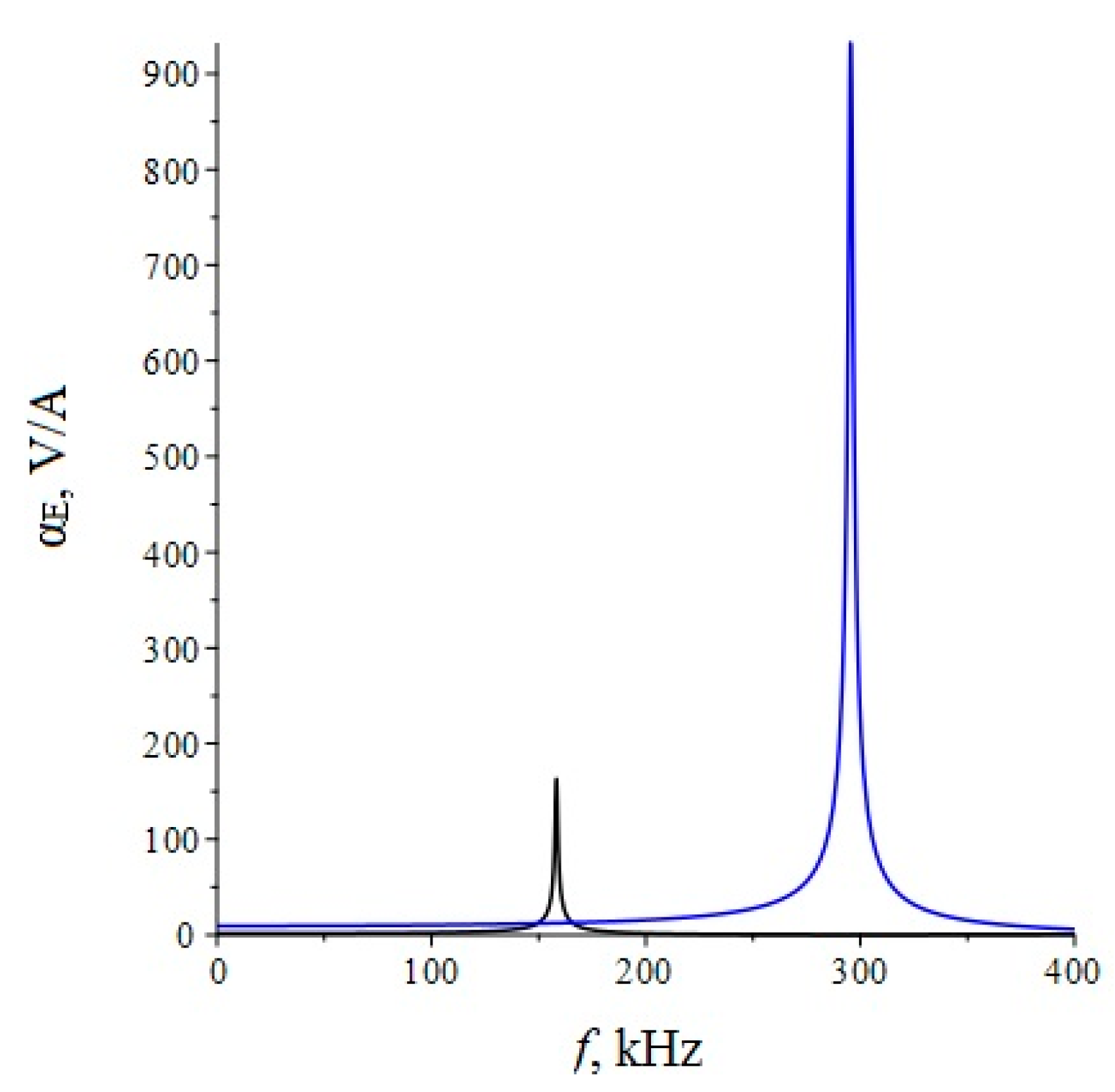
2.2.1. Resonance Regime of the Longitudinal Mode
2.2.2. Resonant Mode of the Bending Mode
- Free Clamping of Both Ends of the ME Composite.
- Cantilever Clamping of ME Composite.
2.2.3. Quasi-Static Mode
3. Longitudinal-Shear and Torsional Modes
3.1. Symmetrical ME Structure
3.1.1. Resonance Mode
3.1.2. Quasi-Static Mode
3.2. Asymmetric ME Structure
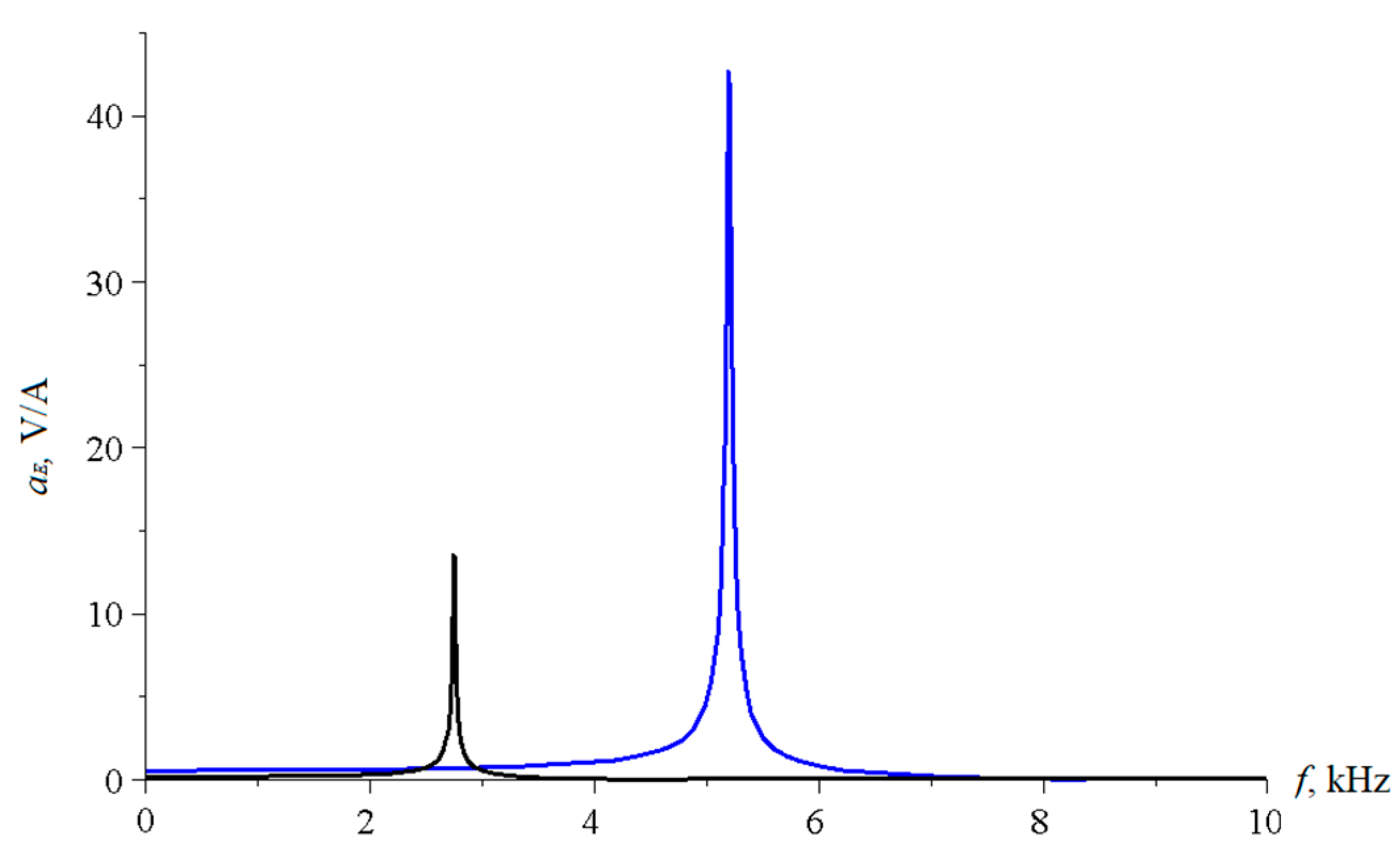
3.2.1. Resonance Regime for the Longitudinal-Shear Mode
3.2.2. Resonant Regime for the Torsional Mode
3.2.3. Quasi-Static Mode
3.3. ME Structure Based on Bimorph Lithium Niobate
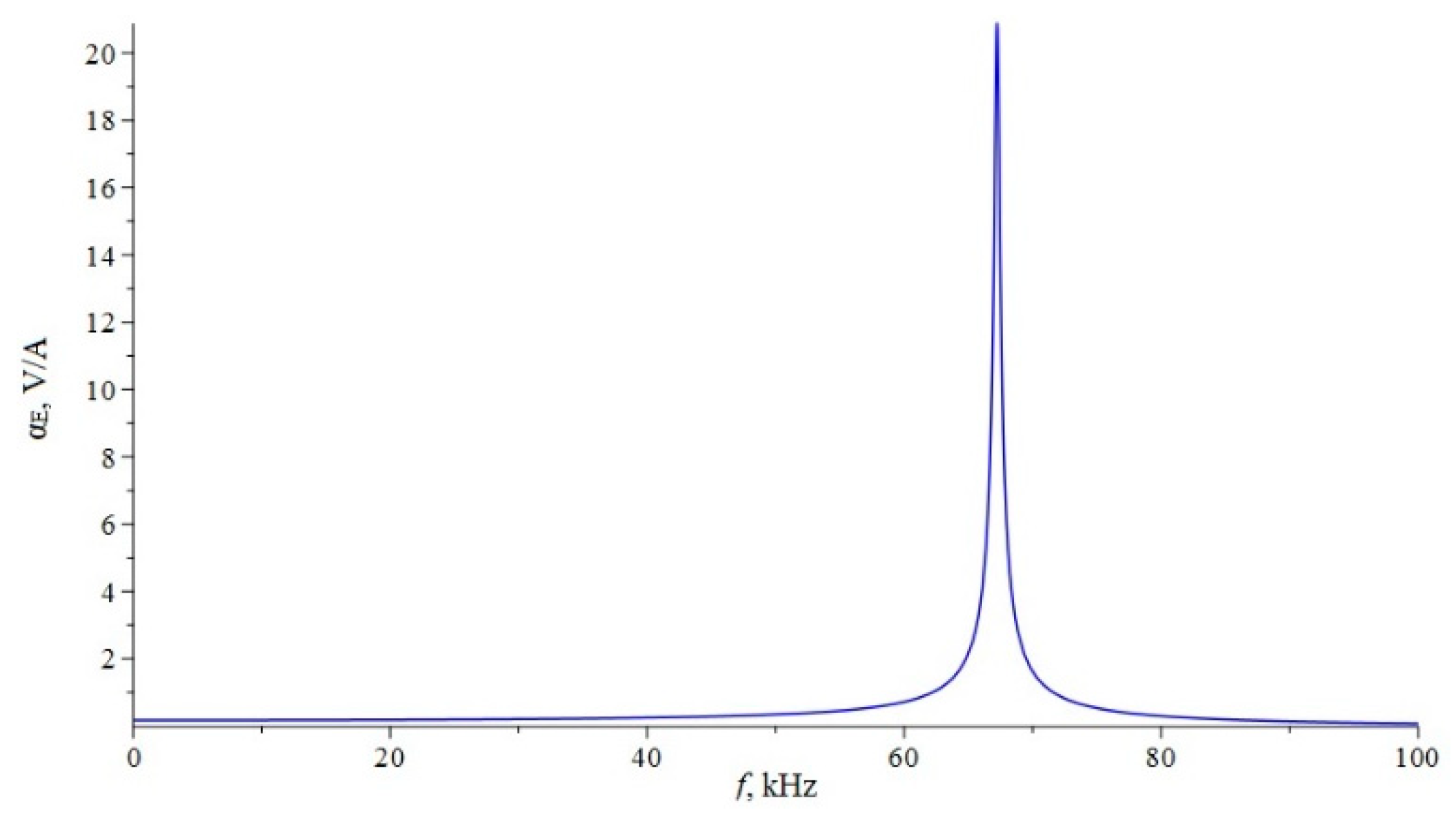
3.3.1. Resonant Regime for the Torsional Mode
3.3.2. Quasi-Static Mode
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nan, C.-W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspectives, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Viehland, D. Magnetoelectricity in Composites; Pan Stanford Publishing Pte. Ltd.: Singapore, 2012; 273p. [Google Scholar]
- Bichurin, M.I.; Petrov, V.M.; Petrov, R.V.; Tatarenko, A.S. Magnetoelectric Composites; Pan Stanford Publishing Pte. Ltd.: Singapore, 2019; 280p. [Google Scholar]
- Harshe, G.; Dougherty, J.O.; Newnham, R.E. Theoretical modelling of multilayer magnetoelectric composites. Int. J. Appl. Electromagn. Mater. 1993, 4, 145. [Google Scholar]
- Bichurin, M.I.; Petrov, V.M.; Srinivasan, G. Theory of low-frequency magnetoelectric coupling in magnetostrictive-piezoelectric bilayers. Phys. Rev. 2003, 68, 054402. [Google Scholar] [CrossRef] [Green Version]
- Bichurin, M.I.; Filippov, D.A.; Petrov, V.M.; Laletsin, V.M.; Paddubnaya, N.N.; Srinivasan, G. Resonance magnetoelectric effects in layered magnetostrictive-piezoelectric composites. Phys. Rev. B 2003, 68, 132408. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Zhai, J. Equivalent circuit method for static and dynamic analysis of magnetoelectric laminated composites. Chin. Sci. Bull. 2008, 53, 2113–2123. [Google Scholar] [CrossRef] [Green Version]
- Chu, Z.; Shi, H.; Shi, W.; Liu, G.; Wu, J.; Yang, J.; Dong, S. Enhanced Resonance Magnetoelectric Coupling in (1-1) Connectivity Composites. Adv. Mater. 2017, 29, 1606022. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Li, J.-F.; Viehland, D. Characterization of magnetoelectric laminate composites operated in longitudinal-transverse and transverse–transverse modes. J. Appl. Phys. 2004, 95, 2625–2630. [Google Scholar] [CrossRef] [Green Version]
- Zhai, J.; Xing, Z.; Dong, S.; Li, J.; Viehland, D. Magnetoelectric Laminate Composites: An Overview. J. Am. Ceram. Soc. 2008, 91, 351–358. [Google Scholar] [CrossRef]
- Petrov, V.M.; Srinivasan, G.; Bichurin, M.I.; Galkina, T.A. Theory of magnetoelectric effect for bending modes in magnetostrictive-piezoelectric bilayers. J. Appl. Phys. 2009, 105, 063911. [Google Scholar] [CrossRef]
- Hasanyan, D.; Gao, J.; Wang, Y.; Viswan, R.; Li, M.; Shen, Y.; Li, J.; Viehland, D. Theoretical and experimental investigation of magnetoelectric effect for bending-tension coupled modes in magnetostrictive-piezoelectriclayered composites. J. Appl. Phys. 2012, 112, 013908. [Google Scholar] [CrossRef] [Green Version]
- Turutin, A.V.; Vidal, J.V.; Kubasov, I.V.; Kislyuk, A.M.; Malinkovich, M.D.; Parkhomenko, Y.N.; Sobolev, N.A. Low-frequency magnetic sensing by magnetoelectric metglas/bidomain LiNbO3 long bars. J. Phys. D Appl. Phys. 2018, 51, 214001. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Petrov, V.M. Modeling of Magnetoelectric Interaction in Magnetostrictive-Piezoelectric Composites. Adv. Condens. Matter Phys. 2012, 798310. [Google Scholar] [CrossRef] [Green Version]
- Yu, G.-L.; Zhang, H.-W.; Bai, F.-M.; Li, Y.-X.; Li, J. Theoretical investigation of magnetoelectric effect in multilayer magnetoelectric composites. Compos. Struct. 2015, 119, 738–748. [Google Scholar] [CrossRef]
- Sokolov, O.V.; Bichurin, M.I. Torsional modes in the magnetoelectric effect for a two-layer ferrimagnet-piezoelectric YIG/GaAs structure. J. Phys. Conf. Ser. 2020, 1658, 012054. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Sokolov, O.V.; Lobekin, V.N. Torsion mode of the magnetoelectric effect in a Metglas/GaAs. IEEE Magn. Lett. 2021, 13, 1–4. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Petrov, V.M.; Leontiev, V.S.; Ivanov, S.N.; Sokolov, O.V. Magnetoelectric effect in layered structures of amorphous ferromagnetic alloy and gallium arsenide. J. Magn. Magn. Mater. 2017, 424, 115. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Petrov, R.V.; Leontiev, V.S.; Sokolov, O.V.; Turutin, A.V.; Kuts, V.V.; Kubasov, I.V.; Kislyuk, A.M.; Temirov, A.A.; Malinkovich, M.D.; et al. Self-Biased Bidomain LiNbO3/Ni/Metglas Magnetoelectric Current Sensor. Sensors 2020, 20, 7142. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Viehland, D. Magnetoelectrics for magnetic sensor applications: Status, challenges and perspectives. Mater. Today 2014, 6, 269. [Google Scholar] [CrossRef]
- Bichurin, M.; Petrov, R.; Sokolov, O.; Leontiev, V.; Kuts, V.; Kiselev, D.; Wang, Y. Magnetoelectric Magnetic Field Sensors: A Review. Sensors 2021, 21, 6232. [Google Scholar] [CrossRef]
- Deng, T.; Chen, Z.; Di, W.; Chen, R.; Wang, Y.; Lu, L.; Luo, H.; Han, T.; Jiao, J.; Fang, B. Significant improving magnetoelectric sensors performance based on optimized magnetoelectric composites via heat treatment. Smart Mater. Struct. 2021, 30, 085005. [Google Scholar] [CrossRef]
- Spetzler, B.; Golubeva, E.V.; Friedrich, R.-M.; Zabel, S.; Kirchhof, C.; Meyners, D.; McCord, J.; Faupel, F. Magnetoelastic Coupling and Delta-E Effect in Magnetoelectric Torsion Mode Resonators. Sensors 2021, 21, 2022. [Google Scholar] [CrossRef] [PubMed]
- Annapureddy, V.; Palneedi, H.; Yoon, W.-H.; Park, D.-S.; Choi, J.-J.; Hahn, B.-D.; Ahn, C.-W.; Kim, J.-W.; Jeong, D.-Y.; Ryu, J. A pT/√ Hz sensitivity ac magnetic field sensor based on magnetoelectric composites using low-loss piezoelectric single crystals. Sens. Actuators A Phys. 2017, 260, 206–211. [Google Scholar] [CrossRef]
- Viehland, D.; Wuttig, M.; McCord, J.; Quandt, E. Magnetoelectric magnetic field sensors. MRS Bull. 2018, 3, 834. [Google Scholar] [CrossRef]
- Bichurin, M.; Petrov, R.; Leontiev, V.; Semenov, G.; Sokolov, O. Magnetoelectric Current Sensors. Sensors 2017, 17, 1271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patil, D.R.; Kumar, A.; Ryu, J. Recent Progress in Devices Based on Magnetoelectric Composite Thin Films. Sensors 2021, 21, 8012. [Google Scholar] [CrossRef]
- García-Arribas, A.; Gutiérrez, J.; Kurlyandskaya, G.V.; Barandiarán, J.M.; Svalov, A.; Fernández, E.; Lasheras, A.; De Cos, D.; Bravo-Imaz, I. Sensor Applications of Soft Magnetic Materials Based on Magneto-Impedance, Magneto-Elastic Resonance and Magneto-Electricity. Sensors 2014, 14, 7602–7624. [Google Scholar] [CrossRef] [Green Version]
- Leung, C.M.; Li, J.-F.; Viehland, D.; Zhuang, X. A review on applications of magnetoelectric composites: From heterostructural uncooled magnetic sensors, energy harvesters to highly efficient power converters. J. Phys. D Appl. Phys. 2018, 51, 263002. [Google Scholar] [CrossRef]
- Zhuang, X.; Leung, C.M.; Li, J.; Srinivasan, G.; Viehland, D. Power Conversion Efficiency and Equivalent Input Loss Factor in Magnetoelectric Gyrators. IEEE Trans. Ind. Electron. 2019, 66, 2499–2505. [Google Scholar] [CrossRef]
- Palneedi, H.; Annapureddy, V.; Priya, S.; Ryu, J. Status and Perspectives of Multiferroic Magnetoelectric Composite Materials and Applications. Actuators 2016, 5, 9. [Google Scholar] [CrossRef] [Green Version]
- Chu, Z.; PourhosseiniAsl, M.; Dong, S. Review of multi-layered magnetoelectric composite materials and devices applications. J. Phys. D Appl. Phys. 2018, 51, 243001. [Google Scholar] [CrossRef]
- Chu, Z.; Annapureddy, V.; PourhosseiniAsl, M.J.; Palneedi, H.; Ryu, J.; Dong, S. Dual-stimulus magnetoelectric energy harvesting. MRS Bull. 2018, 43, 199–205. [Google Scholar] [CrossRef]
- Dong, C.; Wang, X.; Lin, H.; Gao, Y.; Sun, N.X.; He, Y.; Li, M.; Tu, C.; Chu, Z.; Liang, X.; et al. A Portable Very Low Frequency (VLF) Communication System Based on Acoustically Actuated Magnetoelectric Antennas. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 398–402. [Google Scholar] [CrossRef]
- Zaeimbashi, M.; Nasrollahpour, M.; Khalifa, A.; Romano, A.; Liang, X.; Chen, H.; Sun, N.; Matyushov, A.D.; Lin, H.; Dong, C.; et al. Ultra-compact Dual-band Smart NEMS Magnetoelectric Antennas for Simultaneous Wireless Energy Harvesting and Magnetic Field Sensing. Nat. Commun. 2021, 12, 3141. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Chen, H.; Sun, N.X. Magnetoelectric materials and devices. APL Mater. 2021, 9, 041114. [Google Scholar] [CrossRef]
- Elzenheimer, E.; Bald, C.; Engelhardt, E.; Hoffmann, J.; Hayes, P.; Arbustini, J.; Bahr, A.; Quandt, E.; Höft, M.; Schmidt, G. Quantitative Evaluation for Magnetoelectric Sensor Systems in Biomagnetic Diagnostics. Sensors 2022, 22, 1018. [Google Scholar] [CrossRef]
- Tikhonova, S.A.; Evdokimov, P.V.; Filippov, Y.Y.; Safronova, T.V.; Garshev, A.V.; Shcherbakov, I.M.; Dubrov, V.E.; Putlyaev, V.I. Electro- and Magnetoactive Materials in Medicine: A Review of Existing and Potential Areas of Application. Inorg. Mater. 2020, 56, 1319–1337. [Google Scholar] [CrossRef]
- Kopyl, S.; Surmenev, R.; Surmeneva, M.; Fetisov, Y.; Kholkin, A. Magnetoelectric effect: Principles and applications in biology and medicine—A review. Mater. Today Bio 2021, 12, 100149. [Google Scholar] [CrossRef]















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bichurin, M.; Sokolov, O.; Ivanov, S.; Leontiev, V.; Petrov, D.; Semenov, G.; Lobekin, V. Physics of Composites for Low-Frequency Magnetoelectric Devices. Sensors 2022, 22, 4818. https://doi.org/10.3390/s22134818
Bichurin M, Sokolov O, Ivanov S, Leontiev V, Petrov D, Semenov G, Lobekin V. Physics of Composites for Low-Frequency Magnetoelectric Devices. Sensors. 2022; 22(13):4818. https://doi.org/10.3390/s22134818
Chicago/Turabian StyleBichurin, Mirza, Oleg Sokolov, Sergey Ivanov, Viktor Leontiev, Dmitriy Petrov, Gennady Semenov, and Vyacheslav Lobekin. 2022. "Physics of Composites for Low-Frequency Magnetoelectric Devices" Sensors 22, no. 13: 4818. https://doi.org/10.3390/s22134818
APA StyleBichurin, M., Sokolov, O., Ivanov, S., Leontiev, V., Petrov, D., Semenov, G., & Lobekin, V. (2022). Physics of Composites for Low-Frequency Magnetoelectric Devices. Sensors, 22(13), 4818. https://doi.org/10.3390/s22134818





