Path-Planning System for Radioisotope Identification Devices Using 4π Gamma Imaging Based on Random Forest Analysis
Abstract
1. Introduction
2. Investigation of Path-Planning System Using an Integrated Simulation Model
3. Verification of the Path-Planning System
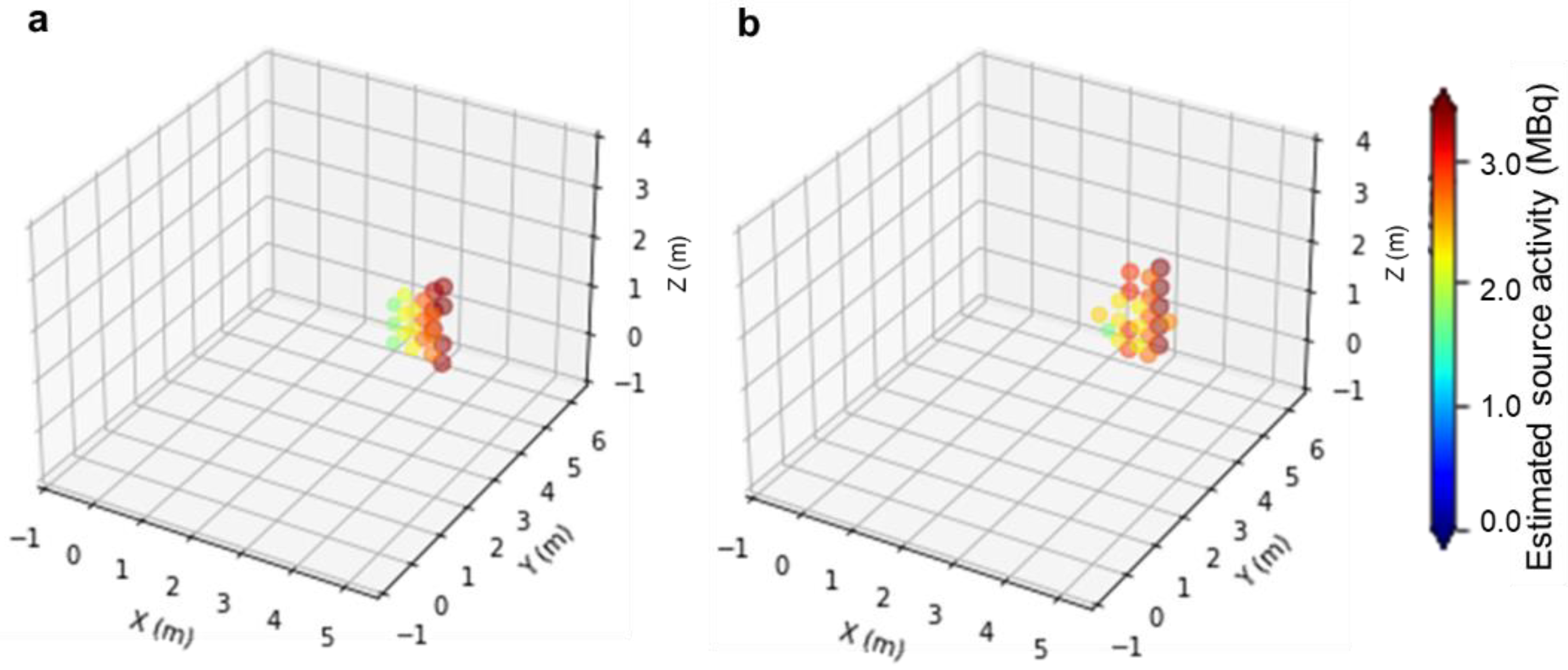
3.1. Verification Based on the Integrated Simulation Model
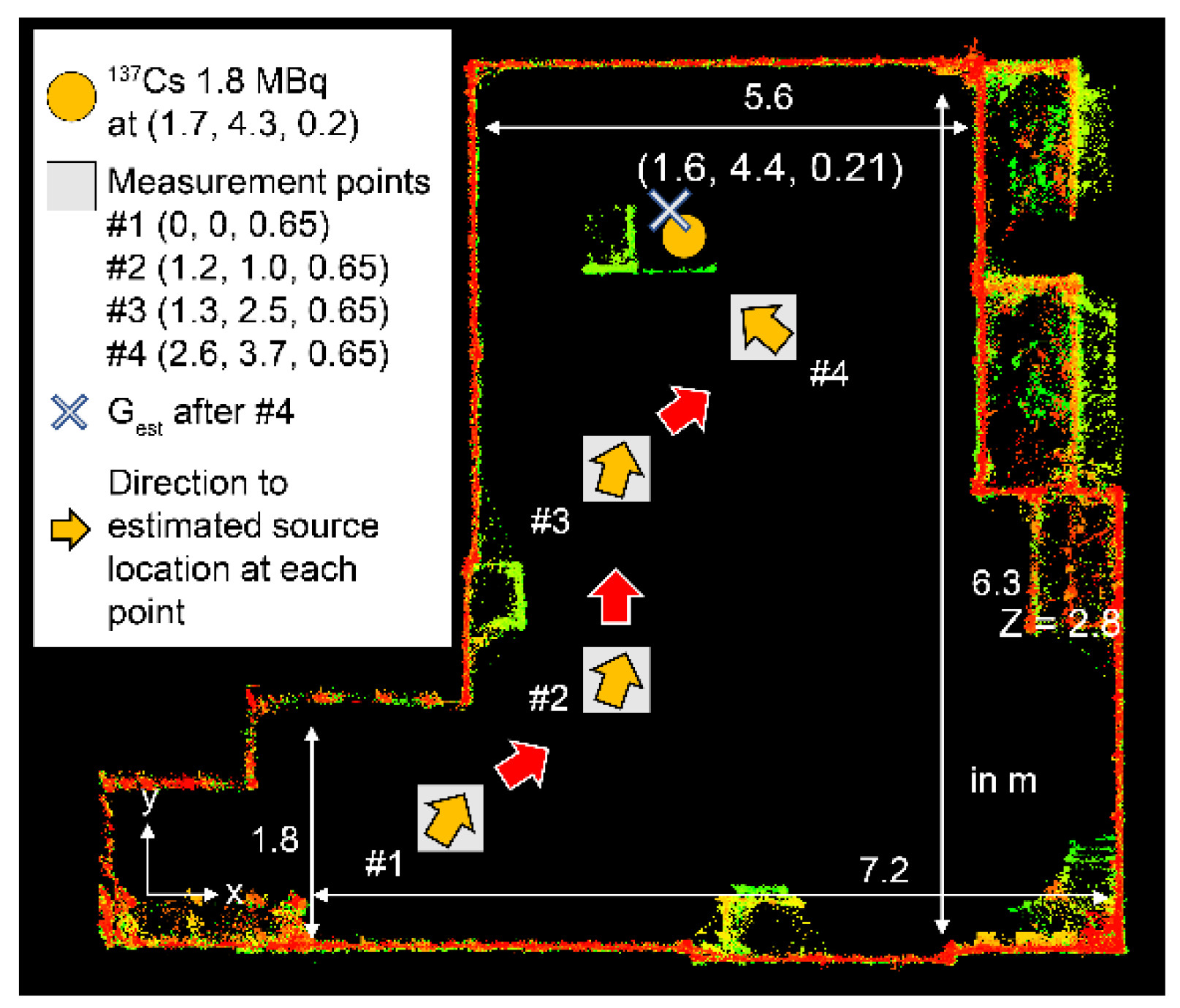
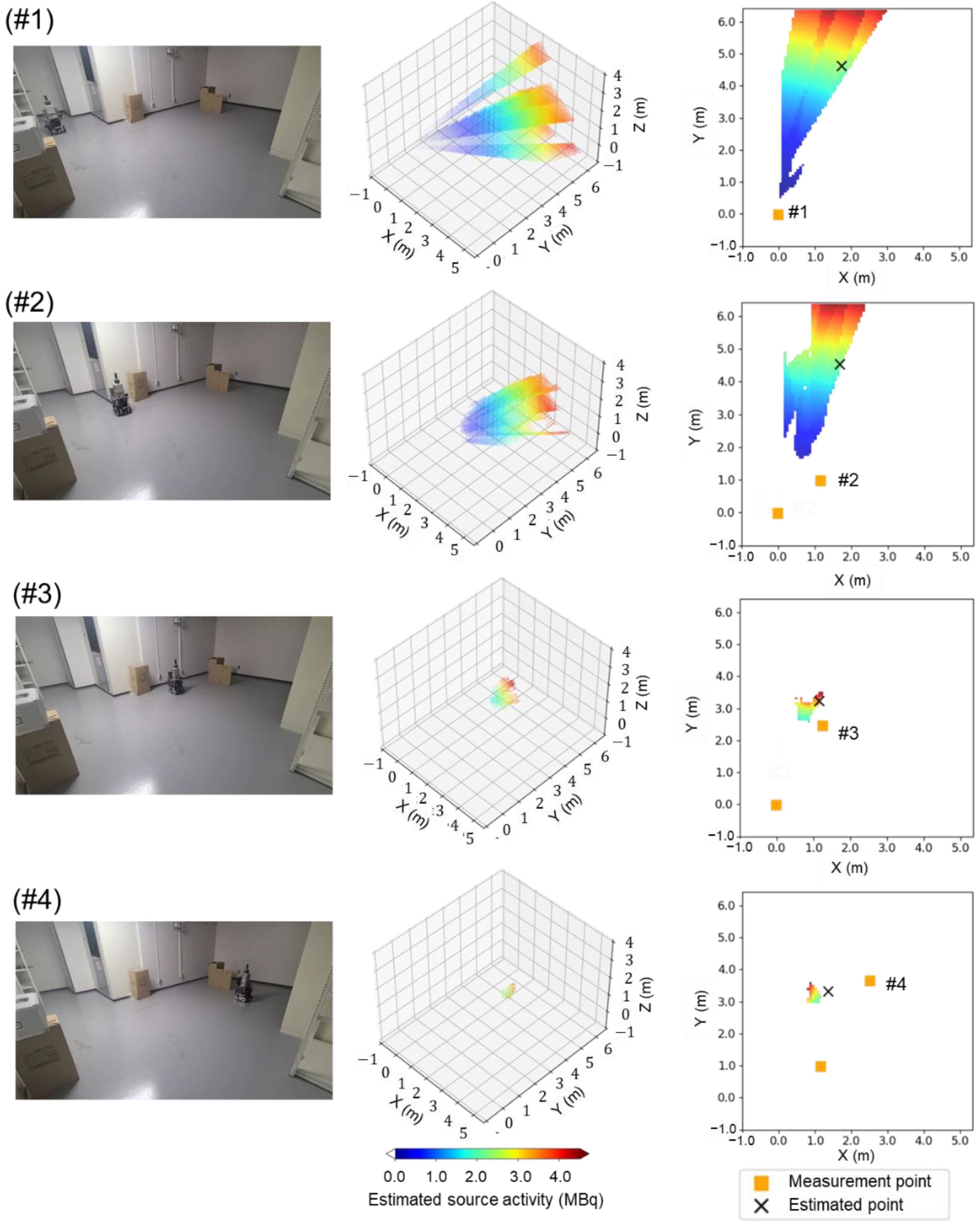
3.2. 137Cs Source Identification by a Prototype Device by 4π Gamma Imaging with the Path-Planning System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IAEA Incident and Trafficking Database (ITDB). Incidents of Nuclear and Other Radioactive Material out of Regulatory Control. Available online: https://www.iaea.org/sites/default/files/20/02/itdb-factsheet-2020.pdf (accessed on 8 March 2022).
- Sharma, M.K.; Alajo, A.B.; Lee, H.K. Three-dimensional localization of low activity gamma-ray sources in real-time scenarios. Nucl. Instrum. Methods Phys. A 2016, 813, 132–138. [Google Scholar] [CrossRef]
- Howse, J.W.; Ticknor, L.O.; Muske, K.R. Least squares estimation techniques for position tracking of radioactive sources. Automatica 2001, 37, 1727–1737. [Google Scholar] [CrossRef]
- Huo, J.; Liu, M.; Neusypin, K.A.; Liu, H.; Guo, M.; Xiao, Y. Autonomous search of radioactive sources through mobile robots. Sensors 2020, 20, 3461. [Google Scholar] [CrossRef] [PubMed]
- Vetter, K.; Barnowski, R.; Cates, J.W.; Haefner, A.; Joshi, T.H.Y.; Pavlovsky, R.; Quiter, B.J. Advances in nuclear radiation sensing: Enabling 3-D gamma-ray vision. Sensors 2019, 19, 2541. [Google Scholar] [CrossRef]
- Sato, Y.; Terasaka, Y.; Utsugi, W.; Kikuchi, H.; Kiyooka, H.; Torii, T. Radiation imaging using a compact Compton camera mounted on a crawler robot inside reactor buildings of Fukushima Daiichi Nuclear Power Station. J. Nucl. Sci. Technol. 2019, 56, 801–808. [Google Scholar] [CrossRef]
- Sato, Y.; Ozawa, S.; Terasaka, Y.; Minemoto, K.; Tamura, S.; Shingu, K.; Nemoto, M.; Torii, T. Remote detection of radioactive hotspot using a Compton camera mounted on a moving multi-copter drone above a contaminated area in Fukushima. J. Nucl. Sci. Technol. 2020, 57, 734–744. [Google Scholar] [CrossRef]
- Takahashi, T.; Kawarabayashi, J.; Tomita, H.; Iguchi, T.; Takada, E. Development of Omnidirectional Gamma-imager with Stacked Scintillators. In Proceedings of the 2013 3rd International Conference on Advancements in Nuclear Instrumentation, Measurement Methods and Their Applications (ANIMMA), Marseille, France, 23–27 June 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Fuwa, Y.; Takahashi, T.; Kawarabayashi, J.; Tomita, H.; Matui, D.; Takada, E.; Iguchi, T. Crystal identification in stacked GAGG scintillators for 4π direction sensitive gamma-ray imager. JPS Conf. Proc. 2016, 11, 070005. [Google Scholar] [CrossRef][Green Version]
- Uema, K.; Tomita, H.; Kanamori, K.; Takahashi, T.; Iguchi, T.; Hori, J.I.; Matsumoto, T.; Shimoyama, T.; Kawarabayashi, J. 4π compton gamma imaging toward determination of radioactivity. JPS Conf. Proc. 2019, 24, 011016. [Google Scholar] [CrossRef][Green Version]
- Mukai, A.; Tomita, H.; Hara, S.; Yamagishi, K.; Terabayashi, R.; Shimoyama, T.; Shimazoe, K. Simplified image reconstruction method in 4π Compton imaging for radioactive source identification. In Proceedings of the 2021 IEEE/SICE International Symposium on System Integration (SII), Fukushima, Japan, 11–14 January 2021; pp. 105–109. [Google Scholar] [CrossRef]
- Tomita, H.; Mukai, A.; Kanamori, K.; Shimazoe, K.; Woo, H.; Tamura, Y.; Hara, S.; Terabayashi, R.; Uenomachi, M.; Nurrachman, A.; et al. Gamma-ray Source Identification by a Vehicle-mounted 4π Compton Imager. In Proceedings of the 2020 IEEE/SICE International Symposium on System Integration (SII), Honolulu, HI, USA, 12–15 January 2020; pp. 18–21. [Google Scholar] [CrossRef]
- Mukai, A.; Hara, S.; Yamagishi, K.; Terabayashi, R.; Shimazoe, K.; Tamura, Y.; Woo, H.; Kishimoto, T.; Kogami, H.; Zhihong, Z.; et al. Optimization of Detector Movement Algorithm Using Decision Trees Analysis for Radiation Source Identification Based on 4π Gamma Imaging. In Proceedings of the 2022 IEEE/SICE International Symposium on System Integration (SII), Narvik, Norway, 9–12 January 2022; pp. 1026–1029. [Google Scholar] [CrossRef]
- Kishimoto, T.; Woo, H.; Komatsu, R.; Tamura, Y.; Tomita, H.; Shimazoe, K.; Yamashita, A.; Asama, H. Path planning for localization of radiation sources based on principal component analysis. Appl. Sci. 2021, 11, 4707. [Google Scholar] [CrossRef]

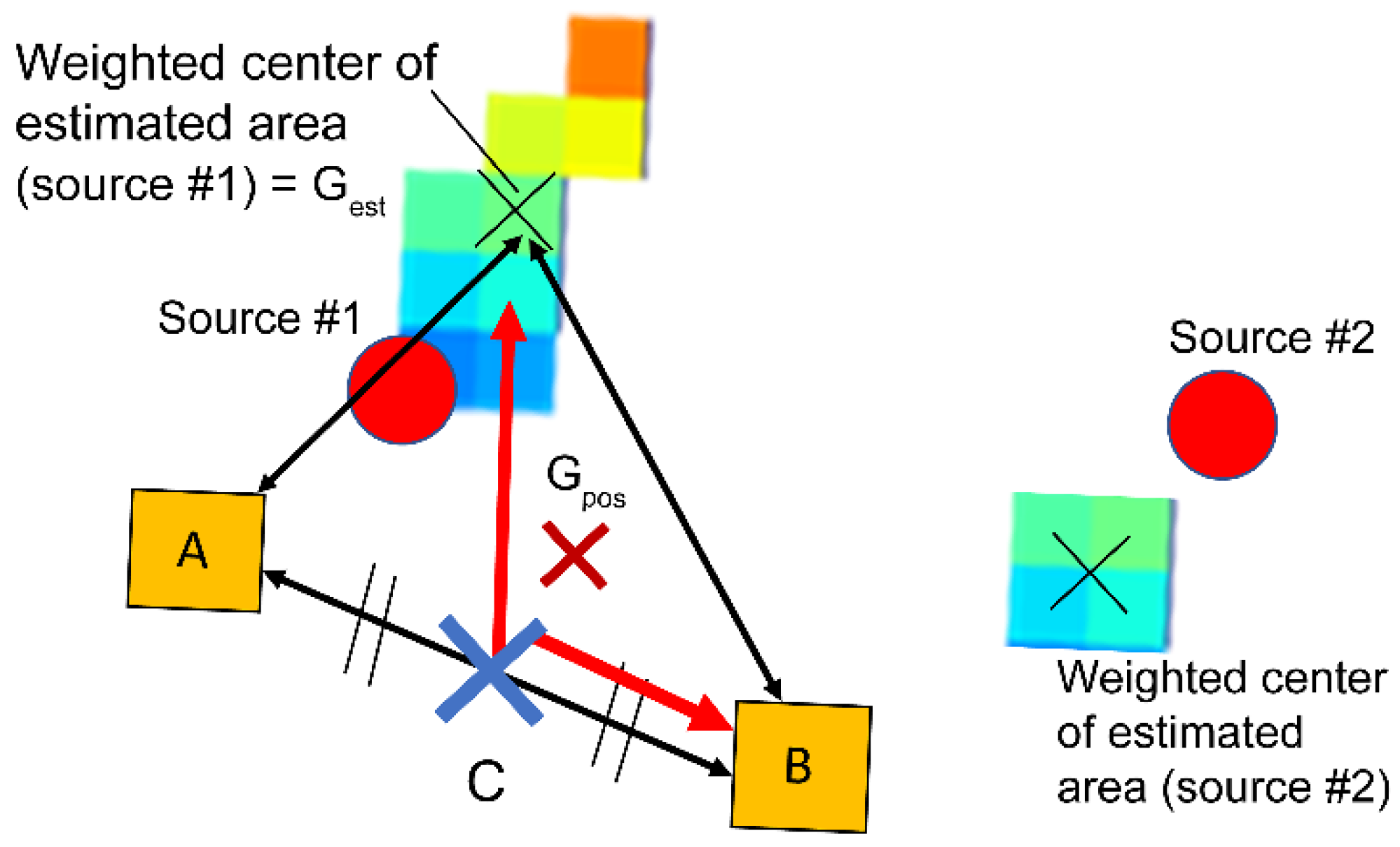
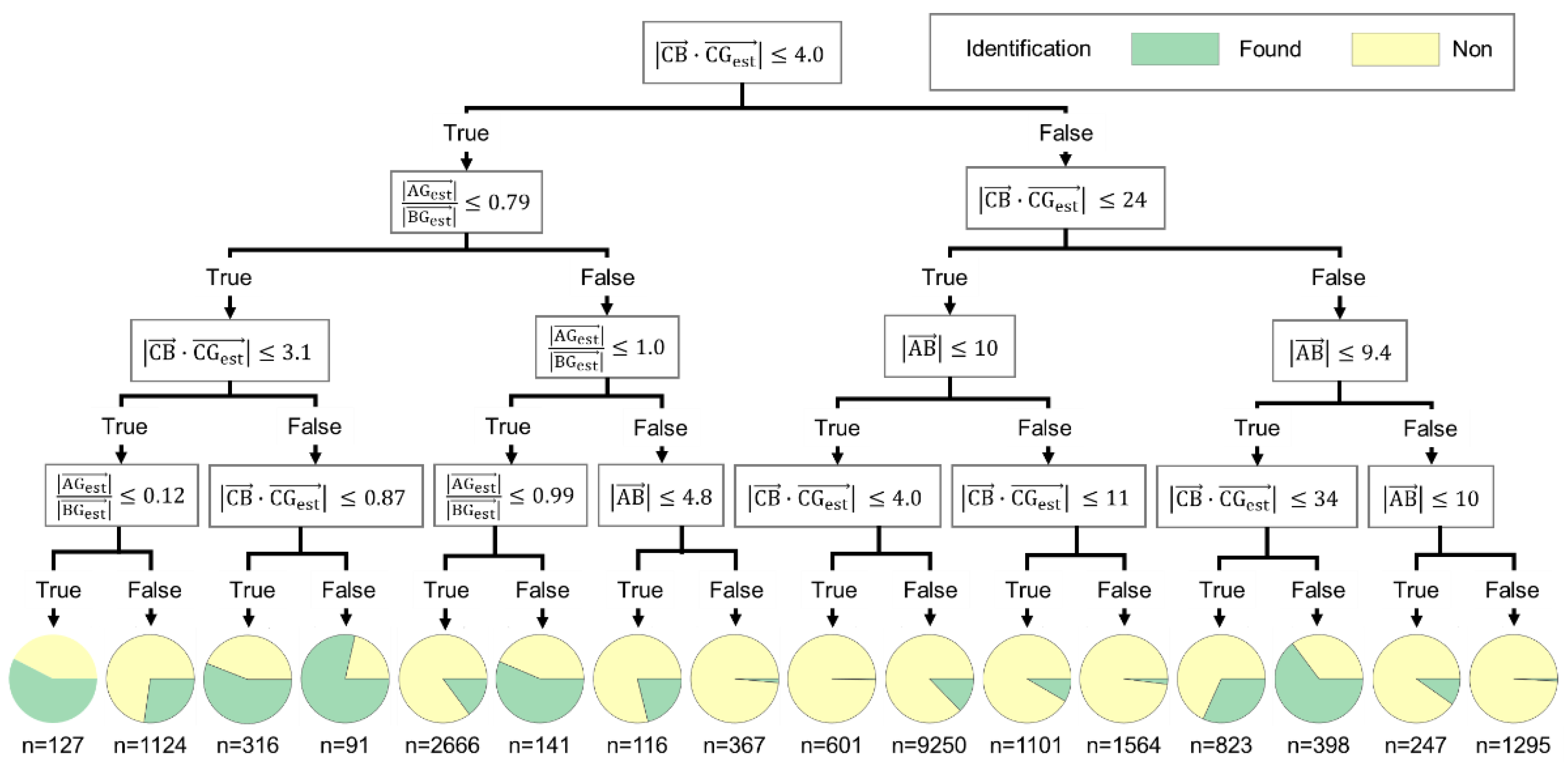
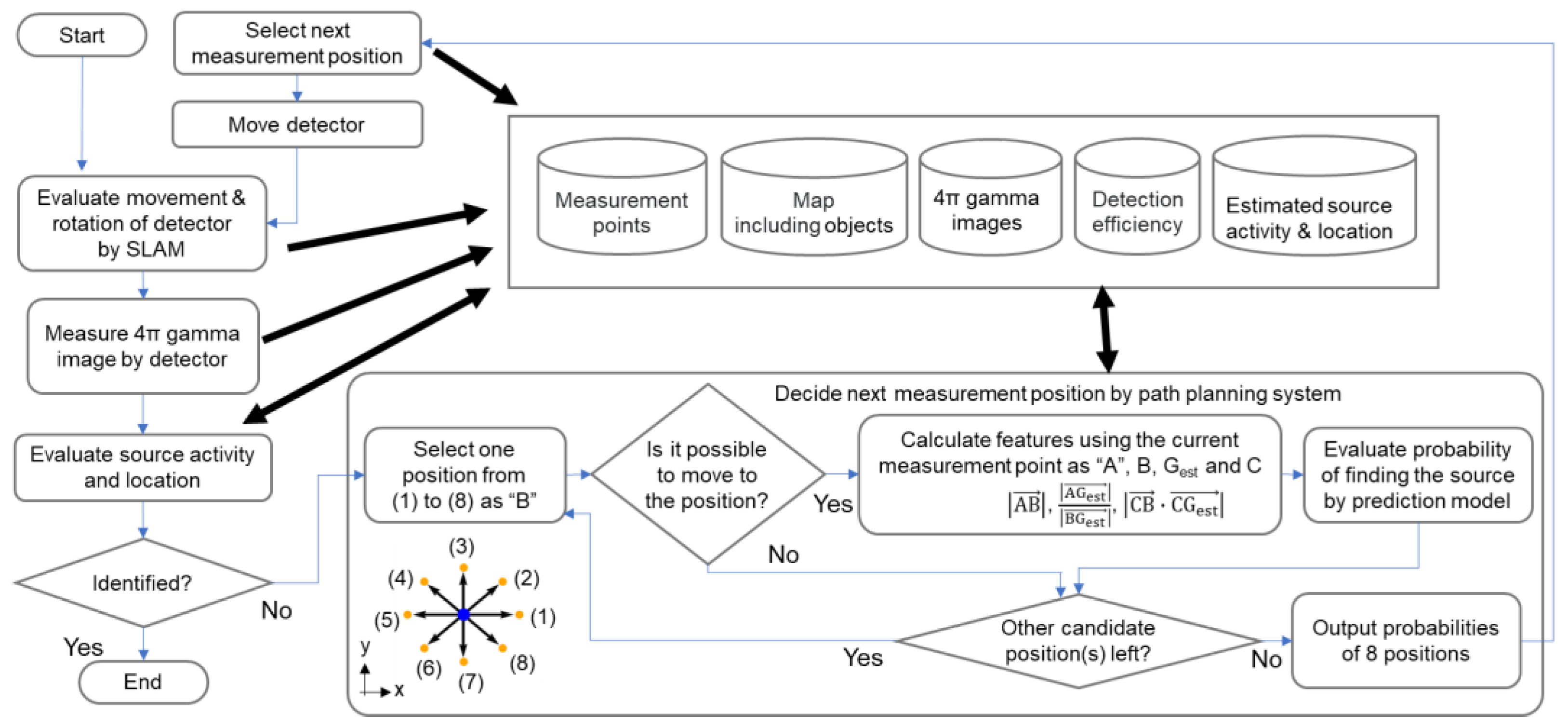
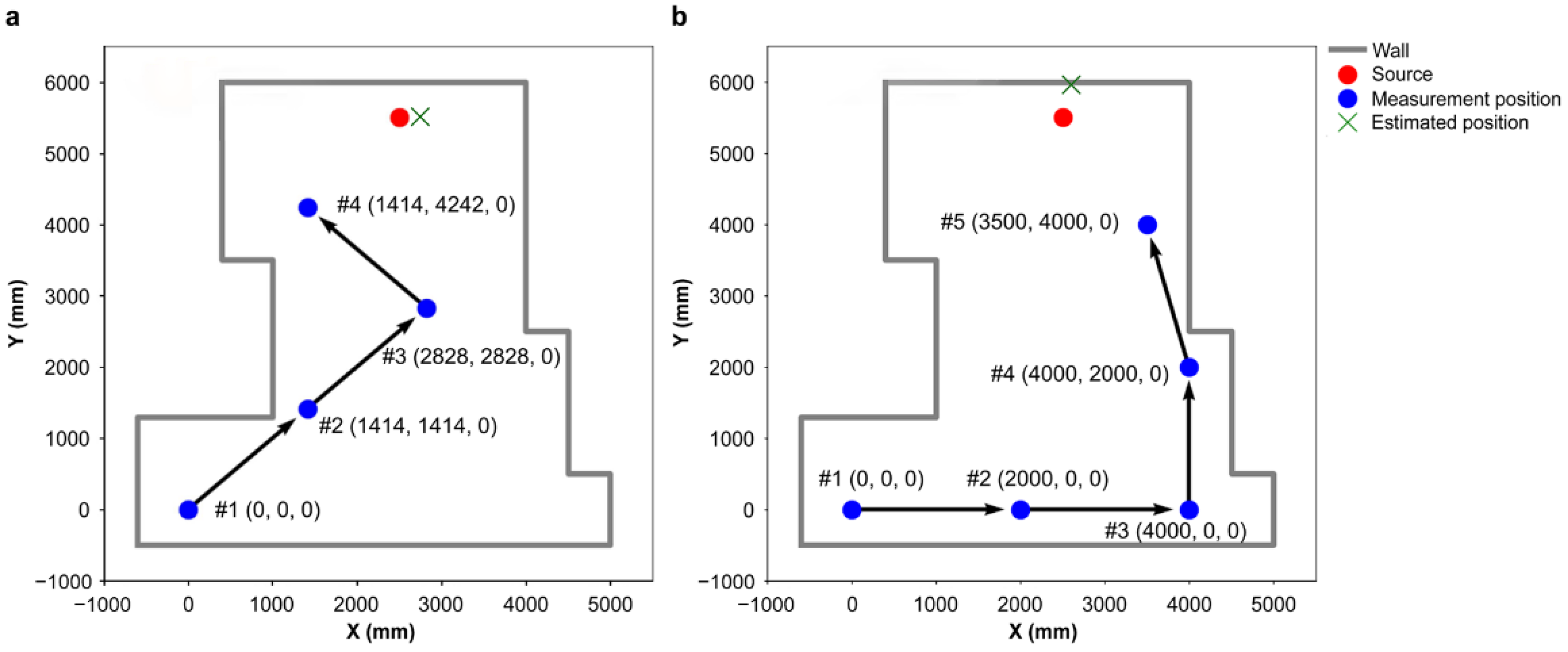

| ∠AGestB | ||||
|---|---|---|---|---|
| 16 | 14 | 15 | 7.9 | 3.9 |
| 5.3 | 2.8 | 2.7 |
| Model based on all 50 trees | 0.36 | 0.26 | 0.39 |
| Decision tree extracted from the model | 0.35 | 0.27 | 0.38 |
| Movement Sequence | #1 | #2 | #3 | #4 |
|---|---|---|---|---|
| Area where a source is located (voxels) | 1208 | 796 | 154 | 22 |
| Estimated source location (m) | (3.8, 5.8, 0.0) | (4.1, 6.3, 0.0) | (3.2, 6.3, 0.1) | (2.8, 5.5, 0.0) |
| Error from true source position (m) | (1.3, 0.3, 0.0) | (1.6, 0.8, 0.0) | (0.7, 0.8, 0.1) | (0.3, 0, 0) |
| Estimated source activity (MBq) | 3.2 ± 3.2 | 3.8 ± 3.0 | 3.5 ± 2.0 | 2.6 ± 0.9 |
| Movement Sequence | #1 | #2 | #3 | #4 | #5 |
|---|---|---|---|---|---|
| Area where a source is located (voxels) | 1208 | 1058 | 746 | 330 | 23 |
| Estimated source location (m) | (3.8, 5.8, 0.0) | (3.8, 6.0, 0.0) | (3.1, 6.1, 0.0) | (3.1, 6.5, 0.0) | (2.6, 5.9, 0.0) |
| Error from true source position (m) | (1.3, 0.3, 0.0) | (1.3, 0.5, 0.0) | (0.6, 0.6, 0.0) | (0.6, 1.0, 0.0) | (0.1, 0.4, 0.0) |
| Estimated source activity (MBq) | 3.2 ± 3.2 | 3.1 ± 2.6 | 2.8 ± 1.9 | 3.2 ± 1.6 | 2.8 ± 0.8 |
| Movement Sequence | #1 | #2 | #3 | #4 |
|---|---|---|---|---|
| Area where a source is located (voxels) | 29,551 | 13,348 | 592 | 58 |
| Estimated source location (m) | (2.3, 5.8, 0.6) | (2.2, 5.7, 0.3) | (1.5, 4.1, 0.4) | (2.0, 4.1, 0.4) |
| Error from true source position (m) | (0.5, 1.5, 0.4) | (0.5, 1.4, 0.1) | (−0.2, −0.2, 0.2) | (0.3, −0.2, 0.2) |
| Estimated source activity (MBq) | 3.1 ± 3.1 | 3.4 ± 3.1 | 1.6 ± 1.0 | 2.1 ± 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomita, H.; Hara, S.; Mukai, A.; Yamagishi, K.; Ebi, H.; Shimazoe, K.; Tamura, Y.; Woo, H.; Takahashi, H.; Asama, H.; et al. Path-Planning System for Radioisotope Identification Devices Using 4π Gamma Imaging Based on Random Forest Analysis. Sensors 2022, 22, 4325. https://doi.org/10.3390/s22124325
Tomita H, Hara S, Mukai A, Yamagishi K, Ebi H, Shimazoe K, Tamura Y, Woo H, Takahashi H, Asama H, et al. Path-Planning System for Radioisotope Identification Devices Using 4π Gamma Imaging Based on Random Forest Analysis. Sensors. 2022; 22(12):4325. https://doi.org/10.3390/s22124325
Chicago/Turabian StyleTomita, Hideki, Shintaro Hara, Atsushi Mukai, Keita Yamagishi, Hidetake Ebi, Kenji Shimazoe, Yusuke Tamura, Hanwool Woo, Hiroyuki Takahashi, Hajime Asama, and et al. 2022. "Path-Planning System for Radioisotope Identification Devices Using 4π Gamma Imaging Based on Random Forest Analysis" Sensors 22, no. 12: 4325. https://doi.org/10.3390/s22124325
APA StyleTomita, H., Hara, S., Mukai, A., Yamagishi, K., Ebi, H., Shimazoe, K., Tamura, Y., Woo, H., Takahashi, H., Asama, H., Ishida, F., Takada, E., Kawarabayashi, J., Tanabe, K., & Kamada, K. (2022). Path-Planning System for Radioisotope Identification Devices Using 4π Gamma Imaging Based on Random Forest Analysis. Sensors, 22(12), 4325. https://doi.org/10.3390/s22124325







