Lamb Waves Propagation Characteristics in Functionally Graded Sandwich Plates
Abstract
:1. Introduction
2. Theoretical Derivation and Numerical Results
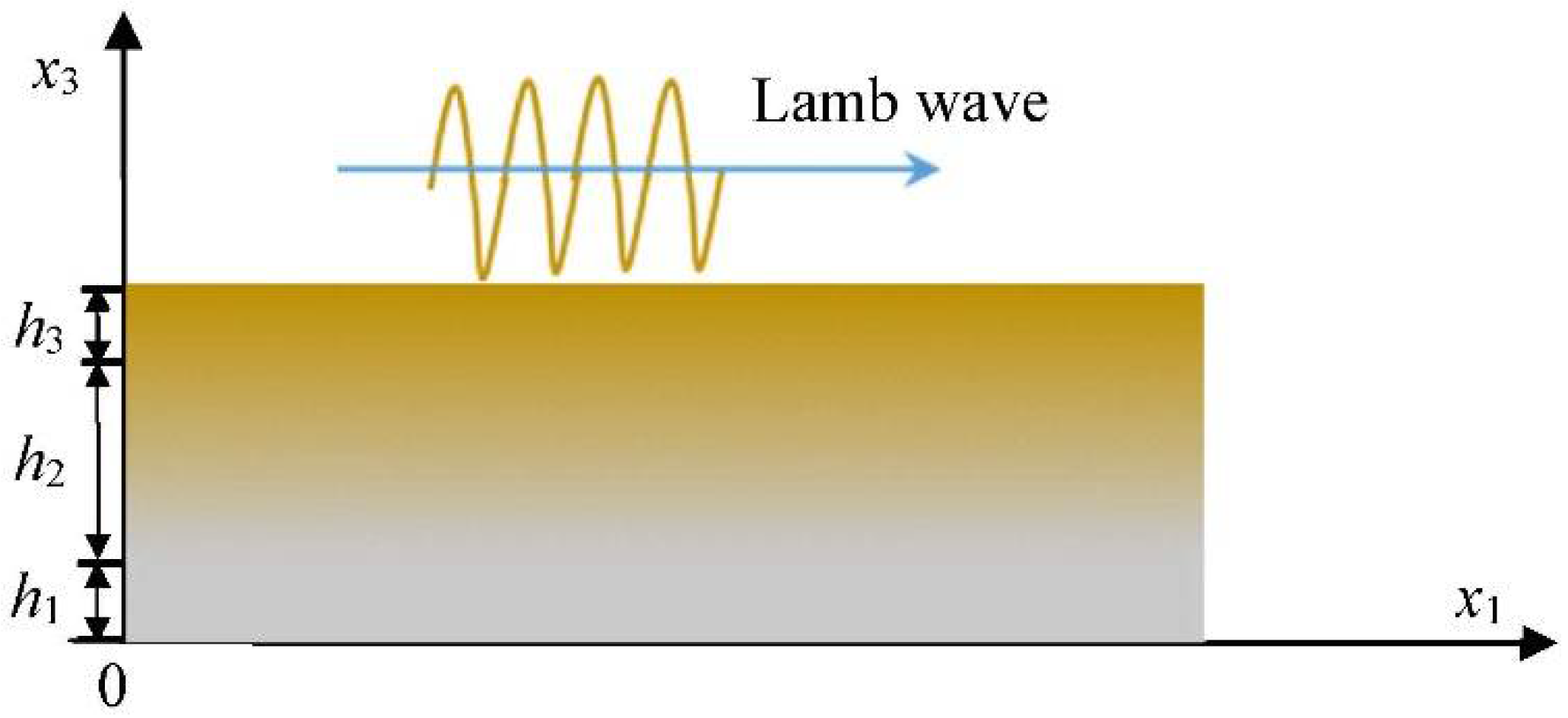
2.1. Modeling
2.2. Legendre Orthogonal Polynomial Expansion
2.3. Numerical Results and Discussion
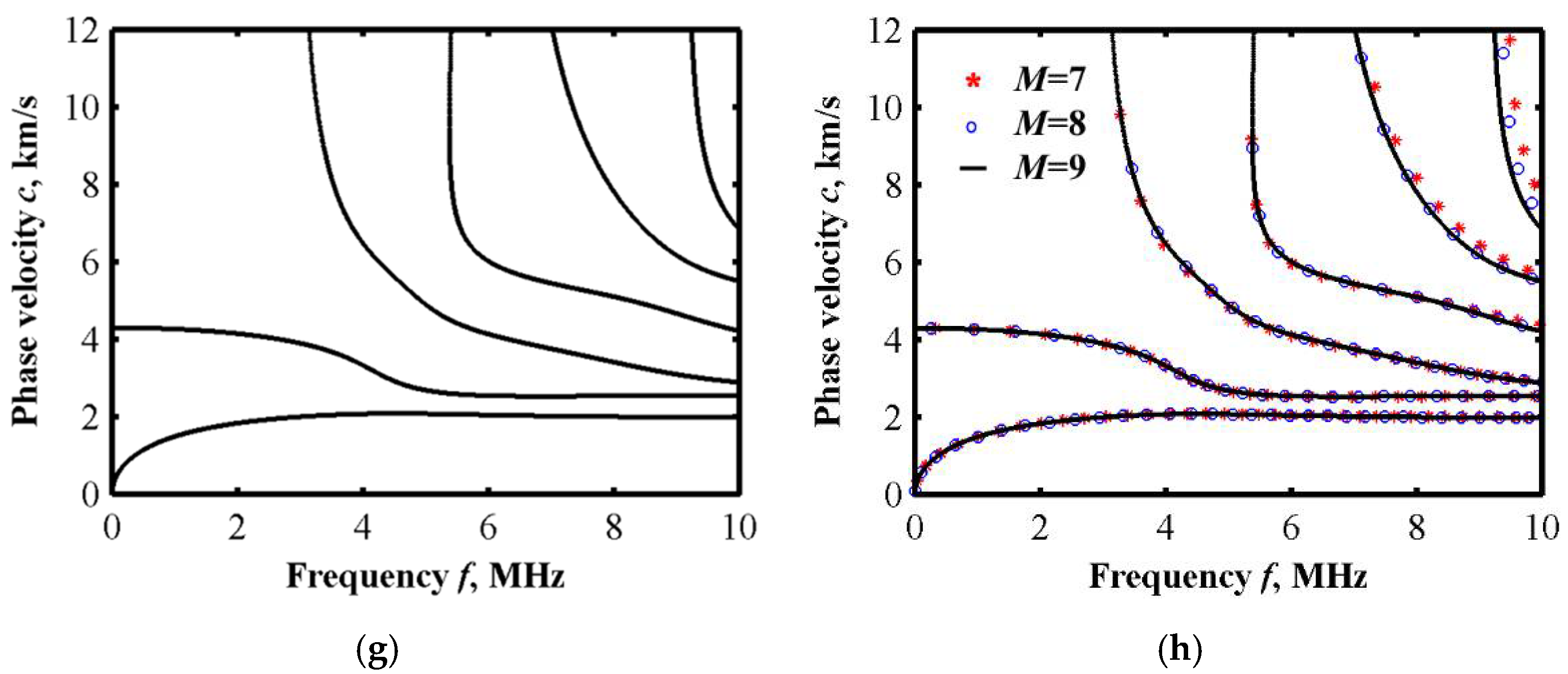
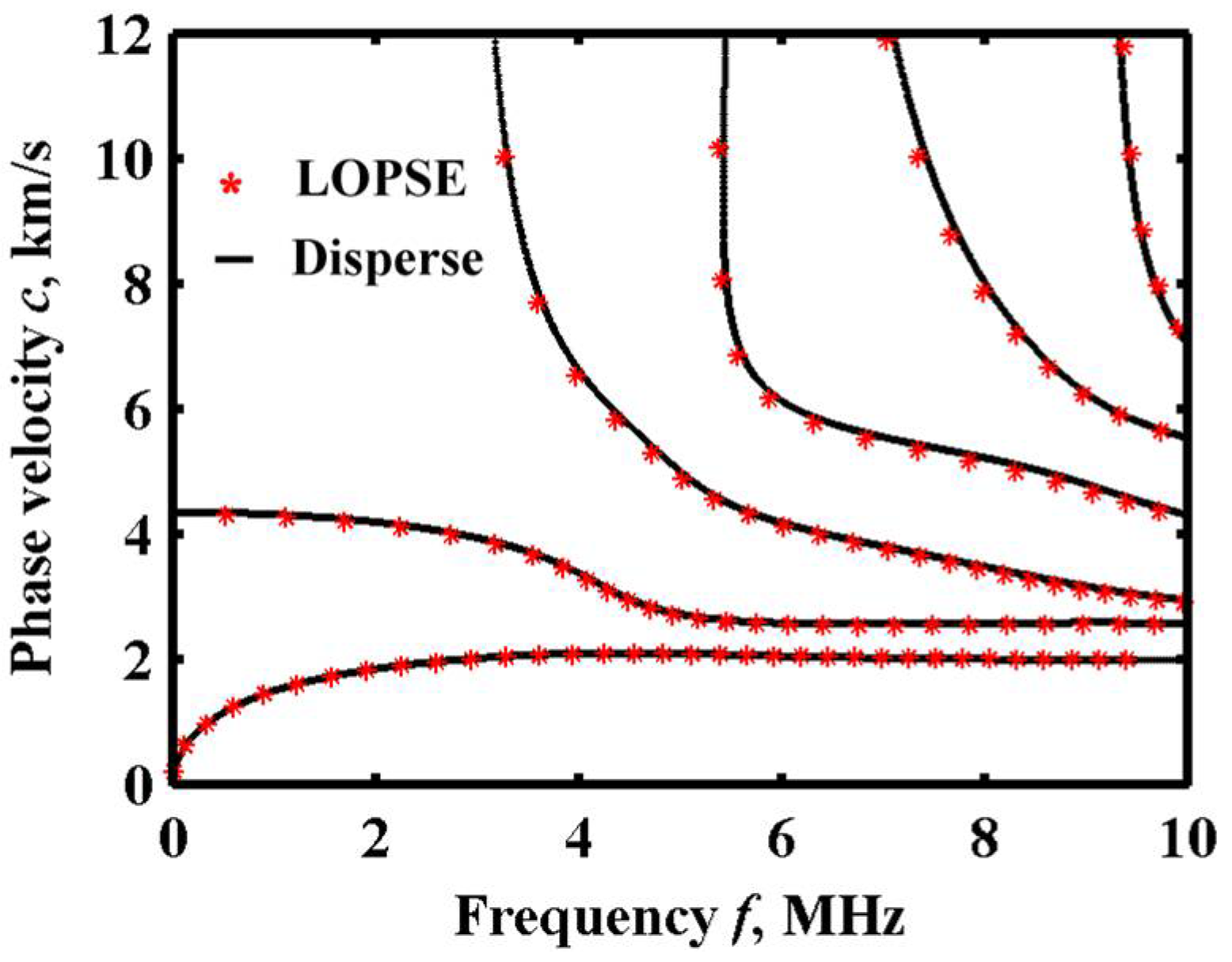
2.3.1. Convergence Analysis of Cutoff Order M
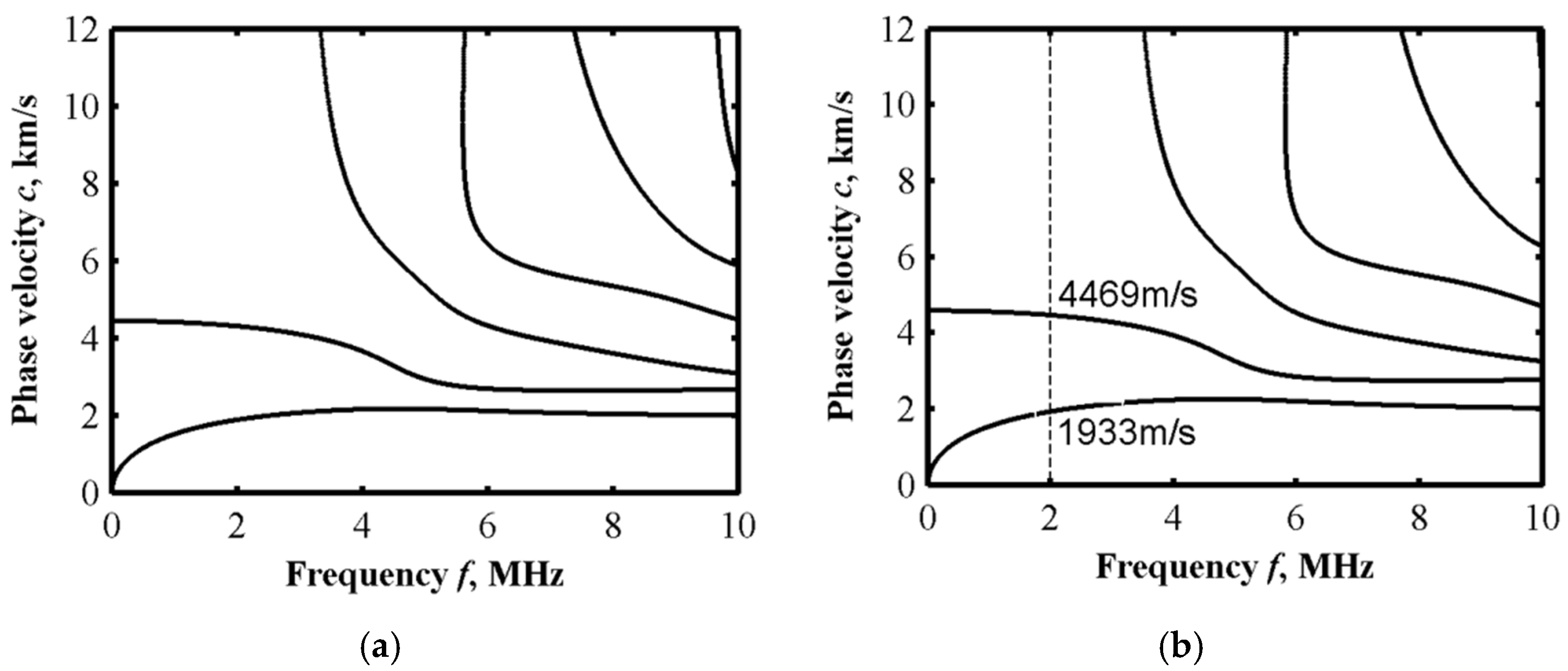
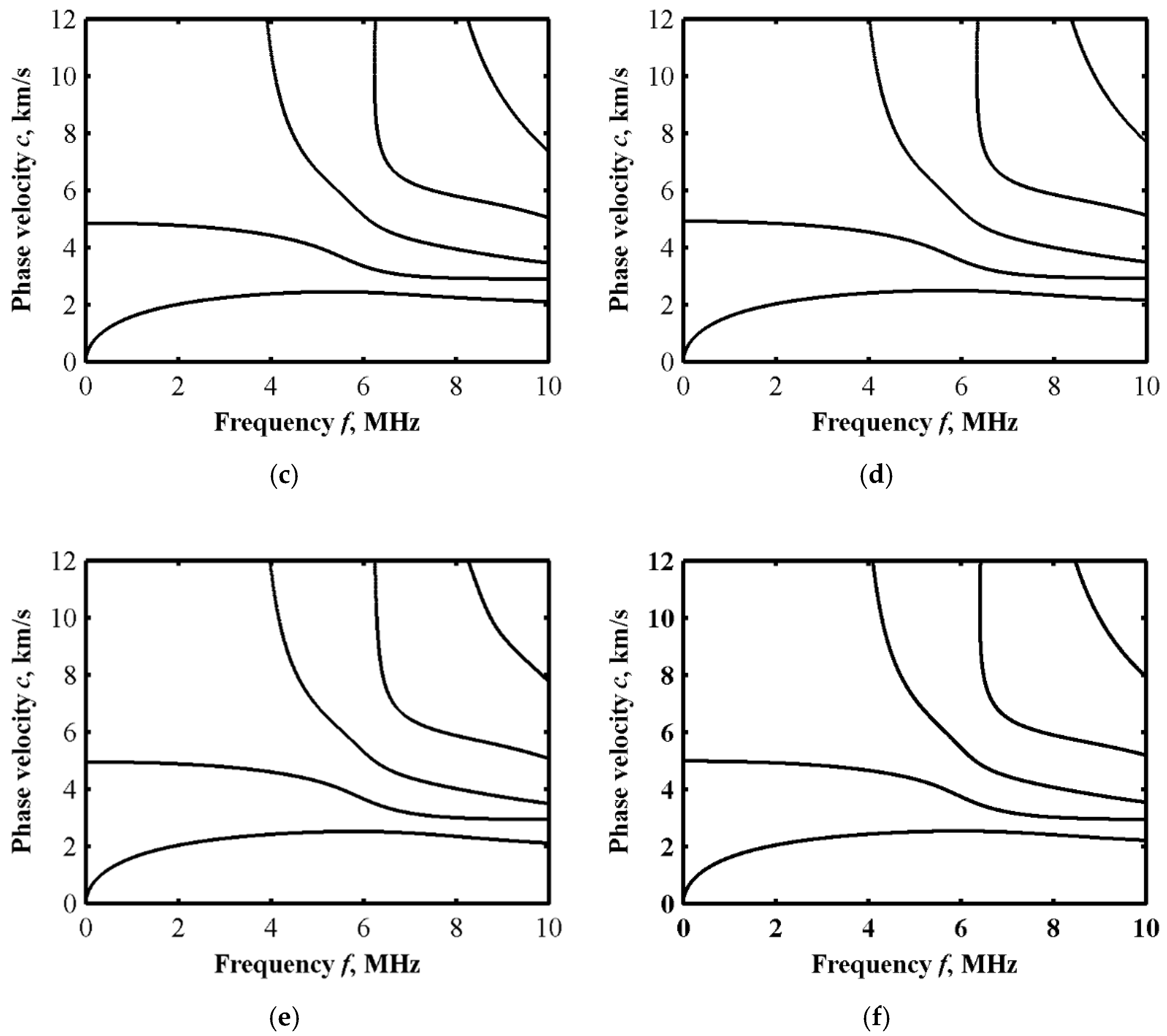
2.3.2. Effect of Volume Fraction n on Dispersion Curves
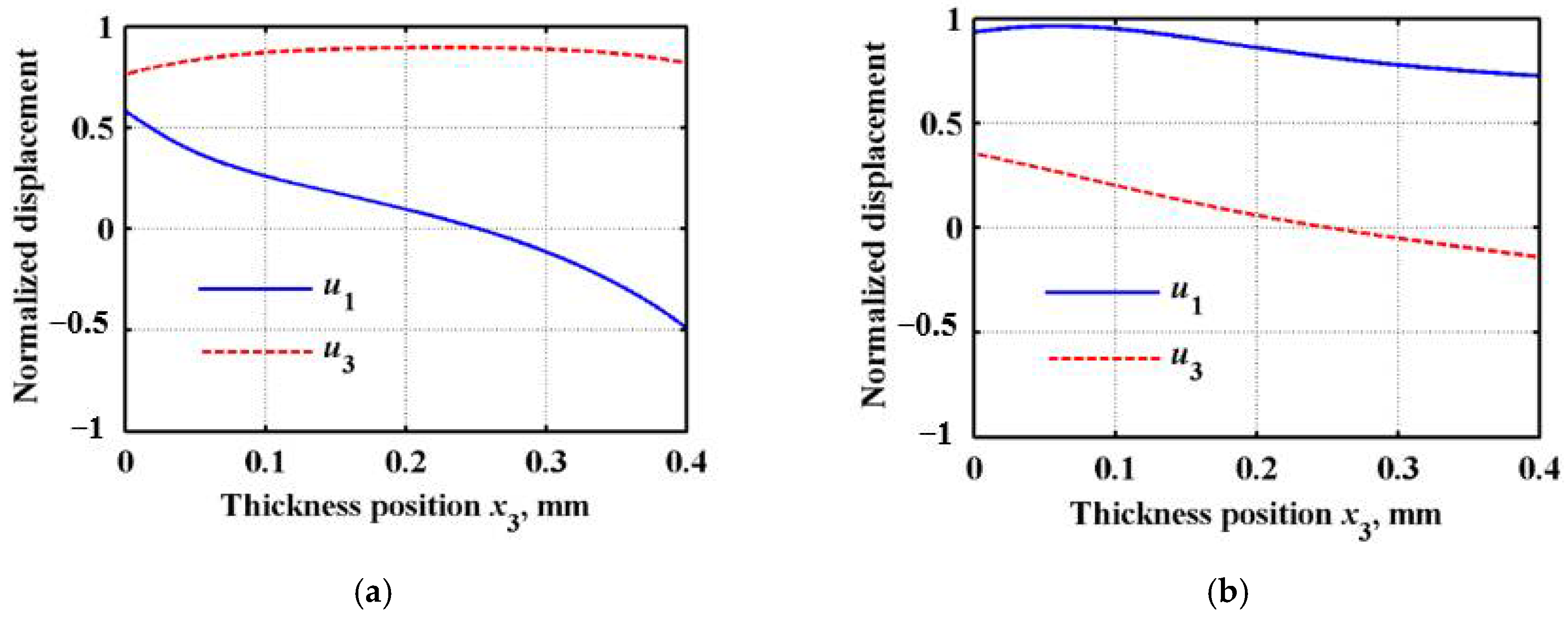
2.3.3. Displacement and Stress Distribution
3. Finite Element Analysis
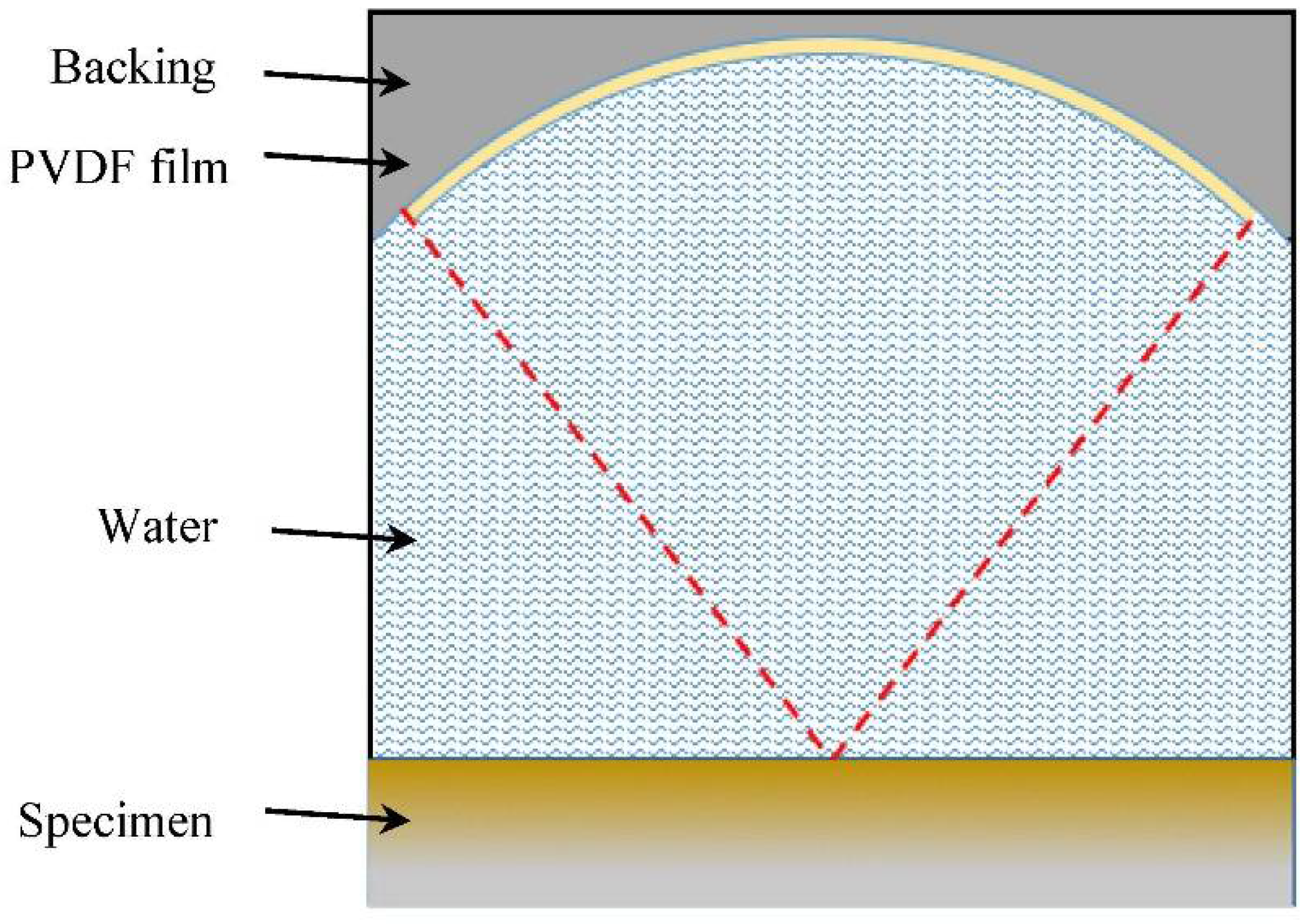
3.1. Simulation Model
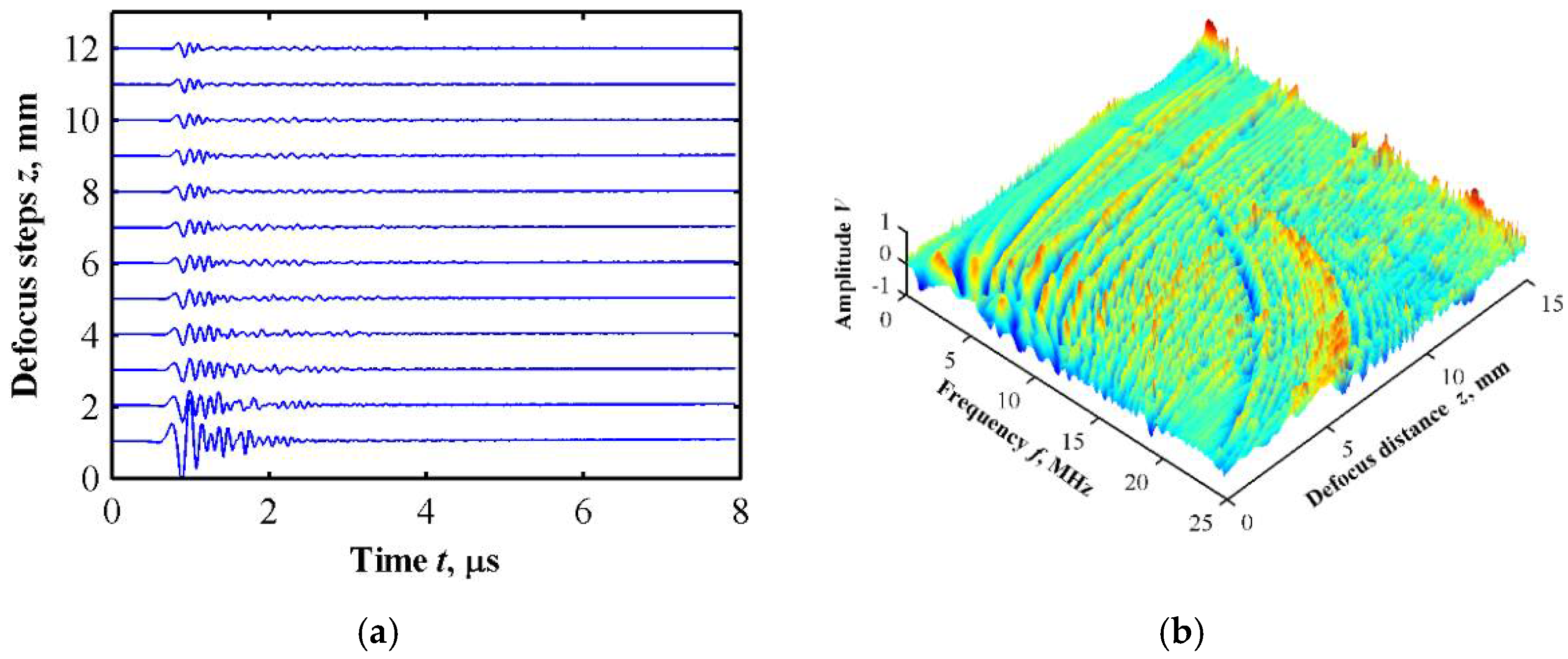
3.2. Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Kumakawa, A.; Niino, M.; Kiyoto, S.; Nagataet, S. Proceedings of the international symposium on functionally gradient materials. J. Am. Ceram. Soc. 1992, 34, 213–219. [Google Scholar]
- Guo, J.; Chen, J.; Pan, E. Size-dependent behavior of functionally graded anisotropic composite pate. Int. J. Eng. Sci. 2016, 106, 110–124. [Google Scholar] [CrossRef]
- Ankit Gupta, M. Talha, Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Sha, G.; Lissenden, C.J. Modeling Magnetostrictive Transducers for Structural Health Monitoring: Ultrasonic Guided Wave Generation and Reception. Sensors 2021, 21, 7971. [Google Scholar] [CrossRef]
- Jie, G.; Yan, L.; Zheng, M.F.; Liu, M.K.; Liu, H.Y.; Wu, B.; He, C.F. Modeling guided wave propagation in functionally graded plates by state-vector formalism and the Legendre polynomial method. Ultrasonics 2019, 99, 105953. [Google Scholar]
- Zhu, J.Y.; Chen, L.Z.; Wu, S.M. Dispersion of Lamb Waves in Layered Plates. J. Vib. Eng. 1998, 3, 366–372. [Google Scholar]
- Wu, R.X.; Yu, L.Z.; Li, X.D.; Qiu, Y. Propagation of Lamb Wave in a Functionally Graded Plate with a Layered Model. Appl. Acoust. 2016, 35, 199–205. [Google Scholar]
- Bruck, H.A. One-dimensional model for designing functionally graded materials to manage stress waves. Int. J. Solids. Struct. 2000, 37, 6383–6395. [Google Scholar] [CrossRef]
- Chen, W.Q.; Wang, H.M.; Bao, R.H. On calculating dispersion curves of waves in a functionally graded elastic plate. Compos. Struct. 2007, 81, 233–242. [Google Scholar] [CrossRef]
- Lefebvre, J.E.; Zhang, V.; Gazalet, J.; Gryba, T. Legendre polynomial approach for modeling free-ultrasonic waves in multilayered plates. J. Appl. Phys. 1999, 85, 3419–3427. [Google Scholar] [CrossRef]
- Yu, J.G.; Lefebvre, J.E.; Guo, Y.; Elmaimouni, L. Wave propagation in the circumferential direction of general multilayered piezoelectric cylindrical plates. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2498–2508. [Google Scholar]
- Salah, I.B.; Wali, Y.; Ghozlen, M.H. Love waves in functionally graded piezoelectric materials by stiffness matrix method. Ultrasonics 2011, 51, 310–316. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.M.; Wang, J.; Zhong, Z.; Du, J. An analysis of surface acoustic wave propagation in functionally graded plates with homotopy analysis method. Acta. Mech. 2009, 208, 249–258. [Google Scholar] [CrossRef]
- Taylor, R.L.; Zienkiewicz, O.C. The Finite Element Method, 6th ed.; McGraw-Hill: London, UK, 2005. [Google Scholar]
- Finnveden, S. Evaluation of modal density and group velocity by a finite element method. J. Sound Vib. 2004, 273, 51–75. [Google Scholar] [CrossRef]
- Cheng, X.; Xu, X.D.; Liu, X.J. Studying the Propagating of Surface Wave Traveling in Functional Gradient by Laser Ultrasonic. Acta Acustica. 2011, 2, 145–149. [Google Scholar]
- Kim, J.H.; Paulino, G.H. Isoparametric Graded Finite Elements for Nonhomogeneous Isotropic and Orthotropic Materials. J. Appl. Mech. 2002, 69, 502–514. [Google Scholar] [CrossRef]
- Zhang, C.; Xiao, J.Y. Research on Finite Element Methods for Functional Graded Material. Aircr. Design 2007, 27, 31–33. [Google Scholar]
- Wang, Y.S.; Gross, D. Analysis of a Crack in a Functionally Gradient Interface Layer under Static and Dynamic Loading. Key Eng. Mater. 2000, 183–187, 331–336. [Google Scholar]
- Gao, J.; Lyu, Y.; Zheng, M.F.; Liu, M.K.; Liu, H.Y.; Wu, B.; He, C.F. Modeling guided wave propagation in multi-layered anisotropic composite laminates by state-vector formalism and the Legendre polynomials. Compos. Struct. 2019, 228, 111319. [Google Scholar] [CrossRef]
- Lowe, M.J.S. Matrix techniques for modeling ultrasonic waves in multilayered media. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 525–542. [Google Scholar] [CrossRef]
- Martínez-Pañeda, E. On the finite element implementation of functionally graded materials. Materials 2019, 12, 287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santare, M.H.; Lambros, J. Use of graded finite elements to model the behavior of nonhomogeneous materials. J. Appl. Mech. 2000, 67, 819–822. [Google Scholar] [CrossRef]
- Gao, J.; Lyu, Y.; Song, G.R.; Liu, M.K.; Zheng, M.F.; He, C.F.; Lee, Y.C. Legendre orthogonal polynomial method in calculating reflection and transmission coefficients of fluid-loaded functionally gradient plates. Wave Motion 2021, 104, 102754. [Google Scholar] [CrossRef]
- Lyu, Y.; He, C.F.; Song, G.R.; Wu, B.; Lee, Y.C. Elastic Properties Inversion of an Isotropic Plate by Hybrid Particle Swarm-Based-Simulated Annealing Optimization Technique from Leaky Lamb Wave Measurements Using Acoustic Microscopy. J. Nondestr. Eval. 2014, 33, 651–662. [Google Scholar]





| Material | C11 (GPa) | C13 (GPa) | C33 (GPa) | C55 (GPa) | ρ (kg/m3) |
|---|---|---|---|---|---|
| Cu | 154.8 | 81.5 | 154.8 | 36.7 | 8292 |
| Steel | 275.0 | 113.2 | 275.0 | 80.9 | 7900 |
| Layer | C11 (GPa) | C13 (GPa) | C33 (GPa) | C55 (GPa) | ρ (kg/m3) |
|---|---|---|---|---|---|
| N = 1 | 154.8 | 81.5 | 154.8 | 36.7 | 8292.0 |
| N = 2 | 157.6 | 82.2 | 157.6 | 37.7 | 8282.9 |
| N = 3 | 160.7 | 83.0 | 160.7 | 38.8 | 8272.8 |
| N = 4 | 164.2 | 84.0 | 164.2 | 40.1 | 8261.5 |
| N = 5 | 168.1 | 85.0 | 168.1 | 41.6 | 8248.5 |
| N = 6 | 172.8 | 86.2 | 172.8 | 43.3 | 8233.3 |
| N = 7 | 178.5 | 87.7 | 178.5 | 45.4 | 8214.7 |
| N = 8 | 186.0 | 89.7 | 186.0 | 48.2 | 8190.2 |
| N = 9 | 197.6 | 92.8 | 197.6 | 52.4 | 8152.6 |
| N = 10 | 275.0 | 113.2 | 275.0 | 80.9 | 7900.0 |
| Material | Density 𝜌 (Kg/m3) | Longitudinal Wave Velocity CL (m/s) | Transverse Wave Velocity CT (m/s) |
|---|---|---|---|
| Back10 | 2975 | 1960 | 1047 |
| PVDF | 1780 | — | — |
| Water | 1000 | 1496 | — |
| Cu | 8292 | 4321 | 2103 |
| FGM layer | 8282.9 | 4357.7 | 2128.5 |
| 8272.8 | 4398.4 | 2156.8 | |
| 8261.5 | 4444.0 | 2188.5 | |
| 8248.5 | 4496.1 | 2224.7 | |
| 8233.3 | 4557.4 | 2267.2 | |
| 8214.7 | 4632.5 | 2319.4 | |
| 8190.2 | 4731.2 | 2388.0 | |
| 8152.6 | 4882.5 | 2493.1 | |
| Steel | 7900 | 5900 | 3200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Zhang, J.; Lyu, Y.; Song, G.; He, C. Lamb Waves Propagation Characteristics in Functionally Graded Sandwich Plates. Sensors 2022, 22, 4052. https://doi.org/10.3390/s22114052
Gao J, Zhang J, Lyu Y, Song G, He C. Lamb Waves Propagation Characteristics in Functionally Graded Sandwich Plates. Sensors. 2022; 22(11):4052. https://doi.org/10.3390/s22114052
Chicago/Turabian StyleGao, Jie, Jianbo Zhang, Yan Lyu, Guorong Song, and Cunfu He. 2022. "Lamb Waves Propagation Characteristics in Functionally Graded Sandwich Plates" Sensors 22, no. 11: 4052. https://doi.org/10.3390/s22114052
APA StyleGao, J., Zhang, J., Lyu, Y., Song, G., & He, C. (2022). Lamb Waves Propagation Characteristics in Functionally Graded Sandwich Plates. Sensors, 22(11), 4052. https://doi.org/10.3390/s22114052






