A Review of Noninvasive Methodologies to Estimate the Blood Pressure Waveform
Abstract
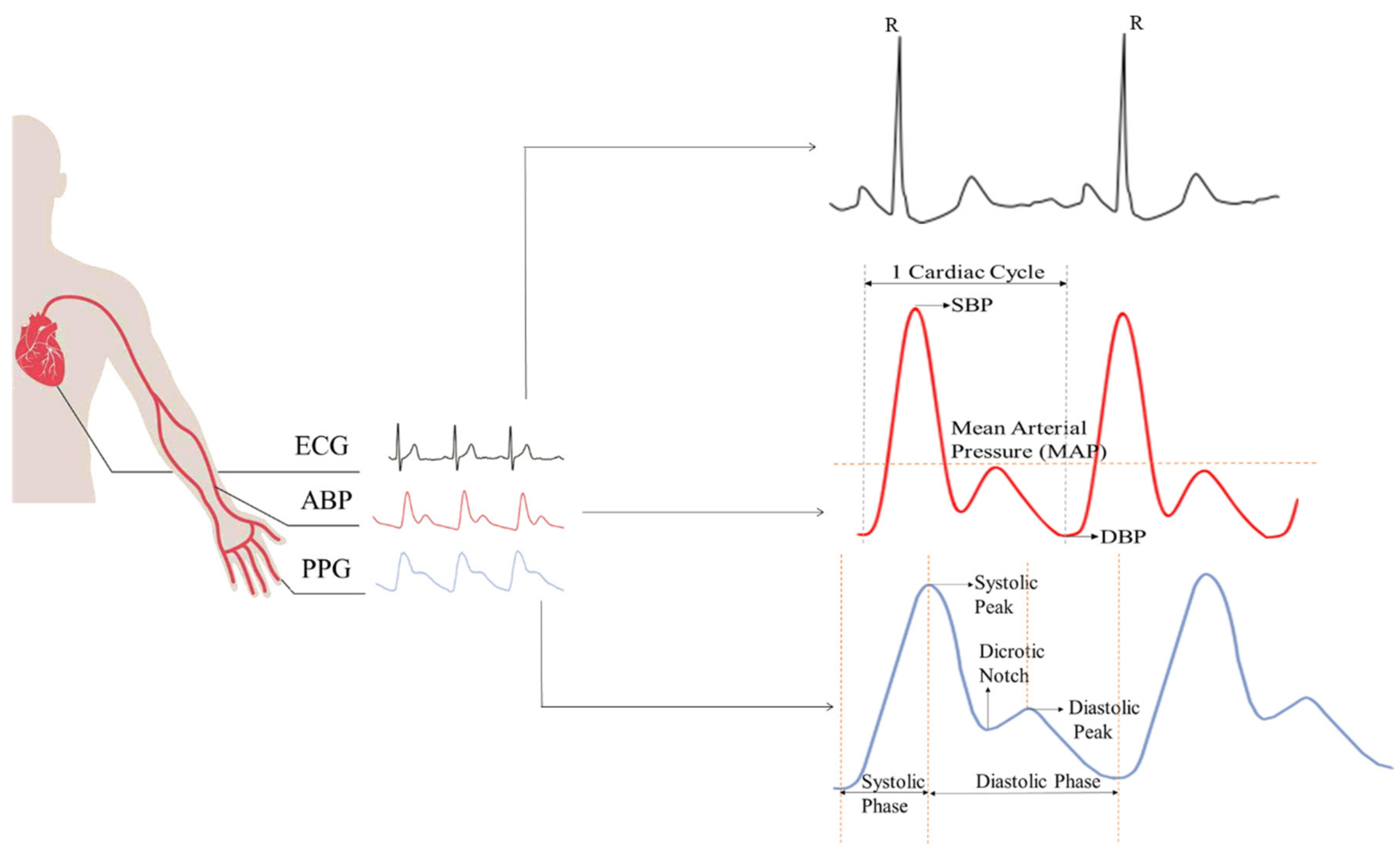
:1. Introduction
2. Searching Strategy
- Hypertension or high blood pressure;
- Arterial waveform;
- Blood pressure waveform;
- Machine learning in ABP waveform;
- Signal processing in ABP waveform.
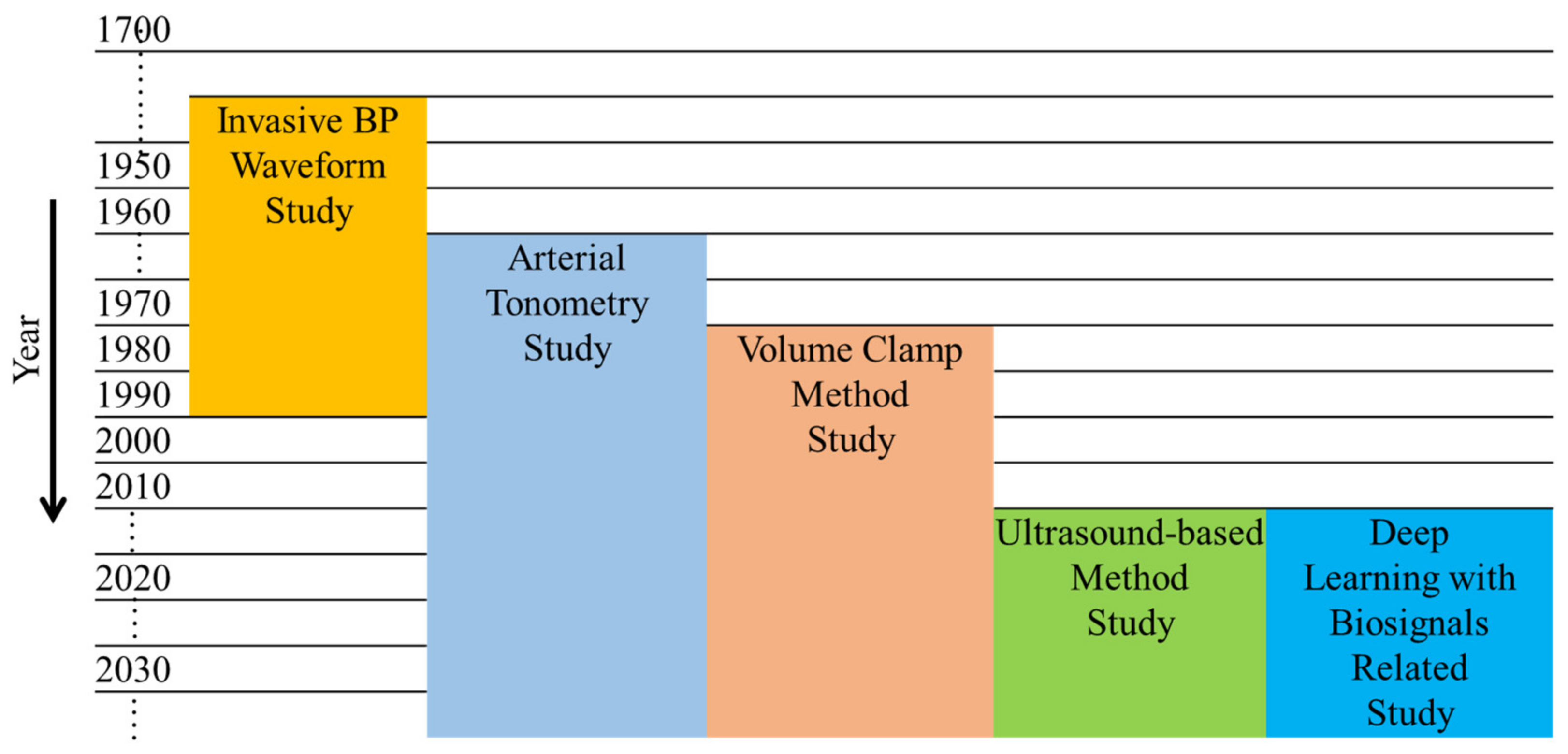
3. Noninvasive BP Waveform Estimation Methods
3.1. Pressure-Based Method
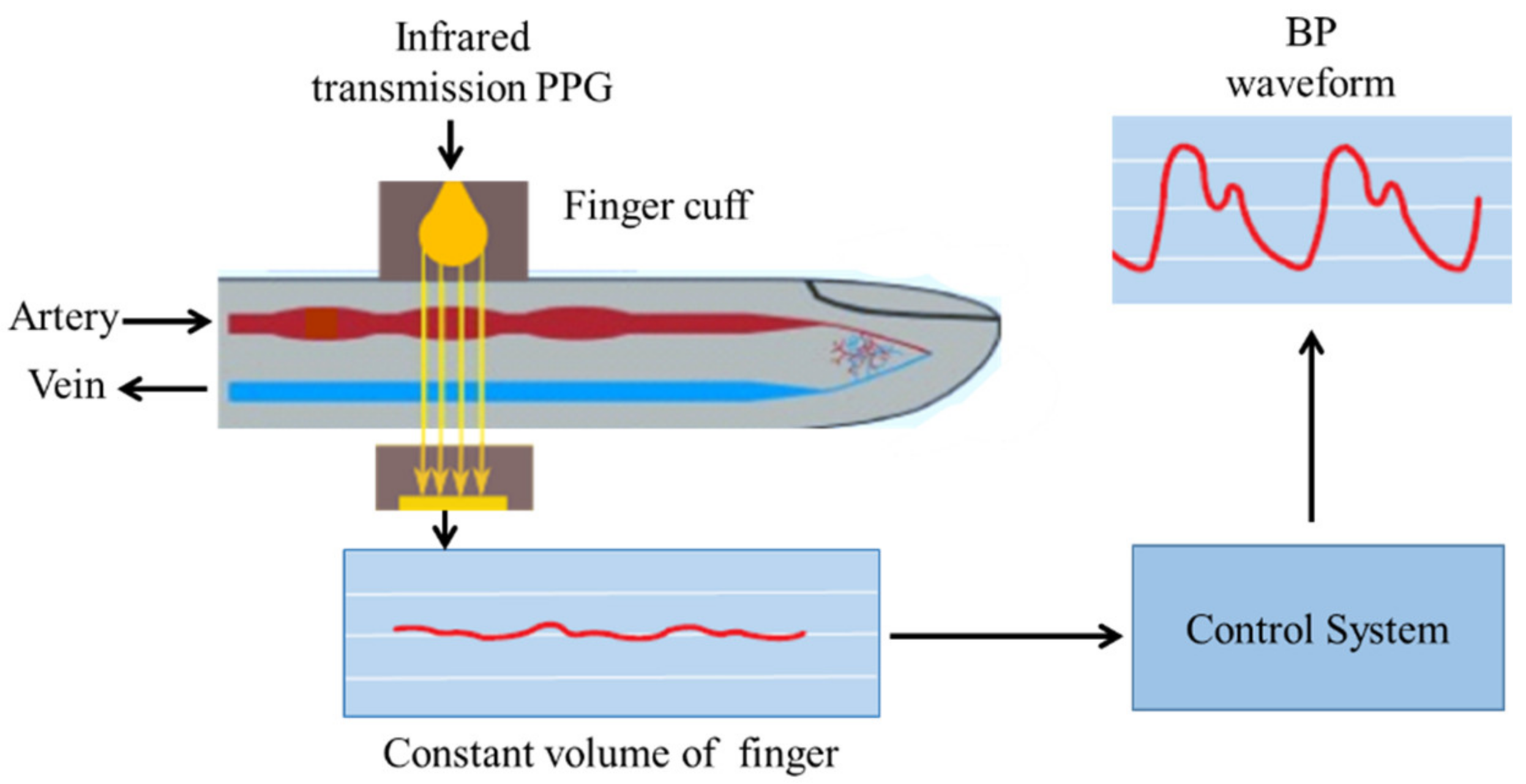
3.1.1. Vascular Unloading Technique
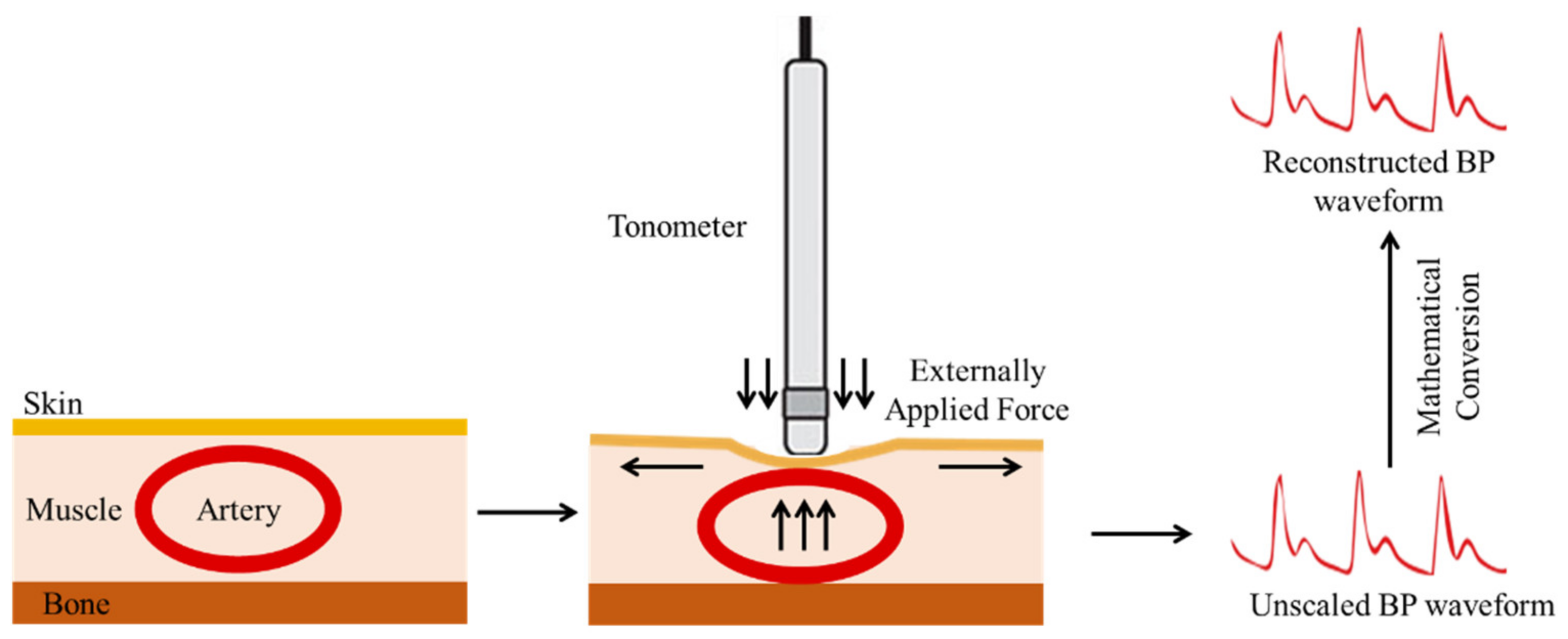
3.1.2. Arterial Tonometry
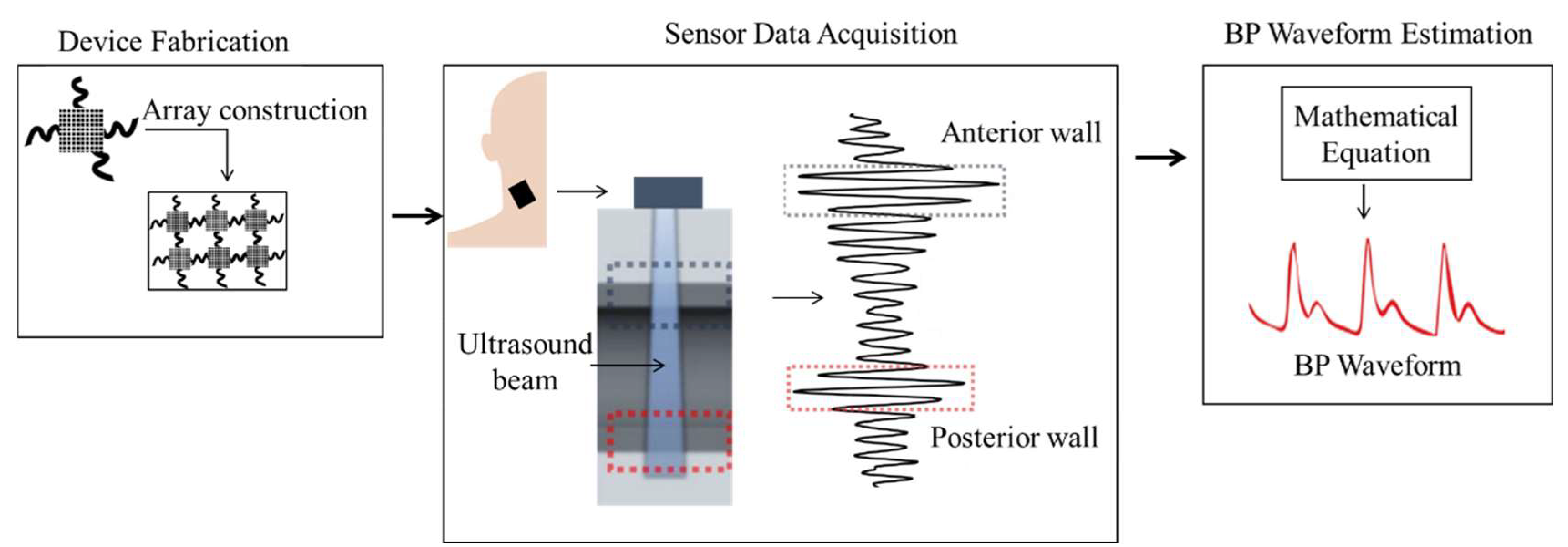
3.2. Ultrasound-Based Method
3.3. Deep-Learning-Based Methods
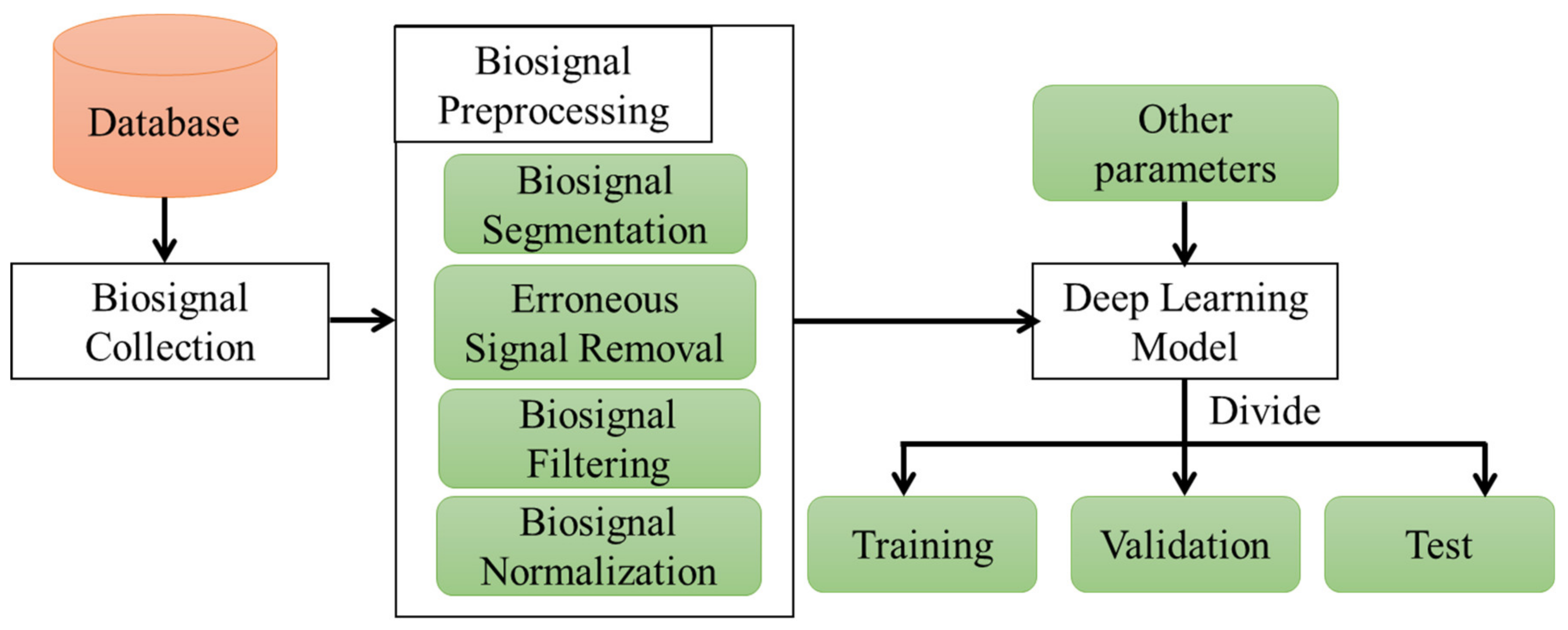
3.3.1. Data Preprocessing
- Segmenting the data to train the model;
- Removing erroneous biosignals that are inaccurate for measurement;
- Filtering the biosignals to remove the baseline wandering and high–frequency noises;
- Normalizing inputs and outputs for accurate training of the model.
3.3.2. Data Availability
4. Result Comparison
5. Commercialization
6. Discussion and Future Prospects
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Esper, S.A.; Pinsky, M.R. Arterial Waveform Analysis. Best Pract. Res. Clin. Anaesthesiol. 2014, 28, 363–380. [Google Scholar] [CrossRef] [PubMed]
- A Global Brief on Hypertension: Silent Killer, Global Public Health Crisis: World Health Day 2013. Available online: https://www.who.int/publications-detail-redirect/a-global-brief-on-hypertension-silent-killer-global-public-health-crisis-world-health-day-2013 (accessed on 3 February 2022).
- Escobar, E. Hypertension and Coronary Heart Disease. J. Hum. Hypertens. 2002, 16, S61–S63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sternlicht, H.; Bakris, G.L. The Kidney in Hypertension. Med. Clin. N. Am. 2017, 101, 207–217. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, F.D.; Whelton, P.K. High Blood Pressure and Cardiovascular Disease. Hypertension 2020, 75, 285–292. [Google Scholar] [CrossRef]
- Monte-Moreno, E. Non-Invasive Estimate of Blood Glucose and Blood Pressure from a Photoplethysmograph by Means of Machine Learning Techniques. Artif. Intell. Med. 2011, 53, 127–138. [Google Scholar] [CrossRef]
- Sun, D.; Zhou, T.; Heianza, Y.; Li, X.; Fan, M.; Fonseca, V.A.; Qi, L. Type 2 Diabetes and Hypertension. Circ. Res. 2019, 124, 930–937. [Google Scholar] [CrossRef]
- Stroke and Hypertension; World Heart Federation: Geneva, Switzerland, 2020.
- Mills, K.T.; Bundy, J.D.; Kelly, T.N.; Reed, J.E.; Kearney, P.M.; Reynolds, K.; Chen, J.; He, J. Global Disparities of Hypertension Prevalence and Control. Circulation 2016, 134, 441–450. [Google Scholar] [CrossRef]
- McGhee, B.H.; Bridges, E.J. Monitoring Arterial Blood Pressure: What You May Not Know. Crit. Care Nurse 2002, 22, 60–79. [Google Scholar] [CrossRef]
- Avolio, A.P.; Butlin, M.; Walsh, A. Arterial Blood Pressure Measurement and Pulse Wave Analysis—Their Role in Enhancing Cardiovascular Assessment. Physiol. Meas. 2009, 31, R1–R47. [Google Scholar] [CrossRef]
- Moxham, D.I. Understanding Arterial Pressure Waveforms. S. Afr. J. Anaesth. Analg. 2003, 9, 40–42. [Google Scholar] [CrossRef]
- Kumar, A.; Anel, R.; Bunnell, E.; Habet, K.; Zanotti, S.; Marshall, S.; Neumann, A.; Ali, A.; Cheang, M.; Kavinsky, C.; et al. Pulmonary Artery Occlusion Pressure and Central Venous Pressure Fail to Predict Ventricular Filling Volume, Cardiac Performance, or the Response to Volume Infusion in Normal Subjects. Crit. Care Med. 2004, 32, 691–699. [Google Scholar] [CrossRef] [PubMed]
- Mf, O. Arterial Pressure Waveforms in Hypertension. Minerva Med. 2003, 94, 229–250. [Google Scholar]
- Spelde, A.; Monahan, C. Invasive Arterial Blood Pressure Monitoring. In Anesthesiology Core Review: Part Two Advanced Exam; Freeman, B.S., Berger, J.S., Eds.; McGraw-Hill Education: New York, NY, USA, 2016. [Google Scholar]
- Mukkamala, R.; Reisner, A.T.; Hojman, H.M.; Mark, R.G.; Cohen, R.J. Continuous Cardiac Output Monitoring by Peripheral Blood Pressure Waveform Analysis. In Proceedings of the Computers in Cardiology, Chalkidiki, Greece, 21–24 September 2003; pp. 255–258. [Google Scholar]
- Lewis, O. Stephen Hales and the Measurement of Blood Pressure. J. Hum. Hypertens. 1994, 8, 865–871. [Google Scholar] [PubMed]
- Tsyrlin, V.A.; Pliss, M.G.; Kuzmenko, N.V. The history of blood pressure measurement: From Hales to our days. Arter. Gipertenz. 2016, 22, 144–152. [Google Scholar] [CrossRef]
- Daniel Bernoulli and the Making of the Fluid Equation. Available online: https://plus.maths.org/content/daniel-bernoulli-and-making-fluid-equation (accessed on 3 February 2022).
- Sutera: The History of Poiseuille’s Law—Google Scholar. Available online: https://scholar.google.com/scholar_lookup?title=The%20history%20of%20Poiseuille%20law&publication_year=1993&author=S.P.%20Sutera&author=R.%20Skalak (accessed on 3 February 2022).
- Peterson, L.H.; Dripps, R.D.; Risman, G.C. A Method for Recording the Arterial Pressure Pulse and Blood Pressure in Man. Am. Heart J. 1949, 37, 771–782. [Google Scholar] [CrossRef]
- Peirce, E.C. Percutaneous Femoral Artery Catheterization in Man with Special Reference to Aortography. Surg. Gynecol. Obs. 1951, 93, 56–74. [Google Scholar]
- Ivar Seldinger, S. Catheter Replacement of the Needle in Percutaneous Arteriography: A New Technique. Acta Radiol. 2008, 49, 47–52. [Google Scholar] [CrossRef]
- Goodman, C.T.; Kitchen, G.B. Measuring Arterial Blood Pressure. Anaesth. Intensive Care Med. 2021, 22, 49–53. [Google Scholar] [CrossRef]
- Hill, B.L.; Rakocz, N.; Rudas, Á.; Chiang, J.N.; Wang, S.; Hofer, I.; Cannesson, M.; Halperin, E. Imputation of the Continuous Arterial Line Blood Pressure Waveform from Non-Invasive Measurements Using Deep Learning. Sci. Rep. 2021, 11, 15755. [Google Scholar] [CrossRef]
- Lam, S.; Liu, H.; Jian, Z.; Settels, J.; Bohringer, C. Intraoperative Invasive Blood Pressure Monitoring and the Potential Pitfalls of Invasively Measured Systolic Blood Pressure. Cureus 2021, 13. [Google Scholar] [CrossRef]
- Zakrzewski, A.M.; Anthony, B.W. Noninvasive Blood Pressure Estimation Using Ultrasound and Simple Finite Element Models. IEEE Trans. Biomed. Eng. 2018, 65, 2011–2022. [Google Scholar] [CrossRef] [PubMed]
- Zakrzewski, A.M.; Huang, A.Y.; Zubajlo, R.; Anthony, B.W. Real-Time Blood Pressure Estimation From Force-Measured Ultrasound. IEEE Trans. Biomed. Eng. 2018, 65, 2405–2416. [Google Scholar] [CrossRef] [PubMed]
- Miao, F.; Wen, B.; Hu, Z.; Fortino, G.; Wang, X.-P.; Liu, Z.-D.; Tang, M.; Li, Y. Continuous Blood Pressure Measurement from One-Channel Electrocardiogram Signal Using Deep-Learning Techniques. Artif. Intell. Med. 2020, 108, 101919. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Liu, J.; Chen, X.; Wang, Y.; Zhao, Z. Continuous Blood Pressure Estimation Based on Multiple Parameters from Eletrocardiogram and Photoplethysmogram by Back-Propagation Neural Network. Comput. Ind. 2017, 89, 50–59. [Google Scholar] [CrossRef]
- Haque, C.A.; Kwon, T.-H.; Kim, K.-D. Cuffless Blood Pressure Estimation Based on Monte Carlo Simulation Using Photoplethysmography Signals. Sensors 2022, 22, 1175. [Google Scholar] [CrossRef] [PubMed]
- Fortin, J.; Marte, W.; Grüllenberger, R.; Hacker, A.; Habenbacher, W.; Heller, A.; Wagner, C.H.; Wach, P.; Skrabal, F. Continuous Non-Invasive Blood Pressure Monitoring Using Concentrically Interlocking Control Loops. Comput. Biol. Med. 2006, 36, 941–957. [Google Scholar] [CrossRef]
- Salvi, P.; Grillo, A.; Parati, G. Noninvasive Estimation of Central Blood Pressure and Analysis of Pulse Waves by Applanation Tonometry. Hypertens. Res. 2015, 38, 646–648. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Hu, H.; Zhang, L.; Huang, Z.; Lin, M.; Zhang, Z.; Yin, Z.; Huang, B.; Gong, H.; et al. Monitoring of the Central Blood Pressure Waveform via a Conformal Ultrasonic Device. Nat. Biomed. Eng. 2018, 2, 687–695. [Google Scholar] [CrossRef]
- Seo, J.; Pietrangelo, S.J.; Lee, H.-S.; Sodini, C.G. Noninvasive Arterial Blood Pressure Waveform Monitoring Using Two- Element Ultrasound System. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 776–784. [Google Scholar] [CrossRef]
- Seo, J.; Pietrangelo, S.J.; Lee, H.-S.; Sodini, C.G. Carotid Arterial Blood Pressure Waveform Monitoring Using a Portable Ultrasound System. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 5692–5695. [Google Scholar]
- Ibtehaz, N.; Rahman, M.S. PPG2ABP: Translating Photoplethysmogram (PPG) Signals to Arterial Blood Pressure (ABP) Waveforms Using Fully Convolutional Neural Networks. arXiv 2020, arXiv:2005.01669. [Google Scholar]
- Athaya, T.; Choi, S. An Estimation Method of Continuous Non-Invasive Arterial Blood Pressure Waveform Using Photoplethysmography: A U-Net Architecture-Based Approach. Sensors 2021, 21, 1867. [Google Scholar] [CrossRef] [PubMed]
- Qin, K.; Huang, W.; Zhang, T. Deep Generative Model with Domain Adversarial Training for Predicting Arterial Blood Pressure Waveform from Photoplethysmogram Signal. Biomed. Signal Process. Control 2021, 70, 102972. [Google Scholar] [CrossRef]
- Sadrawi, M.; Lin, Y.-T.; Lin, C.-H.; Mathunjwa, B.; Fan, S.-Z.; Abbod, M.F.; Shieh, J.-S. Genetic Deep Convolutional Autoencoder Applied for Generative Continuous Arterial Blood Pressure via Photoplethysmography. Sensors 2020, 20, 3829. [Google Scholar] [CrossRef] [PubMed]
- Landry, C.; Peterson, S.D.; Arami, A. Estimation of the Blood Pressure Waveform Using Electrocardiography. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 7060–7063. [Google Scholar]
- Elgendi, M.; Fletcher, R.; Liang, Y.; Howard, N.; Lovell, N.H.; Abbott, D.; Lim, K.; Ward, R. The Use of Photoplethysmography for Assessing Hypertension. npj Digit. Med. 2019, 2, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El-Hajj, C.; Kyriacou, P.A. A Review of Machine Learning Techniques in Photoplethysmography for the Non-Invasive Cuff-Less Measurement of Blood Pressure. Biomed. Signal Process. Control 2020, 58, 101870. [Google Scholar] [CrossRef]
- Barvik, D.; Cerny, M.; Penhaker, M.; Noury, N. Noninvasive Continuous Blood Pressure Estimation from Pulse Transit Time: A Review of the Calibration Models. IEEE Rev. Biomed. Eng. 2022, 15, 138–151. [Google Scholar] [CrossRef]
- Martinez-Ríos, E.; Montesinos, L.; Alfaro-Ponce, M.; Pecchia, L. A Review of Machine Learning in Hypertension Detection and Blood Pressure Estimation Based on Clinical and Physiological Data. Biomed. Signal Process. Control 2021, 68, 102813. [Google Scholar] [CrossRef]
- Priyadarshini, R.G.; Kalimuthu, M.; Nikesh, S.; Bhuvaneshwari, M. Review of PPG Signal Using Machine Learning Algorithms for Blood Pressure and Glucose Estimation. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1084, 012031. [Google Scholar] [CrossRef]
- Sharma, M.; Barbosa, K.; Ho, V.; Griggs, D.; Ghirmai, T.; Krishnan, S.K.; Hsiai, T.K.; Chiao, J.-C.; Cao, H. Cuff-Less and Continuous Blood Pressure Monitoring: A Methodological Review. Technologies 2017, 5, 21. [Google Scholar] [CrossRef] [Green Version]
- Arakawa, T. Recent Research and Developing Trends of Wearable Sensors for Detecting Blood Pressure. Sensors 2018, 18, 2772. [Google Scholar] [CrossRef] [Green Version]
- Peter, L.; Noury, N.; Cerny, M. A Review of Methods for Non-Invasive and Continuous Blood Pressure Monitoring: Pulse Transit Time Method Is Promising? IRBM 2014, 35, 271–282. [Google Scholar] [CrossRef]
- Quan, X.; Liu, J.; Roxlo, T.; Siddharth, S.; Leong, W.; Muir, A.; Cheong, S.-M.; Rao, A. Advances in Non-Invasive Blood Pressure Monitoring. Sensors 2021, 21, 4273. [Google Scholar] [CrossRef] [PubMed]
- Pandit, J.A.; Lores, E.; Batlle, D. Cuffless Blood Pressure Monitoring: Promises and Challenges. CJASN 2020, 15, 1531–1538. [Google Scholar] [CrossRef] [PubMed]
- Meidert, A.S.; Saugel, B. Techniques for Non-Invasive Monitoring of Arterial Blood Pressure. Front. Med. 2018, 4, 231. [Google Scholar] [CrossRef]
- Chung, E.; Chen, G.; Alexander, B.; Cannesson, M. Non-Invasive Continuous Blood Pressure Monitoring: A Review of Current Applications. Front. Med. 2013, 7, 91–101. [Google Scholar] [CrossRef]
- Matthys, K.; Verdonck, P. Development and Modelling of Arterial Applanation Tonometry: A Review. Technol. Health Care 2002, 10, 65–76. [Google Scholar] [CrossRef]
- Wesseling, K.H.; Settels, J.J.; de Wit, B. The Measurement of Continuous Finger Arterial Pressure Noninvasively in Stationary Subjects. In Proceedings of the Biological and Psychological Factors in Cardiovascular Disease; Schmidt, T.H., Dembroski, T.M., Blümchen, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 355–375. [Google Scholar]
- Wesseling, K.H. A Century of Noninvasive Arterial Pressure Measurement: From Marey to Peñáz and Finapres. Homeost. Health Dis. 1995, 36, 50–66. [Google Scholar]
- Wesseling, K.H. Finapres, Continuous Noninvasive Finger Arterial Pressure Based on the Method of Peñáz. In Proceedings of the Blood Pressure Measurements; Meyer-Sabellek, W., Gotzen, R., Anlauf, M., Steinfeld, L., Eds.; Steinkopff: Heidelberg, Germany, 1990; pp. 161–172. [Google Scholar]
- Smith, N.T.; Wesseling, K.H.; de Wit, B. Evaluation of Two Prototype Devices Producing Noninvasive, Pulsatile, Calibrated Blood Pressure Measurement from a Finger. J. Clin. Monit. Comput. 1985, 1, 17–29. [Google Scholar] [CrossRef]
- Molhoek, G.P.; Wesseling, K.H.; Settels, J.J.M.; van Vollenhoven, E.; Weeda, H.W.H.; de Wit, B.; Arntzenius, A.C. Evaluation of the Penàz Servo-Plethysmo-Manometer for the Continuous, Non-Invasive Measurement of Finger Blood Pressure. Basic Res. Cardiol. 1984, 79, 598–609. [Google Scholar] [CrossRef]
- Kurki, T.; Ty Smith, N.; Head, N.; Dec-Silver, H.; Quinn, A. Noninvasive Continuous Blood Pressure Measurement from the Finger: Optimal Measurement Conditions and Factors Affecting Reliability. J. Clin. Monit. Comput. 1987, 3, 6–13. [Google Scholar] [CrossRef]
- Yamakoshi, K.-I.; Shimazu, H.; Togawa, T. Indirect Measurement of Instantaneous Arterial Blood Pressure in the Human Finger by the Vascular Unloading Technique. IEEE Trans. Biomed. Eng. 1980, BME-27, 150–155. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, S.; Yamakoshi, K. Ambulatory Instrument for Monitoring Indirect Beat-to-Beat Blood Pressure in Superficial Temporal Artery Using Volume-Compensation Method. Med. Biol. Eng. Comput. 1996, 34, 441–447. [Google Scholar] [CrossRef] [PubMed]
- Kawarada, A.; Shimazu, H.; Ito, H.; Yamakoshi, K. Ambulatory Monitoring of Indirect Beat-to-Beat Arterial Pressure in Human Fingers by a Volume-Compensation Method. Med. Biol. Eng. Comput. 1991, 29, 55–62. [Google Scholar] [CrossRef]
- Shimazu, H.; Ito, H.; Kawarada, A.; Kobayashi, H.; Hiraiwa, A.; Yamakoshi, K. Vibration Technique for Indirect Measurement of Diastolic Arterial Pressure in Human Fingers. Med. Biol. Eng. Comput. 1989, 27, 130–136. [Google Scholar] [CrossRef] [PubMed]
- Drzewiecki, G.M.; Melbin, J.; Noordergraaf, A. Arterial Tonometry: Review and Analysis. J. Biomech. 1983, 16, 141–152. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. Revolution in Flexible Wearable Electronics for Temperature and Pressure Monitoring—A Review. Electronics 2022, 11, 716. [Google Scholar] [CrossRef]
- Chen, C.-H.; Nevo, E.; Fetics, B.; Pak, P.H.; Yin, F.C.P.; Maughan, W.L.; Kass, D.A. Estimation of Central Aortic Pressure Waveform by Mathematical Transformation of Radial Tonometry Pressure. Circulation 1997, 95, 1827–1836. [Google Scholar] [CrossRef]
- Nelson, M.R.; Stepanek, J.; Cevette, M.; Covalciuc, M.; Hurst, R.T.; Tajik, A.J. Noninvasive Measurement of Central Vascular Pressures With Arterial Tonometry: Clinical Revival of the Pulse Pressure Waveform? Mayo Clin. Proc. 2010, 85, 460–472. [Google Scholar] [CrossRef] [Green Version]
- Arndt, J.O.; Klauske, J.; Mersch, F. The Diameter of the Intact Carotid Artery in Man and Its Change with Pulse Pressure. Pflügers Arch. 1968, 301, 230–240. [Google Scholar] [CrossRef]
- Li, P.; Liu, M.; Zhang, X.; Hu, X.; Pang, B.; Yao, Z.; Chen, H. Novel Wavelet Neural Network Algorithm for Continuous and Noninvasive Dynamic Estimation of Blood Pressure from Photoplethysmography. Sci. China Inf. Sci. 2015, 59, 042405. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Ji, Z.; Wu, H.; Xu, Y. A Non-Invasive Continuous Blood Pressure Estimation Approach Based on Machine Learning. Sensors 2019, 19, 2585. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sideris, C.; Kalantarian, H.; Nemati, E.; Sarrafzadeh, M. Building Continuous Arterial Blood Pressure Prediction Models Using Recurrent Networks. In Proceedings of the 2016 IEEE International Conference on Smart Computing (SMARTCOMP), St. Louis, MO, USA, 18–20 May 2016; pp. 1–5. [Google Scholar]
- Landry, C.; Peterson, S.D.; Arami, A. Nonlinear Dynamic Modeling of Blood Pressure Waveform: Towards an Accurate Cuffless Monitoring System. IEEE Sens. J. 2020, 20, 5368–5378. [Google Scholar] [CrossRef]
- Vijayaraghavan, V. BP-Net: Efficient Deep Learning for Continuous Arterial Blood Pressure Estimation Using Photoplethysmogram. arXiv 2021, arXiv:2111.14558. [Google Scholar]
- Mehrabadi, M.A.; Aqajari, S.A.H.; Zargari, A.H.A.; Dutt, N.; Rahmani, A.M. Novel Blood Pressure Waveform Reconstruction from Photoplethysmography Using Cycle Generative Adversarial Networks. arXiv 2022, arXiv:2201.09976. [Google Scholar]
- Moody, G.B.; Mark, R.G. A Database to Support Development and Evaluation of Intelligent Intensive Care Monitoring. In Proceedings of the Computers in Cardiology 1996, Indianapolis, IN, USA, 8–11 September 1996; pp. 657–660. [Google Scholar]
- Johnson, A.E.W.; Pollard, T.J.; Shen, L.; Lehman, L.H.; Feng, M.; Ghassemi, M.; Moody, B.; Szolovits, P.; Anthony Celi, L.; Mark, R.G. MIMIC-III, a Freely Accessible Critical Care Database. Sci. Data 2016, 3, 160035. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moody, B.; Moody, G.; Villarroel, M.; Clifford, G.; Silva, I. MIMIC-III Waveform Database 2017. Available online: https://physionet.org/content/mimic3wdb/1.0/ (accessed on 21 March 2022).
- Saeed, M.; Villarroel, M.; Reisner, A.T.; Clifford, G.; Lehman, L.-W.; Moody, G.; Heldt, T.; Kyaw, T.H.; Moody, B.; Mark, R.G. Multiparameter Intelligent Monitoring in Intensive Care II: A Public-Access Intensive Care Unit Database. Crit. Care Med. 2011, 39, 952–960. [Google Scholar] [CrossRef] [Green Version]
- O’Brien, E.; Petrie, J.; Littler, W.A.; de Swiet, M.; Padfield, P.L.; Altman, D.; Bland, M.; Coats, A.; Atkins, N. The British Hypertension Society Protocol for the Evaluation of Blood Pressure Measuring Devices. J. Hypertens. 1993, 11, S43–S62. [Google Scholar]
- Stergiou, G.; Alpert, B.; Mieke, S.; Asmar, R.; Atkins, N.; Eckert, S.; Frick, G.; Friedman, B.; Graßl, T.; Ichikawa, T.; et al. A Universal Standard for the Validation of Blood Pressure Measuring Devices: Association for the Advancement of Medical Instrumentation/European Society of Hypertension/International Organization for Standardization (AAMI/ESH/ISO) Collaboration Statement. J. Hypertens. 2018, 36, 472–478. [Google Scholar] [CrossRef]
- White, W.B.; Berson, A.S.; Robbins, C.; Jamieson, M.J.; Prisant, L.M.; Roccella, E.; Sheps, S.G. National Standard for Measurement of Resting and Ambulatory Blood Pressures with Automated Sphygmomanometers. Hypertension 1993, 21, 504–509. [Google Scholar] [CrossRef] [Green Version]
- Baker, S.; Xiang, W.; Atkinson, I. A Hybrid Neural Network for Continuous and Non-Invasive Estimation of Blood Pressure from Raw Electrocardiogram and Photoplethysmogram Waveforms. Comput. Methods Programs Biomed. 2021, 207, 106191. [Google Scholar] [CrossRef]
- Al-Qatatsheh, A.; Morsi, Y.; Zavabeti, A.; Zolfagharian, A.; Salim, N.Z.; Kouzani, A.; Mosadegh, B.; Gharaie, S. Blood Pressure Sensors: Materials, Fabrication Methods, Performance Evaluations and Future Perspectives. Sensors 2020, 20, 4484. [Google Scholar] [CrossRef] [PubMed]
- Bijender; Kumar, A. Flexible and Wearable Capacitive Pressure Sensor for Blood Pressure Monitoring. Sens. Bio-Sens. Res. 2021, 33, 100434. [Google Scholar] [CrossRef]
- Ota, Y.; Kokubo, A.; Yamashita, S.; Kario, K. Development of Small and Lightweight Beat-By-Beat Blood Pressure Monitoring Device Based on Tonometry. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine Biology Society (EMBC), Guadalajara, Mexico, 31 October–4 November 2021; pp. 5455–5458. [Google Scholar]
- AtCor Sphygmocor Xcel—Medaval 2017. Available online: https://medaval.ie/device/atcor-sphygmocor-xcel/ (accessed on 21 March 2022).
- NIBP100A (Vasotrac) Noninvasive BP System User Guide | BIOPAC; BIOPAC Systems, Inc.: Goleta, CA, USA, 2008.
- Friedman, B.H.; Christie, I.C.; Sargent, S.L.; Weaver, J.B. Self-Reported Sensitivity to Continuous Noninvasive Blood Pressure Monitoring via the Radial Artery. J. Psychosom. Res. 2004, 57, 119–121. [Google Scholar] [CrossRef]
- Belani, K.; Ozaki, M.; Hynson, J.; Hartmann, T.; Reyford, H.; Martino, J.-M.; Poliac, M.; Miller, R. A New Noninvasive Method to Measure Blood Pressure: Results of a Multicenter Trial. Anesthesiology 1999, 91, 686. [Google Scholar] [CrossRef] [PubMed]
- Thede, R.C. Wrist-Mounted Blood Pressure Measurement Device. 2003. Available online: https://patents.google.com/patent/US6558335/en (accessed on 21 March 2022).
- Finapres®® NOVA Basic—Finapres. Available online: https://www.finapres.com/product/finapres-nova-basic/ (accessed on 21 March 2022).
- Birch, A.A.; Morris, S.L. Do the Finapres and Colin Radial Artery Tonometer Measure the Same Blood Pressure Changes Following Deflation of Thigh Cuffs? Physiol. Meas. 2003, 24, 653–660. [Google Scholar] [CrossRef] [PubMed]
- Bogert, L.W.J.; van Lieshout, J.J. Non-Invasive Pulsatile Arterial Pressure and Stroke Volume Changes from the Human Finger. Exp. Physiol. 2005, 90, 437–446. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- APC Cardiovascular | CNAPTM Monitor 500. Available online: https://www.apccardiovascular.co.uk/portfolio-item/cnap-monitor-500/ (accessed on 21 March 2022).
- Jagadeesh, A.M.; Singh, N.G.; Mahankali, S. A Comparison of a Continuous Noninvasive Arterial Pressure (CNAPTM) Monitor with an Invasive Arterial Blood Pressure Monitor in the Cardiac Surgical ICU. Ann. Card. Anaesth. 2012, 15, 180. [Google Scholar] [CrossRef]
- Jeleazcov, C.; Krajinovic, L.; Münster, T.; Birkholz, T.; Fried, R.; Schüttler, J.; Fechner, J. Precision and Accuracy of a New Device (CNAPTM) for Continuous Non-Invasive Arterial Pressure Monitoring: Assessment during General Anaesthesia. Br. J. Anaesth. 2010, 105, 264–272. [Google Scholar] [CrossRef] [Green Version]
- Fortin, J.; Rogge, D.E.; Fellner, C.; Flotzinger, D.; Grond, J.; Lerche, K.; Saugel, B. A Novel Art of Continuous Noninvasive Blood Pressure Measurement. Nat. Commun. 2021, 12, 1387. [Google Scholar] [CrossRef]
- Safar, M.E.; Blacher, J.; Pannier, B.; Guerin, A.P.; Marchais, S.J.; Guyonvarc’h, P.-M.; London, G.M. Central Pulse Pressure and Mortality in End-Stage Renal Disease. Hypertension 2002, 39, 735–738. [Google Scholar] [CrossRef] [Green Version]
- Trudeau, L. Central Blood Pressure as an Index of Antihypertensive Control: Determinants and Potential Value. Can. J. Cardiol. 2014, 30, S23–S28. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Townsend, R.R.; Rosendorff, C.; Nichols, W.W.; Edwards, D.G.; Chirinos, J.A.; Fernhall, B.; Cushman, W.C. American Society of Hypertension Position Paper: Central Blood Pressure Waveforms in Health and Disease. J. Am. Soc. Hypertens. 2016, 10, 22–33. [Google Scholar] [CrossRef] [PubMed]
- Sandberg, M.; Zhang, Q.; Styf, J.; Gerdle, B.; Lindberg, L.-G. Non-Invasive Monitoring of Muscle Blood Perfusion by Photoplethysmography: Evaluation of a New Application. Acta Physiol. Scand. 2005, 183, 335–343. [Google Scholar] [CrossRef] [PubMed]
- Hertzman, A.B. The Blood Supply of Various Skin Areas as Estimated by the Photoelectric Plethysmograph. Am. J. Physiol.-Leg. Content 1938, 124, 328–340. [Google Scholar] [CrossRef]
- Maeda, Y.; Sekine, M.; Tamura, T. Relationship Between Measurement Site and Motion Artifacts in Wearable Reflected Photoplethysmography. J. Med. Syst. 2011, 35, 969–976. [Google Scholar] [CrossRef] [PubMed]
- Hossain, S.; Gupta, S.S.; Kwon, T.-H.; Kim, K.-D. Derivation and Validation of Gray-Box Models to Estimate Noninvasive in-Vivo Percentage Glycated Hemoglobin Using Digital Volume Pulse Waveform. Sci. Rep. 2021, 11, 12169. [Google Scholar] [CrossRef]
- Hossain, M.S.; Kim, K.-D. Noninvasive Estimation of Glycated Hemoglobin In-Vivo Based on Photon Diffusion Theory and Genetic Symbolic Regression Models. IEEE Trans. Biomed. Eng. 2022, 69, 2053–2064. [Google Scholar] [CrossRef]
- Lang, Y.; Chen, Z.; Ward, R.; Elgendi, M. Photoplethysmography and Deep Learning: Enhancing Hypertension Risk Stratification. Biosensor 2018, 8, 101. [Google Scholar] [CrossRef] [Green Version]
- Kayid, A.; Khaled, Y.; Elmahdy, M. Performance of CPUs/GPUs for Deep Learning Workloads; German University in Cairo: Cairo, Egypt, 2018. [Google Scholar] [CrossRef]
- Fatahalian, K.; Sugerman, J.; Hanrahan, P. Understanding the efficiency of GPU algorithms for matrix-matrix multiplication. In Proceedings of the ACM SIGGRAPH/EUROGRAPHICS Conference on Graphics Hardware, Grenoble, France, 29–30 August 2004; Association for Computing Machinery: New York, NY, USA; pp. 133–137. [Google Scholar]
| Advantages | Disadvantages |
|---|---|
|
|
| Advantages | Disadvantages |
|---|---|
|
|
| Advantages | Disadvantages |
|---|---|
|
|
| Authors | Pub. Year | Method | Input | Input Length |
|---|---|---|---|---|
| [70] | 2015 | Wavelet neural network | PPG | Not given |
| [72] | 2016 | Long Short-Term Memory (LSTM) | PPG | Not specific |
| [73] | 2020 | Nonlinear autoregressive models with exogenous input (NARX) with ANN | ECG or PPG or both, two BP data | 100 samples |
| [37] | 2020 (preprint server) | U-Net and 1D MultiResUNet | PPG | 8 s |
| [40] | 2020 | Deep convolutional autoencoder (DCAE) | PPG | 5 s |
| [38] | 2021 | 1D U-Net | PPG | 256 samples = 2.048 s with overlapping |
| [39] | 2021 | Regularized deep autoencoder (RDAE) | PPG | 625 samples = 5 s |
| [74] | 2021 (preprint server) | U-Net | PPG | 32 samples |
| [25] | 2021 | 1D V-Net | ECG, PPG, most recent cuff-based SBP, DBP, and MAP values, the time of these values, the standard deviation and median of the pulse arrival time, and pulse rate | 4 s |
| [75] | 2022 (preprint server) | Cycle generative adversarial network (CycleGAN) | PPG | 256 samples = 2.048 s with overlapping |
| Ref. | Advantages | Disadvantages |
|---|---|---|
| [70] |
|
|
| [72] |
|
|
| [73] |
|
|
| [37] |
|
|
| [40] |
|
|
| [38] |
|
|
| [39] |
|
|
| [74] |
|
|
| [25] |
|
|
| [75] |
|
|
| Ref. | Preprocessing Steps | Normalization Equation |
|---|---|---|
| [70,72,74] |
| - |
| [40,73] |
| - |
| [37] |
| |
| [25,38] |
| |
| [39] |
| |
| [75] |
| - |
| Ref | Dataset | # of Subject | Total Data (in hours) | K-Fold Cross-Validation | Train:Val:Test |
|---|---|---|---|---|---|
| [70] | MIMIC | >90 | - | No | Not given |
| [72] | MIMIC | 42 | - | No | 80:10:10 (in total data) |
| [73] | MIMIC II | 15 | - | No | 70:15:15 (in total data) |
| [37] | MIMIC II | 942 | ≈353.5 | Yes (10 Folds) | 78.58:-:21.42 (in total data) |
| [40] | Custom | 18 | ≈50.72 | Yes (10 Folds) | 85:-:15 (in total data) |
| [38] | MIMIC, MIMIC III Waveform | 100 | ≈195 | No | 70:15:15 (in total data) |
| [39] | MIMIC II | 1227 | ≈54.53 | No | 60:20:20 (in subjects) |
| [74] | MIMIC II Waveform database | 948 | ≈353.5 | Yes (10 Folds) | 78.58:-:21.42 |
| [25] | MIMIC III, UCLA | MIMIC-264, UCLA-110 | ≈2516.48 | No | 66:-:33 (in subjects of MIMIC) |
| [75] | MIMIC II Waveform database | 92 | ≈7.67 | Yes (5 Folds) | 80:-:20 |
| Method | Ref. | Year | Performance Metrics (no Unit for r, mmHg for Others) | BHS Grade | AAMI | |||
|---|---|---|---|---|---|---|---|---|
| Waveform | SBP | DBP | MAP | |||||
| Ultrasound-Based | [34] | 2018 | - | ME: 0.05 | ME: 0.28 | - | - | - |
| Pressure-Based | [32] | 2006 | - | - | - | - | - | - |
| [33] | 2015 | - | - | - | - | - | - | |
| Deep Learning-Based | [70] | 2015 | Mean: 3.4094 AMSE: 4.4797 | : 2.32 ± 2.91 | : 1.92 ± 2.47 | - | - | Passed (MAE) |
| [72] | 2016 | RMSE: 6.042 ± 3.26 r: 0.95 MAE: 5.98 ME: −0.214 | RMSE: 2.575 | RMSE: 1.977 | - | - | - | |
| [73] | 2020 | - | - | - | - | - | Failed | |
| [37] | 2020 (preprint server) | : 4.604 ± 5.043 | : 5.727 ± 9.162 | : 3.449 ± 6.147 | : 2.310 ± 4.437 | A | Failed | |
| [40] | 2020 | RMSE: 3.46 MAE: 2.33 r: 0.984 | RMSE: 3.41 MAE: 2.54 r: 0.981 | RMSE: 2.14 MAE: 1.48 r: 0.979 | - | - | Failed (subjects < 85) | |
| [38] | 2021 | r: 0.993 | 3.68 ± 4.42 RMSE: 5.75 r: 0.976 | 1.97 ± 2.92 RMSE: 3.52 r: 0.970 | 2.17 ± 3.06 RMSE: 3.75 r: 0.976 | A | Passed (MAE) | |
| [39] | 2021 | - | 1.648 ± 6.640 MAE: 5.424 | 1.280 ± 3.740 MAE: 3.144 | −0.304 ± 3.412 MAE: 2.885 | SBP:B | Passed (ME) Failed (MAE) | |
| [74] | 2021 (preprint server) | - | −0.225 ± 8.504 MAE: 5.16 | 0.594 ± 4.778 MAE: 2.89 | 0.425 ± 4.784 | SBP:B | Passed (ME) Failed (MAE) | |
| [25] | 2021 | MIMIC RMSE: 5.823 MIMIC r: 0.957 UCLA RMSE: 6.961 UCLA r: 0.947 | 4.297 ± 6.527 2.398 ± 5.623 | −2.497 ± 3.785 | - | - | Passed (ME) | |
| [75] | 2022 (preprint server) | - | 2.89 ± 4.52 RMSE: 5.18 ME: 0.67 r: 0.97 | 3.22 ± 4.67 RMSE: 4.82 ME: 1.78 r: 0.94 | - | A | Passed (MAE, ME) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Athaya, T.; Choi, S. A Review of Noninvasive Methodologies to Estimate the Blood Pressure Waveform. Sensors 2022, 22, 3953. https://doi.org/10.3390/s22103953
Athaya T, Choi S. A Review of Noninvasive Methodologies to Estimate the Blood Pressure Waveform. Sensors. 2022; 22(10):3953. https://doi.org/10.3390/s22103953
Chicago/Turabian StyleAthaya, Tasbiraha, and Sunwoong Choi. 2022. "A Review of Noninvasive Methodologies to Estimate the Blood Pressure Waveform" Sensors 22, no. 10: 3953. https://doi.org/10.3390/s22103953
APA StyleAthaya, T., & Choi, S. (2022). A Review of Noninvasive Methodologies to Estimate the Blood Pressure Waveform. Sensors, 22(10), 3953. https://doi.org/10.3390/s22103953






