Graph Layer Security: Encrypting Information via Common Networked Physics
Abstract
:1. Introduction
1.1. From Public Key Cryptography to Physical Layer Security
1.2. Introducing Graph Layer Security (GLS): Encryption Using Networked Physics
2. Physical Dynamic Model for Data Encryption
3. GLS Encryption Using Physical Networked Dynamic
3.1. GLS Secrecy Rate
3.2. Relay Selection & Weight Computation
3.2.1. GFT Operator-Based Surrogate
3.2.2. Weight Computation
3.2.3. Overall Relay Selection Algorithm
| Algorithm 1 Offline relay selection algorithm |
|
3.3. Active and Passive Attackers
3.3.1. Passive Eavesdropper
3.3.2. Active Attackers
4. Simulations and Results
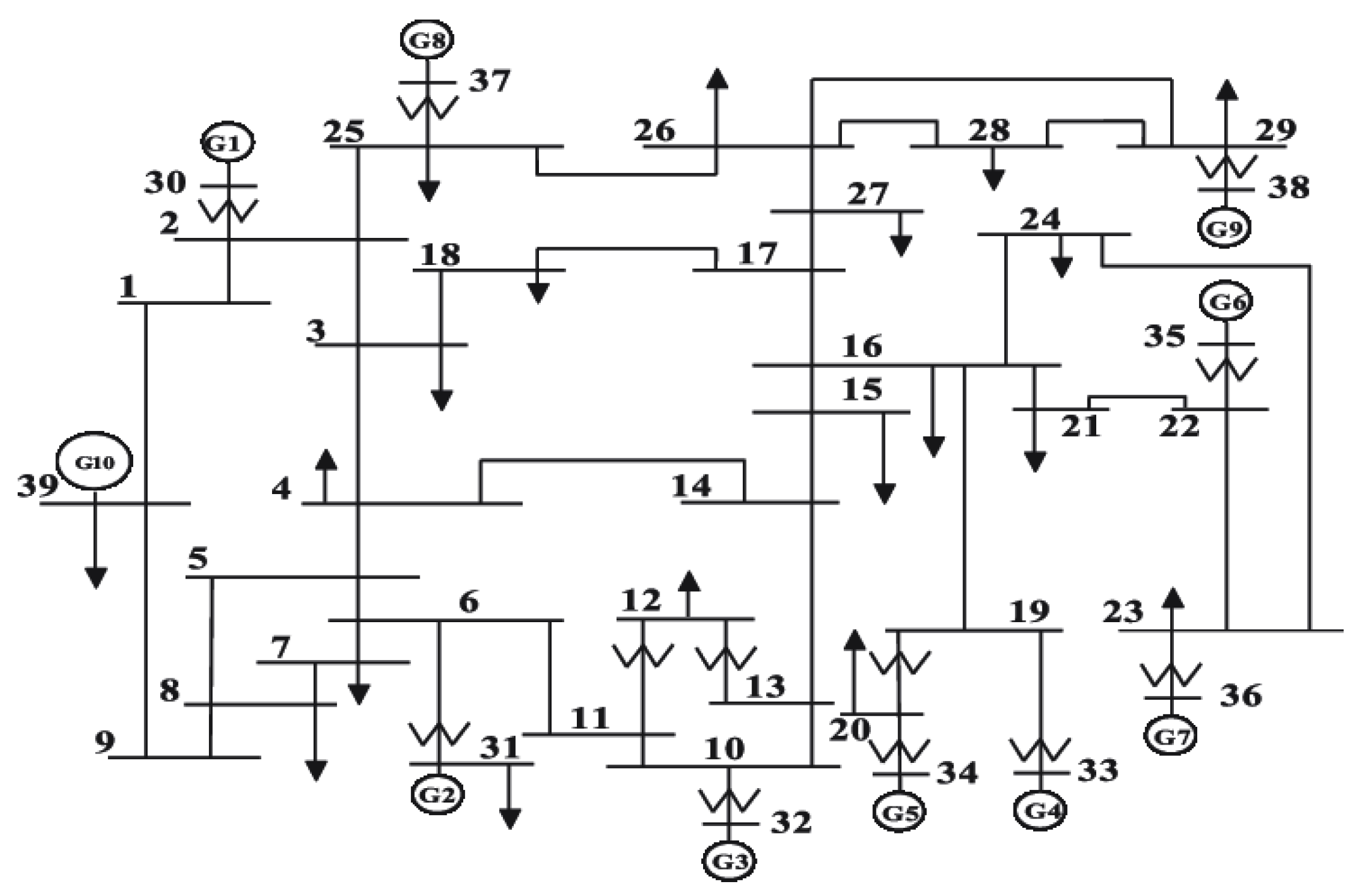
4.1. Experimental Setting
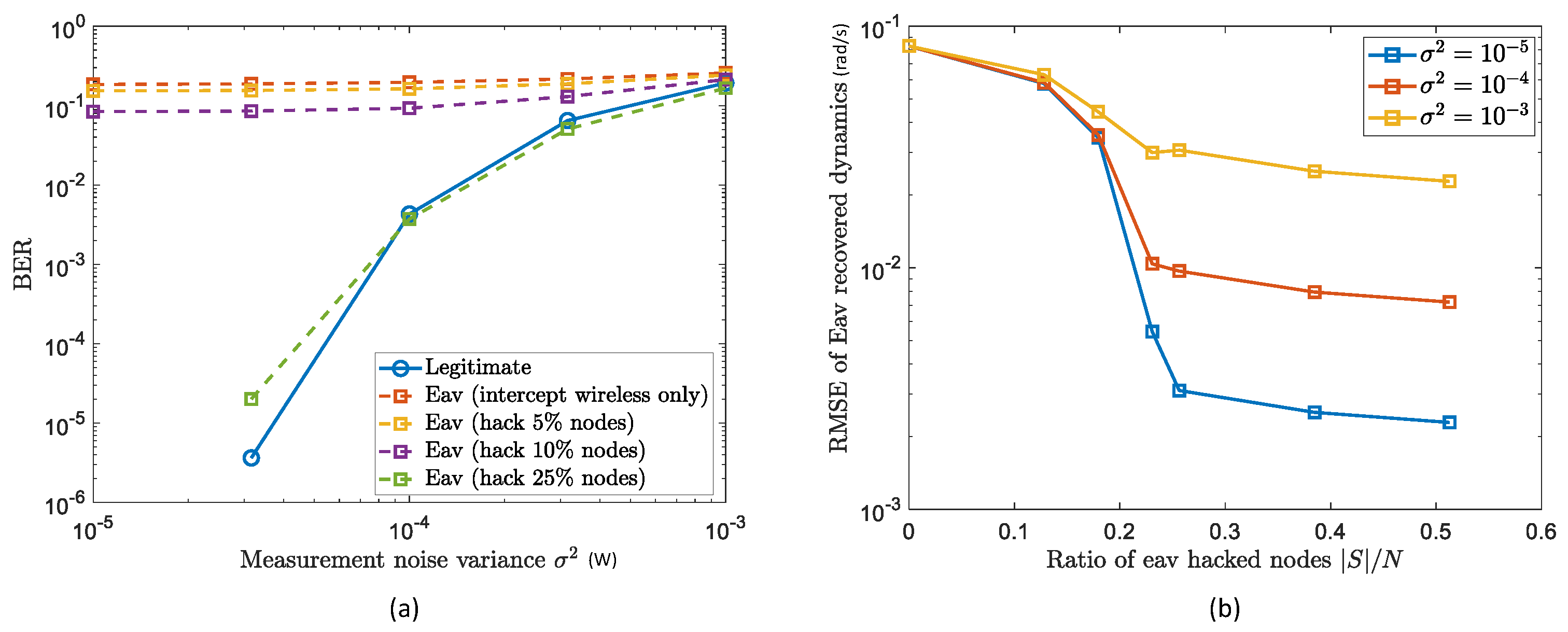
4.2. GLS Performance with Passive Eavesdroppers
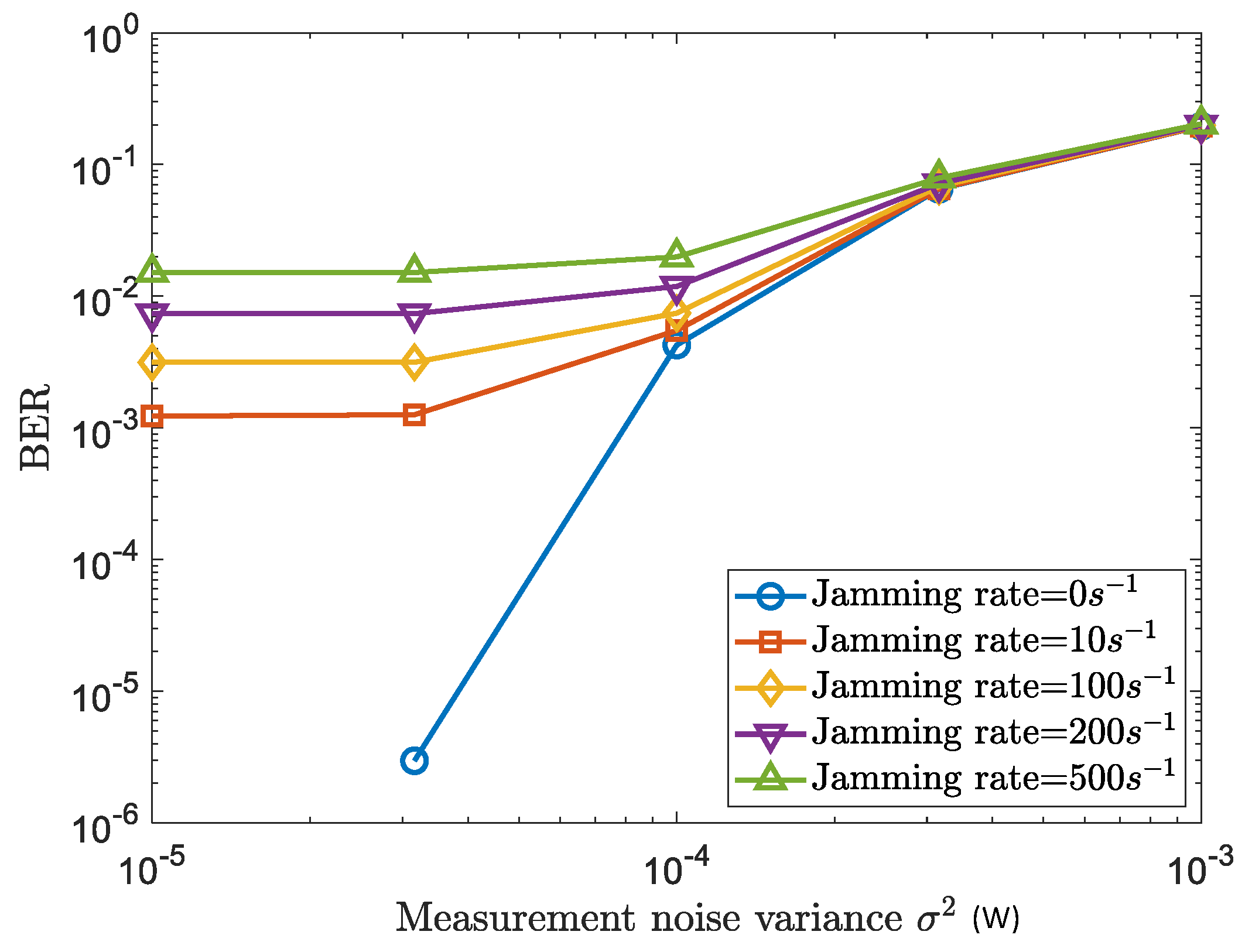
4.3. GLS Performance with Active Attackers
4.4. Comparison with Current PLS
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahlgren, B.; Hidell, M.; Ngai, E.C. Internet of Things for Smart Cities: Interoperability and Open Data. IEEE Internet Comput. 2016, 20, 52–56. [Google Scholar] [CrossRef]
- Wang, L.; Ranjan, R. Processing Distributed Internet of Things Data in Clouds. IEEE Cloud Comput. 2015, 2, 76–80. [Google Scholar] [CrossRef]
- Saeed, N.; Alouini, M.; Al-Naffouri, T.Y. Toward the Internet of Underground Things: A Systematic Survey. IEEE Commun. Surv. Tutor. 2019, 21, 3443–3466. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.; Pagani, A.; Fu, G.; Guymer, I.; Chen, W.; McCann, J.; Guo, W. Optimal Sampling of Water Distribution Network Dynamics Using Graph Fourier Transform. IEEE Trans. Netw. D Eng. 2020, 7, 1570–1582. [Google Scholar] [CrossRef] [Green Version]
- Ayoub, W.; Samhat, A.E.; Nouvel, F.; Mroue, M.; Prevotet, J. Internet of Mobile Things: Overview of LoRaWAN, DASH7, and NB-IoT in LPWANs Standards and Supported Mobility. IEEE Commun. Surv. Tutor. 2019, 21, 1561–1581. [Google Scholar] [CrossRef] [Green Version]
- Poor, H.V.; Schaefer, R.F. Wireless physical layer security. Proc. Natl. Acad. Sci. USA 2017, 114, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, A.; Fakoorian, S.A.A.; Huang, J.; Swindlehurst, A.L. Principles of Physical Layer Security in Multiuser Wireless Networks: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 1550–1573. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Chen, G.; Wong, K.K. Multi-Agent Reinforcement Learning-Based Buffer-Aided Relay Selection in IRS-Assisted Secure Cooperative Networks. IEEE Trans. Inf. Forensics Secur. 2021, 16, 4101–4112. [Google Scholar] [CrossRef]
- Yang, H.; Xiong, Z.; Zhao, J.; Niyato, D.; Xiao, L.; Wu, Q. Deep Reinforcement Learning-Based Intelligent Reflecting Surface for Secure Wireless Communications. IEEE Trans. Wirel. Commun. 2021, 20, 375–388. [Google Scholar] [CrossRef]
- Ye, C.; Reznik, A.; Shah, Y. Extracting Secrecy from Jointly Gaussian Random Variables. In Proceedings of the 2006 IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 2593–2597. [Google Scholar] [CrossRef]
- Ye, C.; Mathur, S.; Reznik, A.; Shah, Y.; Trappe, W.; Mandayam, N.B. Information-Theoretically Secret Key Generation for Fading Wireless Channels. IEEE Trans. Inf. Forensics Secur. 2010, 5, 240–254. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Song, Y.; Zhao, C.; You, X. Secrecy extraction from correlated fading channels: An upper bound. In Proceedings of the 2009 International Conference on Wireless Communications Signal Processing, Nanjing, China, 13–15 November 2009; pp. 1–3. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.; Tang, J.; Zhao, N.; Chen, Y.; Ding, Z.; Wang, X. Beamforming and Jamming Optimization for IRS-Aided Secure NOMA Networks. IEEE Trans. Wirel. Commun. 2021, 21, 1557–1569. [Google Scholar] [CrossRef]
- Pang, X.; Zhao, N.; Tang, J.; Wu, C.; Niyato, D.; Wong, K.K. IRS-Assisted Secure UAV Transmission via Joint Trajectory and Beamforming Design. IEEE Trans. Commun. 2021, 70, 1140–1152. [Google Scholar] [CrossRef]
- Jiang, W.; Chen, B.; Zhao, J.; Xiong, Z.; Ding, Z. Joint Active and Passive Beamforming Design for the IRS-Assisted MIMOME-OFDM Secure Communications. IEEE Trans. Veh. Technol. 2021, 70, 10369–10381. [Google Scholar] [CrossRef]
- Wang, H.M.; Zhang, X.; Jiang, J.C. UAV-Involved Wireless Physical-Layer Secure Communications: Overview and Research Directions. IEEE Wirel. Commun. 2019, 26, 32–39. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Ng, D.W.K.; Ding, Z.; Xu, Y.; Zhong, Z. Physical Layer Security in UAV Systems: Challenges and Opportunities. IEEE Wirel. Commun. 2019, 26, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Duong, T.Q.; Marshall, A.; Woods, R. Key Generation From Wireless Channels: A Review. IEEE Access 2016, 4, 614–626. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Wu, Q.; Cui, M.; Zhang, R. Securing UAV Communications via Joint Trajectory and Power Control. IEEE Trans. Wirel. Commun. 2019, 18, 1376–1389. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Zhang, N.; Zhang, S.; Chen, D.; Sha, X.; Shen, X. On Physical Layer Security: Weighted Fractional Fourier Transform Based User Cooperation. IEEE Trans. Wirel. Commun. 2017, 16, 5498–5510. [Google Scholar] [CrossRef]
- Ai, Y.; Cheffena, M.; Mathur, A.; Lei, H. On Physical Layer Security of Double Rayleigh Fading Channels for Vehicular Communications. IEEE Wirel. Commun. Lett. 2018, 7, 1038–1041. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Pan, C.; Ren, H.; Wang, K.; Nallanathan, A. Artificial-Noise-Aided Secure MIMO Wireless Communications via Intelligent Reflecting Surface. IEEE Trans. Commun. 2020, 68, 7851–7866. [Google Scholar] [CrossRef]
- Zhou, Y.; Yeoh, P.L.; Chen, H.; Li, Y.; Schober, R.; Zhuo, L.; Vucetic, B. Improving Physical Layer Security via a UAV Friendly Jammer for Unknown Eavesdropper Location. IEEE Trans. Veh. Technol. 2018, 67, 11280–11284. [Google Scholar] [CrossRef]
- Guo, W.; Wei, Z.; Li, B. Secure Internet-of-Nano Things for Targeted Drug Delivery: Distance-based Molecular Cipher Keys. In Proceedings of the 2020 IEEE 5th Middle East and Africa Conference on Biomedical Engineering (MECBME), Amman, Jordan, 27–29 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zaman, I.U.; Lopez, A.B.; Faruque, M.A.A.; Boyraz, O. Physical Layer Cryptographic Key Generation by Exploiting PMD of an Optical Fiber Link. J. Light. Technol. 2018, 36, 5903–5911. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Guo, W.; Li, B. A Multi-Eavesdropper Scheme against RIS Secured LoS-dominated Channel. IEEE Commun. Lett. 2022. [Google Scholar] [CrossRef]
- Wei, Z.; Guo, W. Random Matrix based Physical Layer Secret Key Generation in Static Channels. arXiv 2021, arXiv:2110.12785. [Google Scholar]
- Zhang, J.; Rejendran, S.; Sun, Z.; Woods, R.; Hanzo, L. Physical Layer Security for the Internet of Things: Authentication and Key Generation. IEEE Wirel. Commun. 2019, 26, 92–98. [Google Scholar] [CrossRef]
- Qiu, K.; Mao, X.; Shen, X.; Wang, X.; Li, T.; Gu, Y. Time-Varying Graph Signal Reconstruction. IEEE J. Sel. Top. Signal Process. 2017, 11, 870–883. [Google Scholar] [CrossRef]
- Chen, S.; Varma, R.; Sandryhaila, A.; Kovacevic, J. Discrete Signal Processing on Graphs: Sampling Theory. IEEE Trans. Signal Process. 2015, 63, 6510–6523. [Google Scholar] [CrossRef] [Green Version]
- Anis, A.; Gadde, A.; Ortega, A. Efficient Sampling Set Selection for Bandlimited Graph Signals Using Graph Spectral Proxies. IEEE Trans. Signal Process. 2016, 64, 3775–3789. [Google Scholar] [CrossRef]
- Chen, S.; Varma, R.; Singh, A.; Kovacevic, J. Signal Recovery on Graphs: Fundamental Limits of Sampling Strategies. IEEE Trans. Signal Inf. Process. Netw. 2016, 2, 539–554. [Google Scholar] [CrossRef] [Green Version]
- Ortega, A.; Frossard, P.; Kovacevic, J.; Moura, J.M.F.; Vandergheynst, P. Graph Signal Processing: Overview, Challenges, and Applications. Proc. IEEE 2018, 106, 808–828. [Google Scholar] [CrossRef] [Green Version]
- Romero, D.; Ioannidis, V.N.; Giannakis, G.B. Kernel-Based Reconstruction of Space-Time Functions on Dynamic Graphs. IEEE J. Sel. Top. Signal Process. 2017, 11, 856–869. [Google Scholar] [CrossRef] [Green Version]
- Tsitsvero, M.; Barbarossa, S.; Di Lorenzo, P. Signals on Graphs: Uncertainty Principle and Sampling. IEEE Trans. Signal Process. 2016, 64, 4845–4860. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.; Li, B.; Sun, C.; Guo, W. Sampling and Inference of Networked Dynamics Using Log-Koopman Nonlinear Graph Fourier Transform. IEEE Trans. Signal Process. 2020, 68, 6187–6197. [Google Scholar] [CrossRef]
- Sauer, P.W.; Pai, M.A. Power System Dynamics and Stability; Wiley Online Library; Prentice-Hall: Upper Saddle River, NJ, USA, 1998; Volume 101. [Google Scholar]
- Wang, X.; Zhao, J.; Terzija, V.; Wang, S. Fast robust power system dynamic state estimation using model transformation. Int. J. Electr. Power Energy Syst. 2020, 114, 105390. [Google Scholar] [CrossRef]
- Ghahremani, E.; Kamwa, I. Local and Wide-Area PMU-Based Decentralized Dynamic State Estimation in Multi-Machine Power Systems. IEEE Trans. Power Syst. 2016, 31, 547–562. [Google Scholar] [CrossRef]
- Qi, J.; Sun, K.; Kang, W. Optimal PMU Placement for Power System Dynamic State Estimation by Using Empirical Observability Gramian. IEEE Trans. Power Syst. 2015, 30, 2041–2054. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.; Li, B.; Guo, W. Optimal Sampling for Dynamic Complex Networks With Graph-Bandlimited Initialization. IEEE Access 2019, 7, 150294–150305. [Google Scholar] [CrossRef]
- Chang, F.; Onohara, K.; Mizuochi, T. Forward error correction for 100 G transport networks. IEEE Commun. Mag. 2010, 48, S48–S55. [Google Scholar] [CrossRef]


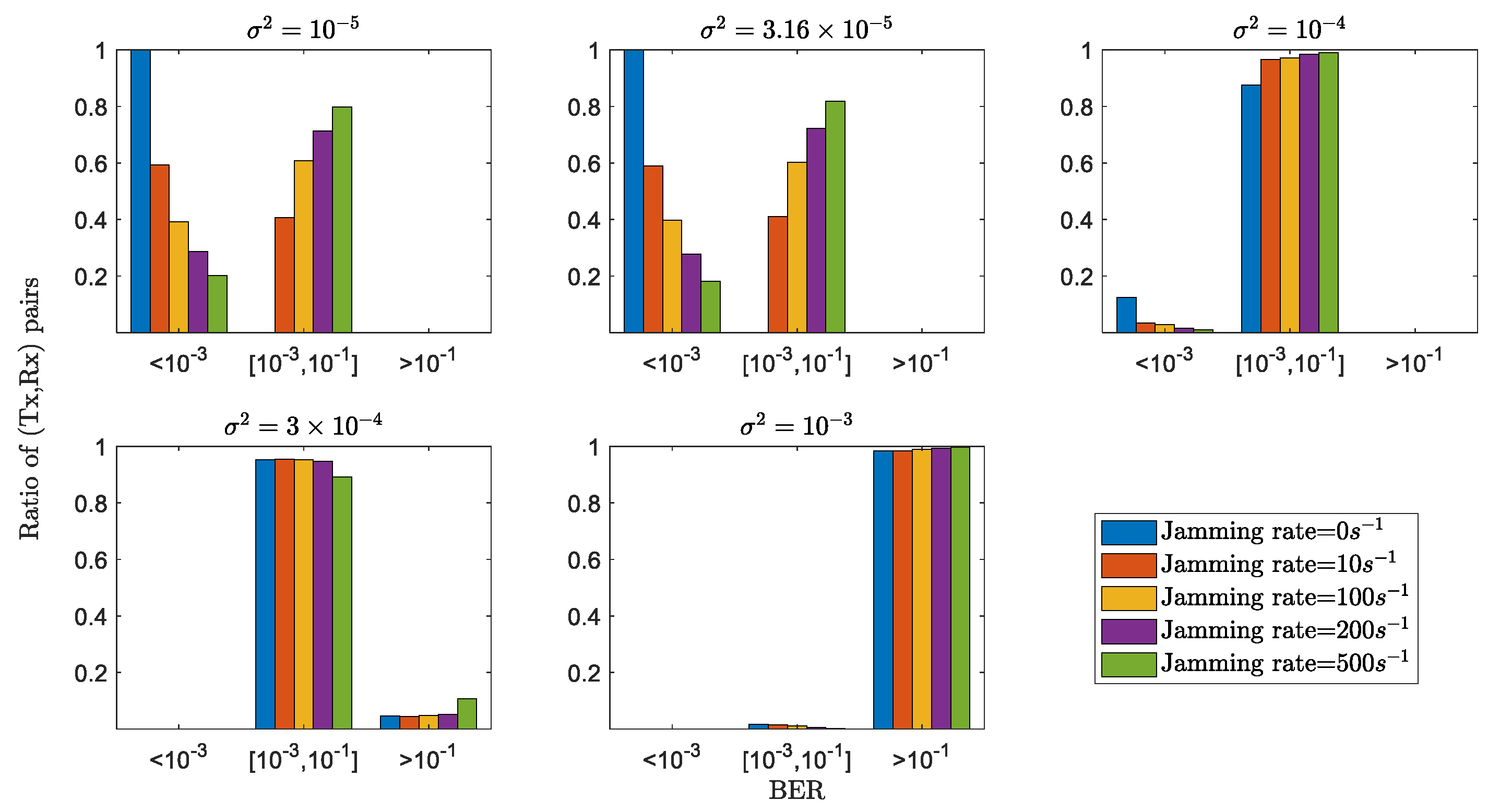
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Wang, L.; Sun, S.C.; Li, B.; Guo, W. Graph Layer Security: Encrypting Information via Common Networked Physics. Sensors 2022, 22, 3951. https://doi.org/10.3390/s22103951
Wei Z, Wang L, Sun SC, Li B, Guo W. Graph Layer Security: Encrypting Information via Common Networked Physics. Sensors. 2022; 22(10):3951. https://doi.org/10.3390/s22103951
Chicago/Turabian StyleWei, Zhuangkun, Liang Wang, Schyler Chengyao Sun, Bin Li, and Weisi Guo. 2022. "Graph Layer Security: Encrypting Information via Common Networked Physics" Sensors 22, no. 10: 3951. https://doi.org/10.3390/s22103951
APA StyleWei, Z., Wang, L., Sun, S. C., Li, B., & Guo, W. (2022). Graph Layer Security: Encrypting Information via Common Networked Physics. Sensors, 22(10), 3951. https://doi.org/10.3390/s22103951






