Measurement of Sea Waves
Abstract
1. Introduction
2. Wave Buoys
2.1. Drifting Buoys
2.2. Moored Buoys
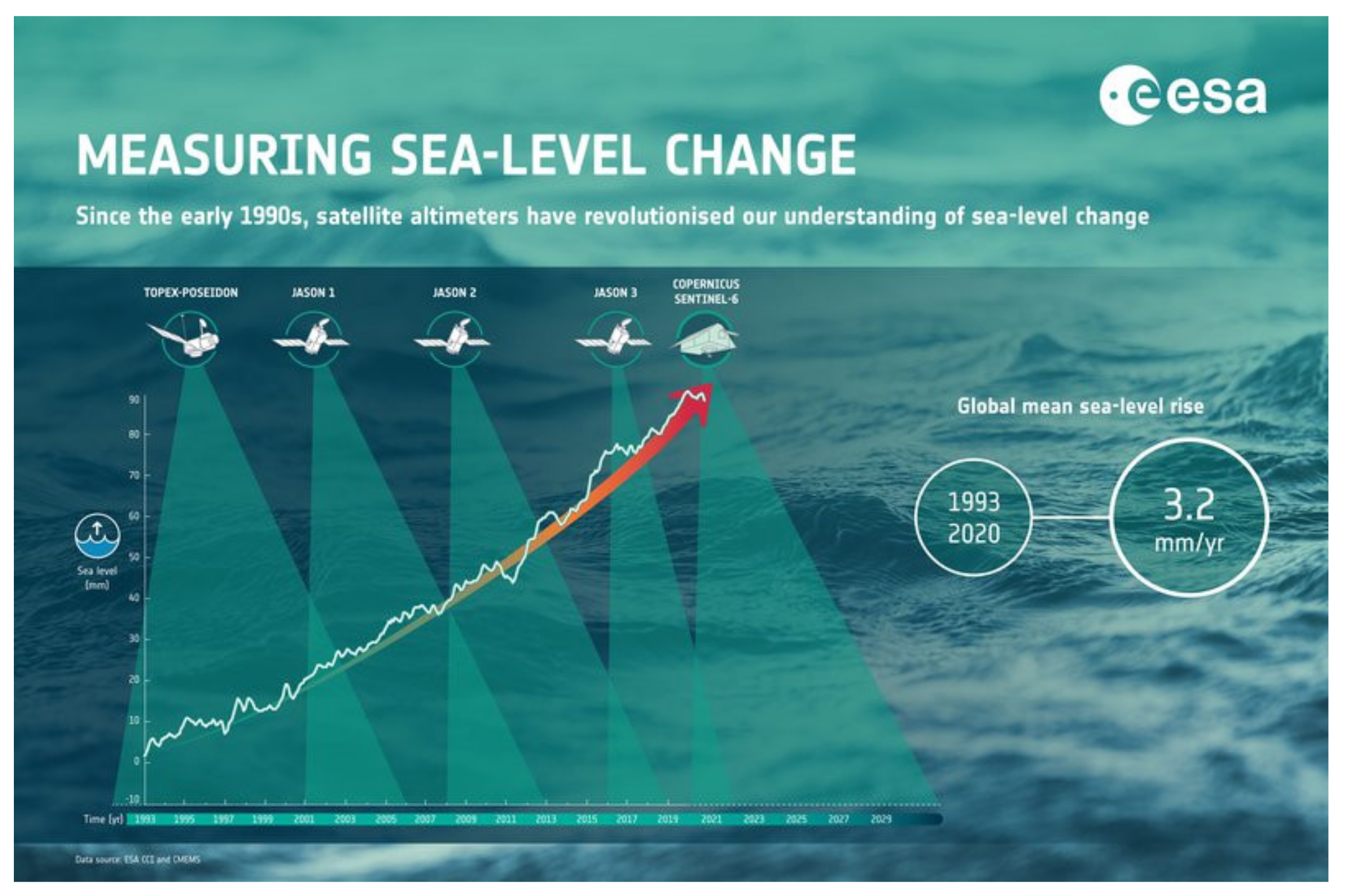
3. Satellite Remote Sensing
3.1. Background
3.2. Review of the Main Marine Value-Added Products
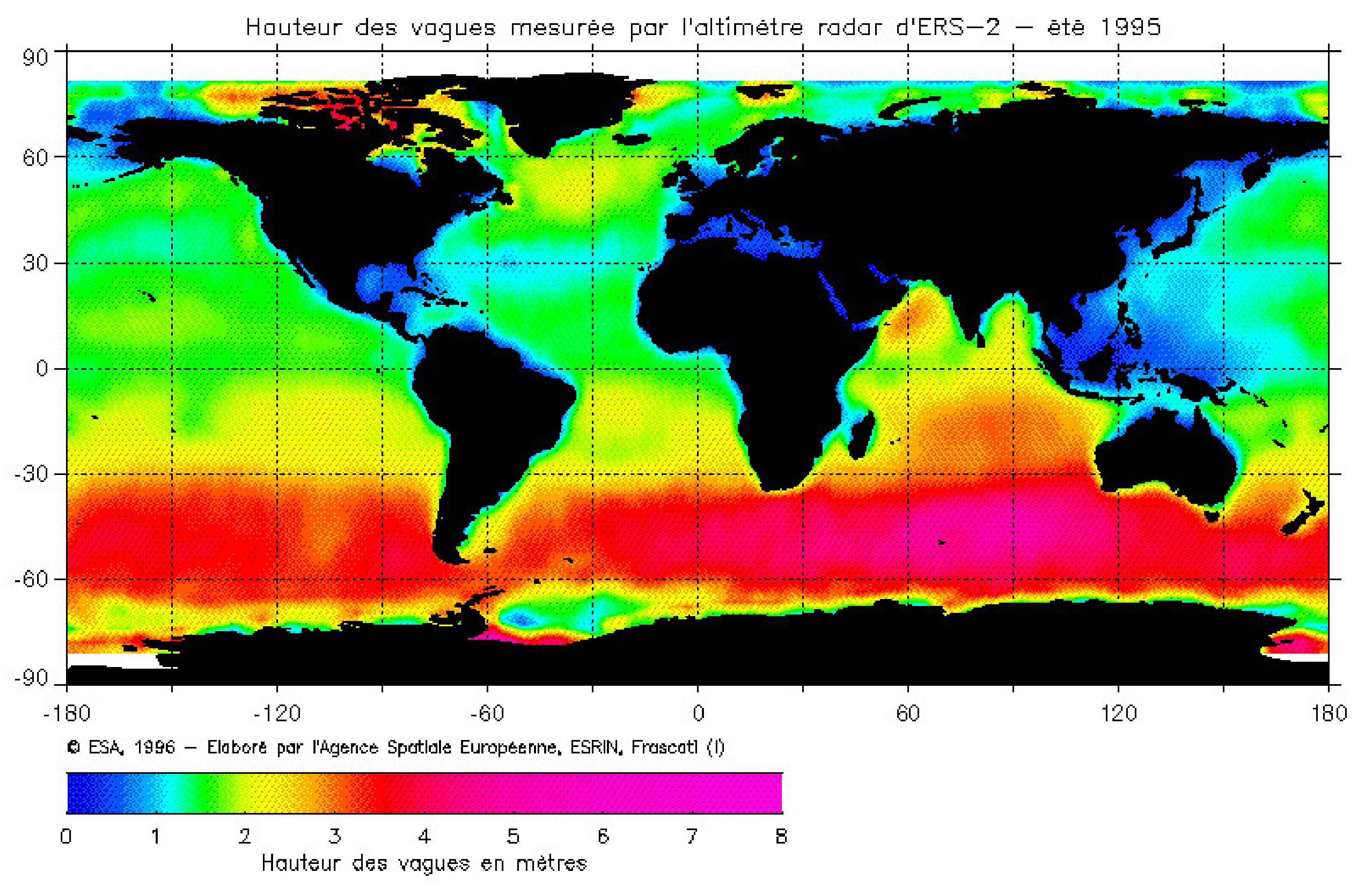
3.3. Sea Waves Monitoring
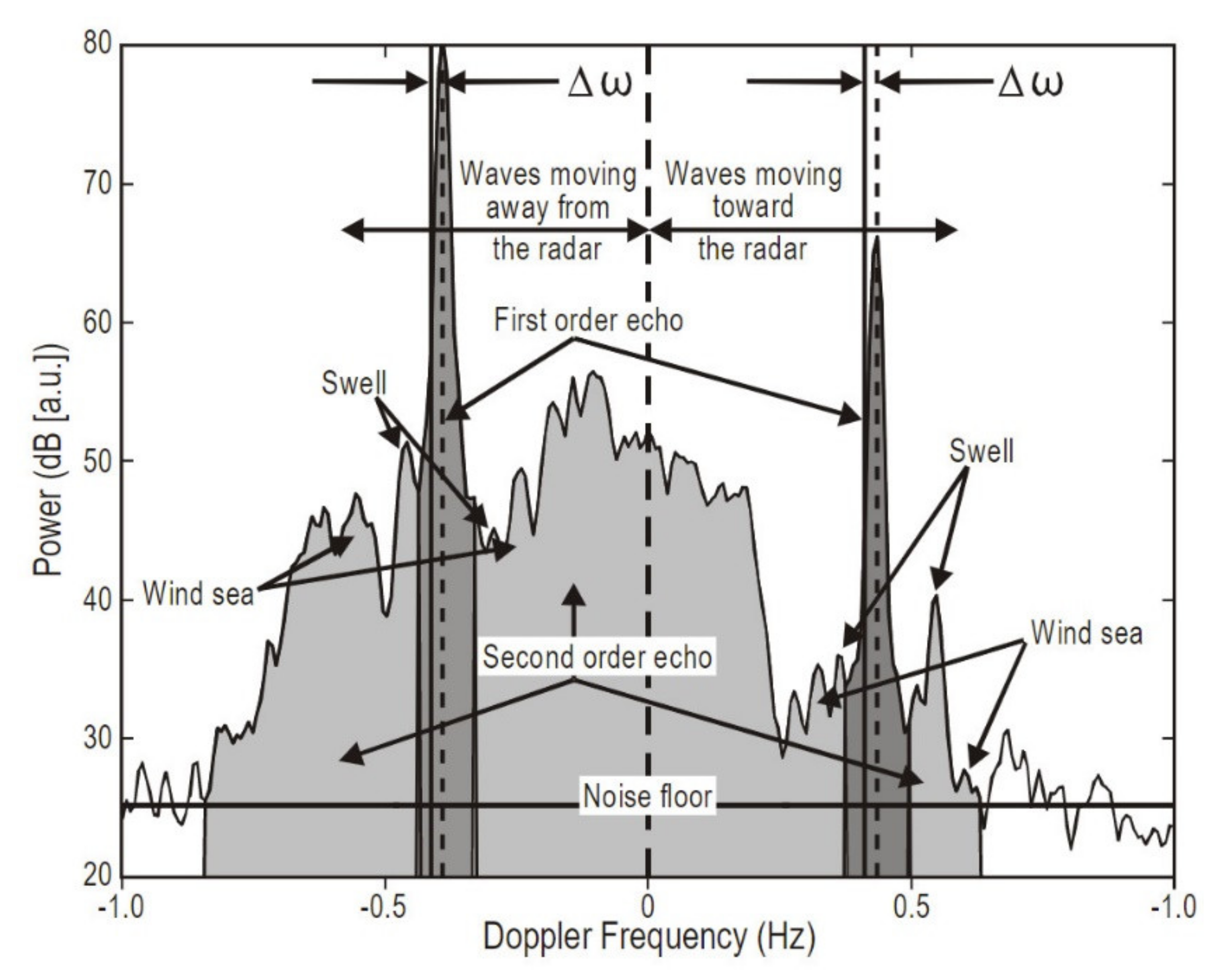
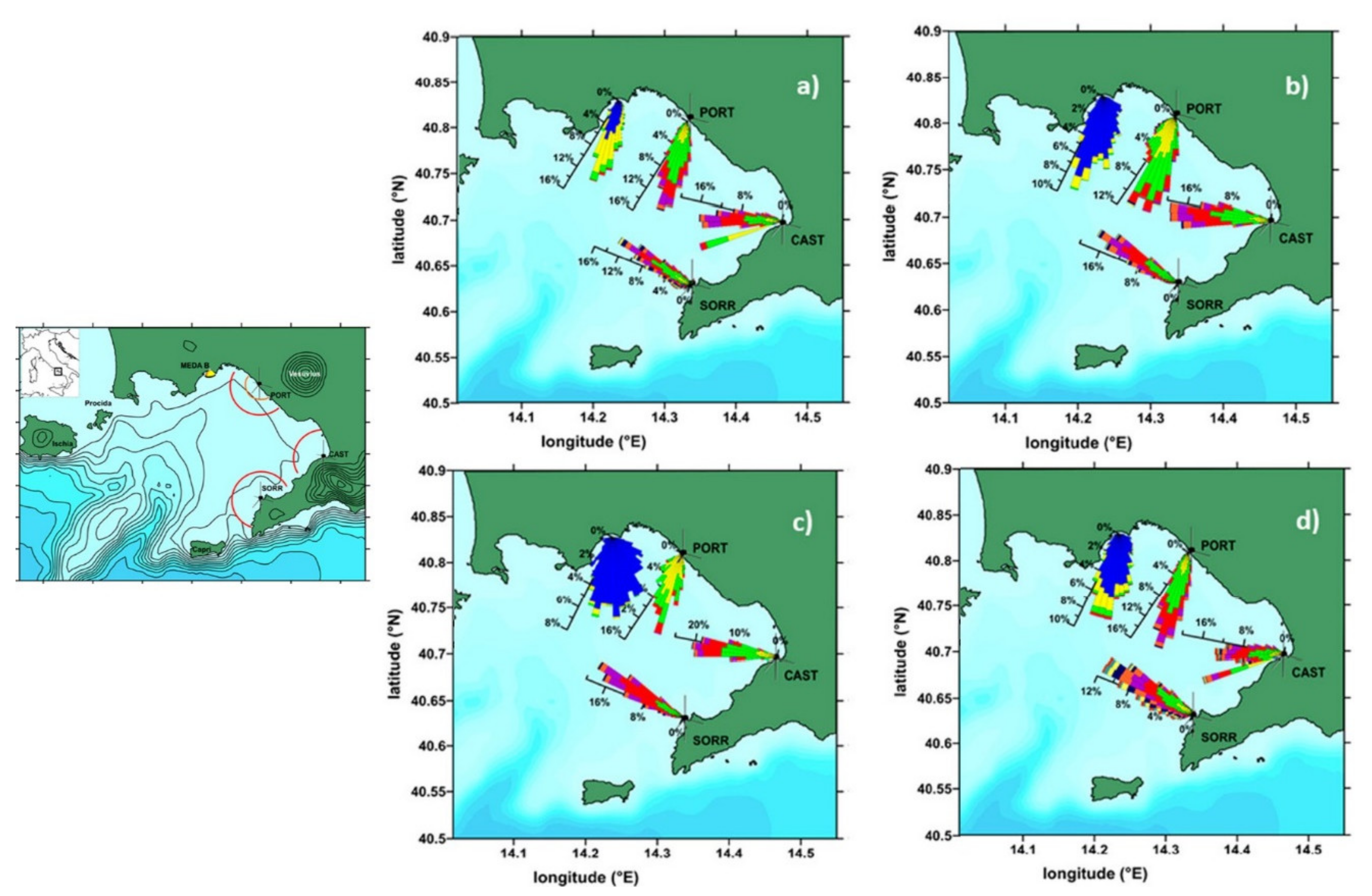
4. Coastal HF Radars
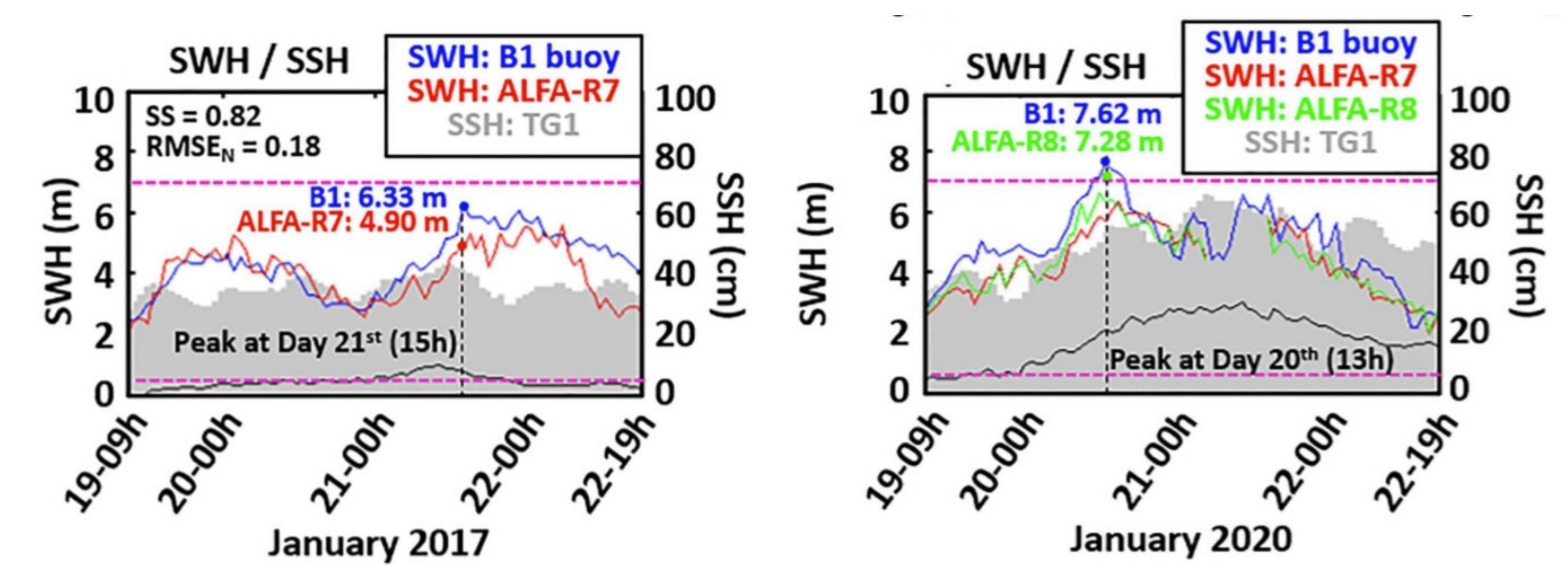
5. Shipboard Sea State Estimation
5.1. Brief Review of the State of the Art
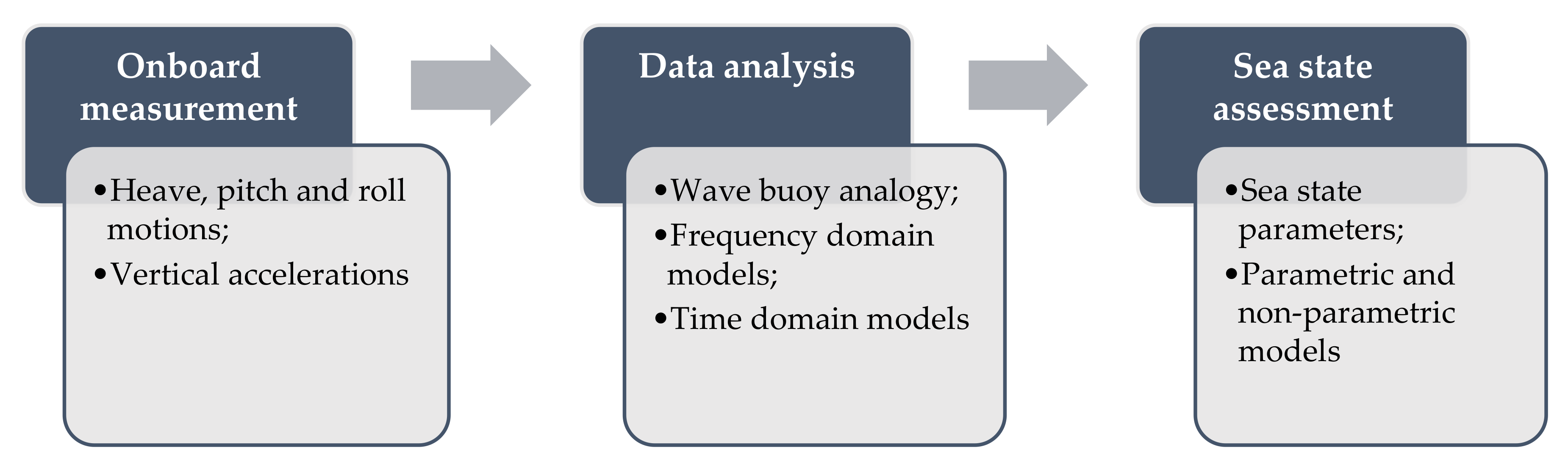
5.2. Methodology
5.2.1. Onboard Measurement
5.2.2. Data Analysis
5.2.3. Assessment of Sea State Parameters
5.3. Future Improvements
- The analysis of nonstationary data that may compromise the accuracy and reliability of sea state estimates;
- The selection of the most suitable ship motions to be endorsed in the assessment of sea state parameters, depending on the ship’s operational conditions;
- The employment of different types of sensors to improve the reliability of the measurement system, based on sensor fusion techniques.
6. Measurement Based on Microseism Observations
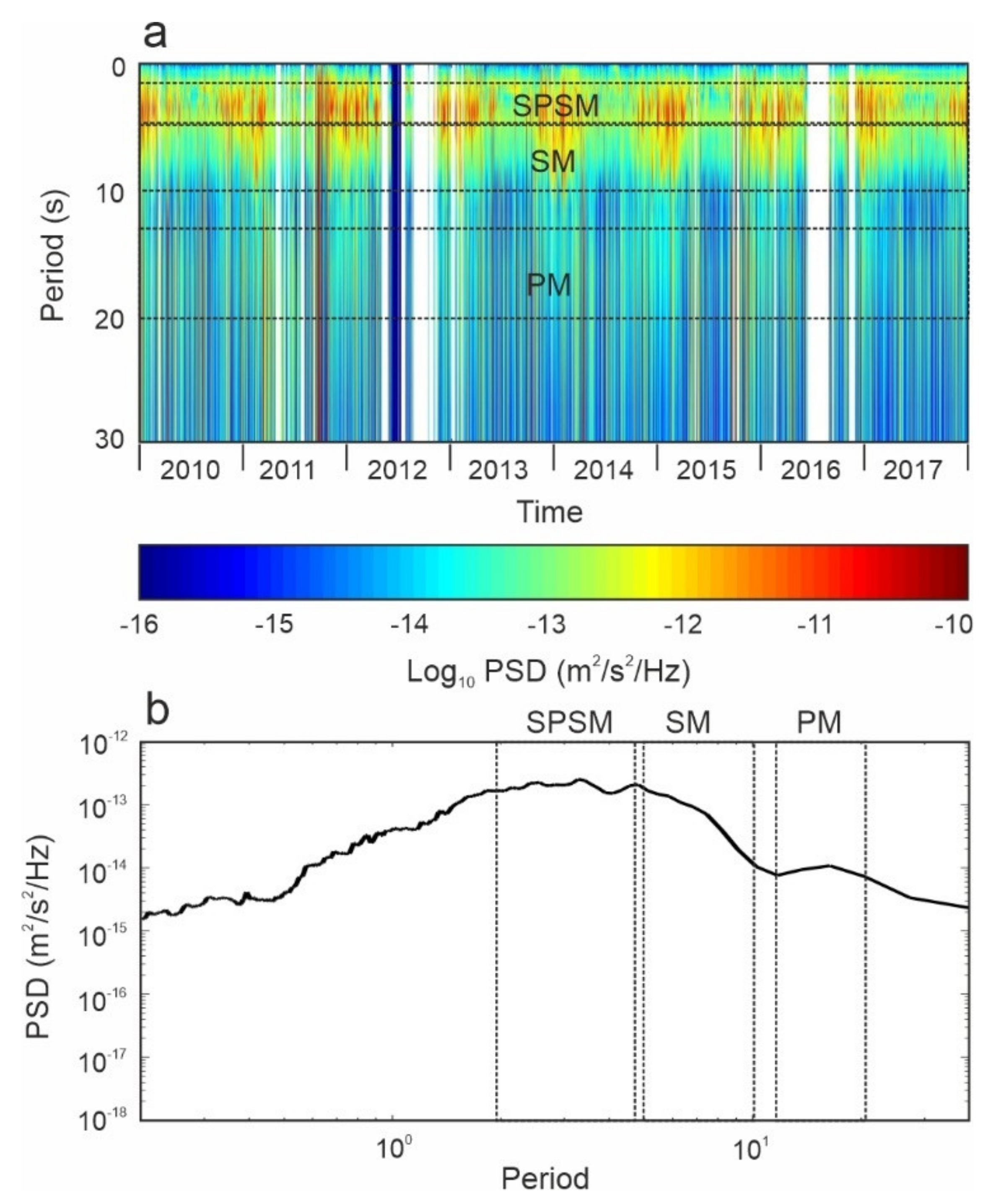
6.1. Microseism
6.2. Applications
6.3. Advantages of Microseism Monitoring
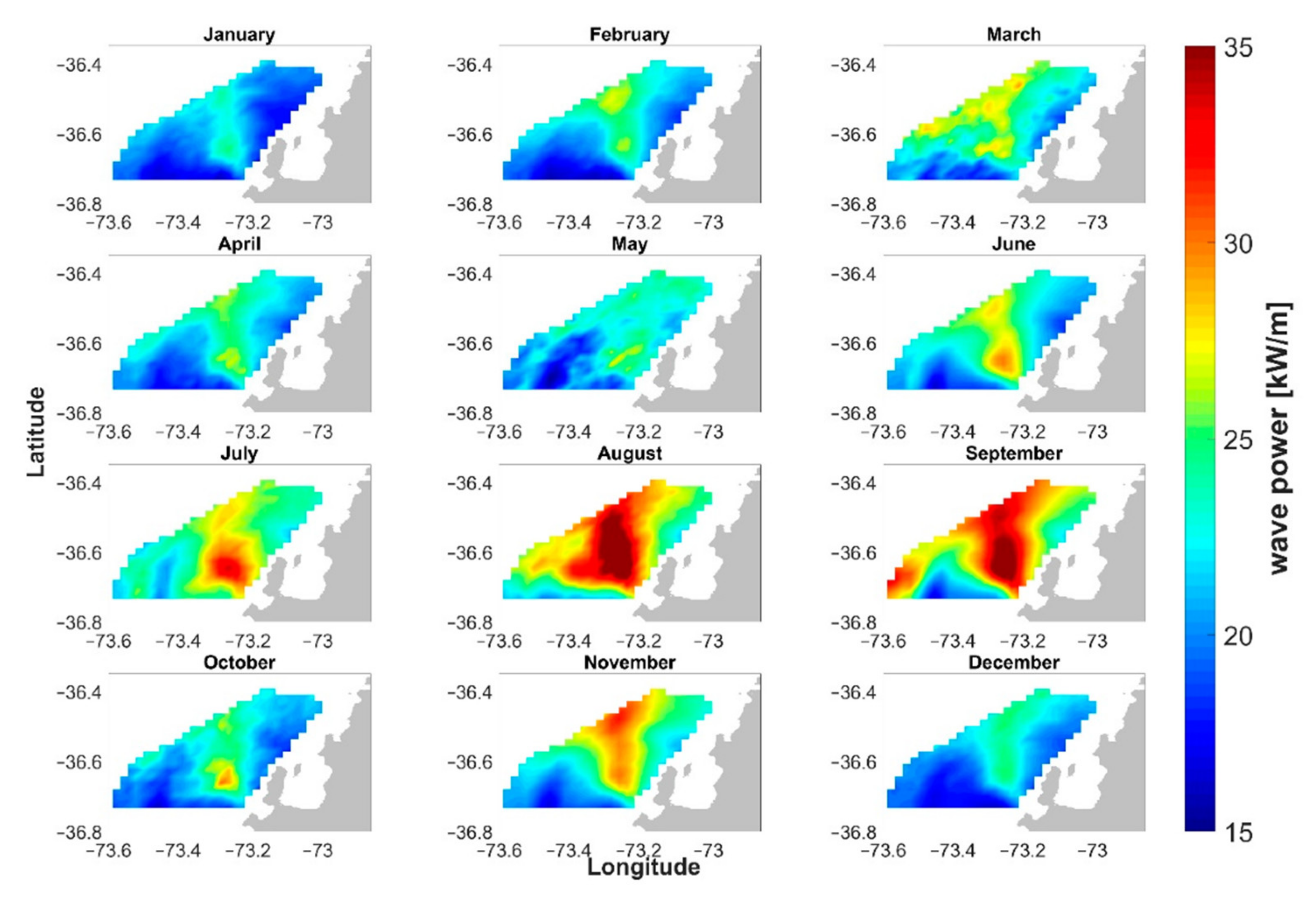
7. Networks for Sea Wave Monitoring
7.1. The Added Value of Networking for Marine Weather Forecasting
7.2. Standards for Design and Management of a Sea-Waves Monitoring Network
7.3. Globally Integrated Sea-Waves Monitoring Networks
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Longuet-Higgins, M.S. On the distribution of the heights of sea waves: Some effects of nonlinearity and finite band width. J. Geophys. Res. 1980, 85, 1519–1523. [Google Scholar] [CrossRef]
- Rossi, G.B.; Crenna, F.; Berardengo, M.; Piscopo, V.; Scamardella, A. Investigation on Spectrum Estimation Methods for Bimodal Sea State Conditions. Sensors 2021, 21, 2995. [Google Scholar] [CrossRef]
- Berardengo, M.; Rossi, G.B.; Crenna, F. Sea Spectral Estimation Using ARMA Models. Sensors 2021, 21, 4280. [Google Scholar] [CrossRef]
- Swail, V.; Jensen, R.; Lee, B.; Turton, J.; Thomas, J.; Gulev, S.; Yelland, M. Wave measurements, needs and developments the next decade. In Proceedings of the OceanObs’09: Sustained Ocean Observations and Information for Society, European Space Agency, Venice, Italy, 21–25 September 2009. [Google Scholar]
- Kuik, A.J.; Ph van Vledder, G.; Holthuijsen, L.H. A Method for the Routine Analysis of Pitch-and-Roll Buoy Wave Data. J. Phys. Oceanogr. 1988, 18, 1020–1034. [Google Scholar] [CrossRef]
- Centurioni, L.; Horányi, A.; Cardinali, C.; Charpentier, E.; Lumpkin, R. A global ocean observing system for measuring sea level atmospheric pressure: Effects and impacts on numerical weather prediction. Bull. Am. Meteorol. Soc. (BAMS) 2017, 98, 231–238. [Google Scholar] [CrossRef]
- Lumpkin, R.; Pazos, M. Measuring surface currents with Surface Velocity Program drifters: The instrument, its data, and some recent results. In Lagrangian Analysis and Prediction of Coastal and Ocean Dynamics (LAPCOD); Griffa, A., Kirwan, A.D., Mariano, A.J., Özgökmen, T., Rossby, H.T., Eds.; Cambridge University Press: Cambridge, UK, 2007; Chapter 2; pp. 39–67. [Google Scholar]
- Centurioni, L.; Braasch, L.; Di Lauro, E.; Contestabile, P.; De Leo, F.; Casotti, R.; Franco, L.; Vicinanza, D. A New Strategic Wave Measurement Station off Naples Port Main Breakwater. In Proceedings of the 35th Conference on Coastal Engineering, Antalya, Turkey, 17–20 November 2016. [Google Scholar]
- Nilsson, J.A.U.; Dobricic, S.; Pinardi, N.; Taillandier, V.; Poulain, P.M. On the assessment of Argo float trajectory assimilation in the Mediterranean Forecasting System. Ocean. Dyn. 2011, 61, 1475–1490. [Google Scholar] [CrossRef] [PubMed]
- D’Asaro, E. Surface Wave Measurements from Subsurface Floats. J. Atmos. Ocean. Technol. 2015, 32, 816–827. [Google Scholar] [CrossRef]
- Wadhams, P.; Comiso, J.C.; Prussen, E.; Wells, S.; Brandon, M.; Aldworth, E.; Viehoff, T.; Allegrino, R.; Crane, D.R. The development of the Odden ice tongue in the Greenland Sea during winter 1993 from remote sensing and field observations. J. Geophys. Res. Ocean. 1996, 101, 18213–18235. [Google Scholar] [CrossRef]
- Liao, Z.; Cheng, B.; Zhao, J.; Vihma, T.; Jackson, K.; Yang, Q.; Yang, Y.; Zhang, L.; Li, Z.; Qiu, Y.; et al. Snow depth and ice thickness derived from SIMBA ice mass balance buoy data using an automated algorithm. Int. J. Digit. Earth 2019, 12, 962–979. [Google Scholar]
- Jackson, K.; Wilkinson, J. A novel and low-cost sea ice mass balance buoy. J. Atmos. Ocean. Technol. 2013, 30, 2676–2688. [Google Scholar] [CrossRef]
- Nicolaus, M.; Hoppmann, M.; Arndt, S.; Hendricks, S.; Katlein, C.; Nicolaus, A.; Rossmann, L.; Schiller, M.; Schwegmann, S. Snow depth and air temperature seasonality on sea ice derived from snow buoy measurements. Front. Mar. Sci. 2021, 8, 655446. [Google Scholar] [CrossRef]
- Voermans, J.; Rabault, J.; Filchuk, K.; Ryzhov, I.; Heil, P.; Marchenko, A.; Collins, C.; Dabboor, M.; Sutherland, G.; Babanin, A. Experimental evidence for a universal threshold characterizing wave-induced sea ice break-up. Cryosphere 2020, 14, 4265–4278. [Google Scholar] [CrossRef]
- Meldrum, D.T. Recent developments at Dunstaffnage: The GPS-Argos drifter, the smart buoy and the mini drifter. In Proceedings of the IEEE Sixth Working Conference on Current Measurement, San Diego, CA, USA, 13 March 1999; pp. 75–81. [Google Scholar]
- O’Reilly, W.C.; Herbers, T.H.C.; Seymour, R.J.; Guza, R.T. A comparison of directional buoy and fixed platform measurements of Pacific swell. J. Atmos. Ocean. Technol. 1996, 13, 231–238. [Google Scholar] [CrossRef]
- Bidlot, J.R.; Holmes, D.J.; Wittmann, P.A.; Lalbeharry, R.; Chen, H.S. Intercomparison of the performance of operational ocean wave forecasting systems with buoy data. Weather Forecast. 2002, 17, 287–310. [Google Scholar] [CrossRef]
- Cavaleri, L. Wave modelling: Missing the peaks. J. Phys. Oceanogr. 2009, 39, 2757–2778. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guide to Wave Analysis and Forecasting, 2nd ed.; (WMO No. 702); WMO: Geneva, Switzerland, 1998; 159p. [Google Scholar]
- Brown, D.T. Mooring Systems. In Handbook of Offshore Engineering; Chakrabarti, S.K., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; Chapter 8; pp. 663–708. [Google Scholar]
- Taft, B.; Teng, C.; Rutledge, T. Low load compliant mooring history and status update. In Proceedings of the OCEANS ’09 “Marine Technology for our Future: Global and Local Challenges”, New Orleans, LA, USA, 26–29 October 2009; pp. 1–9. [Google Scholar]
- Longuet-Higgins, M.S.; Cartwright, D.E.; Smith, N.D. Observations of the directional spectrum of sea waves using the motions of a floating buoy. In Ocean Wave Spectra; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963; pp. 111–136. [Google Scholar]
- Cartwright, D.H.; Smith, N.D. Buoy Techniques for Obtaining Directional Wave Spectra, Buoy Technology; Marine Technology Society: Washington, DC, USA, 1964; pp. 112–121. [Google Scholar]
- Bowden, K.F.; White, R.A. Measurements of the orbital velocities of sea waves and their use in determining the directional spectrum. Geophys. J. Int. 1966, 12, 33–54. [Google Scholar] [CrossRef]
- Barstow, S.F.; Bidlot, J.R.; Caires, S.; Donelan, M.A.; Drennan, W.M.; Dupuis, H.; Graber, H.; Green, J.; Grønlie, Ø.; Guérin, C.; et al. Measuring and analysing the directional spectrum of ocean waves. COST Action 2005, 714, 465. [Google Scholar]
- Mitsuyasu, H.; Tasai, F.; Suhara, T.; Mizuno, S.; Ohkusu, M.; Honda, T.; Rikiishi, K. Observations of the directional spectrum of ocean waves using a cloverleaf buoy. J. Phys. Oceanogr. 1975, 5, 750–760. [Google Scholar] [CrossRef]
- Daidola, J.C.; Basar, N.S.; Reyling, C.J.; Johnson, F.M.; Walker, R.T. Worldwide buoy technology survey. In Coast Guard; Office of Research and Development: Washington, DC, USA, 1991; Volume 1. [Google Scholar]
- Meindl, A. Guide to moored buoys and other ocean data acquisition systems. In IOC-WMO, Data buoy Cooperation Panel—Technical Document No. 8; DBCP: Geneva, Switzerland, 1996. [Google Scholar]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Deutshe Hydrogr. Zeitchrift 1973, 8, 1–95. [Google Scholar]
- Beniot, M. Practical Comparative Performance Survey of Methods Used for Estimating Directional Wave Spectra From Heave-Pitch-Roll Data. In Proceedings of the 23rd Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992; pp. 62–75. [Google Scholar]
- Earle, M. Nondirectional and Directional Wave Data Analysis Procedures (Report No. NDBC Technical Document 96-01); National Oceanic and Atmospheric Administration (NOAA): Slidell, LU, USA, 1996. [Google Scholar]
- Lygre, A.; Krogstad, H.E. Maximum Entropy Estimation of the Directional Distribution in Ocean Wave Spectra. J. Phys. Oceanogr. 1986, 16, 2052–2060. [Google Scholar] [CrossRef]
- Ardhuin, F.; Stopa, J.E.; Chapron, B.; Collard, F.; Husson, R.; Jensen, R.E.; Johannessen, J.; Mouche, A.; Passaro, M.; Quartly, G.D.; et al. Observing Sea States. Front. Mar. Sci. 2019, 6, 124. [Google Scholar] [CrossRef]
- Collins, C.O., III; Lund, B.; Waseda, T.; Graber, H.C. On recording sea surface elevation with accelerometer buoys: Lessons from ITOP (2010). Ocean Dyn. 2014, 64, 895–904. [Google Scholar] [CrossRef]
- O’Reilly, W.C. An Introduction to Directional Wave Observations. In Wave Sensor Technologies Workshop; Alliance for Coastal Technologies: St Petersburg, FL, USA, 7–9 March 2007. [Google Scholar]
- Long, R.B. The statistical evaluation of directional spectrum estimates derived from pitch/roll buoy data. J. Phys. Oceanogr. 1980, 10, 944–952. [Google Scholar] [CrossRef]
- Herber, T.H.C.; Elgar, S.; Guza, R.T. Directional spreading of waves in the nearshore. J. Geophys. Res. 1999, 104, 7683–7693. [Google Scholar] [CrossRef]
- Steele, K.E.; Teng, C.-C.; Wang, D.W. Wave direction wave measurements using pitch-roll buoys. Ocean Eng. 1992, 19, 349–375. [Google Scholar] [CrossRef]
- Bender, L.C.; Guinasso, N.L.; Walpert, J.N.; Howden, S.D. A comparison of two methods for determining wave heights from a discus buoy with a strapped-down accelerometer. In Proceedings of the 11th International Workshop on Wave Hindcasting and Forecasting, Halifax, NS, Canada, 18–23 October 2009. [Google Scholar]
- Cavaleri, L.; Abdalla, S.; Benetazzo, A.; Bertotti, L.; Bidlot, J.R.; Breivik, O.; Carniel, S.; Jensen, R.E.; Portills-Yandun, J.; Rogers, W.E.; et al. Wave modelling in coastal and inner seas. Prog. Oceanogr. 2018, 167, 164–233. [Google Scholar] [CrossRef]
- Jensen, R.E.; Swail, V.; Bouchard, R.H. Quantifying wave measurement differences in historical and present wave buoy systems. Ocean Dyn. 2021, 71, 731–755. [Google Scholar] [CrossRef]
- Doong, D.J.; Lee, B.C.; Kao, C.C. Wave measurements using GPS velocity signals. Sensors 2011, 11, 1043–1058. [Google Scholar] [CrossRef] [PubMed]
- Joodaki, G.; Nahavandchi, H.; Cheng, K. Ocean wave measurement using GPS buoys. J. Geod. Sci. 2013, 3, 163–172. [Google Scholar] [CrossRef]
- Andrews, E.; Peach, L. Wave Monitoring Equipment Comparison: An Evaluation of Current and Emerging In-Situ Ocean Wave Monitoring Technology; Department of Environment and Science: Brisbane, QLD, Australia, 2019. [Google Scholar]
- Herbers, T.H.C.; Jessen, P.F.; Janssen, T.T.; Colbert, D.B.; Mac Mahan, J.H. Observing Ocean Surface Waves with GPS-Tracked Buoys. J. Atmos. Ocean. Technol. 2012, 29, 944–959. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing, Active and Passive; Artech House: Norwood, MA, USA, 1981. [Google Scholar]
- Fu, L.L.; Cazenave, A. (Eds.) Satellite Altimetry and Earth Sciences: A Handbook of Techniques and Applications; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Vignudelli, S.; Kostianoy, A.G.; Cipollini, P.; Benveniste, J. (Eds.) Coastal Altimetry; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Cazenave, A.; Hamlinton, B.; Horwath, M.; Barletta, V.R.; Benveniste, J.; Chambers, D.; Döll, P.; Hogg, A.E.; Legeais, J.F.; Merrifield, M.; et al. Observational Requirements for Long-term Monitoring of the Global Mean Sea Level and Its Components Over the Altimetry Era. Front. Mar. Sci. 2019, 6, 582. [Google Scholar] [CrossRef]
- International Altimetry Team. Altimetry for the future: Building on 25 years of progress. Adv. Space Res. 2021, 68, 319–363. [Google Scholar] [CrossRef]
- Kerkmann, J. Review on Scatterometer Winds; Technical Memorandum, No. 3; EUMETSAT: Darmstadt, Germany, 1998. [Google Scholar]
- Migliaccio, M.; Reppucci, A. A Review of Sea Wind Vector Retrieval By Means of Microwave Remote Sensing. Proc. Eur. Microw. Assoc. 2006, 2, 136–140. [Google Scholar]
- Long, D.G.; Mendel, J.M. Identifiability in Wind Estimation From Scatterometer Measurements. IEEE Trans. Geosci. Remote Sens. 1991, 29, 268–276. [Google Scholar] [CrossRef]
- Soffelen, A.; Portabella, M. On Bayesian Scatterometer Wind Inversion. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1523–1533. [Google Scholar] [CrossRef]
- Nielsen-Englyst, P.; Høyer, J.L.; Pedersen, L.T.; Gentemann, C.L.; Alerskans, E.; Block, T.; Donlon, C. Optimal Estimation of Sea Surface Temperature from AMSR-E. Remote Sens. 2018, 10, 229. [Google Scholar] [CrossRef]
- Goodberlet, M.A.; Swift, C.T.; Wilkerson, J.C. Remote Sensing of Ocean Surface Winds with the Special Sensor Microwave/Imager. J. Geophys. Res. 1989, 94, 14547–14555. [Google Scholar] [CrossRef]
- Wentz, F.; Ricciardulli, L.; Rodriguez, E.; Stiles, B.; Bourassa, M.; Long, D.G.; Hoffman, R.N.; Stoffelen, A.; Verhoef, A.; O’Neill, L.W.; et al. Evaluating and Extending the Ocean Winds Data Climate Record. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2165–2185. [Google Scholar] [CrossRef] [PubMed]
- Bourassa, M.A.; Meissner, T.; Cerovecki, I.; Chang, P.S.; Dong, X.; De Chiara, G.; Donlon, C.; Dukhovskoy, D.S.; Elya, J.; Fore, A.; et al. Remotely Sensed Winds and Wind Stresses for Marine Forecasting and Ocean Modeling. Front. Mar. Sci. 2019, 6, 443. [Google Scholar] [CrossRef]
- Moradi, I.; Franklin Evans, K.; McCarty, W.; Cordero-Fuentes, M.; Gelaro, R.; Black, R.A. Assimilation of Satellite Microwave Observations over the Rainbands of Tropical Cyclones. Mon. Weather Rev. 2020, 148, 4729–4745. [Google Scholar] [CrossRef]
- Yueh, S.H.; Wilson, W.J.; Dinardo, S.J.; Li, F.K. Polarimetric Microwave Brightness Signatures of Ocean Wind Directions. IEEE Trans. Geosci. Remote Sens. 1999, 37, 949–959. [Google Scholar] [CrossRef]
- Le Vine, D.M.; Dinnat, E.P.; Meissner, T.; Wentz, F.J.; Kao, H.-Y.; Lagerloef, G.; Lee, T. Status of Aquarius and Salinity Continuity. Remote Sens. 2018, 10, 1585. [Google Scholar] [CrossRef]
- Font, J.; Camps, A.; Borges, A.; Martìn-Neira, M.; Boutin, J.; Reul, N.; Kerr, Y.H.; Hahne, A.; Mecklenburg, S. SMOS: The Challenging Sea Surface Salinity Measurement From Space. Proc. IEEE 2010, 98, 649–665. [Google Scholar] [CrossRef]
- Kasilingam, D.P.; Shemdin, O.H. Models for Synthetic Aperture Radar Imaging of the Ocean: A Comparison. J. Geophys. Res. 1990, 95, 16263–16276. [Google Scholar] [CrossRef]
- Harger, R.O. The Synthetic Aperture Radar Image of Time-variant Scenes. Radio Sci. 1980, 15, 749–756. [Google Scholar] [CrossRef]
- Hasselmann, K.; Raney, R.K.; Plant, W.J.; Alpers, W.; Shuchman, R.A.; Lyzenga, D.R.; Rufenach, C.L.; Tucker, M.J. Theory of Synthetic Aperture Radar Ocean Imaging: A MARSEN view. J. Geophys. Res. 1985, 90, 4659–4686. [Google Scholar] [CrossRef]
- Vachon, P.W.; Raney, R.K. Ocean waves and optimal SAR processing: Don’t adjust the focus! IEEE Trans. Geosci. Remote Sens. 1992, 30, 627–630. [Google Scholar] [CrossRef]
- Migliaccio, M.; Nunziata, F.; Buono, A. SAR Polarimetry for Sea Oil Slick Observation. Int. J. Remote Sens. 2015, 36, 3243–3273. [Google Scholar] [CrossRef]
- Nunziata, F.; Migliaccio, M.; Brown, C.E. Reflection Symmetry for Polarimetric Observation of Man-made Metallic Targets at Sea. IEEE J. Ocean Eng. 2012, 37, 384–394. [Google Scholar] [CrossRef]
- Raney, R.K. Theory and Measure of Certain Image Norms in SAR. IEEE Trans. Geosci. Remote Sens. 1985, 23, 343–348. [Google Scholar] [CrossRef]
- Delignon, Y.; Garello, R.; Hillion, A. A Statistical Characterization of Sea-State SAR Images. In Proceedings of the Conference Proceedings on Engineering in the Ocean Environment, Washington, DC, USA, 24–26 September 1990. [Google Scholar]
- Migliaccio, M.; Huang, L.; Buono, A. SAR Speckle Dependence on Ocean Surface Wind Field. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5447–5455. [Google Scholar] [CrossRef]
- Nunziata, F.; Gambardella, A.; Migliaccio, M. An Educational SAR Sea Surface Waves Simulator. Int. J. Remote Sens. 2008, 29, 3051–3066. [Google Scholar] [CrossRef]
- Hasselmann, K.; Alpers, W. The Response of Synthetic Aperture Radar To Ocean Surface Waves. In Wave Dynamics and Radio Probing of The Ocean Surface; Phillips, O.M., Hasselmann, K., Eds.; Plenum Press: New York, NY, USA, 1986; pp. 393–402. [Google Scholar]
- Hasselmann, K.; Hasselmann, S. On the nonlinear mapping of an ocean wave spectrum into a SAR image spectrum and its inversion. J. Geophys. Res. 1991, 96, 10713–10729. [Google Scholar] [CrossRef]
- Hasselmann, S.; Brüning Hasselmann, K.; Heimbach, P. An Improved Algorithm for the Retrieval of Ocean Wave Spectra from Synthetic Aperture Radar Image Spectra. J. Geophys. Res. 1996, 101, 16615–16629. [Google Scholar] [CrossRef]
- Engen, G.; Johnsen, H. SAR-Ocean Wave Inversion Using Image Cross Spectra. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1047–1056. [Google Scholar] [CrossRef]
- Bao, M.; Alpers, W. On the Cross Spectrum Between Individual-Look Synthetic Aperture Radar Images of Ocean Waves. IEEE Trans. Geosci. Remote Sens. 1998, 36, 922–932. [Google Scholar]
- Li, H.; Chapron, B.; Mouche, A.; Stopa, J.E. A New Ocean SAR Cross-Spectral Parameter: Definition and Directional Property Using the Global Sentinel-1 Measurements. J. Geophys. Res. 2019, 124, 1566–1577. [Google Scholar] [CrossRef]
- Li, H.; Stopa, J.E.; Mouche, A.; Zhang, B.; He, Y.; Chapron, B. Assessment of Ocean Wave Spectrum using Global Envisat/ASAR Data and Hindcast Simulation. Remote Sens. Environ. 2021, 264, 1–13. [Google Scholar] [CrossRef]
- Hauser, D.; Tourain, C.; Hermozo, L.; Alraddawi, D.; Aouf, L.; Chapron, B.; Dalphinet, A.; Delaye, L.; Dalila, M.; Dormy, E.; et al. New Observations From the SWIM Radar On-Board CFOSAT: Instrument Validation and Ocean Wave Measurement Assessment. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5–26. [Google Scholar] [CrossRef]
- Quach, B.; Glaser, Y.; Stopa, J.E.; Mouche, A.; Sadowski, P. Deep Learning for Predicting Significant Wave Height From Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1859–1867. [Google Scholar] [CrossRef]
- Schuler, D.L.; Lee, J.S.; Kasilingam, D.; Pottier, E. Measurement of Ocean Surface Slopes and Wave Spectra using Polarimetric SAR Image Data. Remote Sens. Environ. 2004, 91, 198–211. [Google Scholar] [CrossRef]
- He, Y.; Shen, H.; Perrie, W. Remote Sensing of Ocean Waves by Polarimetric SAR. J. Atmos. Ocean Technol. 2006, 23, 1768–1773. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; He, Y. Validation of RADARSAT-2 Fully Polarimetric SAR Measurements of Ocean Surface Waves. J. Geophys. Res. 2010, 115, 1–11. [Google Scholar] [CrossRef]
- Shao, W.; Wang, J.; Li, X.; Sun, J. An Empirical Algorithm for Wave Retrieval from Co-Polarization X-Band SAR Imagery. Remote Sens. 2017, 9, 711. [Google Scholar] [CrossRef]
- Pramudya, F.S.; Pan, J.; Devlin, A.T.; Lin, H. Enhanced Estimation of Significant Wave Height with Dual-Polarization Sentinel-1 SAR Imagery. Remote Sens. 2021, 13, 124. [Google Scholar] [CrossRef]
- Kerbaol, V.; Chapron, B.; Vachon, P.W. Analysis of ERS-1/2 Synthetic Aperture Radar Wave Mode Imagettes. J. Geophys. Res. 1998, 103, 7833–7846. [Google Scholar] [CrossRef]
- Grieco, G.; Lin, W.; Migliaccio, M.; Nirchio, F.; Portabella, M. Dependency of the Sentinel-1 azimuth wavelength cut-off on significant wave height and wind speed. Int. J. Remote Sens. 2016, 37, 5086–5104. [Google Scholar] [CrossRef]
- Corcione, V.; Grieco, G.; Portabella, M.; Nunziata, F.; Migliaccio, M. A Novel Azimuth Cut-off Implementation to Retrieve Sea Surface Wind Speed from SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3331–3340. [Google Scholar] [CrossRef]
- Stopa, J.E.; Ardhuin, F.; Chapron, B.; Collard, F. Estimating Wave Orbital Velocity through the Azimuth Cutoff from Space-Borne Satellites. J. Geophys. Res. 2015, 120, 7616–7634. [Google Scholar] [CrossRef]
- Stopa, J.E.; Mouche, A. Significant Wave Heights from Sentinel-1 SAR: Validation and Applications. J. Geophys. Res. 2017, 122, 1827–1848. [Google Scholar] [CrossRef]
- Pleskachevsky, A.; Jacobsen, S.; Tings, B.; Schwarz, E. Estimation of Sea State from Sentinel-1 Synthetic Aperture Radar Imagery for Maritime Situation Awareness. Int. J. Remote Sens. 2019, 40, 4104–4142. [Google Scholar] [CrossRef]
- Vachon, P.W.; Campbell, J.W.M.; Gray, A.L.; Dobson, F.W. Validation of along-Track Interferometric SAR Measurements of Ocean Surface Waves. IEEE Trans. Geosci. Remote Sens. 1999, 37, 150–162. [Google Scholar] [CrossRef]
- Bao, M.; Alpers, W.; Brüning, C. A New Nonlinear Integral Transform Relating Ocean Wave Spectra to Phase Image Spectra of an Along-Track Interferometric Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 1999, 37, 461–466. [Google Scholar]
- He, Y.; Alpers, W. On the Nonlinear Integral Transform of an Ocean Wave Spectrum into an Along-track Interferometric Synthetic Aperture Radar Image Spectrum. J. Geophys. Res. 2003, 108, 1–9. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; He, Y. Remote Sensing of Ocean Waves by Along-track Interferometric Synthetic Aperture Radar. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Schulz-Stellenfleth, J.; Lehner, S. Ocean Wave Imaging Using an Airborne Single Pass Across-Track Interferometric SAR. IEEE Trans. Geosci. Remote Sens. 2001, 39, 38–45. [Google Scholar] [CrossRef]
- Portilla-Yandún, J.; Valladares, C.; Violante-Carvalho, N. A Hybrid Physical-Statistical Algorithm for SAR Wave Spectra Quality Assessment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3943–3948. [Google Scholar] [CrossRef]
- Ferla, M.; Nardone, G.; Orasi, A.; Picone, M.; Zambianchi, E.; Falco, P. Sea-Monitoring Networks. In Measurement for the Sea, Supporting the Marine Environment and the Blue Economy; Daponte, P., Rossi, G.B., Piscopo, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Crombie, D.D. Doppler spectrum of sea echo at 13.56 Mc./s. Nature 1955, 175, 681–682. [Google Scholar] [CrossRef]
- Barrick, D.E. Theory of HF and VHF propagation across the rough sea, 1, The effective surface impedance for a slightly rough highly conducting medium at grazing incidence. Radio Sci. 1971, 6, 517–526. [Google Scholar] [CrossRef]
- Barrick, D.E. Theory of HF and VHF propagation across the rough sea, 2, Application to HF and VHF propagation above the sea. Radio Sci. 1971, 6, 527–533. [Google Scholar] [CrossRef]
- Barrick, D.E. First-order theory and analysis of MF/HF/VHF scatter from the sea. IEEE Trans. Antennas Propag. 1972, 20, 2–10. [Google Scholar] [CrossRef]
- Barrick, D.E. HF radio oceanography—A review. Bound. Layer Meteorol. 1978, 13, 23–43. [Google Scholar] [CrossRef]
- Barrick, D.E.; Evans, M.W.; Weber, B.L. Ocean surface currents mapped by radar. Science 1977, 198, 138–144. [Google Scholar] [CrossRef]
- Paduan, J.D.; Washburn, L. High-frequency radar observations of ocean surface currents. Annu. Rev. Mar. Sci. 2013, 5, 115–136. [Google Scholar] [CrossRef]
- Barrick, D.E. Remote sensing of sea state by radar. In Proceedings of the Ocean 72-IEEE International Conference on Engineering in the Ocean Environment, Newport, RI, USA, 13–15 September 1972; pp. 186–192. [Google Scholar]
- Barrick, D.E. Extraction of wave parameters from measured HF radar sea-echo Doppler spectra. Radio Sci. 1977, 12, 415–424. [Google Scholar] [CrossRef]
- Barrick, D.E. The ocean waveheight nondirectional spectrum from inversion of the HF sea-echo Doppler spectrum. Remote Sens. Environ. 1977, 6, 201–227. [Google Scholar] [CrossRef]
- Lipa, B. Derivation of directional ocean-wave spectra by integral inversion of second-order radar echoes. Radio Sci. 1977, 12, 425–434. [Google Scholar] [CrossRef]
- Lipa, B. Inversion of second-order radar echoes from the sea. J. Geophys. Res. Ocean. 1978, 83, 959–962. [Google Scholar] [CrossRef]
- Wyatt, L. The measurement of the ocean wave directional spectrum from HF radar Doppler spectra. Radio Sci. 1986, 21, 473–485. [Google Scholar] [CrossRef]
- Toro, V.G.; Ocampo-Torres, F.J.; Osuna, P.; García-Nava, H.; Flores-Vidal, X.; Durazo, R. Analysis of fetch-limited wave growth using high-frequency radars in the Gulf of Tehuantepec. Cienc. Mar. 2014, 40, 113–132. [Google Scholar] [CrossRef][Green Version]
- Wyatt, L.R.; Green, J.J.; Middleditch, A. HF radar data quality requirements for wave measurement. Coast. Eng. 2011, 58, 327–336. [Google Scholar] [CrossRef]
- Wyatt, L.R. An evaluation of wave parameters measured using a single HF radar system. Can. J. Remote Sens. 2002, 28, 205–218. [Google Scholar] [CrossRef]
- Piscopo, V.; Rossi, G.B.; Crenna, S.; Gaglione, S.; Scamardella, A.; Uttieri, M.; Zambianchi, E. Measurement of sea waves. In Measurement for the Sea, Supporting the Marine Environment and the Blue Economy; Daponte, P., Rossi, G.B., Piscopo, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Rubio, A.; Mader, J.; Corgnati, L.; Mantovani, C.; Griffa, A.; Novellino, A.; Quentin, C.; Wyatt, L.; Schulz-Stellenfleth, J.; Horstmann, J.; et al. HF radar activity in European coastal seas: Next steps toward a pan-European HF radar network. Front. Mar. Sci. 2017, 4, 8. [Google Scholar] [CrossRef]
- Ranalli, M.; Lagona, F.; Picone, M.; Zambianchi, E. Segmentation of sea current fields by cylindrical hidden Markov models: A composite likelihood approach. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2018, 67, 575–598. [Google Scholar] [CrossRef]
- Saviano, S.; Kalampokis, A.; Zambianchi, E.; Uttieri, M. A year-long assessment of wave measurements retrieved from an HF radar network in the Gulf of Naples (Tyrrhenian Sea, Western Mediterranean Sea). J. Oper. Oceanogr. 2019, 12, 1–15. [Google Scholar] [CrossRef]
- Lorente, P.; Lin-Ye, J.; García-León, M.; Reyes, E.; Fernandes, M.; Sotillo, M.G.; Espino, M.; Ruiz, M.I.; Gracia, V.; Perez, S.; et al. On the Performance of High Frequency Radar in the Western Mediterranean During the Record-Breaking Storm Gloria. Front. Mar. Sci. 2021, 8, 645762. [Google Scholar] [CrossRef]
- Krogstad, H.E.; Wolf, J.; Thompson, S.P.; Wyatt, L.R. Methods for intercomparison of wave measurements. Coast. Eng. 1999, 37, 235–257. [Google Scholar] [CrossRef]
- Atan, R.; Goggins, J.; Harnett, M.; Agostinho, P.; Nash, S. Assessment of wave characteristics and resource variability at a 1/4-scale wave energy test site in Galway Bay using waverider and high frequency radar (CODAR) data. Ocean Eng. 2016, 117, 272–291. [Google Scholar] [CrossRef]
- Fernandes, M.; Fernandes, C.; Barroqueiro, T.; Agostinho, P.; Martins, N.; Alonso-Martirena, A. Extreme wave height events in Algarve (Portugal): Comparison between HF radar systems and wave buoys. In Proceedings of the 5th Jornadas de Engenharia Hidrográfica, Lisboa, Portugal, 19–21 June 2018; pp. 1–5. [Google Scholar]
- Cai, L.; Shang, S.; Wei, G.; He, Z.; Xie, Y.; Liu, K.; Zhou, T.; Chen, J.; Zhang, F.; Li, Y. Assessment of significant wave height in the Taiwan Strait measured by a single HF radar system. J. Atmos. Ocean Technol. 2019, 36, 1419–1432. [Google Scholar] [CrossRef]
- Bué, I.; Semedo, Á.; Catalão, J. Evaluation of HF Radar Wave Measurements in Iberian Peninsula by Comparison with Satellite Altimetry and in Situ Wave Buoy Observations. Remote Sens. 2020, 12, 3623. [Google Scholar] [CrossRef]
- Saviano, S.; Cianelli, D.; Zambianchi, E.; Conversano, F.; Uttieri, M. An integrated reconstruction of the multiannual wave pattern in the Gulf of Naples (South-Eastern Tyrrhenian Sea, Western Mediterranean Sea). J. Mar. Sci. Eng. 2020, 8, 372. [Google Scholar] [CrossRef]
- Lipa, B.; Nyden, B. Directional wave information from the SeaSonde. IEEE J. Ocean. Eng. 2005, 30, 221–231. [Google Scholar] [CrossRef]
- Orasi, A.; Picone, M.; Drago, A.; Capodici, F.; Gauci, A.; Nardone, G.; Inghilesi, R.; Azzopardi, J.; Galea, A.; Ciraolo, G.; et al. HF radar for wind waves measurements in the Malta-Sicily Channel. Measurement 2018, 128, 446–454. [Google Scholar] [CrossRef]
- Saviano, S.; De Leo, F.; Besio, G.; Zambianchi, E.; Uttieri, M. HF radar measurements of surface waves in the Gulf of Naples (Southeastern Tyrrhenian Sea): Comparison with hindcast results at different scales. Front. Mar. Sci. 2020, 7, 492. [Google Scholar] [CrossRef]
- Sotillo, M.G.; Mourre, B.; Mestres, M.; Lorente, P.; Aznar, R.; García-León, M.; Liste, M.; Santana, A.; Espino, M.; Álvarez, E. Evaluation of the operational CMEMS and coastal downstream ocean forecasting services during the storm Gloria (January 2020). Front. Mar. Sci. 2021, 8, 644525. [Google Scholar] [CrossRef]
- Wyatt, L.; Venn, J.; Burrows, G.; Ponsford, A.; Moorhead, M.; van Heteren, J. HF radar measurements of ocean wave parameters during NURWEC. IEEE J. Ocean Eng. 1986, 11, 219–234. [Google Scholar] [CrossRef]
- Lipa, B.J.; Barrick, D.E.; Isaacson, J.; Lilleboe, P.M. CODAR wave measurements from a North Sea semisubmersible. IEEE J. Ocean. Eng. 1990, 15, 119–125. [Google Scholar] [CrossRef]
- Falco, P.; Buonocore, B.; Cianelli, D.; De Luca, L.; Giordano, A.; Iermano, I.; Zambardino, G.; Zambianchi, E. Dynamics and sea state in the Gulf of Naples: Potential use of high-frequency radar data in an operational oceanographic context. J. Oper. Oceanogr. 2016, 9 (Suppl. 1), s33–s45. [Google Scholar] [CrossRef]
- Lopez, G.; Conley, D.C.; Greaves, D. Calibration, validation, and analysis of an empirical algorithm for the retrieval of wave spectra from HF radar sea echo. J. Atmos. Ocean Technol. 2016, 33, 245–261. [Google Scholar] [CrossRef]
- Lopez, G.; Conley, D.C. Comparison of HF radar fields of directional wave spectra against in situ measurements at multiple locations. J. Mar. Sci. Eng. 2019, 7, 271. [Google Scholar] [CrossRef]
- Basañez, A.; Lorente, P.; Montero, P.; Álvarez-Fanjul, E.; Pérez-Muñuzuri, V. Quality Assessment and practical interpretation of the wave parameters estimated by HF Radars in NW Spain. Remote Sens. 2020, 12, 598. [Google Scholar] [CrossRef]
- Long, R.M.; Barrick, D.E.; Largier, J.L.; Garfield, N. Wave observations from central California: SeaSonde systems and in situ wave buoys. J. Sens. 2011, 2011, 728936. [Google Scholar] [CrossRef]
- Lorente, P.; Basañez Mercader, A.; Piedracoba, S.; Pérez-Muñuzuri, V.; Montero, P.; Sotillo, M.G.; Álvarez-Fanjul, E. Long-term skill assessment of SeaSonde radar-derived wave parameters in the Galician coast (NW Spain). Int. J. Remote Sens. 2019, 40, 9208–9236. [Google Scholar] [CrossRef]
- Mundaca-Moraga, V.; Abarca-del-Rio, R.; Figueroa, D.; Morales, J. A Preliminary Study of Wave Energy Resource Using an HF Marine Radar, Application to an Eastern Southern Pacific Location: Advantages and Opportunities. Remote Sens. 2021, 13, 203. [Google Scholar] [CrossRef]
- Thomson, R.E.; Emery, W.J. Data analysis methods in physical oceanography, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2014; p. 638. [Google Scholar]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Wyatt, L.R. Chapter 9—The IMOS Ocean Radar Facility, ACORN. In Coastal Ocean Observing Systems; Academic Press: London, UK, 2015. [Google Scholar]
- Wyatt, L.R. High frequency radar applications in coastal monitoring, planning and engineering. Aust. J. Civ. Eng. 2014, 12, 1–15. [Google Scholar] [CrossRef]
- Wyatt, L.R. Wave and tidal power measurement using HF radar. Int. Mar. Energy J. 2018, 1, 123–127. [Google Scholar] [CrossRef]
- Iermano, I.; Moore, A.M.; Zambianchi, E. Impacts of a 4-dimensional variational data assimilation in a coastal ocean model of southern Tyrrhenian Sea. J. Mar. Syst. 2016, 154, 157–171. [Google Scholar] [CrossRef]
- Siddons, L.A. Data Assimilation of HF Radar Data into Coastal Wave Models. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2007. [Google Scholar]
- Siddons, L.A.; Wyatt, L.R.; Wolf, J. Assimilation of HF radar data into the SWAN wave model. J. Mar. Syst. 2009, 77, 312–324. [Google Scholar] [CrossRef]
- Waters, J.; Wyatt, L.R.; Wolf, J.; Hines, A. Data assimilation of partitioned HF radar wave data into WaveWatch III. Ocean Model. 2013, 72, 17–31. [Google Scholar] [CrossRef]
- Takekuma, K.; Takahashi, T. On the Evaluation of Sea Spectra Based on the Measured Ship Motions. Trans. West Jpn. Soc. Nav. Archit. 1973, 45, 51–57. [Google Scholar]
- Isobe, M.; Kondo, K.; Horikawa, K. Extension of MLM for estimating directional wave spectrum. In Proceedings of the Symposium on Description and Modeling of Directional Seas, Copenhagen, Denmark, 18–20 June 1984. [Google Scholar]
- Kobune, K.; Hashimoto, N. Estimation of directional spectra from the maximum entropy principle. In Proceedings of the 5th International Offshore Mechanics and Arctic Engineering (OMAE) Symposium, Tokyo, Japan, 13–18 April 1986. [Google Scholar]
- Hirayama, T. Real-time estimation of sea spectra based on motions of a running ship. J. Kansai Soc. Nav. Archit. 1988, 204, 21–27. [Google Scholar]
- Iseki, T.; Ohtsu, K.; Fujino, M. A study on estimation of directional spectra based on ship motions. J. Jpn. Inst. Navig. 1982, 86, 179–188. [Google Scholar] [CrossRef][Green Version]
- Iseki, T.; Ohtsu, K. Bayesian estimation of directional wave spectra based on ship motions. Control Eng. Pract. 2000, 8, 215–219. [Google Scholar] [CrossRef]
- Pascoal, R.; Guedes Soares, C.; Sørensen, J. Ocean wave spectral estimation using vessel wave frequency motions. J. Offshore Mech. Arct. Eng. 2007, 129, 90–96. [Google Scholar] [CrossRef]
- Pascoal, R.; Guedes Soares, C. Kalman filtering of vessel motions for ocean wave directional spectrum estimation. Ocean Eng. 2009, 36, 477–488. [Google Scholar] [CrossRef]
- Nielsen, U.D.; Stredulinksy, D.C. Sea state estimation from an advancing ship—A comparative study using sea trial data. Appl. Ocean Res. 2012, 34, 33–44. [Google Scholar] [CrossRef]
- Montazeri, N.; Nielsen, U.D.; Jensen, J.J. Estimation of wind sea and swell using shipboard measurements—A refined parametric modelling approach. Appl. Ocean Res. 2016, 54, 73–86. [Google Scholar] [CrossRef]
- Nielsen, U.D. Transformation of a wave energy spectrum from encounter to absolute domain when observing from an advancing ship. Appl. Ocean Res. 2017, 69, 160–172. [Google Scholar] [CrossRef]
- Brodtkorb, A.H.; Nielsen, U.D.; Sørensen, A. Online wave estimation using vessel motion measurements. In Proceedings of the 11th IFAC Conference on Control Applications in Marine Systems, Robotics and Vehicles CAMS 2018, Opatija, Croatia, 10–12 September 2018. [Google Scholar]
- Piscopo, V.; Scamardella, A.; Gaglione, S. A new wave spectrum resembling procedure based on ship motion analysis. Ocean Eng. 2020, 201, 107137. [Google Scholar] [CrossRef]
- Nielsen, U.D.; Dietz, J. Ocean wave spectrum estimation using measured vessel motions from an in-service container ship. Mar. Struct. 2020, 69, 102682. [Google Scholar] [CrossRef]
- Pennino, S.; Angrisano, A.; Della Corte, V.; Ferraioli, G.; Gaglione, S.; Innac, A.; Martellato, E.; Palumbo, P.; Piscopo, V.; Rotundi, A.; et al. Sea State Monitoring by Ship Motion Measurements Onboard a Research Ship in the Antarctic Waters. J. Mar. Sci. Eng. 2021, 9, 64. [Google Scholar] [CrossRef]
- Nielsen, U.D. A concise account of techniques available for shipboard sea state estimation. Ocean Eng. 2017, 129, 352–362. [Google Scholar] [CrossRef]
- Tannuri, E.A.; Sparano, J.V.; Simos, A.N.; Da Cruz, J.J. Estimating directional wave spectrum based on stationary ship motion measurements. Appl. Ocean Res. 2003, 25, 243–261. [Google Scholar] [CrossRef]
- Nielsen, U.D. Estimations of on-site directional wave spectra from measured ship responses. Mar. Struct. 2006, 19, 33–69. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. A theory of the origin of microseisms: Philosophical Transactions of the Royal Society of London. Ser. A Math. Phys. Sci. 1950, 243, 1–35. [Google Scholar]
- Hasselmann, K. A statistical analysis of the generation of microseisms. Rev. Geophys. 1963, 1, 177–210. [Google Scholar] [CrossRef]
- Ardhuin, F.; Gualtieri, L.; Stutzmann, E. How ocean waves rock the Earth: Two mechanisms explain microseisms with periods 3 to 300 s. Geophys. Res. Lett. 2015, 42, 765–772. [Google Scholar] [CrossRef]
- Ardhuin, F.; Balanche, A.; Stutzmann, E.; Obrebski, M. From seismic noise to ocean wave parameters: General methods and validation. J. Geophys. Res. Ocean 2012, 117, C05002. [Google Scholar] [CrossRef]
- Bromirski, P.D.; Duennebier, F.K.; Stephen, R.A. Mid-Ocean microseisms. Geochem. Geophys. Geosyst. 2005, 6, 1–19. [Google Scholar] [CrossRef]
- Chen, Y.N.; Gung, Y.; You, S.H.; Hung, S.H.; Chiao, L.Y.; Huang, T.Y.; Chen, Y.L.; Jan, S. Characteristics of short period secondary microseisms (SPSM) in Taiwan: The influence of shallow ocean strait on SPSM. Geophys. Res. Lett. 2011, 38, L04305. [Google Scholar] [CrossRef]
- Aster, R.C.; McNamara, D.E.; Bromirski, P.D. Multidecadal climate-induced variability in microseisms. Seismol. Res. Lett. 2008, 79, 194–202. [Google Scholar] [CrossRef]
- Stutzmann, E.; Schimmel, M.; Patau, G.; Maggi, A. Global climate imprint on seismic noise. Geochem. Geophys. Geosyst. 2009, 10, Q11004. [Google Scholar] [CrossRef]
- Tsai, V.C.; McNamara, D.E. Quantifying the influence of sea ice on ocean microseism using observations from the Bering Sea, Alaska. Geophys. Res. Lett. 2011, 38, L22502. [Google Scholar] [CrossRef]
- Anthony, R.E.; Aster, R.C.; Wiens, D.; Nyblade, A.; Anandakrishnan, S.; Huerta, A.; Winberry, J.P.; Rowe, C. The seismic noise environment of Antarctica. Seismol. Res. Lett. 2015, 86, 89–100. [Google Scholar] [CrossRef]
- Anthony, R.E.; Aster, R.C.; McGrath, D. Links between atmosphere, ocean, and cryosphere from two decades of microseism observations on the Antarctic Peninsula. J. Geophys. Res. Earth Surf. 2017, 122, 153–166. [Google Scholar] [CrossRef]
- Cannata, A.; Cannavò, F.; Moschella, S.; Gresta, S.; Spina, L. Exploring the link between microseism and sea ice in Antarctica by using machine learning. Sci. Rep. 2019, 9, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Cannata, A.; Cannavò, F.; Moschella, S.; Di Grazia, G.; Nardone, G.; Orasi, A.; Gresta, S. Unravelling the Relationship Between Microseisms and Spatial Distribution of Sea Wave Height by Statistical and Machine Learning Approaches. Remote Sens. 2020, 12, 761. [Google Scholar] [CrossRef]
- Porritt, R.W.; Miller, M.S.; O’Driscoll, L.J.; Harris, C.W.; Roosmawati, N.; da Costa, L.T. Continent–arc collision in the Banda Arc imaged by ambient noise tomography. Earth Planet. Sci. Lett. 2016, 449, 246–258. [Google Scholar] [CrossRef]
- Tamura, J.; Okada, T. Ambient noise tomography in the Naruko/Onikobe volcanic area, NE Japan: Implications for geofluids and seismic activity. Earth Planet Space 2016, 68, 5. [Google Scholar] [CrossRef]
- Brenguier, F.; Campillo, M.; Takeda, T.; Aoki, Y.; Shapiro, N.M.; Briand, X.; Emoto, K.; Miyake, H. Mapping pressurized volcanic fluids from induced crustal seismic velocity drops. Science 2014, 345, 80–82. [Google Scholar] [CrossRef]
- Cannata, A.; Cannavò, F.; Montalto, P.; Ercoli, M.; Mancinelli, P.; Pauselli, C.; Leto, G. Monitoring crustal changes at volcanoes by seismic noise interferometry: Mt. Etna case of study. J. Volcanol. Geotherm. Res. 2017, 337, 165–174. [Google Scholar] [CrossRef]
- Grevemeyer, I.; Herber, R.; Essen, H.H. Microseismological evidence for a changing wave climate in the northeast Atlantic Ocean. Nature 2000, 408, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Zopf, D.O.; Creech, H.C.; Quinn, W.H. The wavemeter: A land-based system for measuring nearshore ocean waves. Mar. Technol. Soc. J. 1976, 10, 19–25. [Google Scholar]
- Bromirski, P.D.; Flick, R.E.; Graham, N. Ocean wave height determined from inland seismometer data: Implications for investigating wave climate changes in the NE Pacific. J. Geophys. Res. Ocean. 1999, 104, 20753–20766. [Google Scholar] [CrossRef]
- Bromirski, P.D.; Duennebier, F.K. The near-coastal microseism spectrum: Spatial and temporal wave climate relationships. J. Geophys. Res. Solid Earth 2002, 107, ESE 5-1–ESE 5-20. [Google Scholar] [CrossRef]
- Ferretti, G.; Zunino, A.; Scafidi, D.; Barani, S.; Spallarossa, D. On microseisms recorded near the Ligurian coast (Italy) and their relationship with sea wave height. Geophys. J. Int. 2013, 194, 524–533. [Google Scholar] [CrossRef]
- Ferretti, G.; Scafidi, D.; Cutroneo, L.; Gallino, S.; Capello, M. Applicability of an empirical law to predict significant sea-wave heights from microseisms along the Western Ligurian Coast (Italy). Cont. Shelf Res. 2016, 122, 36–42. [Google Scholar] [CrossRef]
- Ferretti, G.; Barani, S.; Scafidi, D.; Capello, M.; Cutroneo, L.; Vagge, G.; Besio, G. Near real-time monitoring of significant sea wave height through microseism recordings: An application in the Ligurian Sea (Italy). Ocean Coast. Manag. 2018, 165, 185–194. [Google Scholar] [CrossRef]
- Moschella, S.; Cannata, A.; Cannavò, F.; Di Grazia, G.; Nardone, G.; Orasi, A.; Picone, M.; Ferla, M.; Gresta, S. Insights into microseism sources by array and machine learning techniques: Ionian and Tyrrhenian Sea case of study. Front. Earth Sci. 2020, 8, 114. [Google Scholar] [CrossRef]
- Gualtieri, L.; Stutzmann, E.; Capdeville, Y.; Ardhuin, F.; Schimmel, M.; Mangeney, A.; Morelli, A. Modelling secondary microseismic noise by normal mode summation. Geophys. J. Int. 2013, 193, 1732–1745. [Google Scholar] [CrossRef]
- Gualtieri, L.; Stutzmann, E.; Juretzek, C.; Hadziioannou, C.; Ardhuin, F. Global scale analysis and modelling of primary microseisms. Geophys. J. Int. 2019, 218, 560–572. [Google Scholar] [CrossRef]
- Daponte, P.; Rossi, G.B.; Piscopo, V. (Eds.) Measurement for the Sea; Springer: Berlin/Heidelberg, Germany, 2021; in press. [Google Scholar]
- Möllhoff, M.; Bean, C.J. Seismic noise characterization in proximity to strong microseism sources in the Northeast Atlantic. Bull. Seismol. Soc. Am. 2016, 106, 464–477. [Google Scholar] [CrossRef]
- Gerstoft, P.; Fehler, M.C.; Sabra, K.G. When Katrina hit California. Geophys. Res. Lett. 2006, 33, L17308. [Google Scholar] [CrossRef]
- Pratt, M.J.; Wiens, D.A.; Winberry, J.P.; Anandakrishnan, S.; Euler, G.G. Implications of sea ice on Southern Ocean microseisms detected by a seismic array in West Antarctica. Geophys. J. Int. 2017, 209, 492–507. [Google Scholar] [CrossRef]
- Woodruff, S.D.; Slutz, R.J.; Jenne, R.L.; Steurer, P.M. A Comprehensive Ocean-Atmosphere Data Set. Bull. Am. Meteorol. Soc. 1987, 68, 1239–1250. [Google Scholar] [CrossRef]
- Freeman, E.; Woodruff, S.D.; Worley, S.J.; Lubker, S.J.; Kent, E.C.; Angel, W.E.; Berry, D.I.; Brohan, P.; Eastman, R.; Gates, L.; et al. ICOADS release 3.0: A major update to the historical marine climate record. Int. J. Climatol. 2017, 37, 2211–2232. [Google Scholar] [CrossRef]
- Komen, G.J.; Cavaleri, L.; Donelan, M.; Hasselmann, K.; Hasselmann, S.; Janssen, P.A.E.M. Dynamics and Modelling of Ocean Waves; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Caires, S.; Sterl, A.; Bidlot, J.R.; Graham, N.; Swail, V. Intercomparison of Different Wind–Wave Reanalyses. J. Clim. 2004, 17, 1893–1913. [Google Scholar] [CrossRef]
- Ardhuin, F.; Magne, R.; Filipot, J.F.; van der Westhyusen, A.; Roland, A.; Quefeulou, P.; Lefèvre, J.M.; Aouf, L.; Babanin, A.; Collard, F. Semi-empirical dissipation source functions for wind-wave models: Part I, definition and calibration and validation at global scales. J. Phys. Oceanogr. 2010, 40, 1917–1941. [Google Scholar] [CrossRef]
- Ribal, A.; Young, I.R. 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 2019, 6, 77. [Google Scholar] [CrossRef] [PubMed]
- Wilkerson, J.C.; Earle, M.D. A study of differences between environmental reports by ships in the voluntary observing programme and measurements from NOAA buoys. J. Geophys. Res. 1990, 95, 3373–3385. [Google Scholar] [CrossRef]
- Ingleby, B. Factors affecting ship and buoy data quality: A data assimilation perspective. J. Atmos. Ocean Technol. 2010, 27, 1476–1489. [Google Scholar] [CrossRef]
- WMO-No. 8. WMO Guide to Meteorological Instruments and Methods of Observation—Vol. III—Observing Systems; WMO: Geneva, Switzerland, 2018. [Google Scholar]
- WMO-No. 1160. Manual on the WMO Integrated Global Observing System; WMO: Geneva, Switzerland, 2019. [Google Scholar]
- WMO-No. 1165. Guide to the WMO Integrated Global Observing System; WMO: Geneva, Switzerland, 2019. [Google Scholar]
- Moltmann, T.; Turton, J.; Zhang, H.M.; Nolan, G.; Gouldman, C.; Griesbauer, L.; Willis, Z.; Piniella, Á.M.; Barrell, S.; Andersson, E.; et al. A Global Ocean Observing System (GOOS), delivered through enhanced collaboration across regions, communities, and new technologies. Front. Mar. Sci. 2019, 6, 291. [Google Scholar] [CrossRef]
- WMO-No. 1093. Executive Summary of the Abridged Final Report with Resolutions and Recommendations of the Fourth Session of the Joint WMO/IOC Technical Commission for Oceanography and Marine Meteorology; WMO: Geneva, Switzerland, 2012. [Google Scholar]
- Centurioni, L.R.; Turton, J.; Lumpkin, R.; Braasch, L.; Brassington, G.; Chao, Y.; Charpentier, E.; Chen, Z.; Corlett, G.; Dohan, K.; et al. Global in situ Observations of Essential Climate and Ocean Variables at the Air–Sea Interface. Front. Mar. Sci. 2019, 6, 419. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Ando, K.; Bourlès, B.; Freitag, H.P.; Lumpkin, R.; Masumoto, Y.; Murty, V.S.N.; Nobre, P.; Ravichandran, M.; Vialard, J.; et al. The global tropical moored buoy array. In Proceedings of the OceanObs’09: Sustained Ocean Observations and Information for Society Conference, Venice, Italy, 21–25 September 2009; Hall, J., Harrison, D.E., Stammer, D., Eds.; European Space Agency: Paris, France, 2009; Volume 2. [Google Scholar]
- Lin, M.; Yang, C. Ocean Observation Technologies: A Review. Chin. J. Mech. Eng. 2020, 33, 32. [Google Scholar] [CrossRef]
- Foltz, G.R.; Brandt, P.; Richter, I.; Rodríguez-Fonseca, B.; Hernandez, F.; Dengler, M.; Rodrigues, R.R.; Schmidt, J.O.; Yu, L.; Lefevre, N.; et al. The Tropical Atlantic Observing System. Front. Mar. Sci. 2019, 6, 206. [Google Scholar] [CrossRef]
- Poli, P.; Emzivat, G.; Blouch, P.; Férézou, R.; Cariou, A. Météo France/E-SURFMAR HRSST (re)calibration. In Proceedings of the Scientific and Technical Workshop on Traceability of Drifter SST Measurements, La Jolla, CA, USA, 13–14 October 2016. [Google Scholar]
- Bencivenga, M.; Nardone, G.; Ruggiero, F.; Calore, D. The Italian Data Buoy Network (RON). Adv. Fluid Mech. IX 2012, 74, 321–332. [Google Scholar]
- Birkemeier, W.A.; Jensen, R.E.; Bernard, L.J.; Bouchard, R. IOOS wave observations, a national perspective. In Proceedings of the OCEANS ‘12 MTS/IEEE: Harnessing the Power of the Ocean, Hampton Roads, VA, USA, 14–19 October 2012. [Google Scholar]
- O’Reilly, W.C.; McGehee, D.D. Design of Regional Wave Monitoring Networks: A Case Study for the Southern California Bight, Miscellaneous Paper CERC; U.S. Army Corps of Engineers—Coastal Engineering Research Center: Washington, WA, USA, 1994. [Google Scholar]
- Bailey, K.; Steinberg, C.; Davies, C.; Galibert, G.; Hidas, M.; McManus, M.A.; Murphy, T.; Newton, J.; Roughan, M.; Schaeffer, A. Coastal mooring observing networks and their data products: Recommendations for the next decade. Front. Mar. Sci. 2019, 6, 180. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossi, G.B.; Cannata, A.; Iengo, A.; Migliaccio, M.; Nardone, G.; Piscopo, V.; Zambianchi, E. Measurement of Sea Waves. Sensors 2022, 22, 78. https://doi.org/10.3390/s22010078
Rossi GB, Cannata A, Iengo A, Migliaccio M, Nardone G, Piscopo V, Zambianchi E. Measurement of Sea Waves. Sensors. 2022; 22(1):78. https://doi.org/10.3390/s22010078
Chicago/Turabian StyleRossi, Giovanni Battista, Andrea Cannata, Antonio Iengo, Maurizio Migliaccio, Gabriele Nardone, Vincenzo Piscopo, and Enrico Zambianchi. 2022. "Measurement of Sea Waves" Sensors 22, no. 1: 78. https://doi.org/10.3390/s22010078
APA StyleRossi, G. B., Cannata, A., Iengo, A., Migliaccio, M., Nardone, G., Piscopo, V., & Zambianchi, E. (2022). Measurement of Sea Waves. Sensors, 22(1), 78. https://doi.org/10.3390/s22010078








